AAJS: An Anti-Malicious Attack Graphic Similarity Judgment System in Cloud Computing Environments
Abstract
1. Introduction
- First, invoke the scalar product protocol [26] and the protocol to determine whether two sets of data correspond to each other [23], a secure search matching protocol (marked as Protocol 1) based on the shape of a graph is proposed. In addition, the possible malicious behaviors of some participants are analyzed.
- Given the possible malicious behaviors under Protocol 1, the corresponding preventive measures are taken. Using the Paillier algorithm, the methods of zero-knowledge proof and cut-choose, a protocol of the anti-malicious attack graphic similarity judgment system is proposed. This protocol has high practical value.
- Using the real/ideal model paradigm, the protocol’s security is proved. The AAJS is the first proposed graphic search similarity matching scheme that anti-malicious attacks in the background of CC and is more efficient than other existing protocols.
2. Preliminary Knowledge
2.1. The Semi-Honest Model and the Malicious Model
- Semi-honest participants fully follow the requirements when executing the agreement. He will derive data information from other participants based on his own input, output, and intermediate results, but will not disclose the data information he holds.
- During the execution of the protocol, malicious participants may not follow the protocol steps to obtain the private information of other participants. In addition, according to the attacker’s intentions, he may change his input, forge output, or terminate the protocol at any time.
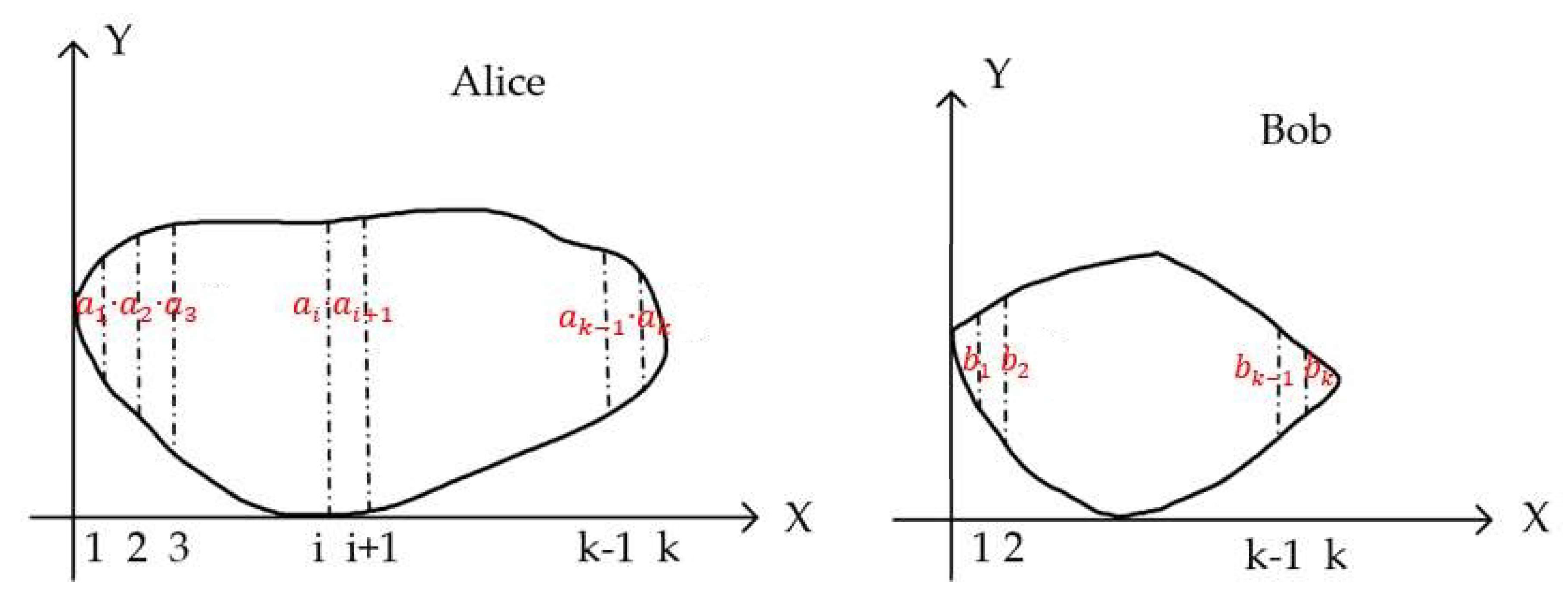
2.2. Problem Description and Transformation Rule
2.3. Paillier Encryption Algorithm
- Key generation: Randomly select two large prime numbers and of equal length (make valid), calculate and , , and define function . The public and private keys are and , respectively. In the above description, the function is defined as the greatest common divisor of and , and the function is defined as the least common multiple of and .
- Encryption: For plaintext , is randomly chosen to encrypt to obtain .
- Decryption: For any ciphertext that satisfies , the private key is used to decrypt the plaintext .
- Additive homomorphism: If , then .
2.4. Scalar Product Algorithm
| Algorithm 1 Computing the scalar product |
| Input: Alice has ; Bob has . Output: Scalar product . Start: Both parties jointly determine a random matrix . 1. A random vector of cardinality generates by Alice ; 2. Then, she computes the addition matrix : ; 3. Alice generates and sends to Bob. 4. Bob generates the scalar product : and the matrix ; 5. Bob sends both and to Alice. 6. Alice generates the subtraction factor ; 7. Alice generates the required scalar product and sends to Bob. |
2.5. Zero-Knowledge Proof
- Bob randomly selects and calculates and sends to Alice.
- Alice calculates and will send to Bob.
- The verifier Bob needs to verify is and whether it is valid or not, if so, it can be considered that Alice knows .
2.6. Security of the Malicious Model
3. The MPC Protocol of Graph Shape Similarity Determination under the Semi-Honest Model
| Protocol 1 Protocol of graph shape similarity determination under the semi-honest model. |
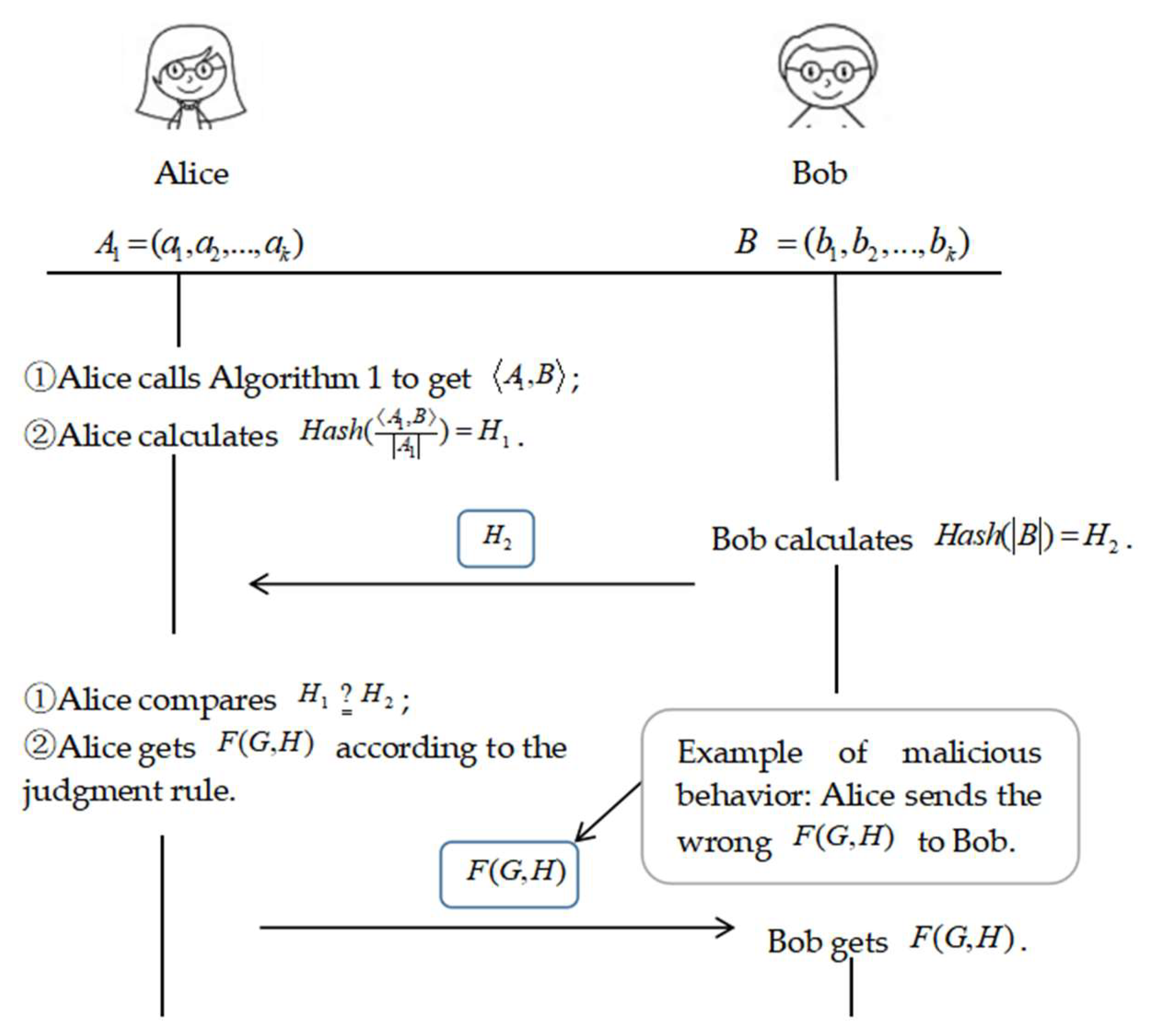
| Input: Alice converts graph into vectors and ; Bob converts the graph to vector . Output: . 1. Alice invokes Algorithm 1 to obtain and , and calculates and . Furthermore, Alice calculates and . 2. Bob calculates the module length of his vector then calculates . 3. Bob sends to Alice, who compares whether and are equal. If , then , at this time . That is, the angle between vector and vector is 0 or , and the two vectors are collinear so that and are proportional. Alice outputs according to the judgment rule. Otherwise, go to the next step. 4. Alice compares whether and are equal. If , then , Alice outputs . Otherwise, Alice outputs . The Protocol ends. |
4. The MPC Protocol of Anti-Malicious Attack Graphic Similarity Judgment System
- In Protocol 1, Alice compares the data. It is unfair to Bob that he can only obtain the calculation results from Alice.
- In step 3 of Protocol 1, the wrong may be sent by Bob to the other party, but doing so is equivalent to providing false inputs and Bob cannot obtain the correct conclusion, hence this situation will not be considered.
- Alice gains the final result in steps 3–4 of Protocol 1, but Bob may gain a wrong result from Alice, and the deception will succeed.
4.1. Specific Protocol
| Protocol 2 Protocol of similarity determination based on graph shape under the malicious model. |
| Input: Alice has and Bob has . Output: . Preparation Stage: Both parties generate public keys, and , and private keys, and , of their own Paillier cryptosystem, respectively, then calculate and , and publish and . Begin: 1. According to the transformation rules, Alice and Bob measure their graphics. Alice obtains and its reverse vector ; Bob obtains . 2. Alice calls Algorithm 1 to obtain and , and calculates and . Furthermore, Alice calculates and . Bob calculates the module length of vector then calculates . 3. Alice and Bob hold and , respectively. random numbers are chosen by each party, and are calculated, respectively. Alice and Bob exchange and . 4. According to the cut-choose method, Alice randomly chooses groups from groups and requires Bob to publish . Then, Alice verifies that . If the verification passes, continue to execute Protocol 2, otherwise terminate Protocol 2. 5. Bob randomly chooses groups from groups and requires Alice to publish . Then, Bob verifies that . 6. One group, and , from the rest, and , are randomly chosen by both parties. Besides, and are selected by Alice and Bob respectively. 7. Alice calculates , and sends to Bob. 8. Bob calculates , and sends to Alice. 9. Alice calculates with , Bob calculates with , and publish , , respectively. 10. According to the ZKP, Alice proves , Bob proves . The party that fails to pass the ZKP is a malicious opponent. 11. If ZKP passes, Bob calculates to obtain then obtains . When , then , that is, . Alice calculates to obtain , then obtains . When , similarly, can be obtained. In this case, there is . At this time, , that is, the angle between vector and vector is 0 or . Since the two vectors are collinear, we can obtain that and are proportional. According to the judgment rule, Alice outputs , and the protocol ends. Otherwise, go to step 12. 12. Alice has and Bob has . Both parties repeat steps 3–11. If , Alice outputs . Otherwise, the graphics are not similar, and Alice outputs . The Protocol ends. |
4.2. Correctness and Security Analysis
- When the parameters meet , the protocol is correct. Assuming that , , , and are not more than bit, it is only necessary to make exceed bit to meet the requirements. Steps 4–5 of Protocol 2 can ensure this.
- The first step in Protocol 2 is the process of both parties to preprocess their graphics to convert them into vectors. The private information in the graphics will not be disclosed.
- In step 2, Alice invokes Algorithm 1 without using the public key encryption algorithm, which achieves information theory security, hence it will not disclose information.
- In step 4, if Alice calculates with a different , and Bob selects the wrong in step 6, this is equal to Alice entering false data. This is unavoidable under ideal conditions.
- In step 9, both parties cannot cheat. Since ZKP can only be passed when the published and are correct.
- Bob may cheat success. The details are as follows: Bob uses the unqualified to calculate , and Alice did not find it in the verification and selected the calculated with unqualified in the subsequent steps. At this time, Alice will obtain the wrong conclusion. According to the above analysis, Bob’s most likely choice is to input a group of wrong data into groups , because, at this time, the probability of successful deception is . If Bob inputs more than groups of wrong , he will be found during verification, and deception will fail. Even if Bob cheats successfully, he cannot obtain any private information belonging to Alice because there are two unknowns in the equation of . The above analysis is the same for Alice, hence Protocol 2 has security [25].
- In Protocol 2, both parties have the same security. In addition, the final result is calculated separately, avoiding the situation that one party informs the wrong conclusion to the other party. In sum, Protocol 2 is anti-malicious.
4.3. Security Proof
- terminates the protocol, and TTP will send to , then: .
- The protocol is executed normally, and receives from TTP. At this time:
- When asks TTP to not send results to , there are:
- Otherwise, then:
5. Protocol Efficiency Analysis
5.1. Computational Complexity Analysis
5.2. Communication Complexity Analysis
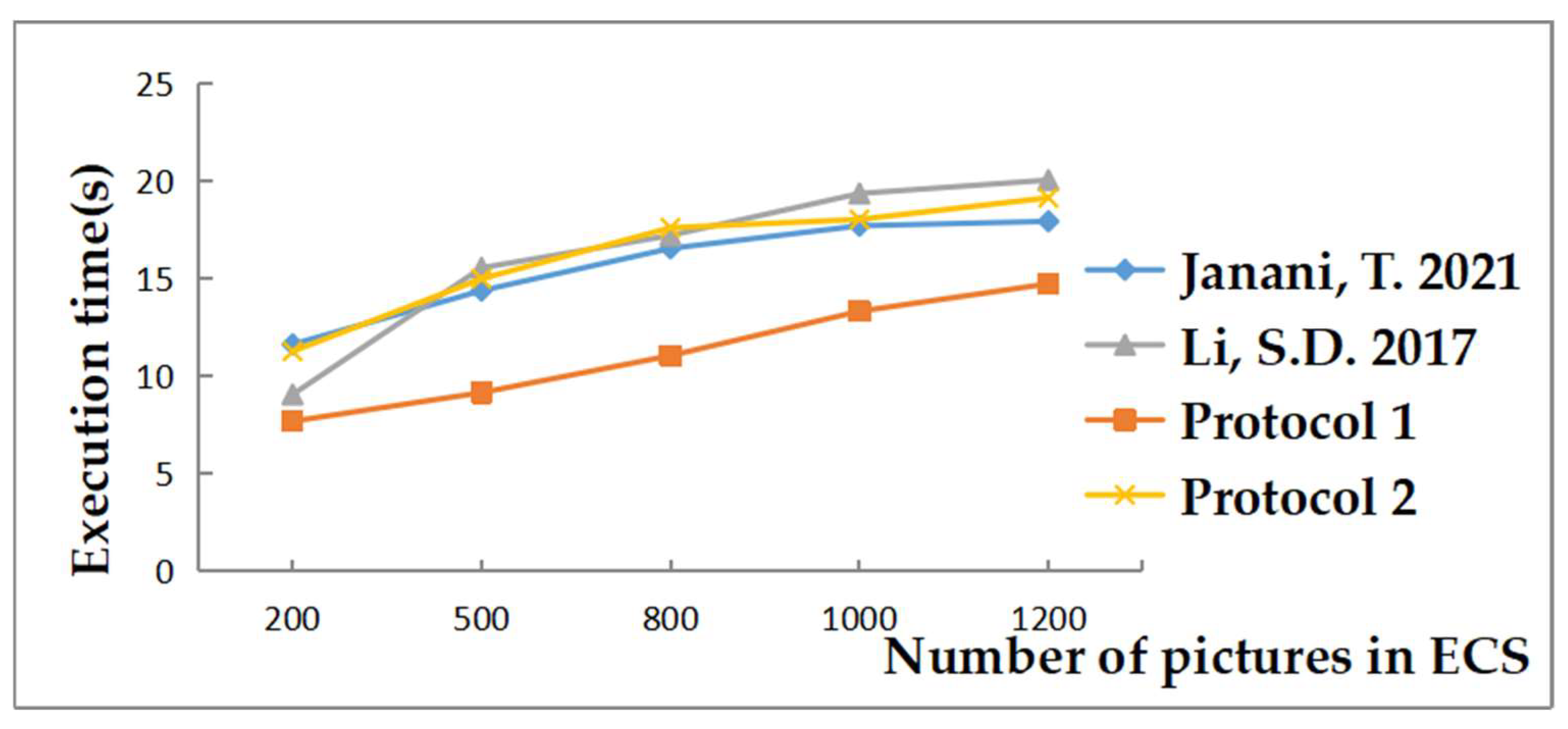
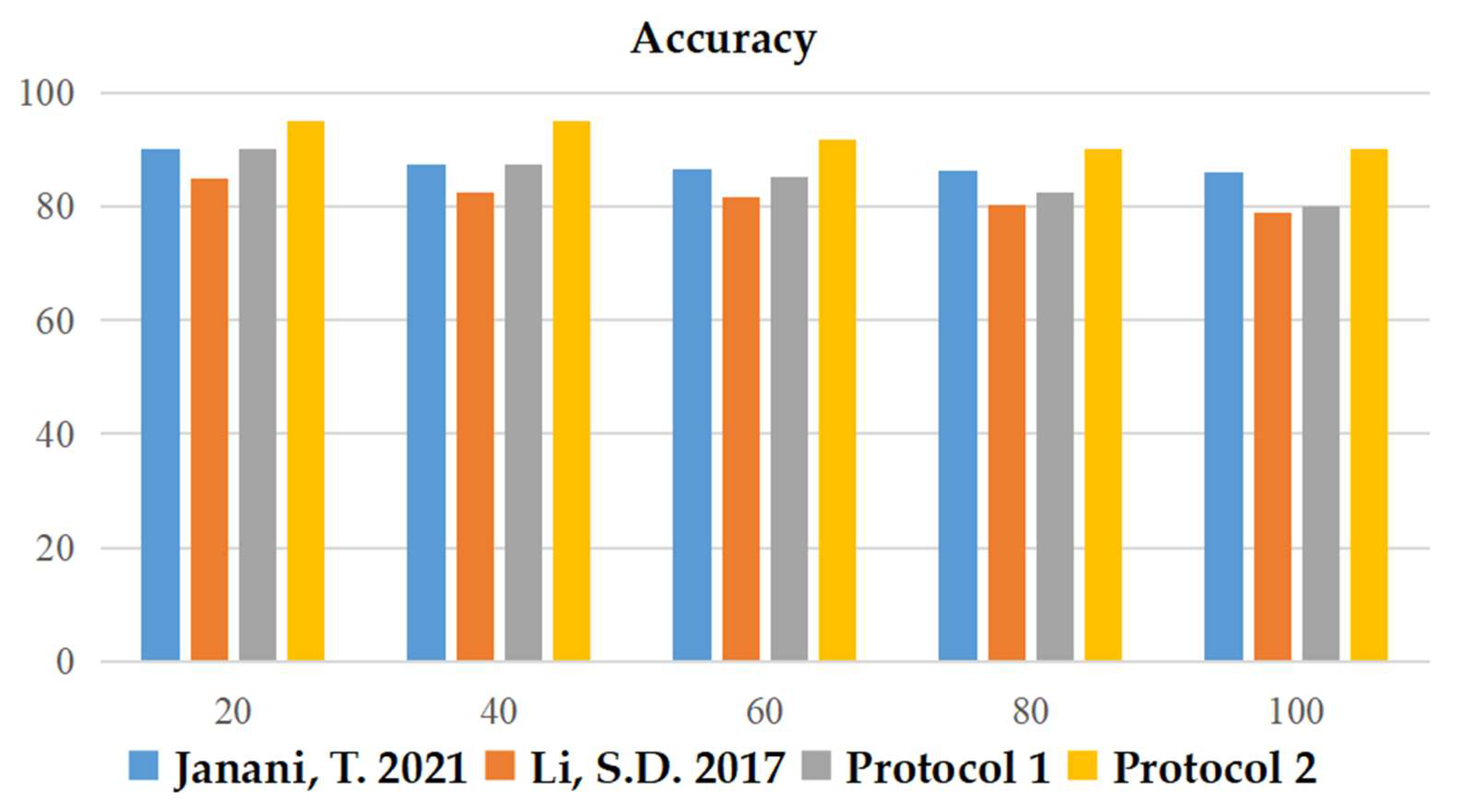
5.3. Experimental Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ( and are large prime numbers of equal length) | |
| represents a set of integers, and subscripts represent elements in the set | |
| represents a set, and represents the number of elements in . Any element in satisfies and | |
| , | Plaintext and ciphertext |
| The public key of Alice’s Paillier encryption system | |
| The public key of Bob’s Paillier encryption system | |
| The private key of Alice’s Paillier encryption system | |
| The public key of Bob’s Paillier encryption system | |
| The process of converting encrypted plaintext into ciphertext | |
| The process of decrypting ciphertext into plaintext | |
| Protocol 2 under the malicious model | |
| Message sequence generated in the process of zero-knowledge proof | |
| The function calculation results of and in the ideal case | |
| The function calculation results of and in the practical case |
References
- Feng, D.G.; Zhang, M.; Zhang, Y.; Xu, Z. Study on Cloud Computing Security. J. Softw. 2011, 22, 71–83. [Google Scholar] [CrossRef]
- Parast, F.K.; Sindhav, C.; Nikam, S.; Yekta, H.I.; Kent, K.B.; Hakak, S. Cloud computing security: A survey of service-based models. Comput. Secur. 2022, 114, 102580. [Google Scholar] [CrossRef]
- Bella, H.K.; Vasundra, S. A study of security threats and attacks in cloud computing. In Proceedings of the 2022 4th International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 20–22 January 2022. [Google Scholar]
- El Kafhali, S.; El Mir, I.; Hanini, M. Security threats, defense mechanisms, challenges, and future directions in cloud computing. Arch. Comput. Methods Eng. 2022, 29, 223–246. [Google Scholar] [CrossRef]
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982), Chicago, IL, USA, 3–5 November 1982. [Google Scholar]
- Gao, C.; Yu, J. SecureRC: A system for privacy-preserving relation classification using secure multi-party computation. Comput. Secur. 2023, 128, 103142. [Google Scholar] [CrossRef]
- Zhang, K.X.; Yang, C.; Li, S.D. Privacy preserving string matching. J. Cryptol. Res. 2022, 9, 619–632. [Google Scholar]
- Stammler, S.; Kussel, T.; Schoppmann, P.; Stampe, F.; Tremper, G.; Katzenbeisser, S.; Hamacher, K.; Lablans, M. Mainzelliste SecureEpiLinker (MainSEL): Privacy-preserving record linkage using secure multi-party computation. Bioinformatics 2022, 38, 1657–1668. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Cao, Z.; Dong, X.; Zhao, X.; Bao, H.; Shen, J. A verifiable privacy-preserving data collection scheme supporting multi-party computation in fog-based smart grid. Front. Comput. Sci.-Chi. 2022, 16, 161810. [Google Scholar] [CrossRef]
- Zhang, E.; Li, H.; Huang, Y.; Hong, S.; Zhao, L.; Ji, C. Practical multi-party private collaborative k-means clustering. Neurocomputing 2022, 467, 256–265. [Google Scholar] [CrossRef]
- Olakanmi, O.O.; Odeyemi, K.O. Trust-aware and incentive-based offloading scheme for secure multi-party computation in Internet of Things. Internet Things 2022, 19, 100527. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, X.; Susilo, W.; Yang, G.; Jiang, Z.L.; Yiu, S.M.; Wang, H. Generic server-aided secure multi-party computation in cloud computing. Comput. Stand. Inter. 2022, 79, 103552. [Google Scholar] [CrossRef]
- Huang, S.; Zeng, Z.; Ota, K.; Dong, M.; Wang, T.; Xiong, N. An intelligent collaboration trust interconnections system for mobile information control in ubiquitous 5G networks. IEEE Trans. Netw. Sci. Eng. 2020, 8, 347–365. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, R.G. Secure multi-party convex hull protocol based on quantum homomorphic encryption. Quantum Inf. Process. 2022, 22, 24. [Google Scholar] [CrossRef]
- Kumar, A.V.; Monica, K.; Mandadi, K. Data Privacy Over Cloud Computing using Multi Party Computation. In Proceedings of the 2023 International Conference on Intelligent Data Communication Technologies and Internet of Things (IDCIoT), Bengaluru, India, 5–7 January 2023. [Google Scholar]
- Jaberi, M.; Mala, H. Privacy-preserving multi-party PCA computation on horizontally and vertically partitioned data based on outsourced QR decomposition. J. Supercomput. 2023, 1–30. [Google Scholar] [CrossRef]
- Cao, Y. Quantum secure two-party Euclidean distance computation based on mutually unbiased bases. Quantum Inf. Process. 2022, 21, 262. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.; Xu, G.; Chen, X.B.; Chen, Y.L. Secure Judgment of Point and Line Relationship Against Malicious Adversaries and Its Applications. J. Internet Technol. 2022, 23, 1019–1027. [Google Scholar]
- Du, W.; Atallah, M.J. Secure multi-party computation problems and their applications: A review and open problems. In Proceedings of the 2001 Workshop on New Security Paradigms, Cloudcroft, New Mexico, 10–13 September 2001. [Google Scholar]
- Song, C.L.; Chen, Z.H. Searchable encryption of graph shape matching in cloud computing. Comput. Eng. Appl. 2022, 1–9. [Google Scholar]
- Bel, K.N.S.; Sam, I.S. Black hole Entropic Fuzzy Clustering-based image indexing and Tversky index-feature matching for image retrieval in cloud computing environment. Inf. Sci. 2021, 560, 1–19. [Google Scholar] [CrossRef]
- Janani, T.; Brindha, M. Secure similar image matching (sesim): An improved privacy preserving image retrieval protocol over encrypted cloud database. IEEE Trans. Multimed. 2021, 24, 3794–3806. [Google Scholar] [CrossRef]
- Chen, Z.H.; Li, S.D.; Huang, Q.; Dong, L.H.; Chen, W. New Solutions to Two Privacy-Preserving Location-Relation Determining Problems. Chin. J. Comput. 2018, 41, 336–348. [Google Scholar]
- Li, S.D.; Yang, X.L.; Zuo, X.J.; Zhou, S.F.; Kang, J.; Liu, X. Privacy-Preserving Graphical Similarity Determination. Acta Electron. Sin. 2017, 45, 2184–2189. [Google Scholar]
- Li, S.D.; Wang, W.L.; Du, R.M. Protocol for millionaires’ problem in malicious models (in Chinese). Sci. Sin. Inform. 2021, 51, 75–88. [Google Scholar] [CrossRef]
- Clifton, C.; Kantarcioglu, M.; Vaidya, J.; Lin, X.; Zhu, M.Y. Tools for privacy preserving distributed data mining. ACM Sigkdd Explor. Newsl. 2002, 4, 28–34. [Google Scholar] [CrossRef]
- Liu, X.M.; Liu, X. Securely Similarity Determination of Convex Geometry Graphics Under the Malicious Model. In Proceedings of the TEPEN 2022: Efficiency and Performance Engineering Network, Baotou, China, 18–21 August 2022. [Google Scholar]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques (EUROCRYPT′99), Prague, Czech Republic, 2–6 May 1999. [Google Scholar]
- Atallah, M.J.; Du, W. Secure multi-party computational geometry. In Algorithms and Data Structures: 7th International Workshop, WADS 2001 Providence, RI, USA, August 8–10, 2001 Proceedings 7; Dehne, F., Sack, J.R., Tamassia, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2125, pp. 165–179. [Google Scholar]
- Sheng, G.; Wen, T.; Guo, Q.; Yin, Y. Privacy preserving inner product of vectors in cloud computing. Int. J. Distrib. Sens. N 2014, 10, 537252. [Google Scholar] [CrossRef]
- Mohammed, N.; Alhadidi, D.; Fung, B.C.; Debbabi, M. Secure two-party differentially private data release for vertically partitioned data. IEEE Trans. Dependable Secur. Comput. 2013, 11, 59–71. [Google Scholar] [CrossRef]
- Vaidya, J.; Clifton, C. Privacy preserving association rule mining in vertically partitioned data. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 23–26 July 2002. [Google Scholar]
- Ben-Sasson, E.; Chiesa, A.; Genkin, D.; Tromer, E.; Virza, M. SNARKs for C: Verifying program executions succinctly and in zero knowledge. In Proceedings of the 33rd Annual Cryptology Conference (CRYPTO 2013), Santa Barbara, CA, USA, 18–22 August 2013. [Google Scholar]
- Goldreich, O. Foundations of Cryptography: Volume 2, Basic Applications; Cambridge University Press: Cambridge, UK, 2009; Volume 2. [Google Scholar]
| Protocol | Computational Complexity | Rounds of Communication | Resist Malicious Attacks |
|---|---|---|---|
| Reference [22] | × | ||
| Reference [23] | 12 | × | |
| Reference [24] | 4 | × | |
| Protocol 1 | 2 | × | |
| Protocol 2 | 5 | √ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Liu, X.; Xiong, N.; Luo, D.; Xu, G.; Chen, X. AAJS: An Anti-Malicious Attack Graphic Similarity Judgment System in Cloud Computing Environments. Electronics 2023, 12, 1983. https://doi.org/10.3390/electronics12091983
Liu X, Liu X, Xiong N, Luo D, Xu G, Chen X. AAJS: An Anti-Malicious Attack Graphic Similarity Judgment System in Cloud Computing Environments. Electronics. 2023; 12(9):1983. https://doi.org/10.3390/electronics12091983
Chicago/Turabian StyleLiu, Xin, Xiaomeng Liu, Neal Xiong, Dan Luo, Gang Xu, and Xiubo Chen. 2023. "AAJS: An Anti-Malicious Attack Graphic Similarity Judgment System in Cloud Computing Environments" Electronics 12, no. 9: 1983. https://doi.org/10.3390/electronics12091983
APA StyleLiu, X., Liu, X., Xiong, N., Luo, D., Xu, G., & Chen, X. (2023). AAJS: An Anti-Malicious Attack Graphic Similarity Judgment System in Cloud Computing Environments. Electronics, 12(9), 1983. https://doi.org/10.3390/electronics12091983







