Terahertz Dual-Band Dual-Polarization 3-Bit Coding Metasurface for Multiple Vortex Beams Generation
Abstract
1. Introduction
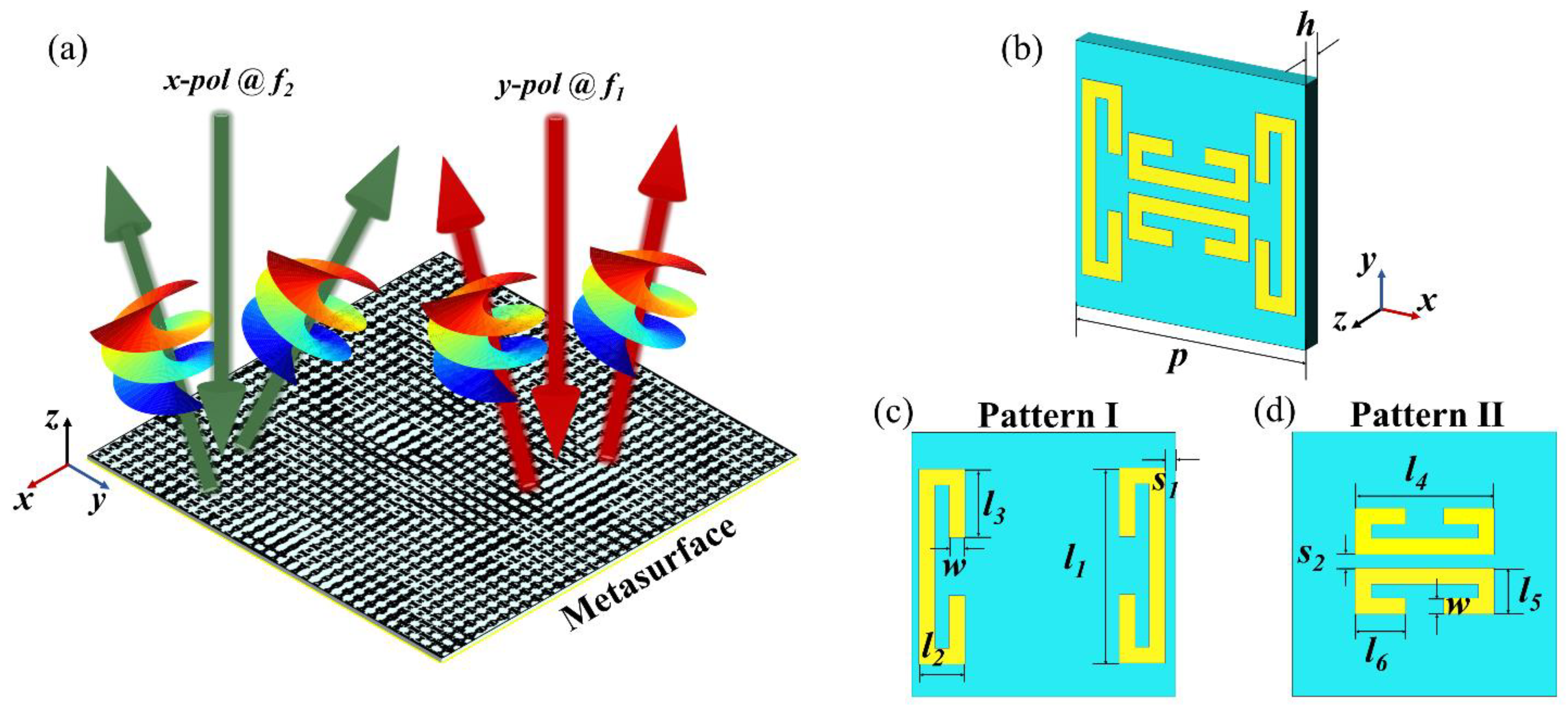
2. Design of Metasurface 3-Bit Unit Cell
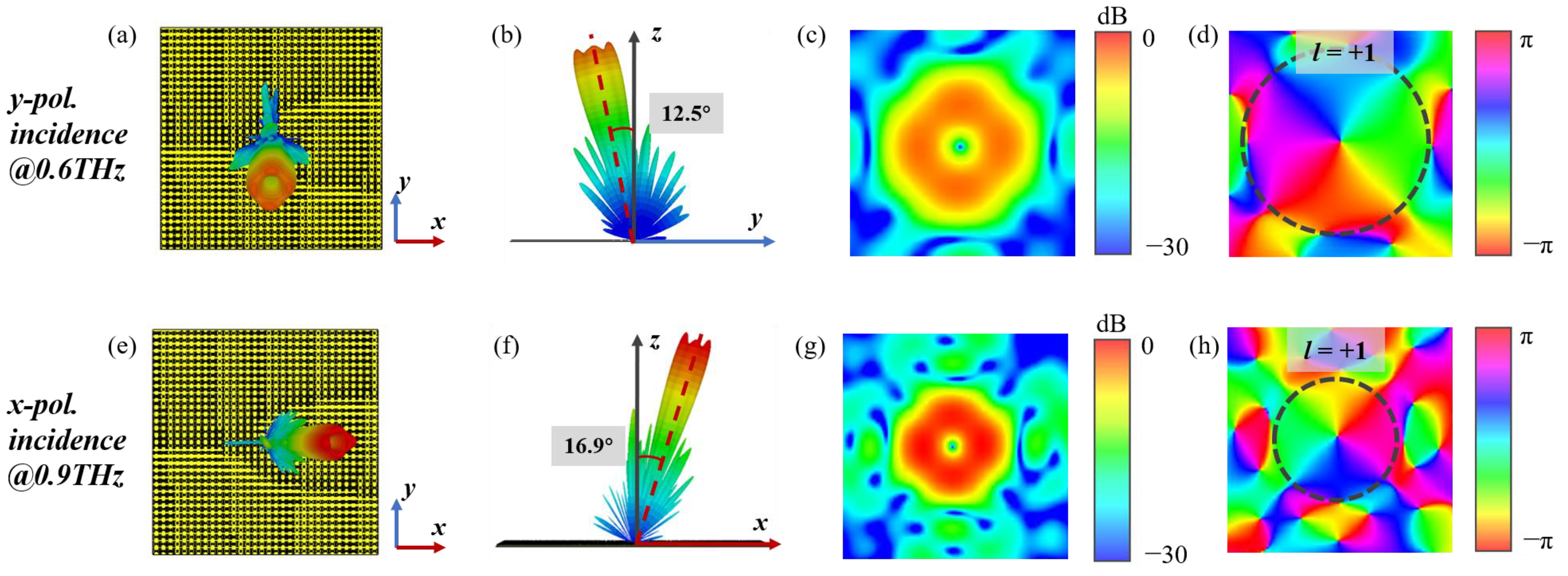
3. Dual-Band Dual-Polarization Single Vortex Beam Metasurface
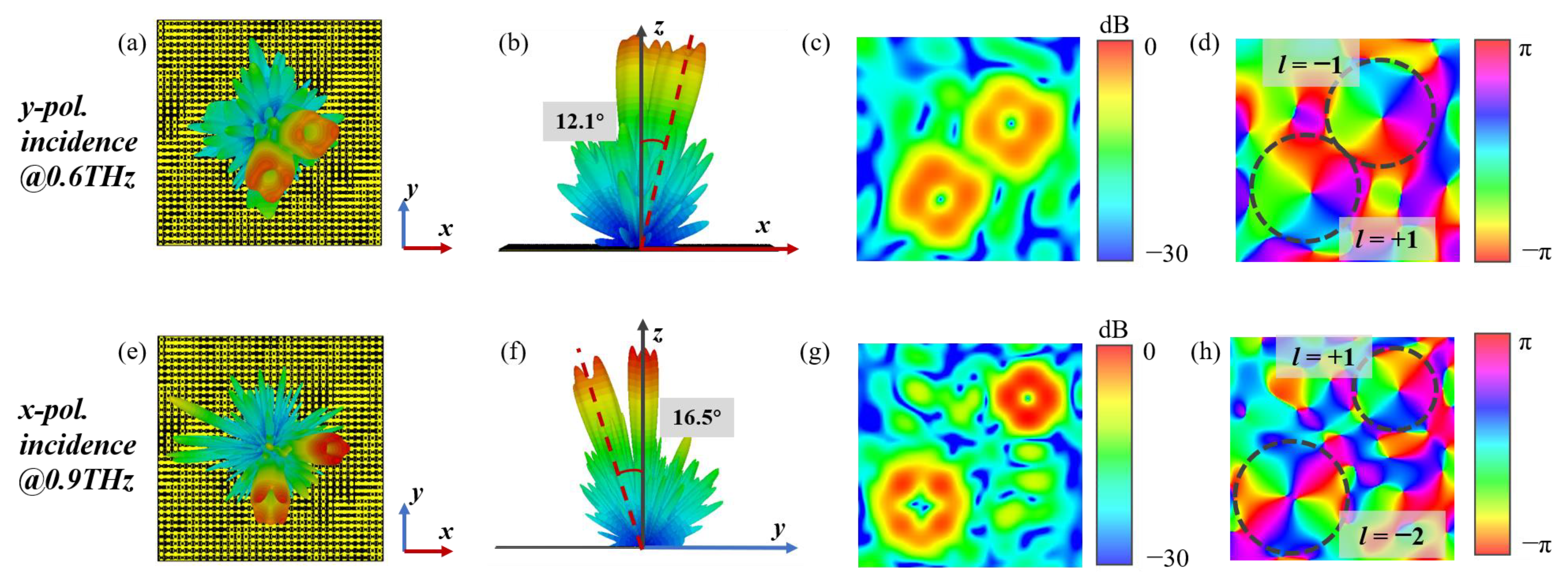
4. Dual-Band Dual-Polarization Multiple Vortex Beams Metasurface
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Siegel, P.H. Terahertz Technology. IEEE Trans. Microw. Theory Tech. 2002, 50, 910–928. [Google Scholar] [CrossRef]
- Federici, J.F.; Schulkin, B.; Huang, F.; Gary, D.; Barat, R.; Oliveira, F.; Zimdars, D. THz imaging and sensing for security applications—explosives, weapons and drugs. Semicond. Sci. Technol. 2005, 20, S266–S280. [Google Scholar] [CrossRef]
- Appleby, R.; Anderton, R.N. Millimeter-wave and submillimeter-wave imaging for security and surveillance. Proc. IEEE 2007, 95, 1683–1690. [Google Scholar] [CrossRef]
- Ma, J.; Shrestha, R.; Adelberg, J.; Yeh, C.-Y.; Hossain, Z.; Knightly, E.; Jornet, J.M.; Mittleman, D.M. Security and Eavesdropping in Terahertz Wireless Links. Nature 2018, 563, 89–93. [Google Scholar] [CrossRef] [PubMed]
- Kleine-Ostmann, T.; Nagatsuma, T. A Review on Terahertz Communications Research. J. Infrared Millim. Terahertz Waves 2011, 32, 143–171. [Google Scholar] [CrossRef]
- Nagatsuma, T.; Ducournau, G.; Renaud, C.C. Advances in Terahertz Communications Accelerated by Photonics. Nat. Photonics 2016, 10, 371–379. [Google Scholar] [CrossRef]
- Woolard, D.L.; Brown, R.; Pepper, M.; Kemp, M. Terahertz frequency sensing and imaging: A time of reckoning future applications? Proc. IEEE 2005, 93, 1722–1743. [Google Scholar] [CrossRef]
- Mittleman, D.M. Twenty Years of Terahertz Imaging [Invited]. Opt. Express 2018, 26, 9417–9431. [Google Scholar] [CrossRef]
- Hillger, P.; Grzyb, J.; Jain, R.; Pfeiffer, U.R. Terahertz imaging and sensing applications with silicon-based technologies. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 1–19. [Google Scholar] [CrossRef]
- Siegel, P.H. Terahertz Technology in Biology and Medicine. IEEE Trans. Microw. Theory Tech. 2004, 52, 2438–2447. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Tamburini, F.; Thidé, B.; Della Valle, M. Measurement of the spin of the M87 black hole from its observed twisted light. Mon. Not. R. Astron. Soc. Lett. 2020, 492, L22–L27. [Google Scholar] [CrossRef]
- Cojoc, D.; Garbin, V.; Ferrari, E.; Businaro, L.; Romanato, F.; Fabrizio, E.D. Laser trapping and micro-manipulation using optical vortices. Microelectron. Eng. 2005, 78–79, 125–131. [Google Scholar]
- Wang, B.; Tanksalvala, M.; Zhang, Z.; Esashi, Y.; Jenkins, N.W.; Murnane, M.M.; Kapteyn, H.C.; Liao, C.-T. Coherent Fourier scatterometry using orbital angular momentum beams for defect detection. Opt. Express 2021, 29, 3342–3358. [Google Scholar] [CrossRef] [PubMed]
- McCarter, M.R.; Saleheen, A.I.U.; Singh, A.; Tumbleson, R.; Woods, J.S.; Tremsin, A.S.; Scholl, A.; DeLong, L.E.; Hastings, J.T.; Morley, S.A.; et al. Antiferromagnetic real-space configuration probed by dichroism in scattered X-ray beams with orbital angular momentum. Phys. Rev. B 2023, 107, L060407. [Google Scholar] [CrossRef]
- Wilig, K.I.; Rizzoli, S.O.; Westphal, V.; Jahn, R.; Hell, S.W. STED microscopy reveals that synaptotagmin remains clustered after synaptic vesicle exocytosis. Nature 2006, 440, 935–939. [Google Scholar] [CrossRef]
- Wang, B.; Brooks, N.J.; Johnsen, P.C.; Jenkins, N.W.; Esashi, Y.; Tanksalvala, M.; Kapteyn, H.C.; Murnane, M.M. High-fidelity ptychographic imaging of highly periodic structures enabled by vortex high harmonic beams. arXiv 2023, 2301, 05563. [Google Scholar]
- Taburini, F.; Mari, E.; Sponselli, A.; Thidé, B.; Bianchini, A.; Romanato, F. Encoding many channels on the same frequency through radio vorticity: First experimental test. New J. Phys. 2012, 14, 033001. [Google Scholar] [CrossRef]
- Thidé, B.; Then, H.; Sjöholm, J.; Palmer, K.; Bergman, J.; Carozzi, T.D.; Istomin, Y.N.; Ibragimov, N.H.; Khamitova, R. Utilization of photon orbital angular momentum in the low-frequency radio domain. Phys. Rev. Lett. 2007, 99, 087701. [Google Scholar]
- Mahmoli, F.E.; Walker, S.D. 4-Gbps uncompressed video transmission over a 60-GHz orbital angular momentum wireless channel. IEEE Wirel. Commun. Lett. 2013, 2, 223–226. [Google Scholar] [CrossRef]
- Nagli, E.; Sciarrino, F.; DeMartini, F.; Marrucci, L.; Piccirillo, B.; Karimi, E.; Santamato, E. Quantum information transfer from spin to orbital angular momentum of photons. Phys. Rev. Lett. 2009, 103, 013601. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Hong, W.; Hao, Z.-C. Generation of electromagnetic waves with arbitrary orbital angular momentum modes. Sci. Rep. 2014, 4, 4814. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Podlipnov, V.V.; Karpeev, S.V.; Ustinov, A.V.; Volotovsky, S.G.; Ganchevskaya, S.V. Spectral control of the orbital angular momentum of a laser beam based on 3D properties of spiral phase plates fabricated for an infrared wavelength. Opt. Express 2020, 28, 18407–18417. [Google Scholar] [CrossRef]
- Guo, Z.-G.; Yang, G.-M. Radial uniform circular antenna array for dual-mode OAM communication. Antennas Wirel. Propag. Lett. 2017, 16, 404–407. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, Z.N.; Liu, Y.; Li, F.; Chen, Y.; Mo, Z. Circular polarization and mode reconfigurable wideband orbital angular momentum patch array antenna. IEEE Trans. Antennas Propag. 2018, 66, 1796–1804. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, X.; Ye, J.; Feng, S.; Sun, W.; Akalin, T.; Zhang, Y. Spatial Terahertz Modulator. Sci. Rep. 2013, 3, 3347. [Google Scholar] [CrossRef]
- Knyazev, B.A.; Choporova, Y.Y.; Mitkov, M.S.; Pavelyev, V.S.; Volodkin, B.O. Generation of terahertz surface plasmon polaritons using nondiffractive Bessel beams with orbital angular momentum. Phys. Rev. Lett. 2015, 115, 163901. [Google Scholar] [CrossRef]
- Zhang, H.; Si, L.; Ma, T.; Dong, L.; Niu, R.; Bao, X.; Sun, H.; Ding, J. Triple-Band Terahertz Chiral Metasurface for Spin-Selective Absorption and Reflection Phase Manipulation. Electronics 2022, 11, 4195. [Google Scholar] [CrossRef]
- Zhang, K.; Yuan, Y.; Zhang, D.; Ding, X.; Ratni, B.; Burokur, S.N.; Lu, M.; Tang, K.; Wu, Q. Phase-engineered metalenses to generate converging and non-diffractive vortex beam carrying orbital angular momentum in microwave region. Opt. Express 2018, 26, 1351–1360. [Google Scholar] [CrossRef]
- Cheng, G.; Si, L.; Tang, P.; Zhuang, Y.; Sun, H.; Ding, J. Topology optimization of the azimuth-rotation-independent polarization conversion metasurface for bandwidth enhancement. Opt. Express 2022, 30, 41340–41349. [Google Scholar] [CrossRef]
- Wong, A.M.H.; Eleftheriades, G.V. Perfect anomalous reflection with a bipartite Huygens’ metasurface. Phys. Rev. X 2018, 8, 011036. [Google Scholar] [CrossRef]
- Zhao, H.; Li, B.; Zhou, J.; Kang, L.; Zhao, Q.; Li, W. Abnormal refraction of microwave in ferrite/wire metamaterials. Opt. Express 2011, 19, 15679–15689. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [PubMed]
- Ni, X.; Ishii, S.; Kildishev, A.V.; Shalaev, V.M. Ultra-thin, planar, Babinet-inverted plasmonic metalenses. Light. Sci. Appl. 2013, 2, e72. [Google Scholar] [CrossRef]
- Yin, X.; Ye, Z.; Rho, J.; Wang, Y.; Zhang, X. Photonic Spin Hall Effect at Metasurfaces. Science 2013, 339, 1405–1407. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.; Cheng, H.; Chen, S.; Tian, J. Manipulation of the Photonic Spin Hall Effect with High Efficiency in Gold-Nanorod-Based Metasurfaces. Adv. Opt. Mater. 2017, 5, 1700413. [Google Scholar] [CrossRef]
- Ni, X.; Wong, Z.J.; Mrejen, M.; Wang, Y.; Zhang, X. An ultrathin invisibility skin cloak for visible light. Science 2015, 349, 1310–1314. [Google Scholar] [CrossRef]
- Yang, Y.; Jing, L.; Zheng, B.; Hao, R.; Yin, W.; Li, E.; Soukoulis, C.M.; Chen, H. Full-polarization 3D metasurface cloak with preserved amplitude and phase. Adv. Mater. 2016, 28, 6866–6871. [Google Scholar] [CrossRef]
- Ni, X.; Kildishev, A.V.; Shalaev, V.M. Metasurface Holograms for Visible Light. Nat. Commun. 2013, 4, 2807. [Google Scholar] [CrossRef]
- Li, L.; JunCui, T.; Ji, W.; Liu, S.; Ding, J.; Wan, X.; BoLi, Y.; Jiang, M.; Qiu, C.-W.; Zhang, S. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 2017, 8, 197. [Google Scholar] [CrossRef]
- Lei, Z.; Jiu-sheng, L. Transmission type Dual-frequency Vortex Beams Generator for Multiple OAM Modes. Opt. Quant. Electron. 2022, 54, 209. [Google Scholar] [CrossRef]
- Xie, R.; Fang, X.; Zhang, D.; Wang, X.; Chen, K.; An, S.; Zheng, B.; Zhang, H.; Feng, Y.; Ding, J. Four-Channel Kaleidoscopic Metasurfaces Enabled by a Single-Layered Single-Cell Quad-Band Meta-Atom. Adv. Theory Sims. 2022, 5, 2100301. [Google Scholar] [CrossRef]
- Tang, Z.; Li, L.; Zhang, H.; Yang, J.; Hu, J.; Lu, X.; Hu, Y.; Qi, S.; Liu, K.; Tian, M.; et al. Multifunctional Janus metasurfaces achieving arbitrary wavefront manipulation at dual frequency. Mater. Des. 2022, 223, 111264. [Google Scholar] [CrossRef]
- Li, J.-S.; Zhang, L.-N. Simple terahertz vortex beam generator based on reflective metasurfaces. Opt. Express 2020, 28, 36403–36412. [Google Scholar] [CrossRef] [PubMed]
- Li, J.-S.; Pan, W.-M. Combination regulation of terahertz OAM vortex beams on multi-bit metasurface. J. Phys. D Appl. Phys. 2022, 55, 235103. [Google Scholar] [CrossRef]
- Wang, T.; Xie, R.; Zhu, S.; Gao, J.; Xin, M.; An, S.; Zheng, B.; Li, H.; Lin, Y.; Zhang, H.; et al. Dual-band high efficiency terahertz meta-devices based on reflective geometric metasurfaces. IEEE Access 2019, 7, 58131–58138. [Google Scholar] [CrossRef]
- Ji, C.; Song, J.; Huang, C.; Wu, X.; Luo, X. Dual-band vortex beam generation with different OAM modes using single-layer metasurface. Opt. Express 2019, 27, 34–44. [Google Scholar] [CrossRef]
- Li, J.; Guo, F.; Zhang, S.; Liu, C. Bidirectional Terahertz Vortex Beam Regulator. Materials 2022, 15, 8639. [Google Scholar] [CrossRef]
- Jie, C.; Jiu-sheng, L. Reflective type metasurface for generating and regulating vortex beam at two frequencies. Opt. Commun. 2022, 524, 128758. [Google Scholar] [CrossRef]
- Wu, R.Y.; Shi, C.B.; Liu, S.; Wu, W.; Cui, T.J. Addition theorem for digital coding metamaterials. Adv. Opt. Mater. 2018, 6, 1701236. [Google Scholar] [CrossRef]
- Liu, S.; Cui, T.J.; Zhang, L.; Xu, Q.; Wang, Q.; Wan, X.; Gu, J.Q.; Tang, W.X.; QingQi, M.; Han, J.G.; et al. Convolution operations on coding metasurface to reach flexible and continuous controls of terahertz beams. Adv. Sci. 2016, 3, 1600156. [Google Scholar] [CrossRef]
- Liu, S.; Cui, T.J.; Xu, Q.; Bao, D.; Du, L.; Wan, X.; Tang, W.X.; Ouyang, C.; Zhou, X.Y.; Yuan, H.; et al. Anisotropic coding metamaterials and their powerful manipulation of differently polarized terahertz waves. Light. Sci. Appl. 2016, 5, e16076. [Google Scholar] [CrossRef]
- Lin, C.; Li, G.Y.L. Terahertz Communications:An Array-of-Subarrays Solution. IEEE Commun. Mag. 2016, 54, 124–131. [Google Scholar] [CrossRef]
- Nanfang, Y.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar]
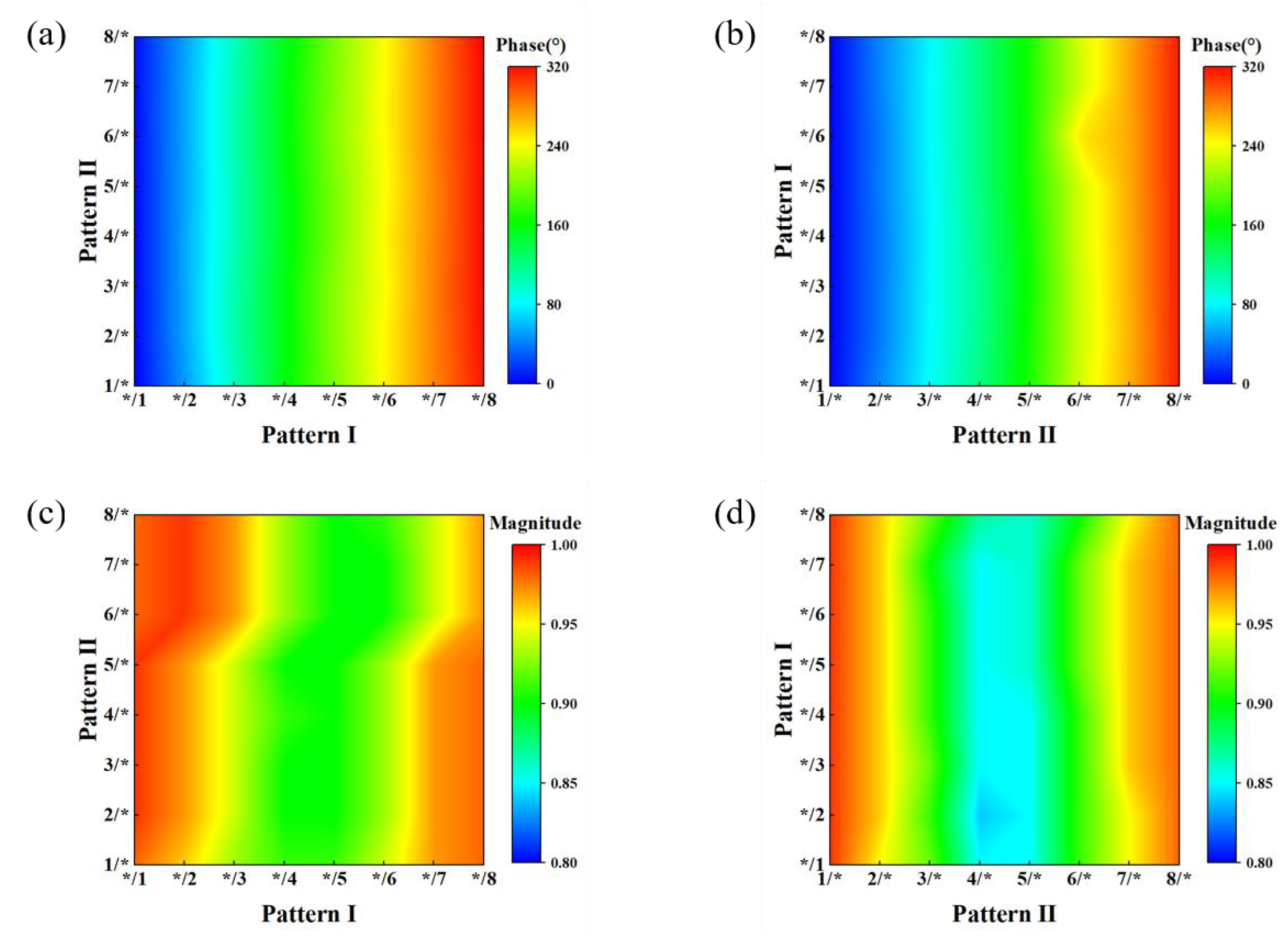


| Pattern I | */1 | */2 | */3 | */4 | */5 | */6 | */7 | */8 |
|---|---|---|---|---|---|---|---|---|
| 70 | 95 | 103 | 102 | 105 | 115 | 120 | 130 | |
| 10 | 15 | 12 | 20 | 21 | 11.5 | 15 | 37 | |
| Phase (°) | 0 | 45 | 90 | 135 | 180 | 215 | 270 | 315 |
| Code | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| Pattern II | 1/* | 2/* | 3/* | 4/* | 5/* | 6/* | 7/* | 8/* |
|---|---|---|---|---|---|---|---|---|
| 40 | 57 | 62 | 65 | 69 | 74 | 80 | 80 | |
| 10 | 10 | 10.5 | 11.2 | 10.5 | 10 | 15 | 33 | |
| Phase (°) | 0 | 45 | 90 | 135 | 180 | 215 | 270 | 315 |
| Code | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, P.; Zheng, X.; Ma, T.; Cheng, G.; Wu, G.; Bao, X.; Sun, H.; Ding, J.; Si, L. Terahertz Dual-Band Dual-Polarization 3-Bit Coding Metasurface for Multiple Vortex Beams Generation. Electronics 2023, 12, 1868. https://doi.org/10.3390/electronics12081868
Tang P, Zheng X, Ma T, Cheng G, Wu G, Bao X, Sun H, Ding J, Si L. Terahertz Dual-Band Dual-Polarization 3-Bit Coding Metasurface for Multiple Vortex Beams Generation. Electronics. 2023; 12(8):1868. https://doi.org/10.3390/electronics12081868
Chicago/Turabian StyleTang, Pengcheng, Xueqi Zheng, Tianyu Ma, Gong Cheng, Genhao Wu, Xiue Bao, Houjun Sun, Jun Ding, and Liming Si. 2023. "Terahertz Dual-Band Dual-Polarization 3-Bit Coding Metasurface for Multiple Vortex Beams Generation" Electronics 12, no. 8: 1868. https://doi.org/10.3390/electronics12081868
APA StyleTang, P., Zheng, X., Ma, T., Cheng, G., Wu, G., Bao, X., Sun, H., Ding, J., & Si, L. (2023). Terahertz Dual-Band Dual-Polarization 3-Bit Coding Metasurface for Multiple Vortex Beams Generation. Electronics, 12(8), 1868. https://doi.org/10.3390/electronics12081868








