Abstract
Currently, DC breakers are commonly used in mainstream protection schemes for DC grids to eliminate faults. However, the cost of high voltage DC (HVDC) breakers is high, and equipping each DC line with DC breakers is expensive. In order to minimize the number of DC breakers while ensuring the reliability of the power supply, a zonal protection strategy suitable for multi-voltage level DC grids is proposed. Subsequently, the qualitative impact of partial power interruption caused by fault DC areas is analyzed in the system. The basic zonal principle of the multi-voltage level DC grid is formulated, taking into account unbalanced power, the mode of system-level control, and the type of converters. Additionally, a time sequence coordination strategy is derived in detail based on the characteristics of DC breakers, AC/DC converters, DC/DC converters, AC breakers, high-speed switches, and other fault removal components. Finally, a seven-terminal DC grid is modeled in the PSCAD/EMTDC simulation platform. According to the simulation analysis, the DC grid can adopt the converter with fault clearing ability or an AC circuit breaker to cooperate with the fast disconnector (FD) to complete fault clearing in the DC fault area under the proposed zonal protection coordination strategy.
1. Introduction
Compared with the traditional transmission system, the multi-voltage level DC grid has high power supply reliability and operation control flexibility. It has significant advantages in achieving reliable transmission of long-distance and large-capacity electric energy, promoting grid connection and the utilization of renewable energy, and improving the security and stability of the regional interconnection of the AC grid, as shown in Figure 1 [1,2]. It is considered to be an effective method to achieve the transformation of an energy structure and the optimal allocation of resources.
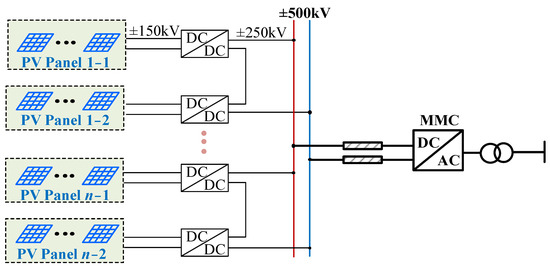
Figure 1.
Multi-voltage level DC grid with distributed renewable energy.
However, unlike the AC grid, the DC grid is a low-damping system. When a DC fault occurs in the DC grid, the fault current rises rapidly, the peak value of the overcurrent is high, there is no zero-crossing [3], and the influence range is wide. Therefore, it is significant to ensure the safe and stable operation of the DC grid and quickly realize DC fault clearing and system recovery. At present, the fault protection methods of the DC grid can be divided into three types:
- Adopting an AC circuit breaker with fast switches [4,5];
- Applying a fault current limiter (FCL) to cooperate with the DC circuit breaker (DCCB) [6,7,8];
- Utilizing the converter with fault self-clearing capability to cooperate with the fast switches [9,10].
When the protection scheme of Type 1 is adopted, the AC circuit breaker is used to clear the fault and the current becomes 0, and then the fast disconnector (FD) plays a role in isolating the fault. In addition, the cost of building the DC grid with protection equipment can be reduced [4]. However, it is pointed out that the action of the AC circuit breaker takes tens of milliseconds, which is a relatively long time to isolate the DC fault [4,5]. In this case, the reliability of the power supply is poor; therefore, the AC circuit breaker is not selected in the fault protection scheme for the future DC grid.
When the protection scheme of Type 2 is adopted, the protection equipment can deal with a large current with small loss and has a good conversion time without causing damage to the system when the fault is disconnected [6]. It is pointed out that when applying a DCCB to isolate the faults in power system, the current can rise quickly to go over the nominal breaking current. Then, FCL can be adopted to reduce the rise rate of faulty current [7]. Therefore, the application of a combination of FCL and DCCB can quickly clear the DC fault while ensuring safe power transmission [8]. However, the current high-voltage DC circuit breaker is expensive and bulky, and the adoption of the full DC circuit breaker configuration scheme also faces the problem of high cost [8].
When the protection scheme of Type 3 is adopted, all the converters directly connected to the fault need to be locked to realize fault clearing by using the FD. It is pointed out in [9] that the converter with fault self-clearing capability to work with fast switches can successfully isolate the fault when the low-voltage port is short-circuited in the system. In this protection type, the application of expensive and immature DCCB can be reduced. However, the converter with fault self-clearing capability cannot cut off by itself and relies on fast switches. As a result, even if the recovery time of the system in this scheme is shorter than that in the AC circuit breaker scheme, it will still cause a short shutdown of the whole system [10].
In order to give consideration to reliability and economy, a combined DC circuit breaker is proposed in [11,12]. The combined DC circuit breakers of all outgoing lines of the same DC bus node share a transfer energy-consuming branch to reduce the number of main disconnectors and reduce the cost. However, when multiple DC lines fail at the same time, the faults cannot be removed normally. In [13], a zonal protection strategy for power transmission is proposed. This protection strategy proposes that DC circuit breakers are only installed on the interconnection lines between different DC areas, which can reduce the number of DC circuit breakers and ensure power transmission in non-fault areas. However, this strategy does not take into account the situation in which the DC grid contains fault self-clearing converters and the time sequence coordination between different fault-clearing elements.
Therefore, this paper proposes a zonal protection strategy for the multi-voltage level DC grid, which can ensure the reliable operation of the system and minimize the investment cost of protection. The main contributions of this research are presented as follows:
- According to the analysis of traveling wave characteristics of a multi-voltage DC power network, a fault detection method based on a single-ended modulus reverse traveling wave is proposed.
- A fault-clearing scheme considering the incomplete configuration of DCCBs in multi-voltage DC networks is proposed. This scheme utilizes the fault-clearing capability of the converter, which greatly saves the cost of multi-voltage DC networks.
In this paper, a seven-terminal DC grid is built on the PSCAD/EMTDC simulation platform to verify the proposed DC grid zonal protection strategy and corresponding time sequence coordination strategy.
The remaining structure of this paper is presented as follows: Section 2 shows the fault detection and identification method for the HVDC grid based on traveling-wave protection; Section 3 introduces the proposed zonal protection strategy for the DC grid; Section 4 presents the time sequence coordination strategy for DC power network zonal protection; Section 5 gives the simulation results and analysis; Section 6 is the conclusion of this paper.
2. Fault Detection and Identification Method for HVDC Grid Based on Traveling Wave Protection
The ultra-high-speed protection of HVDC lines is one of the key technologies that need to be overcome in HVDC grids. In this section, based on the characteristics of single-ended traveling-wave faults mentioned in [14], a fault detection and identification method that can accurately identify fault lines and fault poles is proposed. Based on the wavelet transform, the method of extracting fault features is investigated.
2.1. Fault Traveling Wave Characteristics of DC Grid
The structure of the overhead line tower of the Zhangbei flexible DC power grid is shown in Figure 2. In accordance with the Dubanton formula, the relevant parameters of the DC line were obtained from the height of the line tower and the spacing between the two pole lines in [15].
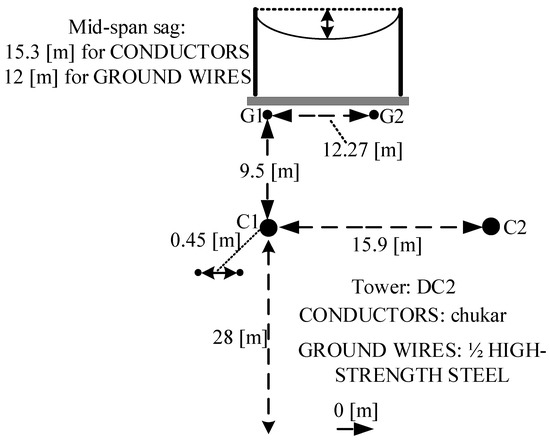
Figure 2.
The structure of the overhead line tower of the Zhangbei flexible DC power grid.
The bipolar DC system is taken as an example to analyze its fault traveling wave characteristics under a single-pole ground fault and double-pole ground fault. Figure 3 shows the fault network diagram of the system at the fault point, in which Rf is the fault transition resistance.
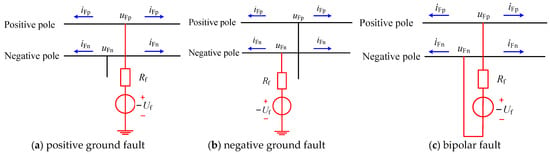
Figure 3.
Fault points in the bipolar system.
According to Figure 3, the modulus’ initial-voltage-fault traveling wave of the bipolar DC system under positive, negative, and bipolar ground fault can be expressed as shown in Equations (1)–(3) [16]:
According to Equations (1)–(3), when the positive and negative ground faults occur on the DC line, the corresponding zero-mode initial-voltage-fault traveling wave polarities are positive and negative, respectively. When a bipolar short-circuit fault occurs, the corresponding zero-mode initial-voltage-fault traveling wave is zero. Therefore, fault pole selection can be effectively performed based on the zero-mode fault traveling wave. For these three faults, there is a negative polarity of the initial-voltage-fault line wave, so the fault line can be discerned based on the polar-mode line wave.
Figure 4a shows the schematic diagram of the HVDC network line boundary. For the convenience of analysis, the initial-fault traveling wave starting from the fault point is represented by the unit step function −ε(t). When the influence of line resistance, conductance and frequency variation characteristics of line parameters are ignored, the initial-fault traveling wave from the fault point will propagate along the line without attenuation and distortion of the line boundary.
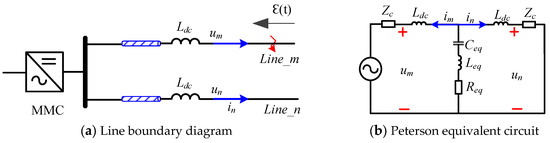
Figure 4.
Boundary of the HVDC grid line.
According to Peterson’s law, the equivalent circuit shown in Figure 4b can be obtained, where Ldc is the inductance of the smoothing reactor and Zc is the wave impedance of the line. When analyzing polar-mode and zero-mode faulted traveling waves, the corresponding polar-mode and zero-mode wave impedances are employed, respectively. Req, Leq and Ceq are the equivalent resistance, equivalent inductance and equivalent capacitance of the MMC converter station.
According to the equivalent circuit shown in Figure 4, the initial-fault-voltage traveling wave and current traveling wave corresponding to measurement points m and n are calculated in the S domain, and their expressions are as follows [17].
According to the relationship between the forward and the reverse traveling waves, the expressions of the forward and the reverse-voltage traveling wave at the measurement points m and n can be obtained, as shown in Equations (6) and (7).
where Umf and Umr are the forward-voltage traveling wave and reverse-voltage traveling wave of the measuring point m, and Unf and Unr are the forward voltage traveling wave and reverse-voltage traveling wave of measuring point n, respectively.
According to the analysis, the voltage fault traveling wave, um(t), at the measuring point m has a step with an amplitude of 2 at t = 0. The reverse-voltage fault traveling wave, umr(t), and the forward-voltage fault traveling wave, umf(t), of the measurement point m have a step with an amplitude of 1 at time t = 0. The remaining fault traveling waves have no step at time t = 0. There is an obvious difference between the reverse-voltage traveling wave of measurement point m and that of measurement point n, that is, the reverse-voltage traveling waves of measurement point m are in step form, while measurement point n has no reverse-voltage traveling waves. For other measurement points in the DC grid except the measurement point at the opposite end of measurement point m, because of the smoothing reactor, the difference in the reverse-voltage traveling wave corresponding to other measurement points and measurement point m is more significant. Therefore, the distinction between internal and external faults can be realized through the reverse-voltage traveling wave.
2.2. Method of Extraction of Fault Traveling Wave Characteristics
According to the above analysis, determining whether or not the reverse-voltage traveling wave has a sudden wave head can help effectively distinguish the internal and external faults. In this paper, the wavelet transform is used to realize the reliable identification of the non-stationary signal wave heads.
The wavelet transform modulus maximum (WTMM) is defined as the local maximum of a signal under a certain scale of the wavelet transform. (Wψf)(2j, x0) is called a modulus maximum of the signal f(t) at the scale of 2j. If any x is satisfied in a certain neighborhood (x0 – ε, x0 + ε) of x0 [18,19]:
Taking the derivative function of the cubic central B-spline function as the mother wavelet, the corresponding low-pass and high-pass filter coefficients are:
The ultrahigh-speed protection is easily affected by noise interference, and noise, as a singular signal, will have a modulus maximum under the wavelet transform. Therefore, it is necessary to further distinguish the modulus maxima of noise interference and the modulus maxima of signal mutations.
The singularity of the signal can be quantitatively described by the Lipschitz index of the signal, but it is difficult to calculate the Lipschitz index according to the definition. The wavelet transform modulus maximum value provides a very convenient method for the calculation of the Lipschitz exponent. It can be proven that there is the following relationship between the Lipschitz exponent and the maximum value of the wavelet transform modulus of the signal at different scales [20]:
Therefore, the Lipschitz exponent of the signal can be calculated by the wavelet transform modulus maxima at different scales. Meanwhile, by comparing the relationship between the modulus maximum of the wavelet transform and the wavelet transform scale j, the noise interference can be effectively distinguished from the actual-fault traveling wave.
2.3. The Overall Process of Traveling Wave Protection
Based on the above analysis, a fault detection and identification method based on single-ended traveling wave protection is designed, and the flow chart is shown in Figure 5 [21,22].
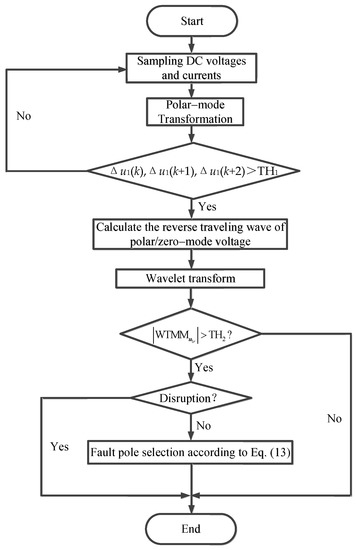
Figure 5.
Flow chart of single-ended traveling wave protection for HVDC grid.
The specific plan for protection implementation is as follows:
- (1)
- The bipolar voltage and current are collected at a sampling rate of 200 kHz.
- (2)
- Based on the starting algorithm, polar-mode transformation is performed on the sampled voltage signal.
- (3)
- The mutation amount is compared with the start threshold to determine whether or not to send a start signal. Protection starts when all three consecutive values, Δu1(k), Δu1(k + 1), and Δu1(k + 2), are greater than the start-up threshold, TH1; otherwise, step (1) is returned to. The protection activation criterion is shown in Equation (11).
- (4)
- When the protection starts, the zero-mode and polar-mode reverse-voltage traveling waves are calculated.
- (5)
- The wavelet transform is performed on the zero-mode and polar-mode inverse-voltage traveling waves and the mode maximum value is obtained. The discriminant formula is shown in Equation (12) to determine whether or not it is a fault in the zone based on the mode maximum value of the reverse-voltage of the polar mode. If it is a fault in the area, then step (6) is performed; otherwise, the process is ended.
- (6)
- If it is judged to be a fault in the area, then whether or not it is noise interference is determined. If it is not noise interference, fault line pole selection is carried out and the discriminant formula is shown in Equation (13); otherwise, the process is ended [22].
3. Zonal Protection Strategy for DC Grid
In Section 2, the fault detection and identification methods of the DC grid are investigated. The large-scale development of a multi-voltage DC grid requires the application of a high-voltage DC circuit breaker or an all-DC circuit breaker in the future. However, the protection scheme in this case will cause a cost problem. Considering the requirements of system economy, this paper proposes a zonal protection strategy. While minimizing the number of DC circuit breakers and reducing the investment cost, it is not necessary to lock all converter stations in the network during fault breaking, which ensures the reliability of the partial power supply of the system.
3.1. Introduction of Zonal Protection
The DC grid is derived from multi-terminal DC transmission systems. Compared to multi-terminal DC transmission systems, DC grids are more complex in structure, more diverse in equipment, and larger in scale. Therefore, more factors need to be considered when developing protection schemes for a large multivoltage-level DC grid. Among the existing protection schemes for simple multiterminal DC transmission systems, the widely accepted scheme is to configure DC breakers on both sides of each DC line, which can prevent the outage of the whole system.
However, for a multivoltage-level DC grid with more terminals and DC lines, the strategy mentioned above has drawbacks: a large number of DC breakers are needed, which will lead to a significant increase in investment costs; false operation of protection will easily occur due to the line coupling being stronger and the identification of the fault line being more difficult. Overall, the strategy of simply setting up DC breakers requires a higher level of selectivity for protection action.
Therefore, a DC network zonal protection strategy is introduced for the multivoltage-level DC grid. Based on the zonal strategy, the DC grid is divided into several small DC areas. In addition, DC breakers or DC/DC converters with fault-clearing capability on the DC contact lines between different DC areas are installed to isolate the faulty DC areas and ensure the normal operation of the nonfaulty DC areas [23]. The number of DC breakers can be sharply reduced, and the shutdown of the entire DC network can be avoided.
A DC zone (DCZ) in a DC network is selected as the research object to illustrate the zonal protection strategy. Assume that the DC zonal DCZ is connected to multiple AC zones (ACZs), ACZ1, ACZ2, ACZi, while the DC side is connected to multiple DC zones, DCZ1, DCZ2, DCZj, as shown in Figure 6. The red line in Figure 6 indicates the protection boundary between the DCZ and each AC system, including the converter with fault self-clearing capability and the AC side circuit breaker without fault self-clearing capability. The blue line in Figure 6 represents the protection boundary between the DCZ and DC areas, including a DCCB and DC/DC converter with fault-blocking capability.
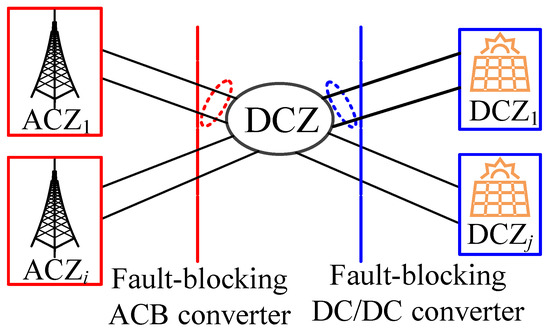
Figure 6.
Schematic diagram of zonal-based protection strategy for DC grid.
When a DC fault occurs in the DCZ, the DC area can be isolated through the protection boundary mentioned above, and the rest of the DC area and the AC power network can be maintained in a normal operation status.
3.2. Influence of DC Network Zonal Protection
The main objective of protecting the DC network is to reduce the damage caused by the fault to the equipment, and the subobjective is to maintain the normal operation of the nonfault area as much as possible to ensure the stable operation of the nonfault DC area and the AC area in the DC network. Specifically, for the DC network, before the DC fault is cleared, the fault current circulating in the power electronics of the system should be less than its overcurrent capacity limit, which is generally twice the rated current [24].
In order to reach the reliability and stability requirements of the DC network, the fault-clearing process should be as short as possible to avoid causing a large number of converters blocking the network to cause a large impact on the AC system. Meanwhile, the restart process should be as fast and smooth as possible in the faut area. The power electronics in the DC network are usually equipped with valve protection, which is set to a reasonable standard, and the overcurrent limit requirements of each power electronic converter can be met before the fault is cleared. Therefore, this paper focuses on the impact of the DC network zonal protection strategy on the whole system.
Taking the zonal protection strategy for the DC grid in Figure 6 as an example, the ACZi and the DCZj are selected to analyze the impact on the system when a fault occurs in the DCZ.
3.2.1. Impact of DCZ Failure on ACZi
After a fault occurs in DCZ, the zonal boundary protection device between the DCZ and ACZi operates, and the power transmission between the DCZ and ACZi is interrupted for a certain period of time. If the sum of the transmitted power of all the AC lines between the DCZ and ACZi is zero, the internal power of the ACZi can be balanced. Moreover, the power transmitted between the DCZ and ACZi can be transferred to the internal AC lines of the ACZi for transmission. However, it may lead to line overload problems. If the sum of the transmitted power of all AC lines between the DCZ and ACZi is not zero, the internal power of the ACZi is unbalanced. In order to maintain the stable operation of the system, the participation of the three lines of defense within the ACZi is required to cut the machine, the load, and even the grid. The impact on the ACZi is related to the amount of unbalanced power and is negatively related to the ACZi system’s strength.
3.2.2. Impact of DCZ Failure on DCZj
When the sum of the transmitted power of all DC lines between the DCZ and DCZj is zero, the internal power of the DCZj can be balanced. In addition, the power transmitted among the DCZs can be transferred to the internal DC lines of the DCZj for transmission, but there may be a line overload problem; if the sum of the transmitted power of all DC lines between the DCZ and DCZj is not zero, the internal power of the DCZj is unbalanced, which will cause active power. At this time, the unbalanced power inside the DCZj will cause active power and DC voltage fluctuations, and even lead to system instability. The DCZj control system is required to coordinate the power balance in the DC region, but its regulation capability is limited and will be constrained by the capacity of the converter station and the nature of the transmission.
In the application of zonal protection, the power transmission interruption capacity between the above-fault DC area and the connected AC/DC area after isolation will directly affect the system’s stability. In addition, the power interruption time in the fault DC area is also an aspect that affects the system’s stability. The time for the power interruption of the fault DC region is defined as toff in Equation (14):
where tc is the time for fault breaking; td is the time for line deionization; tr is the restart time for the fault process in the DC area.
The fault breaking time, tc, and the restart time, tr, for the faulted DC area are defined as follows:
where tc1 is the time for fault detection and identification; tc2 is the time for the fault-clearing element’s action; tr1 is the time for reclosing; tr2 is the time for the restart process of the faulty DC area after successful reclosing.
When there is a permanent fault in the DC area, the time for the power interruption of the faulty DC area is mainly affected by the reclosing time. The restart time of the faulty DC area will be extended until the permanent fault is cleared after the reclosing failure.
When there is a transient fault in the DC region, the power interruption time of the faulty DC region is mainly influenced by the fault breaking time and the line deionization time. In order to meet the speed of protection, the time for the fault detection and identification of the DC network should be as short as 1 to 3 ms [25,26]. The action time of the fault-clearing element is related to the element types. At present, the elements available for fault clearing in the DC network mainly include converters or DC/DC converters with fault self-clearing capability, AC breakers, DC breakers, and FDs. The action time of each fault element is shown in Table 1 [27,28,29]. The time for the DC’s line deionization is about 150 to 500 ms.

Table 1.
The action time of fault-clearing elements.
Therefore, the time for the power interruption of the faulty DC region is mainly related to the type of fault and the fault-clearing elements. Generally, when the interruption time of the fault DC area is long, the impact on the connected AC area and DC regions will be great.
When the DC network adopts a zonal protection strategy, the power exchange capacity between DC regions should be less than the maximum power change of the control system in the respective region. This can prevent the destabilization of the remaining DC regions caused by the excessive amount of unbalanced power after the removal of the faulty DC region. At the same time, in the case of DC networks containing multiple types of converters, a converter with fault self-clearing capability should be divided into the same DC zone. Its fault self-clearing characteristics and fast restart capability can shorten the fault breaking time and the restart time of the faulty DC area, thus shortening the power interruption time, and further reducing the impact on the connected AC and DC areas.
3.3. DC Network Zonal Principles
Based on the analysis of the impact of DC network zonal protection in Section 3.2, the following zonal principles for DC networks can be developed.
The correlation between the exchange capacity, Px,m, and maximum unbalanced power, ΔPm(toff), are presented in Equation (17):
where Px,m is the maximum unbalanced power allowed in the AC or DC region m, which is a function of the power interruption time, toff, in the DC region. When t is smaller, the amount of unbalanced power that the AC or DC region m can withstand is larger.
The exchange capacity is the absolute value of the sum of the transmitted power on all lines:
When the DC network adopts zonal operation due to DC faults, the converter stations within each DC region should satisfy the coordinated control relationship to ensure the stable operation of the nonfaulty DC zone [13,30]. The control methods of individual converter stations within the DC network, Cmode,con, can be constant voltage, Cv, constant power, Cp, active power–voltage droop control, Cpv, and other control methods, as shown in Equation (19).
N converter stations in the nonfaulty DC area should be in one of the following three control modes.
(1) At any moment, there is one and only one main converter station with constant voltage control, and all the remaining converter stations have constant power control, such as master–slave control, and voltage deviation control:
where is the combination of control modes of N converter stations at time t; Nn is the number of n converter stations.
(2) L converter stations adapt active power–voltage droop control and n–L converter stations adapt constant power control.
(3) At any moment there is one and only one converter station with constant voltage control, L converter stations with active power–voltage droop control, and n–L–1 converter stations with constant power control.
DC areas with different voltage levels exist in the DC network and can be connected by DC/DC converters with fault-clearing capability. When there is no significant power exchange, the DC/DC converter with a fault-clearing function can be used as the zonal boundary of DC areas with different voltage levels.
To ensure that the zoning principle is established, in the case of maximizing the overall transmission power of the DC network, the exchange power capacity of each DC region and any AC grid connected to it should be less than the limit power shortage or increase that the AC grid can permanently bear; at the same time, the active power output of each DC region and the active power consumption of the receiving station should be equal. When there is unbalanced power in the power system, it should not exceed the maximum power variation that can be regulated by the control system of the DC region.
4. Time Sequence Coordination Strategy for DC Grid Zonal Protection
As there are more possible fault-clearing elements in the DC network, when a fault occurs in the DC network, it may require the joint participation of different fault-clearing elements. It is necessary to develop a suitable action time sequence to realize the coordination and cooperation of each fault-clearing element to complete fault clearing and realize the smooth recovery of the system quickly and accurately.
First, the action time sequence of the fault DC area boundary and the fault DC area’s internal fault-clearing elements are analyzed during the fault-breaking process in the DC area. When a fault occurs in a DC area, the DC breaker at the boundary of the zone is disconnected or the DC/DC converter with fault self-clearing capability is blocked, and all the converters in the zone are blocked. When the converter without fault-clearing capability is adopted in the system, the AC side’s circuit breaker of the converter should be disconnected.
The fault breaking time, tc, in the DC area can be divided into three types by combining the fault-clearing element action times in Table 1.
(1) If all the converters in the DC area have self-clearing capability and the boundary element between the DC zones is a DC/DC converter with self-clearing capability, the fault breaking time in the DC area should be the converter or DC/DC converter with self-clearing capability at the farthest electrical distance from the fault point, which is within 5 ms.
(2) If all the converters in the DC area have self-clearing capability but the boundary element between the DC area contains DC circuit breakers, the fault interruption time should be the time when the DC circuit breaker at the farthest electrical distance from the fault point operates, which is about 5 ms to 6 ms.
(3) If the DC area contains converters without self-clearing capability, the fault interruption time shall be the time when the nonfaulting circuit breaker at the farthest electrical distance from the fault point operates. The AC side’s circuit breaker of the converter at the farthest electrical distance from the fault point that does not have the ability to clear the fault is completely broken, which happens at a distance of about 45 ms to 50 ms.
Therefore, the restart time will be the shortest when all the converters in the region have self-clearing capability, and the restart time will be the longest when all converters do not have self-clearing capability. The time for line deionization is chosen as 300 ms and the overall protection coordination timing of DC power network zonal protection is shown in Figure 7.
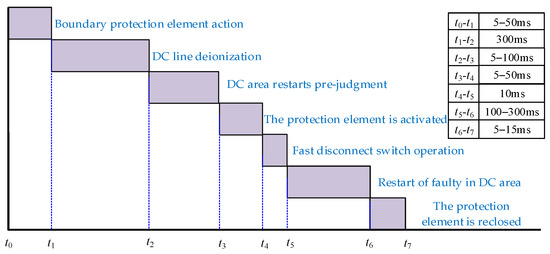
Figure 7.
The overall protection coordination sequence of zonal -based protection.
The definition of each time period in Figure 7 is presented as follows:
- (1)
- t0: the time when a DC line fault occurs.
- (2)
- t0–t1: The protection system detects the fault, the fault DC area boundary protection element acts to complete fault DC area isolation. This time period is the DC area fault breaking time, tc.
- (3)
- t1–t2: the time period for DC line deionization.
- (4)
- t2–t3: The time period over which the faulted DC area restarts prejudgment which is used to determine whether or not the faulted DC area can be restarted directly.
- (5)
- t3–t4: the time period over which the converter with fault self-clearing capability blocks or AC circuit breaker trips when reclosing upon permanent fault.
- (6)
- t4–t5: when the system determines that the fault type is a permanent fault, and FDs on both sides of the faulty DC line act to complete the removal of the faulty line.
- (7)
- t5–t6: sequential unlocking and restarting time of the converter in the faulty DC area.
- (8)
- t6–t7: when the DC circuit breaker or DC/DC converter with self-clearing capability between the faulted DC area and the rest of the connected DC area is reclosed.
The above zonal protection strategy with a time sequence is based on the correct action of the fault-clearing components. Taking into account the possible failure or rejection of the fault-clearing components, corresponding backup protection should be implemented.
Taking the rejection of the DC breaker and quick disconnect switch as an example, if a DC current breaker in the boundary protection element of the faulty DC area rejects, the fault range is extended to the other side of the DC area directly connected to the DC circuit breaker. The action signal should be sent to the boundary protection element of the other side of the DC area to isolate the fault by acting upon the boundary protection element of the other side of the DC area of the DC circuit breaker. The rest of the steps are the same as the those for the correct action of the components.
The FD on one side of the faulty line may refuse to operate during fault clearance in the faulty DC region. In this case, the other connected fault-clearing elements on the bus adjacent to the FD send a trip signal, and the converter connected to this bus is not restarted during the fault recovery process.
The protection process involves multiple converter control systems and other protection components such as DCCBs and FDs. It must rely on the communication system, and fiber optic communication which should be used to shorten the communication delay caused by the signal transmission and to ensure its transmission reliability.
5. Simulation Verification
In order to verify the effectiveness of the proposed zonal protection strategy on the basis of the fault detection method for a DC grid, a seven-terminal DC grid simulation model was built on the PSCAD/EMTDC simulation platform. The seven-terminal DC grid model consisted of four full-bridge MMC converter stations, three half-bridge MMC converter stations and one DC/DC converter with fault-blocking capability. The specific topology is presented in Figure 8 and the related DC grid parameters are given in Table 2 and Table 3. In addition, both ends of each DC line were equipped with DC reactors of a value of 150 mH and the resistance per unit length was 0.01 Ω/km [31].
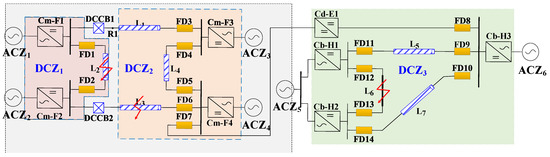
Figure 8.
Topology structure of seven-terminal DC network.

Table 2.
Parameters of converter stations.

Table 3.
Parameters of DC lines.
It is assumed that the maximum unbalanced power of all AC grids is 1000 MW during DC power interruption. According to the zonal protection strategy proposed in this paper, the seven-terminal DC grid shown in Figure 8 can be divided into three DC regions: DCZ1, DCZ2 and DCZ3. The DC circuit breaker was installed on the DC link between DCZ1 and DCZ2 as the DC boundary protection element, and a FD was equipped on the other side. Since DCZ1 had a larger transmission capacity than DCZ2did, when the inter-regional line failed, the locations of the DC circuit breaker and FD could ensure the operation of DC regions with larger transmission capacity. Moreover, the loss of system transmission capacity could be reduced.
The methodology of local detection shown in Section 2 was applied in the DC grid protection process. The overcurrent thresholds of DC circuit breakers DCCB1 and DCCB2 were set to 5 kA and 4 kA, respectively. The overcurrent protection thresholds of all inverters in ±400 kV and ±200 kV DC grids were 8 kA and 4 kA, respectively. Table 4 presents the considered cases for the assumed faults in this section.

Table 4.
Considered cases for the assumed faults.
5.1. Internal Zone and External Zone DC Fault under Four-Terminal DC Grid
In order to verify the effectiveness of the local detection strategy shown in Section 2, DCZ3 was firstly isolated to obtain the four-terminal system to simplify the verification and analysis in this case. The performance of the fault detection and identification method based on single-ended volume traveling wave protection was analyzed and evaluated based on PSCAD/EMTDC. Both sides of each DC line were equipped with DC circuit breakers and smoothing reactors. The value of all smoothing reactors was 200 mH.
Taking the protection of R1 as an example for simulation research, the fault on L1 in Figure 8 is an internal fault for the protection of R1, and the protection should operate reliably. Faults on L2 and L3 are out-of-zone faults for the protection of R1 and should be reliably inoperative. Since the wave process of the fault traveling wave is mainly studied for a very short time after the occurrence of the fault, the control system of the DC system does not act during this period.
When t = 2 s, the midpoint of DC line L1 is set to have a positive, negative, and bipolar metallic grounding short-circuit fault, respectively, and the voltage and current traveling wave changes sampled by the protection of R1 analyzed.
Figure 9a shows that after the positive-fault traveling wave reaches R1, both the polar-mode voltage and the zero-mode voltage of the DC line suddenly drop, and then slowly rise, with a maximum difference of about 800 kV. Figure 9b presents that the polar-mode reverse-voltage traveling wave decreases to −480 kV and remains basically unchanged, while the zero-mode reverse-voltage traveling wave decreases to −500 kV and has a slight rise.
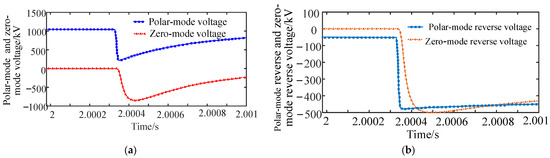
Figure 9.
Positive metal grounding short-circuit fault result: (a) polar-mode and zero-mode voltage waveforms. (b) Traveling wave waveforms of polar-mode reverse-voltage and zero-mode reverse-voltage.
According to Figure 10a, the absolute value of the wavelet modulus maximum of the polar-mode reverse-voltage traveling wave increases at scale to about −590 kV and the noise can be excluded. According to the internal and external zone fault criterion, the fault can be judged as an internal fault from the extreme value of the traveling wavelet mode of the reverse voltage of the polar mode. It can be seen from Figure 10b that the wavelet modulus maximum of the zero-mode inverse voltage traveling wave also has a great value. Similarly to what is shown in Figure 10a, the absolute value of the zero-mode inverse voltage traveling wavelet mode extremes increase at scale to −410 kV. Therefore, according to the fault pole selection criterion, the fault can be judged as a positive fault from the wavelet modulus maximum of the zero-mode reverse-voltage traveling wave.
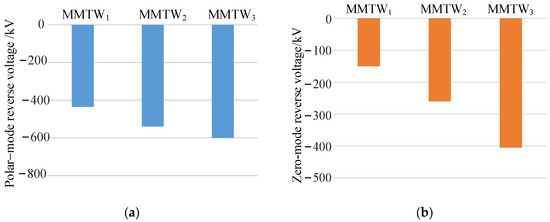
Figure 10.
Wavelet transform results of maximum waveform in the positive pole to ground metal short-circuit fault signal. (a) Polar-mode reverse-voltage traveling wavelet mode maximum waveform; (b) Zero-mode reverse-voltage traveling wavelet mode extreme waveform.
Figure 11a illustrates that when the negative-fault traveling wave reaches R1, the polar-mode voltage of the DC line is similar to the positive fault. Both the polar-mode voltage and the zero-mode voltage of the DC line suddenly drop, and then slowly rise, with a maximum difference of about 800 kV. The zero-mode voltage under a negative fault is the opposite of that under a positive fault which will suddenly increase and then slowly decrease, with a maximum increase of about 800 kV. The polar-mode reverse-voltage traveling wave decreases to −480 kV and remains basically unchanged, while the zero-mode reverse-voltage traveling wave increases to 500 kV and slowly decreases.
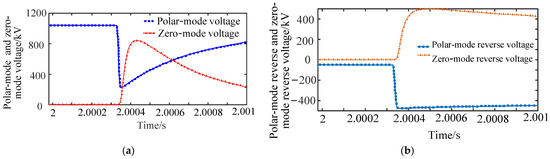
Figure 11.
Negative metal grounding short-circuit fault result: (a) polar-mode and zero-mode voltage waveforms. (b) Traveling wave waveforms of polar-mode reverse and zero-mode reverse voltage.
Similarly, fault feature extraction is performed for the polar-mode reverse-voltage and zero-mode reverse-voltage traveling waves of the DC lines, and the wavelet modulus maxima at each scale are calculated. The calculation results are shown in Figure 12. The calculation result of the wavelet modulus maximum of the polar-mode reverse-voltage traveling wave is similar to that of the positive fault, and it can be determined as an internal zone fault. The wavelet modulus maximum of the zero-mode reverse-voltage traveling wave under a negative fault is exactly the opposite of that under a positive fault. There is a wavelet modulus maximum at each scale, and the value is positive, at about 390 kV. Therefore, according to the fault pole selection criterion, the fault can be determined as a negative fault from the maximum value of the zero-mode reverse-voltage traveling wave wavelet modulus.
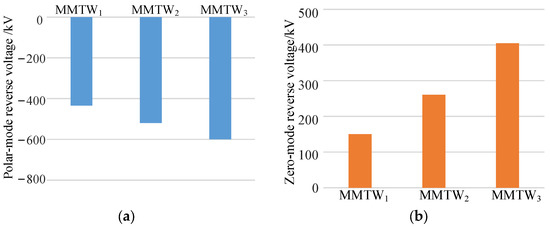
Figure 12.
Wavelet transform results of maximum waveform in the negative pole to ground metal short-circuit fault signal. (a) Polar-mode reverse-voltage traveling wavelet mode maximum waveform; (b) zero-mode reverse-voltage traveling wavelet mode extreme waveform.
The simulation results of when a bipolar metallic ground short-circuit fault occurs at the midpoint of DC line L1 are shown in Figure 13. The occurrence of a bipolar short-circuit fault results in an instantaneous drop of both the polar-mode voltage and polar-mode reverse-voltage traveling waves of the DC line, with a drop amplitude that is approximately twice that of a unipolar fault. The polar-mode voltage subsequently experiences a slow rise to the peak value, while the polar-mode reverse-voltage traveling wave remains unchanged. Conversely, the zero-mode voltage and zero-mode reverse-voltage traveling waves of the DC lines remain unaltered before and after the fault, maintaining a value of zero.
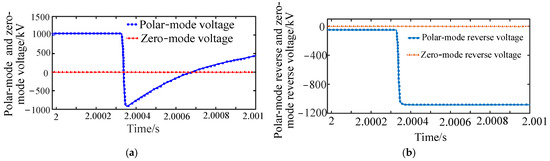
Figure 13.
Bipolar metal grounding short-circuit fault result: (a) polar-mode and zero-mode voltage waveforms. (b) Traveling wave waveforms of polar-mode reverse and zero-mode reverse voltage.
The fault features of a polar-mode reverse-voltage traveling wave and zero-mode reverse-voltage traveling wave of the DC line are extracted, and the wavelet modulus maxima at each scale are calculated. According to Figure 14, there is only one extreme value of the polar-mode reverse-voltage traveling wavelet mode extreme value at each scale. It increases at scale, so the fault can be judged as an internal fault in the region. The zero-mode reverse-voltage wavelet mode maximum value is near zero at each scale, and there is no obvious maximum value, so the fault is judged to be a bipolar fault.
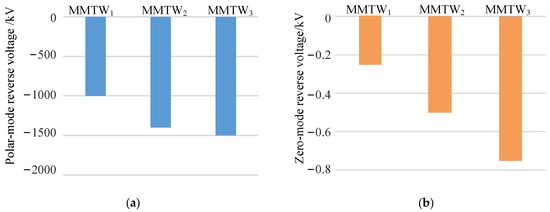
Figure 14.
Wavelet transform results of maximum waveform in the bipolar metal short-circuit fault signal. (a) Polar-mode reverse-voltage traveling wavelet mode maximum waveform; (b) \zero-mode reverse-voltage traveling wavelet mode extreme waveform.
In order to prove the superiority of the fault detection method based on single ended mode inverse traveling waves proposed in this paper, it is compared with voltage differentiation and current differentiation methods [32]. In this paper, it is established that a positive, negative, and neutral metallic fault occurs at the midpoint of the line. The differential variation characteristics of voltage and current on the line are shown in Figure 15. The Voltage differentiation or current differentiation method can be used to realize the pole selection criterion of faults according to the magnitude of the ratio of the fluctuation coefficient when detecting faults. However, in order to ensure the accuracy of protection, at least three sampling points are needed to meet the fault discrimination conditions before fault pole selection can be carried out. The fault discrimination strategy proposed in this paper only needs to meet the discrimination conditions to directly carry out fault pole selection, which has better quick activity.
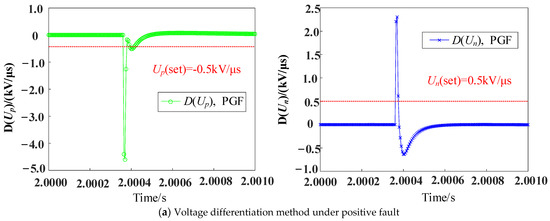
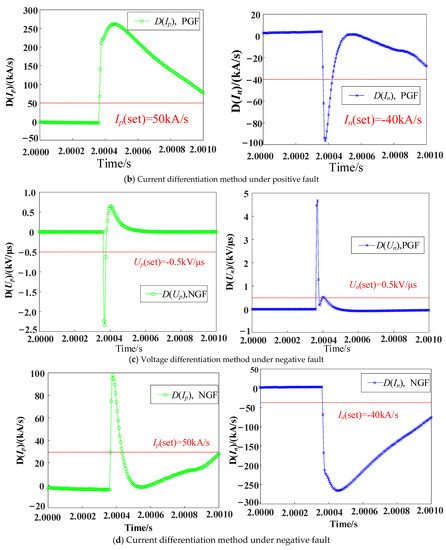
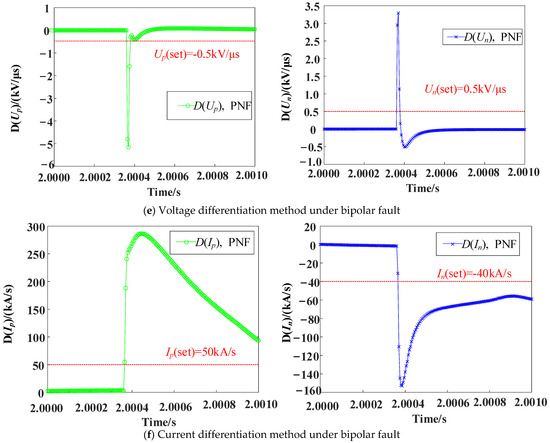
Figure 15.
The differential variation characteristics of voltage and current on the line.
In the DC grid shown in Figure 8, the faults on the DC lines L2, L3 and L4 are all external faults for the protection of R1, and the faults on L2 and L3 are more serious. When a metallic bipolar grounding short-circuit fault occurs outside the protection zone, it is most likely to cause the misoperation of the protection of R1. Therefore, the line wave characteristics of the polar-mode voltage fault in the protection of R1 are analyzed as an example of the fault on L2. When t = 2 s, the DC line L2 has a bipolar metallic grounding short-circuit fault, and the fault location is 1 km away. The simulation results are shown in Figure 16.
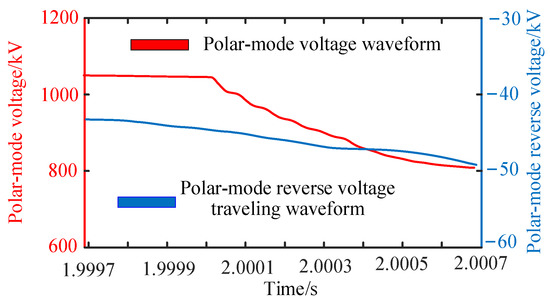
Figure 16.
Characteristics of R1 fault traveling wave of line L2 bipolar metallic short circuit protection.
When line L2 has a bipolar short-circuit fault, the DC line polar-mode voltage in the protection of R1 decreases slowly and the waveform is smooth. The polar-mode reverse-voltage traveling wave also decreases slowly and its amplitude changes slightly. The smoothing reactor has a certain blocking effect on the initial traveling wave of the fault.
To further analyze the impact of the most severe out-of-zone fault on the fault discrimination in the protection of R1, the above polar-mode reverse-voltage traveling wave was subjected to fault feature extraction, and the wavelet mode maximum value at scale j = 3 was calculated. The results are shown in Figure 17. The polar-mode reverse-voltage traveling wavelet mode maxima have no significant wavelet mode maxima at scale j = 3, and the values are all around zero. Therefore, the fault belongs to an out-of-zone fault in the protection of R1, and protection is not carried out.
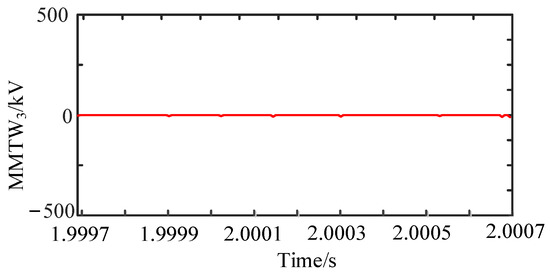
Figure 17.
Wavelet modulus maximum waveform of polar-mode reverse-voltage traveling wave under bipolar short-circuit fault of line L2.
5.2. DC Fault Occurs in DCZ1 under Seven-Terminal DC Grid
According to the simulation results in Section 5.1, the effectiveness of the local detection scheme adopted has been verified, and the subsequent cases will further verify the effectiveness of the proposed zonal protection strategy for the DC network.
In the seven-terminal DC grid shown in Figure 8, the instantaneous bipolar metallic short-circuit fault is set to occur in the DC line L2 inside the DCZ1 at t = 2 s. The fault location is 50 km away from the outlet bus of the converter station Cm-F2, and the fault duration is 0.1 s. According to the zonal protection strategy proposed in this paper, when the DC line L2 has a short-circuit fault, the relay protection on both sides of L2 detect the fault. Subsequently, the locking signal is sent to the converter stations Cm-F1 and Cm-F2, and the tripping signal is sent to the DC circuit breakers DCCB1 and DCCB2. The action signal of the protection boundary element of DCZ1 in the zonal protection process can be obtained as shown in Figure 18.
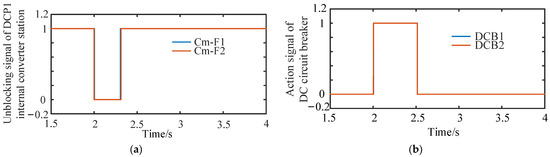
Figure 18.
Protection boundary element action signal in DCZ1. (a) Unblocking signal of converter station in DCZ1; (b) DCZ1 protection boundary of DC circuit breaker action signal.
It can be seen from Figure 18a that the converter stations Cm-F1 and Cm-F2 are relatively close and far away from the fault point. Additionally, the locking time is 2.003 s and 2.002 s, respectively. According to Figure 18b, the DC circuit breakers DCCB2 and DCCB1 are relatively close and far away from the fault point. Additionally, the trip times are 2.005 s and 2.004 s, respectively. Therefore, the fault isolation operation of DCZ1 will be completed in about 5 ms.
It can be seen from Figure 19 that when the fault occurs after 2 s, the active power and DC voltage of the full-bridge converter station in DC regions DCZ1 and DCZ2 fluctuate sharply. However, the fluctuation amplitude of DCZ2 is smaller, and the DC voltage drops to about 500 kV instantaneously, which is not as low as the drop in the full-bridge converter station in DCZ1.
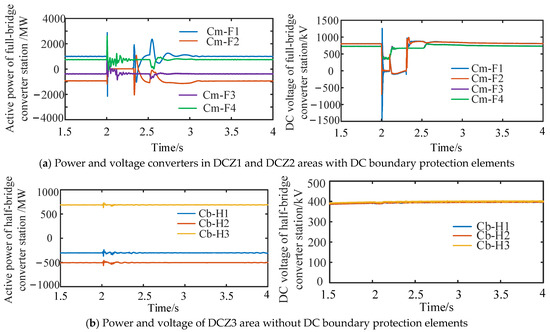
Figure 19.
Simulation results of transient short-circuit fault of DC line in DCZ1.
According to Figure 19, when DCZ1 is isolated, the active power and DC voltage of the full-bridge converter stations Cm-F1 and Cm-F2 will rapidly drop to zero. At the same time, the active power of the full-bridge converter stations Cm-F3 and Cm-F4 quickly recovers to the rated value, but there is still a certain range of fluctuations. When t = 2.1 s, the active power is recovered to the normal value, and the DC voltage is quickly recovered to about 760 kV. During the whole fault isolation process, the active power and DC voltage of the converter stations in DCZ3 fluctuate slightly. After fault isolation, the control mode of the half-bridge converter station Cb-H3 in DCZ3 is changed to constant voltage control.
At t = 2.315 s, after all the converter stations in DCZ1 are unlocked, the DC voltage of Cm-F1 and Cm-F2 rises to about 800 kV, and the active power also begins to recover. At t = 2.515 s, after the DC circuit breakers DCCB1 and DCCB2 coincide, the DC area DCZ1 is reconnected to the system, which will have a large impact on the DC areas of DCZ1 and DCZ2. The active power of all converter stations in DCZ1 and DCZ2 fluctuates briefly, while the active power and DC voltage of all converter stations in DCZ3 almost do not fluctuate. The amplitude of the active power fluctuation of DCZ1 is the largest, and it recovers to the rated value after about 0.4 s.
Subsequently, the DC voltage of all converter stations in DCZ1 drops slightly to 760 kv and then recovers to the rated value after 0.2 s. The DC voltage of the converter station in DCZ2 rises rapidly to 860 kV and then begins to decline slowly, recovering to the rated value in about 0.3 s. The whole DC grid recovers to normal operation after 0.92 s when the fault occurs. The interruption time of DCZ1 exchange power in the DC area is 0.5 s. In the process of fault DC area isolation and reclosing, DCZ2 and DCZ3 have short-term fluctuations in active power and DC voltage but do not affect normal power transmission. When L2 fails, the tripping signal to the DC circuit breakers DCCB1 and DCCB2 are sent. Since DCCB1 and DCCB2 are DC circuit breaker topologies with fault-breaking capabilities, the faults can be quickly cleared. The converter Cd-E1 in region 1 to region 3 does not require to be blocked, so the voltage and current in region 3 (DCZ3) are almost unaffected.
According to the above simulation analysis, the converters in DCZ1 have the ability of fault self-clearing and complete the isolation and restarting of the fault DC area in a short time. DCZ1 and DCZ2 are directly connected, so DCZ2 will be greatly disturbed and impacted during fault isolation and the restart of DCZ1. DCZ1 and DCZ2 are not directly connected, and the electrical distance is far away. Additionally, the internal control of DC converter Cd-E1 can also mitigate the impact, so the fluctuation in active power and DC voltage in DCZ3 is relatively small.
5.3. DC Fault Occurs in DCZ3 under Seven-Terminal DC Grid
In the DC grid shown in Figure 8, the permanent bipolar metallic short-circuit fault is set to occur in the DC line L6 inside DCZ3 at t = 2 s. The fault location is 50 km away from the outlet bus of the converter station Cb-H1. According to the zonal protection strategy proposed in this paper, when the DC line L6 has a short-circuit fault, the relay protection on both sides of L6 detect the fault. Subsequently, the locking signal is sent to the converter stations Cb-H1, Cb-H2, Cb-H3 and the DC/DC converter Cd-E1, and the tripping signal is sent to the AC circuit breakers ACB1, ACB2 and ACB3. The action signal of the protection boundary element of DCZ1 in the zonal protection process can be obtained as shown in Figure 20.
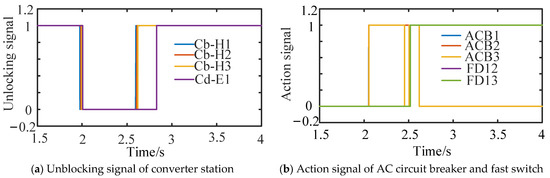
Figure 20.
Protection boundary elements and fast switch action signal in DCZ3.
It can be seen from Figure 20 that the converter stations Cb-H1H and Cd-E1 are the nearest and farthest from the fault point, respectively, corresponding to the fastest and slowest locking times. The blocking times of converter stations Cb-H1, Cb-H2, Cb-H3 and Cd-E1 are about 2.002 s, 2.003 s, 2.004 s and 2.005 s, respectively. Since the converter stations in DCZ3 are all half-bridge MMC and have no fault-clearing capability, the circuit breakers on the AC side of each converter station are further opened.
In the process of fault isolation and reclosure, the active power and DC voltage at the outlet of each converter station in DC regions DCZ1, DCZ2 and DCZ3 are shown in Figure 21. When the fault occurs at 2 s, the active power and DC voltage of all converter stations in DCZ1 and DCZ2 fluctuated slightly and recovered to stability after about 0.1 s. The active power of Cm-F1, Cm-F3 and Cm-F4 remains basically unchanged, while the absorbed active power of Cm-F2 increases from 970 MW to 1120 MW; the active power and DC voltage of the converter station in DCZ3 of the DC region fluctuated sharply and then decreased to 0 after about 0.05 s, at which time the AC circuit breaker was completely disconnected.
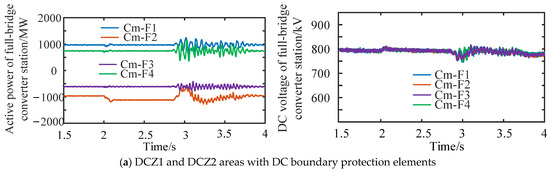
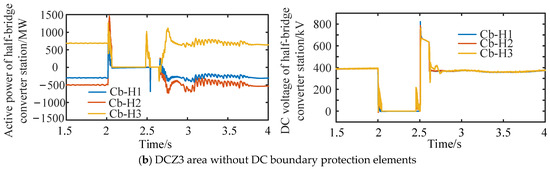
Figure 21.
Simulation results of permanent short-circuit fault of DC line in DCZ3.
At t = 2.454 s, the active power and voltage of the circuit breaker on the AC side of Cb-H3 are increased instantaneously; at t = 2.50 s, the active power drops to 0 after the AC circuit breaker is disconnected. After the fault line is removed, the DC voltage in DCZ3 rises rapidly due to the charging of the submodule capacitor in the DC/DC converter Cd-E1; at t = 2.62 s, after the circuit breakers on the AC side in DCZ3 are closed, the DC voltage in DCZ3 drops to 600 kV instantaneously and then starts to drop slowly; at t = 2.63 s, after the converter stations in DCZ3 are unlocked, the DC bus voltage quickly recovers to 400 kV, and the active power begins to increase; at t = 2.83 s, the DC/DC converter Cd-E1 is unlocked, and the active power and bus DC voltage of the converter stations in the network fluctuate. Moreover, the fluctuation amplitude of Cm-F2 in the converter station is relatively large, and the maximum active power fluctuation amplitude is about 50%. The system returns to stable operation after about 1 s.
According to the above simulation analysis, the internal converter of DCZ3 in the DC area has no fault self-clearing ability and the AC circuit breaker needs to be opened during the process of fault DC area isolation. Therefore, it would take a long time for fault isolation. The converter in DCZ3 is unlocked, and the fault DC area is reclosed after the AC circuit breaker is reclosed. Subsequently, the fault DC area is restarted, and it would take a relative long time. DCZ3 and DCZ2 are connected through DC/DC converter Cd-E1, and there is no direct connection with DCZ1. Therefore, in the process of fault isolation and restart of DCZ3, DCZ1 and DCZ2 are subject to less disturbance and impact and can quickly recover to stable operation after internal adjustment.
In Section 5.1, the fault characteristics of positive, negative, and bipolar line faults in a four-terminal DC network model were shown. Based on the traveling wave characteristics of multivoltage DC power systems, the effectiveness of the proposed fault detection method based on the single-ended module reverse traveling wave was verified through faults set internally and externally to the zone.
In Section 5.2 and Section 5.3, a seven-terminal DC network was utilized and a fault-clearing scheme in which the DCCB is not fully configured in a multi-voltage DC network was considered. When the faults occur in the DCZ1 and DCZ3 regions, respectively, the fault-clearing ability of the converter is utilized to reduce the application of DCCBs, which can greatly save the cost of multivoltage DC networks.
6. Conclusions
This paper proposes a zonal protection strategy for large-scale DC power networks. The DC network is divided into three DC regions, and the DC circuit breaker between the DC regions is adopted to isolate the faulty DC regions quickly. The converter or AC circuit breaker with fault-clearing capability is applied in combination with a fast isolation switch to complete fault-clearing in the faulty DC area. In this paper, a fault detection method based on single-ended-mode reverse traveling waves was proposed based on the analysis of the traveling wave characteristics of multivoltage DC networks. In addition, the zonal protection strategy proposed in this paper considered the corresponding partition principle and realized the configuration of parts of DC circuit breakers in a multivoltage DC network to clear a fault. This scheme makes use of the fault-clearing ability of the converter and greatly saves the cost of a multivoltage DC network. Based on the proposed zonal protection strategy, the time sequence of different fault-clearing elements in the network was coordinated. Depending on the type of converter stations in the fault area, the breaking time and restart time could be further obtained to guarantee the normal operation of the DC system.
Author Contributions
Conceptualization, Y.H., J.L. and Y.W.; methodology, T.L. and W.Z.; software, R.M. and Y.L.; validation, Y.H. and J.L.; formal analysis, R.M.; investigation, T.L.; resources, W.Z.; data curation, C.G. and J.L.; writing—original draft preparation, Y.L. and C.G.; writing—review and editing, Y.H. and Y.L; visualization, T.L. and Y.W.; supervision, J.L. and Y.W.; project administration, Y.H. and Y.W.; funding acquisition, Y.H. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (52207126), the National Natural Science Foundation of China (U22B6006), and the Science and Technology Project of State Grid Corporation of China (SGSCJY00GHJS2200046).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
| HVDC | high voltage DC |
| FD | fast disconnector |
| FCL | fault current limiter |
| DCCB | DC circuit breaker |
| WTMM | Wavelet transform modulus maximum |
| DCZ | DC zone |
| ACZ | AC zone |
References
- Jiang, Q.; Li, B.; Zhang, Y.; Wang, Z.; Liu, T.; Wang, T.; Zhang, M. Analysis of power flow transfer characteristics and stability improvement method of DC grid considering converter’s safety boundary. Energy Rep. 2023, 9, 1720–1730. [Google Scholar] [CrossRef]
- Xiao, F.; Cao, K.; Tang, J.; Liu, D.; Rao, Y.; Xiong, P. Study on coordinated multi-objective reactive control system of AC/DC power grid based on new-generation synchronous condenser. Energy Rep. 2023, 9, 2140–2148. [Google Scholar] [CrossRef]
- Yuan, S.; Yan, J.; Yu, Y.; Zhao, C.; Su, G.; Li, X. Calculation method of short-circuit fault current in flexible DC grid. Energy Rep. 2022, 8, 461–468. [Google Scholar] [CrossRef]
- Dantas, R.; Liang, J.; Ugalde-Loo, C.E.; Adamczyk, A.; Barker, C.; Whitehouse, R. Progressive Fault Isolation and Grid Restoration Strategy for MTDC Networks. IEEE Trans. Power Deliv. 2017, 33, 909–918. [Google Scholar] [CrossRef]
- Wang, S.; Ugalde-Loo, C.E.; Li, C.; Liang, J.; Adeuyi, O.D. Bridge-Type Integrated Hybrid DC Circuit Breakers. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 1134–1151. [Google Scholar] [CrossRef]
- Xu, J.; Song, B.; Lu, Y.; Zhao, C.; Li, G.; Liang, J. A Multi-Port Current-Limiting Hybrid DC Circuit Breaker. IEEE Trans. Power Deliv. 2020, 36, 1672–1682. [Google Scholar] [CrossRef]
- Kong, L.; Nian, H. Parameters Selection Method of Circuit Breaker and Fault Current Limiter in Mesh-Type DC Microgrid. IEEE Access 2021, 9, 35514–35523. [Google Scholar] [CrossRef]
- Keshavarzi, D.; Farjah, E.; Ghanbari, T. Hybrid DC Circuit Breaker and Fault Current Limiter with Optional Interruption Capability. IEEE Trans. Power Electron. 2017, 33, 2330–2338. [Google Scholar] [CrossRef]
- Diao, X.; Liu, F.; Song, Y.; Xu, M.; Zhuang, Y.; Zha, X. A Novel Fault Ride-Through Topology with High Efficiency and Fast Fault Clearing Capability for MVdc PV System. IEEE Trans. Ind. Electron. 2022, 70, 1501–1511. [Google Scholar] [CrossRef]
- Yan, S.; He, Z.; Yang, J.; Kong, M.; Hu, M. Optimized Protection Strategies for HVDC Grid with Fault-blocking Modular Multilevel Converters for Overhead Line Applications. J. Mod. Power Syst. Clean Energy 2020, 8, 1168–1177. [Google Scholar] [CrossRef]
- Kontos, E.; Schultz, T.; Mackay, L.; Ramirez-Elizondo, L.; Bauer, P. Multi-Line Breaker for HVdc Applications. IEEE Trans. Power Deliv. 2017, 33, 1469–1478. [Google Scholar] [CrossRef]
- Li, C.; Liang, J.; Wang, S. Interlink hybrid DC circuit breaker. IEEE Trans. Ind. Electron. 2018, 65, 8677–8686. [Google Scholar] [CrossRef]
- Rahman, M.H.; Xu, L.; Yao, L. DC Fault Protection Strategy Considering DC Network Partition. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016. [Google Scholar]
- Yang, Y.; Huang, C.; Zhou, D.; Li, Y. Fault detection and location in multi-terminal DC microgrid based on local measurement. Electr. Power Syst. Res. 2021, 194, 107047. [Google Scholar] [CrossRef]
- Dommel, B. EMTP Theory Book; Microtran Power System Analysis Corporation: Vancouver, BC, Canada, 1996. [Google Scholar]
- Zhang, Y.; Tai, N.; Xu, B. Fault Analysis and Traveling-Wave Protection Scheme for Bipolar HVDC Lines. IEEE Trans. Power Deliv. 2012, 27, 1583–1591. [Google Scholar] [CrossRef]
- Chen, L.; Pei, X.; Wei, X.; Li, P.; Tang, G. An effective ultra-high-speed identification scheme of lightning strokes suitable for VSC-based DC grids. CSEE J. Power Energy Syst. 2022, 1–13. [Google Scholar] [CrossRef]
- Lan, T.; Xiao, H.; Li, Y.; Chen, J. Enhanced Current Differential Protection for HVDC Grid Based on Bergeron Model: A Parameter Error Tolerable Solution. IEEE Trans. Power Deliv. 2020, 36, 1869–1881. [Google Scholar] [CrossRef]
- Dong, Z.; Xie, H.; Han, P.; Wang, N.-L.; Jia, Z.-Z. Denoising Realization Based on Wavelet Transform Modulus Maximum. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; Volume 3, pp. 1472–1476. [Google Scholar] [CrossRef]
- Ke, L.; Houjun, W. A Novel Wavelet Transform Modulus Maxima Based Method of Measuring Lipschitz Exponent. In Proceedings of the 2007 International Conference on Communications, Circuits and Systems, Kokura, Japan, 11–13 July 2007; pp. 628–632. [Google Scholar] [CrossRef]
- Ikhide, M.; Tennakoon, S.; Griffiths, A.; Ha, H. Aspects of Travelling Wave Based Protection Philosophy for Consideration in DC Grids of the Future. In Proceedings of the 2019 IEEE 15th Brazilian Power Electronics Conference and 5th IEEE Southern Power Electronics Conference (COBEP/SPEC), Santos, Brazil, 1–4 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, C.; He, J.; Ni, P. A novel protection scheme for MMC-MTDC transmission lines based on fault coefficient. CSEE J. Power Energy Syst. 2022, 1–8. [Google Scholar] [CrossRef]
- Assis, K.; Almeida, R.; Reed, M.; Santos, A.; Dinarte, H.; Chaves, D.; Li, H.; Yan, S.; Nejabati, R.; Simeonidou, D. Protection by diversity in elastic optical networks subject to single link failure. Opt. Fiber Technol. 2023, 75, 103208. [Google Scholar] [CrossRef]
- Jejurkar, P.D.; Awale, R. Effectiveness of hybrid differential-adaptive overcurrent protection scheme for microgrid. Mater. Today Proc. 2022, 69, 592–602. [Google Scholar] [CrossRef]
- Li, T.; Li, Y.; Zhu, Y.; Liu, N.; Chen, X. DC fault current approximation and fault clearing methods for hybrid LCC-VSC HVDC networks. Int. J. Electr. Power Energy Syst. 2022, 143, 108467. [Google Scholar] [CrossRef]
- Xue, S.; Liu, B.; Wang, S.; Chen, X.; Zhu, X.; Lu, J. A modular hybrid DC circuit breaker with fault current self-adaptive control and protection coordination. Int. J. Electr. Power Energy Syst. 2021, 134, 107434. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Y.; Qin, L.; Liu, K.; Blaabjerg, F. Quantitative criteria of considering AC infeed in DC fault assessment of modular multilevel converters. Int. J. Electr. Power Energy Syst. 2022, 141, 107874. [Google Scholar] [CrossRef]
- Xi, J.; Pei, X.; Song, W.; Niu, L.; Liu, Y.; Zeng, X. Integration of superconducting fault current limiter with solid-state DC circuit breaker. Int. J. Electr. Power Energy Syst. 2023, 145, 108630. [Google Scholar] [CrossRef]
- Haseeb, M.; Thomas, M.J. Disconnector switching induced transient voltage and radiated fields in a 1100 kV gas insulated substation. Electr. Power Syst. Res. 2018, 161, 86–94. [Google Scholar] [CrossRef]
- Yu, Z.; Niu, S.; Huo, C.; Chen, N.; Song, K.; Wang, X.; Bai, Y. Multi-objective partition planning for multi-infeed HVDC system. Glob. Energy Interconnect. 2021, 4, 81–90. [Google Scholar] [CrossRef]
- Tang, S.; Chen, M.; Jia, G.; Zhang, C.; Jiang, F.; He, Z.; Yang, H.; Li, W. Centralized Locating Strategy of Fault Current Limiters in MMC-Based Multiterminal HVdc Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 7032–7044. [Google Scholar] [CrossRef]
- Liang, H.; Li, H.; Wang, G. A Single-Phase-to-Ground Fault Detection Method Based on the Ratio Fluctuation Coefficient of the Zero-Sequence Current and Voltage Differential in a Distribution Network. IEEE Access 2023, 11, 7297–7308. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).