Bidirectional CLLLC Resonant Converter Based on Frequency-Conversion and Phase-Shift Hybrid Control
Abstract
:1. Introduction
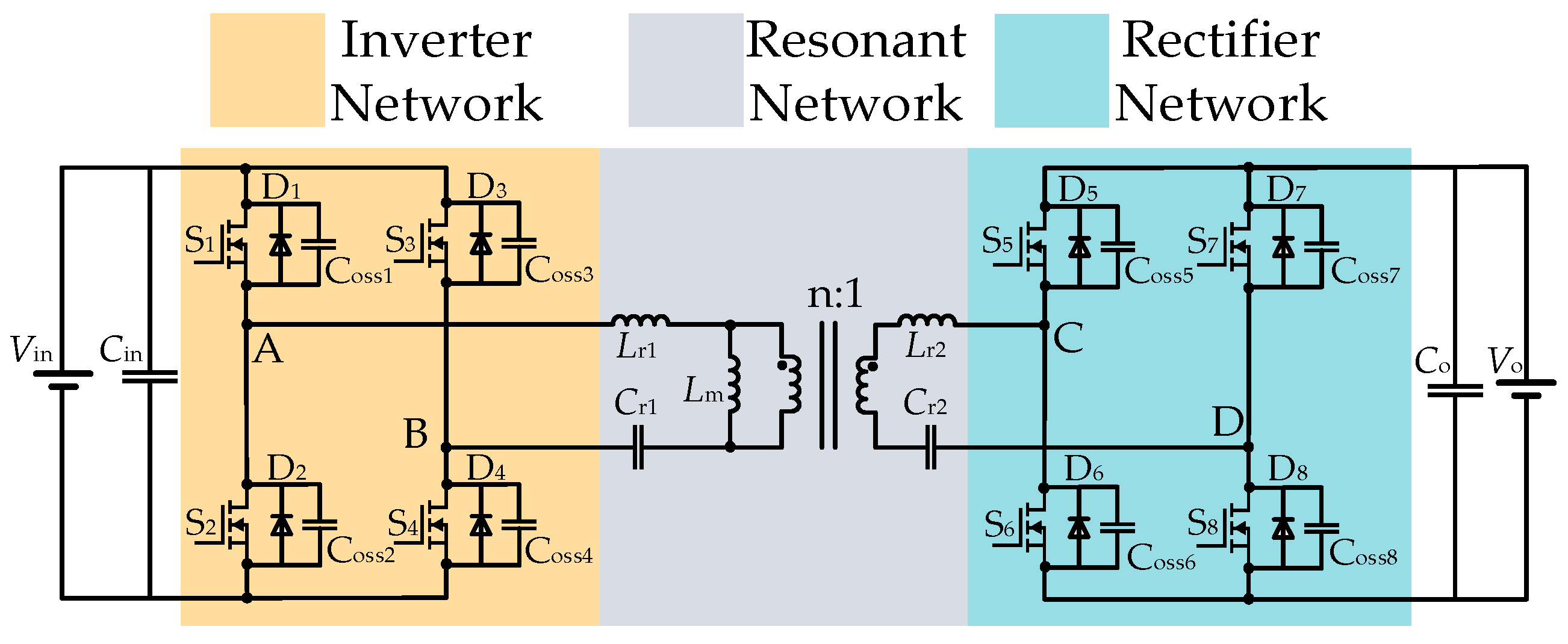
2. System Structure and Characteristic Analysis
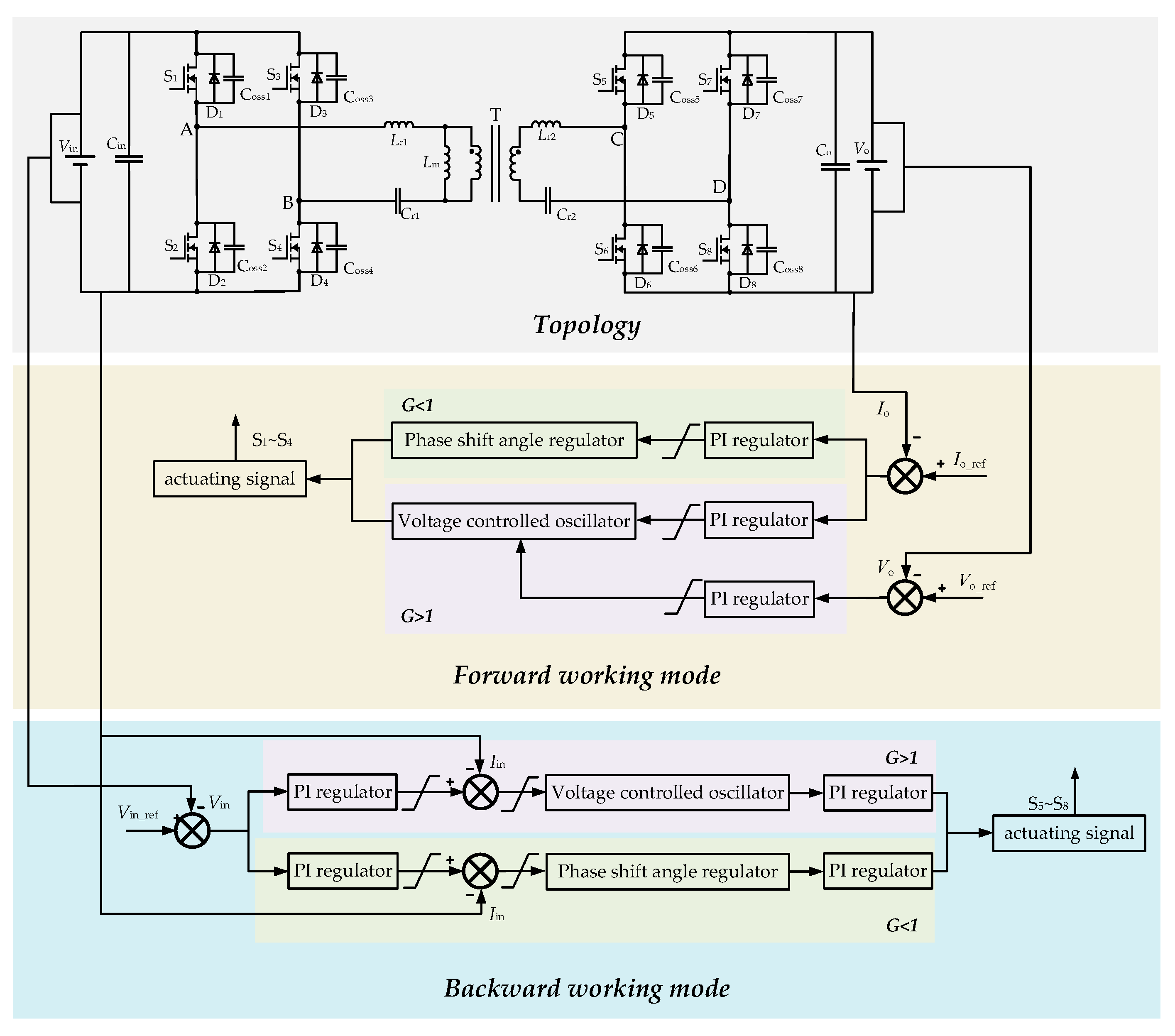
2.1. Birirectional CLLLC Resonant Converter
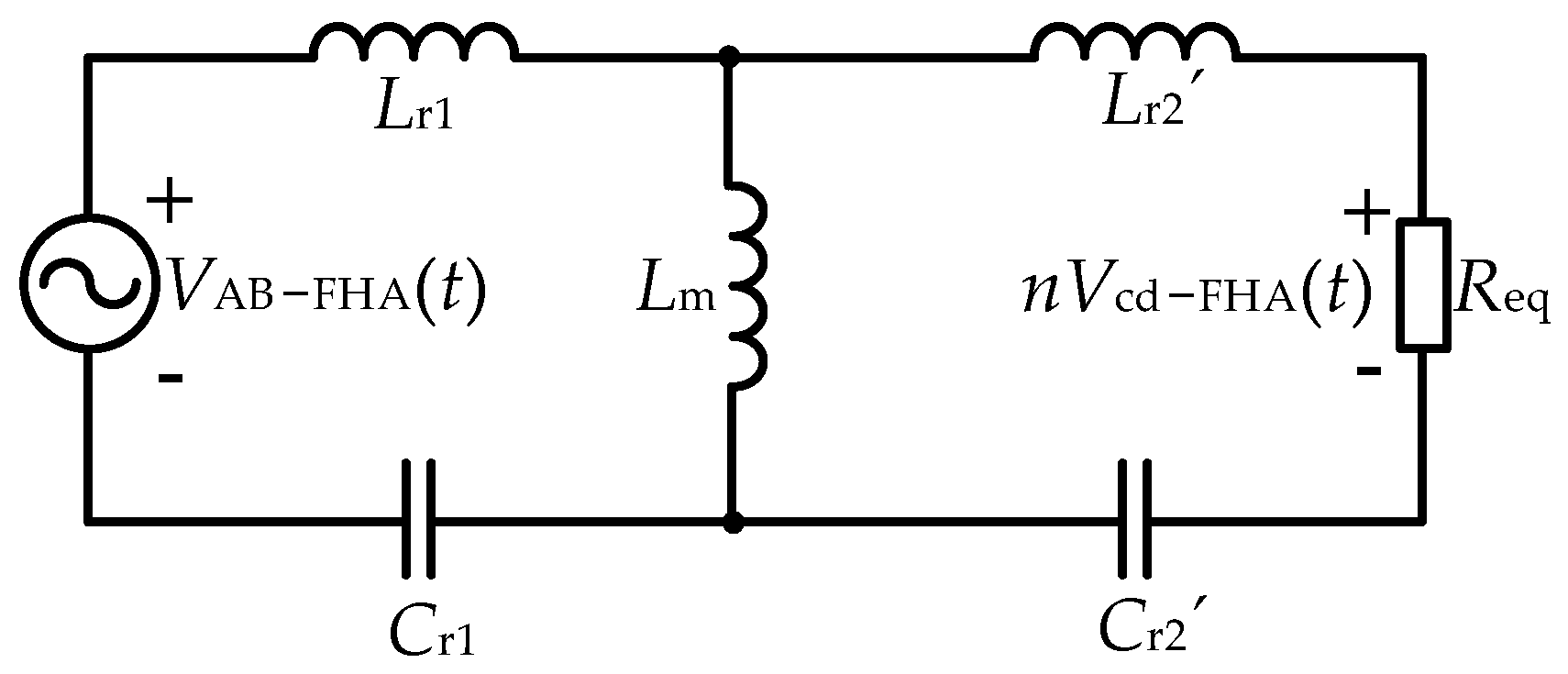
2.2. Working Characteristics of Frequency-Conversion Control
- (1)
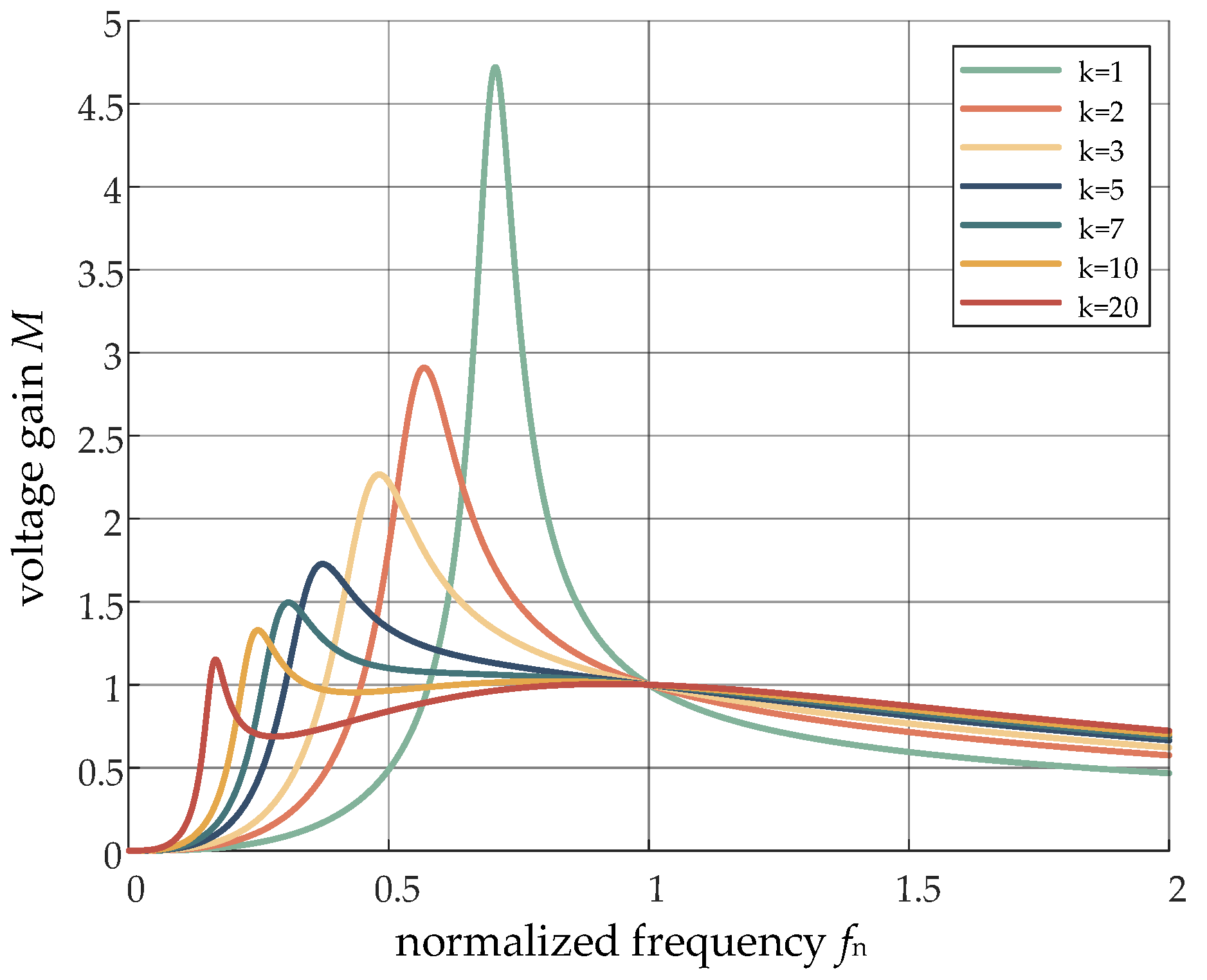
- Influence of inductance factor k on voltage gain
- (2)
- Influence of quality factor Q on voltage gain
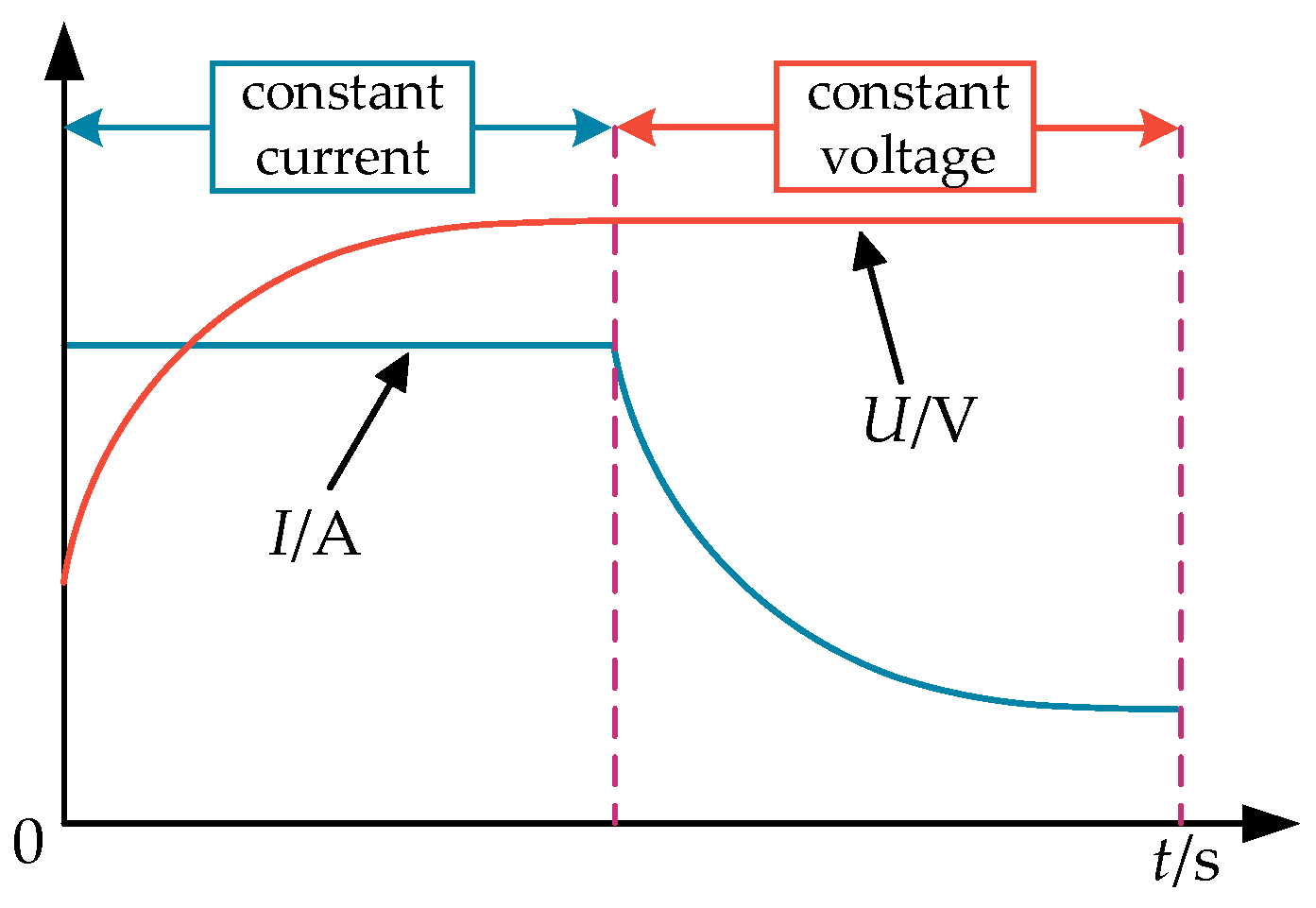
2.3. Working Characteristics of Phase-Shift Control
3. Resonant Network Parameter Design
- (1)
- Turn ratio of transformer n
- (2)
- Transformer normalized voltage gain M
- (3)
- Parameter design of inductance coefficient k and quality factor Q
- (4)
- Design of resonant inductor and resonant capacitor
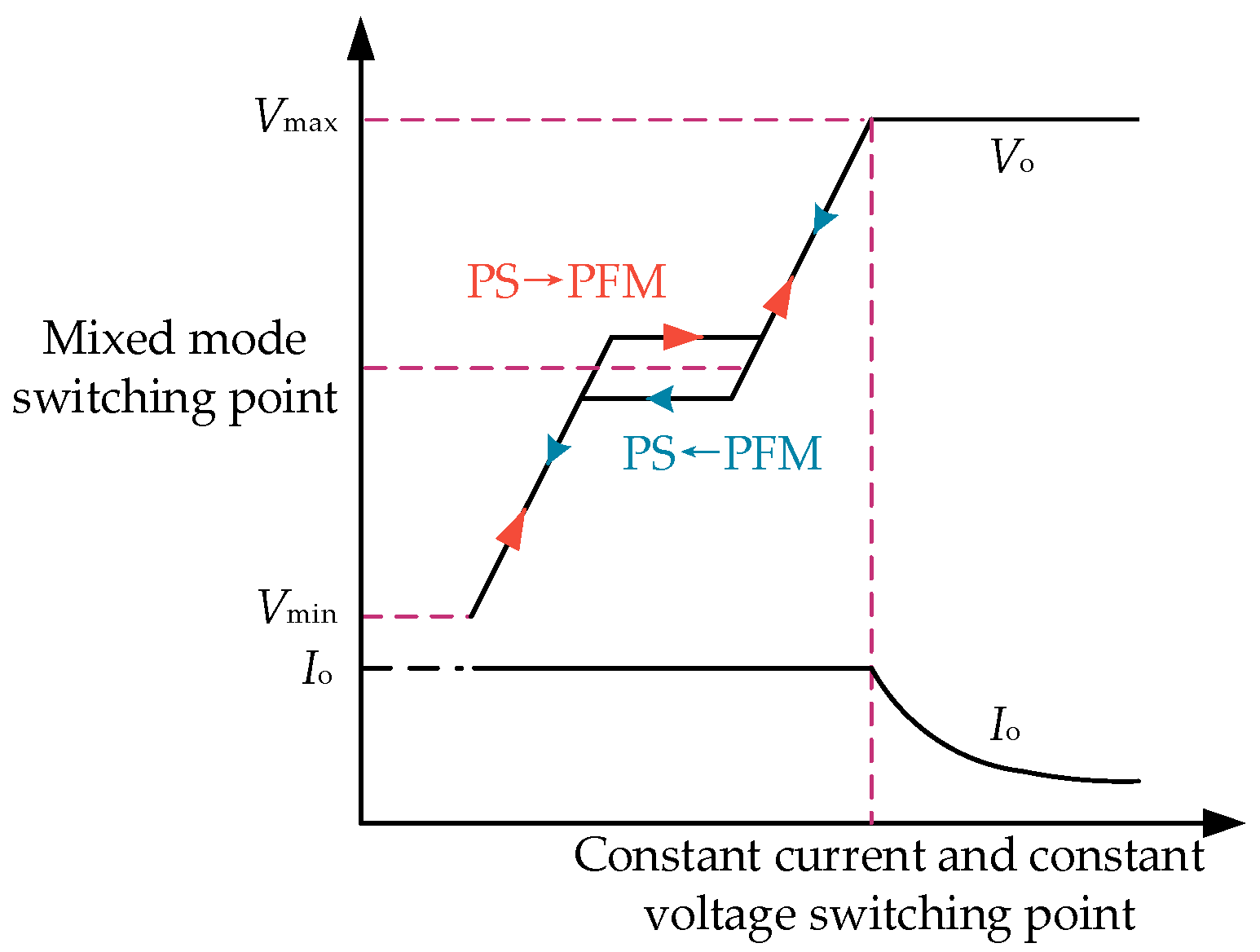
4. Frequency-Conversion and Phase-Shift Hybrid Control Strategy
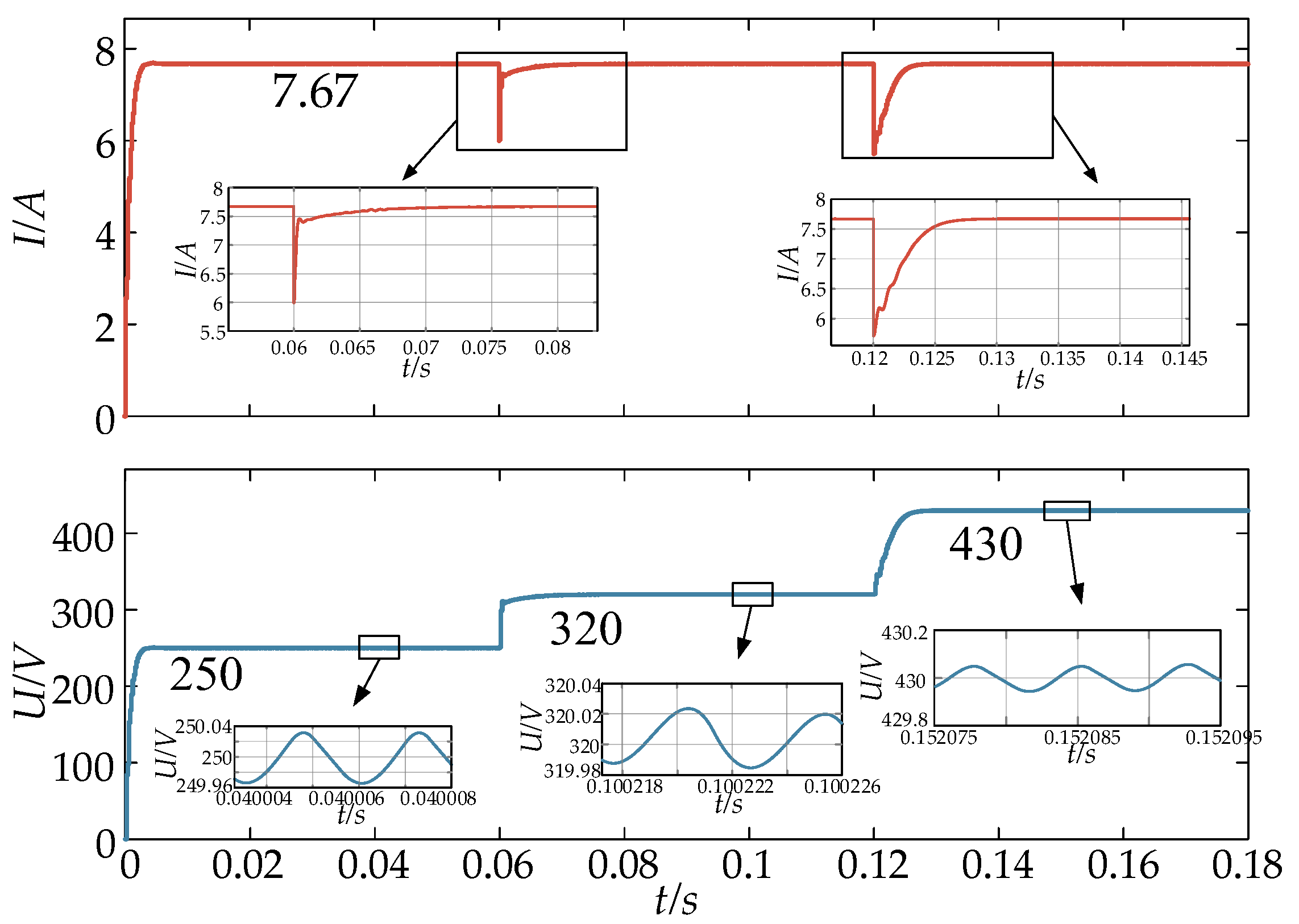
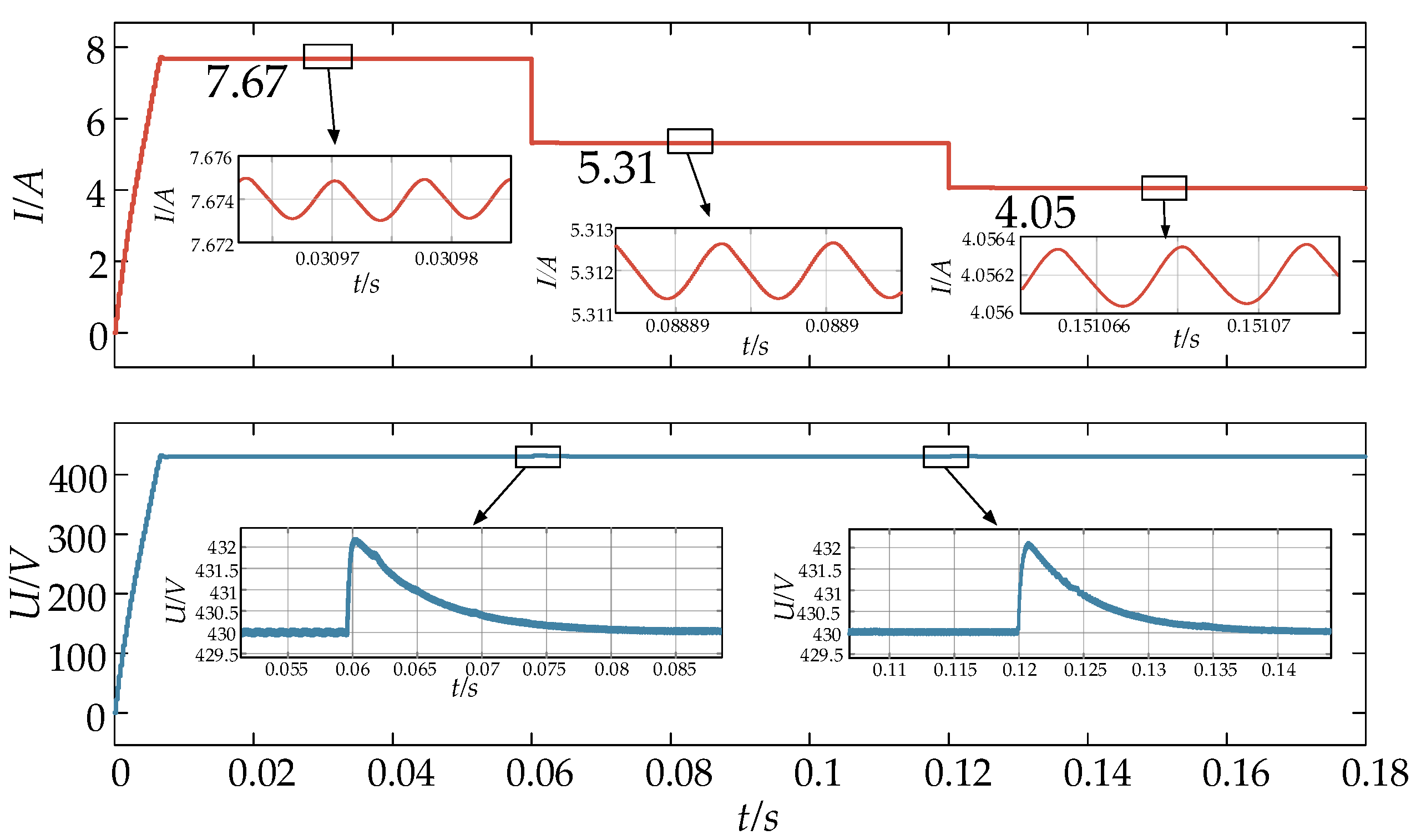
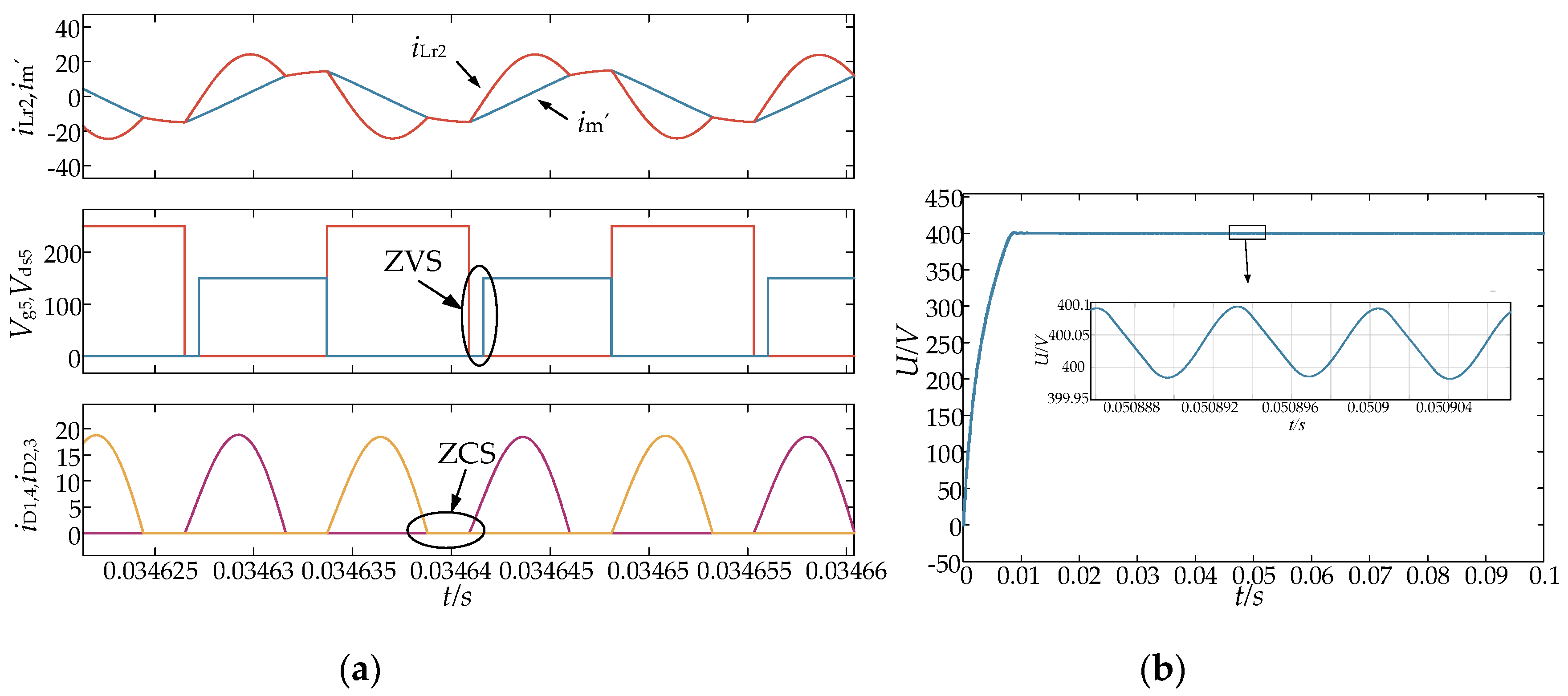
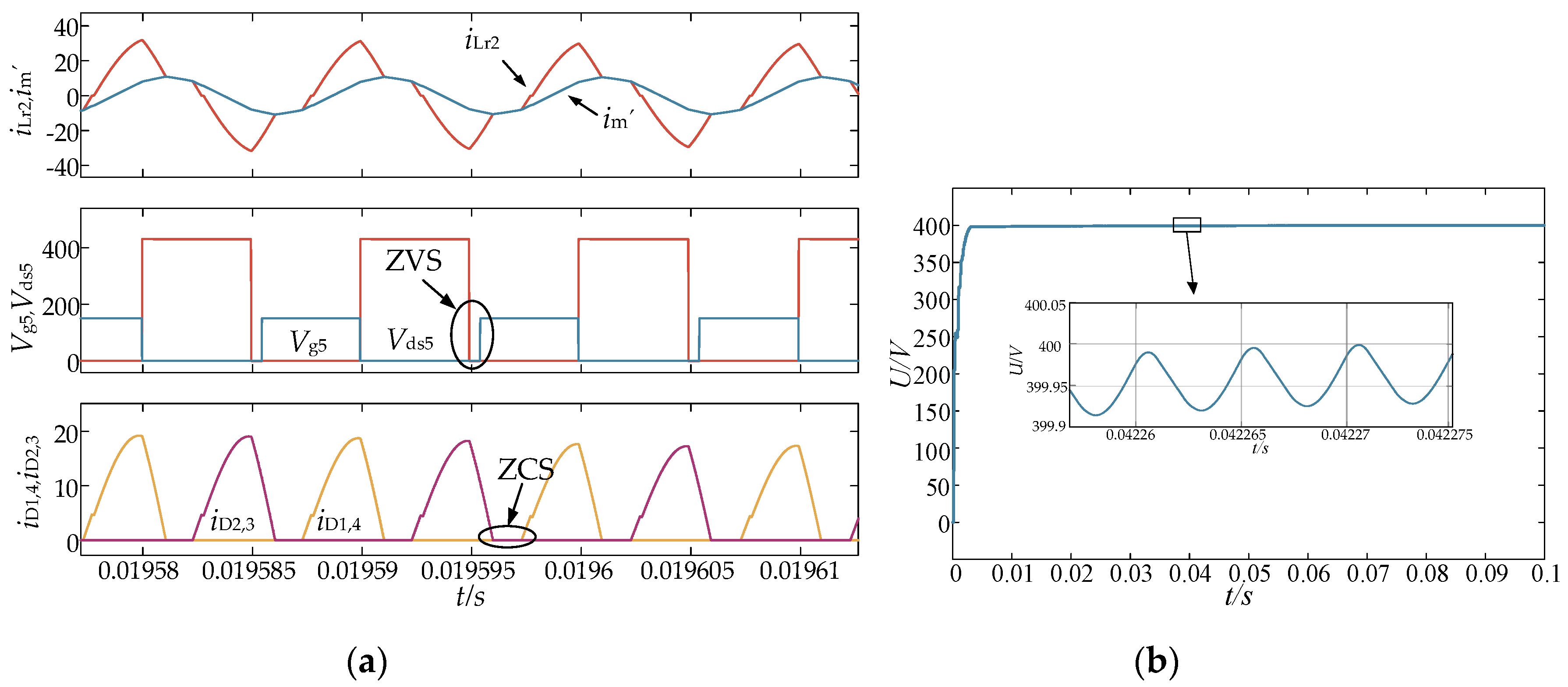
5. Simulation Analysis
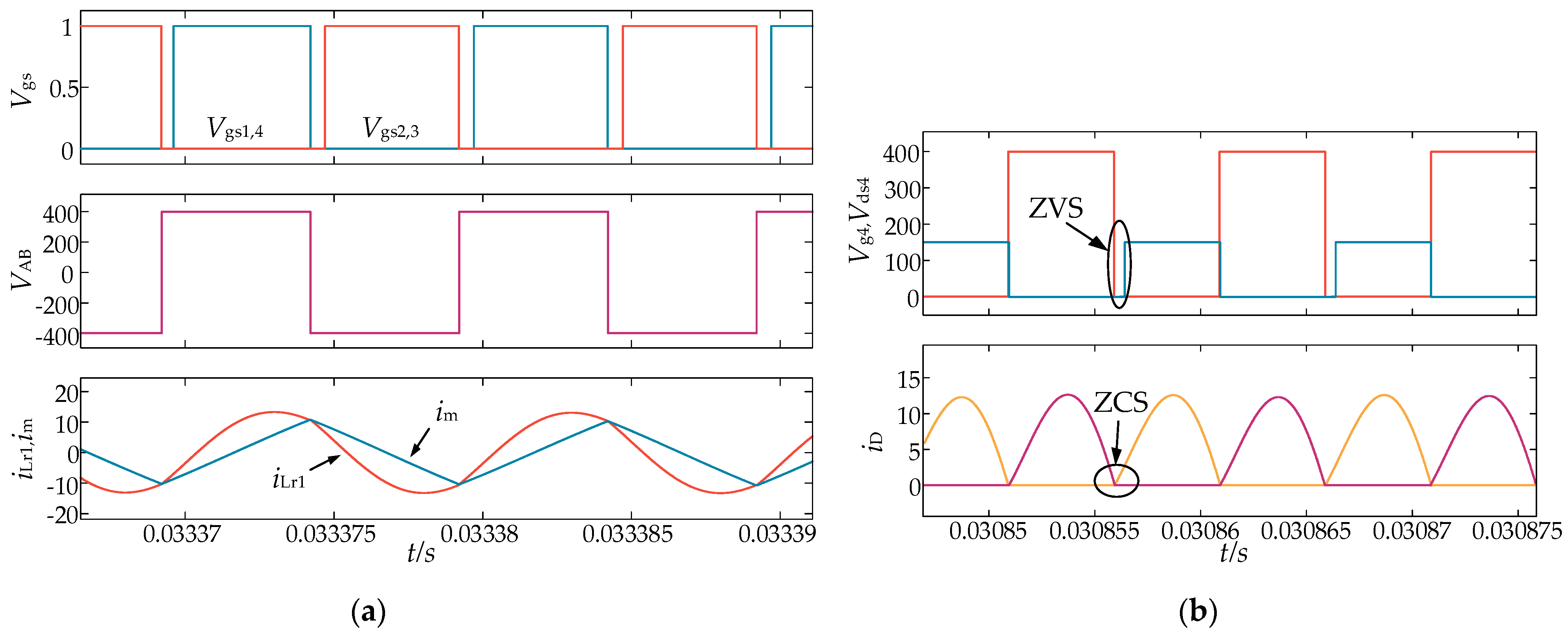
5.1. Forward Simulation
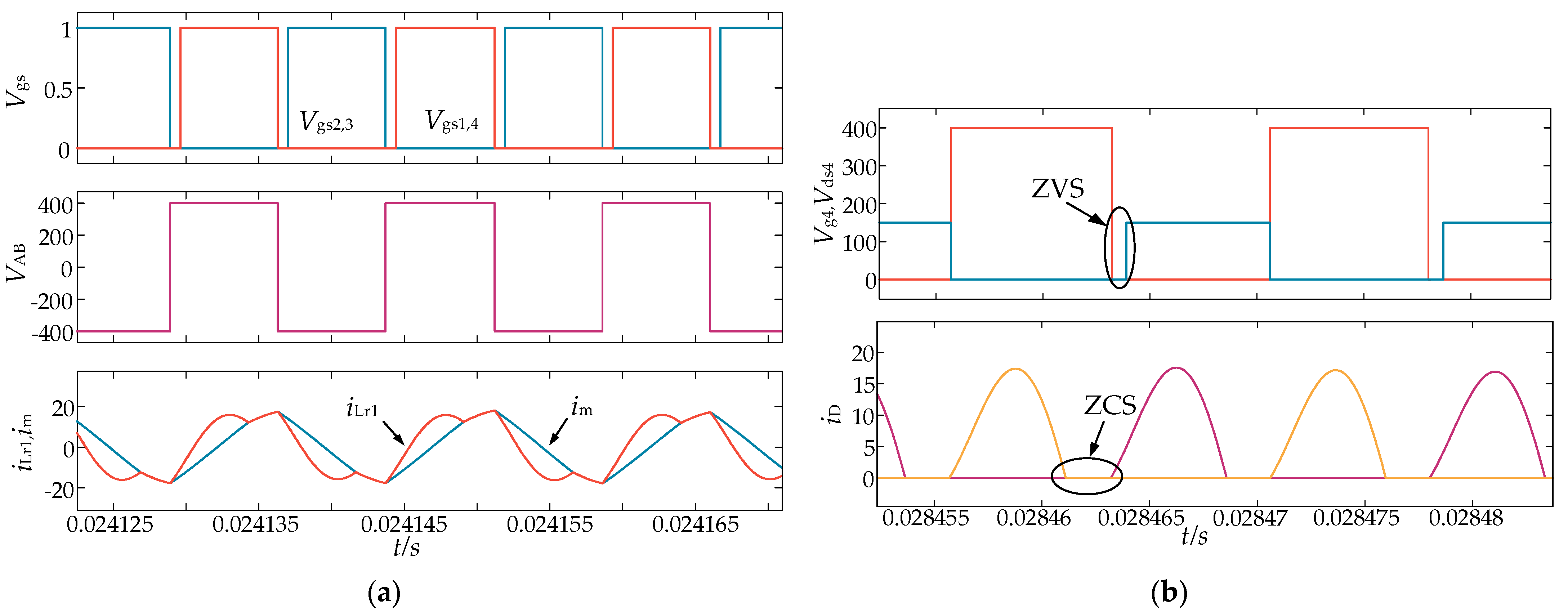
5.2. Reverse Simulation
6. Conclusions
- (1)
- Due to its complete symmetrical and good soft-switching characteristics, the bidirectional CLLLC resonant converter solves the problem where the traditional LLC resonant converter has different resonant states during the forward and reverse operations, and cannot achieve soft switching at the same time and is difficult to control.
- (2)
- The hybrid control method of frequency conversion and phase shift adopts frequency-conversion control at a higher voltage gain and phase-shift control at a lower voltage gain. It solves the problem of low voltage gain of the single frequency-conversion control method in the step-down mode, effectively broadens the output voltage range of the bidirectional CLLLC converter, and is suitable for wide-range output occasions. At the same time, it achieves zero-voltage switching and zero-current switching in the full load range, and has a high operating efficiency. This control method is convenient and easy to implement.
- (3)
- The control method proposed in this paper is superior to the traditional control method in reducing the switching frequency-conversion range and improving the efficiency of the converter, which is helpful in the popularization and application of the high-efficiency and high-power bidirectional DC/DC converter in the distributed new energy generation.
- (4)
- In the actual debugging process, it is difficult to establish an accurate model of a bidirectional CLLLC circuit. In the later stage, it is necessary to further analyze the circuit model to design more appropriate closed-loop control parameters and test how well it actually works.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, D.Y.; Zhao, Q.L.; Li, J. Wide Output Range Multi-Level LLC Resonant Converter with Fixed-Frequency. Chin. J. Electr. Eng. 2022, 43, 1973–1984. [Google Scholar] [CrossRef]
- Yu, W.H.; Guo, Y.; Shang, Z.; Zhang, Y.C.; Xu, S.M. A Review on Comprehensive Recycling of Spent Power Lithium-ion Battery in China. eTransportation 2022, 11, 100155. [Google Scholar] [CrossRef]
- Li, H.M.; Zhang, H.G.; Cui, C. Review of PWM Soft-Switching DC-DC Converter for on-Board Chargers. Chin. J. Electr. Eng. 2017, 32, 59–70. [Google Scholar]
- Ding, C.; Li, Y.; Jiang, L.; Wan, J.H.; Liu, F. Analysis of Soft Switching Voltage Boundary of LLC Resonant Converter for EV DC Charging System. Trans. China Electrotech. Soc. 2022, 37, 3–11. [Google Scholar]
- Wang, Y.J.; Wang, L.; Mince, L.; Chen, Z.H. A review of Key Issues for Control and Management in Battery and Ultra-capacitor Hybrid Energy Storage Systems. eTransportation 2022, 4, 100064. [Google Scholar] [CrossRef]
- Esteban, F.D.; Serra, F.M.; De Angelo, C.H. Control of a DC-DC Dual Active Bridge Converter in DC Microgrids Applications. IEEE Lat. Am. Trans. 2021, 19, 1261–1269. [Google Scholar] [CrossRef]
- Xiong, F.; Wu, L.; Liu, Z.; Hao, L. Current Sensorless Control for Dual Active Bridge DC/DC Converter with Estimated Load-Current Feedforward. IEEE Trans. Power Electron. 2018, 33, 3552–3566. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.F. An Optimized Phase-Shift Modulation for Fast Transient Response in a Dual-Active-Bridge Converter. IEEE Trans. Power Electron. 2014, 29, 2661–2665. [Google Scholar]
- Bal, S.; Yelaverthi, D.B.; Rathore, A.K.; Srinivasan, D. Improved Modulation Strategy Using Dual Phase Shift Modulation for Active Commutated Current-Fed Dual Active Bridge. IEEE Trans. Power Electron. 2018, 33, 7359–7375. [Google Scholar] [CrossRef]
- Guan, Q.X.; Zhang, Y.; Zhao, P.H.; Kang, Y. Zero-voltage Soft-switching Conditions and Loss Balance Method of Three Level ANPC-DAB. Proc. CSEE 2021, 41, 4603–4616. [Google Scholar]
- Hu, Y.; Zhang, T.H.; Yang, L.X.; Guan, X.Q. Comparative Study of Reactive Power Optimization and Current Stress Optimization of DAB Converter with Dual Phase Shift Control. Proc. CSEE 2020, 40, 243–253. [Google Scholar]
- Peiwen, H.E.; Mallik, A.; Sankar, A. Design of a 1-MHz High-efficiency High-power-density Bidirectional GaN-based CLLC Converter for Electric Vehicles. IEEE Trans. Veh. Technol. 2019, 68, 213–223. [Google Scholar]
- Kim, K.; Youn, H.; Baek, J.; Jeong, Y.; Moon, G. Analysis on Synchronous Rectifier Control to Improve Regulation Capability of High-frequency LLC Resonant Converter. IEEE Trans. Power Electron. 2018, 33, 7252–7259. [Google Scholar]
- Yuan, Y.S.; Lai, L. A Compound Resonant Full-bridge Converter Suitable for Wide Range Output. Proc. CSEE 2020, 40, 6694–6704. [Google Scholar]
- Zhu, H.Y.; Zhuo, F.; Zhao, F.Z.; Wang, F. Analysis and Design of Multiple Phase-shift Control for CLLC Resonant Converter Under Light-load Conditions Based on Multi-harmonic Impedance Model. Proc. CSEE 2021, 41, 326–339. [Google Scholar]
- Zhao, L.; Pei, Y.Q.; Liu, X.H.; Fang, W.J. Design Methodology of CLLC Resonant Converters for Electric Vehicle Battery Chargers. Proc. CSEE 2020, 40, 4965–4977. [Google Scholar]
- Mumtahina, U.; Wolfs, P.J. Multimode Optimization of the Phase-shifted LLC Series Resonant Converter. IEEE Trans. Power Electron. 2018, 33, 10478–10489. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, J.; Wu, X.; Sheng, K.; Wang, Y. A Bidirectional LLC Resonant Converter with Automatic Forward and Backward Mode Transition. IEEE Trans. Power Electron. 2015, 30, 757–770. [Google Scholar] [CrossRef]
- Yuan, Y.S.; Lai, L. A Multi-mode Current-fed LCL Resonant Converter. Proc. CSEE 2020, 40, 3259–3270. [Google Scholar]
- Zuo, Y.; Pan, X.; Wang, C. A Reconfigurable Bidirectional Isolated LLC Resonant Converter for Ultra-Wide Voltage-Gain Range Applications. IEEE Trans. Ind. Electron. 2022, 69, 5713–5723. [Google Scholar] [CrossRef]
- Sun, X.N.; Chen, M.; Li, B.D.; Zhang, D.B.; Wang, X.Q. Efficiency Optimization of CLLC Resonant Converter Based on Analysis of the Ratio of Inductances. Proc. CSEE 2021, 41, 2825–2834. [Google Scholar]
- Wei, Y.; Luo, Q.; Mantooth, H.A. An LLC and LCL-T Resonant Tanks Based Topology for Battery Charger Application. CPSS Trans. Power Electron. Appl. 2021, 6, 263–275. [Google Scholar] [CrossRef]
- Liu, B.L.; Zhang, X.D.; Li, Y.; Wu, W. Variable Frequency-phase Shift Control Method for LLC Resonant Converter Applied to Electric Vehicle Charging. J. Power Supply 2020, 18, 43–52. [Google Scholar]
- Pan, J.; Shi, D.; Liu, S.L. Wide Output Dual Full Bridge LLC Resonant Converter with Hybrid Control Strategy. J. Power Supply 2023, 1–16. Available online: http://kns.cnki.net/kcms/detail/12.1420.TM.20220307.1010.004.html (accessed on 28 February 2023).
- Tao, W.D.; Wang, Y.B.; Zhang, F.Y. Pulse Frequency Modulation and Phase Shift Combined Control Method for Bidirectional LLC Resonant Converter. Trans. China Electrotech. Soc. 2018, 33, 5856–5863. [Google Scholar]
- Liu, T.; Yang, X.-G.; Ge, S.; Leng, Y.; Wang, C.-Y. Ultrafast Charging of Energy-dense Lithium-ion Batteries for Urban Air Mobility. eTransportation 2021, 7, 100103. [Google Scholar] [CrossRef]



| Main Indicator | Parameter |
|---|---|
| input voltage range | 390–410 V |
| rated input voltage | 400 V |
| output voltage range | 250–430 V |
| rated output voltage | 320 V |
| maximal output power | 3.3 kW |
| resonant frequency | 100 kHz |
| Main Indicator | Parameter |
|---|---|
| primary-side resonant inductor (Lr1) | 18.76 |
| primary-side resonant capacitor (Cr1) | 135.02 |
| secondary-side resonant inductance (Lr2) | 12.01 |
| secondary-side resonant capacitor (Cr2) | 210.97 |
| magnetizing inductance (Lm) | 93.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, N.-Z.; Feng, Y.; Chen, Z.-Y.; Wu, X.-G. Bidirectional CLLLC Resonant Converter Based on Frequency-Conversion and Phase-Shift Hybrid Control. Electronics 2023, 12, 1605. https://doi.org/10.3390/electronics12071605
Jin N-Z, Feng Y, Chen Z-Y, Wu X-G. Bidirectional CLLLC Resonant Converter Based on Frequency-Conversion and Phase-Shift Hybrid Control. Electronics. 2023; 12(7):1605. https://doi.org/10.3390/electronics12071605
Chicago/Turabian StyleJin, Ning-Zhi, Yu Feng, Ze-Yu Chen, and Xiao-Gang Wu. 2023. "Bidirectional CLLLC Resonant Converter Based on Frequency-Conversion and Phase-Shift Hybrid Control" Electronics 12, no. 7: 1605. https://doi.org/10.3390/electronics12071605
APA StyleJin, N.-Z., Feng, Y., Chen, Z.-Y., & Wu, X.-G. (2023). Bidirectional CLLLC Resonant Converter Based on Frequency-Conversion and Phase-Shift Hybrid Control. Electronics, 12(7), 1605. https://doi.org/10.3390/electronics12071605







