Chiplet Multi-Objective Optimization Algorithm Based on Communication Consumption and Temperature
Abstract
1. Introduction
2. Related Works
3. Chiplet Multi-Objective Optimization Method
3.1. Thermal Module Establishment
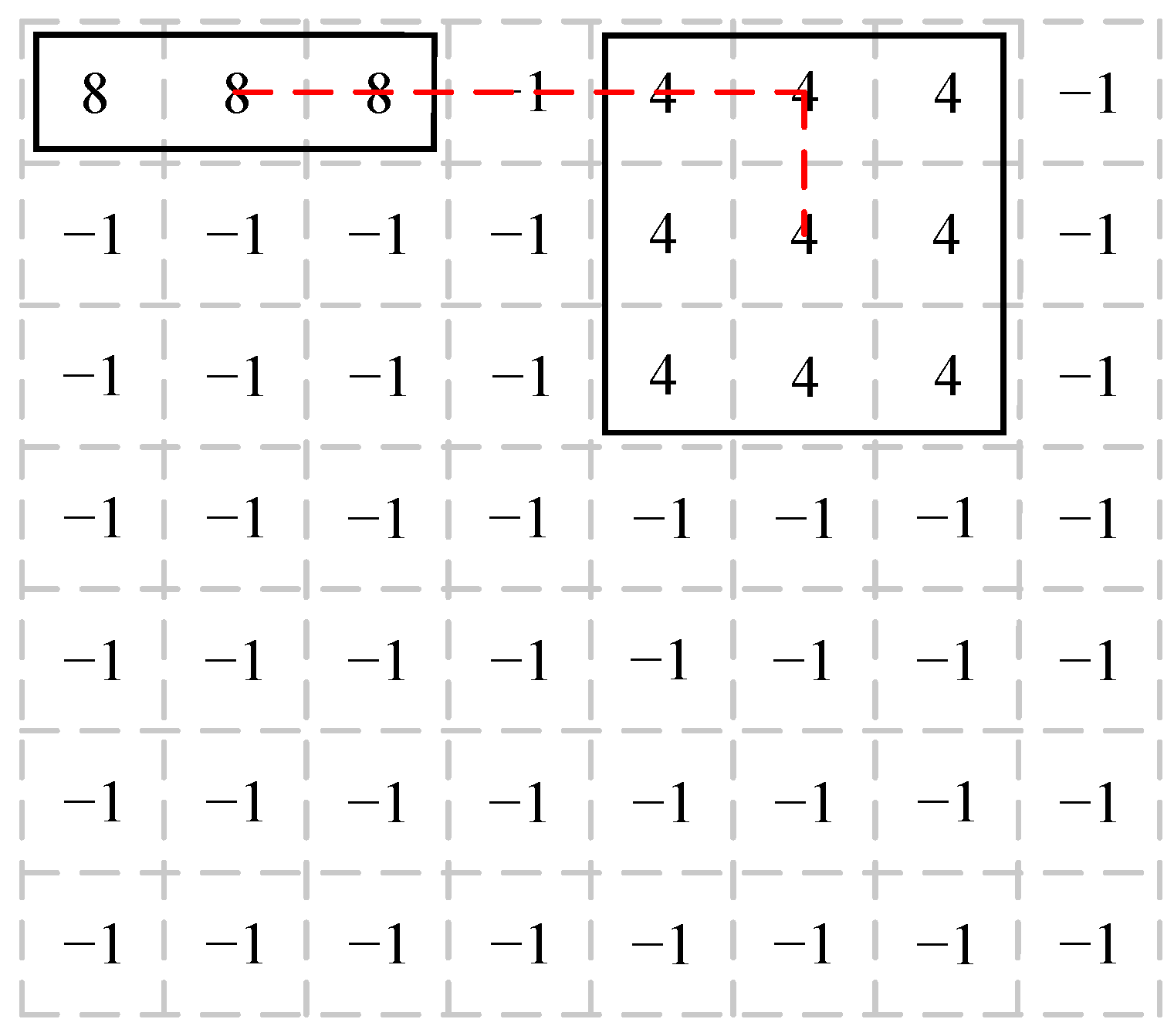
3.2. Chiplet Multi-Objective Optimization Algorithm Description
3.2.1. Topology Generation
3.2.2. The Number and Location of the Initial Nodes
| Algorithm 1 Initial node generation |
| Input: topology length N1, width N2. chiplet length L0, width W0. |
| Output: number of schemes, M. Initial node matrix, initial_node []. |
| 1.int x = ceil ((N1 − L0 + 1)/2); |
| 2.int y = ceil ((N2 − W0 + 1)/2); |
| 3.int M = x × y; |
| 4.int k = 0; |
| 5.for (int i = 0; i < x; i++) |
| 6.{ |
| 7. for (int j = 0; j < y; j++) |
| 8. { |
| 9. initial_node[k] = i + j × N1; |
| 10. k++; |
| 11. } |
| 12.} |
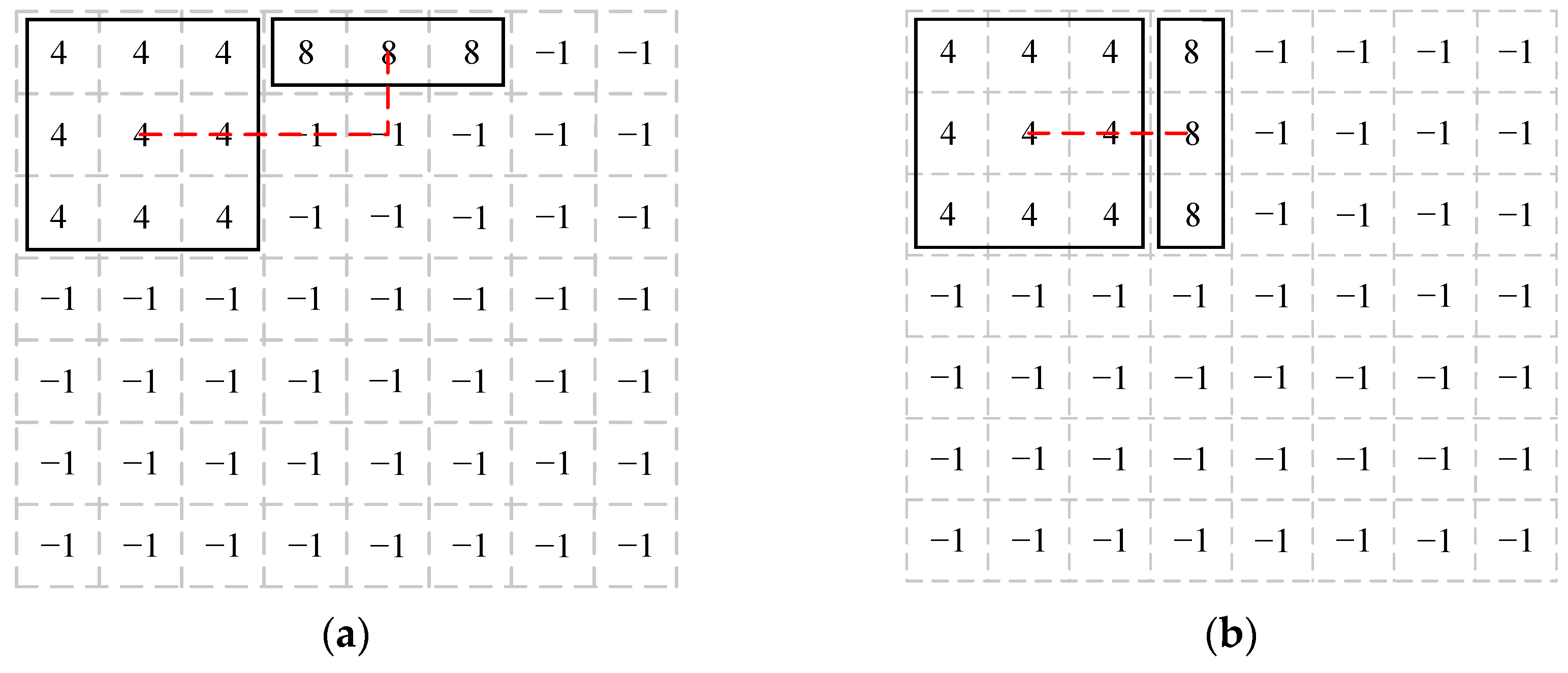
3.2.3. Selecting Mapping Area
| Algorithm 2 Next chiplet selection |
| Input: topology length N1, width N2 chiplet length L, width W. mapping flag matrix, mflag []. counting matrix, count []. |
| Output: selection flag matrix, sflag []. |
| 1.for (int k = 0; k < L × W; k++) |
| 2. { |
| 3. for (int w = 0; w < W; w++) |
| 4. { |
| 5. for (int l = 0; l < L; l++) |
| 6. { |
| 7. if (mflag [k + l + w × N1]) == −1 && |
| 8. L1 <= (N1 − k % N1) && W <= N2 − floor (k/N1)) |
| 9. count[k]++; |
| 10. } |
| 11. } |
| 12. } |
| 13.for (int k = 0; k < L × W; k++) |
| 14. { |
| 15. if (count[k] == L1 × W1) |
| 16. { |
| 17. sflag[k1] = 1; |
| 18. } |
| 19. } |
3.2.4. Computing Heuristic Information and Mapping Chiplets
| Algorithm 3 Heuristic information caculation |
| Input: chiplet number NR; mapping flag matrix mapflag[]; distance matrix D[][]; mapping matrix map[]; the number of node being mapped k; weighing factor α;maximum and minimum heuristic factors, , , , ; output: optimal node node; |
| 1.for(int i = 0; i < NR; i++) |
| 2.{ |
| 3. for(int j = i + 1; j < NR; j++) |
| 4. { |
| 5. if(mapflag[i]== −2&&mapflag[j]== −2) |
| 6. comcost+=D[i][j] × cost[i][j] × 0.186; |
| 7. } |
| 8.} |
| 9. for( int i = 0; i < NR; i++) |
| 10.{ |
| 11. if( i ! = k&&map[i]== −2) |
| 12. { |
| 13. temcost+=power[mapp[i]]/D[map[i]]D[map[k]]; |
| 14. } |
| 15.} |
| 16. cost = α* (comcost − )/( − ) + (1 − α) × (temcost − )/ |
| 17. ( − ); |
| 18.if(cost < cost_min) |
| 19.{ |
| 20. cost_min = cost; |
| 21. node = i; |
| 22.} |
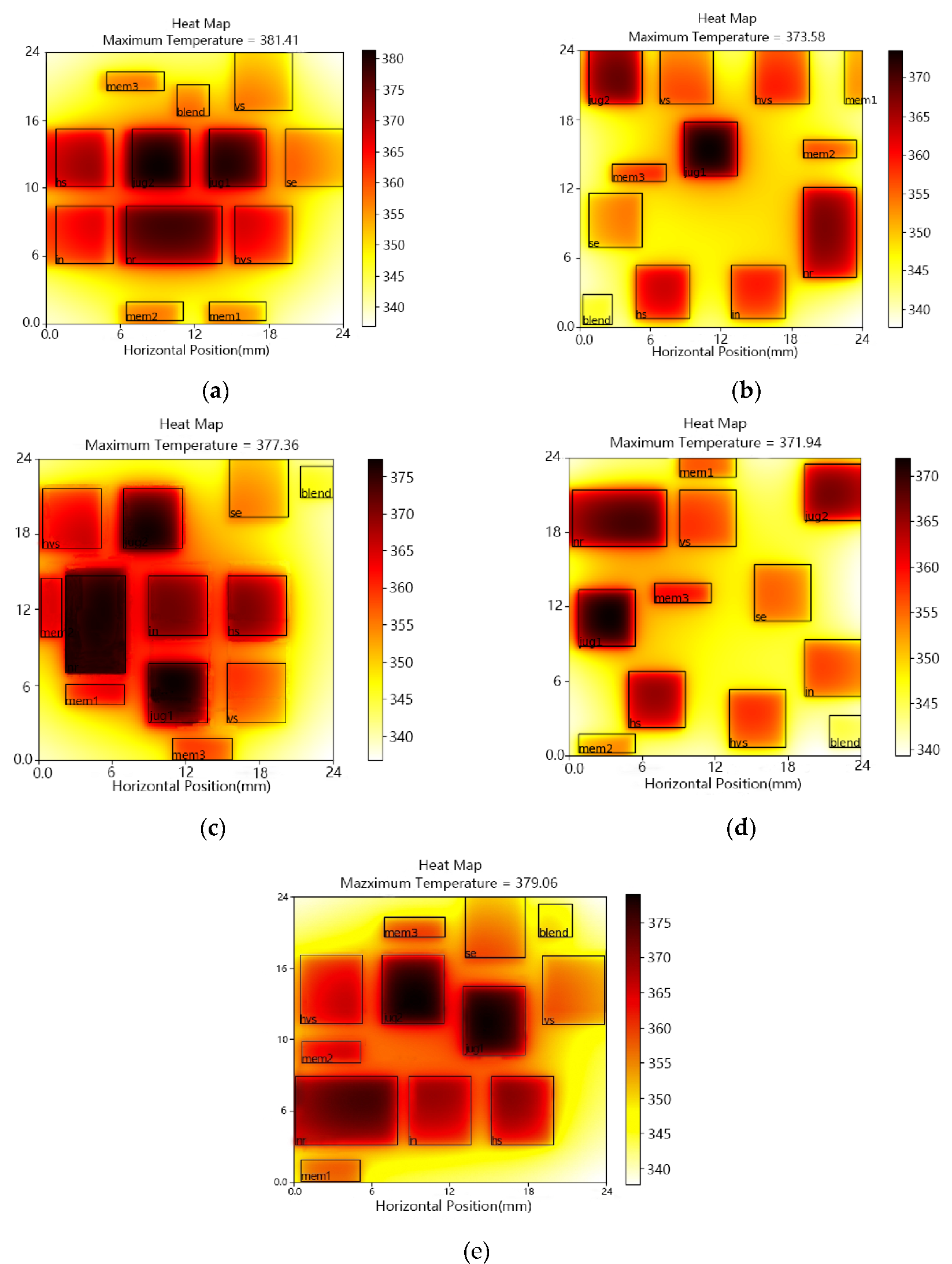
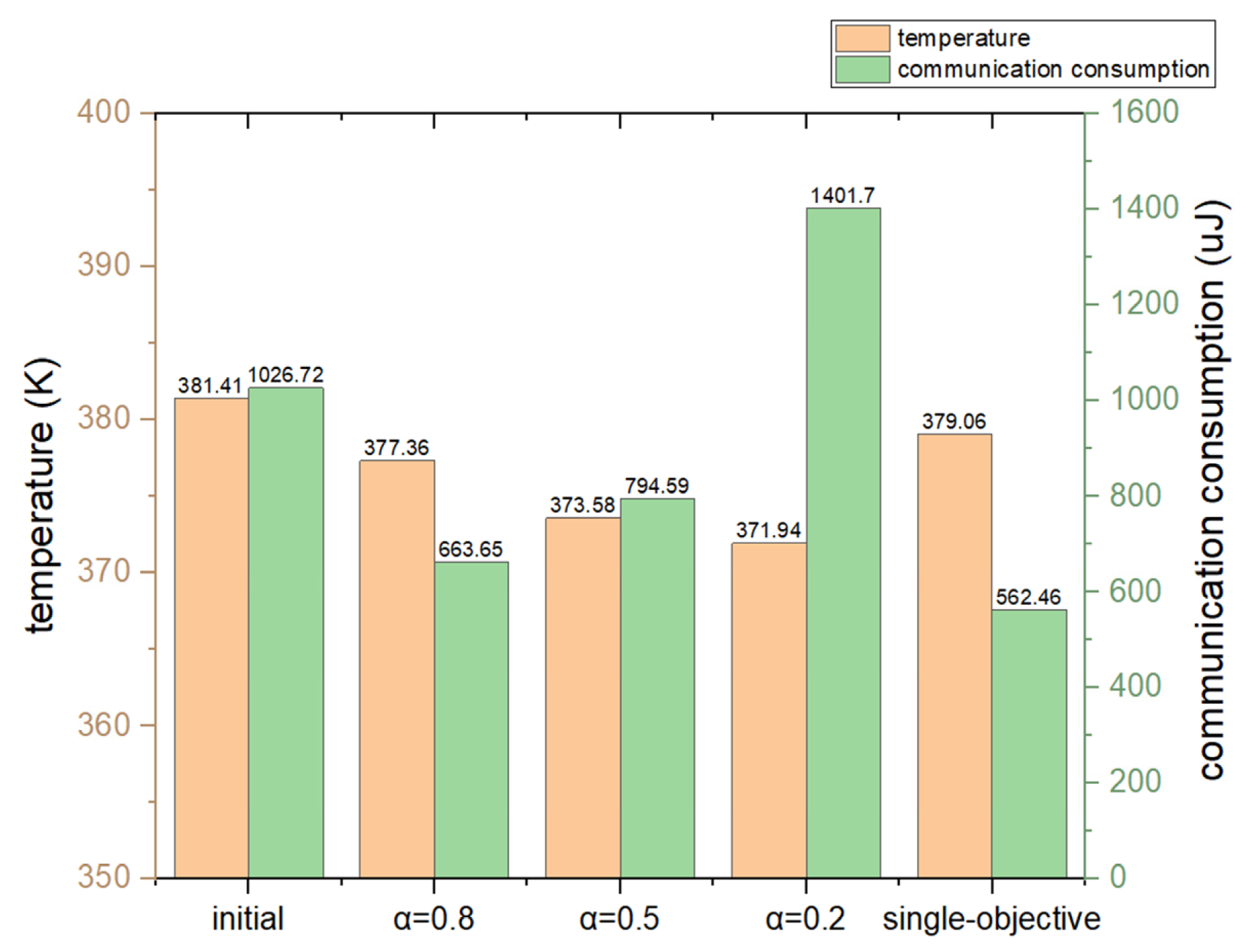
4. Evaluation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moore, G.E. Cramming more components onto integrated circuits. Proc. IEEE 1998, 86, 82–85. [Google Scholar] [CrossRef]
- Kabir, M.D.A.; Peng, Y. Holistic Chiplet—Package Co-Optimization for Agile Custom 2.5-D Design. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 11, 715–726. [Google Scholar] [CrossRef]
- Lim, S.P.S.; Chidambaram, V.; Jaafar, N.; Seit, W. Development of 2.5 D high density device on large ultra-thin active interpose. In Proceedings of the 2019 IEEE 21st Electronics Packaging Technology Conference (EPTC), Singapore, 4–6 December 2019; pp. 247–252. [Google Scholar]
- Chaware, R.; Nagarajan, K.; Ramalingam, S. Assembly and reliability challenges in 3D integration of 28nm FPGA die on a large high density 65nm passive interposer. In Proceedings of the 2012 IEEE 62nd Electronic Components and Technology Conference, San Diego, CA, USA, 29 May–1 June 2012; pp. 279–283. [Google Scholar]
- Coskun, A.; Eris, F.; Joshi, A.; Kahng, A.B.; Ma, Y.; Narayan, A.; Srinivas, V. Cross-layer co-optimization of network design and chiplet placement in 2.5-D systems. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 39, 5183–5196. [Google Scholar] [CrossRef]
- Vivet, P.; Guthmuller, E.; Thonnart, Y.; Pillonnet, G.; Fuguet, C.; Miro-Panades, I.; Moritz, G.; Durupt, J.; Bernard, C.; Varreau, D.; et al. IntAct: A 96-core processor with six chiplets 3D-stacked on an active interposer with distributed interconnects and integrated power management. IEEE J. Solid-State Circuits 2020, 56, 79–97. [Google Scholar] [CrossRef]
- Kim, J.; Chekuri, V.C.K.; Rahman, N.M.; Dolatsara, M.A.; Torun, H.; Swaminathan, M.; Mukhopadhyay, S.; Lim, S.K. Silicon vs. Organic Interposer: PPA and Reliability Tradeoffs in Heterogeneous 2.5 D Chiplet Integration. In Proceedings of the 2020 IEEE 38th International Conference on Computer Design (ICCD), Hartford, CT, USA, 18–21 October 2020; pp. 80–87. [Google Scholar]
- Li, T.; Hou, J.; Yan, J.; Liu, R.; Yang, H.; Sun, Z. Chiplet heterogeneous integration technology—Status and challenges. Electronics 2020, 9, 670. [Google Scholar] [CrossRef]
- Gupta, P.; Iyer, S.S. Goodbye, motherboard. Bare chiplets bonded to silicon will make computers smaller and more powerful: Hello, silicon-interconnect fabric. IEEE Spectr. 2019, 56, 28–33. [Google Scholar] [CrossRef]
- Coudrain, P.; Charbonnier, J.; Garnier, A.; Vivet, P.; Vélard, R.; Vinci, A.; Ponthenier, F.; Farcy, A.; Segaud, R.; Chausse, P.; et al. Active interposer technology for chiplet-based advanced 3D system architectures. In Proceedings of the 2019 IEEE 69th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 28–31 May 2019; pp. 569–578. [Google Scholar]
- Datta, S.; Dutta, S.; Grisafe, B.; Smith, J.; Srinivasa, S.; Ye, H. Back-end-of-line compatible transistors for monolithic 3-D integration. IEEE Micro 2019, 39, 8–15. [Google Scholar] [CrossRef]
- Chen, T.C.; Chang, Y.W. Modern floorplanning based on B/sup*/-tree and fast simulated annealing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2006, 25, 637–650. [Google Scholar] [CrossRef]
- Coskun, A.K.; Atienza, D.; Rosing, T.S.; Brunschwiler, T.; Michel, B. Energy-efficient variable-flow liquid cooling in 3D stacked architectures. In Proceedings of the 2010 Design, Automation & Test in Europe Conference & Exhibition (DATE 2010), Dresden, Germany, 8–12 March 2010; pp. 111–116. [Google Scholar]
- Eris, F.; Joshi, A.; Kahng, A.B.; Ma, Y.; Mojumder, S.; Zhang, T. Leveraging thermally-aware chiplet organization in 2.5 D systems to reclaim dark silicon. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 19–23 March 2018; pp. 1441–1446. [Google Scholar]
- Ebrahimi, M.; Weldezion, A.Y.; Daneshtalab, M. NoD: Network-on-Die as a standalone NoC for heterogeneous many-core systems in 2.5 D ICs. In Proceedings of the 2017 19th International Symposium on Computer Architecture and Digital Systems (CADS), Kish Island, Iran, 21–22 December 2017; pp. 1–6. [Google Scholar]
- Kim, J.; Murali, G.; Park, H.; Qin, E.; Kwon, H.; Chaitanya, V.; Chekuri, K.; Dasari, N.; Singh, A.; Lee, M.; et al. Architecture, chip, and package co-design flow for 2.5 D IC design enabling heterogeneous IP reuse. In Proceedings of the 56th Annual Design Automation Conference 2019, Las Vegas, NV, USA, 2–6 June 2019; pp. 1–6. [Google Scholar]
- Kabir, M.A.; Peng, Y. Chiplet-package co-design for 2.5 D systems using standard ASIC CAD tools. In Proceedings of the 2020 25th Asia and South Pacific Design Automation Conference (ASP-DAC), Beijing, China, 13–16 January 2020; pp. 351–356. [Google Scholar]
- Yin, J.; Lin, Z.; Kayiran, O.; Poremba, M.; Altaf, M.S.B.; Jerger, N.E.; Loh, G.H. Modular routing design for chiplet-based systems. In Proceedings of the 2018 ACM/IEEE 45th Annual International Symposium on Computer Architecture (ISCA), Los Angeles, CA, USA, 2–6 June 2018; pp. 726–738. [Google Scholar]
- Park, H.; Kim, J.; Chekuri, V.C.K.; Dolatsara, M.A.; Nabeel, M.; Bojesomo, A.; Patnaik, S.; Sinanoglu, O.; Swaminathan, M.; Mukhopadhyay, S.; et al. Design flow for active interposer-based 2.5-D ICs and study of RISC-V architecture with secure NoC. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 2047–2060. [Google Scholar] [CrossRef]
- Liu, Y.; Ruan, Y.; Lai, Z.; Jing, W. Energy and thermal aware mapping for mesh-based NoC architectures using multi-objective ant colony algorithm. In Proceedings of the 2011 3rd International Conference on Computer Research and Development, Shanghai, China, 11–13 March 2011; pp. 407–411. [Google Scholar]
- Ma, Y.; Delshadtehrani, L.; Demirkiran, C.; Abellan, J.L.; Joshi, A. TAP-2.5 D: A thermally-aware chiplet placement methodology for 2.5 D systems. In Proceedings of the 2021 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 1–5 February 2021; pp. 1246–1251. [Google Scholar]
- Healy, M.; Vittes, M.; Ekpanyapong, M.; Ballapuram, C.S.; Lim, S.K.; Lee, H.H.S.; Loh, G.H. Multiobjective microarchitectural floorplanning for 2-D and 3-D ICs. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2006, 26, 38–52. [Google Scholar] [CrossRef]
- Liu, Y.; Ruan, Y.; Lai, Z. New heuristic algorithms for low-energy mapping and routing in 3D NoC. Int. J. Comput. Appl. Technol. 2013, 47, 1–13. [Google Scholar] [CrossRef]
- Skadron, K.; Stan, M.; Barcella, M.; Dwarka, A.; Huang, W.; Li, Y.; Ma, Y.; Naidu, A.; Parikh, D.; Re, P.; et al. HotSpot: Techniques for modeling thermal effects at the processor-architecture level. In Proceedings of the 8th THERMINIC Workshop, Madrid, Spain, 1–4 October 2002. [Google Scholar]
- Huang, W.; Stan, M.R.; Skadron, K.; Sankaranarayanan, K.; Ghosh, S.; Velusam, S. Compact thermal modeling for temperature-aware design. In Proceedings of the 41st Annual Design Automation Conference, San Diego, CA, USA, 7–11 June 2004; pp. 878–883. [Google Scholar]
- Stan, M.R.; Skadron, K.; Barcella, M.; Huang, W.; Sankaranarayanan, K.; Velusamy, S. Hotspot: A dynamic compact thermal model at the processor-architecture level. Microelectron. J. 2003, 34, 1153–1165. [Google Scholar] [CrossRef]
- Skadron, K.; Stan, M.R.; Sankaranarayanan, K.; Huang, W.; Velusamy, S.; Tarjan, D. Temperature-aware microarchitecture: Modeling and implementation. ACM Trans. Archit. Code Optim. 2004, 1, 94–125. [Google Scholar]
- Jaspers, E.G.; De With, P.H.N. Chip-set for video display of multimedia information. IEEE Trans. Consum. Electron. 1999, 45, 706–715. [Google Scholar] [CrossRef]
- Huang, W.; Ghosh, S.; Velusamy, S.; Sankaranarayanan, K.; Skadron, K.; Stan, M.R. HotSpot: A compact thermal modeling methodology for early-stage VLSI design. IEEE Trans. Very Large Scale Integr. Syst. 2006, 14, 501–513. [Google Scholar] [CrossRef]
- Kahng, A.B.; Li, B.; Peh, L.S.; Samadi, K. ORION 2.0: A fast and accurate NoC power and area model for early-stage design space exploration. In Proceedings of the 2009 Design, Automation & Test in Europe Conference & Exhibition, Nice, France, 20–24 April 2009; pp. 423–428. [Google Scholar]
- Sun, H.; Peng, X.; Cang, D.; Zhao, J.; Liu, Y. New Heuristic Algorithm for Low Energy Mapping for 2.5-D Integration. Electronics 2022, 11, 1817. [Google Scholar] [CrossRef]

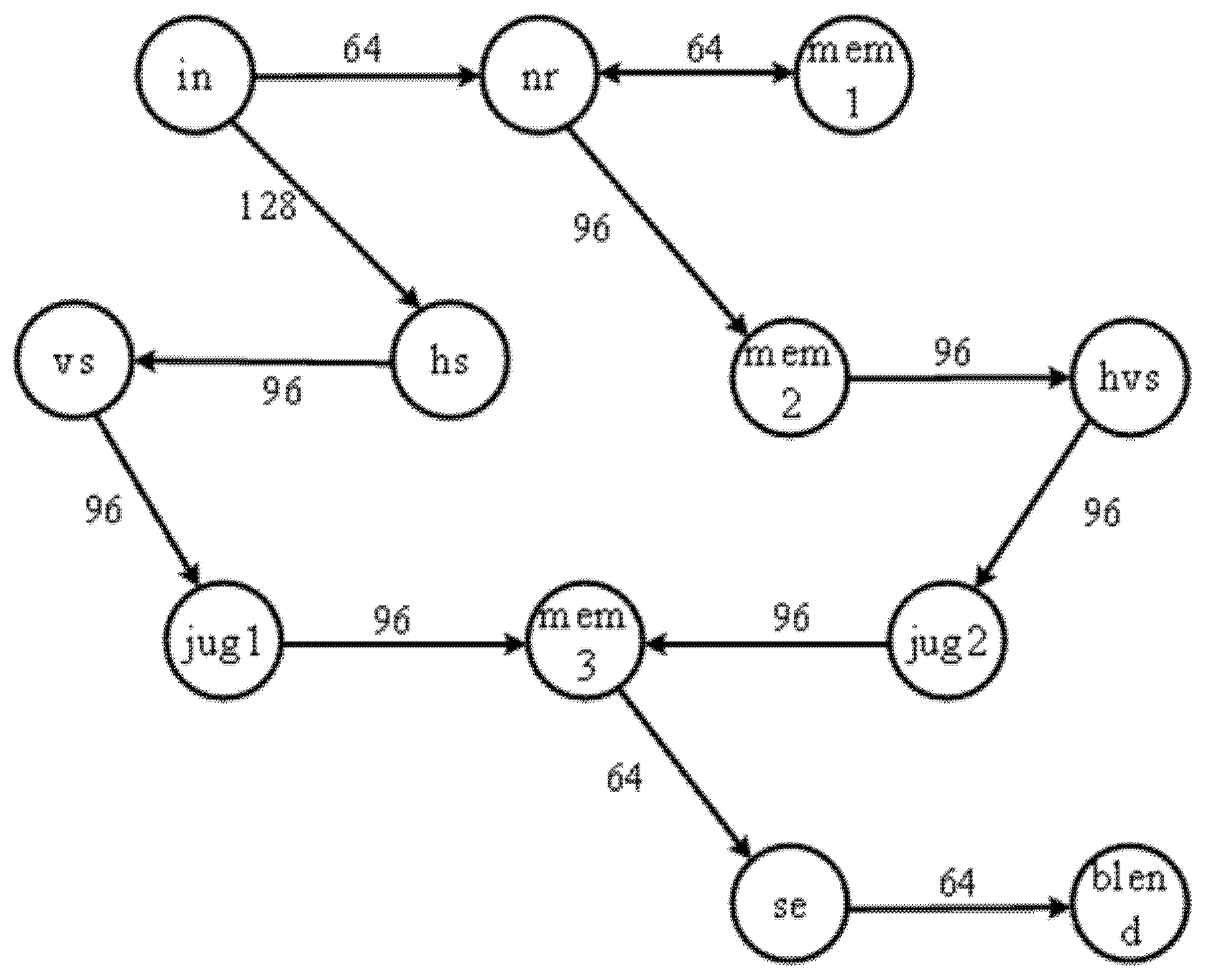
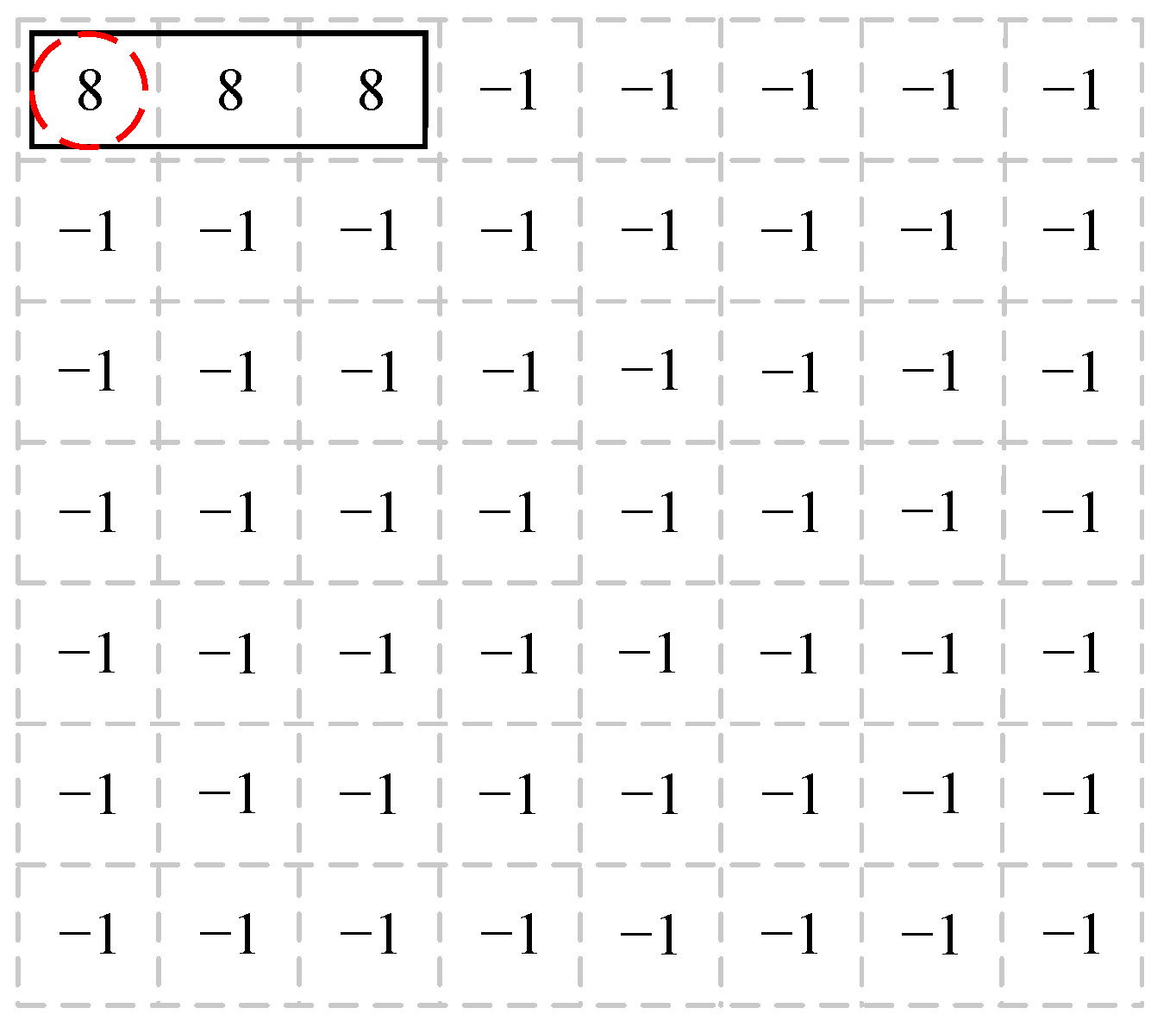

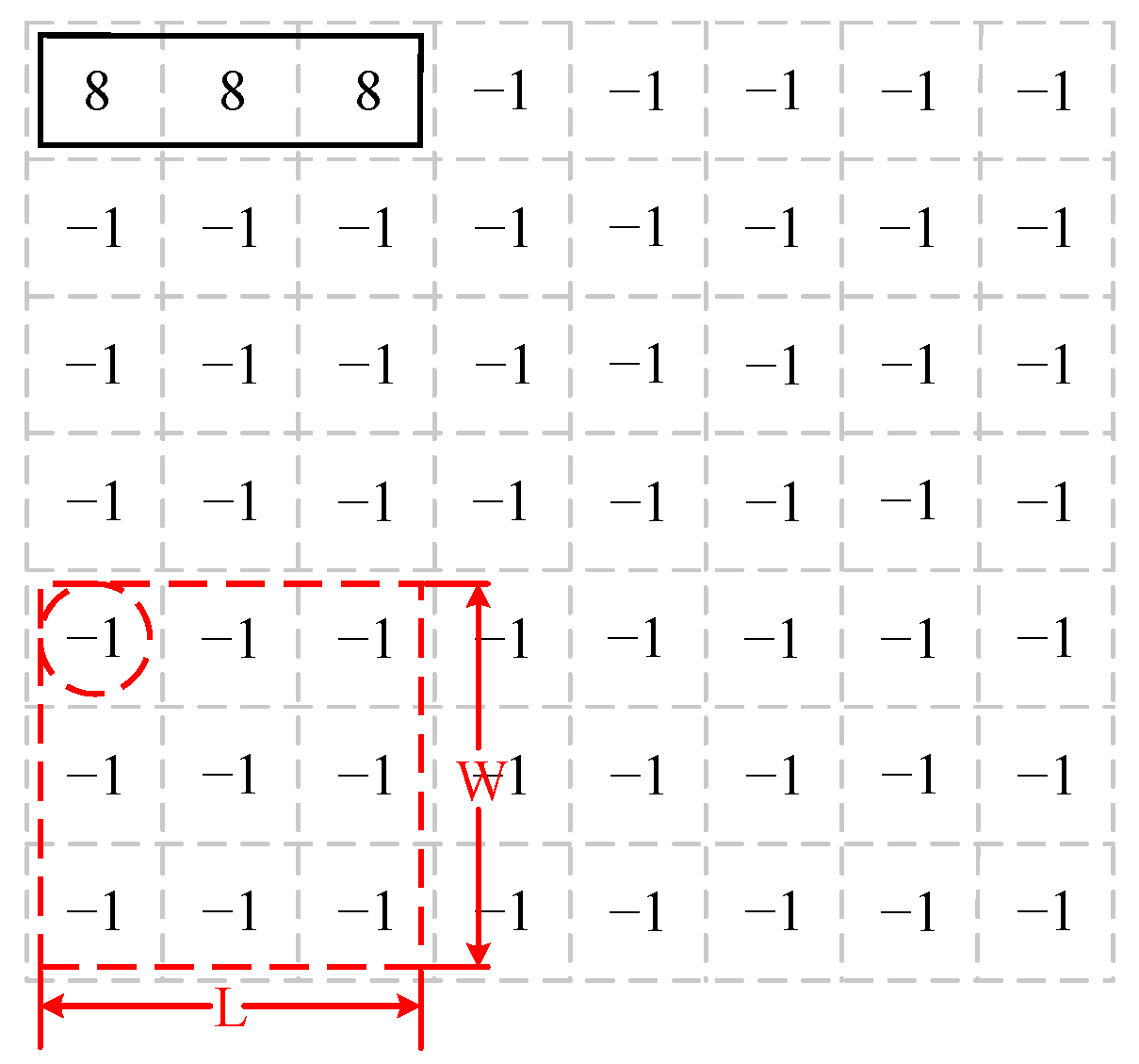
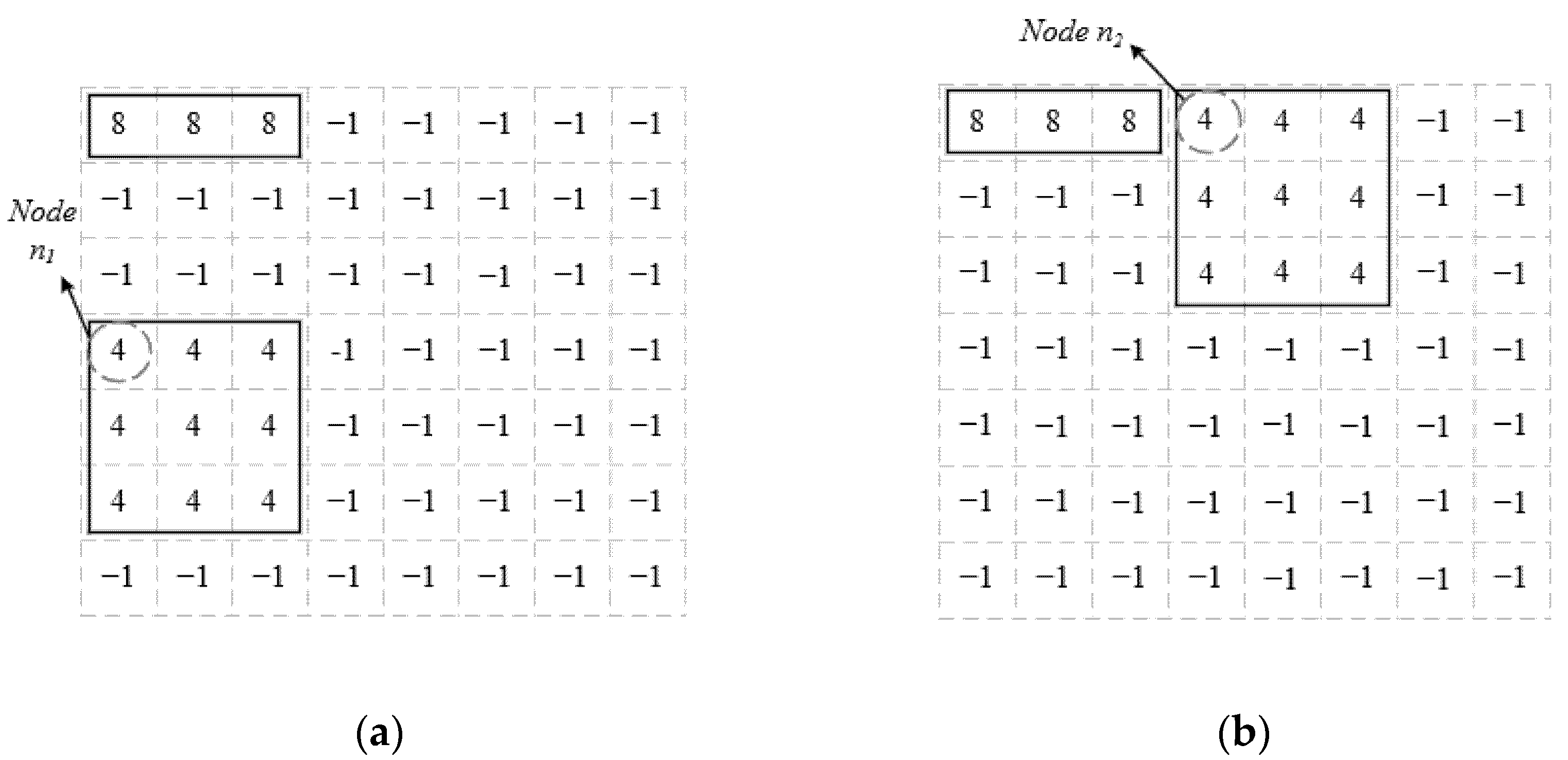

| Priority | Chiplet Number | Chiplet Name | Communication Data (Mbit/s) |
|---|---|---|---|
| 1 | 8 | mem3 | 256 |
| 2 | 4 | hs | 224 |
| 1 | nr | 224 | |
| 3 | 0 | in | 192 |
| 3 | vs | 192 | |
| 5 | mem2 | 192 | |
| 6 | hvs | 192 | |
| 7 | jug1 | 192 | |
| 9 | jug2 | 192 | |
| 4 | 10 | se | 128 |
| 2 | mem1 | 64 | |
| 5 | 11 | blend | 64 |
| Chiplet Name | Chiplet Theoretical Size (mm2) | Chiplet Actual Size (mm2) | Power (W) |
|---|---|---|---|
| mem3 | 6.0 × 2.0 | 4.5 × 1.5 | 10 |
| hs | 6.0 × 6.0 | 4.5 × 4.5 | 40 |
| nr | 8.0 × 6.0 | 7.5 × 4.5 | 70 |
| in | 6.0 × 6.0 | 4.5 × 4.5 | 30 |
| vs | 6.0 × 6.0 | 4.5 × 4.5 | 20 |
| mem2 | 6.0 × 2.0 | 4.5 × 1.5 | 10 |
| hvs | 6.0 × 6.0 | 4.5 × 4.5 | 30 |
| jug1 | 6.0 × 6.0 | 4.5 × 4.5 | 50 |
| jug2 | 6.0 × 6.0 | 4.5 × 4.5 | 50 |
| se | 6.0 × 6.0 | 4.5 × 4.5 | 20 |
| mem1 | 6.0 × 2.0 | 4.5 × 1.5 | 10 |
| blend | 4.0 × 4.0 | 2.5 × 2.5 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Peng, X.; Cang, D.; Zhao, J.; Liu, Y.; Fang, J. Chiplet Multi-Objective Optimization Algorithm Based on Communication Consumption and Temperature. Electronics 2023, 12, 1604. https://doi.org/10.3390/electronics12071604
Sun H, Peng X, Cang D, Zhao J, Liu Y, Fang J. Chiplet Multi-Objective Optimization Algorithm Based on Communication Consumption and Temperature. Electronics. 2023; 12(7):1604. https://doi.org/10.3390/electronics12071604
Chicago/Turabian StyleSun, Haiyan, Xinwei Peng, Dongqing Cang, Jicong Zhao, Yanhua Liu, and Jiaen Fang. 2023. "Chiplet Multi-Objective Optimization Algorithm Based on Communication Consumption and Temperature" Electronics 12, no. 7: 1604. https://doi.org/10.3390/electronics12071604
APA StyleSun, H., Peng, X., Cang, D., Zhao, J., Liu, Y., & Fang, J. (2023). Chiplet Multi-Objective Optimization Algorithm Based on Communication Consumption and Temperature. Electronics, 12(7), 1604. https://doi.org/10.3390/electronics12071604





