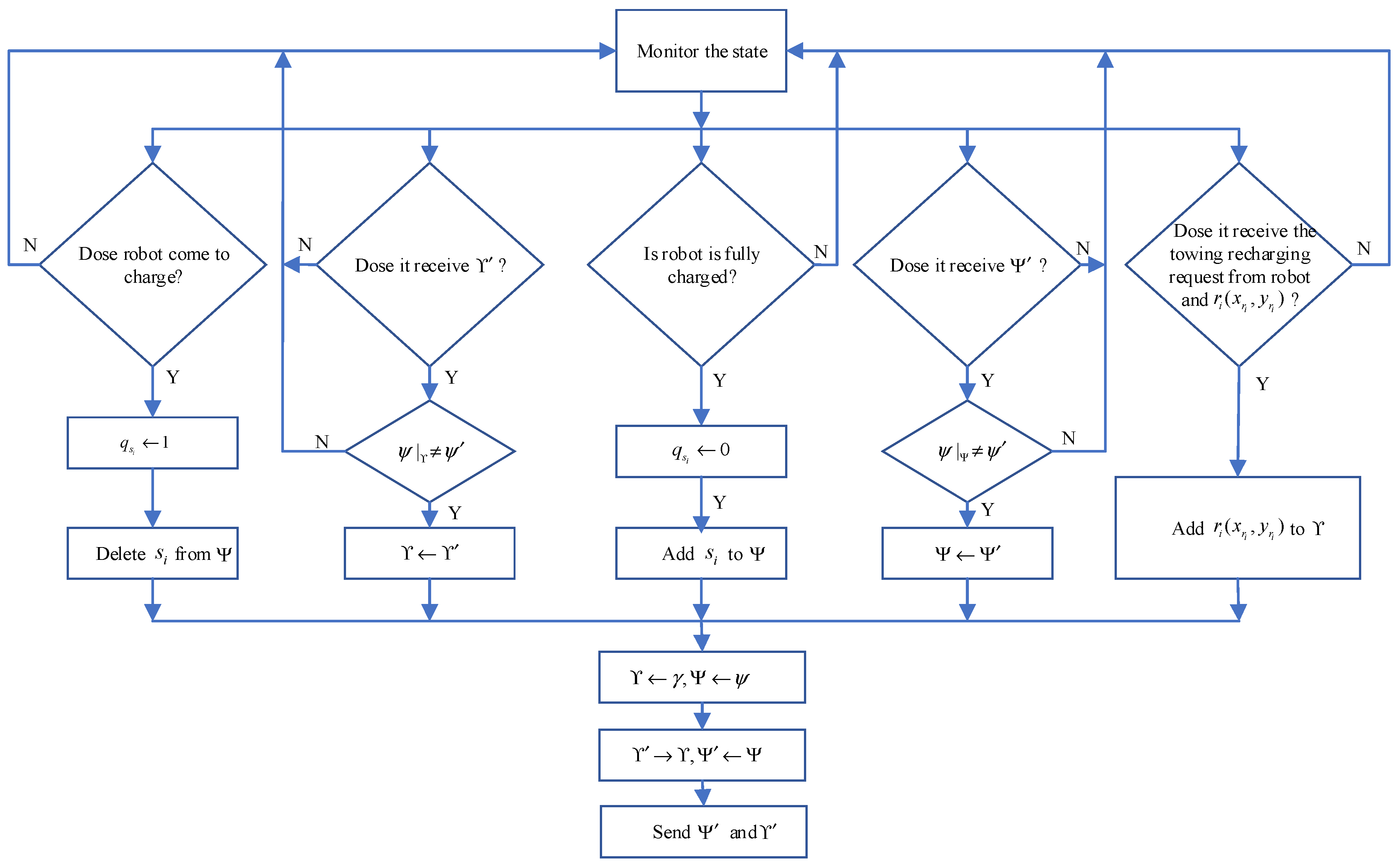
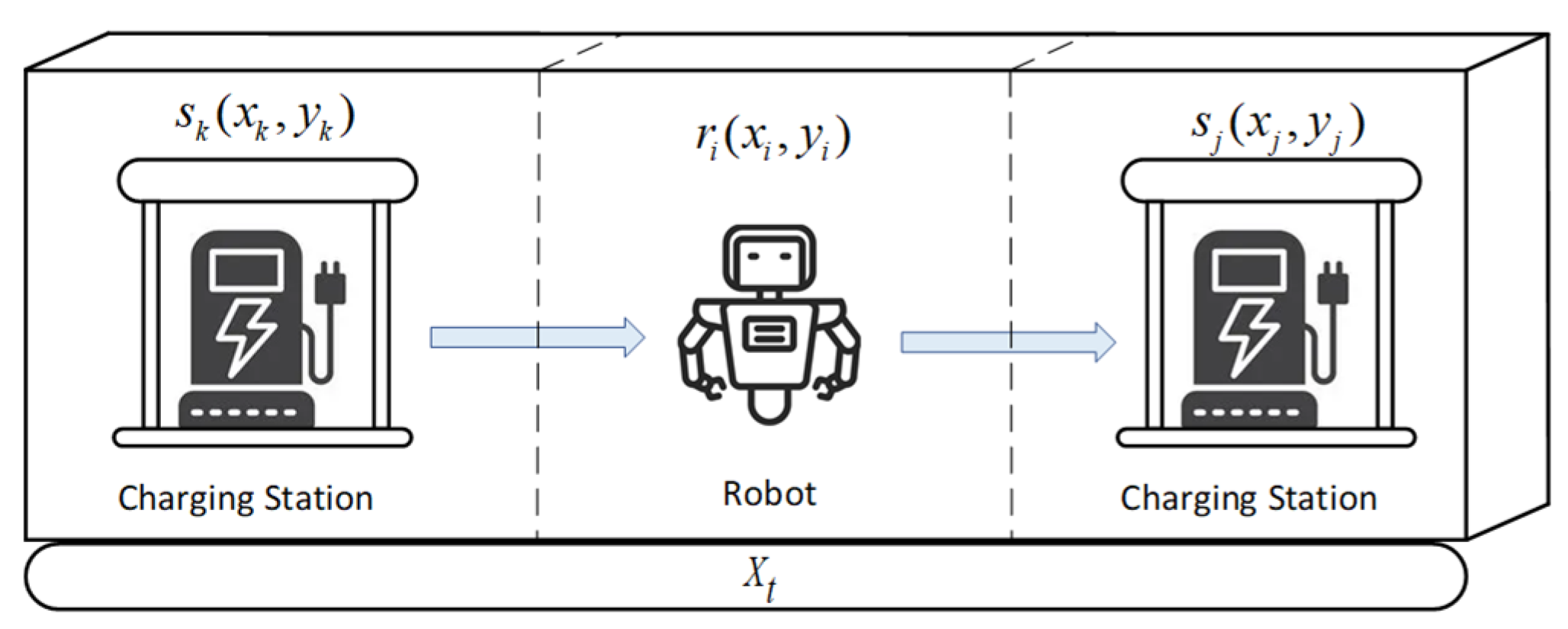
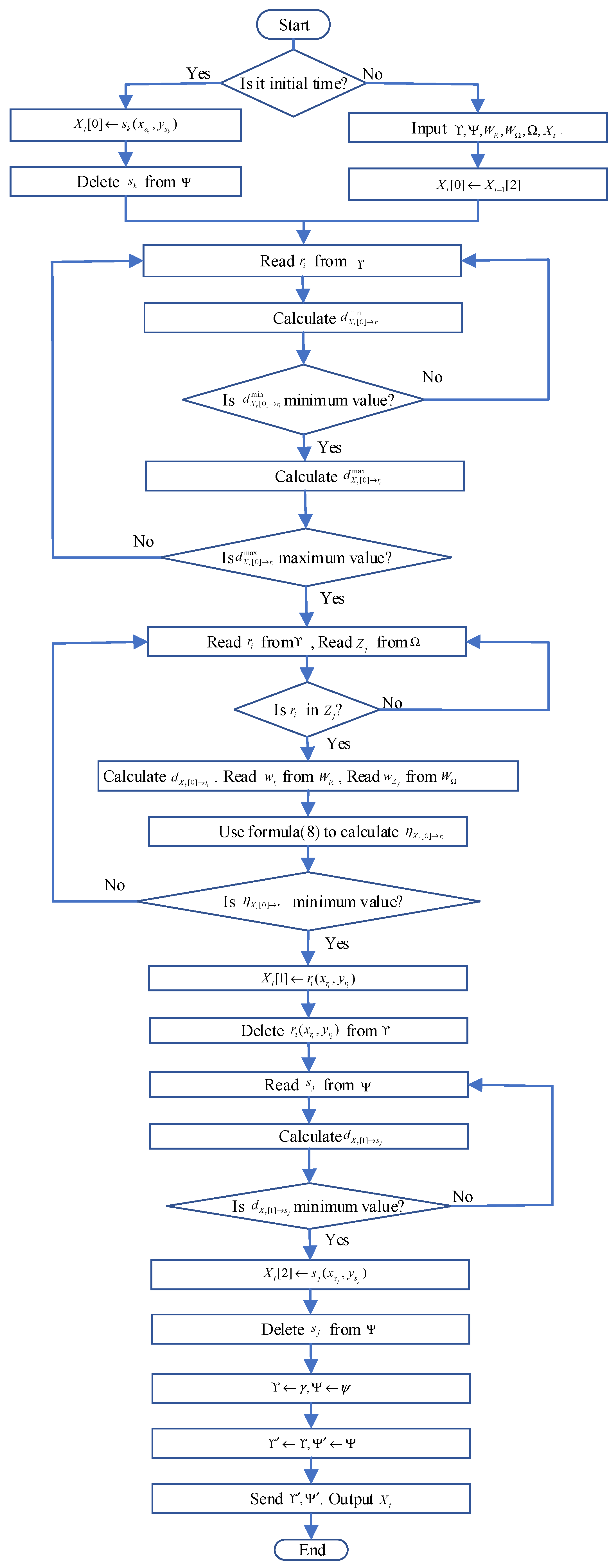
In this section we simulated the towing recharging optimization scheme. We use MATLAB 2020a tool for simulation verification. It is possible and independent for robots to send requests to be towed for recharging in each room. The position of the robot, charging station and robot-trailer adopts two-dimensional Cartesian coordinate system, with the lower left corner of the space as the coordinate origin.
5.2. Simulation 2
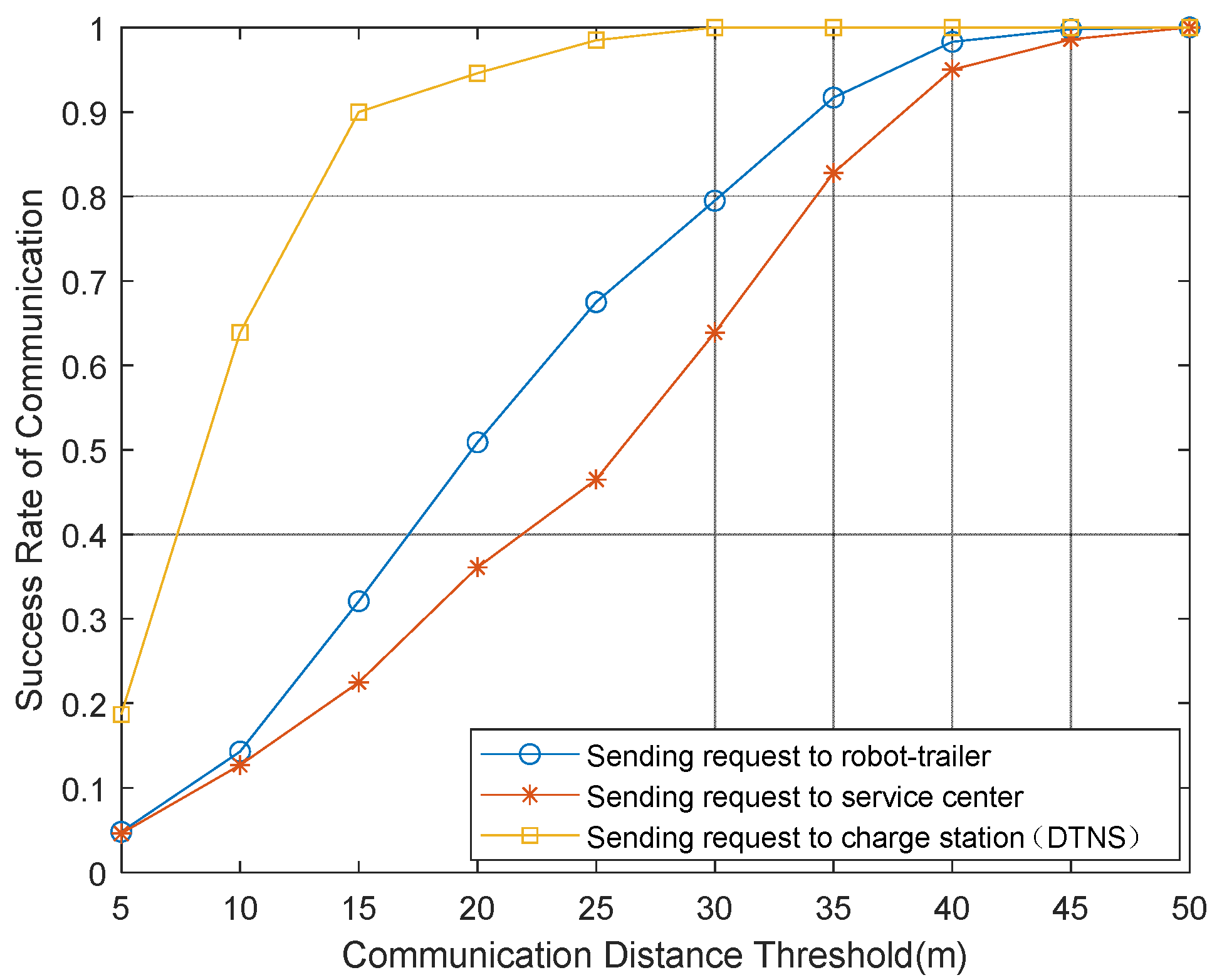
This simulation is to verify the superiority of scheduling efficiency. We compare the delay expectation and delay time between the DTNS scheduling algorithm and the FCFS [
30] scheduling algorithm. The service space of this experiment is set in a space of 40 m × 40 m, as shown in
Figure 7.
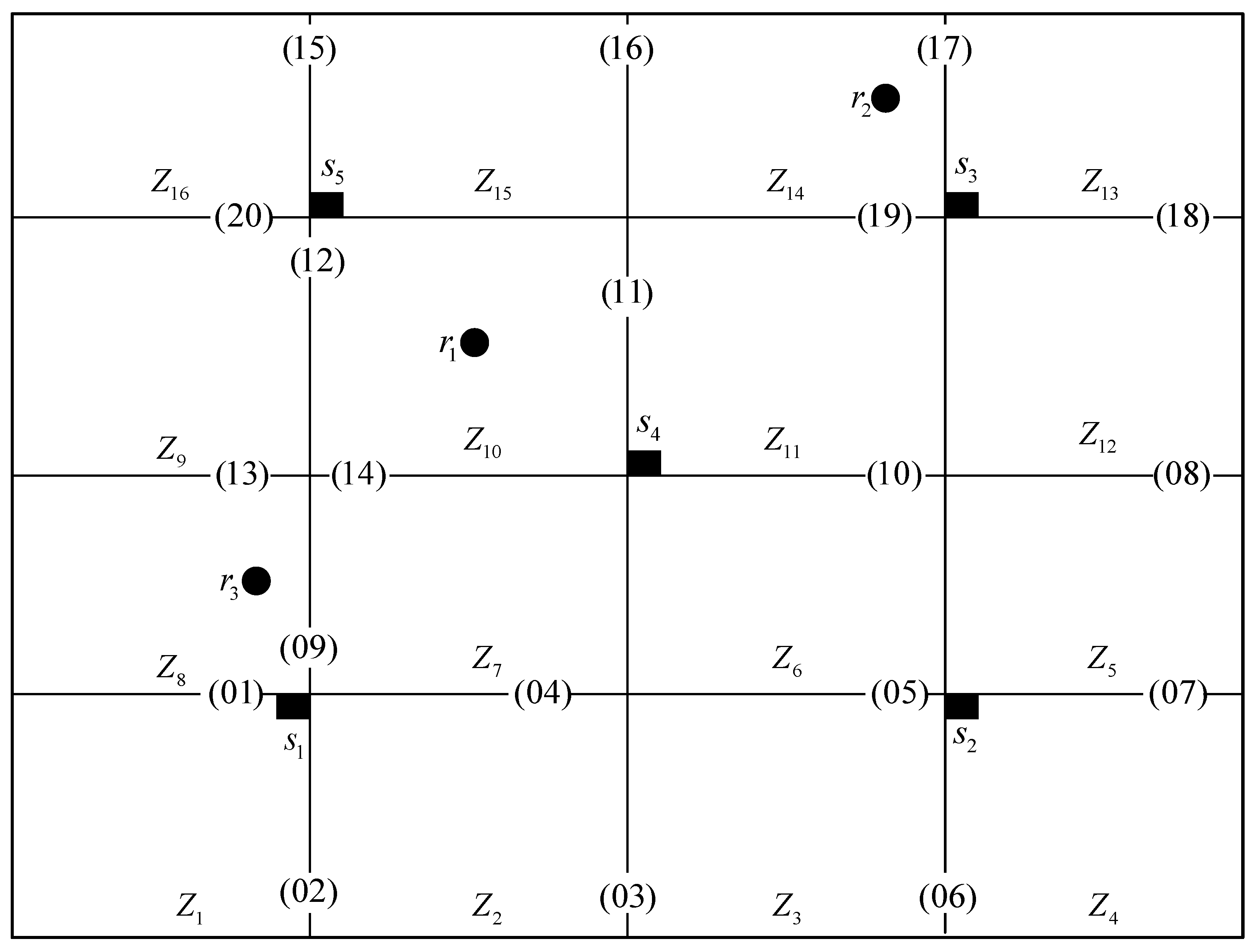
In
Figure 7, the black square
![Electronics 12 01402 i001 Electronics 12 01402 i001]()
represents the deployed charging station, the black blob
![Electronics 12 01402 i002 Electronics 12 01402 i002]()
represents the position of the robot to be transported for charging, bracketed number
represents the door and its number, and the coordinates of each door are shown in
Table 1.
Five charging stations are deployed in the service space, and the location of each charging station is shown in
Table 2. The charging stations can communicate with each other.
There are 16 rooms in the service space, which are connected with each other. The influence degree of the room is a set of random values, as shown in
Table 3.
Six robots are deployed, and the task weight of each robot is shown in
Table 4.
The queue
of robots waiting to be towed is set as shown in
Table 5.
The queue
of idle and available charging stations is shown in
Table 6.
All robot-trailers are set to drive at a uniform speed, and the driving speed is set to 1 m/s. , and are adjustment coefficients which values are set to 1. In this Simulation, we compare the DTNS proposed in this paper with the FCFS scheduling. In practice, it takes time for robot-trailer to load and unload robots. Because we are concerned with the comparison of scheduling efficiency, the time of robot-trailer loading and unloading robots in DTNS and FCFS scheduling algorithms is the same, so the time comparison in this experiment is not included in the time of robot-trailer loading and unloading robots. We discuss three conditions of two scenarios. The first scenario is that when the robot-trailer plans the path, no other robot sends a charging request. The second scenario is that when the robot-trailer plans the path, other robots send the request to be towed for recharging.
Scenario 1: we first discuss the efficiency of the scheduling algorithm when there is only one robot-trailer. If the initial position of the robot-trailer
is at
, the charging path obtained by using FCFS and DTNS is shown in
Table 7.
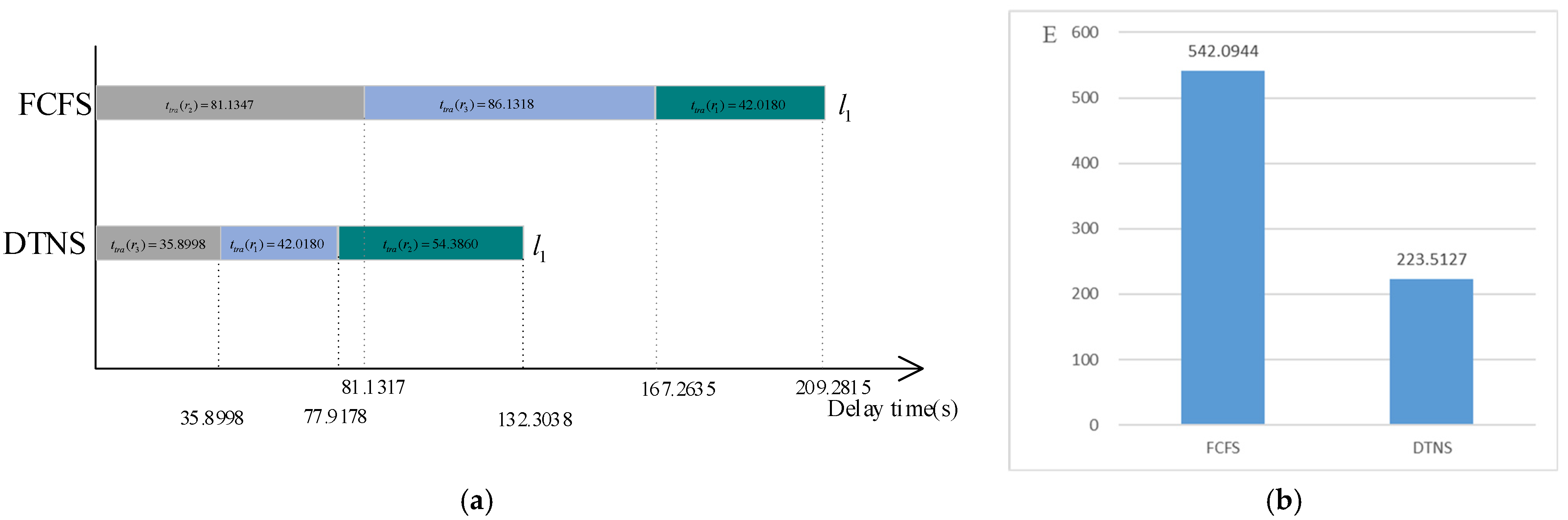
The towing service time of each requesting robot and the delay expectation of the whole robot service system are shown in
Figure 8, where
represents the service time of towing robot
to charge. For the FCFS scheduling, the delay time of robots
,
and
is 81.1317 s, 167.2635 s and 209.2815 s respectively. For the DTNS scheduling, the delay time of robots
,
and
is 35.8998 s, 77.9178s and 132.3038 s respectively. The delay expectation of the whole robot service system is 542.0944 for FCFS algorithm and 223.5127 for DTNS algorithm.
Under the condition of two robot trailers, let the initial position of the robot-trailer
be at
and the initial position of the robot-trailer
be at
. Suppose
gets the data a little earlier than
. The charging paths obtained by using the two scheduling algorithms are shown in
Table 8.
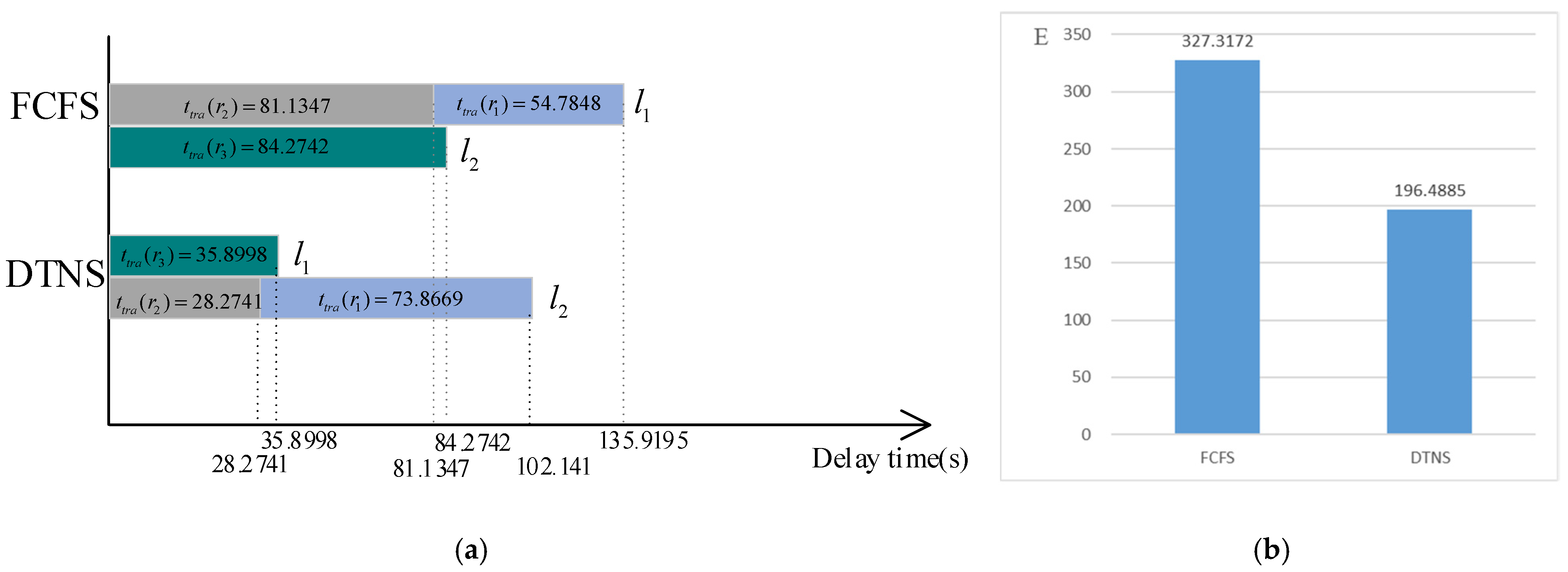
The towing charging service time of each requesting robot and the delay expectation of the whole robot service system are shown in
Figure 9. For the FCFS algorithm, the delay time of robots
,
and
is 135.9195 s, 81.1347 s and 84.2742 s respectively. For the DTNS algorithm, the delay time of robots
,
and
is 102.141 s, 28.2741 s and 35.8998 s respectively. The delay expectation of the whole robot service system is 327.3172 for FCFS algorithm and 196.4885 for DTNS algorithm.
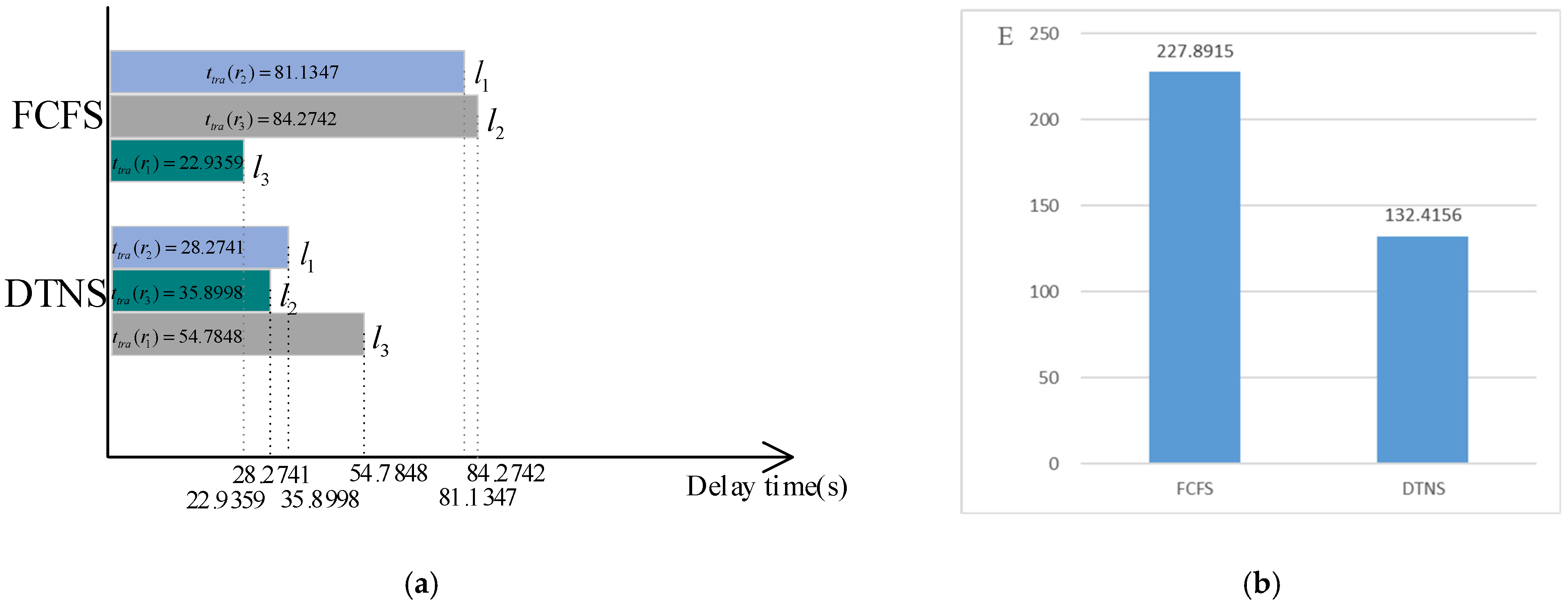
Under the condition of three robot-trailers, the initial position of the robot-trailer
is set at
, the initial position of the robot-trailer
is set at
, and the initial position of the robot-trailer
is set at
. The charging path obtained is shown in
Table 9.
The towing charging service time of each requesting robot and the delay expectation of the whole robot service system are shown in
Figure 10. For the FCFS algorithm, the delay time of robots
,
and
is 22.9359 s, 81.1347 s and 84.2742 s respectively. For the DTNS algorithm, the delay time of robots
,
and
is 54.7848 s, 28.2741 s and 35.8998 s respectively. The delay expectation of the whole robot service system is 227.8915 for FCFS algorithm and 132.4156 for DTNS algorithm.
As can be seen from
Figure 8b,
Figure 9b and
Figure 10b, the delay expectation of the proposed DTNS is lower than that of FCFS, with a difference of nearly half. As the number of robot-trailers increases, the delay expectation of the two models decreases. As can be seen from
Figure 8a,
Figure 9a and
Figure 10a, the delay time of the proposed DTNS is less than that of FCFS.
Table 7,
Table 8 and
Table 9 show that most of the paths obtained by DTNS are shorter than those obtained by FCFS.
Scenario 2: It is assumed that during the execution of scheduling planning, a robot sends a towing recharging request. Suppose that after towing the robot in the dataset for 30 s, sent a towed charging request and entered dataset . At the same time, the charging station has a robot fully charged to leave, which is idle and available, and its coordinates are stored in the dataset . The model of this work is low cache path planning, which can be processed immediately, while the first come first service model will be processed after all three robots are charged. Similarly, this experiment is divided into three conditions for discussion.
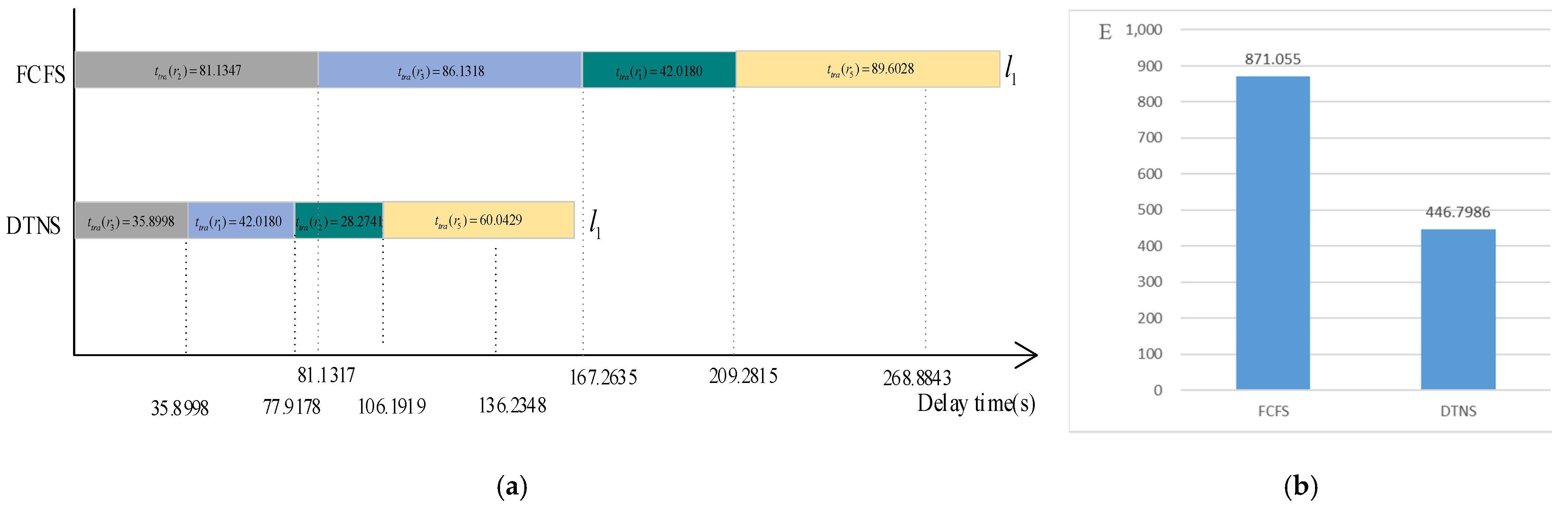
Under the condition of one robot trailers, the initial position of the robot-trailer is set at
. Using two scheduling models, the charging paths are shown in
Table 10.
The towing charging service time of each requesting robot and the delay expectation of the whole robot service system are shown in
Figure 11. For the FCFS algorithm, the delay time of robots
,
and
is 209.2815 s, 81.1347 s and 167.2635 s respectively. The delay time for robot
is 81.1317 + 86.1318 + 42.0180 + 89.6028 − 30 = 268.8843 s. For the DTNS algorithm, the delay time of robots
,
and
is 77.9178 s, 106.1919 s and 35.8998 respectively. The delay time for robot
is 35.8998 + 42.0180 + 28.2741 + 60.0429 − 30 = 136.2348 s. The delay expectation of the whole robot service system is 871.055 for FCFS algorithm and 446.7986 for DTNS algorithm.
Comparing
Figure 8a with
Figure 11a, it is found that due to the entry of
and
, the delay time of the robot
is less, because it is sent to a charging station
closer to it. The first come first service model needs to wait until it is all run before dealing with the following
and
.
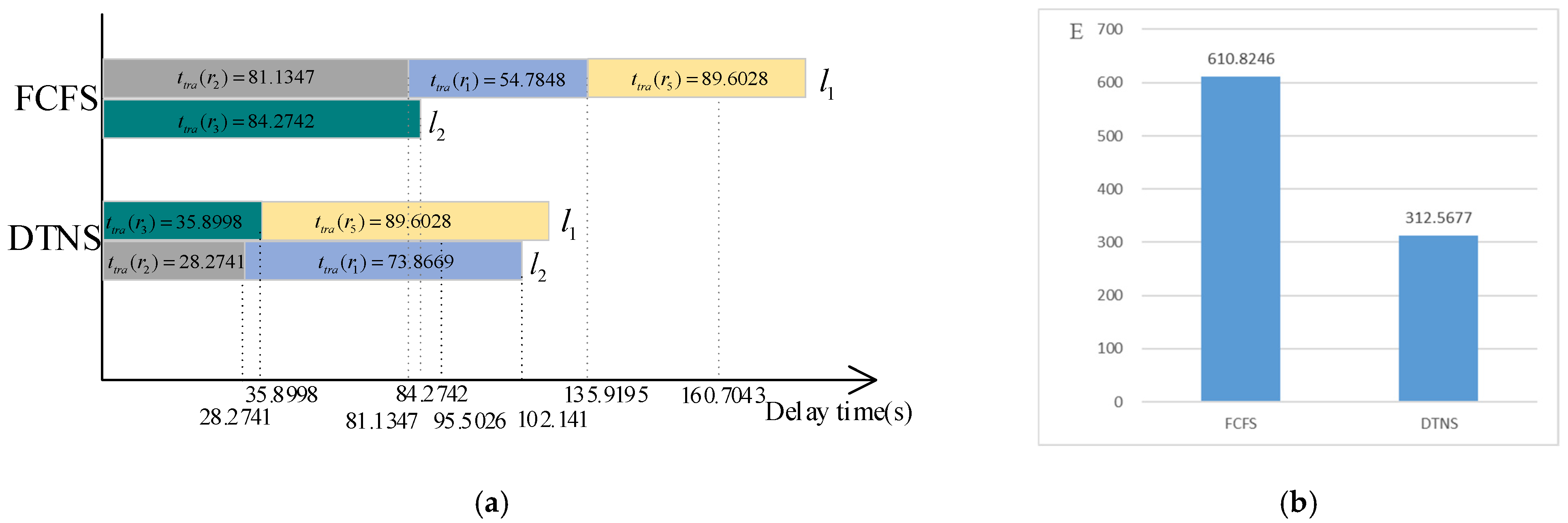
Under the condition of two robot trailers, let the initial position of the robot-trailer
be at
and the initial position of the robot-trailer
be at
. The charging paths obtained by using the two scheduling models are shown in
Table 11.
The towing charging service time of each requesting robot and the delay expectation of the whole robot service system are shown in
Figure 12. For the FCFS algorithm, the delay time of robots
,
and
is 235.9195 s, 81.1347 s and 84.2742 s respectively. The delay time for robot
is 81.1317 + 54.7848 + 89.6028-30 = 160.7043 s. For the DTNS algorithm, the delay time of robots
,
and
is 102.141 s, 28.2741 s and 35.8998 s respectively. The delay time for robot
is 35.8998 + 89.6028-30 = 95.5026 s. The delay expectation of the whole robot service system is 610.8246 for FCFS algorithm and 312.5677 for DTNS algorithm.
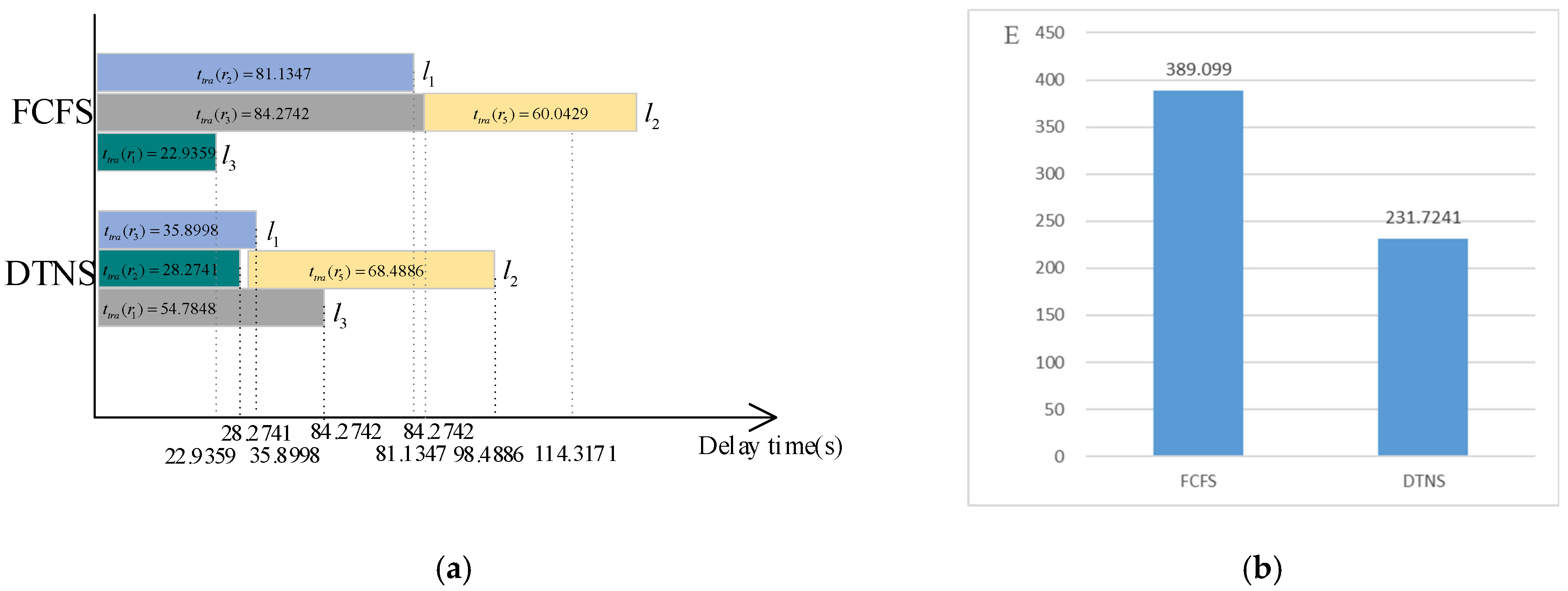
Under the condition of three robot-trailers, the initial position of the robot-trailer
is set at
, the initial position of the robot-trailer
is set at
, and the initial position of the robot-trailer
is set at
. The charging path obtained is shown in
Table 12.
The towing charging service time of each requesting robot and the delay expectation of the whole robot service system are shown in
Figure 11. For the FCFS, the delay time of robots
,
and
is 22.9359 s, 81.1347 s and 84.2742 s respectively. The delay time for robot
is 84.2742 + 60.0429 - 30 = 114.3171 s. For the DTNS algorithm, the delay time of robots
,
and
is 54.7848 s, 28.2741 s and 35.8998 s respectively. The delay time for robot
is 30 + 68.4886 = 98.4886 s. The time for the robot-trailer to finish serving the robot is 28.2741 s. Wait until 30 s,
is stored in dataset
. The delay expectation of the whole robot service system is 871.055 for FCFS algorithm and 446.7986 for DTNS algorithm.
As can be seen from
Figure 11a,
Figure 12a and
Figure 13a, the delay time of DTNS model is less than that of FCFS model.
Table 10,
Table 11 and
Table 12 show that the most of paths obtained by most DTNS is shorter than that obtained by FCFS. For the FCFS scheduling model, it is necessary to wait until all three robots are serviced before serving the incoming robot
. However, after 30 s, the DTNS scheduling model can serve the incoming robot
as long as there is free robot-trailer available. For the scenario 2, it can be seen from
Figure 11b,
Figure 12b and
Figure 13b, because there are more robots serving, the overall service delay is higher than that of the first scenario, but the overall trend is decreasing with the increase of robot trailers. The delay expectation of DTNS scheduling model proposed in this paper is lower than that of FCFS.
 represents the deployed charging station, the black blob
represents the deployed charging station, the black blob  represents the position of the robot to be transported for charging, bracketed number represents the door and its number, and the coordinates of each door are shown in Table 1.
represents the position of the robot to be transported for charging, bracketed number represents the door and its number, and the coordinates of each door are shown in Table 1.