Abstract
Knowledge Graph Embedding (KGE) is a powerful way to express Knowledge Graphs (KGs), which can help machines learn patterns hidden in the KGs. Relation patterns are useful hidden patterns, and they usually assist machines to predict unseen facts. Many existing KGE approaches can model some common relation patterns like symmetry/antisymmetry, inversion, and commutative composition patterns. However, most of them are weak in modeling noncommutative composition patterns. It means these approaches can not distinguish a lot of composite relations like “father’s mother” and “mother’s father”. In this work, we propose a new KGE method called QuatRotatScalE (QRSE) to overcome this weakness, since it utilizes rotation and scaling transformations of quaternions to design the relation embedding. Specifically, we embed the relations and entities into a quaternion vector space under the difference norm KGE framework. Since the multiplication of quaternions does not satisfy the commutative law, QRSE can model noncommutative composition patterns naturally. The experimental results on the synthetic dataset also support that QRSE has this ability. In addition, the experimental results on real-world datasets show that QRSE reaches state-of-the-art in link prediction problem.
1. Introduction
Knowledge Graph (KG) is composed by structured, objective facts. The facts are usually expressed in the form of triples as (h, r, t), where h, r, and t express the head entity, the relation, and the tail entity, respectively. For example, (China, located_in, Asia). Knowledge graphs have successfully supported many applications in various fields, such as recommender systems [1], question answering [2], information retrieval [3], and natural language processing [4]. KGs have also attracted increased attention from both industry and academic communities. However, real-world knowledge graphs, such as Dbpedia [5], Freebase [6], Yago [7], and WordNet [8], are usually incomplete, which restricts their applications. Thus, knowledge graph completion has become a widely studied subject. This subject is usually formulated as a link prediction problem, i.e., predicting the missing links that should be in the knowledge graph. Generally speaking, it asks us to design an agent that takes the query as input and outputs some entities. The query may contain a head entity and a relation or a tail entity and a relation. Every outputted entity should be able to form a plausible triple together with the query.
So far, the fundamental way to deal with the link prediction problem is Knowledge Graph Embedding (KGE) in industry and academia [9,10,11,12,13]. In this way, the agent needs to learn a low-dimensional vector representation, also called embedding, for each entity and relation. We have to design a scorer that can grade any triple in the embedding form for its plausibility. When predicting the unknown entity, the agent only needs to grade all possible triples (composed by the query with each candidate entity) and then take the candidate entities of high score triples as the predicted result.
There are two reasons why these knowledge-graph embedding methods can tackle the link prediction problem effectively. On the one hand, there are many utilizable relation patterns in real-world KGs, such as symmetry/antisymmetry, inversion, and composition. These relation patterns are generally presented as natural redundancies in KGs, such as triple (China, located_in, Asia) and triple (Asia, includes, China) may exist in some KGs simultaneously, and they are describing the same fact. Here, located_in and includes are inverse relations for each other. On the other hand, existing KGE models have been able to model most relation patterns, i.e., evaluate the plausibility of triples by utilizing the relation patterns. For example, TransE [10] can model inversion patterns. When there are many natural redundancies relevant to located_in and includes in training KG, even if it has only seen triple (China, located_in, Asia) but not seen triple (Asia, includes, China), the TransE model can still mark a high plausibility score for triple (Asia, includes, China).
However, as far as we know, almost none of the existing KGE models can perfectly model the aforementioned relation patterns. For example, RotatE [13] declares that it can model all of the relation patterns, but it still has a fatal defect in modeling the composition patterns: It can only model commutative composition patterns, but can not model noncommutative composition patterns. This defect is also existing in some other KGE models which claim themselves can model composition patterns, such as TransE. Briefly speaking, a composition pattern implies the relation pattern that in the shape of , where ⊕ means the ordered composition of and . If composition pattern exists in some KG, it means that KG has frequent natural redundancies in the form of , can be any entity. If and are both in a KG, we call a commutative composition pattern, such as and . Otherwise, if only is in the KG, it is a noncommutative composition pattern, such as .
Both of RotatE and TransE model the noncommutative composition pattern as the commutative composition pattern by mistake. This mistake will bring severely ridiculous inferences. For example, they will infer (i.e., mark a high score for) triple (Mary, is_the_father_of, Barbara) based on existing triples (Mary, is_the_mother_of, James) and (James, is_the_husband_of, Barbara). The primary cause of this mistake is that they have not taken the design inspiration of their models carefully. They both expect to express a fact triple (h, r, t) through an equation relevant to the embeddings of h, r, and t (noted as boldface letters h, r, and t): , where ⊙ is some binary operation. Thus, they design the score function in the form of , and we can see that the closer the equation is to hold, the higher the plausibility score is. TransE embeds entities and relations into the real number vector space and takes the addition in that space as ⊙, while RotatE replaces the real numbers with the complex numbers and takes the element-wise multiplication as ⊙. Since these two operations both satisfy the commutative law, the corresponding two models can only model commutative composition patterns.
Inspired by QuatE [14], which will be discussed in Section 2.1.2, we propose a new KGE model called QuatRotatScalE (or QRSE, for short) in this paper. The main difference from TransE and RotatE is it embeds entities and relations into the quaternion [15] vector space and takes the element-wise multiplication in that space as ⊙. Because the quaternion multiplication generally does not satisfy the commutative law (but there are special cases where the law holds), QRSE can model both composition patterns. Furthermore, we can prove that QRSE can also model the rest relation patterns. Thus it has become one of the KGE models that can model most relation patterns up to now. We evaluated QRSE and compared it with many baselines in two well-established and widely used real-world datasets FB15k-237 [16] and WN18RR [17]. The results indicate our method has reached the state-of-the-art in link prediction problem.
2. Related Work
At present, there are two classes of methods to solve the knowledge graph completion or link prediction problem. One class of methods is the KGE methods, and the other is the path-finding methods. Both of them are introduced below:
2.1. KGE Method
Embedding methods are widely used in many fields of machine learning since the embeddings of sentences, graphs, and many other data types can be easily transferred to various downstream tasks with only a little task-specific fine-tuning. For example, studies [18,19] first learn the embeddings of sentences and then use these embeddings to perform sentiment classification. Study [20] first learns an embedding for each graph, then use these embeddings to predict the missing labels of graphs. In addition, some other studies learn an embedding vector for each object (i.e., the node in a graph) of a given Heterogeneous Information Network (HIN) in a (semi-)supervised [21] or self-supervised [22] manner. Taking advantage of the learned embeddings of objects, they can fulfill many tasks, e.g., object classification, clustering, and visualization.
In knowledge graph completion or link prediction problem, Knowledge Graph Embedding methods are also the most studied methods. Let us use to represent the set of all entities and use to represent the set of all relations in KG. KGE methods need to assign a vector representation to every entity and relation , noted in boldface letters and , respectively. or is also called the embedding of e or r. In addition to this, KGE methods still need to design a score function to mark the plausibility of the triple (h, r, t). The objective of optimization is to mark high scores for the true triples and low scores for the false triples. Based on the type of score function, we can further divide the KGE methods into two sorts, KGE based on difference norm and KGE based on semantic matching:
2.1.1. KGE Based on Difference Norm
The common motivation of this sort of method is they want to use a triple approximate equation to describe any triple (h, r, t), and the strict equation should hold for fact triples. As for the unknown triples, they think the proximity of the two sides can reflect the plausibility of the triple. Thus, the score functions of these methods are always in the form of .
Among them, there is a kind of method that is widely studied, called translational methods. We call them “translational” because the origin of this kind of method, TransE, uses the translation transformation to design the triple approximate equation. Precisely, it chooses the real number vector space as the embedding space and regards the relation embedding as a translation transformation from head entity embedding to tail entity embedding . So it designs the triple approximate equation as . Following TransE, many improvements have emerged. TransH [23] claims it is better to assign a hyperplane in embedding space for every relation (the hyperplane’s normal vector noted as ), and only regards as a translation from the projection of to the projection of on that hyperplane. Hence the triple approximate equation of TransH is , where is the identity matrix. TransR [24] generalizes TransH, it assigns a linear map to every relation r, noted as transfer matrix . This linear map maps and into the relation space. Then TransR utilizes the images of and in the relation space with to design the triple approximate equation in TransE’s style: . Further, StransE [25] assigns each relation r two different transfer matrices and . Similarly, the triple approximate equation is designed as . These derivative methods of TransE are collectively known as TransX. Their score functions can be written in the form of , where denotes a matrix multiplication concerning relation r.
Since the large number of the derivative methods of TransE, some literature uses the translational methods to refer to KGE based on difference norm in general. But this is not accurate enough. Some other methods do not turn to translation transformation to design their triple approximate equations, such as TorusE [26] and RotatE. TorusE chooses a compact Lie group as its embedding space and can be regarded as a special case of RotatE when the embedding modulus are fixed [13]. RotatE embeds entities and relations into the complex number vector space . It wants to replace the translation in with the rotation in . Specifically, for each element of , RotatE fixes it as a unitary complex number (i.e., ). Hence the complex multiplication between the i-th element of (i.e., ) and means rotates in its complex plane with angle (i.e., the argument of complex ). Let us use ∘ to denote the Hadamard (element-wise) product between two complex vectors, the triple approximate equation of RotatE is .
There are some KGE methods with score functions belonging to a special case of difference norm, which is in the form of , where ⊙ is some binary operation. When the ideal optimization is achieved, the triple approximate equations of these methods hold: . This property is useful to explain some abilities to model relation patterns. For example, TransE and RotatE are two of these methods, and because their binary operations are both associative and commutative, they can only model commutative composition patterns. For more details, please see Section 5.
2.1.2. KGE Based on Semantic Matching
The intuition of this sort of method is to measure the plausibility of a triple by inspecting the matching degree of the latent semantics of the two entities and the relation.
There is a family of methods called bilinear models that design score functions as bilinear maps of head and tail entities. RESCAL [9] may be the first bilinear model. It selects real vector space as the embedding space of entities and assigns a real matrix to each relation r. Then it directly applies to define a bilinear map as the score function. To reduce the complexity of , DistMult [11] restricts to be a diagonal matrix. So DistMult can express as a vector in and rewrite the score function in the form of the multi-linear dot product of , , and . To overcome DistMult’s weakness in modeling antisymmetry relation pattern, ComplEx [12] extends the embedding space into the complex vector space , and modifies the score function. QuatE [14] further develops ComplEx, it extends the embedding space into the quaternion vector space to obtain better expression ability. DualE [27] uses the dual quaternion vectors to design the embeddings of entities and relations, and chooses the dual quaternion inner product as the score function. DihEdral [28] designs entity embeddings with real vectors, and designs relation embeddings with dihedral group vectors, where each dihedral group is expressed as a second-order discrete real matrix. Although its score function is a bilinear form, which belongs to the type of semantic matching, it is theoretically proven that this score function is equivalent to a difference norm function in the form of for optimizing relation embeddings. So DihEdral has the ability to model composition patterns like TransE and RotatE. Furthermore, since the multiplication of dihedral groups generally does not satisfy the commutative law, DihEdral can model noncommutative composition patterns. However, because the relation embeddings take discrete values, DihEdral has to use special treatments of the relation embeddings during the training process, and the actual performance is easily affected by special treatments. As for QuatE and DualE, their relation embeddings have the potential to model noncommutative composition patterns for the (dual) quaternion multiplication generally does not satisfy the commutative law. Nevertheless, because their score functions belong to the type of semantic matching and lack the theoretical equivalence to a difference norm function in the form of like DihEdral at present, their abilities to model the composition patterns have no strict theoretical guarantees. More precisely, their triple approximate equations, if any, do not necessarily hold when the ideal optimization is achieved, which is a crucial but easily overlooked step for a rigorous proof.
Apart from bilinear models, some models based on neural networks emerged recently. Such as ConvE [17] and ConvKB [29] take the convolutional neural networks to construct the score functions.
Some mentioned KGE methods are listed in Table 1 with their score functions. Their abilities to model the relation patterns are shown in Table 2. We can see that our QRSE can model all relation patterns, which is a rare ability.

Table 1.
Score functions and embedding spaces of several KGE models. means the multi-linear dot product of vector , , and ; denotes conjugate for a complex or quaternion vectors; denotes the real part of a complex number or quaternion; ⊗ indicates the Hadamard (element-wise) product between two quaternion vectors. Note that we report an equivalent formulation for QuatE to show the inheritance relationship with ComplEx.

Table 2.
The modeling ability comparison for various relation patterns among different models (partial reference from [13]).
Additionally, “supervised relation composition” [30] is a method that can model composition patterns under supervision. But it is not a KGE method. Its goal is to design and train a function model that can take the embeddings of two relations as input and output the embedding of the composite relation of these two relations. The relation embeddings used are provided by an existing KGE model and are fixed once obtained. The supervisory information used for training is mined from the original KGs by another method. This method and the KGE models mentioned before belong to different research directions. The direction of KGE models studies how to directly model relation patterns (including composition patterns) by training entity and relation embeddings from the original KGs.
2.2. Path-Finding Method
This class of methods does not need score function to predict unknown entities, such as MINERVA [31], MultiHopKG [32], and DeepPath [33]. Instead, they should start from the query entity node and follow the direction implied by the query relation to search the KG for the unknown entity. Compared with KGE methods, their results are explainable to some extent since they can provide the inference paths as evidence, but the lack of precision is their weakness at present.
3. Preliminaries
Before introducing our proposed method, let us briefly explain the related concepts and geometric meaning of quaternions.
3.1. A Brief Introduction of Quaternion
As an extened number system from the complex numbers , quaternions [15] have to import three fundamental quaternion units , , and , which are not existing in the real numbers. Each quaternion q can be expressed as , where a, b, c, and d are all real numbers. The addition of quaternions is defined as . The multiplication between any two fundamental quaternion units are defined as and . Obviously, this multiplication is associative but not commutative. For completeness, we also confirm the multiplication between any one in , and a real number is commutative and associative. To obey the distributive law, we consequently get the multiplication between two arbitrary quaternions as:
We can conclude that the multiplication of quaternions (also known as the Hamilton product) holds the associative and distributive law, but does not hold the commutative law in general. Nevertheless, there are some special cases where the commutative law holds.
Some useful concepts of quaternions are listed as follows (let ):
Modulus: The modulus of q is written as and is defined as . Since the set of quaternions is a linear space isomorphic to with basis , modulus means the length of q intuitively. In addition, if , q is called a unit quaternion.
Real and imaginary part: Similar to complex numbers, real number a is the real part of q, and real vector is the imaginary part of q. Sometimes we would like to express q in the form of for convenience. Then, the multiplication of quaternions can be written as , where · is the dot product and × is the cross product.
Conjugate: The conjugate of q is the quaternion . It has thses properties: (1) ; (2), and from (1), (2) we get (3) . As a corollary, the product of two unit quaternions is also a unit quaternion.
Reciprocal: If , the reciprocal of q is the quaternion such that , and it is equivalent to define .
3.2. The Geometric Meaning of the Multiplication of Quaternions
To see the geometric meaning of the multiplication of quaternions, we have to view the as a linear space isomorphic to with an orthonormal basis . Any q in can be expressed in the form as , where and . This is because if we could set , , and , whereas if we could set and choose and arbitrarily. Note that is a unit quaternion and implies the direction of q, while implies the length of q.
Take another quaternion from , then the product means a new quaternion reached via two steps from p: (1) changing the direction of p according to , (2) stretching the length by times. So we only have to see what is the change implied by .
Without loss of generality, we suppose and is not parallel with . Thus we can find another orthonormal basis of : . Here, and . Besides, we confirm the coordinates of p under this basis is , where and . Thus we can split p into two parts: , where and . So we only have to see what do and mean.
Since , this product and are both in the plane with basis . And we can show the transformation from to the product by their coordinates under basis as:
So means rotates with angle counterclockwise in plane . In the same way, since , this product and are both in the plane with basis . And we can show the transformation from to the product by their coordinates under basis as:
So means rotates with angle counterclockwise in plane .
In a word, the change implied by is: (1) Split p into two components and , where is in plane and is in plane ; (2) Rotate and with angle counterclockwise in each plane simultaneously, as shown in Figure 1; (3) Add two new components together.
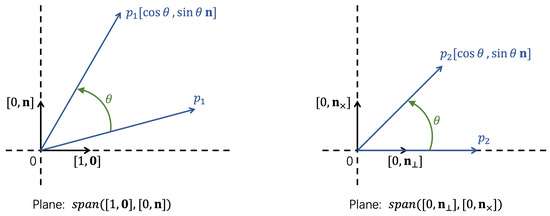
Figure 1.
How do and rotate when they are multiplied by on the right.
As a special case, when or is parallel with , . Thus at that time, only means the rotation in plane . Moreover, the geometric meaning of is almost the same with , except that the rotation for is clockwise.
4. Proposed Method
Now we start to introduce our proposed KGE model. The embedding spaces of entities and relations are both the quaternion vector space . For any and , their embeddings are noted as and in lower case bold letters, respectively. The i-th elements of and are written as () and () for every integer i from 1 to k. Our model is based on difference norm, so we first define its triple approximate equation as for any triple (h, r, t). Here, ⊗ denotes the Hadamard (element-wise) product between two quaternion vectors. So this triple approximate equation is equivalent to asking for for all . In consequence, we get our score function:
Here, is the abbreviation of , for any quaternion vector . is a hyperparameter.
According to the geometric meaning of the quaternion multiplication, we can explain the purpose of this triple approximate equation intuitively: We treat each element of relation embedding (written in the form of ) as a two-step transformation from to : (1) Rotate in two planes ( and ) counterclockwise with angle ; (2) Stretch with scaling factor . Thus we refer to our model as QuatRotatScalE (or QRSE, for short) due to we use Quaternions with Rotation and Scaling transformations to design the Embedding model.
Optimization
The general objective of KGE models is to return high scores for true triples and low scores for false triples. We adopt negative sampling as our training style to avoid the efficiency loss brought by the huge number of entities like most of the other KGE methods. The training KG usually only contains true triples (positive samples, noted as ) without false triples (negative samples). Thus we apply a common way (i.e., corrupting the positive samples) to obtain the negative samples. Suppose (h, r, t) is a positive sample, we can get two sets of negative samples by replacing the head or tail entity with other entities: and . The size of negative samples and is fixed and much smaller than .
Following RotatE [13], we use the loss function on each triple (h, r, t) in the training KG as
where is the sigmoid function, is a fixed margin, and is or . In practice, is regenerated in the same way ( or ) for every positive sample in one training batch. Once it turns to the next training batch, should switch the regenerating way. is the distribution of self-adversarial negative sampling proposed by RotatE [13] and is defined as
where is the temperature of sampling. The self-adversarial negative sampling can moderate the low efficiency of the uniform negative sampling. We also take Adam as our optimizer. Moreover, plays a role of importance sampling ratio in L, so it need not backpropagate gradients through it.
5. Theoretic Analysis
5.1. Relation Patterns
As mentioned in introduction Section 1, modeling (i.e., identifying and utilizing) the relation patterns in KGs are the fundamental for KGE models to solve the link prediction problem. There are three types of relation patterns, which are very powerful and widely exist in various KGs [12,13,16,34,35]:
Symmetry/antisymmetry: A relation r is symmetric (antisymmetric) if , ().
Inversion: Relation is inverse to relation if , .
Composition: Relation is composed of relation and relation if , . We adopt form to describe this composition pattern for simplicity. Moreover, if both of and make sense, is a commutative composition pattern. Otherwise, if only holds, it is a noncommutative composition pattern.
5.2. Abilities to Model Relation Patterns
In this subsection, we prove that QRSE can model symmetry/antisymmetry, inversion, and composition patterns. Additionally, TransE and RotatE are unable to model noncommutative composition patterns. Next, if triple (h, r, t) is in the knowledge graph, we write it in the embedding space as for QRSE because its score function is a special case of difference norm and when the ideal optimization is achieved, we can directly get (we can replace ⊗ with + or ∘ for TransE or RotatE for the same reason).
- QRSE can model symmetry/antisymmetry patterns:Suppose and . We can get . It means for any , . If , can be any quaternion. But if , must satisfies:, . , . Thus is 1 or . In a word, if satisfies , models a symmetry pattern, otherwise, it models a antisymmetry pattern.
- QRSE can model inversion patterns:Suppose and . We can get . It means for any , . If , and can be any quaternions. But if , and must satisfy:Define for all . We can conclude that if , and model an inversion pattern.
- QRSE can model composition patterns:Suppose , , and . We can get . It means for any , . If , , , and can be any quaternions. But if , , , and must satisfy:Moreover, if we still suppose , , and . Then if for all , , , and must satisfy: . This means . If we note and , then we will get:We can conclude that if , , , and model a composition pattern. Moreover, if is parallel with for all , it is a commutative composition pattern, otherwise, it is a noncommutative composition pattern.
- TransE and RotatE can not model noncommutative composition patterns, and they can only model commutative composition patterns:For TransE, we suppose , , , , , but , which means the composition of relation and is noncommutative. From the first three equations we get , and from the fourth and fifth equations we get . Because , we get , which contradicts the condition. Therefore TransE can not model noncommutative composition patterns. If we replace the condition with , then the composition of relation and becomes commutative composition. In this case the previous contradiction disappears, which means TransE can model commutative composition patterns.As for RotatE, we suppose , , , , , but , which means the composition of relation and is noncommutative. Since (the multiplication of complex numbers satisfies the commutative law), we can get in the same way as TransE, which contradicts the condition. So RotatE can not model noncommutative composition patterns. If we replace the condition with , then the composition of relation and becomes commutative composition. In this case the previous contradiction disappears, which means RotatE can model commutative composition patterns.
6. Experiments
In this section, we first evaluate QRSE with RotatE on a small knowledge graph made up of two families. This experiment will verify the superiority of QRSE in modeling noncommutative composition relation patterns. Then we evaluate QRSE and compare it with many baselines in two well-established and widely used real-world datasets.
6.1. Experiment on a KG about Two Families
There are 10 entities and 4 relations in the training KG. Each entity is a member of one family, and each relation is a type of kinship. Such as triple (Am1, son, Am2) means Am1 has a son called Am2. All of the triples in the training KG are shown in Figure 2, where each directed edge represents a triple, and its direction is from the head entity to the tail entity. Furthermore, the test set contains two triples: (Bm1, daughter_of_son, Bw3) and (Bm1, son_of_daughter, Bm3). We let models predict the head or tail entity for each test triple, so there are 4 queries during the test process.
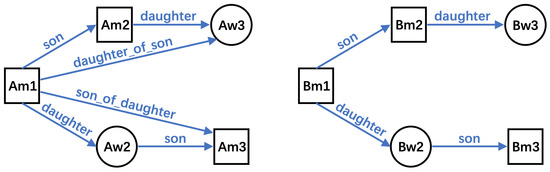
Figure 2.
The structure of the training KG, where each directed edge represents a triple.
Since we need 2 and 4 real numbers to determine a complex number and a quaternion respectively, we take (i.e., embedding dimension ) and (i.e., ) as the entity embedding spaces for RotatE and QRSE. Thus in practice, we can express the entity embeddings of RotatE and QRSE as 20-D real vectors. Except for the embedding dimension k, we keep other hyperparameters the same for two models: batch size , self-adversarial sampling temperature , fixed margin , learning rate , negative sampling size , and the order of norm in score function .
We use Hit@1 to measure the performance of models, which means the proportion of the correctly answered queries (i.e., the true answer’s score is ranked first) among all test queries. The test performances of RotatE and QRSE are shown in Figure 3. We can see that QRSE gets the best Hit@1 value 1.00 quickly, and after that, it keeps this Hit@1 value all the time during the training process. RotatE also gets the best Hit@1 value quickly; however, after that, it’s Hit@1 value is always fluctuating between 0.5 and 1.00 randomly. To explain this phenomenon, we inspected the detailed scores and embeddings at step 16,000, which is large enough to ensure the convergence of the two models.
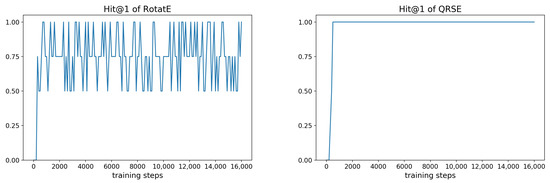
Figure 3.
The Hit@1 performance of RotatE and QRSE on the test set along with the training process.
The top 3 scores for all test queries are shown in Table 3. For the two queries to predict the head entity Bm1, the scores of Bm1 are much higher than the second candidate entities for both RotatE and QRSE. However for the two queries to predict the tail entities Bm3 and Bw3, only QRSE keeps the large gap between the first and the second score, whereas RotatE gives very close scores for the top 2 candidate entities on both of the two queries. This result reveals that, for RotatE, the score ranks for the top 2 candidates are unstable and easily affected by the random noise on the two queries to predict the tail. That is why the Hit@1 of RotatE fluctuates during training. Moreover, for RotatE, the top 2 candidate entities are Bm3 and Bw3 for both of the two tail queries. Thus we guess the embeddings of these two entities are also very close.

Table 3.
The detailed test results of RotatE and QRSE at training step 16,000.
Figure 4 shows the embeddings of Bm3 and Bw3 in RotatE and QRSE. As we guessed, the two embeddings are very close in RotatE but different in QRSE. This result verified that RotatE is unable to model noncommutative composition patterns, but QRSE can. Let us use the bold type to indicate the embeddings as before. For RotatE, along with the training process, Bw3 will close to , and Bm2 will close to . Hence Bw3 will close to . Similarly, Bm3 will close to . Because , Bw3 will close to Bm3. For QRSE, in general, so Bw3 will not close to Bm3.
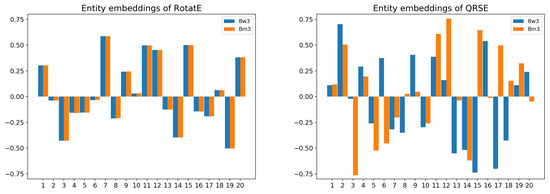
Figure 4.
The entity embeddings of RotatE and QRSE on training step 16,000. The 10-D complex or 5-D quaternion vectors are expressed in the corresponding 20-D real vectors.
We can also show this fact by directly inspecting the relation embeddings of the two models in Figure 5. Note that and are not the relations in KG but the combinations made up of the relations in KG. Their “embeddings” are calculated from the embeddings of some relations (e.g., the “embedding” of is in QRSE). Obviously, the embeddings of son_of_daughter and daughter_of_son are almost the same in RotatE, since they are both approaching during training. However, they are different in QRSE since the embeddings of son_of_daughter is approaching while the other is approaching during training.
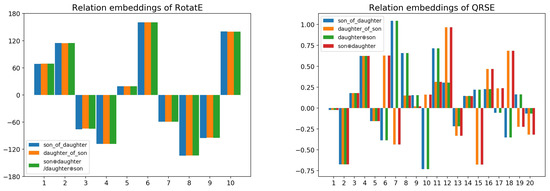
Figure 5.
The relation embeddings of RotatE and QRSE on training step 16,000. A relation embedding of RotatE has 10 complex numbers with modulus 1, which are determined by their 10 arguments. Thus we express it by its 10 arguments in angle degrees. For QRSE, we continue use the corresponding 20-D real vectors for each relation embedding.
6.2. Experiment on Real-World Datasets
6.2.1. Experimental Setting
We still evaluated our method on two well-established and widely used real-world knowledge graphs, FB15k-237 [16] and WN18RR [17], with several strong baselines.
FB15k-237 is selected from FB15k [10], which is a subset of Freebase and mainly records the facts about movies, actors, and sports. Because FB15k suffers from test leakage through inverse relations: there are too many inversion patterns in KG, which are too easy to model, and even a simple rule-based model can perform well [17]. To make the results more reliable, FB15k-237 removed these inverse patterns. The statistics of FB15k-237 are 14,541 entities, 237 relations, 272,115 training triples, 17,535 validation triples, and 20,466 test triples.
WN18RR is selected from WN18 [10], which is a subset of WordNet and records lexical relations between words. WN18 also suffers from test leakage through inverse relations, so WN18RR removed its inverse patterns too. The statistics of WN18RR are 40,943 entities, 11 relations, 86,835 training triples, 3034 validation triples, and 3134 test triples.
The ranges of the hyperparameters for the grid search are following RotatE as embedding dimension , batch size , and fixed margin . Moreover, we searched self-adversarial sampling temperature in , learning rate in , negative sampling size in , and the order p of norm in score function in . The embeddings are also uniformly initialized.
From each test triple (h, r, t), we generate two queries: (?, r, t) and (h, r, ?). Given each query, we can make a candidate triple by placing a candidate entity on the place of the entity to predict. The score of each candidate entity is just the score of its corresponding candidate triple. While ranking all the scores, we omit the scores of those candidate triples that already exist in training, validation, and test set, except the true answer for the query. This process is called “filtered” in some literature and is widely adopted in existing methods to avoid possibly flawed evaluation.
6.2.2. Results
We adopt these standard evaluation measures for both of the datasets: the mean reciprocal rank of the true answers (MRR), the proportion of queries whose true answers are ranked in the top k (Hit@k).
The link prediction results on real-world datasets are shown in Table 4. The result of TransE is taken from [29]. The results of DistMult, ComplEx, and ConvE are taken from [17]. The results of RotatE and DualE are taken from [13,27], respectively. The results of DihEdral(STE) and DihEdral(Gumbel) are taken from [28], where STE and Gumbel are two special treatments of the discrete relation embeddings. The results of QuatE and QuatE(TC) are taken from [14], where TC indicates the corresponding model using type constraints [36]. From this table, we can see that QRSE outperforms RotatE largely on all datasets and evaluation measures. This result supports our analysis of the modeling ability of the composition patterns. Compared with DihEdral(STE) and DihEdral(Gumbel), we find QRSE outperforms both of them on the two real-world datasets, whereas DihEdral(STE) is better than DihEdral(Gumbel) on FB15k-237 and just the opposite on WN18RR. This means the performance of DihEdral is easily affected by special treatments, and DihEdral can not perform well on the two real-world datasets simultaneously. Compared with DualE and QuatE, we find QRSE outperforms both of them too. This means that among all methods using (dual) quaternions so far, QRSE has explored the greatest potential of the (dual) quaternion space in the implementation of knowledge graph embedding. Because type constraints [36] can integrate prior knowledge into various KGE models and can significantly improve their performance in link prediction tasks, QRSE and most baselines display the results without it for fairness except QuatE(TC). Surprisingly, we can even see that QRSE is superior to QuatE with type constraints overall slightly. The success on this unfair comparison further demonstrates the excellence of QRSE. Overall, our QRSE has reached the state-of-the-art in link prediction problem on real-world datasets.

Table 4.
Link prediction results on the FB15k-237 and WN18RR datasets. Numbers in boldface are the best, and underlined numbers are the second best.
7. Conclusions and Future Work
We proposed a novel knowledge graph embedding model QRSE based on quaternions. QRSE is a KGE model that can model the noncommutative composition patterns. Besides, it can also model many other relation patterns, such as symmetry/antisymmetry, inversion, and commutative composition patterns. We varified these properties by theoretical proofs and experiments. From the definition of the triple approximate equation of QRSE, we can easily see that QRSE is a generalization of RotatE. Conversely, in some special cases, QRSE will degenerate to RotatE. For example, the case when the coefficients of and are fixed as 0 for all quaternions in all embeddings, and the modulus of all quaternions in relation embeddings are fixed as 1. Before QRSE, QuatE has already generalized ComplEx through replacing the complex numbers with quaternions. However, QuatE only takes advantage of that quaternions are more expressive than complex numbers. While our method not only leverages the expression advantage but also exploits the noncommutative property of quaternion multiplication to model the noncommutative composition patterns. The results of experiments on real-world datasets show that QRSE reaches the state-of-the-art on the link prediction problem. For future work, our plan is to combine QRSE with deep models for natural language processing. With its help, we expect deep models to achieve higher accuracy on question answering tasks and make the model’s answers more interpretable.
Author Contributions
Conceptualization, C.X., C.F., D.C. and X.H.; methodology, C.X.; software, C.X.; validation, C.X. and C.F.; formal analysis, C.X.; investigation, C.X.; resources, D.C. and X.H.; data curation, C.X.; writing—original draft preparation, C.X.; writing—review and editing, C.X., C.F., D.C. and X.H.; visualization, C.X.; supervision, D.C. and X.H.; project administration, D.C. and X.H.; funding acquisition, D.C. and X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by The National Nature Science Foundation of China (Grant Nos.: 62273302, 62036009, U1909203, 61936006), in part by Innovation Capability Support Program of Shaanxi (Program No. 2021TD-05).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study and the code are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Zhang, F.; Yuan, N.J.; Lian, D.; Xie, X.; Ma, W. Collaborative Knowledge Base Embedding for Recommender Systems. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 353–362. [Google Scholar] [CrossRef]
- Hao, Y.; Zhang, Y.; Liu, K.; He, S.; Liu, Z.; Wu, H.; Zhao, J. An End-to-End Model for Question Answering over Knowledge Base with Cross-Attention Combining Global Knowledge. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, ACL 2017, Vancouver, BC, Canada, 30 July–4 August 2017; Volume 1, pp. 221–231. [Google Scholar] [CrossRef]
- Xiong, C.; Power, R.; Callan, J. Explicit Semantic Ranking for Academic Search via Knowledge Graph Embedding. In Proceedings of the 26th International Conference on World Wide Web, WWW 2017, Perth, Australia, 3–7 April 2017; pp. 1271–1279. [Google Scholar] [CrossRef]
- Yang, B.; Mitchell, T.M. Leveraging Knowledge Bases in LSTMs for Improving Machine Reading. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, ACL 2017, Vancouver, BC, Canada, 30 July–4 August 2017; Volume 1, pp. 1436–1446. [Google Scholar] [CrossRef]
- Auer, S.; Bizer, C.; Kobilarov, G.; Lehmann, J.; Cyganiak, R.; Ives, Z.G. DBpedia: A Nucleus for a Web of Open Data. In Proceedings of the The Semantic Web, 6th International Semantic Web Conference, 2nd Asian Semantic Web Conference, ISWC 2007 + ASWC 2007, Busan, Republic of Korea, 11–15 November 2007; pp. 722–735. [Google Scholar] [CrossRef]
- Bollacker, K.D.; Evans, C.; Paritosh, P.; Sturge, T.; Taylor, J. Freebase: A collaboratively created graph database for structuring human knowledge. In Proceedings of the ACM SIGMOD International Conference on Management of Data, SIGMOD 2008, Vancouver, BC, Canada, 10–12 June 2008; pp. 1247–1250. [Google Scholar] [CrossRef]
- Suchanek, F.M.; Kasneci, G.; Weikum, G. Yago: A core of semantic knowledge. In Proceedings of the 16th International Conference on World Wide Web, WWW 2007, Banff, AB, Canada, 8–12 May 2007; pp. 697–706. [Google Scholar] [CrossRef]
- Miller, G.A. WordNet: A Lexical Database for English. Commun. ACM 1995, 38, 39–41. [Google Scholar] [CrossRef]
- Nickel, M.; Tresp, V.; Kriegel, H. A Three-Way Model for Collective Learning on Multi-Relational Data. In Proceedings of the 28th International Conference on Machine Learning, ICML 2011, Bellevue, Washington, DC, USA, 28 June–2 July 2011; pp. 809–816. [Google Scholar]
- Bordes, A.; Usunier, N.; García-Durán, A.; Weston, J.; Yakhnenko, O. Translating Embeddings for Modeling Multi-relational Data. In Proceedings of the Advances in Neural Information Processing Systems 26: 27th Annual Conference on Neural Information Processing Systems 2013, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 2787–2795. [Google Scholar]
- Yang, B.; Yih, W.; He, X.; Gao, J.; Deng, L. Embedding Entities and Relations for Learning and Inference in Knowledge Bases. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex Embeddings for Simple Link Prediction. In Proceedings of the 33nd International Conference on Machine Learning, ICML 2016, New York, NY, USA, 19–24 June 2016; pp. 2071–2080. [Google Scholar]
- Sun, Z.; Deng, Z.; Nie, J.; Tang, J. RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zhang, S.; Tay, Y.; Yao, L.; Liu, Q. Quaternion Knowledge Graph Embeddings. In Proceedings of the Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019; pp. 2731–2741. [Google Scholar]
- Hamilton, W.R. LXXVIII. On quaternions; or on a new system of imaginaries in Algebra: To the editors of the Philosophical Magazine and Journal. Philos. Mag. J. Sci. 1844, 25, 489–495. [Google Scholar] [CrossRef]
- Toutanova, K.; Chen, D. Observed versus latent features for knowledge base and text inference. In Proceedings of the 3rd Workshop on Continuous Vector Space Models and their Compositionality, Beijing, China, 31 July 2015; pp. 57–66. [Google Scholar]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2D Knowledge Graph Embeddings. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, (AAAI-18), the 30th innovative Applications of Artificial Intelligence (IAAI-18), and the 8th AAAI Symposium on Educational Advances in Artificial Intelligence (EAAI-18), New Orleans, LA, USA, 2–7 February 2018; pp. 1811–1818. [Google Scholar]
- Chen, L.; Wang, F.; Yang, R.; Xie, F.; Wang, W.; Xu, C.; Zhao, W.; Guan, Z. Representation learning from noisy user-tagged data for sentiment classification. Int. J. Mach. Learn. Cybern. 2022, 13, 3727–3742. [Google Scholar] [CrossRef]
- Zhao, W.; Guan, Z.; Chen, L.; He, X.; Cai, D.; Wang, B.; Wang, Q. Weakly-Supervised Deep Embedding for Product Review Sentiment Analysis. IEEE Trans. Knowl. Data Eng. 2018, 30, 185–197. [Google Scholar] [CrossRef]
- Yang, Y.; Guan, Z.; Zhao, W.; Weigang, L.; Zong, B. Graph Substructure Assembling Network with Soft Sequence and Context Attention. IEEE Trans. Knowl. Data Eng. 2022, 1. [Google Scholar] [CrossRef]
- Yang, Y.; Guan, Z.; Li, J.; Zhao, W.; Cui, J.; Wang, Q. Interpretable and Efficient Heterogeneous Graph Convolutional Network. IEEE Trans. Knowl. Data Eng. 2023, 35, 1637–1650. [Google Scholar] [CrossRef]
- Yang, Y.; Guan, Z.; Wang, Z.; Zhao, W.; Xu, C.; Lu, W.; Huang, J. Self-supervised Heterogeneous Graph Pre-training Based on Structural Clustering. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 16–19 May 2022; Oh, A.H., Agarwal, A., Belgrave, D., Cho, K., Eds.; 2022. [Google Scholar]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge Graph Embedding by Translating on Hyperplanes. In Proceedings of the 28th AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; pp. 1112–1119. [Google Scholar]
- Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning Entity and Relation Embeddings for Knowledge Graph Completion. In Proceedings of the 29thh AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 2181–2187. [Google Scholar]
- Nguyen, D.Q.; Sirts, K.; Qu, L.; Johnson, M. STransE: A novel embedding model of entities and relationships in knowledge bases. In Proceedings of the NAACL HLT 2016, The 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, San Diego, CA, USA, 12–17 June 2016; pp. 460–466. [Google Scholar]
- Ebisu, T.; Ichise, R. TorusE: Knowledge Graph Embedding on a Lie Group. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, (AAAI-18), the 30th innovative Applications of Artificial Intelligence (IAAI-18), and the 8th AAAI Symposium on Educational Advances in Artificial Intelligence (EAAI-18), New Orleans, LA, USA, 2–7 February 2018; pp. 1819–1826. [Google Scholar]
- Cao, Z.; Xu, Q.; Yang, Z.; Cao, X.; Huang, Q. Dual quaternion knowledge graph embeddings. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021; Volume 35, pp. 6894–6902. [Google Scholar]
- Xu, C.; Li, R. Relation Embedding with Dihedral Group in Knowledge Graph. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 263–272. [Google Scholar]
- Nguyen, D.Q.; Nguyen, T.D.; Nguyen, D.Q.; Phung, D.Q. A Novel Embedding Model for Knowledge Base Completion Based on Convolutional Neural Network. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT, New Orleans, LA, USA, 1–6 June 2018; Volume 2, pp. 327–333. [Google Scholar]
- Chen, W.; Hakami, H.; Bollegala, D. Learning to compose relational embeddings in knowledge graphs. In Proceedings of the Computational Linguistics: 16th International Conference of the Pacific Association for Computational Linguistics, PACLING 2019, Hanoi, Vietnam, 11–13 October 2019; Revised Selected Papers 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 56–66. [Google Scholar]
- Das, R.; Dhuliawala, S.; Zaheer, M.; Vilnis, L.; Durugkar, I.; Krishnamurthy, A.; Smola, A.; McCallum, A. Go for a Walk and Arrive at the Answer: Reasoning Over Paths in Knowledge Bases using Reinforcement Learning. In Proceedings of the 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Lin, X.V.; Socher, R.; Xiong, C. Multi-Hop Knowledge Graph Reasoning with Reward Shaping. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; pp. 3243–3253. [Google Scholar]
- Xiong, W.; Hoang, T.; Wang, W.Y. DeepPath: A Reinforcement Learning Method for Knowledge Graph Reasoning. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, EMNLP 2017, Copenhagen, Denmark, 9–11 September 2017; pp. 564–573. [Google Scholar]
- Guu, K.; Miller, J.; Liang, P. Traversing Knowledge Graphs in Vector Space. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, EMNLP 2015, Lisbon, Portugal, 17–21 September 2015; pp. 318–327. [Google Scholar]
- Lin, Y.; Liu, Z.; Luan, H.; Sun, M.; Rao, S.; Liu, S. Modeling Relation Paths for Representation Learning of Knowledge Bases. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, EMNLP 2015, Lisbon, Portugal, 17–21 September 2015; pp. 705–714. [Google Scholar]
- Krompaß, D.; Baier, S.; Tresp, V. Type-constrained representation learning in knowledge graphs. In Proceedings of the The Semantic Web-ISWC 2015: 14th International Semantic Web Conference, Bethlehem, PA, USA, 11–15 October 2015; Proceedings, Part I 14. Springer: Berlin/Heidelberg, Germany, 2015; pp. 640–655. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
