An Encryption Application and FPGA Realization of a Fractional Memristive Chaotic System
Abstract
1. Introduction
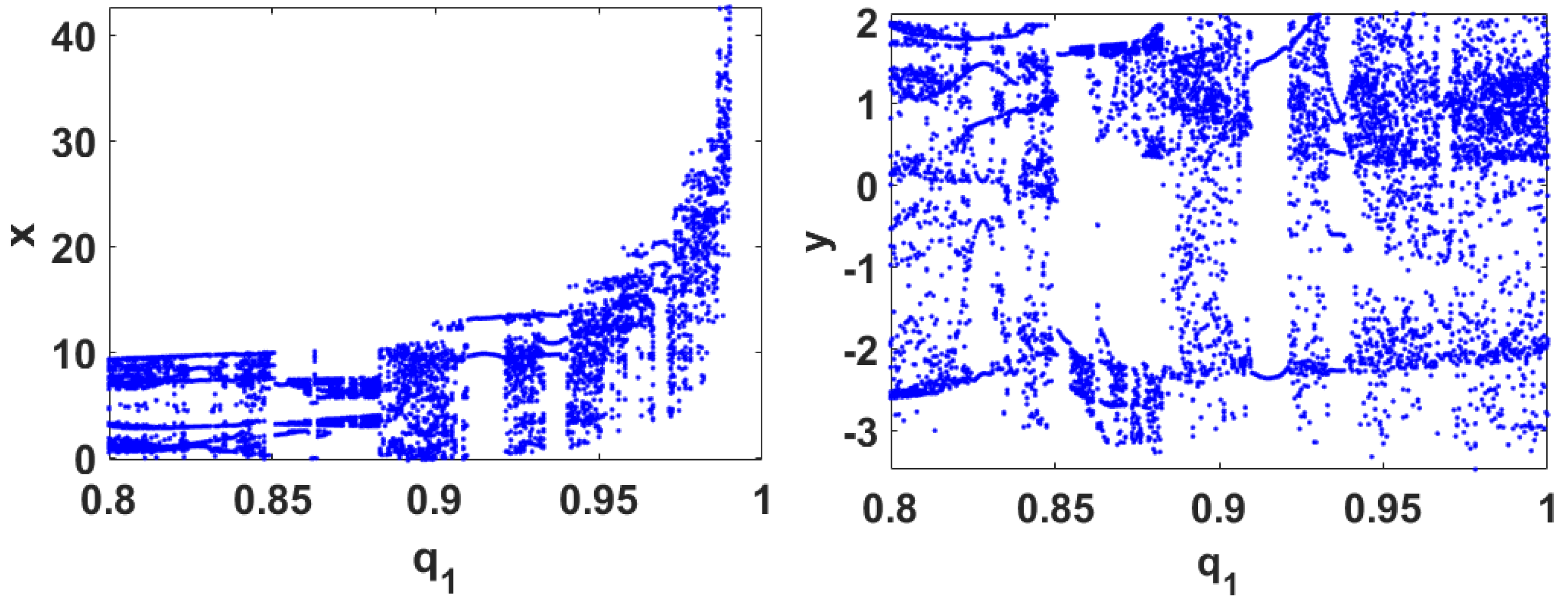
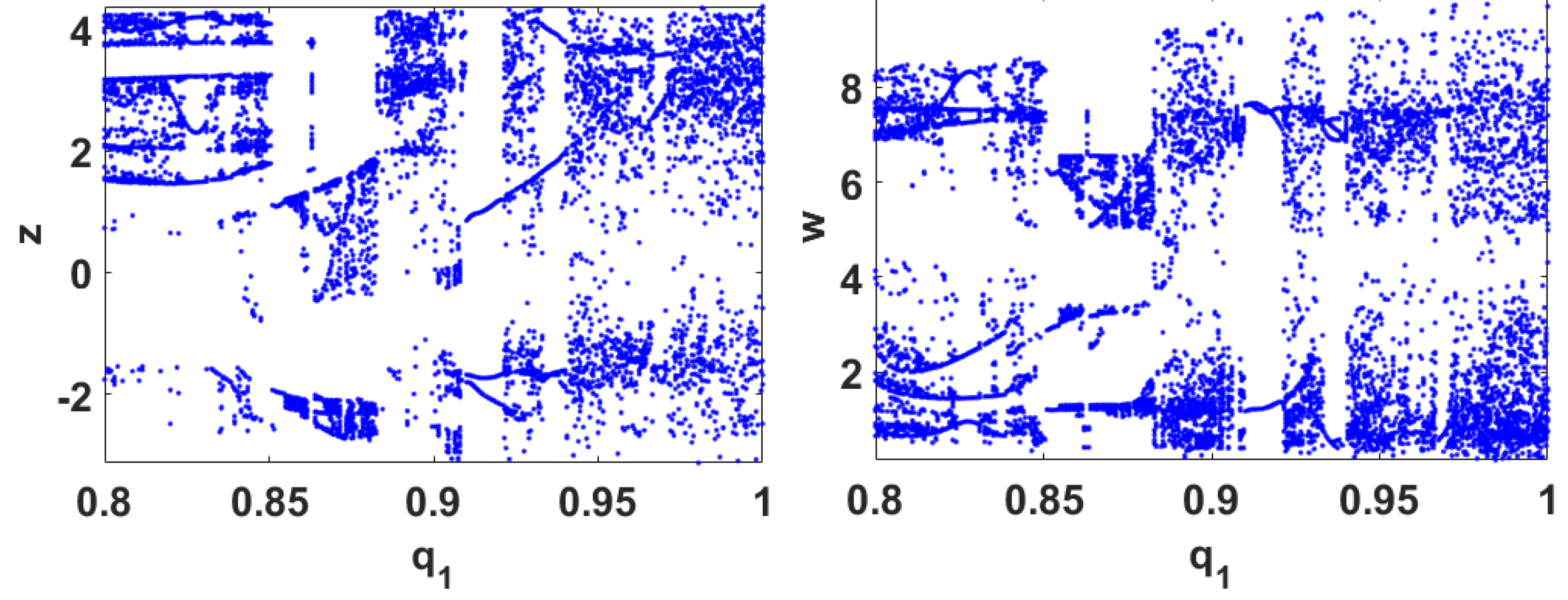
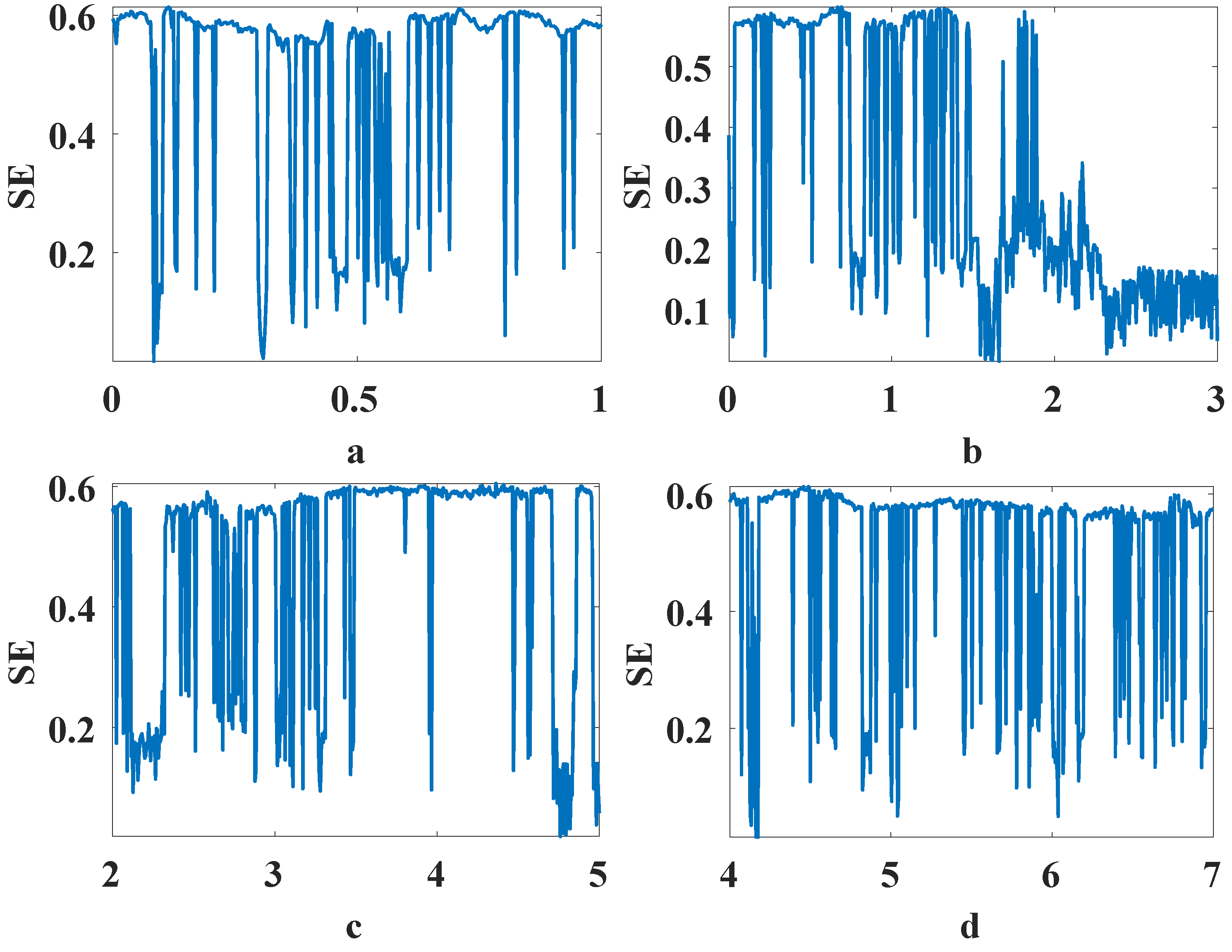
2. The Proposed Fractional-Order Memristive Chaotic System
3. A PRNG and the Encryption Scheme
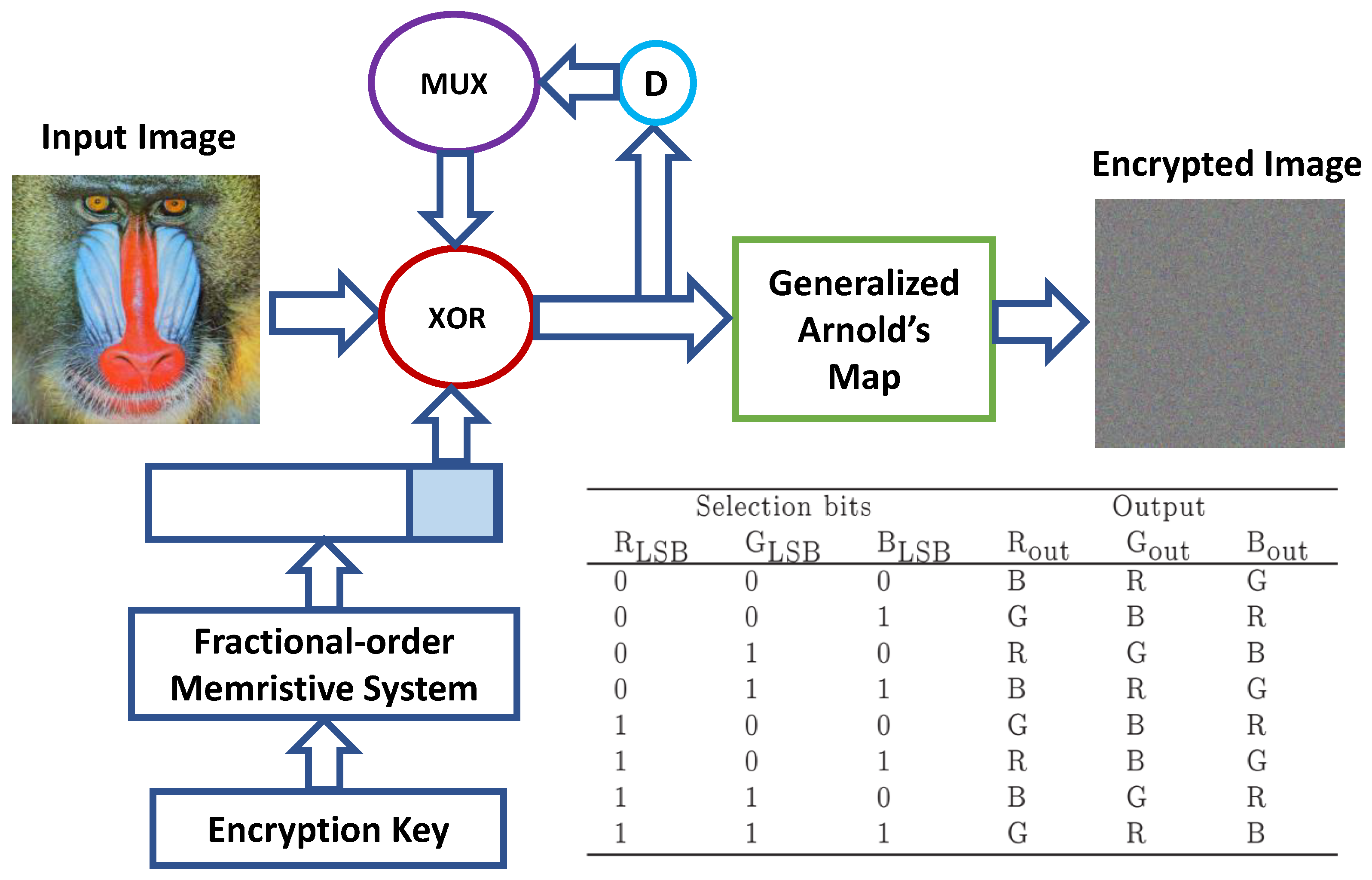
3.1. Encryption Scheme
3.2. Performance Evaluation
3.2.1. Statistical Tests
3.2.2. Key Space and Key Sensitivity
3.2.3. Resistance to Differential Attacks
4. FPGA Implementation and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Aliabadi, F.; Majidi, M.H.; Khorashadizadeh, S. Chaos synchronization using adaptive quantum neural networks and its application in secure communication and cryptography. Neural Comput. Appl. 2022, 34, 6521–6533. [Google Scholar] [CrossRef]
- Hosny, K.M.; Abd Elaziz, M.; Darwish, M.M. Color face recognition using novel fractional-order multi-channel exponent moments. Neural Comput. Appl. 2021, 33, 5419–5435. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Ren, F.; Yang, Z. Design of a high throughput pseudo-random number generator based on discrete hyper-chaotic system. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 806–810. [Google Scholar]
- Yang, F.; Mou, J.; Liu, J.; Ma, C.; Yan, H. Characteristic analysis of the fractional-order hyperchaotic complex system and its image encryption application. Signal Process. 2020, 169, 107373. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Tolba, M.F.; Said, L.A.; Madian, A.H.; Radwan, A.G. FPGA implementation of fractional-order integrator and differentiator based on Grünwald Letnikov’s definition. In Proceedings of the 2017 29th International Conference on Microelectronics (ICM), Singapore, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Tour, J.M.; He, T. Electronics: The fourth element. Nature 2008, 453, 42–43. [Google Scholar] [CrossRef] [PubMed]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Kokate, P.P. Memristor-based chaotic circuits. IETE Tech. Rev. 2009, 26, 417–429. [Google Scholar] [CrossRef]
- Chen, M.; Sun, M.; Bao, H.; Hu, Y.; Bao, B. Flux–charge analysis of two-memristor-based Chua’s circuit: Dimensionality decreasing model for detecting extreme multistability. IEEE Trans. Ind. Electron. 2019, 67, 2197–2206. [Google Scholar] [CrossRef]
- Chai, X.; Zheng, X.; Gan, Z.; Han, D.; Chen, Y. An image encryption algorithm based on chaotic system and compressive sensing. Signal Process. 2018, 148, 124–144. [Google Scholar] [CrossRef]
- Li, H.; Hua, Z.; Bao, H.; Zhu, L.; Chen, M.; Bao, B. Two-dimensional memristive hyperchaotic maps and application in secure communication. IEEE Trans. Ind. Electron. 2020, 68, 9931–9940. [Google Scholar] [CrossRef]
- Bao, B.; Qian, H.; Wang, J.; Xu, Q.; Chen, M.; Wu, H.; Yu, Y. Numerical analyses and experimental validations of coexisting multiple attractors in Hopfield neural network. Nonlinear Dyn. 2017, 90, 2359–2369. [Google Scholar] [CrossRef]
- ElSafty, A.H.; Tolba, M.F.; Said, L.A.; Madian, A.H.; Radwan, A.G. A study of the nonlinear dynamics of human behavior and its digital hardware implementation. J. Adv. Res. 2020, 25, 111–123. [Google Scholar] [CrossRef]
- Wang, L.; Dong, T.; Ge, M.F. Finite-time synchronization of memristor chaotic systems and its application in image encryption. Appl. Math. Comput. 2019, 347, 293–305. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Kacar, S.; Pham, V.T.; Alsaadi, F.E. A new fractional-order hyperchaotic memristor oscillator: Dynamic analysis, robust adaptive synchronization, and its application to voice encryption. Appl. Math. Comput. 2020, 383, 125310. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kengne, L.K.; Kuate, P.D.K.; Chen, C. Two-memristor-based chaotic system with infinite coexisting attractors. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 2197–2201. [Google Scholar] [CrossRef]
- Chai, X.; Gan, Z.; Yang, K.; Chen, Y.; Liu, X. An image encryption algorithm based on the memristive hyperchaotic system, cellular automata and DNA sequence operations. Signal Process. Image Commun. 2017, 52, 6–19. [Google Scholar] [CrossRef]
- Hu, Y.; Li, Q.; Ding, D.; Jiang, L.; Yang, Z.; Zhang, H.; Zhang, Z. Multiple coexisting analysis of a fractional-order coupled memristive system and its application in image encryption. Chaos Solitons Fractals 2021, 152, 111334. [Google Scholar] [CrossRef]
- Li, P.; Xu, J.; Mou, J.; Yang, F. Fractional-order 4D hyperchaotic memristive system and application in color image encryption. EURASIP J. Image Video Process. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Sayed, W.S.; Radwan, A.G. Generalized switched synchronization and dependent image encryption using dynamically rotating fractional-order chaotic systems. AEU-Int. J. Electron. Commun. 2020, 123, 153268. [Google Scholar] [CrossRef]
- Rahman, Z.A.S.; Jasim, B.H.; Al-Yasir, Y.I.; Abd-Alhameed, R.A. High-Security Image Encryption Based on a Novel Simple Fractional-Order Memristive Chaotic System with a Single Unstable Equilibrium Point. Electronics 2021, 10, 3130. [Google Scholar] [CrossRef]
- Tolba, M.F.; AbdelAty, A.M.; Soliman, N.S.; Said, L.A.; Madian, A.H.; Azar, A.T.; Radwan, A.G. FPGA implementation of two fractional order chaotic systems. AEU-Int. J. Electron. Commun. 2017, 78, 162–172. [Google Scholar] [CrossRef]
- Sayed, W.S.; Radwan, A.G.; Fahmy, H.A.; El-Sedeek, A. Software and hardware implementation sensitivity of chaotic systems and impact on encryption applications. Circuits Syst. Signal Process. 2020, 39, 5638–5655. [Google Scholar] [CrossRef]
- Sayed, W.S.; Mohamed, S.M.; Elwakil, A.S.; Said, L.A.; Radwan, A.G. Numerical Sensitivity Analysis and Hardware Verification of a Transiently-Chaotic Attractor. Int. J. Bifurc. Chaos 2022, 32, 2250103. [Google Scholar] [CrossRef]
- Soriano-Sánchez, A.G.; Posadas-Castillo, C.; Platas-Garza, M.A.; Arellano-Delgado, A. Synchronization and FPGA realization of complex networks with fractional–order Liu chaotic oscillators. Appl. Math. Comput. 2018, 332, 250–262. [Google Scholar]
- Chen, H.; Cheng, K.; Lu, Z.; Fu, Y.; Li, L. Hyperbolic CORDIC-based architecture for computing logarithm and its implementation. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2652–2656. [Google Scholar] [CrossRef]
- Sayed, W.S.; Roshdy, M.; Said, L.A.; Radwan, A.G. Design and FPGA verification of custom-shaped chaotic attractors using rotation, offset boosting and amplitude control. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3466–3470. [Google Scholar] [CrossRef]
- Mohamed, S.M.; Sayed, W.S.; Radwan, A.G.; Said, L.A. FPGA Implementation of Reconfigurable CORDIC Algorithm and a Memristive Chaotic System With Transcendental Nonlinearities. IEEE Trans. Circuits Syst. I Regul. Pap. 2022. [Google Scholar] [CrossRef]
- Mohamed, S.M.; Sayed, W.S.; Said, L.A.; Radwan, A.G. Reconfigurable FPGA Realization of Fractional-Order Chaotic Systems. IEEE Access 2021, 9, 89376–89389. [Google Scholar] [CrossRef]
- Gu, J.; Li, C.; Chen, Y.; Iu, H.H.; Lei, T. A conditional symmetric memristive system with infinitely many chaotic attractors. IEEE Access 2020, 8, 12394–12401. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, H. Complexity analysis and DSP implementation of the fractional-order Lorenz hyperchaotic system. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef]
- Sayed, W.S.; Radwan, A.G.; Fahmy, H.A.; Elsedeek, A. Trajectory control and image encryption using affine transformation of lorenz system. Egypt. Inform. J. 2021, 22, 155–166. [Google Scholar] [CrossRef]
- Radwan, A.G.; AbdElHaleem, S.H.; Abd-El-Hafiz, S.K. Symmetric encryption algorithms using chaotic and non-chaotic generators: A review. J. Adv. Res. 2016, 7, 193–208. [Google Scholar] [CrossRef] [PubMed]
- Weber, A.G. The USC-SIPI Image Database: Version 5, Original Release; Signal and Image Processing Institute, Department of Electrical Engineering, University of Southern California: Los Angeles, CA, USA, 1997. [Google Scholar]
- Bassham, L.E.; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Barker, E.B.; Leigh, S.D.; Levenson, M.; Vangel, M.; Banks, D.L.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Technical Report; Booz-Allen and Hamilton Inc.: Mclean, VA, USA, 2010. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. Cyber J. Multidiscip. J. Sci. Technol. J. Sel. Areas Telecommun. (JSAT) 2011, 1, 31–38. [Google Scholar]





| Performance Measure | Equation |
|---|---|
| Correlation coefficient | , where , |
| , (height) width). | |
| Mean squared error | MSE , where are the original |
| incorrectly decrypted image pixels. | |
| Entropy | , where is the probability of symbol . |
| Number of pixels | |
| change rate | , |
| Unified average | |
| changing intensity | , |
| where is the ciphered pixel and | |
| is the ciphered pixel corresponding to a slightly modified original image. |
| Image | Horizontal | Vertical | Diagonal | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R | G | B | R | G | B | R | G | B | |
| Baboon | |||||||||
| Peppers | |||||||||
| Barb | |||||||||
| Lake | |||||||||
| Baboon | Peppers | Barb | Lake | Baboon [34] | Peppers [34] | ||
|---|---|---|---|---|---|---|---|
| Entropy | |||||||
| MSE | 8609 | 10151 | 8540 | 10115 | 8710 | 8798 | |
| Key sens. | Entropy | ||||||
| MSE | 8502 | 9935 | 8408 | 9950 | 8701 | 8034 | |
| DA | NPCR (%) | ||||||
| UACI (%) |
| Test | PRNG | Baboon | Peppers | Barb | Lake | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| PV | PP | PV | PP | PV | PP | PV | PP | PV | PP | |
| Frequency | ✔ | 1 | ✔ | 1 | ✔ | 1 | ✔ | ✔ | 1 | |
| Block frequency | ✔ | 1 | ✔ | 1 | ✔ | 1 | ✔ | ✔ | ||
| Cumulative sums | ✔ | 1 | ✔ | 1 | ✔ | 1 | ✔ | 1 | ✔ | 1 |
| Runs | ✔ | 1 | ✔ | ✔ | 1 | ✔ | 1 | ✔ | 1 | |
| Longest run | ✔ | 1 | ✔ | 1 | ✔ | 1 | ✔ | ✔ | 1 | |
| Rank | ✔ | 1 | ✔ | 1 | ✔ | 1 | ✔ | 1 | ✔ | 1 |
| FFT | ✔ | 1 | ✔ | ✔ | 1 | ✔ | 1 | ✔ | ||
| Non-overlapping template | ✔ | ✔ | ✔ | ✔ | ✔ | |||||
| Overlapping template | ✔ | 1 | ✔ | ✔ | ✔ | 1 | ✔ | 1 | ||
| Universal | ✔ | ✔ | 1 | ✔ | 1 | ✔ | 1 | ✔ | ||
| Approximate entropy | ✔ | ✔ | ✔ | ✔ | 1 | ✔ | ||||
| Random excursions | ✔ | ✔ | 1 | ✔ | 1 | ✔ | ✔ | 1 | ||
| Random excursions variant | ✔ | ✔ | 1 | ✔ | 1 | ✔ | ✔ | |||
| Serial | ✔ | ✔ | 1 | ✔ | 1 | ✔ | 1 | ✔ | 1 | |
| Linear complexity | ✔ | ✔ | 1 | ✔ | 1 | ✔ | 1 | ✔ | 1 | |
| Final result | Passed | Passed | Passed | Passed | Passed | |||||
| Total Slices | Total Slice LUTs | Total Slice Regs | DSPs | Max Freq (MHz) | Throughput (Gbit/s) | Order | Params. | |
|---|---|---|---|---|---|---|---|---|
| Proposed | 6269 | 23,929 | 4599 | 144 | 12.368 | 0.396 | Fractional | 8 |
| [30] | 951 | 3440 | 374 | 84 | 14.009 | 0.4483 | Integer | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, S.M.; Sayed, W.S.; Madian, A.H.; Radwan, A.G.; Said, L.A. An Encryption Application and FPGA Realization of a Fractional Memristive Chaotic System. Electronics 2023, 12, 1219. https://doi.org/10.3390/electronics12051219
Mohamed SM, Sayed WS, Madian AH, Radwan AG, Said LA. An Encryption Application and FPGA Realization of a Fractional Memristive Chaotic System. Electronics. 2023; 12(5):1219. https://doi.org/10.3390/electronics12051219
Chicago/Turabian StyleMohamed, Sara M., Wafaa S. Sayed, Ahmed H. Madian, Ahmed G. Radwan, and Lobna A. Said. 2023. "An Encryption Application and FPGA Realization of a Fractional Memristive Chaotic System" Electronics 12, no. 5: 1219. https://doi.org/10.3390/electronics12051219
APA StyleMohamed, S. M., Sayed, W. S., Madian, A. H., Radwan, A. G., & Said, L. A. (2023). An Encryption Application and FPGA Realization of a Fractional Memristive Chaotic System. Electronics, 12(5), 1219. https://doi.org/10.3390/electronics12051219










