Research on Testing Method for Shielding Effectiveness of Irregular Cavity Based on Field Distribution Characteristics
Abstract
:1. Introduction
2. Electromagnetic Topology Calculation Model of Shielding Effectiveness of Irregular Cavity
2.1. Electromagnetic Topology Modle
- -
- is the voltage vector.
- -
- is the unit hypermatrix.
- -
- S is the scattering matrix.
- -
- is the propagation matrix.
- -
- is the source vector.
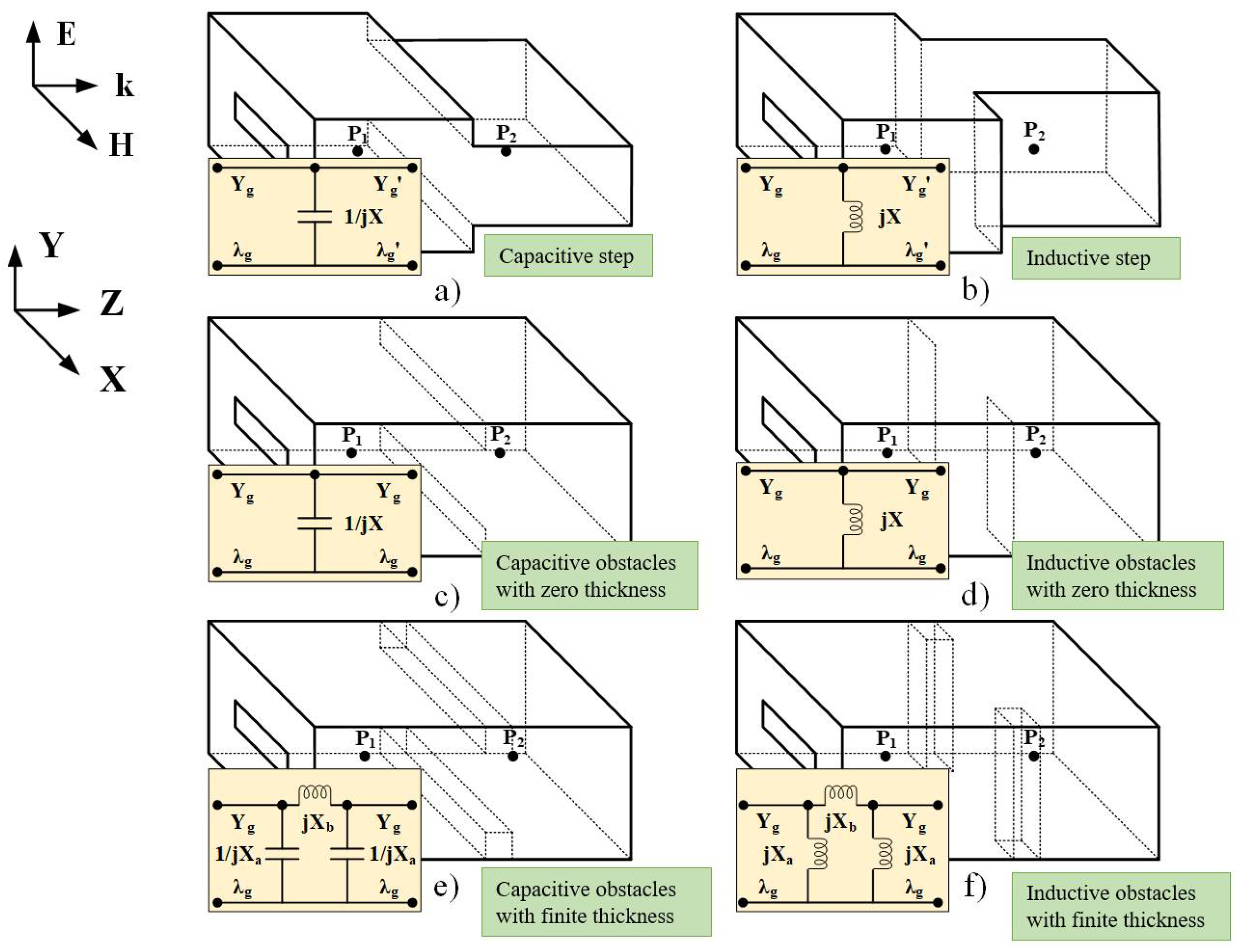
2.2. Irregular Cavity Classification
- 1.
- Capacitive step
- 2.
- Inductive step
- 3.
- Capacitive obstacles with a zero thickness value
- 4.
- Inductive obstacles with a zero thickness value
- 5.
- Capacitive obstacles with finite thickness
- 6.
- Inductive obstacles with finite thickness
3. Simulation Analysis of Field Distribution in Irregular Cavity
3.1. Simulation Parameters of Irregular Cavity Field Distribution
3.2. Simulation Results of Field Distribution in the Irregular Cavity
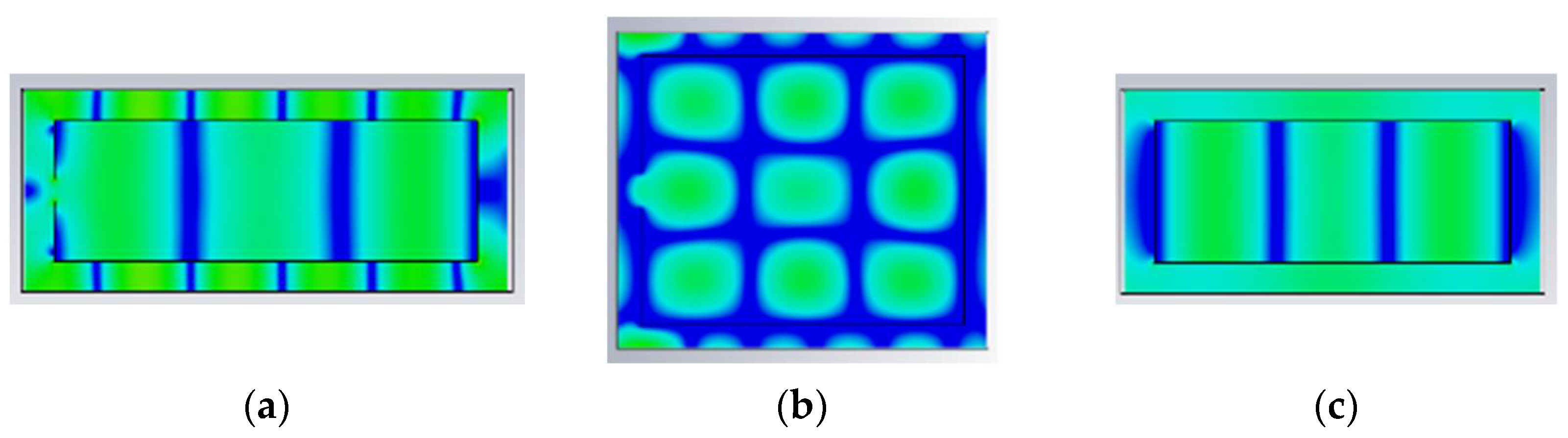
3.2.1. Basic Model Field Distribution
3.2.2. Field Distributions of Capacitive Step and Inductive Step
3.2.3. Field Distributions of Capacitive and Inductive obstacles with a Finite Thickness
3.2.4. Field Distributions of Capacitive and Inductive Obstacles with Zero Thickness
3.3. Analysis of Field Distribution in Special-Shaped Cavity
- 1.
- The effects of irregular structures.
- 2.
- Selection of observation points.
- Irregular cavities mean that the distributions of the front and back parts are different, with the cavity of the step structure being the most obvious part. As the step structure changes the size of the front and back parts of the cavity, and the change in the size of the capacitive step is the height direction, the mode transmission has only a small effect on the overall field distribution since there is no mode transmission in the height direction of the back part of the cavity in the Mode303. However, there are changes in the length direction of the back part of the cavity in the inductive steps, resulting in the coupling of the modes in the front and back parts of cavities.
- The regular cavity is similar to the irregular cavity of the thick block type on the whole, which is mainly reflected in the cross-coupling of the inductive thick block appearance mode.
- As there is a small volume in the cavity that the thin plate takes up, the capacitive thin plate has only a small effect on the field distribution of the cavity. In contrast, the inductive thin plate has more significant effects, which is similar to the inductive thick block.
4. Characterization and Test Method of Shielding Effectiveness of Irregular Cavity
4.1. Characterization of Shielding Effectiveness of Irregular Cavity
4.2. Test Method for Shielding Effectiveness of Irregular Cavity
5. Measurement for Shielding Effectiveness of Irregular Cavity
5.1. Test Parameters
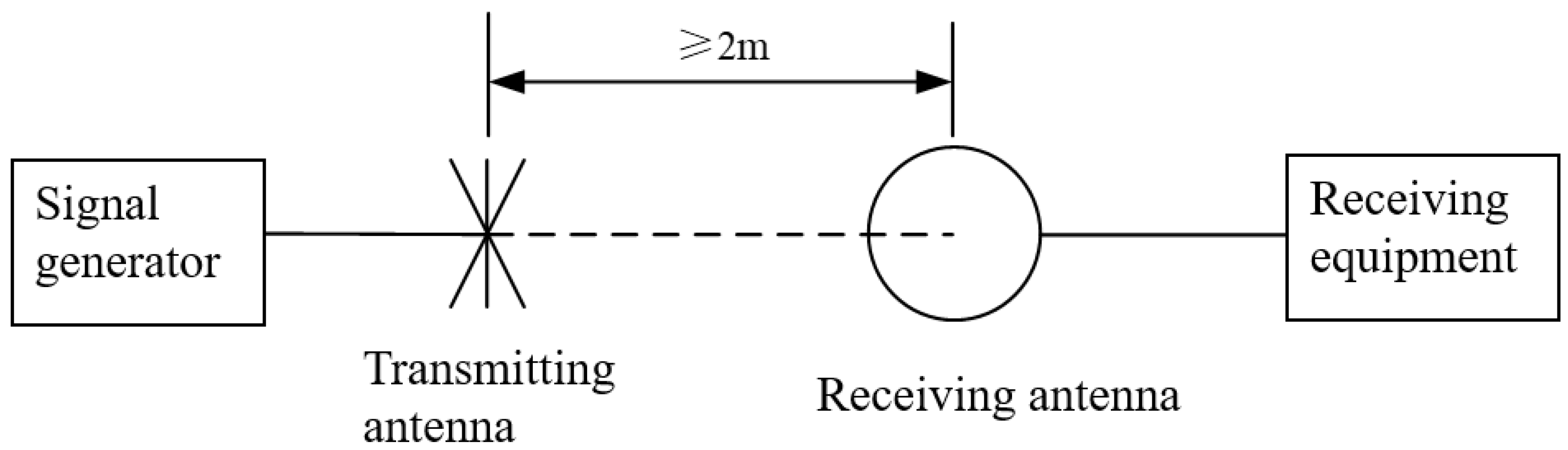
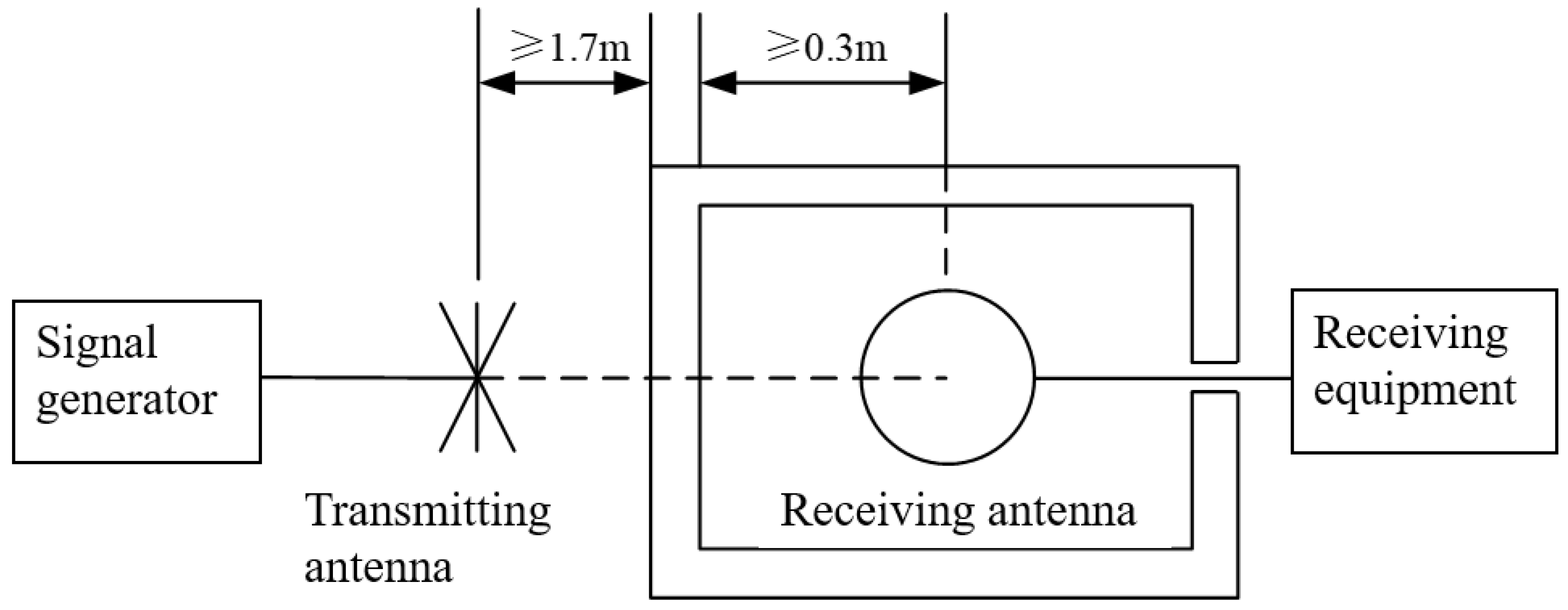
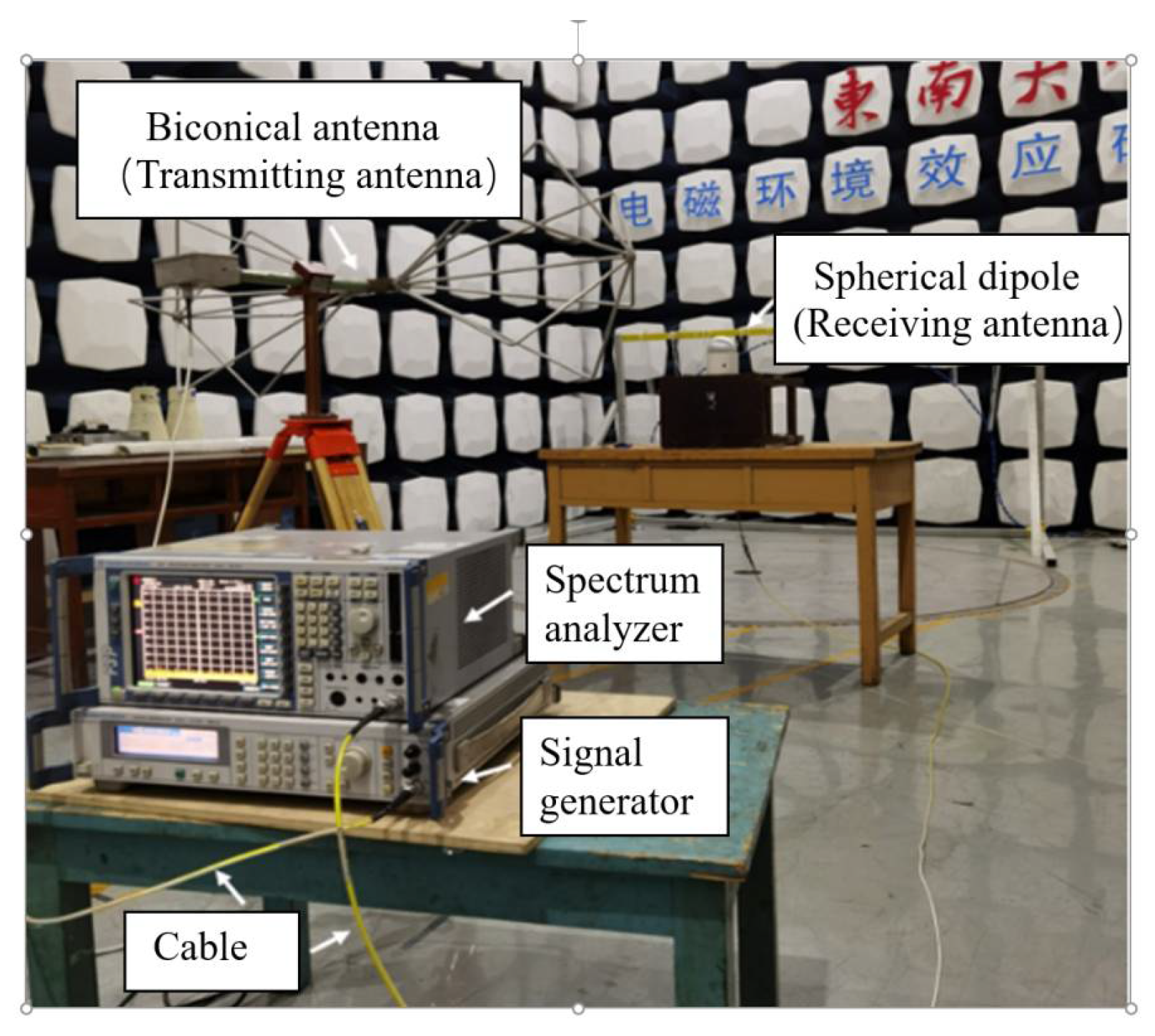
5.2. Test Layout
5.2.1. Reference Test Arrangement
5.2.2. Shield Test Arrangement
5.3. Test Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jóskiewicz, Z.; Janukiewicz, J. Experimental Study of the Shielding Effectiveness Performance Degradation for a Shielding Material Used in Protective Storage Pouch. In Proceedings of the 2020 International Symposium on Electromagnetic Compatibility-EMC EUROPE, Rome, Italy, 23–25 September 2020; pp. 1–4. [Google Scholar]
- Li, H.; Bao, X.; Zhou, H. Electromagnetic Pulse Propagation over Large Area Simulation through Massively Parallel Adaptive Mesh Refinement FDTD. In Proceedings of the 2019 International Symposium on Electromagnetic Compatibility-EMC EUROPE, Barcelona, Spain, 2–6 September 2019. [Google Scholar]
- Xiao, L.; Wang, X.H.; Wang, B.Z.; Zheng, G.; Chen, P. An Efficient Hybrid Method of Iterative MoM-PO and Equivalent Dipole-Moment for Scattering From Electrically Large Objects. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1723–1726. [Google Scholar] [CrossRef]
- Geng, L.; Liu, X.; He, H. Analytical formulation for the coupling coefficient of equivalent impedance to calculated shielding effectiveness by TLM. In Proceedings of the 2017 IEEE 5th International Symposium on Electromagnetic Compatibility (EMC-Beijing), Beijing, China, 28–31 October 2017. [Google Scholar]
- Cruciani, S.; Feliziani, M.; Maradei, F. Prediction of shielding effectiveness in graphene enclosures by FEM-INBC method. In Proceedings of the 2015 Asia-Pacific Symposium on Electromagnetic Compatibility, Taipei, Taiwan, 26–29 May 2015. [Google Scholar]
- Wang, C.F. Development of Higher-Order DG-FETD Tool for Efficient Modeling of Complex Electromagnetic Structures. In Proceedings of the 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Atlanta, GA, USA, 7–12 July 2019. [Google Scholar]
- Li, M.; Liu, B.; Wei, Q.; Yu, K.; Wang, C.; Zeng, X. Time-Frequency Analysis on Earth Fault Signal Response Based on the BLT Equation for MultiBranch Distribution Networks. In Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, China, 20–23 September 2020; pp. 1–5. [Google Scholar]
- Choo, J.; Choo, J.; Kim, Y.H. Shielding Effectiveness of Open Cabinet Containing Digital Modules Using Ferrite Sheet. IEEE Trans. Magn. 2017, 53, 2900609. [Google Scholar] [CrossRef]
- Konefal, T.; Dawson, J.F.; Marvin, A.C.; Robinson, M.P.; Porter, S.J. A fast multiple mode intermediate level circuit model for the prediction of shielding effectiveness of a rectangular box containing a rectangular aperture. IEEE Trans. Electromagn. Compat. 2005, 47, 678–691. [Google Scholar] [CrossRef] [Green Version]
- Robinson, M.P.; Benson, T.M.; Christopoulos, C.; Dawson, J.F.; Ganley, M.D.; Marvin, A.C.; Porter, S.J.; Thomas, D.W. Analytical formulation for the shielding effectiveness of enclosures with apertures. IEEE Trans. Electromagn. Compat. 1998, 40, 240–248. [Google Scholar] [CrossRef] [Green Version]
- Solin, J.R. Formula for the field excited in a rectangular cavity with a small aperture. IEEE Trans. Electromagn. Compat. 2011, 53, 82–90. [Google Scholar] [CrossRef]
- Solin, J.R. Formula for the field excited in a rectangular cavity with an electrically large aperture. IEEE Trans. Electromagn. Compat. 2012, 54, 188–192. [Google Scholar] [CrossRef]
- Lee, J.G.; Eom, H.J.; Kim, B.W.; Park, H.H. Shielding effectiveness of enclosure with thick multiple apertures. Microw. Opt. Technol. Lett. 2001, 29, 178–181. [Google Scholar] [CrossRef]
- Wallyn, W.; Zutter, D.D.; Laermans, E. Fast shielding effectiveness prediction for realistic rectangular enclosures. IEEE Trans. Electromagn. Compat. 2003, 45, 639–643. [Google Scholar] [CrossRef]
- Park, H.H.; Eom, H.J. Electromagnetic penetration into a rectangular cavity with multiple rectangular apertures in a conducting plane. IEEE Trans. Electromagn. Compat. 2000, 42, 303–307. [Google Scholar] [CrossRef]
- Konefal, T.; Dawson, J.F.; Marvin, A.C.; Robinson, M.P.; Porter, S.J. A fast circuit model description of the shielding effectiveness of a box with imperfect gaskets or apertures covered by thin resistive sheet coatings. IEEE Trans. Electromagn. Compat. 2006, 48, 134–144. [Google Scholar] [CrossRef]
- Lehman, T.H.; Miller, E.K. The elementary statistical properties of electromagnetic fields in complex cavities. In Proceedings of the ICAP 91, Seventh International Conference on Antennas and Propagation, York, UK, 15–18 April 1991; Volume 2, pp. 938–941. [Google Scholar]
- Hill, D.A. Plane wave integral representation for fields in reverberation chambers. IEEE Trans. Electromagn. Compat. 1998, 40, 209–217. [Google Scholar] [CrossRef] [Green Version]
- Hill, D.A.; Ladbury, J.M. Spatial-correlation functions of fields and energy density in a reverberation chamber. IEEE Trans. Electromagn. Compat. 2002, 44, 95–101. [Google Scholar] [CrossRef]
- Gradoni, G.; Antonsen, T.M.; Ott, E.; Anlage, S.M. Random coupling model for the radiation of statistical sources inside cavities. In Proceedings of the 2016 46th European Microwave Conference, London, UK, 4–6 October 2016. [Google Scholar]
- Gil, J.G.; Drikas, Z.B.; Andreadis, T.D.; Anlage, S.M. Prediction of Induced Voltages on Ports in Complex, Three-Dimensional Enclosures With Apertures, Using the Random Coupling Model. IEEE Trans. Electromagn. Compat. 2016, 58, 1535–1540. [Google Scholar] [CrossRef]
- The Certification of Aircraft Electrical and Electronic Systems for Operation in the High-Intensity Radiated Fields (HIRF) Environment; AA AC 20-158A (05/14); Federal Aviation Administration: Washington, DC, USA, 2014.
- IEEE Std 299-2006; IEEE Standard Method for Measuring the Effectiveness of Electromagnetic Shielding Enclosures. IEEE: Piscataway, NJ, USA, 2006.
- IEEE Std 299.1-2013; IEEE Standard Method for Measuring the Shielding Effectiveness of Enclosures and Boxes Having All Dimensions between 0.1 m and 2 m. IEEE: Piscataway, NJ, USA, 2013.
- IEC TS 61587-3-2013; Mechanical Structures for Electronic Equipment–Test for IEC 60917 and IEC 60297–Part 3: Electromagnetic Shielding Performance Tests for Cabinets, Racks and Subracks. IEC: Geneva, Switzerland, 2013.
- Pan, Y.; Ren, J.; Zhou, Z.; Zhang, T. Research on Calculation Method of Shielding Effectiveness of Irregular Cavity. In Proceedings of the 2021 IEEE 5th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Xi’an, China, 15–17 October 2021. [Google Scholar]
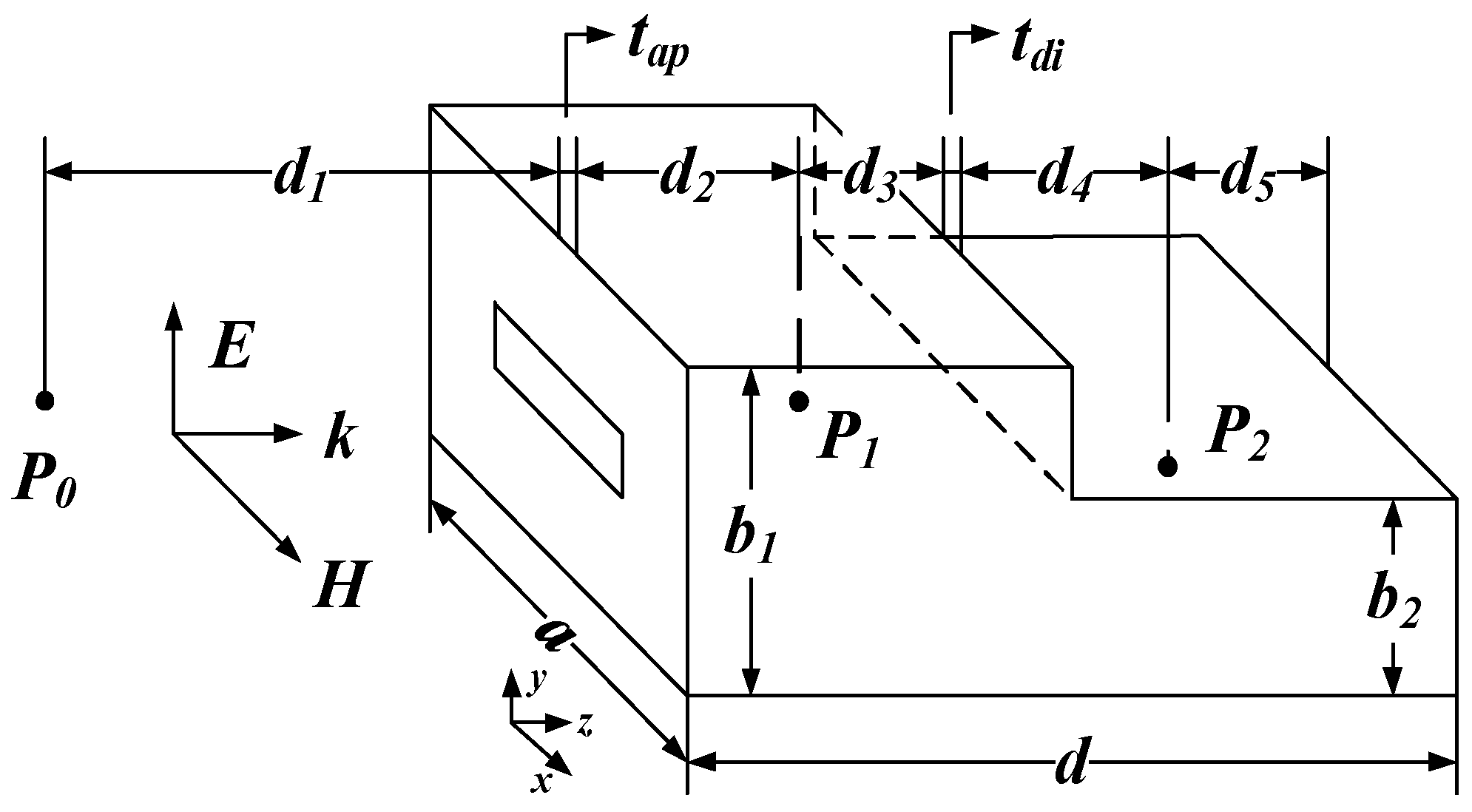
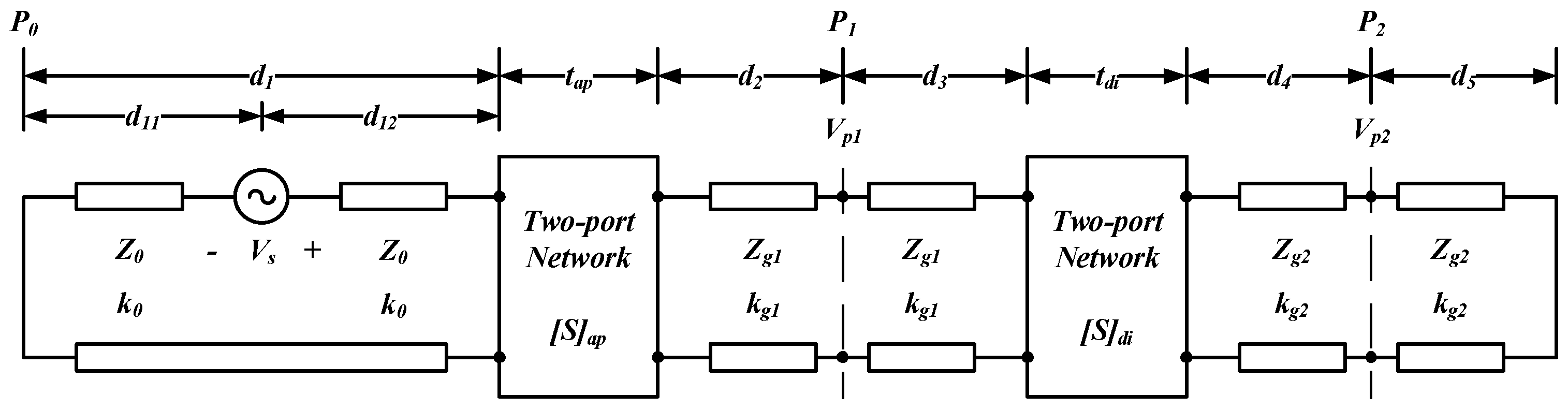

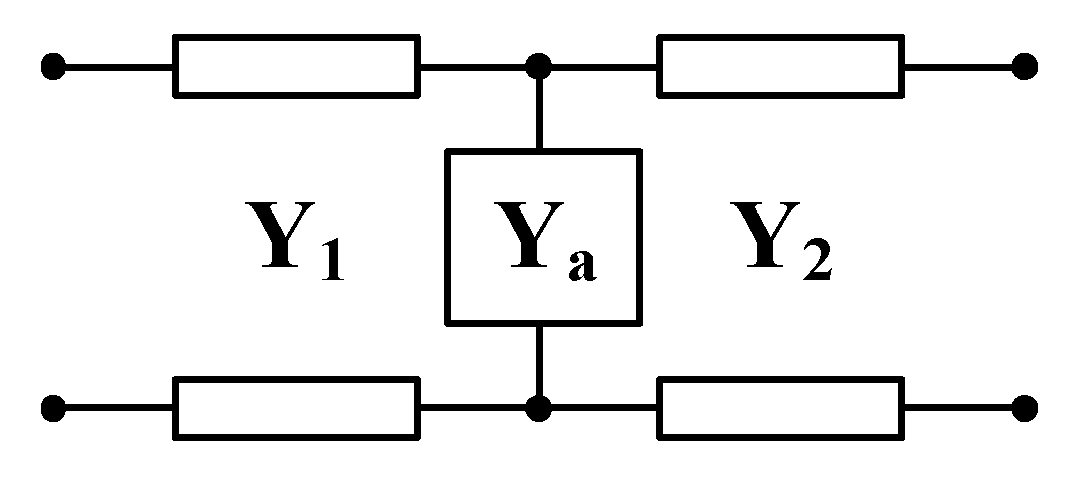
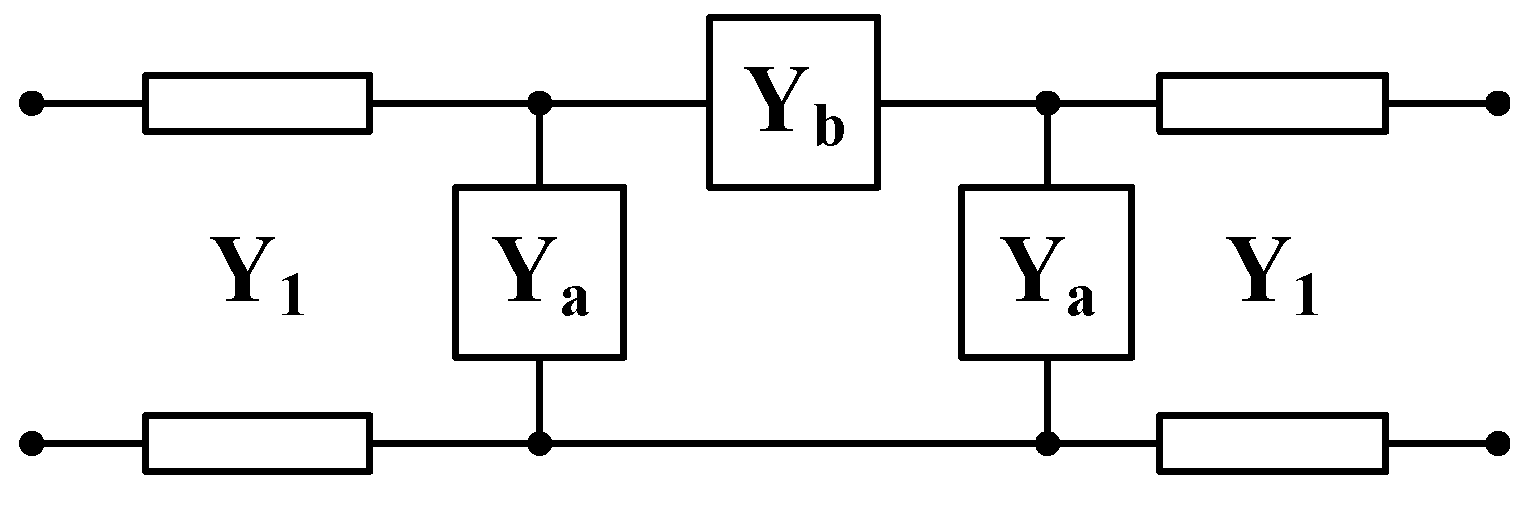








| Numbering | Type | Heteromorphic Structure Parameters |
|---|---|---|
| 1 | Capacitive step | 300 × 20 × 160 mm3 |
| 2 | Inductive step | 30 × 120 × 160 mm3 |
| 3 | Capacitive obstacles with a zero thickness value | 300 × 20 × 1 mm3, d2 +d3 = 180 mm |
| 4 | Inductive obstacles with a zero thickness value | 25 × 120 × 1 mm3, d2 +d3 = 180 mm |
| 5 | Capacitive obstacles with a finite thickness | 300 × 10 × 40 mm3, d2 +d3 = 200 mm |
| 6 | Inductive obstacles with a finite thickness | 20 × 120 × 40 mm3, d2 +d3 = 200 mm |
| Test Frequency Band | Location and Number of Observation Points |
|---|---|
| 20 MHz~0.8 fr | Single point: Cavity center position |
| 0.8 fr~1 GHz | Multi-point: the center position of the x-direction, the y-direction or the center position of the multi-segment division, and the center position of the multi-segment division in the z-direction |
| Figure | Type of Transmitting Antenna | Polarization Direction | Shielding Effectiveness/dB |
|---|---|---|---|
| 30 | Biconical antenna | Horizontal | 38.08 |
| Vertical | 34.34 | ||
| 50 | Biconical antenna | Horizontal | 34.5 |
| Vertical | 35.85 | ||
| 80 | Biconical antenna | Horizontal | 32.97 |
| Vertical | 33.11 | ||
| 100 | Biconical antenna | Horizontal | 43.06 |
| Vertical | 42.82 | ||
| 100 | Periodic log antenna | Horizontal | 46.23 |
| Vertical | 42.63 | ||
| 200 | Periodic log antenna | Horizontal | 34.14 |
| Vertical | 31.92 | ||
| 300 | Periodic log antenna | Horizontal | 26.54 |
| Vertical | 31.49 | ||
| 500 | Periodic log antenna | Horizontal | 25.07 |
| Vertical | 28.24 | ||
| 800 | Periodic log antenna | Horizontal | 18.21 |
| Vertical | 19.2 | ||
| 1000 | Periodic log antenna | Horizontal | 14.26 |
| Vertical | 16.68 |
| Frequency/MHz | Polarization Direction | No.1 SE/dB | No.2 SE/dB | No.3 SE/dB | No.4 SE/dB | No.5 SE/dB |
|---|---|---|---|---|---|---|
| 500 | Horizontal | 25.07 | 24.79 | 26.59 | 24.83 | 24.25 |
| Vertical | 28.24 | 28.72 | 27.19 | 28.78 | 27.7 | |
| 800 | Horizontal | 18.21 | 17.88 | 18.12 | 18.89 | 18.03 |
| Vertical | 19.2 | 20.85 | 18.65 | 20.03 | 19.07 | |
| 1000 | Horizontal | 14.26 | 14.51 | 14.29 | 15.08 | 14.85 |
| Vertical | 16.68 | 16.64 | 17.44 | 17.04 | 17.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Pan, Y.; Zhou, Z.; Zhang, T. Research on Testing Method for Shielding Effectiveness of Irregular Cavity Based on Field Distribution Characteristics. Electronics 2023, 12, 1035. https://doi.org/10.3390/electronics12041035
Ren J, Pan Y, Zhou Z, Zhang T. Research on Testing Method for Shielding Effectiveness of Irregular Cavity Based on Field Distribution Characteristics. Electronics. 2023; 12(4):1035. https://doi.org/10.3390/electronics12041035
Chicago/Turabian StyleRen, Jinjing, Yuhao Pan, Zhongyuan Zhou, and Tao Zhang. 2023. "Research on Testing Method for Shielding Effectiveness of Irregular Cavity Based on Field Distribution Characteristics" Electronics 12, no. 4: 1035. https://doi.org/10.3390/electronics12041035
APA StyleRen, J., Pan, Y., Zhou, Z., & Zhang, T. (2023). Research on Testing Method for Shielding Effectiveness of Irregular Cavity Based on Field Distribution Characteristics. Electronics, 12(4), 1035. https://doi.org/10.3390/electronics12041035





