1. Introduction
Traditionally, multimedia applications require high data processing speed due to the need to process the large amounts of data in real time. The performance of digital filters, windowing and Fourier transform blocks, and other arithmetic processors is mainly determined by the speed of the multipliers; so, the development of high-speed multipliers is relevant [
1,
2,
3]. The situation is similar when implementing the convolutional neural networks; the number of multipliers on each layer can be very large [
4,
5,
6,
7]. The hardware implementation of signal processing systems for many applications is based on the Field-Programmable Gate Array (FPGA). FPGA architecture allows for the continuous processing of input data due to the maximum parallelization of the calculations. FPGAs have embedded hardware multipliers, but multiplication can also be implemented using the logic cells. In some cases, the use of the logical cells is preferable. This is because the number of multipliers in an FPGA is limited, and their location and digit capacity are fixed. Moreover, the logic cells of modern FPGAs have an improved architecture which increases the performance of the arithmetic circuits [
8].
To increase the multiplication speed, various algorithmic methods have been developed. The first group of methods is based on decreasing the number of partial products by processing several digits of a multiplier simultaneously. These methods are based on Booth’s algorithm [
9], which performs multiplication by two digits at once, halving the number of partial products. A modified Booth’s algorithm [
10] is also used. It reduces the number of partial products by less than half but does not require any preliminary operations to compute the partial products. Subsequent modifications of Booth’s multipliers dealt with improving accuracy [
11,
12], minimizing the complexity of the design [
13], and accelerating the operation [
13,
14,
15]. There are also known extensions of Booth’s algorithm to perform more complex operations, such as the multiplication of three arguments [
16,
17]. The second group of multiplication optimization methods is related to paralleling the summation of partial products because the classical methods of summation (iterative and linear) are slow. One of the most effective methods of acceleration is based on the Wallace tree [
18], which implements the addition of different bits of partial products at the same time. Wallace tree implementations are also constantly being modified to minimize hardware costs [
19] and delays [
20,
21,
22]. Pipelining is used to improve the performance of multipliers [
23]. Often, all of these methods are used simultaneously [
24,
25,
26].
The improvement of the time characteristics of multipliers can be achieved by using tabular methods [
27,
28]. The choice of a specific optimization method depends on the hardware implementation technology. For FPGA-based digital design, tabular methods are most often used [
29,
30,
31], as well as the methods focused on paralleling computational operations [
32,
33,
34]. This makes it possible to obtain simple, fast computational blocks.
Constant coefficient multipliers are a special class of multipliers; these units perform multiplication by a fixed constant. These multipliers are often found in many signal processing applications where one of the multiplication arguments is constant. They can be filter coefficients, window function values, Fourier transform coefficients, and weights of a neural network. Traditionally the usual multipliers are used for signal multiplication by a constant, i.e., the multiplication is performed according to the same algorithm as the multiplication of one signal by another with an unknown value. At the same time, the constant coefficient multipliers can be optimized to be simpler and faster than the general purpose multipliers.
The configurable logic blocks of FPGAs designed to implement logic functions consist of a look-up table (LUT) with 4–6 inputs, depending on the FPGA family, the flip-flops, and the multiplexers. Due to this structural feature, when implementing arithmetic on an FPGA it is possible to use table methods based on the different table algorithms. These are, for example, the constant factor multiplier method based on canonical recoding, using the special algorithms to find the optimal chains of adders, subtractors, and shift elements [
35]; the constant factor multiplier construction method, using fine-grained FPGA memory resources and the special table search method [
36]; and the method using the pre-computation of partial products [
37].
In our paper, we have integrated different approaches to building the fast multipliers and evaluated the possibilities and effectiveness of their implementations in FPGA technologies. This paper is structured as follows. In
Section 2, we consider the multiplication acceleration method based on Booth’s algorithm (multiplication by two digits at a time) with maximal parallelization of partial product addition. We also propose the modification of this algorithm by the multiplication by three digits at a time.
Section 3 describes the implementation of the considered methods of multiplying two input binary codes as well as the input binary code by a constant on the FPGA. The results of the development are discussed in
Section 4, and the conclusion is given in
Section 5.
3. Designing a Multiplier on the FPGA Basis
To determine the efficiency of the proposed method, we compared its characteristics with the implementation of the modified Booth’s algorithm, performing multiplication by two digits at a time, as presented in
Section 2.1. We also analyzed the characteristics of the multipliers with an embedded FPGA multiplier. All the compared variants of the multiplier per constant were described in the Verilog HDL language; the RTLs were generated for Cyclone 10 LP chips using Intel
® Quartus
® Prime. Altera’s ModelSim was used to simulate the synthesized multipliers. The frequency response analysis of the developed circuits was performed using the TimeQuest Timing Analyzer (Intel
® Quartus
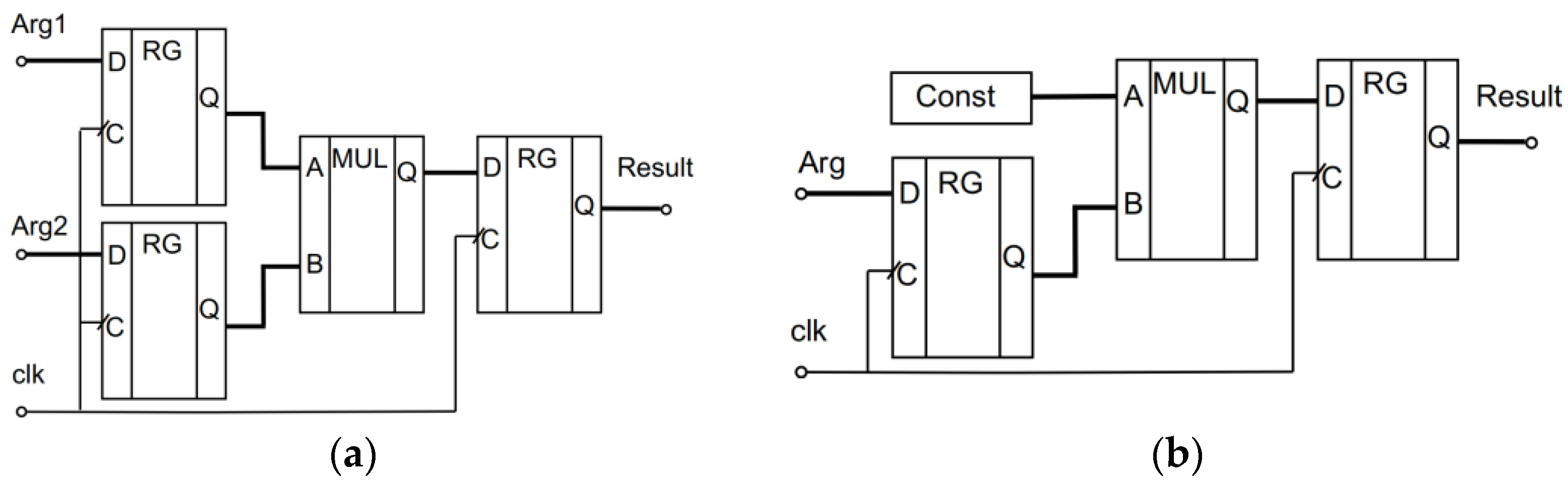
® Prime utility). For the correct timing analysis, we used the test setup shown in
Figure 5.
The proposed architecture is used to determine the Fmax; this frequency is calculated only for the paths where the source and target registers or ports are controlled by the same clock.
3.1. Hardware Implementation of the Modified Booth’s Algorithm
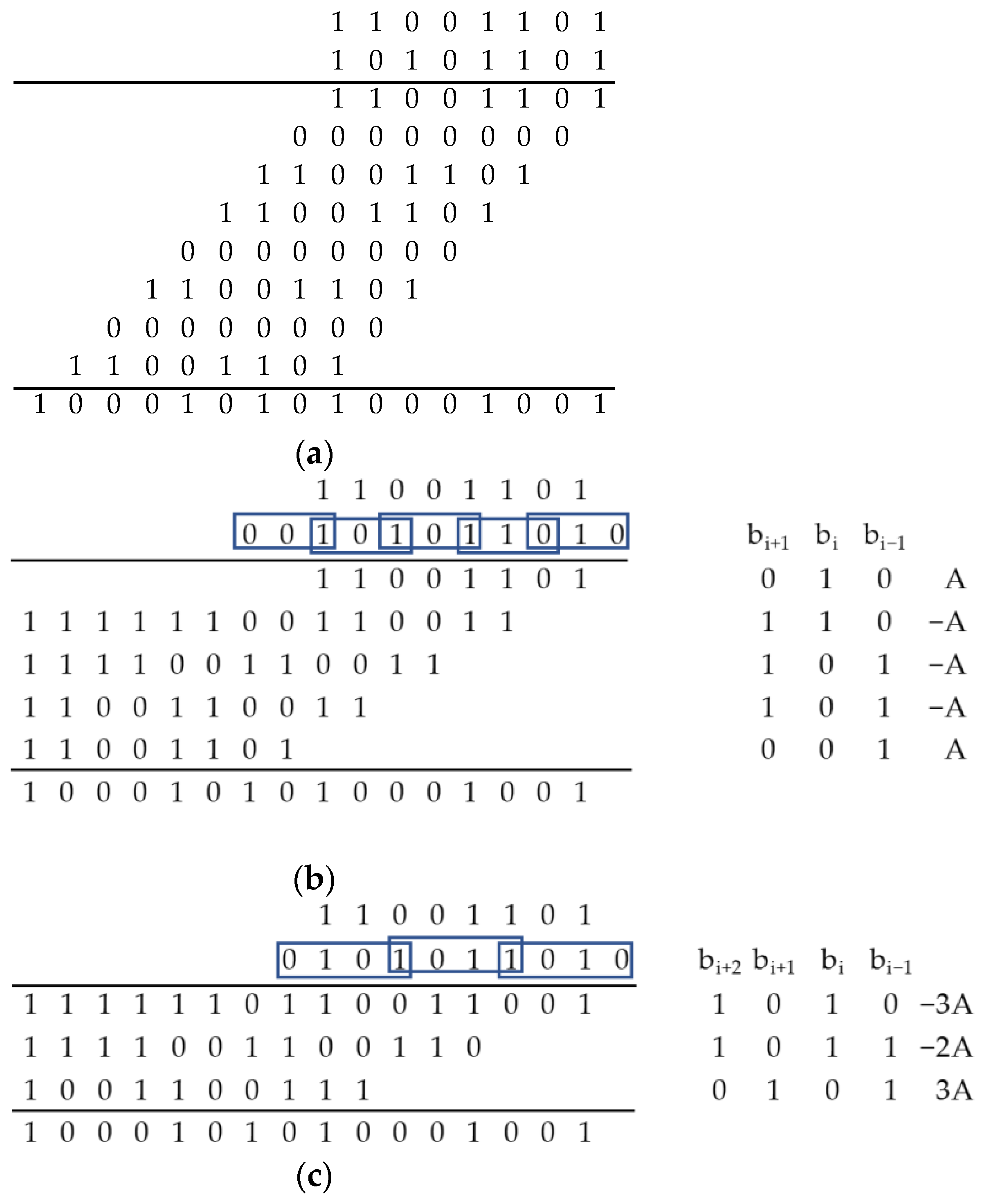
To perform the research, the modified Booth’s algorithm was implemented in two variants: the multiplication of two arguments and the multiplication of an argument by a constant.
3.1.1. Implementation of Two Binary Code Multiplication
For the investigation, we used a parameterized description of the multiplier, allowing for a rapid change in its digit capacity.
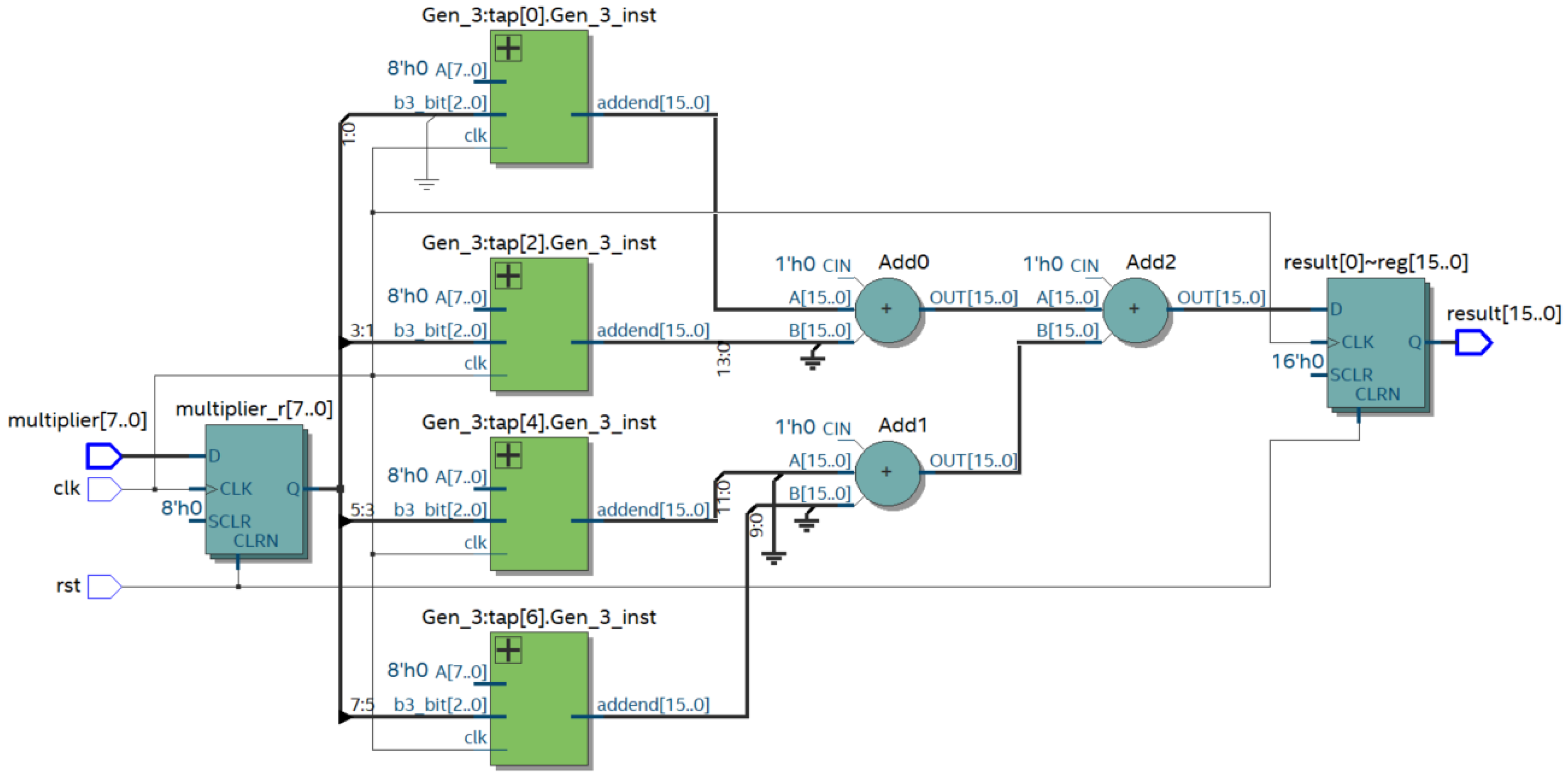
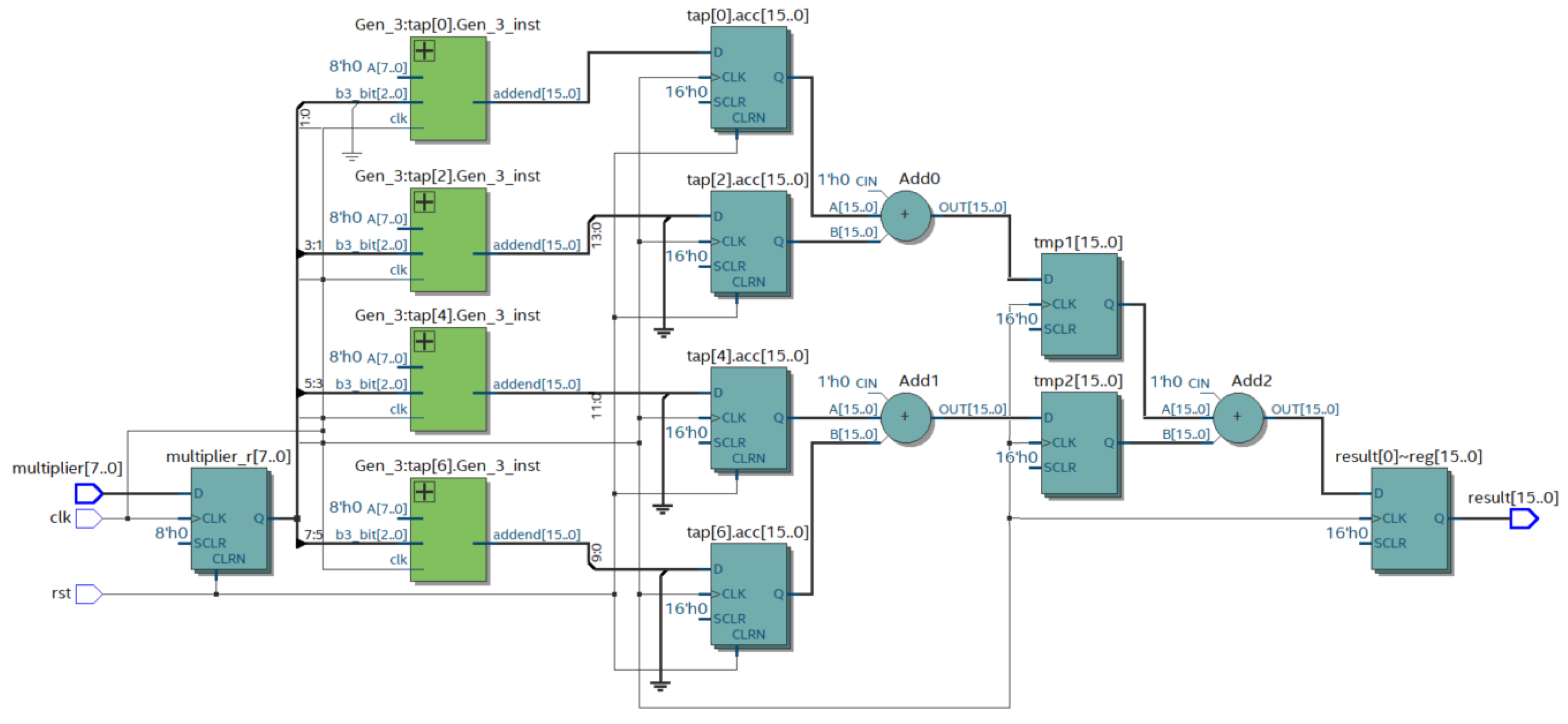
Figure 6 shows the result of compiling the prepared Verilog HDL description with a bit size of n = 8.
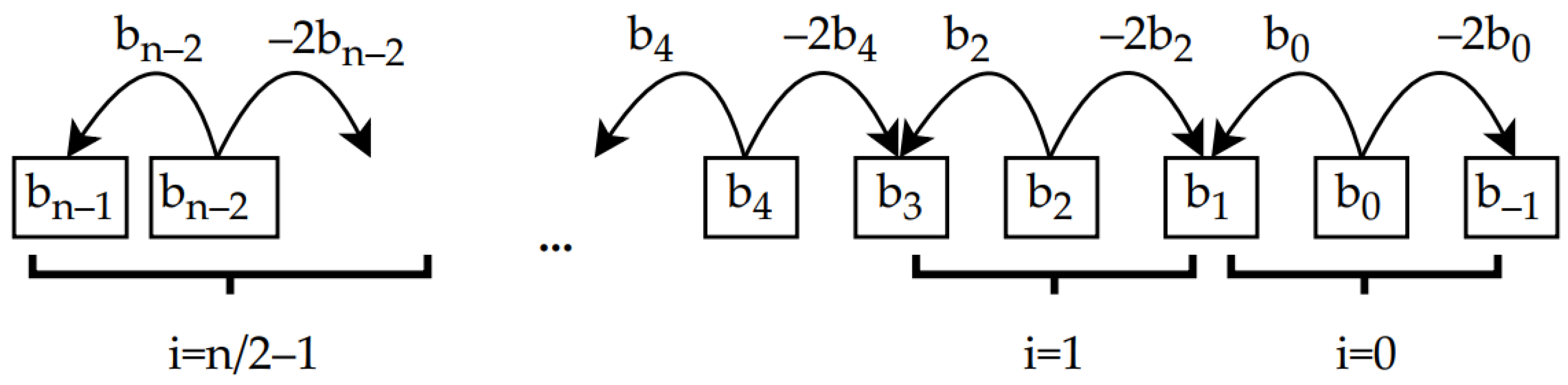
The multiplier uses partial product generation modules (modules Gen_3) based on the three bits of the multiplier. These modules generate PPs according to the rules shown in
Table 1. The summation of the PPs is performed pairwise; three adders are used for the 8-bit multiplier. In the study, we evaluated the change in the maximum frequency of the module, as well as the required resources of the FPGA Cyclone 10 LP for multiplication as a function of the digit capacity of the codes to be multiplied. The results are presented in
Table 4.
The table shows the maximum possible frequencies of the multiplier. These frequencies were calculated using the Slow1 and Slow2 models corresponding to the different operating parameters (voltage and temperature) considered in the static time analysis. The following characteristics are used: Slow1—1200 mV, 100 °C.; Slow 2—1200 mV, −40 °C. The models are based on determining the lowest speed-up for the different paths; the model is built for the chip with the worst speed-up. For both models, there is a decreasing trend in frequency with the minor spikes.
3.1.2. Implementation of the Constant Coefficient Multiplier
Figure 7 shows the RTL of the 8-bit constant coefficient multiplier (CCM). The FPGA distributed memory is used to store the constants. The basis of distributed memory is LUTs; in most FPGA families, they have six inputs and allow for the storage of 64 bits. This type of memory is quite flexible and supports a variety of data widths, unlike block memory, where the bit depth of the stored words and their number can take certain values depending on the type of block memory. The flexibility of distributed memory and its high speed make it ideal for storing partial products.
The partial product generation modules (Gen_3) for the CCM are designed using distributed FPGA memory, which stores the pre-calculated partial products for the constant multiplicand. The modules Gen_3 select the partial product from the memory according to the value of three bits of the multiplier. The maximum frequency Fmax of the multiplier and the required FPGA resources were analyzed during the study of this module.
Table 5 shows the dependence of the analyzed parameters on the digit capacity of the arguments.
Analysis of the RTL multiplier presented in
Figure 7 shows that it can be easily pipelined.
Figure 8 illustrates a pipeline implementation of the Booth’s multiplier. The productivity of the pipeline circuit depends on the number of stages and the ratio of the combinational and the register parts performance. It tends to the value t/m, where t is the working time of the original circuit, and m is the number of pipeline steps.
The increment of the hardware costs to implement the pipeline method of processing depends on the number of registers entered. The maximum effect is given by the pipelining of the summing. Although pipelining leads to additional hardware, it speeds up the multiplication operation by 2–3 times.
Table 6 shows the characteristics of the pipelined constant coefficient of the Booth’s multiplier.
3.2. Hardware Implementation of the Proposed Algorithm for Multiplying by Three Bits at a Time
The proposed multiplication algorithm for multiplying by three bits at a time has also been implemented and investigated in two variants: the multiplication of two arguments and the multiplication of an argument by a constant.
3.2.1. Implementation of Two Binary Code Multiplication
The parameterized description was used to investigate the three-bits-at-a-time multiplier (TBTM). The parametrization makes it possible to easily change the digit capacity of the arguments and to analyze the evolution of the maximum frequency Fmax of the unit and to estimate the hardware cost of the multiplier implementation.
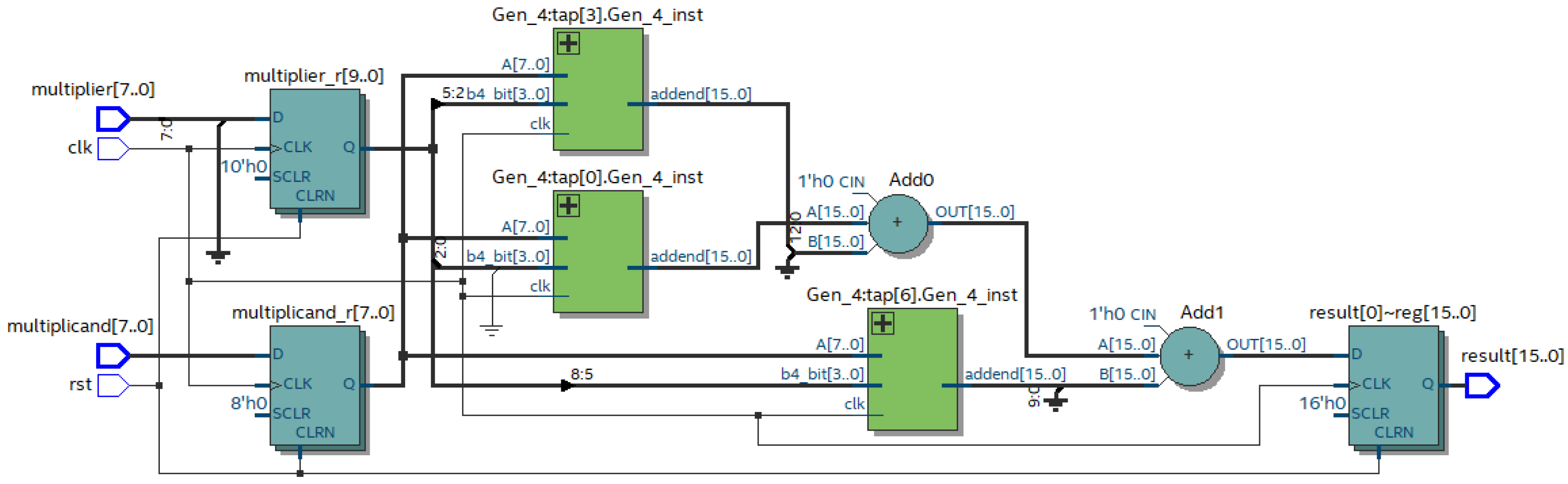
Figure 9 shows the result of the compiling of the prepared Verilog HDL description for the eight-bit implementation.
The multiplier uses partial product generation modules (Gen_4) based on the four analyzed bits of the multiplier. These modules generate PPs for the multiplicand according to the rules presented in the
Table 2. The summation of the three PPs is performed using two adders.
A comparison of
Figure 6 and
Figure 9 shows the reduction in the blocks for the formation of the PPs with some of their complications, as well as the reduction in the number of adders. The multiplication of the eight-digit arguments requires three PPs and consequently needs two adders for their addition. The implementation of Booth’s algorithm forms four PPs and requires three adders. The characteristics of the multiplier realizing the proposed algorithm for the different argument digit capacities are presented in
Table 7.
3.2.2. Implementation of the Constant Coefficient Multiplier
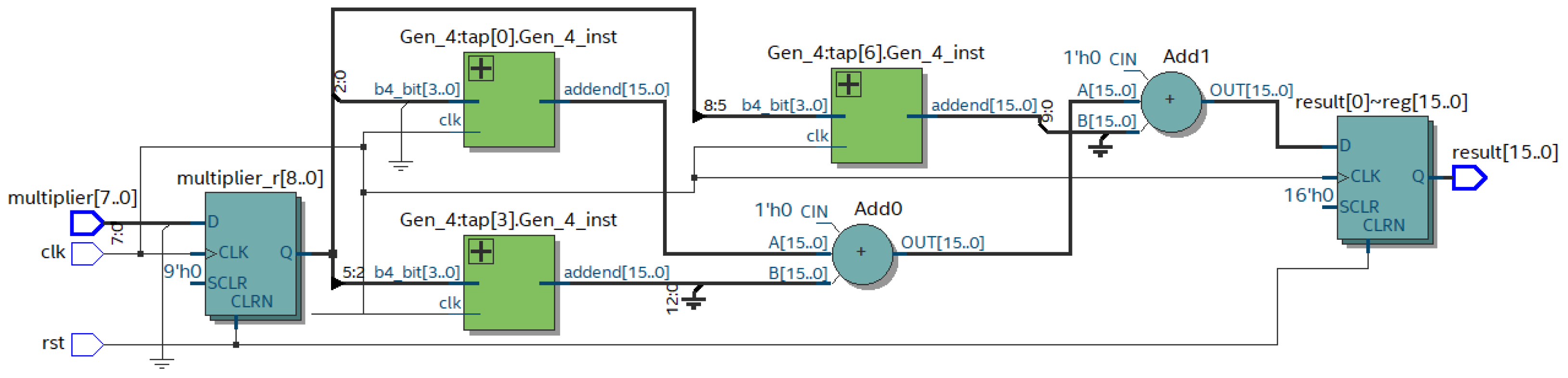
Figure 10 shows the RTL of the hardware implementation of the proposed algorithm that performs multiplication by a constant.
The Gen_4 modules of the CCM implement a selection of the partial product stored in the FPGA’s distributed memory. The address for the selection is generated based on the four bits of the multiplier.
Table 8 shows the characteristics of the CCM that implement the proposed algorithm for the different digit capacities of the arguments.
4. Discussion
This paper presents an analysis of several variants of the implementation of the input code multipliers by a constant. One is based on Booth’s algorithm, the other implements multiplication by three digits at once. The comparison was made for the variant of multiplication of two codes and a code by a constant because the implementations of these methods on the FPGA basis were different. To ensure a correct comparison, we disabled the optimization when compiling in Quartus Prime. This guaranteed that all of the elements provided in the Verilog HDL description were preserved.
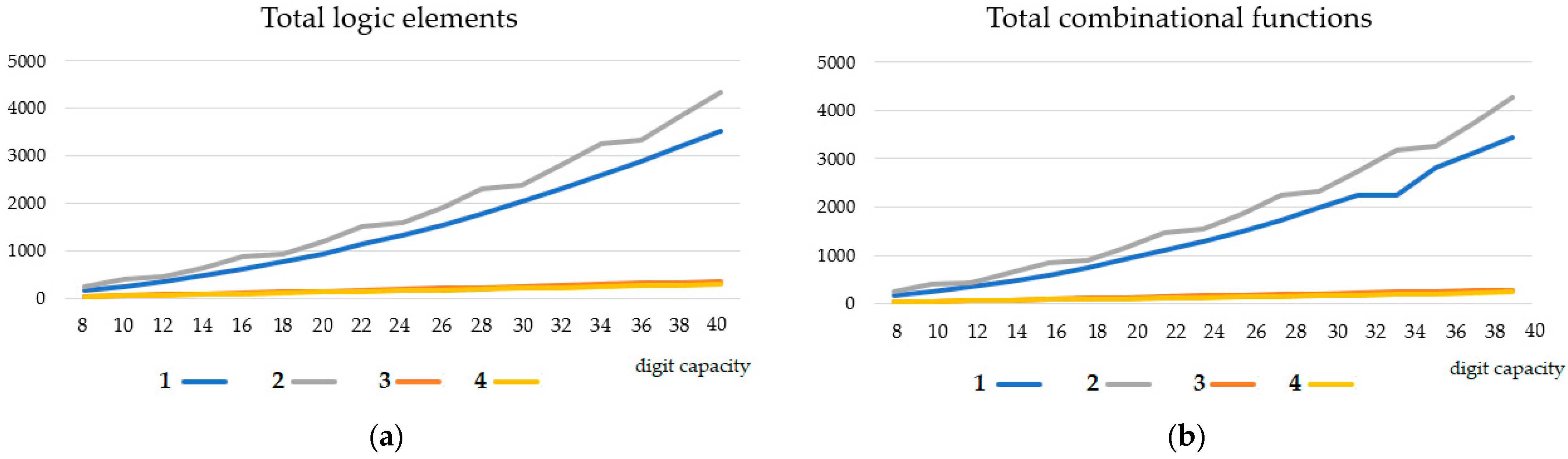
Table 9 integrates the characteristics of the two code multipliers and the constant code multipliers realized by Booth’s algorithm and by the proposed algorithm for the multiplication of three digits at once. The table shows the maximum frequency Fmax for the Slow1 model and the total number of logic elements (LE) used. The results of the Slow2 timing analysis model and the number of combinational functions have the same trends. The number of registers is constant for all the multipliers because, according to
Figure 5, the registers are used to fix the arguments and results, and their number does not depend on the realized algorithm.
The analysis of the table shows that the maximum possible frequency Fmax when realizing the multiplication of two arguments in the Booth’s multiplier (in the column Booth’s MUL Fmax) is higher than in the three-bit multiplier (in the column TBTM Fmax). This is due to the fact that for the generation of the PPs in the Booth’s multiplier the elementary operations—shift, inversion, and increment—are sufficient. The proposed algorithm requires more time-consuming calculations, such as when calculating the partial products of 3A and −3A. The situation changes when the input code is multiplied by a constant. As the PPs are pre-calculated, no complex operations are required and the maximum possible frequency Fmax in the Booth’s multiplier (in the Booth’s CCM Fmax column) is lower than the Fmax of the three-bit multiplier (in the TBT CCM Fmax column). In the hardware cost analysis, the situation is the opposite. The generation of the partial products during computation requires a lot of FPGA resources. If the precalculated partial products are stored in the distributed memory, the hardware costs are reduced.
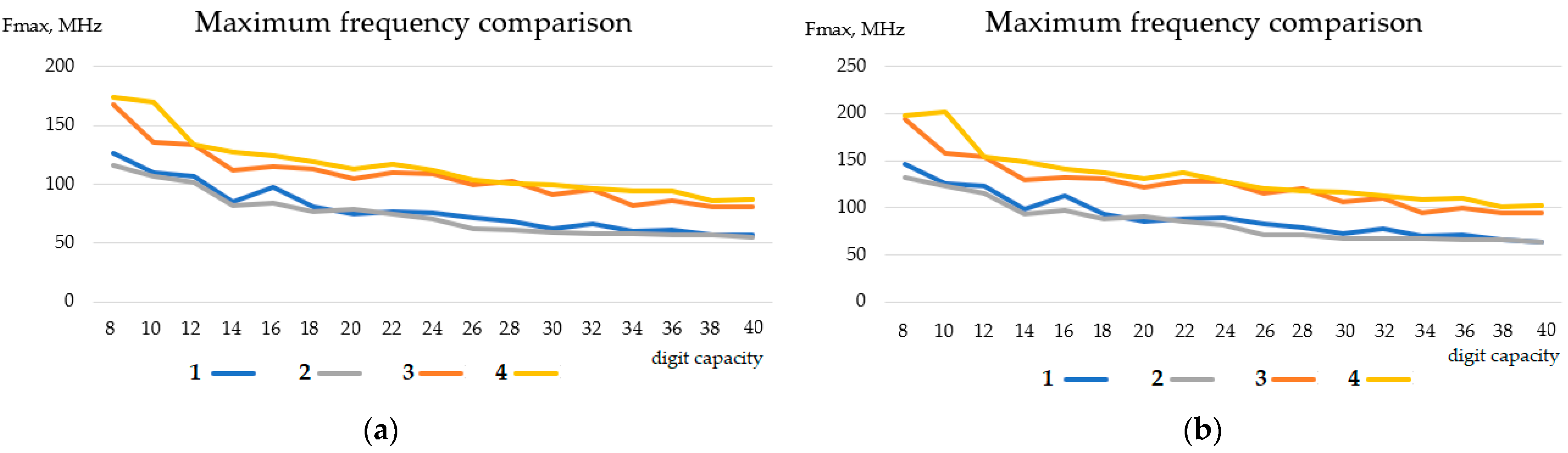
Figure 11 shows the growth of the maximum frequency with the increasing digit capacity. The comparison was made for two timing models (Slow1 and Slow2); as can be seen in the figure, the frequency trends are the same.
Figure 12 shows the dependence of the hardware costs on the multiplier’s digit capacity.
The analysis shows that the hardware costs increase significantly when the multiplication of two arguments is implemented; at the same time, there is a minimal increase when multiplying by a constant. In other words, it is obvious that if multiplication by a constant is required, it is necessary to use an appropriate multiplier and not to replace it with a universal one that multiplies the arguments.
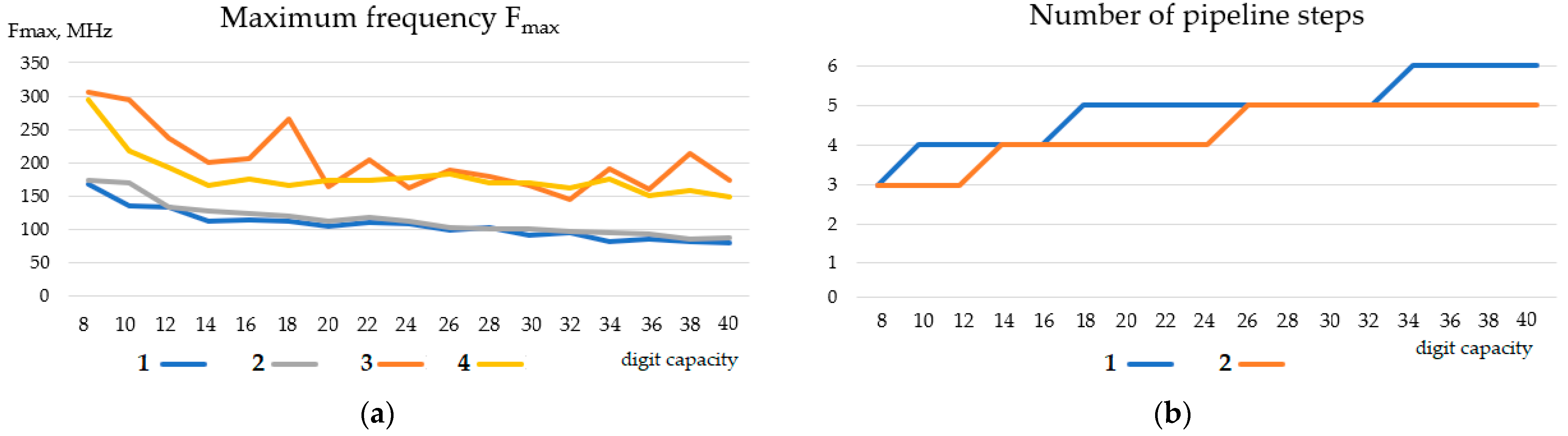
Piping allows the raising of the frequency of the multiplier.
Figure 13 illustrates the frequency change when the multiplier is pipelined. The maximum frequency after pipelining in the implementation of Booth’s algorithm for some bits exceeds the frequencies of the device by the proposed algorithm. However, in the proposed algorithm the reducing of the number of partial products and the corresponding reduction in the adder numbers leads to a decreasing of the pipeline stages number, as shown in
Figure 13b. In most cases, reducing the number of pipeline steps in the TBT multiplier decreases the time required to obtain a multiplication result.
We also compared the considered solutions with the characteristics of the devices designed using embedded FPGA multipliers with different argument digit capacities.
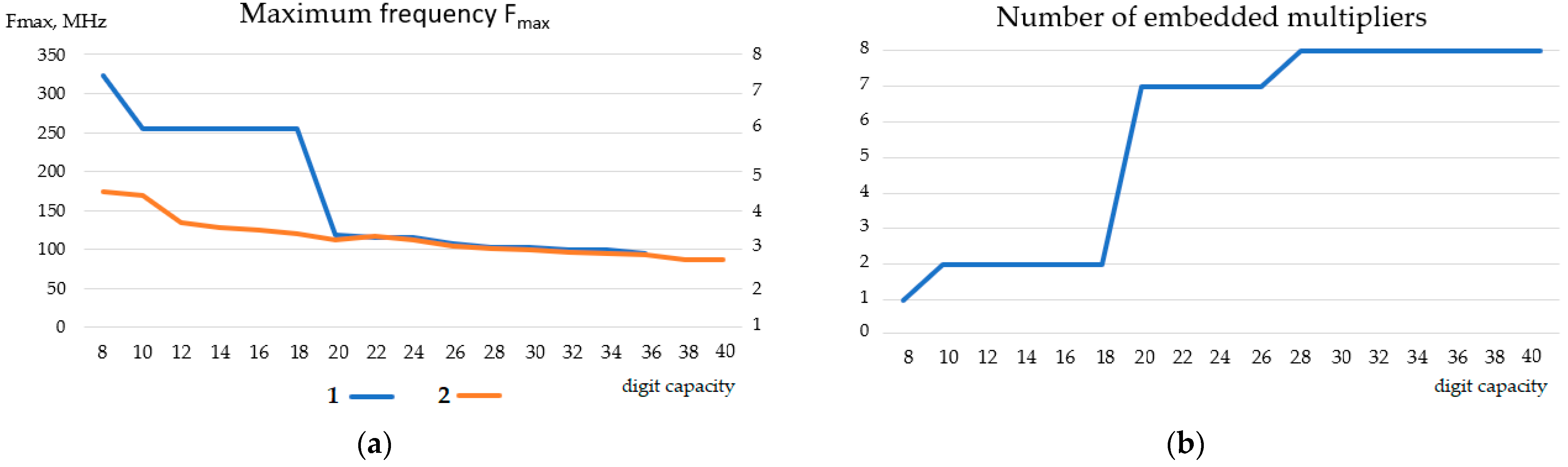
Figure 14 shows a comparison of the TBTM-based and the FPGA embedded multiplier-based constant coefficient multipliers.
The embedded FPGA multipliers are configured as 9 × 9 or 18 × 18 units. This explains the nature of the graphs in
Figure 14a. Embedded multipliers are fast, and when multiplying arguments with a digit capacity not greater than 18, they operate at maximum frequency. This frequency exceeds the frequency of the proposed three-bits-at-a-time multiplier by about twice. When the multiplier capacity exceeds 18 digits, the frequency decreases sharply and becomes the same as the frequency of the TBTM. This is due to the need of the cascading multiplier and the corresponding complication of the FPGA internal resources routing. In this case, the number of multipliers required increases dramatically. As
Figure 14b shows, seven embedded multipliers are required to multiply two codes with a bit capacity of more than 18 bits. This is why there are sharp drops in the maximum frequency (
Figure 14a) at the points corresponding to the digit capacities n = 10 and n = 20. That is, when cascading fast embedded multipliers, the time characteristics of the multiplier device fall sharply. Setting up embedded multipliers for multiplication by a constant does not change the timing characteristics of the resulting unit.
Multiplication operands based on logical cell tables have no limitations in capacity. The number and location of the built-in multipliers are fixed, while LUT-based multipliers can be placed anywhere, and their number is limited only by the size of the reconfigurable matrix.
The effectiveness of the proposed approach of multiplication by a constant using a combination of three-digit multiplication methods with the tabular generation of partial products can be illustrated by the FIR filter design. We compared three implementations of a 32nd order lowpass FIR filter with 20-bit coefficients and 20-bit input codes. In the first version, the filter coefficients were stored in the distributed memory, and the hardware implementation of the multiplication was not specified. In the Verilog HDL program, the multiplication operator was used. In the second version, the multiplication by coefficients was performed using Booth’s CCM. The third version used the developed three-bits-at-a-time multipliers to multiply by the coefficients.
Table 10 shows the hardware cost of the filter implementation, and
Table 11 presents the frequency characteristics of the three FIR filter variants considered.
Analysis of the data in the tables shows that the filter built using the proposed three-bits-at-a-time multipliers has the best frequency and hardware cost characteristics.
5. Conclusions
In the paper, we proposed an approach to the implementation of multiplication that performs multiplication by three digits. The rate of the multipliers implementing multiplication on a group of bits depends on the number of grouped bits and the depth of the tree realizing the parallel summation of the partial products. Our approach reduces the number of partial products and the depth of the tree, thus increasing the performance of the module. The proposed solution reduces the performance difference between the embedded FPGA multipliers and the multipliers implemented on logical cells. A comparison of the developed multipliers with Altera’s multiplying library of parameterized modules showed the advantage of the proposed multiplication by three digits at a time.
The paper can be used by designers of digital circuits to select an optimal method of multiplier implementation on FPGAs with regard to their design constraints.
Further development of the method of multiplication by a group of digits can be associated with the creation of algorithms and hardware modules multiplying by four, five, and more digits at a time.