A 22.3-Bit Third-Order Delta-Sigma Modulator for EEG Signal Acquisition Systems
Abstract
:1. Introduction
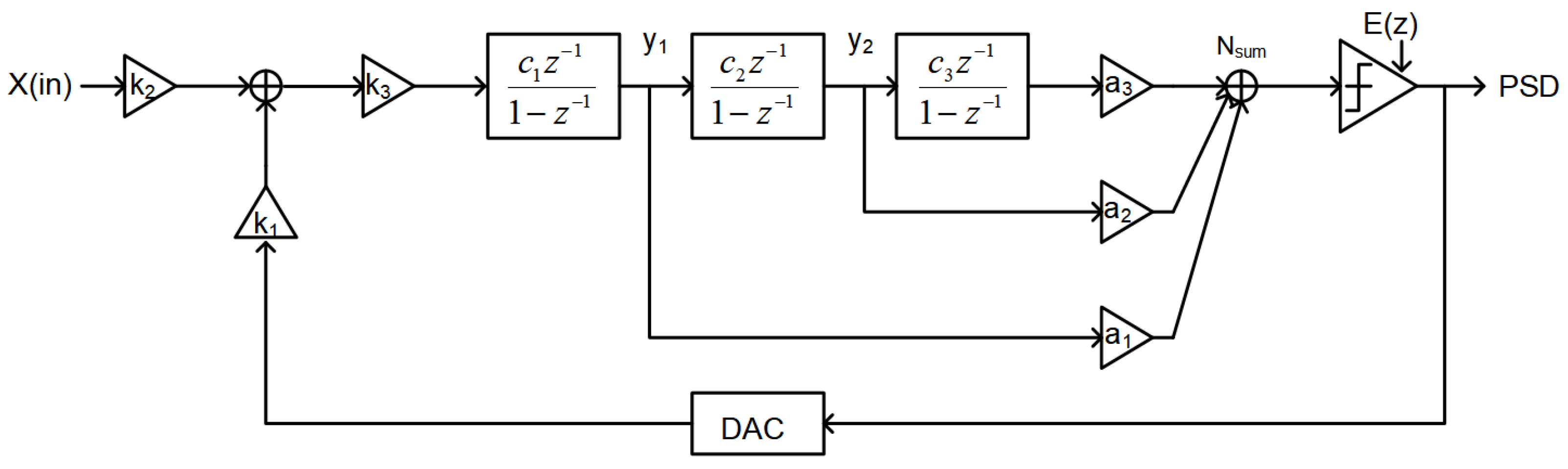
2. Thermal Noise Analysis and Proposed Topology Design
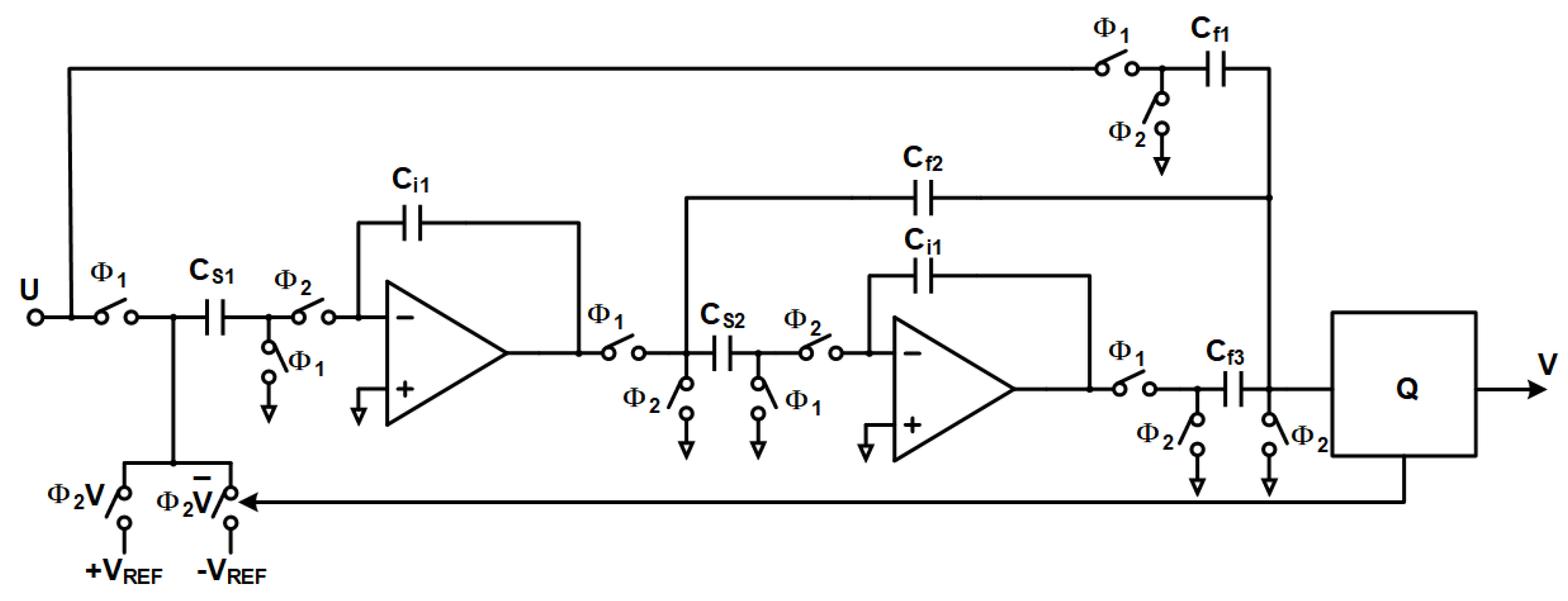
3. Circuit Implementation
3.1. Integrator Output Swings
3.2. OTA Requirements
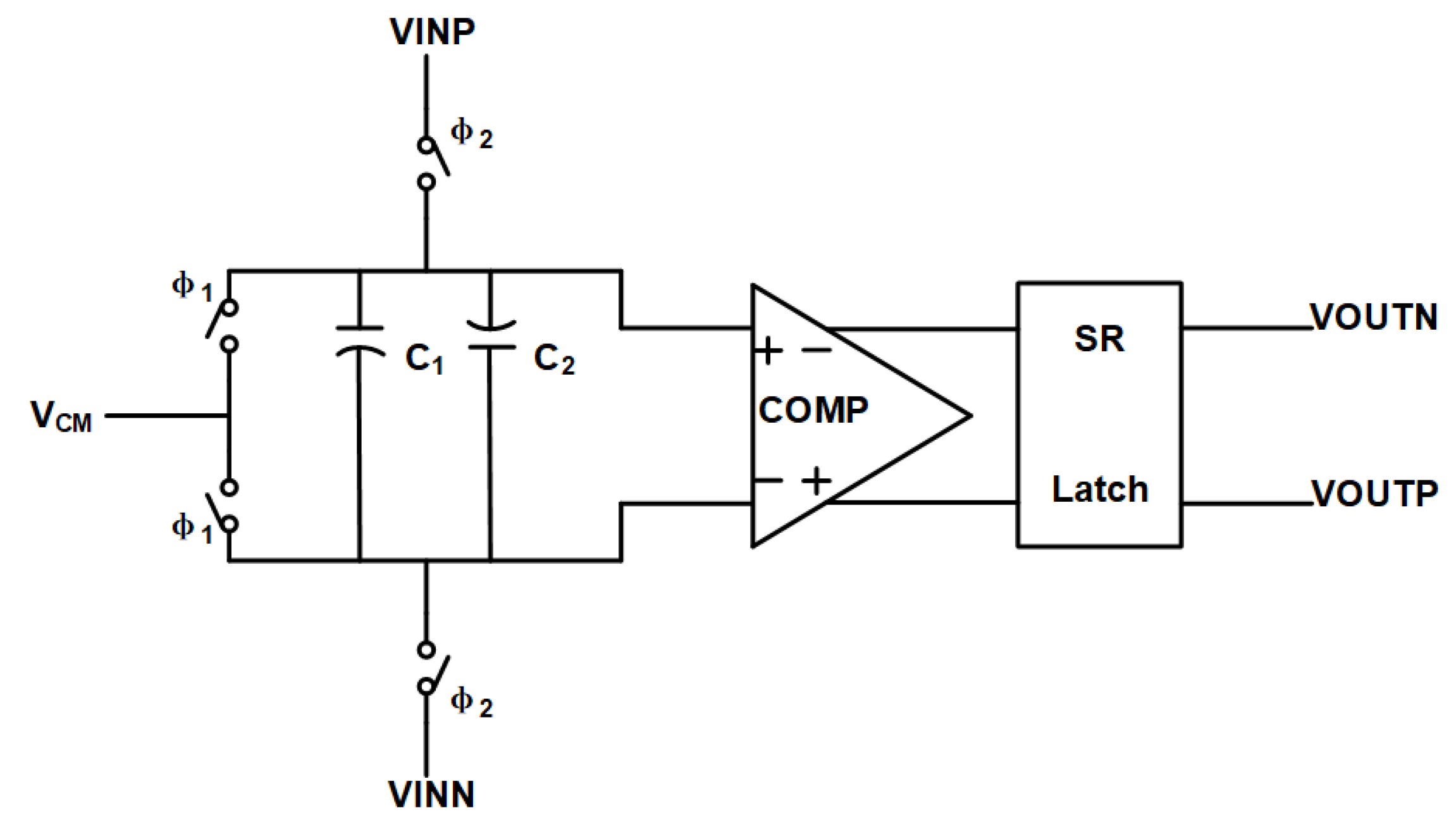
3.3. Single-Bit Quantizer Circuit
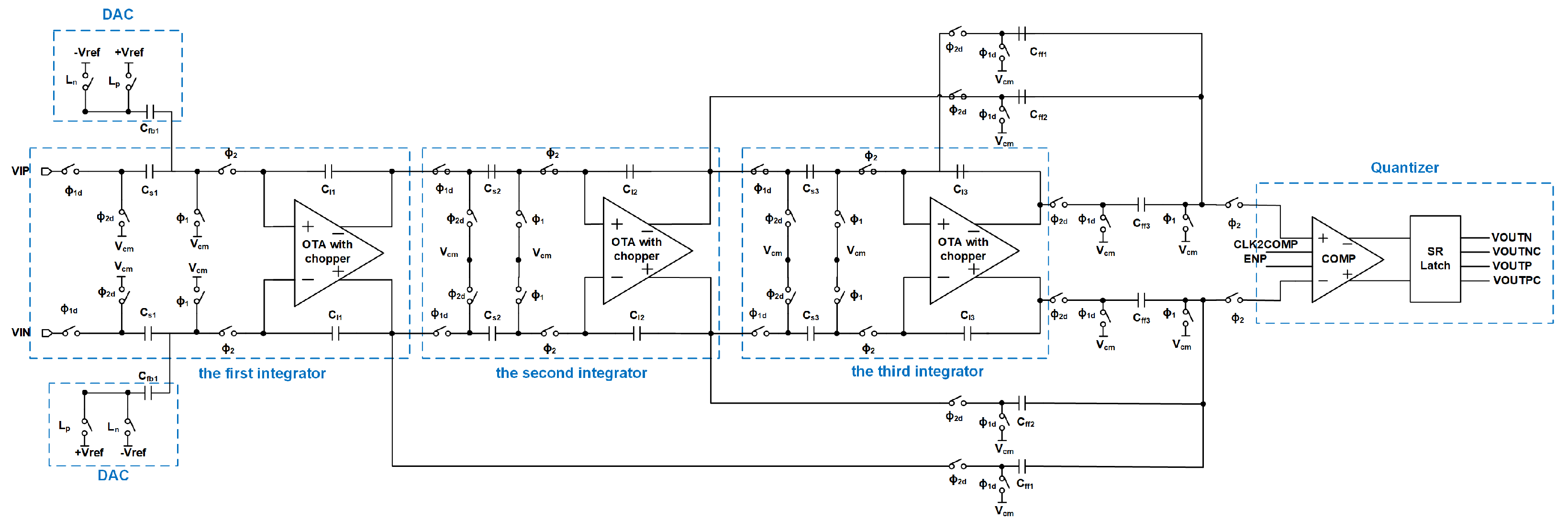
3.4. Complete Modulator Circuit Implementation
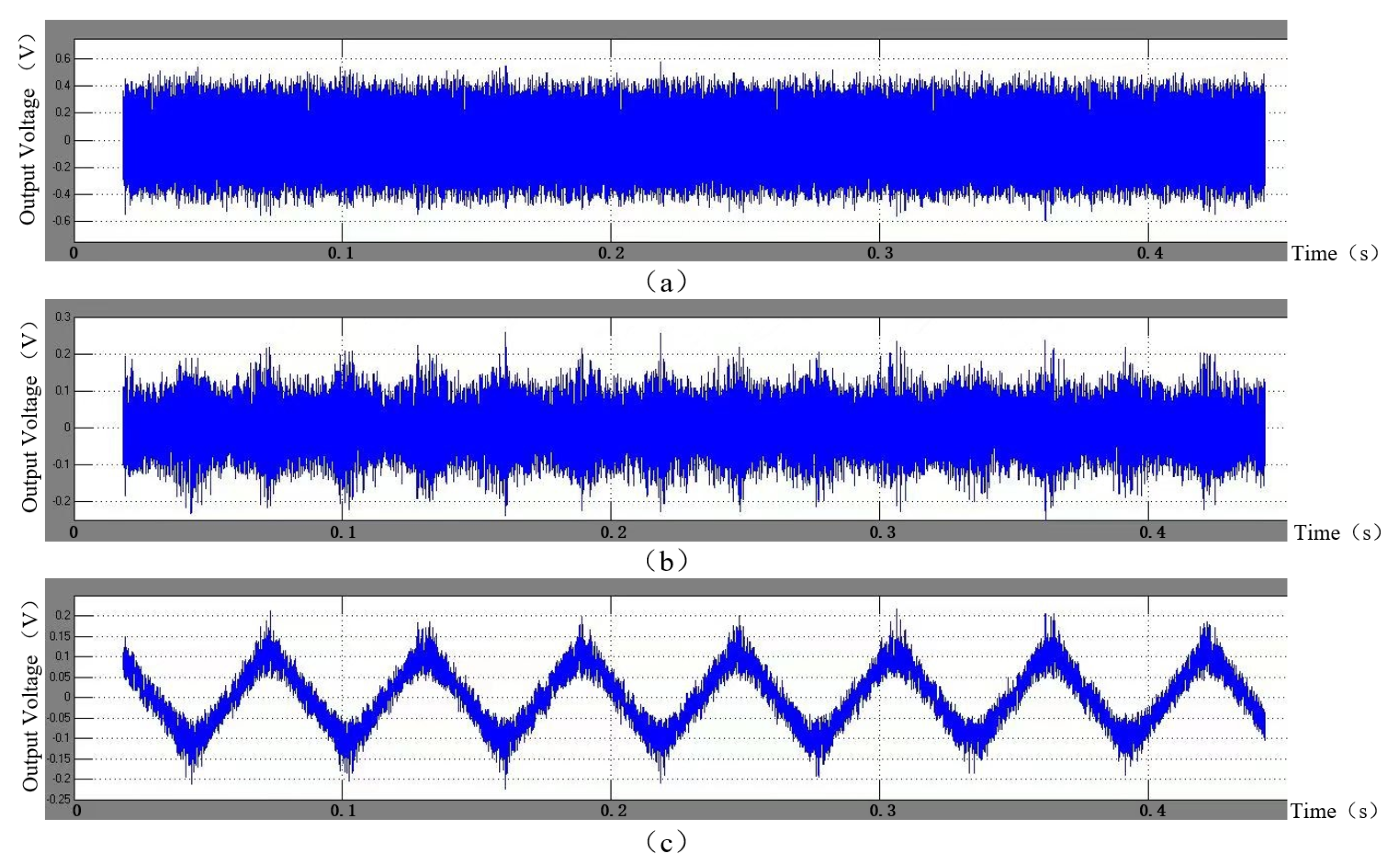
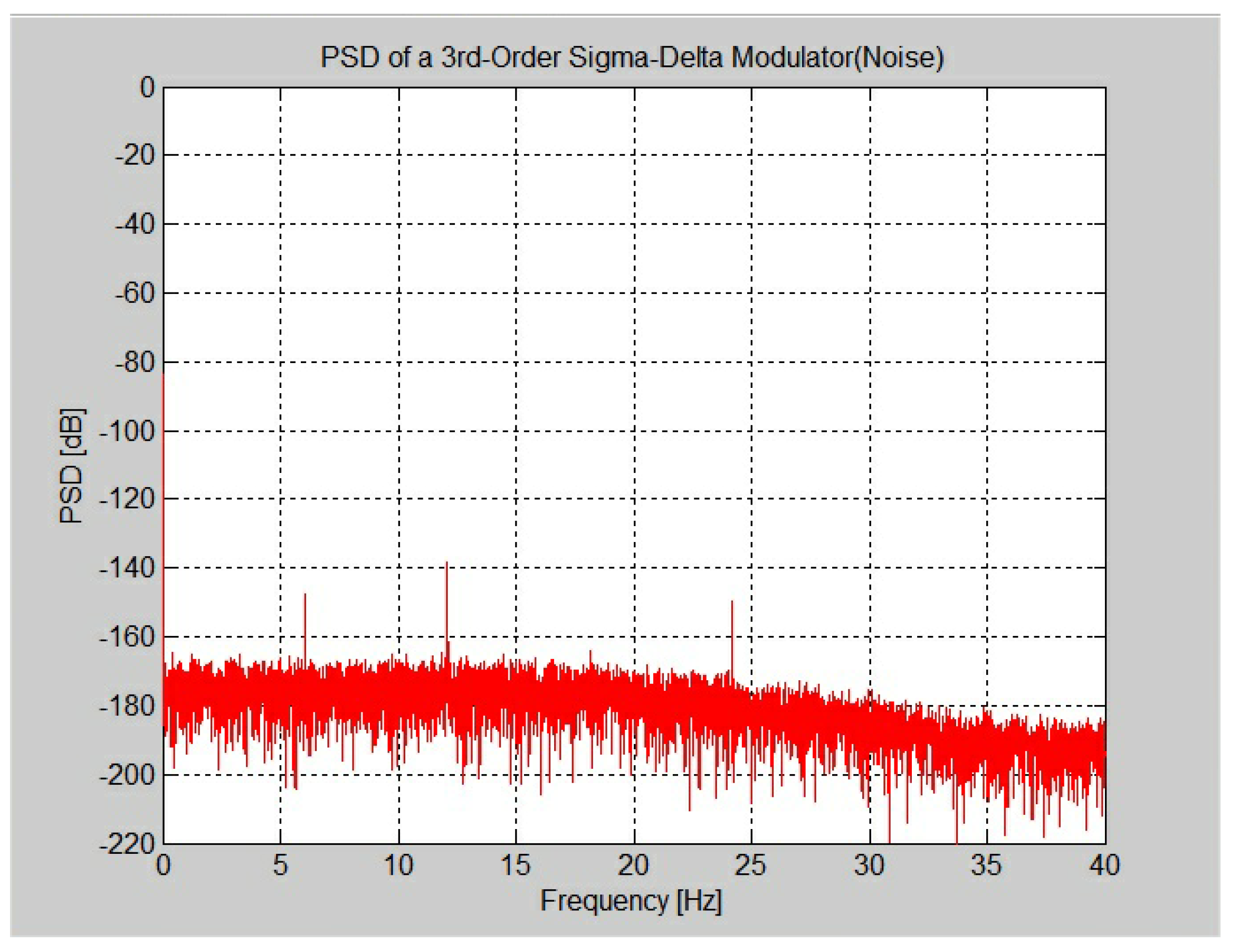
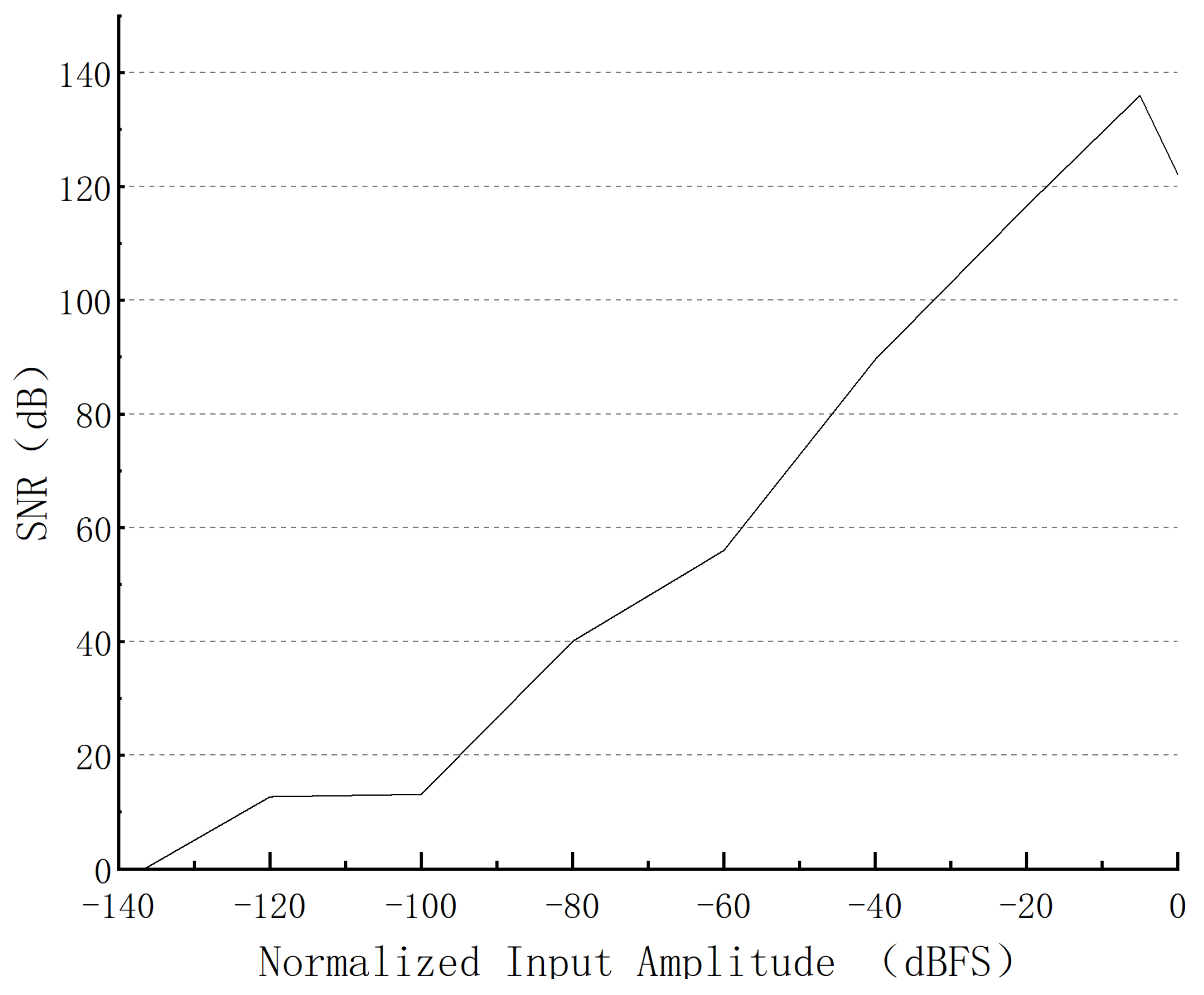
4. Measurement Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EEG | Electroencephalography |
| AFE | Analog-front-end |
| CMRR | Common-mode-rejection-ratio |
| EOV | Electrode-offset-voltage |
| SNR | Signal to noise ratio |
| SNDR | Signal to noise and distortion ratio |
| OSR | Oversampling ratio |
| NS | Noise shaping |
| MASH | Multistage noise-shaping |
| DEM | Dynamic element matching |
| GBW | Gain bandwidth |
| DR | Dynamic range |
| CMFB | Common-mode feedback |
| ENOB | Effective number of bits |
| FOM | Figure of merit |
| DT | Discrete time |
| MB | Multi-bit |
| CT | Continuous time |
| SB | Single-bit |
| OTA | Operational transconductance amplifier |
| PSD | Power spectrum density |
References
- Yazıcıoglu, R.; Merken, P.; Puers, R.; Hoof, C. A 200 μW eight-channel acquisition ASIC for ambulatory EEG systems. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 3–7 February 2008. [Google Scholar]
- Webster, J.G. Medical Instrumentation: Application and Design; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Van Rijn, A.M.; Peper, A.; Grimbergen, C. High-quality recording of bioelectric events. Part 1. Interference reduction, theory and practice. Med. Biol. Eng. Comput. 1990, 28, 389–397. [Google Scholar] [CrossRef]
- Yokus, M.A.; Jur, J.S. Fabric-based wearable dry electrodes for body surface biopotential recording. IEEE Trans. Biomed. Eng. 2015, 63, 423–430. [Google Scholar] [CrossRef] [PubMed]
- Tohidi, M.; Madsen, J.K.; Moradi, F. Low-power high-input-impedance EEG signal acquisition SoC with fully integrated IA and signal-specific ADC for wearable applications. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 1437–1450. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.; Duan, Q.; Yeo, J.; Roh, J.; Kim, J.; Kim, D. A delta–sigma modulator for low-power analog front ends in biomedical instrumentation. IEEE Trans. Instrum. Meas. 2016, 65, 1530–1539. [Google Scholar] [CrossRef]
- Lee, I.; Kim, B.; Lee, B.G. A low-power incremental delta–sigma ADC for CMOS image sensors. IEEE Trans. Circuits Syst. II Express Briefs 2015, 63, 371–375. [Google Scholar] [CrossRef]
- Nikas, A.; Jambunathan, S.; Klein, L.; Voelker, M.; Ortmanns, M. A continuous-time delta-sigma modulator using a modified instrumentation amplifier and current reuse DAC for neural recording. IEEE J. Solid-State Circuits 2019, 54, 2879–2891. [Google Scholar] [CrossRef]
- Boni, A.; Giuffredi, L.; Pietrini, G.; Ronchi, M.; Caselli, M. A low-power sigma-delta modulator for healthcare and medical diagnostic applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 207–219. [Google Scholar] [CrossRef]
- Edward, A.; Liu, Q.; Briseno-Vidrios, C.; Kinyua, M.; Soenen, E.G.; Karşılayan, A.I.; Silva-Martinez, J. A 43-mW MASH 2-2 CT ΔΣ Modulator Attaining 74.4/75.8/76.8 dB of SNDR/SNR/DR and 50 MHz of BW in 40-nm CMOS. IEEE J. Solid-State Circuits 2016, 52, 448–459. [Google Scholar] [CrossRef]
- Nowacki, B.; Paulino, N.; Goes, J. 15.3 A 1V 77 dB-DR 72 dB-SNDR 10 MHz-BW 2-1 MASH CT ΔΣM. In Proceedings of the 2016 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 31 January–4 February 2016; pp. 274–275. [Google Scholar]
- Chebli, R.; Sawan, M. Fully integrated high-voltage front-end interface for ultrasonic sensing applications. IEEE Trans. Circuits Syst. Regul. Pap. 2007, 54, 179–190. [Google Scholar] [CrossRef]
- Rabii, S.; Wooley, B.A. The Design of Low-Voltage, Low-Power Sigma-Delta Modulators; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 483. [Google Scholar]
- Johansson, J.; Neubauer, H.; Hauer, H. A 16-bit 60 μW multi-bit ΣΔ modulator for portable ECG applications. In Proceedings of the ESSCIRC 2004-29th European Solid-State Circuits Conference (IEEE Cat. No. 03EX705), Estoril, Portugal, 16–18 September 2003; pp. 161–164. [Google Scholar]
- Singh, G.; Wu, R.; Chae, Y.; Makinwa, K.A. A 20bit continuous-time ΣΔ modulator with a Gm-C integrator, 120dB CMRR and 15 ppm INL. In Proceedings of the 2012 Proceedings of the ESSCIRC (ESSCIRC), Bordeaux, France, 17–21 September 2012; pp. 385–388. [Google Scholar]
- Xu, L.; Gönen, B.; Fan, Q.; Huijsing, J.H.; Makinwa, K.A. 5.2 A 110 dB SNR ADC with ±30 V input common-mode range and 8 μV Offset for current sensing applications. In Proceedings of the 2015 IEEE International Solid-State Circuits Conference-(ISSCC) Digest of Technical Papers, San Francisco, CA, USA, 22–26 February 2015; pp. 1–3. [Google Scholar]
- Liang, J.; Sin, S.W.; Seng-Pan, U.; Maloberti, F.; Martins, R.P.; Jiang, H. A high DR high-input-impedance programmable-gain ECG acquisition interface with non-inverting continuous time sigma-delta modulator. In Proceedings of the 2019 IEEE Asian Solid-State Circuits Conference (A-SSCC), Macau, China, 4–6 November 2019; pp. 309–312. [Google Scholar]






| Feed-Forward Coefficients | Integrator Coefficients | Other Coefficients |
|---|---|---|
| a = 2 | b = 1/3 | k = 2 |
| a = 3 | b = 1/4 | k = 2 |
| a = 4 | b = 1/16 | k = 1/2 |
| Supply voltage | 5 V |
| Analog power consumption | A |
| Peak SNR | 136 dB |
| Dynamic range | 137 dB |
| Sampling frequency | kHz |
| Signal bandwidth | 100 Hz |
| Oversampling ratio | 512 |
| Modulator core size | 1.41 mm |
| Figure of merit | 188 |
| References | 2003 [14] | 2012 [15] | 2015 [16] | 2019 [17] | 2019 [8] | 2022 [9] | This Work |
|---|---|---|---|---|---|---|---|
| Techn. [nm] | 350 | 700 | 180 | 65 | 180 | 90 | 500 |
| Supply [V] | 2.6 | 5 | 5 | 1 | 1.8 | 1.2 | 3.3∼5 |
| Arch. | DT-MB | CT-MB | DT-SB | CT-SB | CT-SB | DT-SB | DT-SB |
| BW [Hz] | 45 | 10 | 100 | 150 | 250 | 250 | 100 |
| ENOB [b] | 14.7 | 16.7 | 16.4 | 12.2 | 12.7 | 14.8 | 22.3 |
| DR [dB] | 98 | 121 | 110.1 | 99.3 | 90 | 95.6 | 137 |
| Cons. [A] | 23 | 240 | 101 | 20.8 | 12.8 | 25 | 700 |
| Area. [mm] | 0.7 | N.D | 0.8 | 0.225 | 0.088 | 0.39 | 1.41 |
| S.FOM [dB] | 156.8 | 160.2 | 163.1 | 167.8 | 153.1 | 164.8 | 188 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Liu, F.; Fu, L.; Li, Q.; Kang, J.; Chen, K.; Huo, Z. A 22.3-Bit Third-Order Delta-Sigma Modulator for EEG Signal Acquisition Systems. Electronics 2023, 12, 4866. https://doi.org/10.3390/electronics12234866
Wang Q, Liu F, Fu L, Li Q, Kang J, Chen K, Huo Z. A 22.3-Bit Third-Order Delta-Sigma Modulator for EEG Signal Acquisition Systems. Electronics. 2023; 12(23):4866. https://doi.org/10.3390/electronics12234866
Chicago/Turabian StyleWang, Qianqian, Fei Liu, Liyin Fu, Qianhui Li, Jing Kang, Ke Chen, and Zongliang Huo. 2023. "A 22.3-Bit Third-Order Delta-Sigma Modulator for EEG Signal Acquisition Systems" Electronics 12, no. 23: 4866. https://doi.org/10.3390/electronics12234866
APA StyleWang, Q., Liu, F., Fu, L., Li, Q., Kang, J., Chen, K., & Huo, Z. (2023). A 22.3-Bit Third-Order Delta-Sigma Modulator for EEG Signal Acquisition Systems. Electronics, 12(23), 4866. https://doi.org/10.3390/electronics12234866








