Research on the Prediction Method of Clock Tester Calibration Data Based on Radial Basis Function Neural Network
Abstract
:1. Introduction
2. Basic Theory and Problem Description
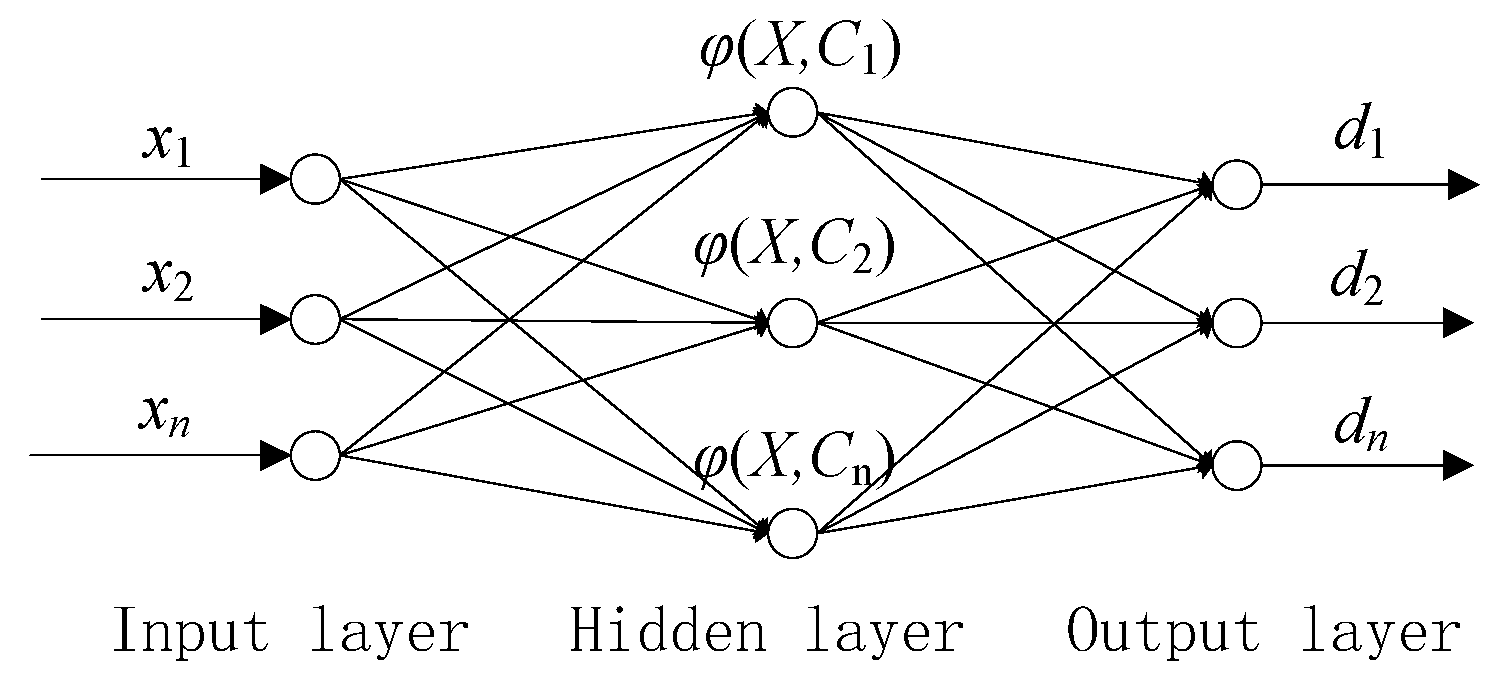
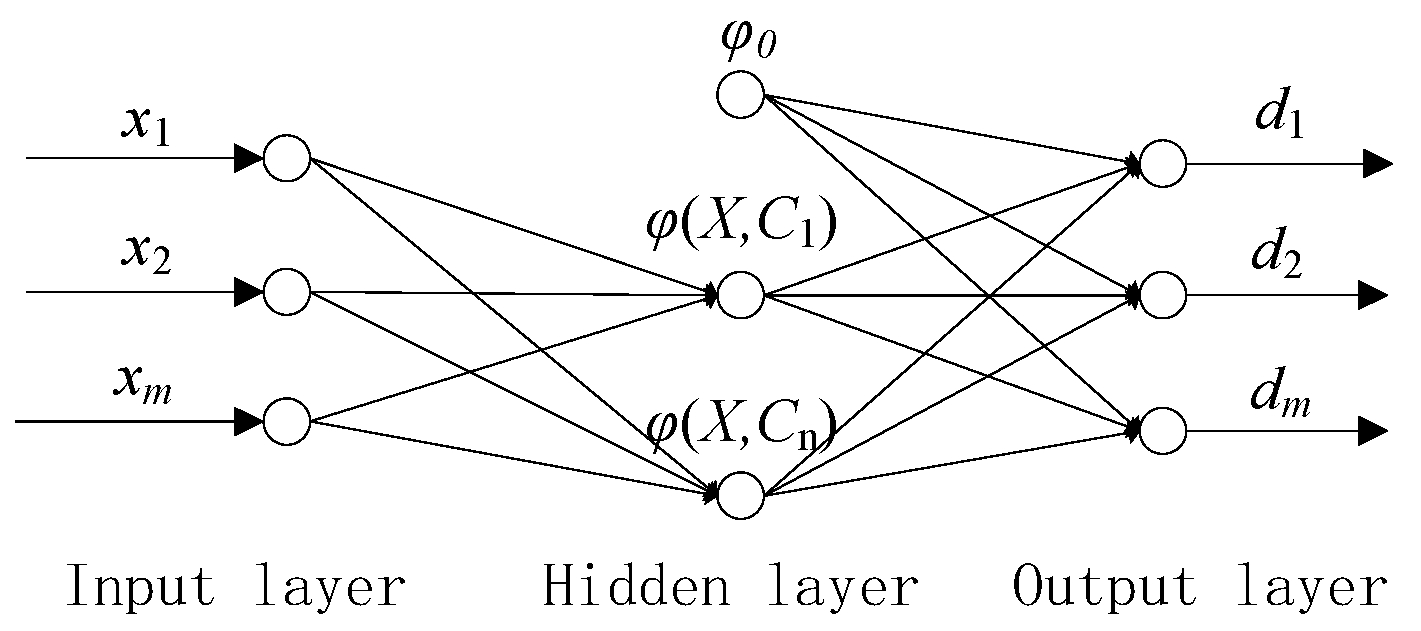
2.1. Principles of Radial Basis Function Neural Networks
2.2. Problem Description
3. Prediction Model
3.1. Factors Affecting Calibration Parameters
- (1)
- Measurement Repeatability
- (2)
- Accuracy of Reference Standards
- (3)
- Uncertainty Calculation
3.2. Data Analysis and Preprocessing
3.3. Model Construction
- Step 1:
- Obtain the measurement data of five clock testers of the same model produced by the same manufacturer and year for a certain unit for 4 consecutive years.
- Step 2:
- Classify the obtained data according to the measurement method, preprocess the data according to the calibration specifications of the clock tester, and obtain stability- and accuracy-related data.
- Step 3:
- Decommon the data related to measurement stability and accuracy and amplify the error to obtain the feature data.
- Step 4:
- Normalize the feature data.
- Step 5:
- Build time-driven prediction models and data-driven prediction models and classify feature data.
- Step 6:
- Train the two models based on the prediction target to obtain corresponding prediction models and achieve calibration data prediction.
- Step 7:
- Verify the effectiveness of the RBF neural network prediction method using test samples.
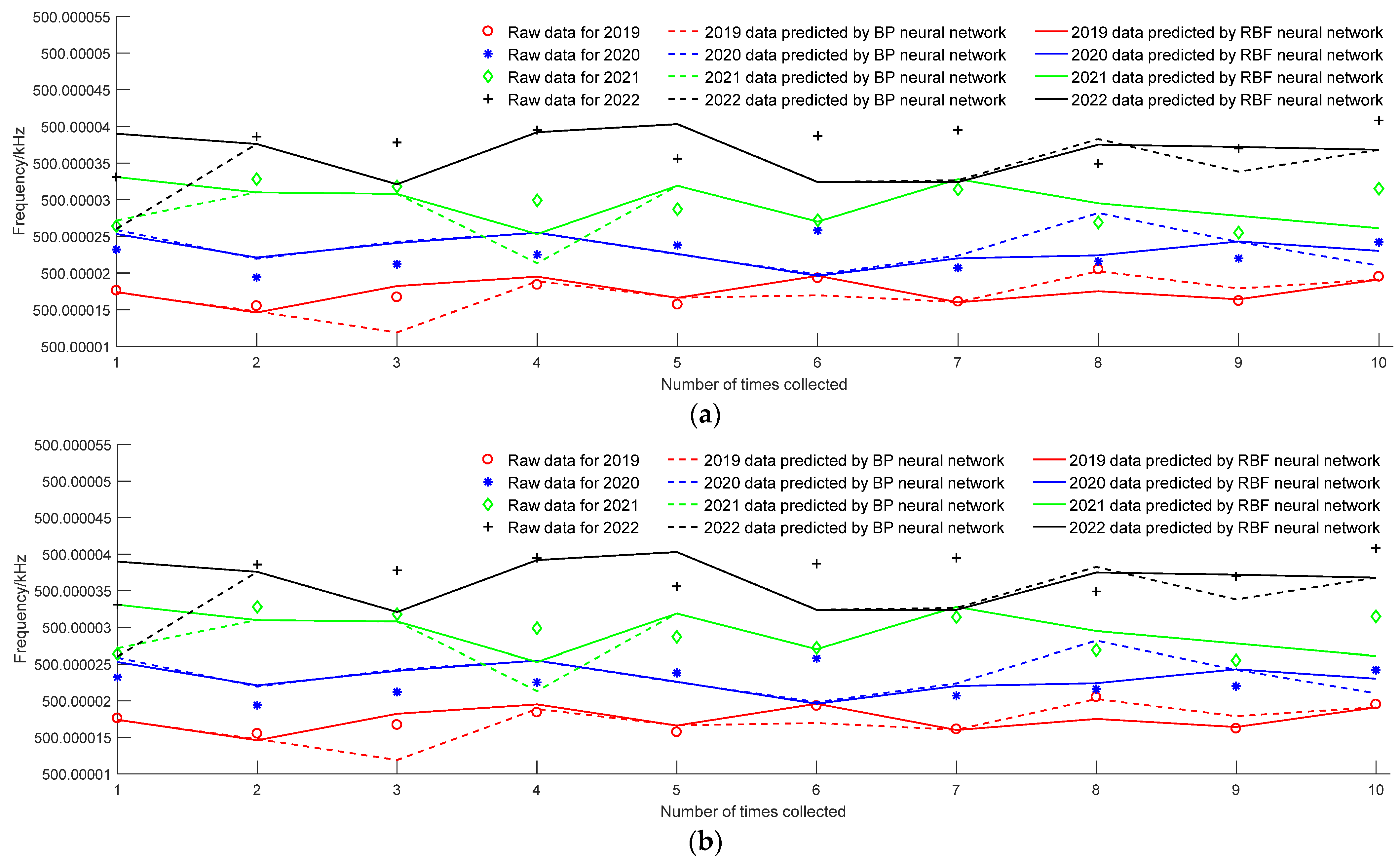
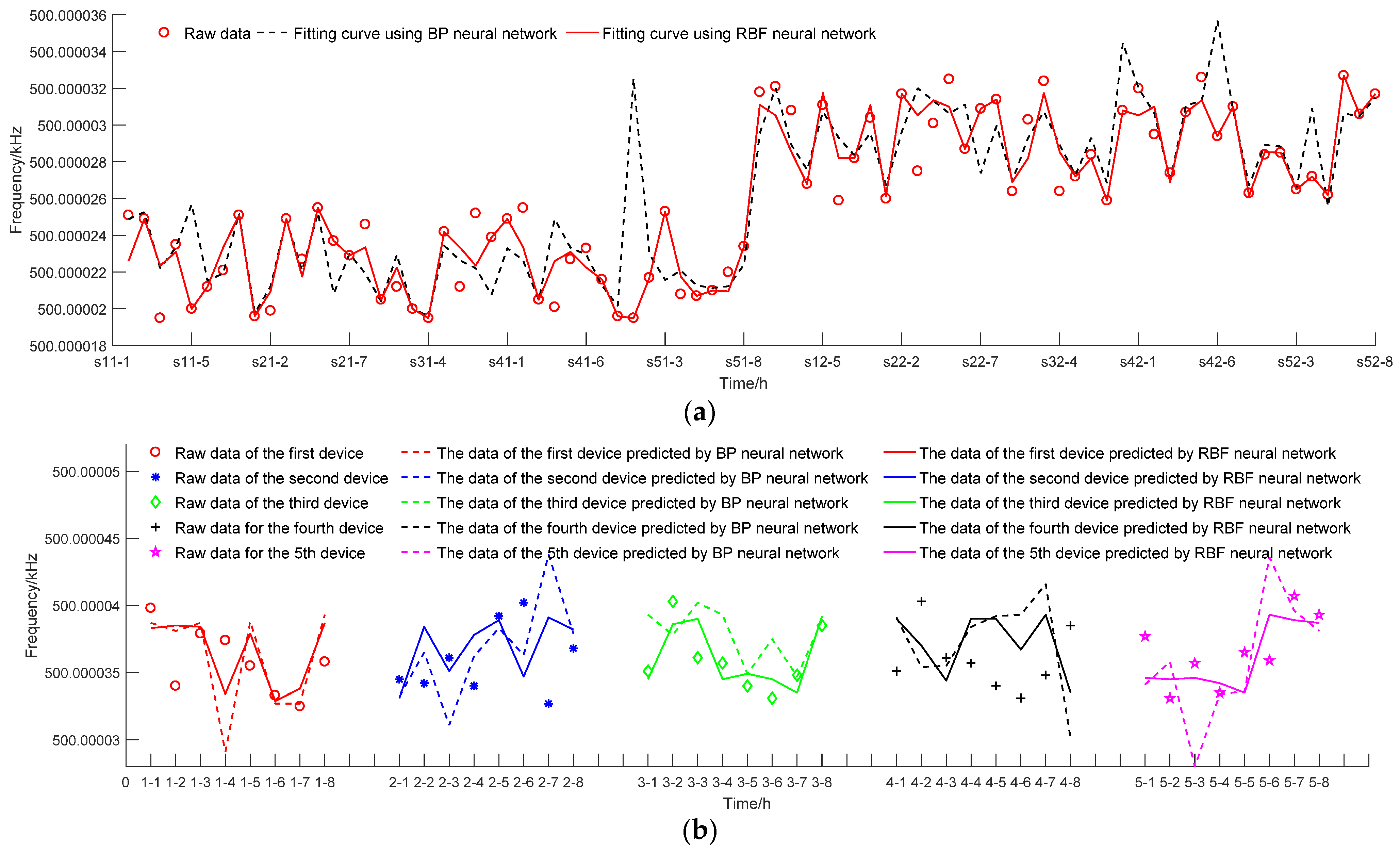
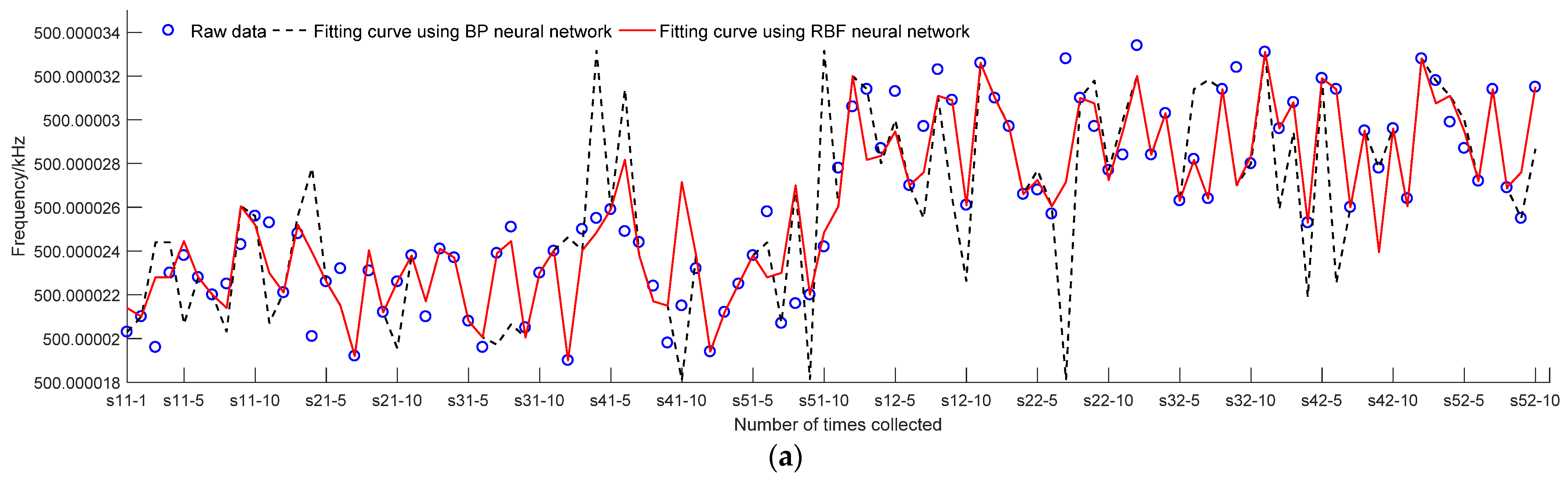
4. Simulation Analysis
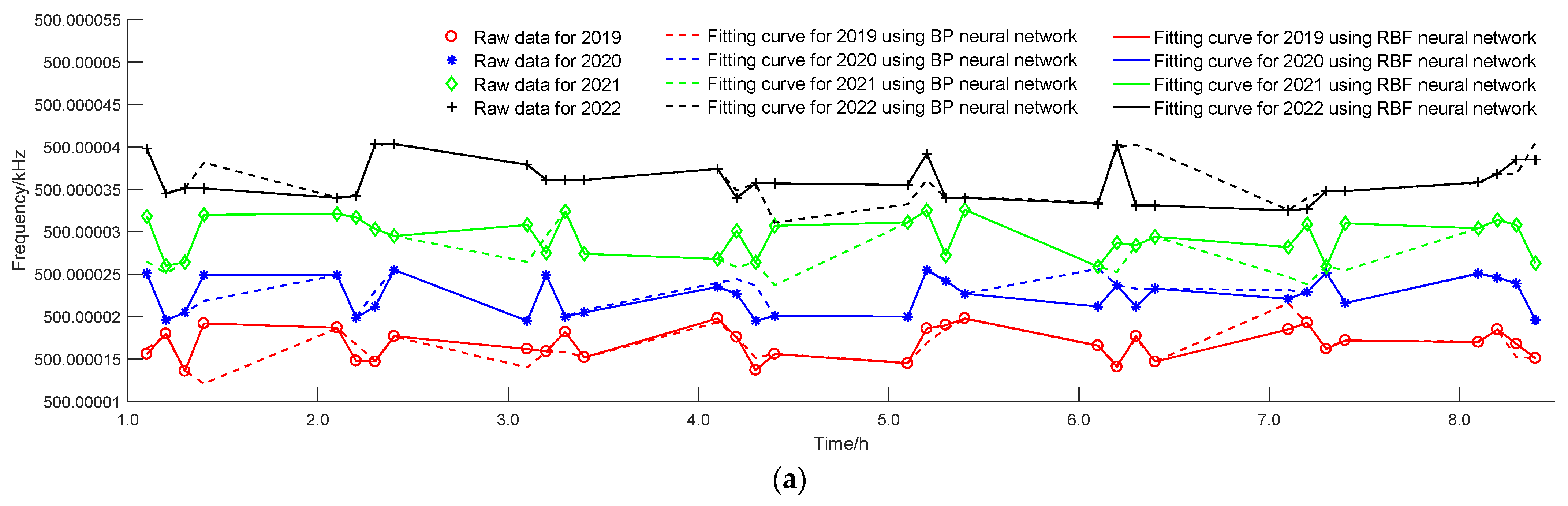
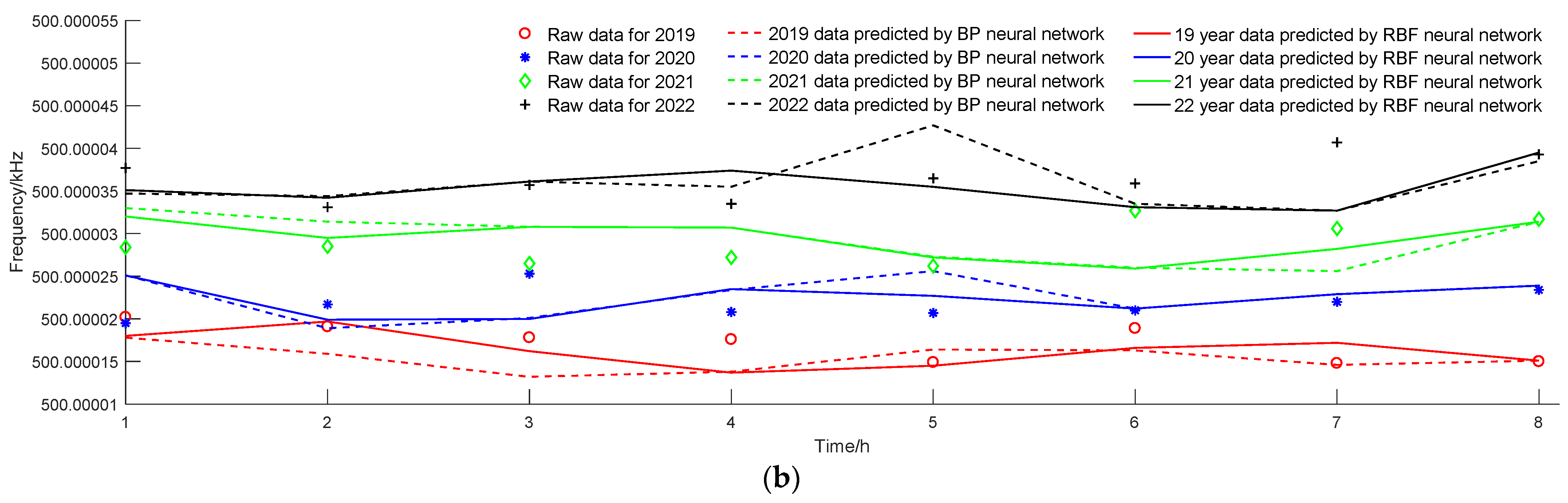
4.1. Time-Driven Model
4.2. Data-Driven Model
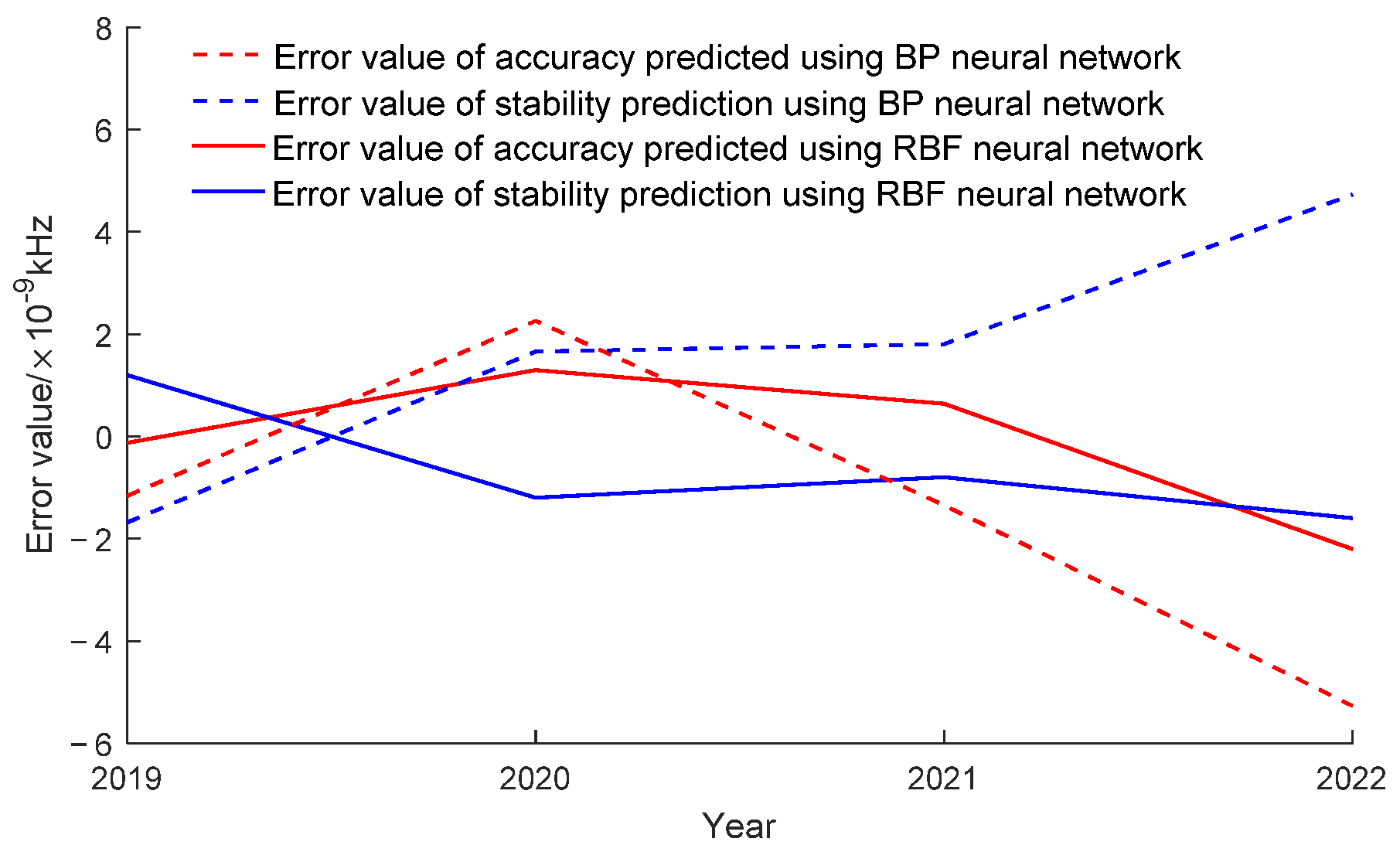
4.3. Error Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, X. Discussion on the Calibration Method of Clock Tester. Ind. Metrol. 2017, 27, 44. [Google Scholar]
- JJF1662-2017; Clock Tester Calibration Specification. Standards Press of China: Beijing, China, 2017.
- Liu, P.; Yin, C.; Jia, N.; Fan, X.; Yang, Q. Short-term Wind Power Prediction Based on Niche Genetic Algorithm and Radial Basis Function Surrogate Model. Acta Energ. Solaris Sin. 2013; in press. [Google Scholar]
- Feng, B.; Wang, S.; Feng, M. Application of Improved Radial Basis Interpolation Method in Ship Shape Optimization. J. South China Univ. Technol. Nat. Sci. Ed. 2022, 50, 57–64. [Google Scholar]
- Xue, P.; Hao, P.; Wang, H. Novel Gear Fault Diagnosis Method Based on RBF Neural Network. Control Decis. 2022, 37, 409–416. [Google Scholar]
- Wang, B.; Zhao, H. Small Obiect Detection in Hyperspectral Images Based on Radial Basis Activation Function. Acta Opt. Sin. 2021, 41, 95–105. [Google Scholar]
- Ren, X.; Wang, Y.; Wang, Q. Beam Pattern Optimization Method Based on Radial Basis Function Neural Network. J. Electron. Inf. Technol. 2021, 43, 3695–3702. [Google Scholar]
- Hu, M.; Wang, L.; Yang, F.; Zhou, Y. Weighted Radial Basis Collocation Method for the Nonlinear Inverse Helmholtz Problems. Mathematics 2023, 11, 662. [Google Scholar] [CrossRef]
- Yin, C.; Ji, Q.; Wen, C. An Adaptive Terminal Sliding Mode Control of Stone-carving Robotic Manipulators Based on Radial Basis Function Neural Network. Appl. Intell. 2022, 52, 16051–16068. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhao, H.; Wang, Z.; Zheng, M.; Xun, Q. Radial Basis Function Neural Network Optimal Modeling for Phase-Only Array Pattern Nulling. IEEE Trans. Antennas Propag. 2021, 69, 7971–7975. [Google Scholar] [CrossRef]
- Marcin, K. Nature-Inspired Algorithm Implemented for Stable Radial Basis Function Neural Controller of Electric Drive with Induction Motor. Energies 2020, 13, 6541. [Google Scholar]
- Ludovico, O.; Fabio, T.; Mauro, Z. Adaptive Maximum Torque per Ampere Control of Synchronous Reluctance Motors by Radial Basis Function Networks. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2531–2539. [Google Scholar]
- Lashkenari, M.; Bagheri, M.; Tatar, A.; Rezazadeh, H.; Inc, M. A Further Study in The Prediction of Viscosity for Iranian Crude Oil Reservoirs by Utilizing a Robust Radial Basis Function (RBF) Neural Network Model. Neural Comput. Appl. 2023, 35, 10663–10676. [Google Scholar] [CrossRef]
- Luo, J.; Shan, Y.; Liu, X.; Zhang, Y.; Jiang, E.; Kong, D. A Rapid Method to Predict Biaxial Fatigue Life of Automotive Wheels Using Proper Orthogonal Decomposition and Radial Basis Function Algorithm. Adv. Eng. Softw. 2023, 186, 103543. [Google Scholar] [CrossRef]
- Mohammad, A.; Awadh, A.; Aiesh, A.; Aiesh, Q.; Ljaz, A.; Alhashim, H.; Ehsan, E. Developing a Model Based on the Radial Basis Function to Predict the Compressive Strength of Concrete Containing Fly Ash. Buildings 2022, 12, 1743. [Google Scholar]
- Hao, G.; Guo, J.; Zhang, W.; Chen, Y.; David, A. High-precision Chaotic Radial Basis Function Neural Network Model: Data Forecasting for The Earth Electromagnetic Signal Before a Strong Earthquake. Geosci. Front. 2022, 13, 101315. [Google Scholar] [CrossRef]
- Stephen, O.; Agbotiname, I.; Daniel, A. Radial Basis Function Neural Network Path Loss Prediction Model for LTE Networks in Multitransmitter Signal Propagation Environments. Int. J. Commun. Syst. 2020, 34, e4680. [Google Scholar]
- Zhang, S.; Ge, Z.; Fan, X.; Huang, H.; Long, X. Prediction Method of Thermal Conductivity of Nanofluids Based on Radial Basis Function. J. Therm. Anal. Calorim. 2020, 141, 859–880. [Google Scholar] [CrossRef]
- Tao, W.; Chen, J.; Gui, Y. Coking Energy Consumption Radial Basis Function Prediction Model Improved by Differential Evolution Algorithm. Meas. Control 2019, 52, 1122–1130. [Google Scholar] [CrossRef]
- Yoon, S.; Jeon, H.; Kum, D. Predictive Cruise Control Using Radial Basis Function Network-Based Vehicle Motion Prediction and Chance Constrained Model Predictive Control. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3832–3843. [Google Scholar] [CrossRef]
- Roshani, M.; Sattari, M.; Muhammad, A.; Roshani, G.; Nazemi, B.; Corniani, E.; Nazemi, E. Application of GMDH Neural Network Technique to Improve Measuring Precision of a Simplified Photon Attenuation Based Two-Phase Flowmeter. Flow Meas. Instrum. 2020, 75, 101804. [Google Scholar] [CrossRef]
- Qin, X.; Liu, Z.; Liu, Y.; Liu, S.; Yang, B.; Yin, L.; Liu, M.; Zheng, W. User OCEAN Personality Model Construction Method Using a BP Neural Network. Electronics 2022, 11, 3022. [Google Scholar] [CrossRef]
- Lv, C.; Liu, Y.; Liu, J.; Yu, Z. Application of Generalized Radial Basis Function Neural Network to Thermal Error Modeling. Opt. Precis. Eng. 2015, 23, 1705–1713. [Google Scholar]



| Sample Number | Time | Measurement Conditions | Partial Measurement Data/kHz |
|---|---|---|---|
| 20163320 | 15 April 2019 | Stability measurement conditions: measure every 1 h | 500.0000156\500.0000187 500.0000162\500.0000198 |
| 20163340 | 14 April 2020 | Accuracy measurement conditions: random measurement | 500.0000253\500.0000221 500.0000248\500.0000201 |
| 20163366 | 12 April 2021 | Stability measurement conditions: measure every 1 h | 500.0000264\500.0000303 500.0000324\500.0000264 |
| 20163355 | 20 May 2022 | Accuracy measurement conditions: random measurement | 500.0000329\500.0000324 500.0000370\500.0000390 |
| 20163352 | 21 May 2022 | Stability measurement conditions: measure every 1 h | 500.0000377\500.0000331 500.0000357\500.0000335 |
| Time | Practical Stability | Stability Prediction Using BP Neural Network | Stability Prediction Using RBF Neural Network |
|---|---|---|---|
| 2019 | 1.080 × 10−8 | 0.912 × 10−8 | 1.200 × 10−8 |
| 2020 | 1.160 × 10−8 | 1.326 × 10−8 | 1.040 × 10−8 |
| 2021 | 1.300 × 10−8 | 1.481 × 10−8 | 1.220 × 10−8 |
| 2022 | 1.520 × 10−8 | 1.993 × 10−8 | 1.360 × 10−8 |
| Time | Practical Stability | Accuracy Prediction Using BP Neural Network | Accuracy Prediction Using RBF Neural Network |
|---|---|---|---|
| 2019 | 3.510 × 10−8 | 3.394 × 10−8 | 3.498 × 10−8 |
| 2020 | 4.488 × 10−8 | 4.714 × 10−8 | 4.618 × 10−8 |
| 2021 | 5.842 × 10−8 | 5.708 × 10−8 | 5.906 × 10−8 |
| 2022 | 7.510 × 10−8 | 6.983 × 10−8 | 7.290 × 10−8 |
| Equipment Number | Practical Stability | Stability Prediction Using BP Neural Network | Stability Prediction Using RBF Neural Network |
|---|---|---|---|
| 20163320 | 1.460 × 10−8 | 2.036 × 10−8 | 1.167 × 10−8 |
| 20163340 | 1.500 × 10−8 | 2.537 × 10−8 | 1.202 × 10−8 |
| 20163366 | 1.440 × 10−8 | 1.082 × 10−8 | 1.154 × 10−8 |
| 20163355 | 1.440 × 10−8 | 2.298 × 10−8 | 1.159 × 10−8 |
| 20163352 | 1.520 × 10−8 | 3.134 × 10−8 | 1.171 × 10−8 |
| Equipment Number | Practical Accuracy | Accuracy Prediction Using BP Neural Network | Accuracy Prediction Using RBF Neural Network |
|---|---|---|---|
| 20163320 | 7.436 × 10−8 | 7.282 × 10−8 | 7.341 × 10−8 |
| 20163340 | 7.142 × 10−8 | 6.974 × 10−8 | 7.282 × 10−8 |
| 20163366 | 7.456 × 10−8 | 7.133 × 10−8 | 7.150 × 10−8 |
| 20163355 | 7.110 × 10−8 | 7.358 × 10−8 | 7.335 × 10−8 |
| 20163352 | 7.510 × 10−8 | 7.361 × 10−8 | 7.386 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Zheng, X.; Zhao, C. Research on the Prediction Method of Clock Tester Calibration Data Based on Radial Basis Function Neural Network. Electronics 2023, 12, 4677. https://doi.org/10.3390/electronics12224677
Yu M, Zheng X, Zhao C. Research on the Prediction Method of Clock Tester Calibration Data Based on Radial Basis Function Neural Network. Electronics. 2023; 12(22):4677. https://doi.org/10.3390/electronics12224677
Chicago/Turabian StyleYu, Meixia, Xiaoping Zheng, and Chuanhui Zhao. 2023. "Research on the Prediction Method of Clock Tester Calibration Data Based on Radial Basis Function Neural Network" Electronics 12, no. 22: 4677. https://doi.org/10.3390/electronics12224677
APA StyleYu, M., Zheng, X., & Zhao, C. (2023). Research on the Prediction Method of Clock Tester Calibration Data Based on Radial Basis Function Neural Network. Electronics, 12(22), 4677. https://doi.org/10.3390/electronics12224677





