A Target Detection Method of Distributed Passive Radar without Direct-Path Signal
Abstract
1. Introduction
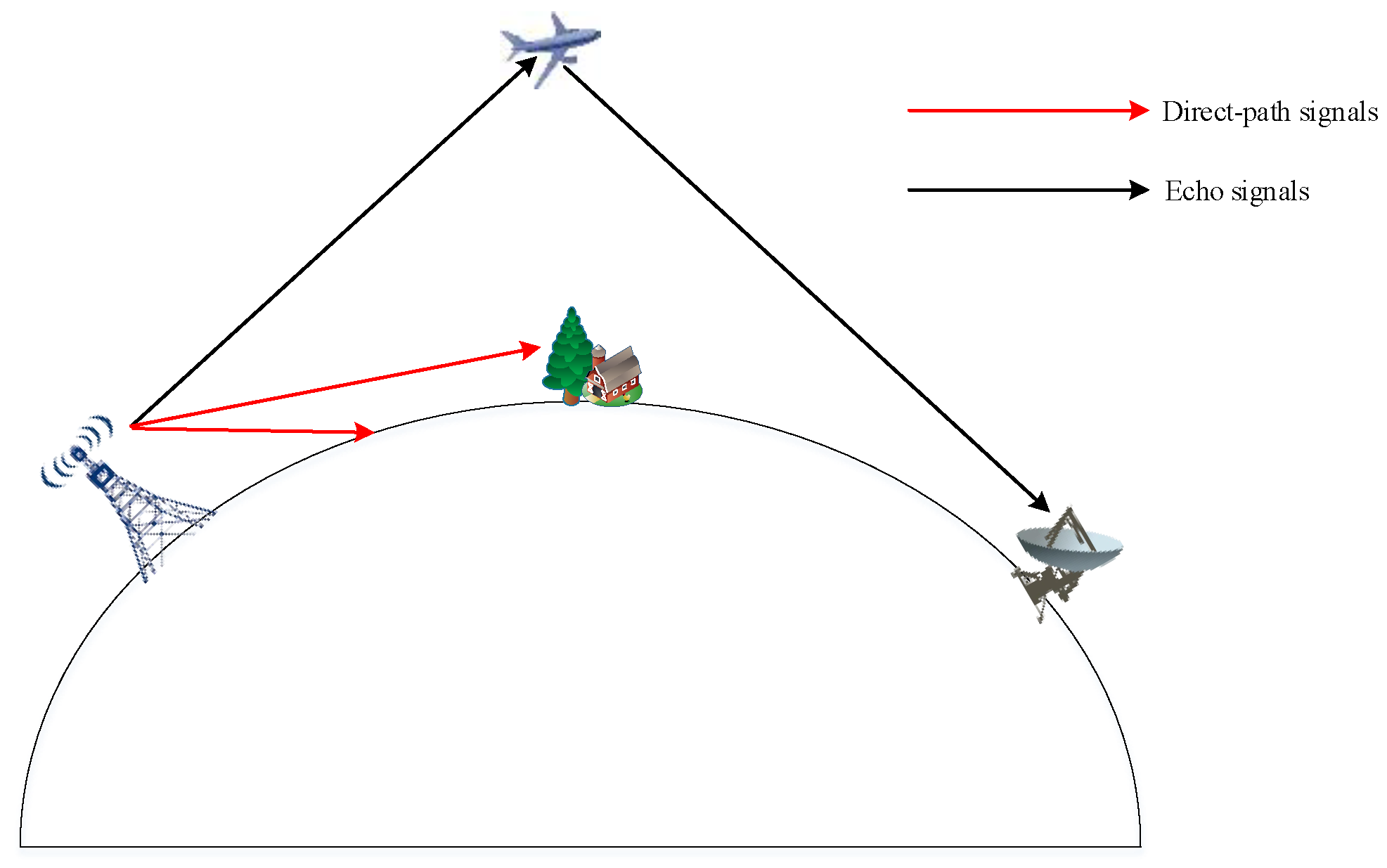
2. The Scene of Without-Direct-Path Signals
3. GLRT Detection Algorithm
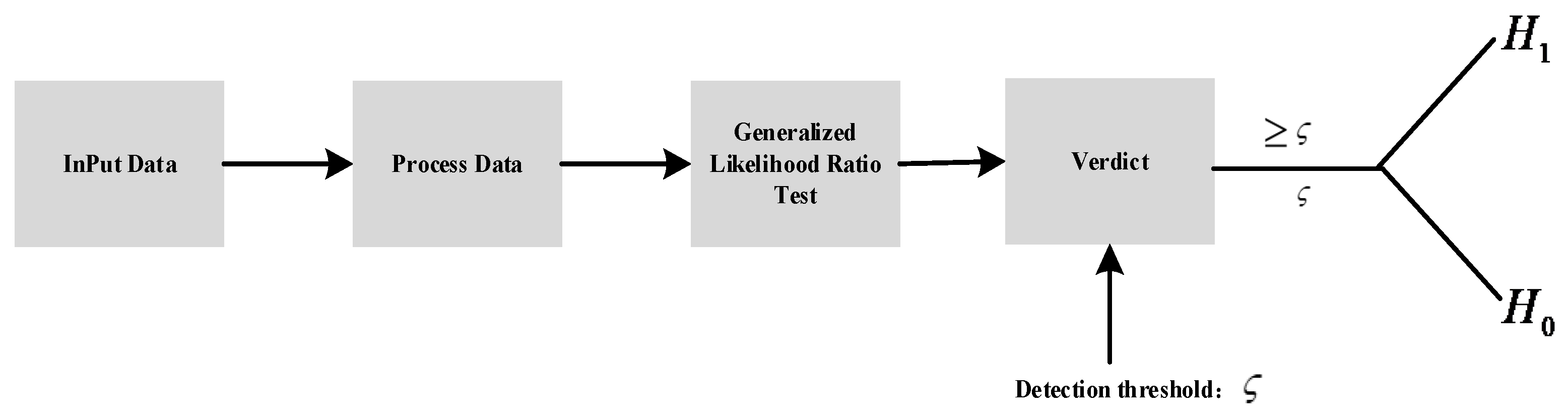
3.1. Detection Algorithm
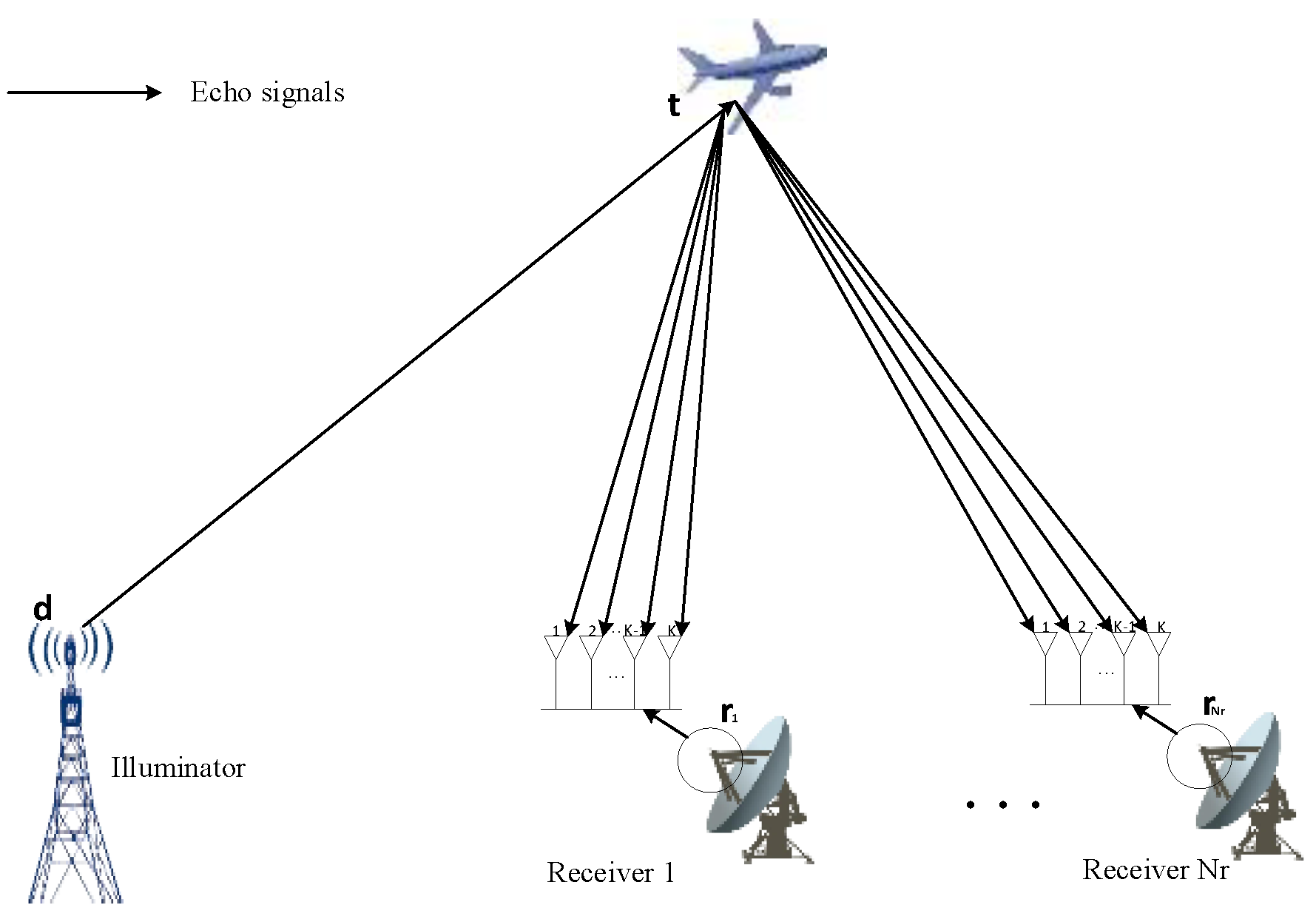
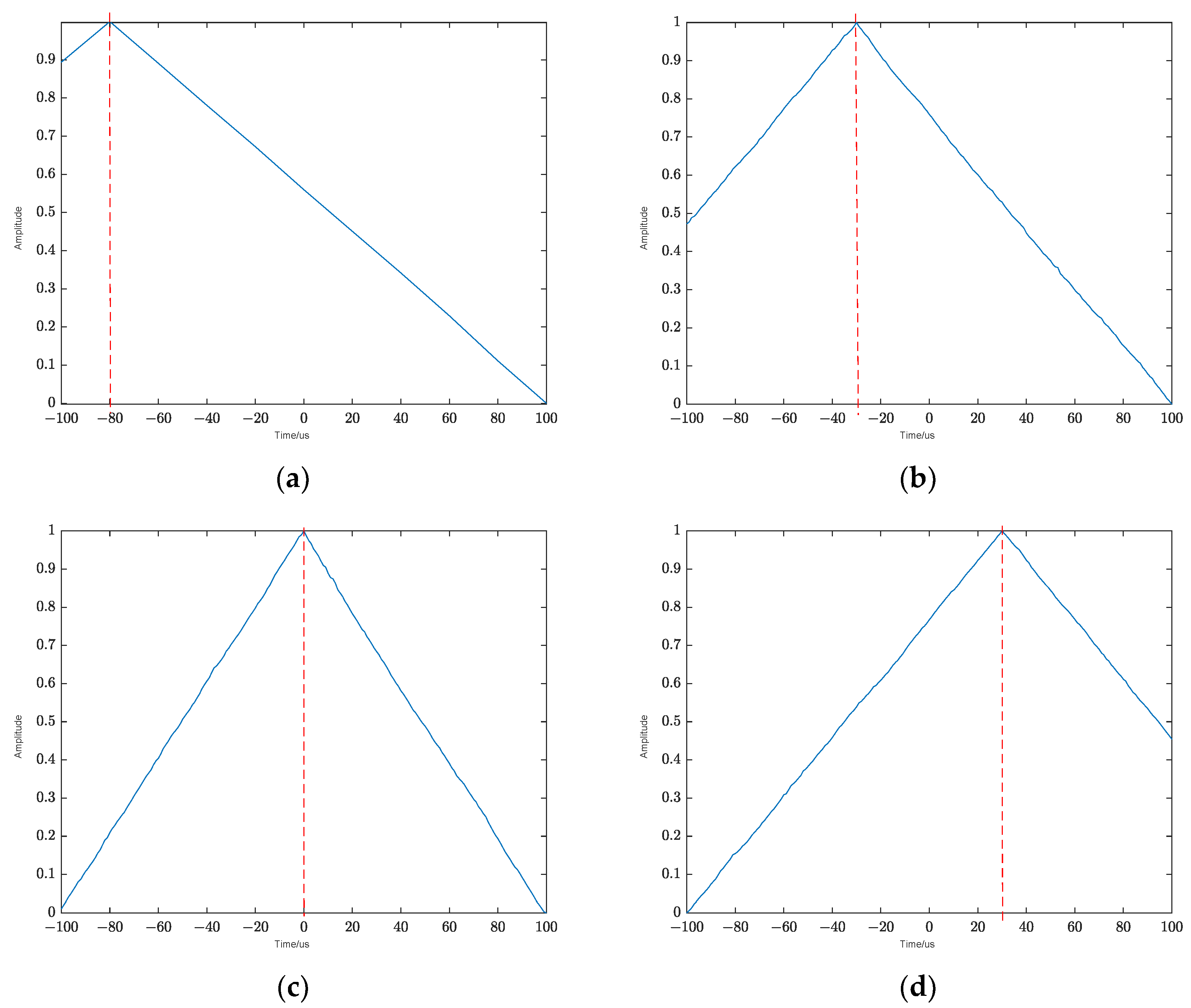
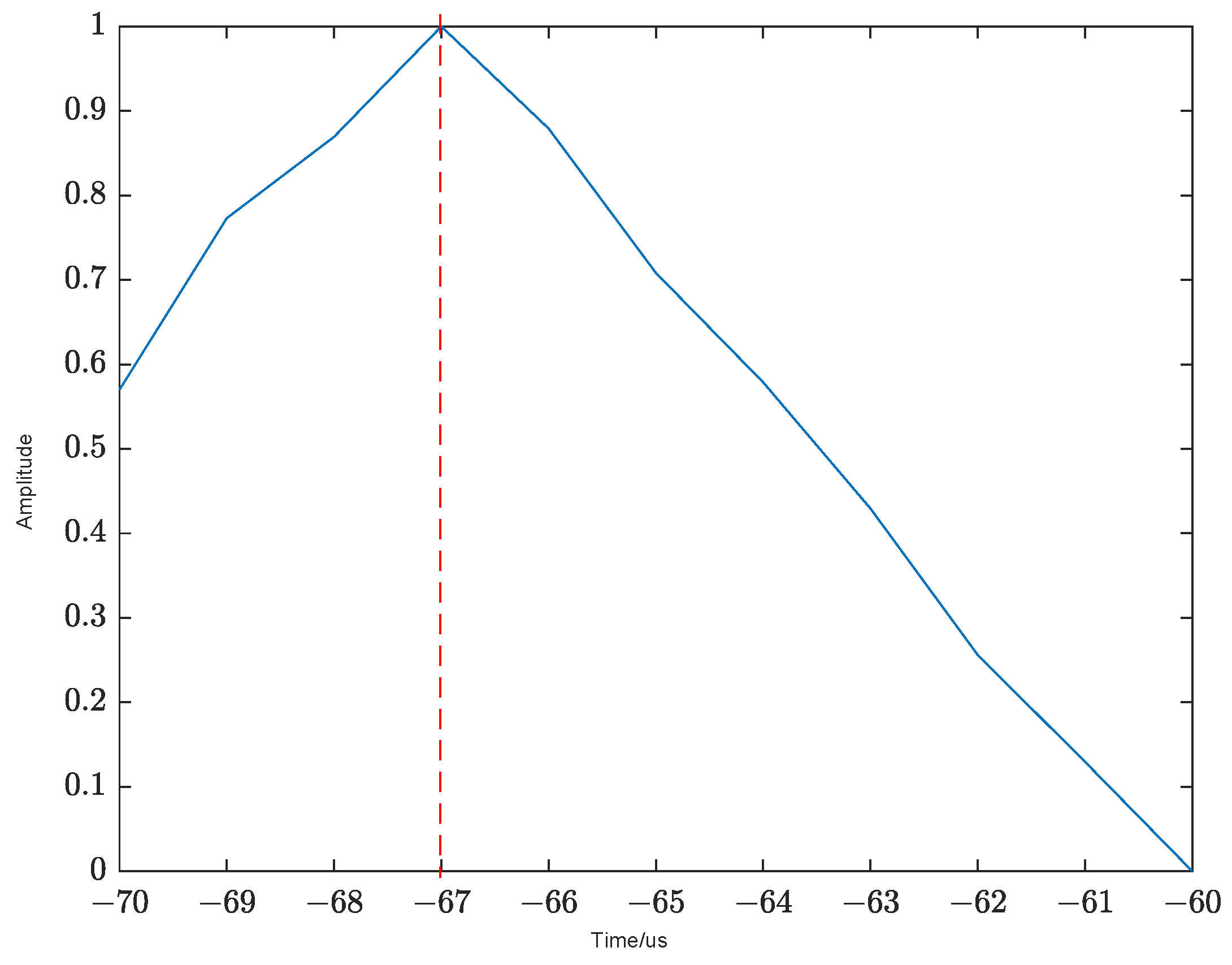
3.2. The Estimation of Time Delay of Arrival (TDOA)
- Generate the scheme of TDOA estimation;
- Set the time delay interval , according to the distance between stations, set the search range as , and set the scheme . There are auxiliary receivers, easy to know is a finite collection. The number of elements is , and can be expressed as
- For any , represents the th echo data from the receivers moving to the right time units;
- Initialize the dimensional vector and set all the entries in to 0;
- Estimate the TDOA according to the scheme;
- Go through all the schemes in the set , and repeat the following (2) and (3) for each scheme until the collection is traversed and step 3 is entered;
- The echo data of each channel was arranged as dimensional vector in chronological order; that is , the echo data of channel was merged into a dimensional matrix ;
- Make a calculation of
- Put in the corresponding position of vector , let us say ;
- Traverse the vector to find the maximum value, as shown in (17);
- Record the position of the maximum value in , and find out the corresponding scheme of the same position as in and , so as to determine the delay time , as shown in Equation (18).
4. Experiments
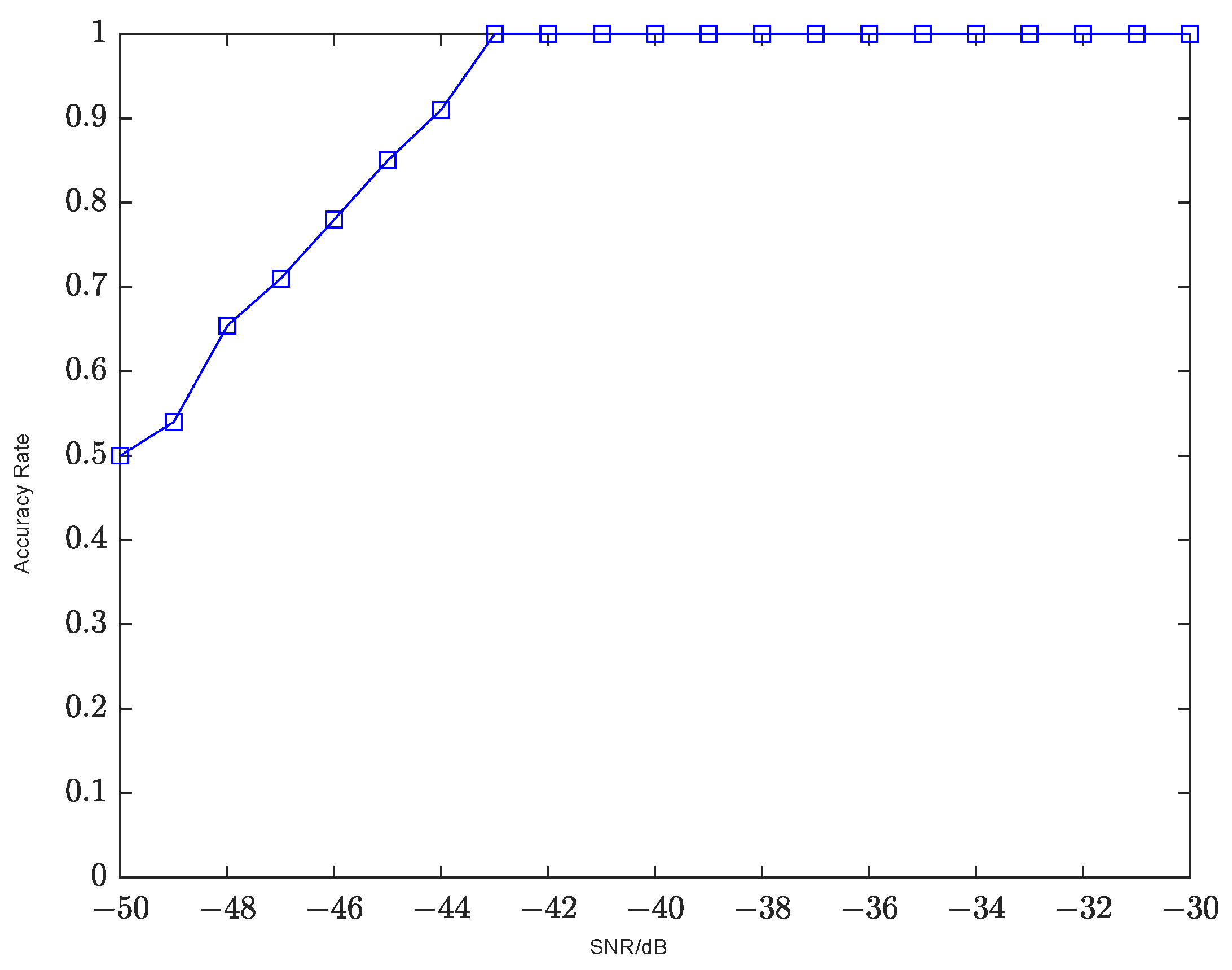
4.1. Detection Performance
4.2. Verify the Accuracy of TDOA Estimation
4.3. The Influence of Different Algorithms on Detection Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, L.; Li, J.; Stoica, P. Target detection and parameter estimation for MIMO radar systems. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 927–939. [Google Scholar] [CrossRef]
- Bekkerman, I.; Tabrikian, J. Target detection and localization using MIMO radars and sonars. IEEE Trans. Signal Process. 2006, 54, 3873–3883. [Google Scholar] [CrossRef]
- Blasone, G.P.; Colone, F.; Lombardo, P. Dual cancelled channel STAP for target detection and DOA estimation in Passive Radar. Sensors 2021, 21, 4569. [Google Scholar] [CrossRef] [PubMed]
- Zaimbashi, A. A unified framework for multistatic passive radar target detection under uncalibrated receivers. IEEE Trans. Signal Process. 2021, 69, 695–708. [Google Scholar] [CrossRef]
- Blasone, G.P.; Colone, F.; Lombardo, P. Passive Radar STAP detection and DOA estimation under antenna calibration errors. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2725–2742. [Google Scholar] [CrossRef]
- Viswanathan, R.; Varshney, P.K. Distributed Detection with Multiple Sensors, I. Fundamentals. Proc. IEEE 1997, 85, 54–63. [Google Scholar] [CrossRef]
- Tao, R.; Gao, Z.; Wang, Y. Side Peaks Interference Suppression in DVB-T Based Passive Radar. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3610–3619. [Google Scholar] [CrossRef]
- Jichuan, L.; Yaodong, Z.; Yongke, Z.; Xiaode, L. Direct path wave purification for passive radar with normalized least mean square algorithm. In Proceedings of the 2013 IEEE International Conference on Signal Processing, Communication and Computing (ICSPCC 2013), Kunming, China, 5–8 August 2013. [Google Scholar]
- Hack, D.E.; Patton, L.K.; Himed, B.; Saville, M.A. Detection in Passive MIMO Radar Networks. IEEE Trans. Signal Process. 2014, 62, 2999–3012. [Google Scholar] [CrossRef]
- Cui, G.; Liu, J.; Li, H.; Himed, B. Signal detection with noisy reference for passive sensing. Signal Process. 2015, 108, 389–399. [Google Scholar] [CrossRef]
- Ying, T.; Zuo, W.; Gao, J. Weak target detection method based on hypothesis test theory in non-cooperative passive detection. Acta Aeronaut. Astronaut. Sin. 2016, 37, 626–636. [Google Scholar]
- Chen, G.; Wang, J.; Zuo, L. Two-stage clutter and interference cancellation method in passive bistatic radar. IET Signal Process. 2020, 14, 342–351. [Google Scholar] [CrossRef]
- Liu, J.; Lia, H.; Himed, B. On the performance of the cross-correlation detector for passive radar applications. Signal Process. 2015, 113, 32–37. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Liu, J.; Himed, B. Joint delay and doppler estimation for passive sensing with direct-path interference. IEEE Trans. Signal Process. 2016, 64, 630–640. [Google Scholar] [CrossRef]
- Zaimbashi, A.; Derakhtian, M.; Sheikhi, A. GLRT-based CFAR detection in passive bistatic radar. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 134–159. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Himed, B. Two target detection algorithms for passive multistatic radar. IEEE Trans. Signal Process. 2014, 62, 5930–5939. [Google Scholar] [CrossRef]
- Chen, W.S.; Reed, I.S. A new CFAR detection test for radar. Digit. Signal Process. Acad. Press 1991, 1, 198–214. [Google Scholar] [CrossRef]
- Wang, H.; Cai, L. On adaptive spatial-temporal processing for airborne surveillance radar systems. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 660–670. [Google Scholar] [CrossRef]
- Kraut, S.; Scharf, L.L. The CFAR adaptive subspace detector is a scale-invariant GLRT. IEEE Trans. Signal Process. 1999, 47, 2538–2541. [Google Scholar] [CrossRef]
- Conte, E.; De Maio, A.; Ricci, G. GLRT-based adaptive detection algorithms for range-spread targets. IEEE Trans. Signal Process. 2001, 49, 1336–1348. [Google Scholar] [CrossRef]
- Bandiera, F.; Besson, O.; Orlando, D. GLRT-based direction detectors in homogeneous noise and subspace interference. IEEE Trans. Signal Process. 2007, 55, 2386–2394. [Google Scholar] [CrossRef]
- Sohn, K.J.; Li, H.; Himed, B. Parametric GLRT for multichannel adaptive signal detection. IEEE Trans. Signal Process. 2007, 55, 5351–5360. [Google Scholar] [CrossRef]
- Kraut, S.; Scharf, L.L.; McWhorter, L.T. Adaptive subspace detectors. IEEE Trans. Signal Process. 2001, 49, 1–16. [Google Scholar] [CrossRef]
- Bialkowski, K.S.; Clarkson, I.V.L.; Howard, S.D. Generalized canonical correlation for passive multistatic radar detection. In Proceedings of the IEEE Statistical Signal Processing Workshop (SSP), Nice, France, 28–30 June 2011; pp. 417–420. [Google Scholar]
- Horn, R.; Johnson, C. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Chen, Y.; Wu, Y.; Chen, N. New approximate distributions for the generalized likelihood ratio test detection in passive radar. IEEE Signal Process. Lett. 2019, 26, 685–689. [Google Scholar] [CrossRef]
- Liu, R.; Dai, W.; Zhang, C. Multi-target Detection by Distributed Passive Radar Systems without Reference Signals. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 10–13 April 2022; pp. 1–5. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Number of receivers | 4 |
| Sampling frequency | 100 MHz |
| Destination location | (0, 50, 0) km |
| Receivers position | (10, 0, 0) km, (−10, 0, 0) km (0, 10, 0) km, (0, −10, 0) km |
| Illuminator location | (0, 0, 0) km |
| Target speed | 0 |
| Signal length | 0.01 s |
| SNR | −40 dB |
| Type of signal | DVB-T |
| SNR/dB | −10 | −11 | −12 | −13 | −14 | −15 | −16 | −17 | −18 | −19 |
| DP | 1 | 1 | 1 | 1 | 1 | 0.999 | 0.98 | 0.929 | 0.842 | 0.722 |
| SNR/dB | −20 | −21 | −22 | −23 | −24 | −25 | −26 | −27 | −28 | −29 |
| DP | 0.639 | 0.549 | 0.479 | 0.456 | 0.429 | 0.426 | 0.407 | 0.427 | 0.407 | 0.39 |
| SNR/dB | −30 | −31 | −32 | −33 | −34 | −35 | −36 | −37 | −38 | −39 |
| DP | 0.423 | 0.408 | 0.382 | 0.398 | 0.392 | 0.409 | 0.433 | 0.396 | 0.399 | 0.403 |
| SNR/dB | −10 | −11 | −12 | −13 | −14 | −15 | −16 | −17 | −18 | −19 |
| DP | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.999 |
| SNR/dB | −20 | −21 | −22 | −23 | −24 | −25 | −26 | −27 | −28 | −29 |
| DP | 0.995 | 0.987 | 0.94 | 0.851 | 0.724 | 0.649 | 0.553 | 0.5 | 0.439 | 0.444 |
| SNR/dB | −30 | −31 | −32 | −33 | −34 | −35 | −36 | −37 | −38 | −39 |
| DP | 0.414 | 0.464 | 0.427 | 0.412 | 0.401 | 0.405 | 0.402 | 0.407 | 0.378 | 0.418 |
| SNR/dB | −10 | −11 | −12 | −13 | −14 | −15 | −16 | −17 | −18 | −19 |
| DP | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| SNR/dB | −20 | −21 | −22 | −23 | −24 | −25 | −26 | −27 | −28 | −29 |
| DP | 1 | 1 | 1 | 1 | 1 | 0.997 | 0.984 | 0.956 | 0.845 | 0.762 |
| SNR/dB | −30 | −31 | −32 | −33 | −34 | −35 | −36 | −37 | −38 | −39 |
| DP | 0.661 | 0.535 | 0.497 | 0.476 | 0.435 | 0.422 | 0.419 | 0.455 | 0.411 | 0.414 |
| SNR/dB | −10 | −11 | −12 | −13 | −14 | −15 | −16 | −17 | −18 | −19 |
| DP | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| SNR/dB | −20 | −21 | −22 | −23 | −24 | −25 | −26 | −27 | −28 | −29 |
| DP | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| SNR/dB | −30 | −31 | −32 | −33 | −34 | −35 | −36 | −37 | −38 | −39 |
| DP | 1 | 0.96 | 0.91 | 0.83 | 0.81 | 0.7 | 0.419 | 0.63 | 0.57 | 0.57 |
| Parameters | Value |
|---|---|
| Number of receivers | 2 |
| SNR | −40 dB |
| Signal length | 0.1 s |
| Sampling frequency | 100 MHz |
| Time moving interval | 0.001 ms |
| Target speed | 0 |
| Receivers position | (10, 0, 0) km, (−10, 0, 0) km |
| Illuminator location | (0, 0, 0) km |
| Parameters | Value |
|---|---|
| The location of illuminator | |
| The location of receiver | |
| The location of target | |
| Temperature | |
| Bandwidth | |
| The gain of transmitter | 10 dB |
| The gain of receiver | 10 dB |
| Type of signal | DVB-T |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Wang, C.; Wang, L. A Target Detection Method of Distributed Passive Radar without Direct-Path Signal. Electronics 2023, 12, 433. https://doi.org/10.3390/electronics12020433
Zhu H, Wang C, Wang L. A Target Detection Method of Distributed Passive Radar without Direct-Path Signal. Electronics. 2023; 12(2):433. https://doi.org/10.3390/electronics12020433
Chicago/Turabian StyleZhu, Huijie, Changlong Wang, and Lu Wang. 2023. "A Target Detection Method of Distributed Passive Radar without Direct-Path Signal" Electronics 12, no. 2: 433. https://doi.org/10.3390/electronics12020433
APA StyleZhu, H., Wang, C., & Wang, L. (2023). A Target Detection Method of Distributed Passive Radar without Direct-Path Signal. Electronics, 12(2), 433. https://doi.org/10.3390/electronics12020433






