Numerical Robustness Evaluation of Floating-Point Closed-Loop Control Based on Interval Analysis
Abstract
1. Introduction
2. Interval- versus Floating-Point Arithmetic
2.1. Interval Arithmetic
2.2. Sources of Inaccuracy in Interval Computations
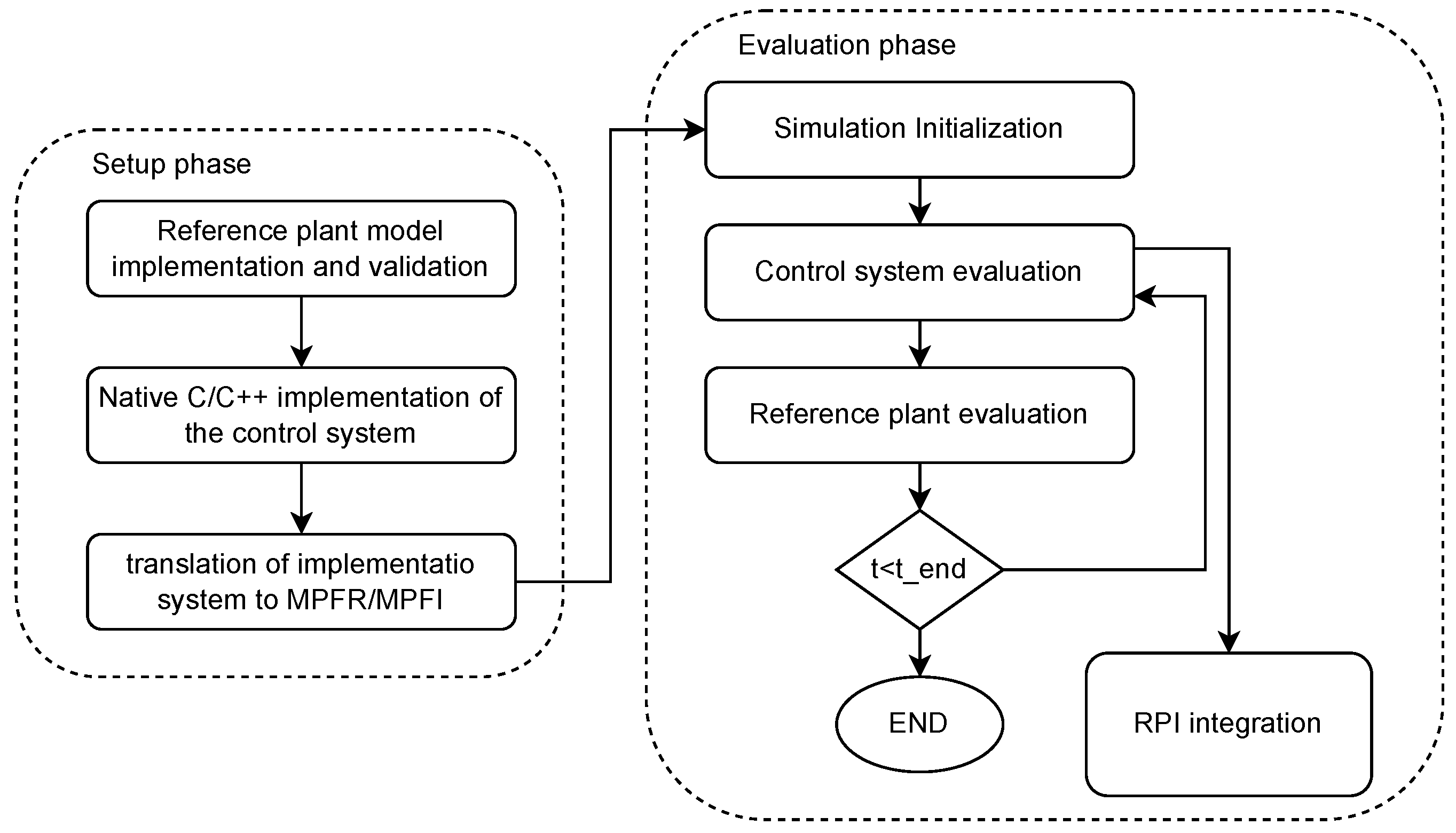
3. Verification of Closed-Loop Floating-Point Core
3.1. Setup Phase
3.2. Evaluation Phase
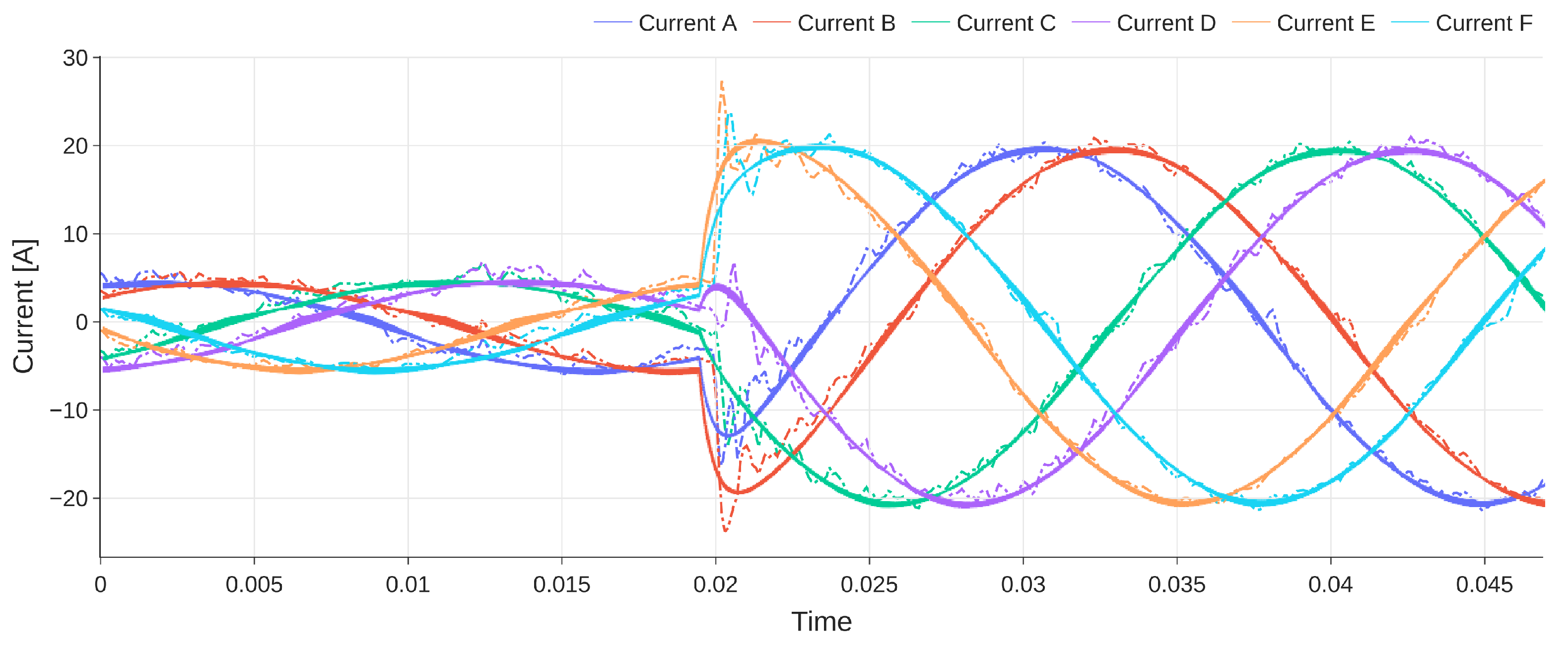
4. Case Study
4.1. System and Control Architecture
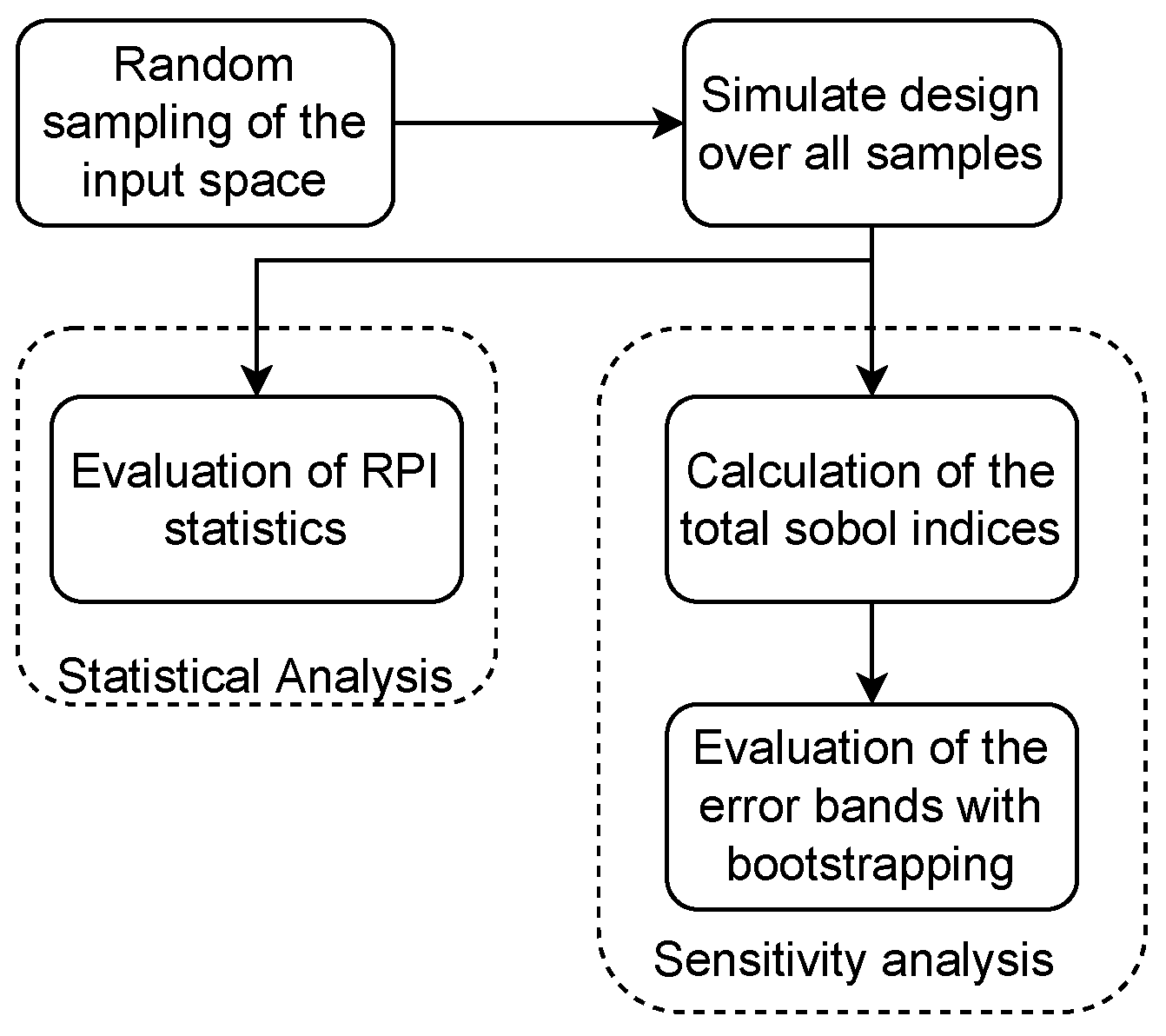
4.2. Sensitivity Analysis
4.3. Statistical Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| List of Abbreviations | |
| Carbon dioxide | |
| Nitrogen oxides | |
| FPU | Floating-point unit |
| MPFI | Multiple-Precision Floating-Point Interval Library |
| MVDC | Medium-voltage DC |
| OAT | One-at-a-time |
| PI | Proportional integral |
| PIR | Proportional integral resonant |
| PLECS | Piecewise Linear Circuit Simulator |
| PMSM | Permanent magnet synchronous machine |
| RPI | Robustness performance indicator |
| VSD | Vector space decomposition |
| List of Symbols | |
| Simulation time | |
| Confidence interval width for the xth quantity of interest | |
| Sobol Sensitivity index | |
| Mean value of the input random variable X not connected to the examined parameter | |
| Variance of the input random variable X connected to the examined parameter | |
| Output random variable | |
References
- Directorate-General for Mobility and Transport (European Commission); Directorate-General for Research and Innovation (European Commission). Flightpath 2050: Europe’s Vision for Aviation: Maintaining Global Leadership and Serving Society’s Needs; Publications Office: Geneva, Switzerland, 2011. [Google Scholar] [CrossRef]
- Gibson, A.; Hall, D.; Waters, M.; Masson, P.; Schiltgen, B.; Foster, T.; Keith, J. The Potential and Challenge of TurboElectric Propulsion for Subsonic Transport Aircraft. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar] [CrossRef]
- Golovanov, D.; Gerada, D.; Sala, G.; Degano, M.; Trentin, A.; Connor, P.H.; Xu, Z.; Rocca, A.L.; Galassini, A.; Tarisciotti, L.; et al. 4-MW Class High-Power-Density Generator for Future Hybrid-Electric Aircraft. IEEE Trans. Transp. Electrif. 2021, 7, 2952–2964. [Google Scholar] [CrossRef]
- Trentin, A.; Sala, G.; Tarisciotti, L.; Galassini, A.; Degano, M.; Connor, P.H.; Golovanov, D.; Gerada, D.; Xu, Z.; La Rocca, A.; et al. Research and Realization of High-Power Medium-Voltage Active Rectifier Concepts for Future Hybrid-Electric Aircraft Generation. IEEE Trans. Ind. Electron. 2021, 68, 11684–11695. [Google Scholar] [CrossRef]
- Savi, F.; Barater, D.; Buticchi, G.; Gerada, C.; Wheeler, P. A Scalable System Architecture for High-Performance Fault Tolerant Machine Drives. IEEE Open J. Ind. Electron. Soc. 2021, 2, 428–440. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Dai Pre, M. Strategies for the Fault-Tolerant Current Control of a Five-Phase Permanent-Magnet Motor. IEEE Trans. Ind. Appl. 2007, 43, 960–970. [Google Scholar] [CrossRef]
- Kiselev, A.; Catuogno, G.R.; Kuznietsov, A.; Leidhold, R. Finite-Control-Set MPC for Open-Phase Fault-Tolerant Control of PM Synchronous Motor Drives. IEEE Trans. Ind. Electron. 2020, 67, 4444–4452. [Google Scholar] [CrossRef]
- Sanchez-Stern, A.; Panchekha, P.; Lerner, S.; Tatlock, Z. Finding Root Causes of Floating Point Error. SIGPLAN Not. 2018, 53, 256–269. [Google Scholar] [CrossRef]
- Das, A.; Briggs, I.; Gopalakrishnan, G.; Krishnamoorthy, S.; Panchekha, P. Scalable yet Rigorous Floating-Point Error Analysis. In Proceedings of the SC20: International Conference for High Performance Computing, Networking, Storage and Analysis, Atlanta, GA, USA, 9–19 November 2020; pp. 1–14. [Google Scholar] [CrossRef]
- Delmas, D.; Goubault, E.; Putot, S.; Souyris, J.; Tekkal, K.; Védrine, F. Towards an Industrial Use of FLUCTUAT on Safety-Critical Avionics Software. In Formal Methods for Industrial Critical Systems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 53–69. [Google Scholar]
- Higham, N.J. Accuracy and Stability of Numerical Algorithms, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Boldo, S.; Melquiond, G. Computer Arithmetic and Formal Proofs: Verifying Floating-Point Algorithms with the Coq System; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Muller, J.M. Arithmétique des Ordinateurs; Masson: Paris, France, 1989. [Google Scholar]
- Muller, J.M. Ordinateurs en quête d’arithmétique. La Rech. 1995, 26, 772–777. [Google Scholar]
- Ménissier-Morain, V. Arbitrary precision real arithmetic: Design and algorithms. J. Log. Algebr. Program. 2005, 64, 13–39. [Google Scholar] [CrossRef]
- Tucker, W. Validated Numerics: A Short Introduction to Rigorous Computations; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Moore, R.E.; Kearfott, R.B.; Cloud, M.J. Introduction to Interval Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009. [Google Scholar]
- Hansen, E.; Walster, G.W. Global Optimization Using Interval Analysis; Pure and Applied Mathematics Series; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- IEEE Std 1788-2015; IEEE Standard for Interval Arithmetic. IEEE SA: Piscataway, NJ, USA, 2015. Available online: https://standards.ieee.org/ieee/1788/4431/ (accessed on 29 December 2022).
- Revol, N.; Rouillier, F. Motivations for an Arbitrary Precision Interval Arithmetic and the MPFI Library. Reliab. Comput. 2005, 11, 275–290. [Google Scholar] [CrossRef]
- MPFI Boost Multiprecision Library. Available online: https://www.boost.org/doc/libs/1_76_0/libs/multiprecision/doc/html/boost_multiprecision/tut/interval/mpfi.html (accessed on 19 December 2022).
- Duracz, J.; Farjudian, A.; Konečný, M.; Taha, W. Function Interval Arithmetic. In Mathematical Software—ICMS 2014; Hong, H., Yap, C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8592, pp. 677–684. [Google Scholar]
- Tucker, W. A rigorous ODE solver and Smale’s 14th problem. Found. Comput. Math. 2002, 2, 53–117. [Google Scholar] [CrossRef]
- Wang, S.; Pei, K.; Whitehouse, J.; Yang, J.; Jana, S. Formal Security Analysis of Neural Networks Using Symbolic Intervals. In Proceedings of the 27th USENIX Conference on Security Symposium (SEC’18), Baltimore, MD, USA, 15–17 August 2018; pp. 1599–1614. [Google Scholar]
- Neumaier, A. The Wrapping Effect, Ellipsoid Arithmetic, Stability and Confidence Regions. In Validation Numerics: Theory and Applications; Albrecht, R., Alefeld, G., Stetter, H.J., Eds.; Springer: Vienna, Austria, 1993; pp. 175–190. [Google Scholar] [CrossRef]
- Savi, F.; Harikumaran, J.; Barater, D.; Buticchi, G.; Gerada, C.; Wheeler, P. Femtocore: An Application Specific Processor for Vertically Integrated High Performance Real-Time Controls. IEEE Open J. Ind. Electron. Soc. 2021, 2, 479–488. [Google Scholar] [CrossRef]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so many published sensitivity analyses are false: A systematic review of sensitivity analysis practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Sobol, I. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Sobol, I. On the distribution of points in a cube and the approximate evaluation of integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Hervé Monod, C.N.; Makowski, D. Uncertainty and Sensitivity Analysis for Crop Models; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Yepes, A.G.; Freijedo, F.D.; Doval-Gandoy, J.; López, O.; Malvar, J.; Fernandez-Comesaña, P. Effects of Discretization Methods on the Performance of Resonant Controllers. IEEE Trans. Power Electron. 2010, 25, 1692–1712. [Google Scholar] [CrossRef]



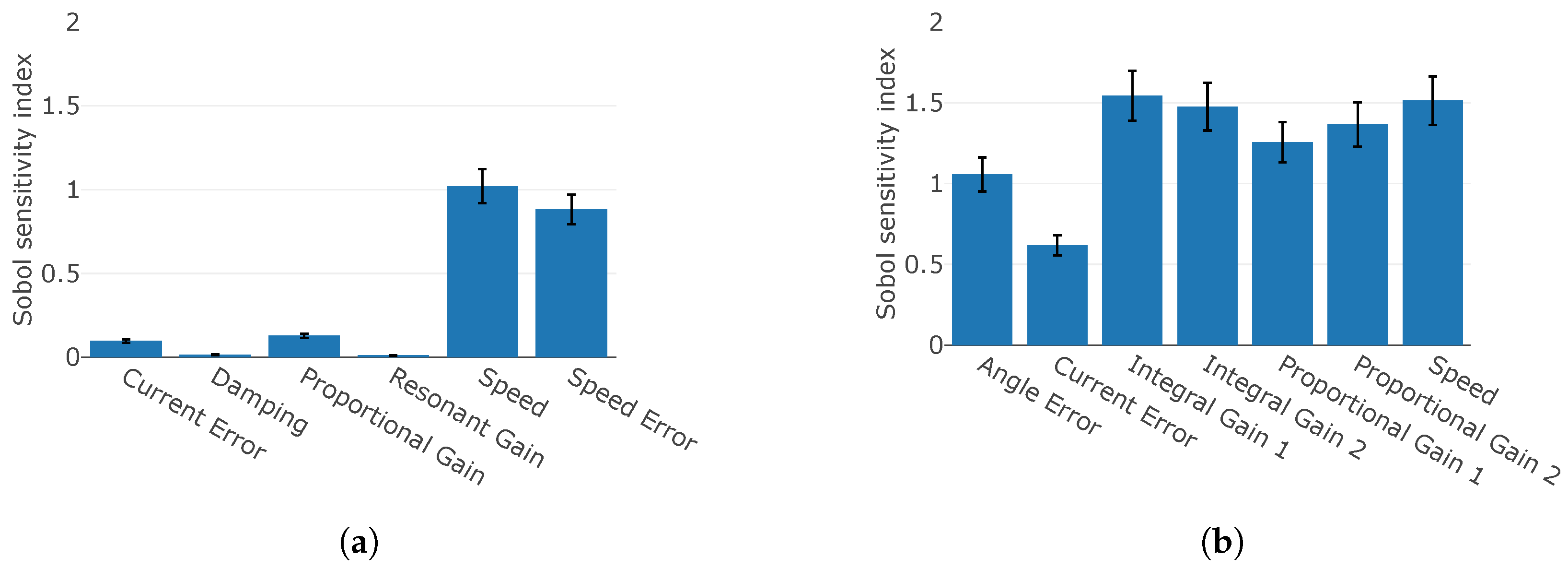

| Parameter | Value |
|---|---|
| DC-link voltage | |
| Motor rated power | |
| Stator inductance | |
| Stator resistance | |
| Switching frequency | |
| Pole pairs | 4 |
| Resonant Control | VSD Control |
|---|---|
| Proportional gain | Proportional gain for controllers |
| Resonant gain | Integral gain for controllers |
| Damping | Proportional gain for and 0 controllers |
| Current sensor error | Integral gain for and 0 controllers |
| Frequency sensor error | Current sensor error |
| Speed | Angle sensor error |
| Speed |
| Technique | Mean RPI | Median RPI | Variance |
|---|---|---|---|
| Resonant | |||
| VSD |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savi, F.; Farjudian, A.; Buticchi, G.; Barater, D.; Franceschini, G. Numerical Robustness Evaluation of Floating-Point Closed-Loop Control Based on Interval Analysis. Electronics 2023, 12, 390. https://doi.org/10.3390/electronics12020390
Savi F, Farjudian A, Buticchi G, Barater D, Franceschini G. Numerical Robustness Evaluation of Floating-Point Closed-Loop Control Based on Interval Analysis. Electronics. 2023; 12(2):390. https://doi.org/10.3390/electronics12020390
Chicago/Turabian StyleSavi, Filippo, Amin Farjudian, Giampaolo Buticchi, Davide Barater, and Giovanni Franceschini. 2023. "Numerical Robustness Evaluation of Floating-Point Closed-Loop Control Based on Interval Analysis" Electronics 12, no. 2: 390. https://doi.org/10.3390/electronics12020390
APA StyleSavi, F., Farjudian, A., Buticchi, G., Barater, D., & Franceschini, G. (2023). Numerical Robustness Evaluation of Floating-Point Closed-Loop Control Based on Interval Analysis. Electronics, 12(2), 390. https://doi.org/10.3390/electronics12020390






