Seismoelectric Effect of Oil-Wetted Porous Media Containing Two-Phase Flow
Abstract
:1. Introduction
2. Methods
2.1. Seismoelectric Effect under Steady Conditions
2.2. Seismoelectric Effect under Time-Harmonic Conditions
2.3. Verification of the Validity of the Flux-Averaging Method
3. Simulation and Discussion
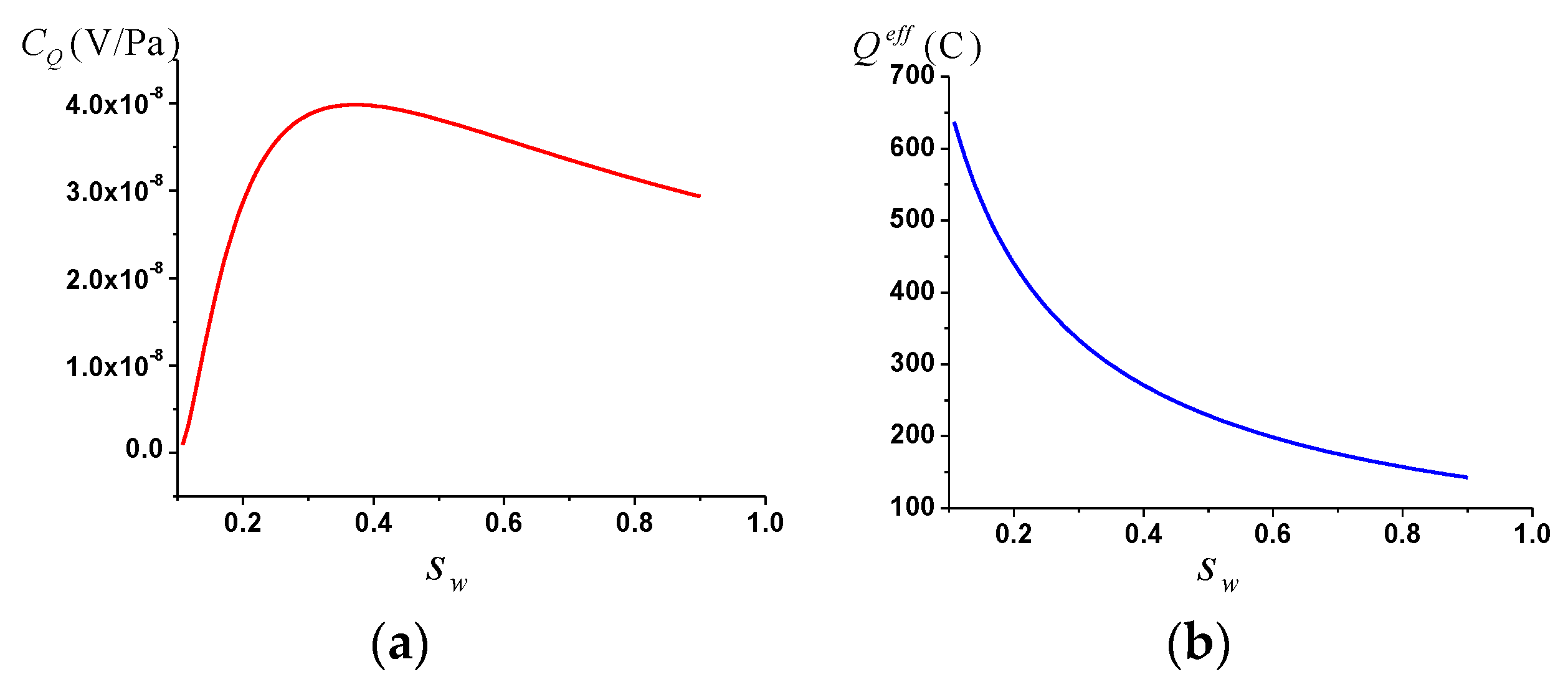
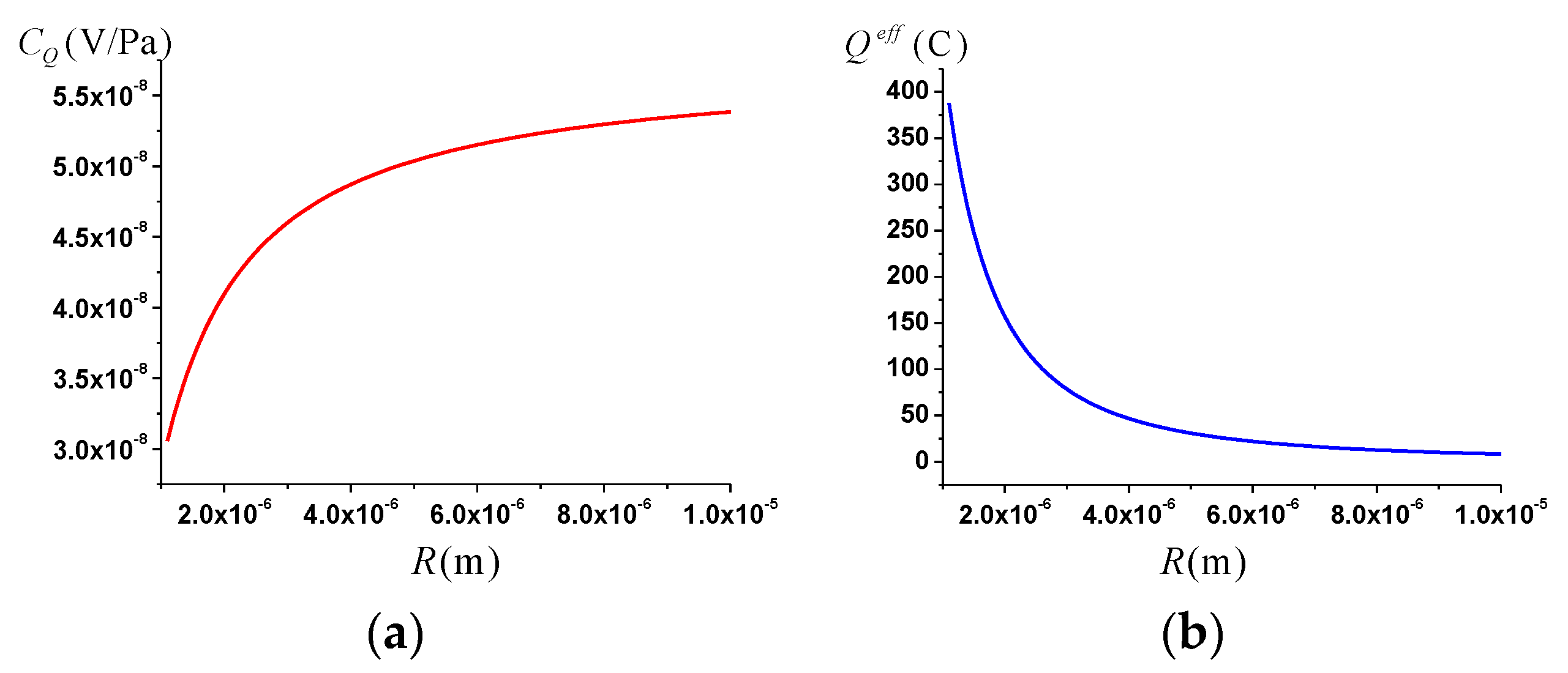
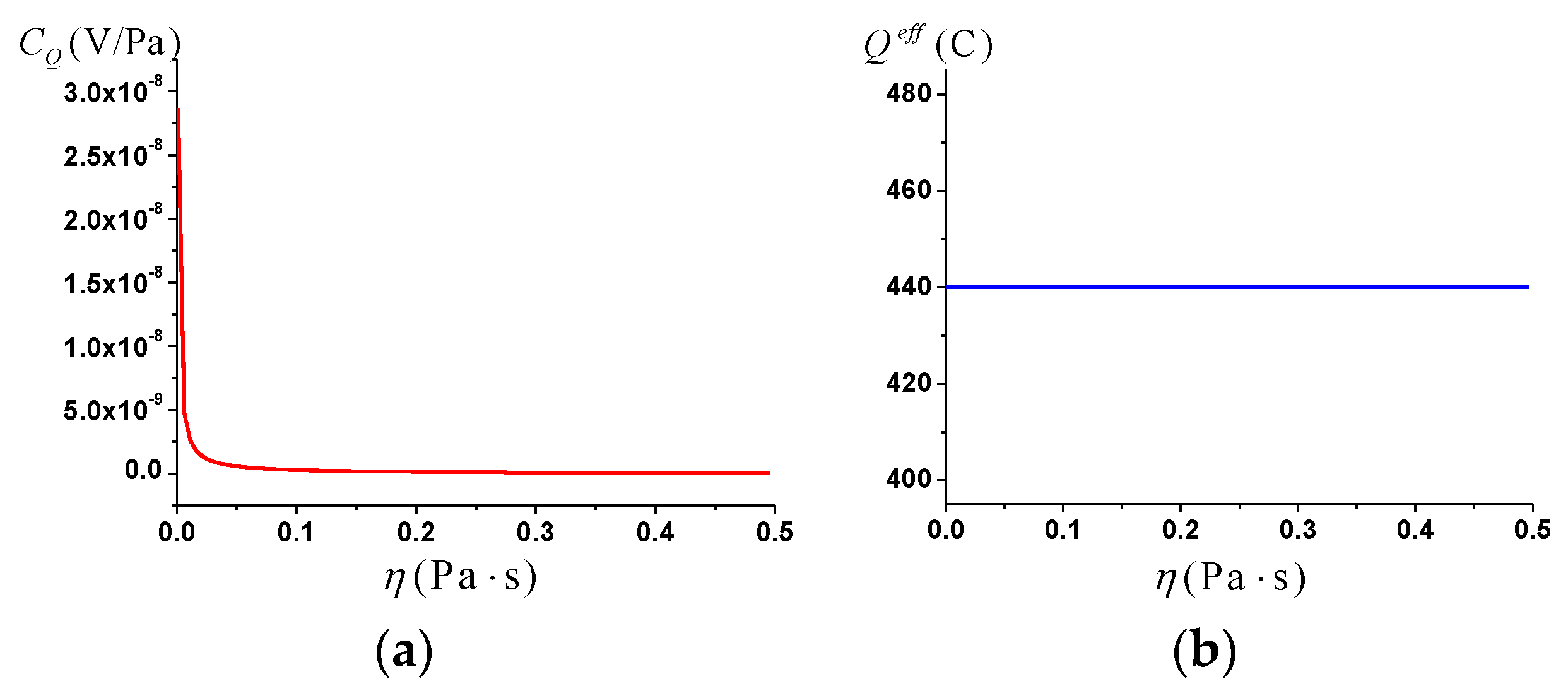
3.1. The Streaming Potential Coupling Coefficient
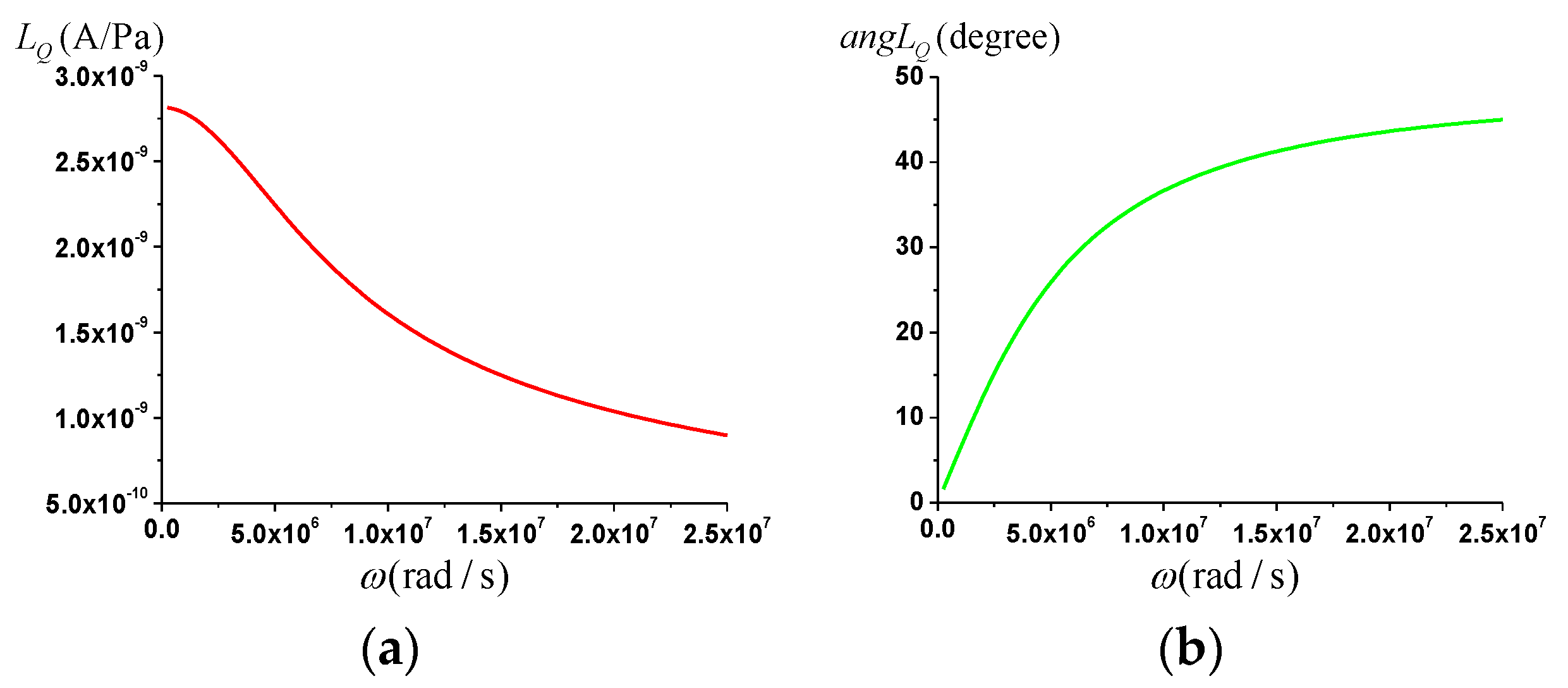
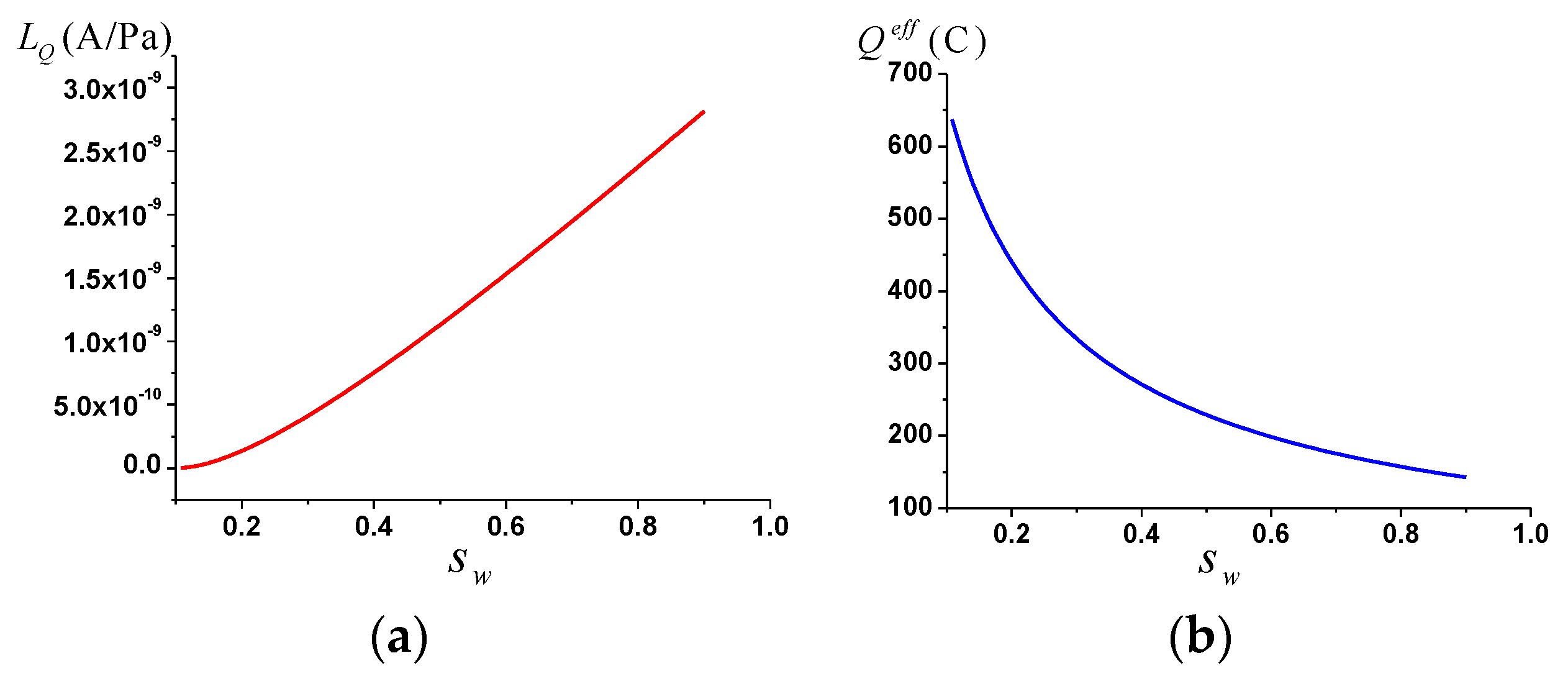
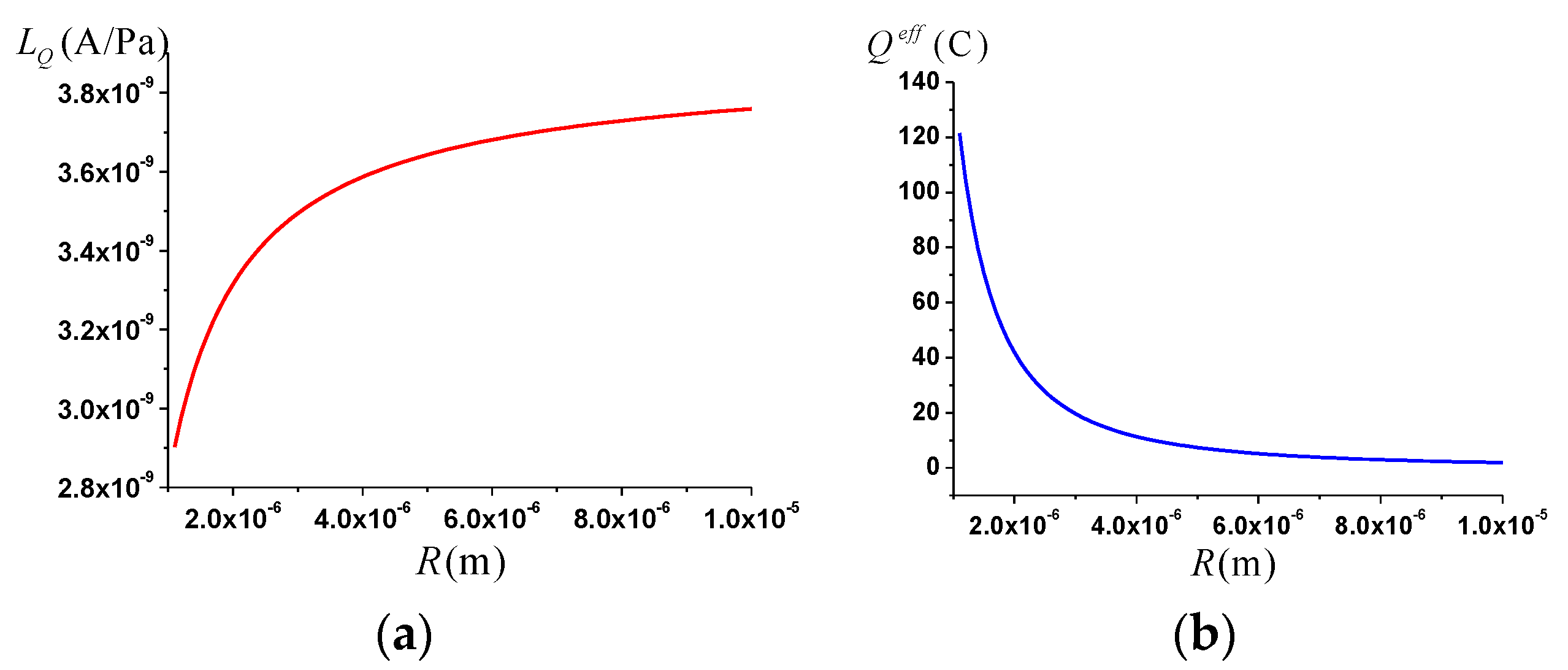
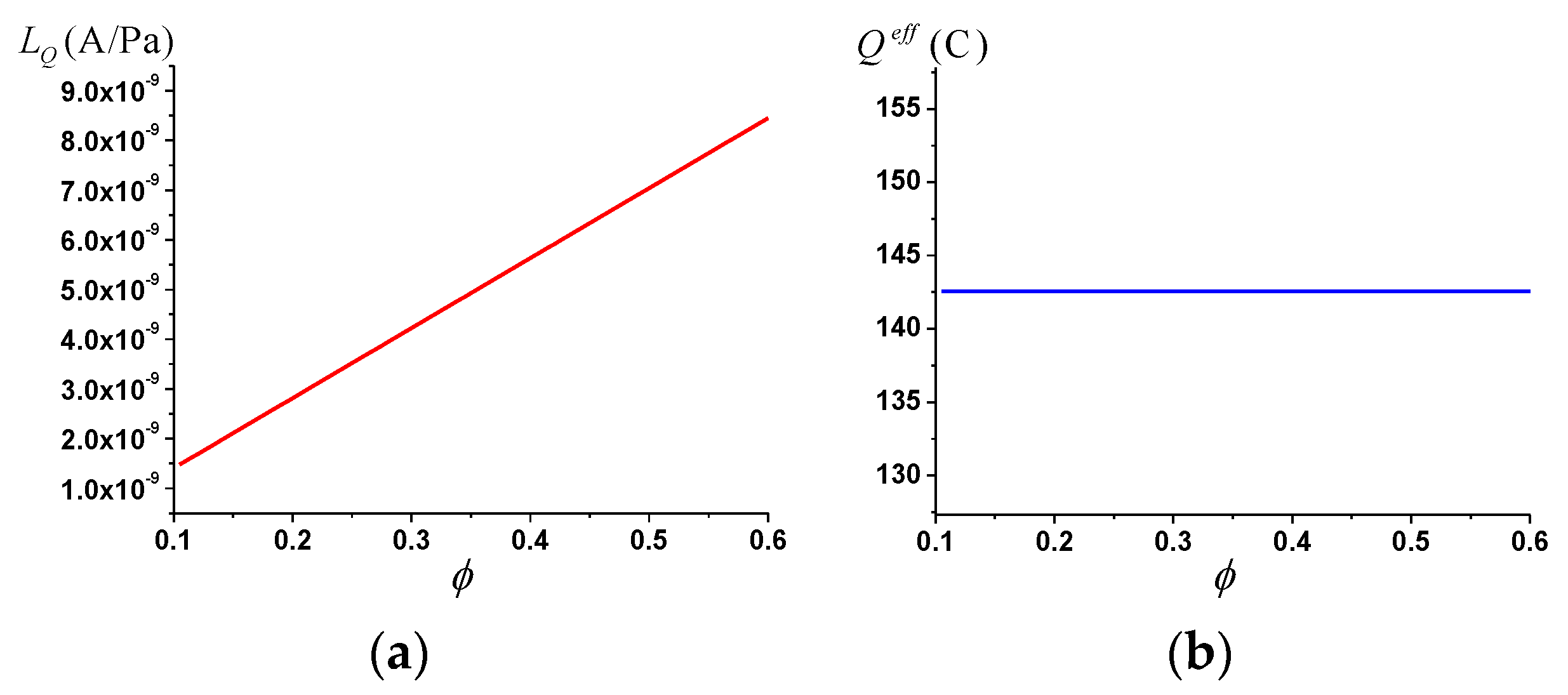
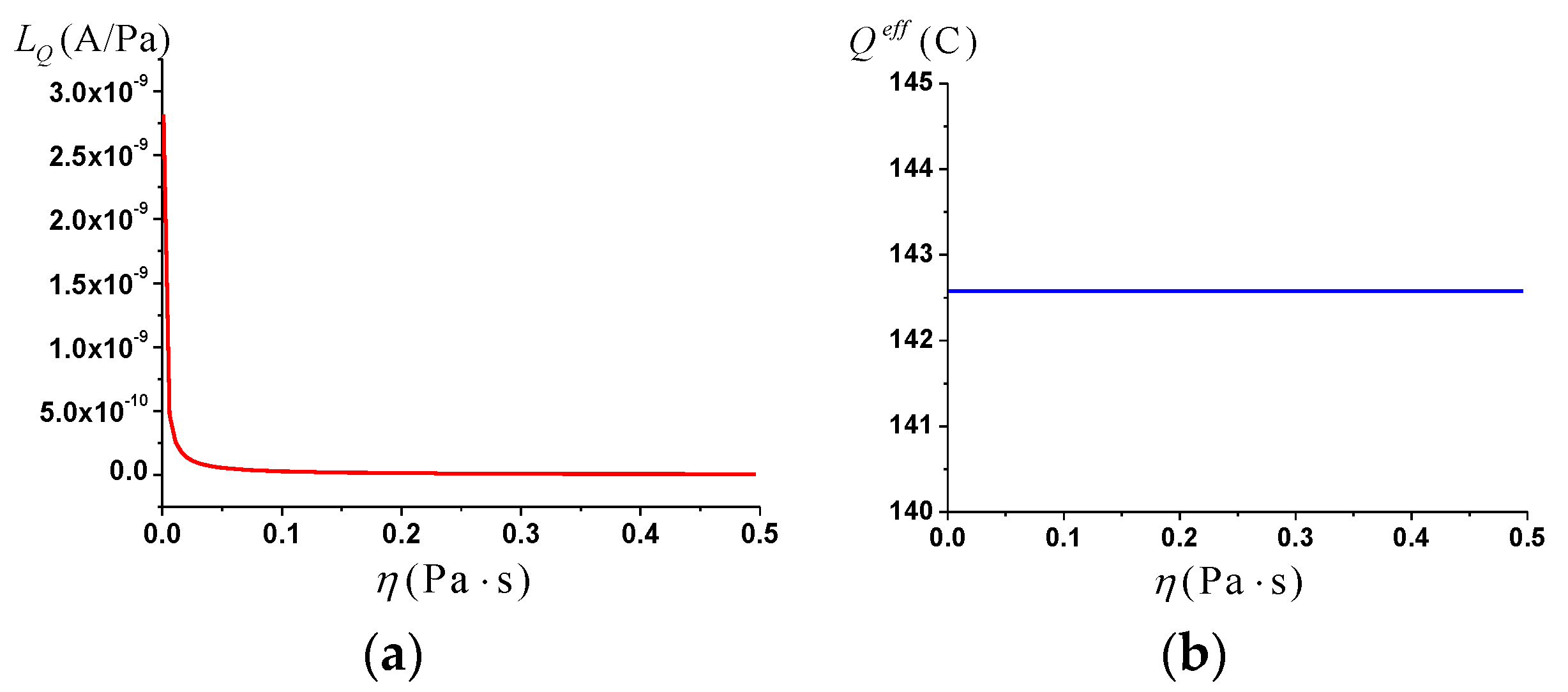
3.2. The Streaming Current Coupling Coefficient
4. Conclusions
- (1)
- The streaming potential coupling coefficient has a non-monotonic relationship with water saturation.
- (2)
- The streaming potential coupling coefficient is positively correlated with pore size and porosity.
- (3)
- The streaming potential coupling coefficient is negatively correlated with water viscosity.
- (4)
- For ideal soil with the same porosity, the larger the soil particle size, the greater the streaming potential coupling coefficient.
- (1)
- The amplitude of the streaming current coupling coefficient gradually decreases with an increase in the frequency, and the phase gradually increases with an increase in the frequency, finally resulting in a constant value ().
- (2)
- The streaming current coupling coefficient is positively correlated with water saturation, porosity and pore size.
- (3)
- The streaming current coupling coefficient is negatively correlated with water viscosity.
- (4)
- For ideal soil with the same porosity, the larger the soil particle size, the greater the streaming current coupling coefficient.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Revil, A.; Jardani, A.; Sava, P.; Haas, A. The Seismoelectric Method: Theory and Applications, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 258–259. [Google Scholar]
- Jackson, M.D. Characterization of multiphase electrokinetic coupling using a bundle of capillary tubes model. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Jackson, M.D. Multiphase electrokinetic coupling: Insights into the impact of fluid and charge distribution at the pore scale from a bundle of capillary tubes model. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Frenkel, J. On the theory of seismic and seismoelectric phenomena in a moist soil. J. Eng. Mech. 2005, 131, 879–887. [Google Scholar] [CrossRef] [Green Version]
- Packard, R.G. Streaming potentials across glass capillaries for sinusoidal pressure. J. Chem. Phys. 1953, 21, 303–307. [Google Scholar] [CrossRef]
- Pride, S.; Morgan, F.D. On the importance of electrokinetic forces in the acoustics of porous media. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 1989; pp. 579–581. [Google Scholar]
- Pride, S.R.; Morgan, F.D. Electrokinetic dissipation induced by seismic waves. Geophysics 1991, 56, 914–925. [Google Scholar] [CrossRef]
- Pride, S. Governing equations for the coupled electromagnetics and acoustics of porous media. Phys. Rev. B 1994, 50, 15678. [Google Scholar] [CrossRef] [PubMed]
- Wurmstich, B.; Morgan, F.D. Modeling of streaming potential responses caused by oil well pumping. Geophysics 1994, 59, 46–56. [Google Scholar] [CrossRef]
- Revil, A.; Cerepi, A. Streaming potentials in two-phase flow conditions. Geophys. Res. Lett. 2004, 31, 293–317. [Google Scholar] [CrossRef]
- Linde, N.; Jougnot, D.; Revil, A.; Matthäi, S.K.; Arora, T.; Renard, D.; Doussan, C. Streaming current generation in two-phase flow conditions. Geophys. Res. Lett. 2007, 34, L03306. [Google Scholar] [CrossRef] [Green Version]
- Allègre, V.; Jouniaux, L.; Lehmann, F.; Sailhac, P. Streaming potential dependence on water-content in Fontainebleau sand. Geophys. J. Int. 2010, 182, 1248–1266. [Google Scholar] [CrossRef]
- Allegre, V.; Maineult, A.; Lehmann, F.; Lopes, F.; Zamora, M. Self-potential response to drainage–imbibition cycles. Geophys. J. Int. 2014, 197, 1410–1424. [Google Scholar] [CrossRef]
- Allègre, V.; Jouniaux, L.; Lehmann, F.; Sailhac, P.; Toussaint, R. Influence of water pressure dynamics and fluid flow on the streaming-potential response for unsaturated conditions. Geophys. Prospect. 2015, 63, 694–712. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Ma, D.; Zhang, Y.; Liu, Y.; Ma, Y.; Hu, D. Insights into Controlling Factors of Pore Structure and Hydraulic Properties of Broken Rock Mass in a Geothermal Reservoir. Lithosphere 2021, 2021, 3887832. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Zhang, J. Solid grain migration on hydraulic properties of fault rocks in underground mining tunnel: Radial seepage experiments and verification of permeability prediction. Tunn. Undergr. Space Technol. 2022, 126, 104525. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Zhang, J.; Liu, X.; Li, Z. Numerical Simulation of Water–Silt Inrush Hazard of Fault Rock: A Three-Phase Flow Model. Rock Mech. Rock Eng. 2022, 55, 5163–5182. [Google Scholar] [CrossRef]
- Alkafeef, S.; Gochin, R.J.; Smith, A.L. The effect of double layer overlap on measured streaming currents for toluene flowing through sandstone cores. Colloids Surf. A Physicochem. Eng. Asp. 2001, 195, 77–80. [Google Scholar] [CrossRef]
- Alkafeef, S.F.; Smith, A.L. Asphaltene adsorption isotherm in the pores of reservoir rock cores. In Proceedings of the SPE International Symposium on Oilfield Chemistry, The Woodlands, TX, USA, 2–4 February 2005. [Google Scholar]
- Alkafeef, S.F.; Algharaib, M.K.; Alajmi, A.F. Hydrodynamic thickness of petroleum oil adsorbed layers in the pores of reservoir rocks. J. Colloid Interface Sci. 2006, 298, 13–19. [Google Scholar] [CrossRef]
- Dullien, F. Porous Media: Fluid Transport and Pore Structure; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Hui, M.H.; Martin, J.B. Pore-scale modeling of three-phase flow and the effects of wettability. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 3–5 April 2000. [Google Scholar]
- Van Dijke, M.I.J.; Sorbie, K.S.; McDougall, S.R. Saturation-dependencies of three-phase relative permeabilities in mixed-wet and fractionally wet systems. Adv. Water Resour. 2001, 24, 365–384. [Google Scholar] [CrossRef]
- Ishido, T.; Mizutani, H. Experimental and theoretical basis of electrokinetic phenomena in rock-water systems and its applications to geophysics. J. Geophys. Res. Solid Earth 1981, 86, 1763–1775. [Google Scholar] [CrossRef]
- Warden, S.; Garambois, S.; Jouniaux, L.; Brito, D.; Sailhac, P.; Bordes, C. Seismoelectric wave propagation numerical modelling in partially saturated materials. Geophys. J. Int. 2013, 194, 1498–1513. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. Aime 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Waxman, M.H.; Smits, L.J.M. Electrical conductivities in oil-bearing shaly sands. Soc. Pet. Eng. J. 1968, 8, 107–122. [Google Scholar] [CrossRef]
- Saunders, J.H.; Jackson, M.D.; Pain, C.C. Fluid flow monitoring in oil fields using downhole measurements of electrokinetic potential. Geophysics 2008, 73, E165–E180. [Google Scholar] [CrossRef]
- Stachurski, J.; MichaŁek, M. The effect of the ζ potential on the stability of a non-polar oil-in-water emulsion. J. Colloid Interface Sci. 1996, 184, 433–436. [Google Scholar] [CrossRef] [PubMed]
- Sherwood, J.D. Streaming potential generated by two-phase flow in a capillary. Phys. Fluids 2007, 19, 053101. [Google Scholar] [CrossRef]
- Revil, A.; Linde, N.; Cerepi, A.; Jougnot, D.; Matthäi, S.; Finsterle, S. Electrokinetic coupling in unsaturated porous media. J. Colloid Interface Sci. 2007, 313, 315–327. [Google Scholar] [CrossRef] [Green Version]
- Hiemenz, P.C. Principles of Colloid and Surface Chemistry; Marcel Dekker: New York, NY, USA, 1986. [Google Scholar]
- Keh, H.J.; Liu, Y.C. Electrokinetic flow in a circular capillary with a surface charge layer. J. Colloid Interface Sci. 1995, 172, 222–229. [Google Scholar] [CrossRef]
- Yang, J.; Grundke, K.; Bellmann, C.; Michel, S.; Kostiuk, L.W.; Kwok, D.Y. Oscillating streaming potential and electro-osmosis of multilayer membranes. J. Phys. Chem. B 2004, 108, 2103–2110. [Google Scholar] [CrossRef]

| Model Parameters | |
|---|---|
| Porosity | |
| Static permeability | |
| Conductivity of oil-wetted porous media containing two-phase flow | |
| Aqueous-phase conductivity | |
| Relative conductivity | |
| Water permeability | |
| Relative permeability of water phase | |
| Water saturation | |
| Residual water saturation | |
| Residual oil saturation | |
| Shear potential | |
| Dielectric constant | |
| Electrostatic potential of electric double layer | |
| Debye length | |
| Salinity | |
| Boltzmann constant | |
| Electron charge | |
| Effective viscosity of two-phase flow | |
| Water-phase viscosity | |
| Oil-phase viscosity | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Sun, X.; Nie, Z. Seismoelectric Effect of Oil-Wetted Porous Media Containing Two-Phase Flow. Electronics 2023, 12, 346. https://doi.org/10.3390/electronics12020346
Zhao Y, Sun X, Nie Z. Seismoelectric Effect of Oil-Wetted Porous Media Containing Two-Phase Flow. Electronics. 2023; 12(2):346. https://doi.org/10.3390/electronics12020346
Chicago/Turabian StyleZhao, Yongpeng, Xiangyang Sun, and Zaiping Nie. 2023. "Seismoelectric Effect of Oil-Wetted Porous Media Containing Two-Phase Flow" Electronics 12, no. 2: 346. https://doi.org/10.3390/electronics12020346
APA StyleZhao, Y., Sun, X., & Nie, Z. (2023). Seismoelectric Effect of Oil-Wetted Porous Media Containing Two-Phase Flow. Electronics, 12(2), 346. https://doi.org/10.3390/electronics12020346






