Abstract
As a mainstream approach in the quantum machine learning field, variational quantum algorithms (VQAs) are frequently mentioned among the most promising applications for quantum computing. However, VQAs suffer from inefficient training methods. Here, we propose a pretraining strategy named near Clifford circuits warm start (NCC-WS) to find the initialization for parameterized quantum circuits (PQCs) in VQAs. We explored the expressibility of NCCs and the correlation between the expressibility and acceleration. The achieved results suggest that NCC-WS can find the correct initialization for the training of VQAs to achieve acceleration.
1. Introduction
With the rapid development of quantum computing hardware [1,2,3,4], we are entering the noisy intermediate-scale quantum (NISQ) era [5]. Variational quantum algorithms (VQAs) [6,7,8] are one of the most important applications on NISQ devices, which could be used to demonstrate the quantum advantage over classical computers. VQAs are optimization-based (or learning-based) approaches that use parameterized quantum circuits (PQCs) running on a quantum computer, and then outsource the parameter update to a classical optimizer. As the quantum analog of highly successful machine-learning methods, they have been implemented to solve a wide range of problems, including quantum chemistry [9,10,11], classification [12,13,14,15], image generation and recognition [16,17,18,19], and optimization problems [20,21].
The main obstacles to applying VQAs to achieve quantum advantages are the training efficiency of a PQC. Because the estimation of the expectation values requires repeatedly running and taking measurements of a PQC with the same initial state, the number of the measurements and the number enormously increase with the number of the qubits and trainable parameters. To address the issue of accelerating the training process of a VQA, a variety of improved approaches have been proposed, such as distributed VQA schemes by simultaneously training with multiple quantum processors [22,23], higher-efficiency estimation methods with fewer measurement shots [24,25,26], and parameter initialization by a pretraining process [27,28,29].
In this paper, we propose a new parameter initialization method named near Clifford circuit warm start (NCC-WS) to accelerate the VQAs. We used a near Clifford circuit (NCC) [30,31], which includes Clifford gates and a limited number of T gates, to classically pretrain PQCs with the same structure. Compared with randomly initialized parameters in conventional VQA, the NCC-WS provides a good guess of the initial parameters, which can significantly increase the convergence rate of VQAs. Meanwhile, for an NCC that can be efficiently simulated by a classical computer, the computational overhead of the NCC-WS is negligible. We investigated the relationship between T gate ratio in NCCs and its expressibility, and we explained the role of T gate in enhancing the expressibilities of the NCCs from the perspective of numerical experiments. We further investigated the correlation between the pretraining effect and the expressivity of NCCs, which demonstrates the advantage of NCC-WS in accelerating VQAs.
2. Method
We consider a “composite" training process consisting of two pieces, as schematically depicted in Figure 1. We first perform a discrete optimization training with an NCC, and then transform it into a PQC with continuous parameters for a secondary optimization that has the same structure as the NCC.
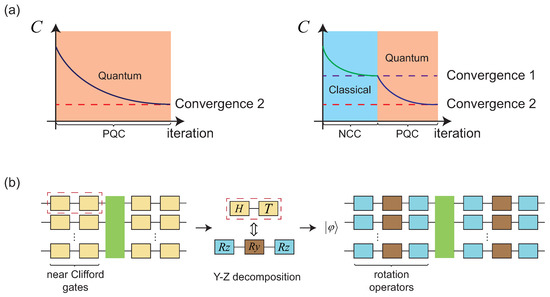
Figure 1.
Schematic diagram of NCC-WS. (a) Left: A diagram of the training process of conventional VQAs with random initialization parameters. The cost function C gradually converges to the optimum with iterations. Right: A diagram showing the application of NCC-WS before the second-stage VQAs training. The cost function C associated with machine learning task first converges once after NCC-WS, which is performed by a classical computer. The optimal circuit obtained from NCC-WS is then transformed into a PQC with the same structure. On this basis, the cost function C reaches a new convergence due to the improved expressivity of PQC, which is performed by a quantum computer. Compared with conventional VQAs, the training of VQAs after NCC-WS is initialized with better parameters so that fewer iterations are needed to achieve the same or even better training results, where the cost of NCC-WS is negligible. (b) The process of converting an NCC into an equivalent PQC with the same structure as the former.
In the NCC-WS stage, we leverage a classical optimization algorithm to pretrain an NCC consisting of discrete quantum gates. The Clifford circuit (CC) is composed of a Hardmard gate (H gate), phase gate (S gate), and two qubit control-NOT (CNOT) gates. To further increase the expressibility, we usually considers a near Clifford circuit (NCC) constructed by Clifford gates and a few T gates. Gottesman–Knill theorem [32], as well as more recent studies [33,34], highlights that an NCC with n qubits and T gates can be classically simulated in time . Therefore, the NCC-WS can be performed on a classical computer with a low computational cost. The classical training strategy of an NCC is not unique. In this study, we employed the simulated annealing algorithm to train the NCC. Specifically, we considered a random NCC consisting of trainable single qubit layers interlaced with CNOT layers. The single qubit gates are chosen from the gate set with a certain probability distribution. In each iteration, we randomly change part of single qubit gates with the same probability, and compare the new cost value to the previous one . Based on the idea of annealing, we accept the updated NCC with certainty when is better than ; otherwise, we accept with probability in the opposite case, where the inverse temperature increases with iterations.
After the NCC-WS, we obtain a relatively optimal quantum circuit. However, because the CCs and NCCs are not sufficient for universal quantum computation, the cost function may not converge to the optimal value. Therefore, we needed to continue to optimize the training results with PQC on this basis. We can use decomposition [35] to convert the single qubit gate U in the NCC into the rotation gates about the z and y axes, i.e., where (for ). In this way, an NCC can be converted into an equivalent hardware-efficient PQC, where circuits of this form are a natural choice due to a straightforward evaluation of the gradient with respect to most objective functions [36,37], as shown in Figure 1b.
Compared with random initializations, the training of VQAs after NCC-WS starts from a better initial point, which directly accelerates the convergence of VQAs. A well set of initial parameters will allow the cost function to achieve optimal value in fewer iterations. Another potential advantage of NCC-WS is the ability to escape from local traps in the landscape of cost function. The landscape of cost function usually becomes more rugged when parameter space increases, such that the cost function more easily fall into the trap of local minima [38]. The simulated annealing algorithm [39] is a probability check method that may accept a new solution that is even worse than previous solution, so it is possible to move away from the local optimal solution and thus search for the global minimum cost function.
3. Expressibility
An empirical intuition is that the better the expressibility of an NCC, the more likely we are able to obtain better initial parameters for the training of VQAs. Therefore, to evaluate the quality of initial parameters obtained by NCC-WS, we first need to investigate the expressibility of an NCC. We introduce a descriptor [40] to quantify the expressibility of a quantum circuit. is defined as a circuit’s ability to generate states that are well representative of the Hilbert space, which can be quantified by the Kullback–Leibler (KL) divergence between the probability distributions,
where is the estimated probability distribution of fidelities resulting from sampling states from a quantum circuit with initial state for each qubit, and is the probability density function of fidelities for the uniform distribution of states, i.e., the ensemble of Haar random states, where F is fidelity, and N corresponds to the dimension of Hilbert space.
We were particularly interested in the additional T gates in an NCC, which improves the expressibility of pure Clifford circuits [31]. However, the number of T gates in an NCC that can drive the best expressibility is not logically and tightly answered. We numerically simulated the variation in the expressibility with the probability of initializing a single qubit gate to T gate on a six-qubits NCC, as shown in Figure 2a. To investigate the relationship between non-Cliffordness and expressivity, we considered a more general case, that the probability of T gate ranges from 0 to in steps of .
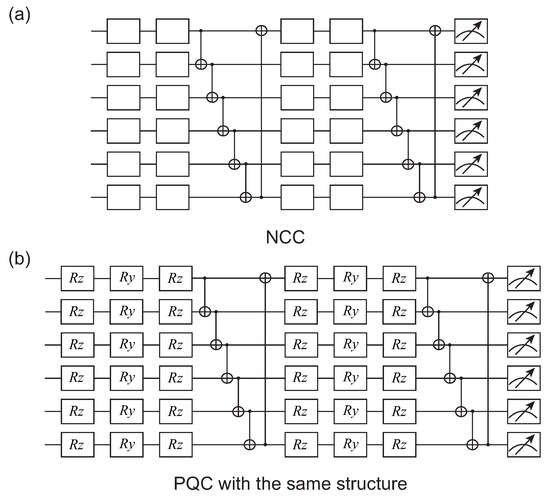
Figure 2.
The ansatz in numerical simulation. (a) A cluster of NCCs, where each single-bit gate is selected with a certain probability from the following gates: H gate, S gate, I gate, and T gate. (b) PQC with the same structure as NCC in (a).
Figure 3 displays the simulated data of the estimated fidelities, which were normalized to a discrete probability density function. As a reference, we show the curve of when . A bin number of 200 was used to generate the histogram Figure 3a–f. Above subgraphs, the KL divergence (Here, the area of each bar in histogram represents the probability of occurrence of the estimated fidelity in corresponding bin. Similarly, the integration of the curve representing over each interval also has the same meaning. The vectors for acquiring KL divergence were obtained by arranging the probabilities calculated from above two ways according to the fidelity interval from smallest to largest.) between and are reported to quantify the expressibility, in which a smaller value corresponds to more favorable expressibility. Although the KL divergence varies with bin number, the observations coming from the relative quantitative comparisons among circuits remain the same. Additionally, the degree of fitting between the histogram and curve in each subgraph visually demonstrates the appropriateness of the expressibility of the corresponding circuit.
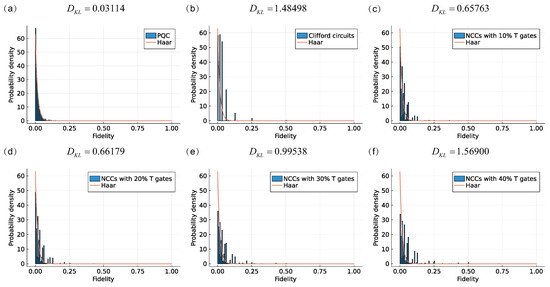
Figure 3.
Histograms of estimated fidelities normalized to a discrete probability density function. NCC and PQC diagrams are shown in Figure 2a,b, respectively, and we set the probability of T gate appearing from 0 (CC) to with step . For NCC (PQC), 2000 sample pairs of gate sequences (circuit parameter vectors) were uniformly generated, corresponding to 4000 states in Hilbert space using Yao in Julia. Histograms of estimated fidelities normalized to a discrete probability density function are shown with the computed KL divergence above the histograms.
As shown in Figure 3a–f, under the condition that the total number of gates is constant, we see that the expressibility of NCCs with a probability of a T gate is closest to that of Haar states in addition to PQCs. It means that there is no strict positive correlation between NCC expressivity and the number of T gates, and only the correct proportion of T gate can maximize the expressibility of an NCC.
4. Numerical Simulation
In this section, we demonstrate the application of NCC-WS VQA for classifying the handwritten digits 0 and 1 on MNIST, which contains a total of 3112 examples, to further explore whether there is a link between the acceleration effect and the expressibility. The settings on NCCs and PQC remained the same as those in the previous section.
We first encoded a classical example (a matrix) in the MNIST dataset into the quantum state (6 qubits) by amplitude encoding, i.e.,
where represents the kth sample in training set, which arranges the elements in the matrix into a vector.
To calibrate the training effect, we employed the mean square error (MSE) [41] cost function C, defined as
where is the predicted label, and is the real label.
According to parameter-shift rule, (jth component of parameter vector ) satisfies
where donates the output of VQA with shifted parameter at the tth iteration, and donates the unit vector.
In NCC-WS phase, we utilize an annealing algorithm (When , the probability of accepting satisfies , where is inverse temperature.) for discrete gate sequence updates, where increases by 1.25 times per iteration, varying from 10 to . In the VQA phase after NCC-WS, we leveraged the vanilla SGD (Vanilla SGD as a common classical optimizer to update the parameters in PQC from to , i.e., , where is the fixed learning rate.) with to update the parameters of rotation gates in PQC, and the batch size was set as 10. To ensure the accuracy of the experimental results, a total of 30 independent experiments were run by setting random initialization (random NCC gate sequence for NCC-WS VQA and random initial parameter vector for conventional VQA) for each setting.
Figure 4 displays the simulation results. In Figure 4a, the yellow C curve, representing NCC with T gates, has the minimum convergence value in all curves; the purple curve, representing NCC with the worst expressibility, is just the opposite, which reveals that there is a positive correlation between the expressibility of an NCC in NCC-WS and the convergence value of cost function C, i.e., the better the expressibility, the smaller the convergence value of C. This is easy to understand because the NCCs with good expressibility can characterize more quantum states to be retrieved, which makes the output of NCCs closer to the target quantum states.
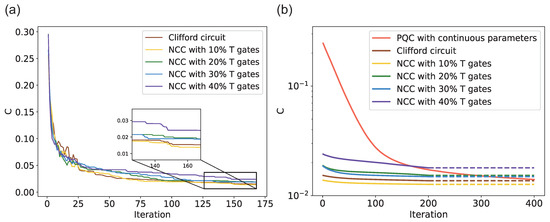
Figure 4.
Simulation results of NCC-WS training for classification task on MNIST. (a) The average C during pretraining plotted as a function of iteration past the probability of T gate appearing in NCC used in warm start, for iterations from 1 to 168, and the probability ranging from 0 to in steps of . All curves eventually converge steadily around 0.02, where the yellow curve that has largest expressibility value has the minimum convergence value. (b) Comparison of the training effect of conventional VQA and NCC-WS VQA with settings in (a) for classification task, where the dashed lines are numerical extensions of the corresponding experimental results and do not represent the real training. We observe that there exists an obvious difference at the beginning of training, where NCC-WS VQA has noticeable smaller C value. However, the initial parameters superiority found by NCC-WS will not necessarily be retained, where the cost value of conventional VQA, i.e., the orange curve, is smaller than that of NCC-WS VQA with , , and T gates, although it still has a slow decreasing trend after 400 iterations.
As shown in Figure 4b, comparing the second stage training in the NCC-WS VQA and the conventional VQA, the cost function C of the former is closer to convergence at the beginning, which demonstrates the powerful acceleration effect of NCC-WS. Noticeably, although NCCs with different expressibilities are capable of accelerating VQAs, the quality of initializations searched by NCC-WS are closely related to the expressibility of an NCC. NCCs with better expressibility have more potential to find better initializations.
Additionally, NCC-WS VQA has good scalability. The reasons are as follows: (1) The complexity of simulating an NCC is when the number of T gates is limited [42,43], which means that it is efficient when the scale of the system is large. (2) From the perspective of the principle of NCC-WS, this approach is applicable to larger systems. Essentially, NCC-WS will firstly determine an approximate range of the target quantum state by roughly searching in Hilbert space, then VQAs continues to perform a precise search, where these two phases are implemented on a clssical computer and quantum computer, respectively. Therefore, the feasibility of NCC-WS VQA is independent of system size.
5. Conclusions and Outlook
In summary, our results showed that warm start using NCCs with good expressibility can dramatically accelerate the training of VQAs by achieving a “good" initialization for PQCs used in VQAs. Another elegant feature of our method is its generality, as our approach is independent of the VQAs, which is promising for application to a wide range of problems.
Furthermore, we would like to emphasize the issue of T gates so that the readers can make the appropriate trade-offs when employing this method. Our results showed that the addition of the T gates is just an additional feature accelerating the conventional VQAs, because it also exponentially increases the difficulty of the simulation [42,43], which means that we need to balance the pros and cons, rather than adding T gates to an system.
Author Contributions
Methodology, Y.-F.N.; Validation, Y.-F.N.; Writing – original draft, Y.-F.N.; Writing—review & editing, S.Z. and W.-S.B.; Supervision, S.Z. and W.-S.B.; Project administration, W.-S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Youth Talent Lifting Project (grant no. 2020-JCJQ-QT-030), National Natural Science Foundation of China (grant nos. 11905294 and 12274464), China Postdoctoral Science Foundation, and the Open Research Fund from State Key Laboratory of High Performance Computing of China (grant no. 201901-01).
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, W.-S.; Cao, S.; Chen, F.; Chen, M.-C.; Chen, X.; Chung, T.-H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef] [PubMed]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef]
- Huang, H.-L.; Wu, D.; Fan, D.; Zhu, X. Superconducting quantum computing: A review. Sci. China Inf. Sci. 2020, 63, 1. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L.; et al. Variational quantum algorithms. Nat. Rev. Phys. 2021, 3, 625. [Google Scholar] [CrossRef]
- Benedetti, M.; Fiorentini, M.; Lubasch, M. Hardware-efficient variational quantum algorithms for time evolution. Phys. Rev. Res. 2021, 3, 033083. [Google Scholar] [CrossRef]
- Huang, H.-L.; Xu, X.-Y.; Guo, C.; Tian, G.; Wei, S.-J.; Sun, X.; Bao, W.-S.; Long, G.-L. Near-Term Quantum Computing Techniques: Variational Quantum Algorithms, Error Mitigation, Circuit Compilation, Benchmarking and Classical Simulation. arXiv 2022, arXiv:2211.08737. [Google Scholar]
- Hempel, C.; Maier, C.; Romero, J.; McClean, J.; Monz, T.; Shen, H.; Jurcevic, P.; Lanyon, B.P.; Love, P.; Babbush, R.; et al. Quantum Chemistry Calculations on a Trapped-Ion Quantum Simulator. Phys. Rev. X 2018, 8, 031022. [Google Scholar] [CrossRef]
- Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.M.; Gambetta, J.M. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242. [Google Scholar] [CrossRef]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.-H.; Zhou, X.-Q.; Love, P.J.; Aspuru-Guzik, A.; O’brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 1. [Google Scholar] [CrossRef] [PubMed]
- Mitarai, K.; Negoro, M.; Kitagawa, M.; Fujii, K. Quantum circuit learning. Phys. Rev. A 2018, 98, 032309. [Google Scholar] [CrossRef]
- Schuld, M.; Bocharov, A.; Svore, K.M.; Wiebe, N. Circuit-centric quantum classifiers. Phys. Rev. A 2020, 101, 032308. [Google Scholar] [CrossRef]
- Ding, C.; Xu, X.-Y.; Niu, Y.-F.; Zhang, S.; Bao, W.-S.; Huang, H.-L. Active Learning on a Programmable Photonic Quantum Processor. arXiv 2022, arXiv:2208.02104. [Google Scholar]
- Gong, M.; Huang, H.-L.; Wang, S.; Guo, C.; Li, S.; Wu, Y.; Zhu, Q.; Zhao, Y.; Guo, S.; Qian, H.; et al. Quantum Neuronal Sensing of Quantum Many-Body States on a 61-Qubit Programmable Superconducting Processor. arXiv 2022, arXiv:2201.05957. [Google Scholar]
- Cong, I.; Choi, S.; Lukin, M.D. Quantum convolutional neural networks. Nat. Phys. 2019, 15, 1273. [Google Scholar] [CrossRef]
- Wei, S.; Chen, Y.; Zhou, Z.; Long, G. A quantum convolutional neural network on NISQ devices. AAPPS Bull. 2022, 32, 2. [Google Scholar] [CrossRef]
- Liu, J.; Lim, K.H.; Wood, K.L.; Huang, W.; Guo, C.; Huang, H.-L. Hybrid quantum-classical convolutional neural networks. Sci. China Phys. Mech. Astron. 2021, 64, 290311. [Google Scholar] [CrossRef]
- Huang, H.-L.; Du, Y.; Gong, M.; Zhao, Y.; Wu, Y.; Wang, C.; Li, S.; Liang, F.; Lin, J.; Xu, Y.; et al. Experimental Quantum Generative Adversarial Networks for Image Generation. Phys. Rev. Appl. 2021, 16, 024051. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
- Guerreschi, G.G.; Matsuura, A.Y. QAOA for Max-Cut requires hundreds of qubits for quantum speed-up. Sci. Rep. 2019, 9, 6903. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Qian, Y.; Tao, D. Accelerating variational quantum algorithms with multiple quantum processors. arXiv 2021, arXiv:2106.12819. [Google Scholar]
- Niu, Y.-F.; Zhang, S.; Ding, C.; Bao, W.-S.; Huang, H.-L. Parameter-Parallel Distributed Variational Quantum Algorithm. arXiv 2022, arXiv:2208.00450. [Google Scholar]
- Huang, H.-Y.; Kueng, R.; Preskill, J. Predicting many properties of a quantum system from very few measurements. Nat. Phys. 2020, 16, 1050. [Google Scholar] [CrossRef]
- Hadfield, C.; Bravyi, S.; Raymond, R.; Mezzacapo, A. Measurements of Quantum Hamiltonians with Locally-Biased Classical Shadows. Commun. Math. Phys. 2022, 391, 951. [Google Scholar] [CrossRef]
- Ding, C.; Xu, X.-Y.; Niu, Y.-F.; Bao, W.-S.; Huang, H.-L. Noise-Resistant Quantum State Compression Readout. arXiv 2021, arXiv:2109.06805. [Google Scholar]
- Grant, E.; Wossnig, L.; Ostaszewski, M.; Benedetti, M. An initialization strategy for addressing barren plateaus in parametrized quantum circuits. Quantum 2019, 3, 214. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, S.-T.; Choi, S.; Pichler, H.; Lukin, M.D. Quantum Approximate Optimization Algorithm: Performance, Mechanism, and Implementation on Near-Term Devices. Phys. Rev. X 2020, 10, 021067. [Google Scholar] [CrossRef]
- Dborin, J.; Barratt, F.; Wimalaweera, V.; Wright, L.; Green, A.G. Matrix product state pre-training for quantum machine learning. Quantum Sci. Technol. 2022, 7, 035014. [Google Scholar] [CrossRef]
- Ravi, G.S.; Gokhale, P.; Ding, Y.; Kirby, W.M.; Smith, K.N.; Baker, J.M.; Love, P.J.; Hoffmann, H.; Brown, K.R.; Chong, F.T. CAFQA: A classical simulation bootstrap for variational quantum algorithms. arXiv 2022, arXiv:2202.12924. [Google Scholar]
- Selinger, P. Efficient Clifford+T approximation of single-qubit operators. arXiv 2012, arXiv:1212.6253. [Google Scholar] [CrossRef]
- Bennett, C.H.; DiVincenzo, D.P. Quantum information and computation. Nature 2000, 404, 247. [Google Scholar] [CrossRef] [PubMed]
- Qassim, H.; Wallman, J.J.; Emerson, J. Clifford recompilation for faster classical simulation of quantum circuits. Quantum 2019, 3, 170. [Google Scholar] [CrossRef]
- Bennink, R.S.; Ferragut, E.M.; Humble, T.S.; Laska, J.A.; Nutaro, J.J.; Pleszkoch, M.G.; Pooser, R.C. Unbiased simulation of near-Clifford quantum circuits. Phys. Rev. A 2017, 95, 062337. [Google Scholar] [CrossRef]
- Nielson, M.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Romero, J.; Babbush, R.; McClean, J.R.; Hempel, C.; Love, P.J.; Aspuru-Guzik, A. Strategies for quantum computing molecular energies using the unitary coupled cluster ansatz. Quantum Sci. Technol. 2018, 4, 014008. [Google Scholar] [CrossRef]
- Guerreschi, G.G.; Smelyanskiy, M. Practical optimization for hybrid quantum-classical algorithms. arXiv 2017, arXiv:1701.01450. [Google Scholar]
- Ge, X.; Wu, R.-B.; Rabitz, H. The optimization landscape of hybrid quantum–classical algorithms: From quantum control to NISQ applications. Annu. Rev. Control 2022, 54, 314–323. [Google Scholar] [CrossRef]
- Lundy, M.; Mees, A. Convergence of an annealing algorithm. Math. Program. 1986, 34, 111. [Google Scholar] [CrossRef]
- Sim, S.; Johnson, P.D.; Aspuru-Guzik, A. Expressibility and Entangling Capability of Parameterized Quantum Circuits for Hybrid Quantum-Classical Algorithms. Adv. Quantum Technol. 2019, 2, 1900070. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79. [Google Scholar] [CrossRef]
- Bravyi, S.; Gosset, D. Improved Classical Simulation of Quantum Circuits Dominated by Clifford Gates. Phys. Rev. Lett. 2016, 116, 250501. [Google Scholar] [CrossRef] [PubMed]
- Bravyi, S.; Smith, G.; Smolin, J.A. Trading Classical and Quantum Computational Resources. Phys. Rev. X 2016, 6, 021043. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).