Abstract
With the increasing demand for target sensing in future mobile communication networks, integrated sensing and communications (ISAC) not only brings new system architecture and multi-functional integration, but also introduces new challenges. In order to further reduce the data volume of the sensing system signal processing, this paper proposes a waveform optimization design method and target parameter estimation technique for a compressed sensing multiple-input multiple-output (MIMO) radar based on a 2D antenna array. This scheme enables accurate estimation of target angles in the sparse time-domain sampling scenario and L-shaped antenna array. In this paper, extensive simulation results demonstrate the good performance of the proposed scheme for various compression ratios and signal-to-noise ratios (SNRs).
1. Introduction
At present, the devices used for communication and sensing are still in a state of independent separation or coexistence in adjacent frequency bands. Communication and sensing processes use different waveforms, spectra, antennas, processors, and other hardware equipment resources, resulting in low efficiency of overall resource utilization. With the continuous development of 5G technology and the global research layout of 6G technology, in order to meet the demands for high-precision wireless network connections such as the industrial internet of things, smart cities, and remote healthcare in the future, the network’s requirements for positioning and sensing capabilities are gradually increasing [1]. The integration, forming integrated sensing and communication (ISAC) technology, provides a new system or network architecture, enabling integration to achieve the symbiosis and reciprocity between communication and sensing through reasonable resource reuse design. Therefore, compared to traditional communication networks that only support communication capabilities, the ISAC poses new requirements and challenges for the management technology of radio resources and the design of network architecture [2].
Compared to traditional communication networks, the introduction of radar sensing capability will add signal processing processes for sensing in communication systems, resulting in additional computational resource requirements. For high range resolution radars, sensing requires a greater bandwidth compared to traditional communication. By introducing compressed sensing (CS) technology, sampling can be carried out at a lower sampling rate than Nyquist under the same bandwidth requirements, and the amount of data to be processed can be significantly reduced on the digital signal processing side, which can greatly alleviate the pressure on the hardware and computing power of the ISAC system [3]. In addition, multiple-input multiple-output (MIMO) technology can greatly improve the overall performance of systems in both wireless communication and radar sensing fields. The design of MIMO technology for ISAC is still a popular research issue [4]. Therefore, in order to meet the continuous evolution of the current 5G communication system for the ISAC and further improve the sensing performance in limited computing resources, this paper will focus on the optimal design of the sensing waveform for the MIMO radar based on the compressed sensing (CS) technology. The new design waveform can fully adapt to the compressed sensing system and reduce the data size for computation in the sparse signal processing process. In order to achieve sparse recovery for limited data with high probability, the sensing matrix, which can used for reconstruct the original signal of CS technology, needs to satisfy the restricted isometric properties (RIP) [5], which means that the sensing matrix should be as orthogonal as possible. Compressed sensing in the context of MIMO radars has been studied in [6,7]; it takes advantage of the sparsity of targets in the target space to perform multi-target detection and estimation through sparse recovery methods. Regarding a CS-based MIMO radar, waveform optimization can be widely achieved from multiple dimensions such as the frequency domain, time domain, spatial domain, and computing power domain.
In the frequency domain, there are several techniques to further improve the detection performance of CS-based MIMO radars. For example, significant range resolution gains can be achieved by using a stepping frequency scheme during transmission [8,9], in which optimal or near-optimal measurement matrices have been designed to improve the detection performance by minimizing the coherence and/or signal inference ratio (SIR) of the measurement matrix. Considering the spectrum policy of mobile communication systems, various operators of the wireless network will be strictly limited in frequency usage for ISAC in future 5G and 6G communication systems, making it difficult to achieve frequency hopping compression from the frequency domain dimension.
In the time domain, optimizing the waveform to improve the performance of the sparse recovery in CS-based MIMO radars has been investigated in several previous works. These optimization methods can compress the radar sampling signal in the time domain while ensuring sensing accuracy of the radar as much as possible, thereby reducing the complexity of the sampling and subsequent processing. To effectively reconstruct the target scene, a waveform design method to reduce the correlations between target responses has been introduced in [6]. The waveform design problem considers beam-pattern design and optimizes phase hopping signals with the objective of minimizing coherence. In [10], the power allocation and waveform design problems are proposed for the widely separated and colocated setting using an orthogonal Hadamard sequence as the initialization. In [11], a new iteration algorithm was proposed for a joint design transmission waveform and sensing matrix, which then initialized the transmission waveform as a random complex vector. Study [12] proposed a formal algorithm for the joint design of radar waveforms and receiver filters of CS-based MIMO radar systems for extended target detection, and radar waveforms are designed based on Alltop sequences. It is not difficult to find that in order to explore the principle of waveform optimization under compressed sensing conditions, these studies first selected a relatively simple waveform to intuitively demonstrate the effectiveness of the method, but such ideal waveforms can not be directly used in practical applications.
Then, in the spatial domain, a waveform design approach based on given antenna locations where the design criterion focuses on the coherence of the sensing matrix has been presented in [13], and it also optimized the allocation of the total power budget among transmitters. The study considered a one-dimensional array structure, specifically assuming that transmitters and receivers are randomly distributed within a small area, forming a colocated CS-based MIMO radar system. A similar antenna configuration was used in [10]. In [14], an optimal design of frequency hopping waveforms based on a linear array arrangement has been introduced. The waveform design problem can be simplified into a frequency code selection scheme, and then an iterative process was used to minimize the block coherence criterion for selection. Furthermore, study [6] considered the uniform linear array for TX and RX antennas. In order to verify the impact of the designed optimized waveforms on the sparse recovery performance, the above studies are all based on the assumption of one-dimensional arrays such as the uniform line array (ULA) for azimuth estimation. There is indeed little research on extending these methods to actual two-dimensional angle space. In the actual radar sensing process, it is necessary to simultaneously estimate the target’s azimuth and elevation angles.
At last, in the computing power domain, a CS-based MIMO radar can realize the estimation of range, velocity, and angle. Compared to the basic functional requirements of range and speed, the estimation of direction of arrival (DOA) in the future wireless network will become more important. Therefore, for the angle estimation method of CS-based MIMO radar, in [15,16], the radar waveforms and receiver filters were jointly optimized with respect to a mutual coherence criterion. The Regularized Orthogonal Matched Basis Pursuit (ROMP) algorithm was used as the CS recovery algorithm in the studies. Moreover, the Orthogonal Matching Pursuit (OMP) algorithm was used in [6,11], and the Dantzig selector was used in [10]. After research, it was found that the commonly used sparse recovery methods in previous works were greedy algorithms such as OMP or convex relaxation algorithms, but these methods may not perform well when dealing with highly correlated or high-dimensional signal problems.
To address the above issues, the contributions in this article are as follows:
- In the time domain for compressed optimization, compared to ideal orthogonal MIMO waveforms such as the Hadamard sequence and Alltop sequence as the initial waveform, this work will use a Hadamard-coded waveform as the initial waveform which is more suitable for millimeter wave radar;
- In the spatial domain for compressed optimization, unlike most previous studies that have considered one-dimensional linear arrays that can only estimate the azimuth information of the target, this paper extends the research to CS-based MIMO radar systems based on L-shaped arrays and redesigned waveform optimizations;
- In the computational power domain, due to the use of a two-dimensional array based MIMO radar scenarios in this article, sparse recovery belongs to the problem of high correlation and high-dimensional signals, and algorithms such as OMP will no longer be applicable. Therefore, in order to achieve higher resolution and accuracy, this article introduces the Sparse Bayesian Learning (SBL) algorithm for the sparse estimation of both azimuth and elevation angles.
The rest of the paper is organized as follows. In Section 2, the signal model and the expression of waveform design questions are discussed. In Section 3, the sparse recovery algorithm and optimization techniques have been introduced. The numerical experiments and performance validation of the proposed methods are presented in Section 4. Finally, Section 5 and Section 6 contain the discussions and conclusions for this article.
2. Waveform Design for CS-Based MIMO Radar
2.1. Signal Model
In this paper, we consider a colocated MIMO radar system based on an L-shaped array, as shown in Figure 1. It is assumed that the L-shaped array consists of two mutually vertical uniform line arrays, where the X-axis is the transmitting array with M antennas and the Y-axis is the receiving array with N antennas, the reference antenna element (transmitting and receiving shared antenna) is at the coordinate origin. The transmitting and receiving antenna elements are separated by a distance of and , respectively. M transmitting antennas transmit orthogonal waveforms with the same bandwidth and center frequency. Lowercase bold letters denote vectors and capital bold letters denote matrices. Superscripts and denote, respectively, the transpose and Hermitian transpose. ⊗ denotes the Kronecker tensor product.
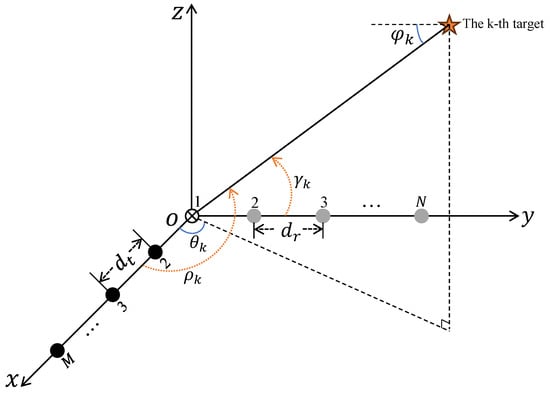
Figure 1.
Colocated MIMO radar system based on an L-shaped array.
Let us assume that there are K targets to be estimated in the far field of the antennas, ignoring the clutter. A clutter suppression filter can be used at the receiver if the clutter interference in the environment is large [17]. Therefore, the following studies in this paper do not consider clutter. In the general case, the targets are located in different range cells and are moving. Therefore, we would require searching for targets in a three-dimensional (3D) space, i.e., range-speed-DOA space. For simplicity, we assume that all the targets are not moving and located in the same range cell, thus the only parameters that need to be estimated are the target azimuth angles and elevation angles , . We can be positioned in two dimensions by , and . Although, in the following, we focus on DOA estimation only, the results can be easily extended to the case of moving targets.
To mathematically describe the radar signals, let denote the transmitted waveform of the m-th transmitting antenna, where L denotes the number of samples in a pulse period. Then, the matrix of the transmitted waveforms corresponding to the transmitting array is denoted by , where each column corresponds to a transmitter and rows encode the time instances. Assuming that the angles between the k-th target and the X-axis and Y-axis are , , respectively, from the geometric relationship in Figure 1, we can know that
then, the transmit steering vector corresponding to X-axis and receive steering vector corresponding to Y-axis of the k-th target can be given by
The received signal (without matched filtering) at the n-th receive antenna can be represented as
where is an matrix that contains the transmit waveforms as its columns, is the reflection coefficient (RCS) of the k-th target, and stands for the additive noise vector at the n-th receiver, which is modeled by a circularly symmetric complex Gaussian random vector with variance . As a result, the target echo signal matrix of the L-shaped array MIMO radar can be expressed as
where is the transmit steering matrix, is the receive steering matrix, is the diagonal matrix, and is the additive noise matrix. At the n-th receive antenna, the dimensional received signal is linearly compressed via the measurement matrix to obtain a dimensional observed signal, which can be expressed as
where the size of is . Similarly, we can obtain the matrix form .
In general, the azimuth and elevation angles of each target are real numbers. However, in practice, due to quantization and other resolution-limiting factors, the estimated angles by the radar have finite precision and belong to a finite set. Therefore, we discretize the angle space into a linearly spaced grid with discrete angles, as shown in Figure 2. Define the azimuth angle space as , the elevation angle space as , and normally . As a result, the angle between the target and the X-axis and Y-axis is discretized as and , respectively. In addition, the discretization step is small enough so that the error of the nearest neighbor grid from the exact azimuth and elevation angles of the targets is tolerable. Hence, in the rest of the paper, we only consider the case where each target falls on some angle grid point. This way, Equation (6) can be rewritten as
where
is regarded as the sparse basis matrix for the n-th receiver, and is the K-sparse vector of target’s reflection coefficients (), where
Since the radar is colocated, the vector is the same for all receive antennas.
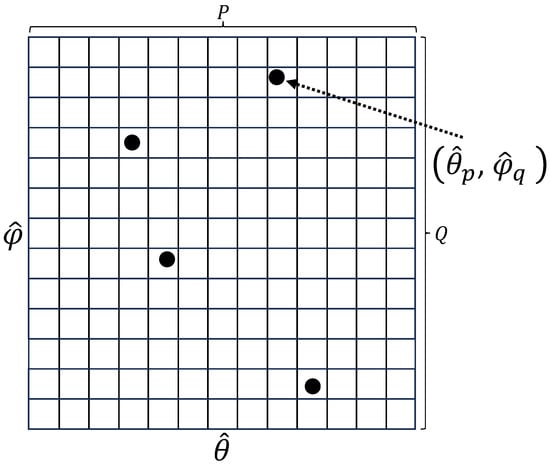
Figure 2.
Illustration of discrete angle space.
By concatenating the observation data from each receive antenna into a column vector, we construct , which can express as
according to the formulation of compressed sensing, denotes the sensing matrix. We let , which denotes the noise vector. If the number of targets is significantly smaller than , then can be regarded as a sparse vector, where the locations of non-zero elements indicate the target angles. Up to this point, the radar parameter estimation problem is transformed into a sparse recovery problem in compressed sensing, and could be found as the sparse solution of Equation (10). Provided that is sparse enough, a variety of CS methods are available for the sparse recovery of , such as Basis Pursuit [18], Orthogonal Matching Pursuit [19,20], Regularized Orthogonal Matching Pursuit [21], the NESTA method [22], and so on.
2.2. Reconstruction Performance Analysis
In Section 2.1, we have transformed the problem of target parameter estimation in CS-based MIMO radars into a sparse recovery problem. Therefore, in order to improve the performance of radar systems, it becomes essential to increase the probability of successful sparse recovery. To achieve sparse recovery with high probability, the sensing matrix needs to satisfy the restricted isometry property (RIP) [5], which can be understood as follows: the sub-matrices composed of any K columns selected from the sensing matrix are approximately orthogonal to each other. Although RIP is a strong sufficient condition for stable recovery, it is an NP-hard problem to verify it for a specific matrix. In deterministic scenarios where a is given, it is common to evaluate the coherence of the matrix:
where stands for the l-th column of . is known as the coherence of the sensing matrix (CSM) and reflects the lower bound on the performance of the sensing matrix; in other words, it reflects the recovery performance determined by the two columns of the sensing matrix with the worst orthogonality. For design purposes, it is desirable to keep as small as possible to improve the upper limit of sparsity, the accuracy, and stability of target parameter estimation [23].
2.3. Waveform Design
RIP signifies that the sparse vector can be accurately recovered with a high probability if the sensing matrix is orthogonal. This is impossible for a fat measurement matrix; however, we can optimize the sensing matrix to be as orthogonal as possible by minimizing the difference between the Gram matrix and an identity matrix. The Gram matrix is a symmetric matrix, and the diagonal elements actually correspond to the auto-correlation coefficients of the column vectors in the sensing matrix, while the off-diagonal elements correspond to the cross-correlation coefficients between the different column vectors in the sensing matrix. Meanwhile, according to the definition of , it can be seen that happens to be the maximum value of the absolute value of all the off-diagonal elements of the normalized Gram matrix. Previous work has studied waveform design methods that aim to minimize [6], essentially also making the sensing matrix as orthogonal as possible.
Our design approach focuses on minimizing the coherence of the overall sensing matrix by optimizing the transmit waveforms, in order to improve the performance of CS-based MIMO radars [13]. As a design criterion, we seek to minimize the difference between the Gram matrix and an identity matrix while maintaining a fixed total transmit power. The objective function is given by
where , denotes the total transmit power, and the size of the identity matrix is . The l-th column of the overall sensing matrix equals
where , ⊗ is the Kronecker product, and , it holds that . As a result, we can rewrite Equation (12) and then further formulate the following optimization problem to find waveforms:
where the first term, denoted by SCSM, represents the sum of the square magnitude of the cross-correlation between different columns in the sensing matrix. The second term aims to maintain the norm of all columns close to . s are the columns of that implicitly depend on . The objective function in Equation (14) is not necessarily convex but can be transformed into a convex function. The derivation will be shown as follows.
For the sake of simplicity, we can simplify the inner product of s by using some properties of the Kronecker product, as shown in the following
where , is a constant that does not affect the optimization procedure, so it can be ignored. It is readily apparent that is not a positive semidefinite (PSD) matrix unless , which leads to a non-convex objective function. To address this issue, we split into and , where and , as a result [10]
Clearly, both and are the Hermitian matrices. As is known, if all eigenvalues (denoted by ) are greater than or equal to zero, a Hermitian matrix is positive semidefinite. Accordingly, we define b and d as non-negative real scalars that let and . Then, the first term of Equation (16) can be rewritten as
where is a constant that does not affect the objective function. In this way, Equation (17) is convex since and are PSD matrices. Performing the same procedure on , we can obtain
In the same way, the second term in the objective function of Equation (14) can be rewritten as
Finally, the objective function is transformed into a convex function. However, we can see that the constraint of Equation (14) is a quadratic equality constraint, which is not a convex set. Thus, we replace it with a local affine approximation as follows [10]
where is the estimate of at the last iteration.
In summary, the convex problem of optimizing waveforms with a total power constraint can be formulated as
3. Waveform Optimization and CS Recovery Algorithms for MIMO Radar
3.1. Optimization Algorithm Based on Simulated Annealing
The solution to Equation (21) can be obtained with the Simulated Annealing algorithm (SA) [24]. SA is a global optimization algorithm capable of conducting randomized searches in the solution space to find a globally optimal solution, or an approximation of it. SA is usually a good choice for problems where there may be multiple locally optimal solutions to the objective function. Consequently, it finds widespread application in various optimization problems, especially in the field of traditional radar waveform design [6]. The process of the Algorithm 1 is shown as follows.
| Algorithm 1 Simulated Annealing Algorithm | |
| Input: the initial solution, i.e., initial waveform vector , the objective function . | |
| Output: the best solution, i.e., optimized waveform . | |
| : | Initialization. Initial temperature, cooling schedule, Markov chain length. |
| : | IGenerate a new neighboring solution by applying a small perturbation or modified-tion to the current solution, and calculate the objective function value . |
| : | Verify the constraint and new solution. |
| if meet the constraint | |
| if < | |
| accept the new solution | |
| else | |
| accept the new solution in terms of the Metropolis criterion | |
| else | |
| discard the new solution | |
| end | |
| : | Update the temperature according to the cooling schedule. The acceptance probability of worse solutions decreases gradually as the temperature decreases. |
| : | Check if the stopping criteria are met. If met, terminate the iteration process and return the best solution as the final output, otherwise, repeat steps 2 to 4. |
3.2. CS Recovery Algorithm Based on Sparse Bayesian Learning
In this paper, we use the Sparse Bayesian Learning (SBL) method [25,26] to recover the sparse vector in Equation (10), which contains the angle information of all targets. SBL uses the sparse prior information of the signal to build a hierarchical probability model and perform sparse reconstruction by the maximum a posteriori (MAP) probability function to obtain the parameter estimation of targets. In the field of DOA estimation, SBL is an effective method. When applied to CS-based MIMO radar, it can estimate the target direction efficiently and has excellent performance in the case of limited observation data. In the case of a 2D array MIMO radar, the sparse recovery accuracy of the SBL algorithm is much better than the OMP algorithm. The process of the Algorithm 2 is shown as follows.
| Algorithm 2 Sparse Bayesian Learning Algorithm | |
| Input: the observation vector , the sensing matrix . | |
| Output: the estimated angles of targets. | |
| : | Initialization. Initialize the sparse coefficient estimation vector randomly, representing the weights of received signals at different DOA angles. |
| : | Calculate the likelihood function of the current sparse coefficient vector. |
| : | Update the sparse coefficient vector by the Expectation-Maximization (EM) algorithm. |
| : Calculate the posterior distribution of DOA angles, given the observed data. | |
| : Maximize the MAP function to update the sparse coefficient vector. | |
| : | Check if the stopping criteria are met. If met, terminate the iteration process, otherwise, repeat steps 2 to 3. |
| : | DOA Estimation. Use the updated sparse coefficient vector to calculate the estimated angles of targets and return the result. |
4. Simulation
4.1. Simulation Configuration
First of all, let us discuss the initial waveform . In addition to the general requirements for radar waveforms such as good resolution, low sidelobes, etc., MIMO radar waveforms should also possess good orthogonality. However, strictly speaking, the ideal orthogonal MIMO waveform does not exist [27]. To be closer to practical radar systems, we use a Hadamard-coded waveform as the initial waveform, unlike the ideal orthogonal waveforms used in other literature. We consider a colocated MIMO radar system based on an L-shaped array, as shown in Figure 1, where and the number of transmit antennas is . The Hadamard coding waveform is a kind of slow-time code division multiple access (CDMA) waveform. For the scenario with 8 transmit antennas, each antenna transmits a chirp signal with the same bandwidth and carrier frequency. The initial phases of eight consecutive pulse signals transmitted by eight antennas are modulated by a Hadamard matrix.
The parameter settings of the simulation are given in Table 1. The transmitted waveform is an orthogonal Hadamard-coded waveform with unit power. The received signal is corrupted by zero-mean complex Gaussian noise. The measurement matrix is chosen as a Gaussian random matrix with , and denotes the compression ratio. There are three targets on the angle grid . It should be noted that, in CS-based scenarios, the angular grid can range from to . However, there might be some prior information about the DOA of targets, or the antennas are not omnidirectional, so only part of the angles are illuminated. In these cases, the angle grid can be limited to a small range. Therefore, to keep the computational complexity low, we consider here a small grid located in the middle of the angle space for the performance evaluation. The reflection coefficients s come from a complex Gaussian distribution with zero mean. Each simulation is run 2000 times based on the Monte Carlo method. In each run, three targets are randomly placed on the angle grids.

Table 1.
The parameter settings of the simulation.
4.2. Simulation Results
In this section, simulation experiments are performed to illustrate the effectiveness of the proposed waveform design scheme. Our main focus is to evaluate the incoherence of the sensing matrix and the CS-based multi-target detection and parameter estimation performance for the MIMO radar in the above configuration.
(1) Incoherence: First, analyze the incoherence of the sensing matrix. Using the Gram matrix mentioned in Equation (12), calculate the absolute value of normalized coherence coefficients between the different columns of the sensing matrix. All normalized coherence coefficients are counted in steps of 0.01, and then histograms are plotted. The statistical result is shown in Figure 3. It can be seen that normalized coherence coefficients are more concentrated around 0 after optimization. Since the coherence between the target returns from different search cells is large in the 2D array, the maximum value of normalized coherence coefficients, i.e., , is close to 1. Therefore, we use the average normalized coherence coefficient denoted by ACSM to measure the incoherence of the sensing matrix, which is more intuitive. The ACSMs before and after optimization at different compression ratios are given in Table 2. It can be seen that the ACSM is lower after optimization. These two simulation experiments show that the optimized sensing matrix has better incoherence, i.e., better orthogonality, and is therefore more likely to satisfy the RIP criterion, which provides improved sparse reconstruction performance.
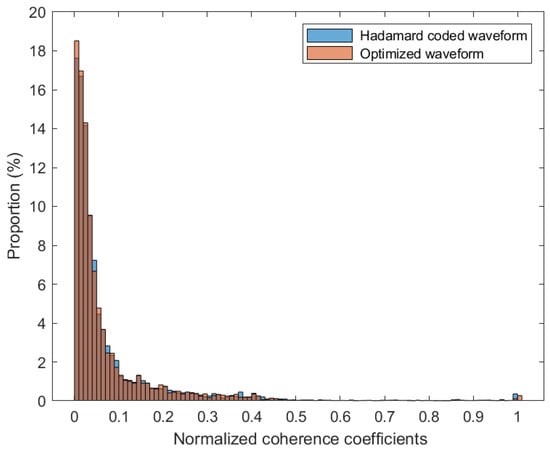
Figure 3.
Histograms of normalized coherence coefficients with M = 8, N = 20 and .

Table 2.
Average normalized coherence coefficients of the sensing matrix with , .
(2) Target Parameter Estimation: To verify the effectiveness of the optimized waveform, we examine the root mean squared error (RMSE) of the target scene recovery (i.e., angle estimation) for different signal-to-noise ratio (SNR) values and different compression ratios . In the cases of with , Figure 4 and Figure 5 demonstrate the RMSE curves of the angle estimation produced by the initial waveform (Hadamard coded waveform), the proposed waveform optimization scheme, and the initial waveform without compression for different SNRs, respectively. From the figure, we can see that the performance improvement due to the optimized waveform is evident. Under the same SNR condition, the optimized waveform has a smaller target parameter estimation error, indicating that the effectiveness and robustness of the CS-MIMO radar are improved. The RMSE of angle estimation decreases as the SNR increases. Moreover, the performance improvement due to the optimized waveform is more obvious when the SNR is low, indicating that when the noise interference is high, the waveform optimization scheme can well compensate for the performance loss caused by noise. Although the target parameter estimation performance in compressed perception scenarios is consistently worse than in general scenarios without compression, the smaller amount of data to be processed in compressed perception reduces the signal processing complexity of the system. Thus, a better balance between the accuracy and complexity of the system can be achieved by our waveform optimization scheme.
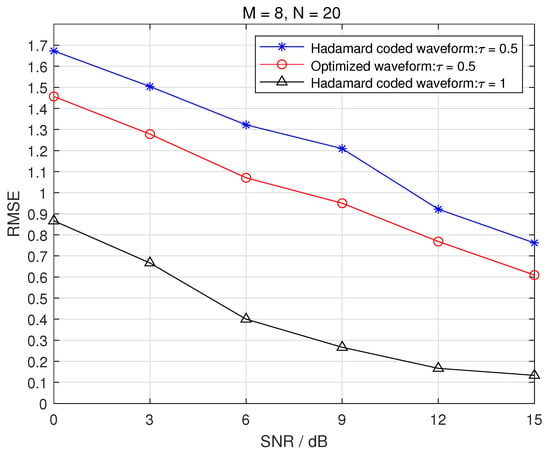
Figure 4.
The recovery results for different values of SNR with .
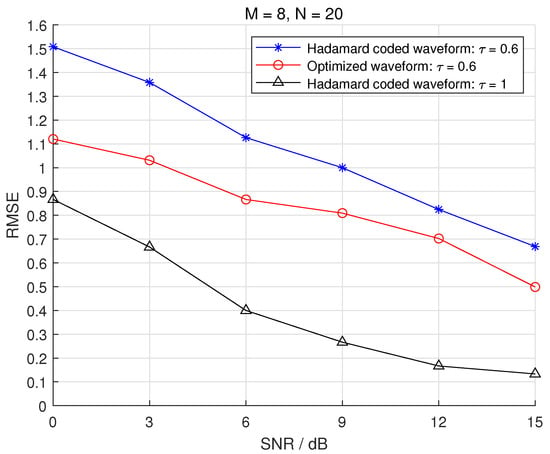
Figure 5.
The recovery results for different values of SNR with .
Figure 6 shows the recovery results for different compression ratios in the conditions of and . From the figure, we can clearly see that the optimized waveform has a better target parameter estimation performance than the initial waveform, regardless of the compression ratio. It is worth noting that the performance improvement is particularly significant at the low compression ratio. In conclusion, we have learned that applying compressive sensing to MIMO radar systems offers numerous benefits. However, the reduction in data volume may lead to a loss of accuracy during parameter estimation. In such cases, using the waveform optimization scheme can improve the performance of CS-based MIMO radar systems.
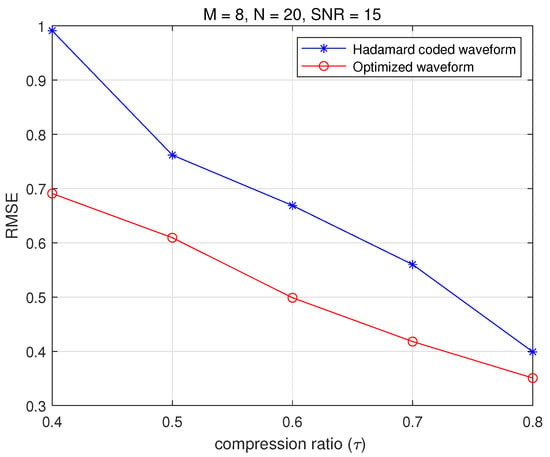
Figure 6.
The recovery results for different compression ratios with , and .
The case of with a different number of receiving antennas is shown in Figure 7. One can see that the waveform optimization scheme has improved RMSE performance as compared to the initial waveform. Again, increasing the number of receiving antennas can improve the target parameter estimation performance of the CS-based MIMO radar when all other conditions are the same. The performance gain with the increase in the number of receiving antennas is more prominent at low SNR. This is because using more receiving antennas effectively increases the array aperture. However, it is important to note that the number of antennas and apertures cannot be increased without limitations, otherwise the practical requirements such as hardware cost, amount of data for signal processing, and size of the radar cannot be met, especially in the field of automotive radar. In this context, our proposed waveform optimization scheme is particularly applicable as it achieves a significant improvement in the performance of the CS-based MIMO radar at a relatively low cost.
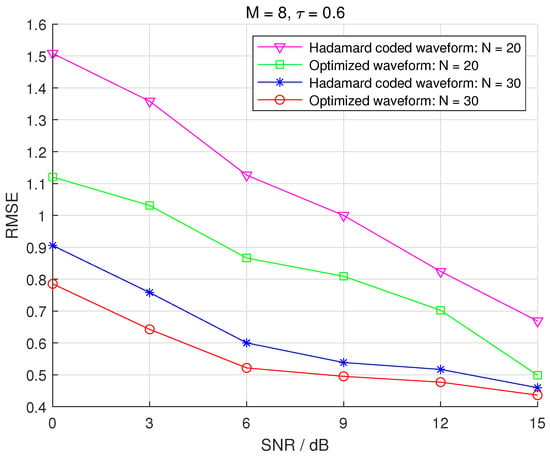
Figure 7.
When and , the recovery results for different values of SNR with different receiving antennas.
5. Discussion
For the sake of simplicity, the objective function in Equation (14) only pertains to the DOA. However, in the general scenario where targets are situated in different range cells and are moving, a range-dependent time delay will be introduced into the waveforms, and a Doppler shift will manifest in the phase term. In this case, when formulating the signal model, the sparse basis matrix has to be represented based on a three-dimensional space and the targets require to be searched in the 3D space. The method proposed in this paper can be easily extended to accommodate the aforementioned model involving range, speed, and angle, but the computational complexity will increase significantly. Therefore, it becomes crucial to propose a more efficient optimization algorithm in future work.
6. Conclusions
We propose a novel waveform design scheme for colocated CS-based MIMO radars. Under the constraint of fixed total transmit power, we optimize the transmit waveform to minimize the difference between the Gram matrix of the sensing matrix and an identity matrix, thus achieving maximum orthogonality of the sensing matrix. Unlike the one-dimensional arrays considered in most of the previous studies, we consider a MIMO radar system based on an L-shaped array with the capability of estimating both the azimuth and elevation angles of the targets. It is more widely used in real-life applications. Furthermore, we use the SBL algorithm for sparse recovery, which is more suitable for 2D array MIMO radar systems. In simulation experiments, we optimize a Hadamard-coded waveform that can be used in practical application scenarios. The simulation results show that under the condition of a 0.5 compression rate of the received data, the MIMO sensing performance has an overall improvement of more than 10% in the range of 0 dB∼15 dB SNR, compared to the non-optimized waveform, and under the condition of 15dB SNR, the MIMO sensing performance has an overall improvement of more than 10% in the range of 0.4∼0.8 compression ratio, compared to the non-optimized waveform. It proves that our waveform design scheme can significantly improve the performance of the radar system.
Author Contributions
Methodology, Y.L. (Yiwen Liu) and X.L.; software, Y.L. (Yifu Liu); validation, C.P. and Y.L. (Yifu Liu); investigation, X.L. and Y.Z.; resources, C.P.; writing—original draft preparation, Y.L. (Yiwen Liu); writing—review and editing, X.L.; project administration, Y.Z.; funding acquisition, C.P. All authors have read and agreed to the published version of the manuscript.
Funding
This researchwas funded by National Key R&D Program of China (Grant No. 2022YFB2902400).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ISAC | Integrated sensing and communications |
| MIMO | Multiple-input multiple-output |
| CS | Compressed sensing |
| RCS | Reflection coefficient |
| RIP | Restricted isometry property |
| CSM | Coherence of the sensing matrix |
| SCSM | The sum of the cross-correlation |
| PSD | Positive semidefinite |
| SA | Simulated annealing |
| SBL | Sparse Bayesian learning |
| MAP | Maximum a posteriori |
| DOA | Direction of arrival |
| CDMA | Code division multiple access |
| ASCM | Average normalized coherence coefficient |
References
- Liu, A.; Huang, Z.; Li, M.; Wan, Y.; Li, W.; Han, T.X.; Liu, C.; Du, R.; Tan, D.K.P.; Lu, J.; et al. A Survey on Fundamental Limits of Integrated Sensing and Communication. IEEE Commun. Surv. Tutorials 2022, 24, 994–1034. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, F.; Jing, X.; Mu, J. Integrating Sensing and Communications for Ubiquitous IoT: Applications, Trends, and Challenges. IEEE Netw. 2021, 35, 158–167. [Google Scholar] [CrossRef]
- Cohen, D.; Eldar, Y.C. Sub-Nyquist Radar Systems: Temporal, Spectral, and Spatial Compression. IEEE Signal Process. Mag. 2018, 35, 35–58. [Google Scholar] [CrossRef]
- Liu, F.; Zheng, L.; Cui, Y.; Masouros, C.; Petropulu, A.P.; Griffiths, H.; Eldar, Y.C. Seventy Years of Radar and Communications: The road from separation to integration. IEEE Signal Process. Mag. 2023, 40, 106–121. [Google Scholar] [CrossRef]
- Candès, E.J. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Vaidyanathan, P.P. Compressed Sensing in MIMO Radar. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 41–44. [Google Scholar]
- Gogineni, S.; Nehorai, A. Target Estimation Using Sparse Modeling for Distributed MIMO Radar. IEEE Trans. Signal Process. 2011, 59, 5315–5325. [Google Scholar] [CrossRef]
- Gurbuz, A.C.; McClellan, J.H.; Scott, W.R. A Compressive Sensing Data Acquisition and Imaging Method for Stepped Frequency GPRs. IEEE Trans. Signal Process. 2009, 57, 2640–2650. [Google Scholar] [CrossRef]
- Yu, Y.; Petropulu, A.P.; Poor, H.V. CSSF MIMO RADAR: Low-Complexity Compressive Sensing Based MIMO Radar That Uses Step Frequency. arXiv 2011, arXiv:1101.2719. [Google Scholar]
- Yu, Y.; Sun, S.; Madan, R.N.; Petropulu, A. Power Allocation and Waveform Design for the Compressive Sensing Based MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 898–909. [Google Scholar] [CrossRef]
- Chen, P.; Wu, L. Joint Design Transmission Waveform and Sensing Matrix for the Compressive Sensing Radar. In Proceedings of the 2014 9th International Symposium on Communication Systems, Networks & Digital Sign (CSNDSP), Manchester, UK, 23–25 July 2014; pp. 558–563. [Google Scholar]
- Rogers, C.A.; Popescu, D.C. Compressed Sensing MIMO Radar System for Extended Target Detection. IEEE Syst. J. 2021, 15, 1381–1389. [Google Scholar] [CrossRef]
- Ajorloo, A.; Amini, A.; Bastani, M.H. A Compressive Sensing-Based Colocated MIMO Radar Power Allocation and Waveform Design. IEEE Sensors J. 2018, 18, 9420–9429. [Google Scholar] [CrossRef]
- Gogineni, S.; Nehorai, A. Frequency-Hopping Code Design for MIMO Radar Estimation Using Sparse Modeling. IEEE Trans. Signal Process. 2012, 60, 3022–3035. [Google Scholar] [CrossRef]
- Daniel, A.; Popescu, D.C. MIMO Radar Waveform Design for Multiple Extended Targets Using Compressed Sensing. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 0567–0572. [Google Scholar]
- Daniel, A.; Popescu, D.C. Multiple Extended Target Detection Using MIMO Radar and Compressed Sensing. In Proceedings of the 2014 IEEE Military Communications Conference, Baltimore, MD, USA, 6–8 October 2014; pp. 777–782. [Google Scholar]
- Urkowitz, H. Filters for Detection of Small Radar Signals in Clutter. J. Appl. Phys. 2004, 24, 1024–1031. [Google Scholar] [CrossRef]
- Chen, S.; Donoho, D. Application of Basis Pursuit in Spectrum Estimation. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP ’98 (Cat. No.98CH36181). Seattle, WA, USA, 15 May 1998; pp. 1865–1868. [Google Scholar]
- Cai, T.T.; Wang, L. Orthogonal Matching Pursuit for Sparse Signal Recovery With Noise. IEEE Trans. Inf. Theory 2011, 57, 4680–4688. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal Recovery from Random Measurements via Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Needell, D.; Vershynin, R. Uniform Uncertainty Principle and Signal Recovery via Regularized Orthogonal Matching Pursuit. Found. Comput. Math. 2009, 9, 317–334. [Google Scholar] [CrossRef]
- Becker, S.; Bobin, J.; Candès, E.J. NESTA: A Fast and Accurate First-Order Method for Sparse Recovery. SIAM J. Imaging Sci. 2011, 4, 1–39. [Google Scholar] [CrossRef]
- Donoho, D.L.; Elad, M.; Temlyakov, V.N. Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Trans. Inf. Theory 2005, 52, 6–18. [Google Scholar] [CrossRef]
- Kirpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Readings Comput. Vis. 1987, 220, 606–615. [Google Scholar]
- Dai, J.; Bao, X.; Xu, W.; Chang, C. Root Sparse Bayesian Learning for Off-Grid DOA Estimation. IEEE Signal Process. Lett. 2017, 24, 46–50. [Google Scholar] [CrossRef]
- Groll, H.; Mecklenbrauker, C.; Gerstoft, P. Sparse Bayesian Learning for Directions of Arrival on an FPGA. In Proceedings of the 2018 IEEE Statistical Signal Processing Workshop (SSP), Freiburg im Breisgau, Germany,, 10–13 June 2018; pp. 623–627. [Google Scholar]
- Sun, H.; Brigui, F.; Lesturgie, M. Analysis and comparison of MIMO radar waveforms. In Proceedings of the 2014 International Radar Conference, Lille, France, 13–17 October 2014; pp. 1–6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).