Abstract
How to rapidly adapt to new tasks and improve model generalization through few-shot learning remains a significant challenge in meta-learning. Model-Agnostic Meta-Learning (MAML) has become a powerful approach, with offers a simple framework with excellent generality. However, the requirement to compute second-order derivatives and retain a lengthy calculation graph poses considerable computational and memory burdens, limiting the practicality of MAML. To address this issue, we propose Evolving MAML (Evo-MAML), an optimization-based meta-learning method that incorporates evolving gradient within the inner loop. Evo-MAML avoids the second-order information, resulting in reduced computational complexity. Experimental results show that Evo-MAML exhibits higher generality and competitive performance when compared to existing first-order approximation approaches, making it suitable for both few-shot learning and meta-reinforcement learning settings.
1. Introduction
Meta-learning aims to rapidly learn new tasks by leveraging prior knowledge from related tasks [1,2]. A popular optimization-based meta-learning method is Model-Agnostic Meta-Learning (MAML) [3], which tries to identify initialization parameters that are sensitive to related tasks, thereby enhancing generalization ability. MAML-based meta-learning algorithms have seen a variety of successful applications [4,5] in enhancing generalization and addressing various learning issues throughout the years. For example, researchers have concentrated on studying generalization bounds and convergence rates to support clarity-aware minimization [6]. Others have investigated the application of evolutionary approaches to compute second-order gradients and increase algorithm performance [7]. Furthermore, researchers looked at the initial conditions for training agents in order to improve few-shot learning [3,8,9]. Furthermore, the combination of MAML with reinforcement learning has shown good performance in a variety of control tasks [10].
Despite the appealing properties of MAML, its meta-learning process depends on the computation of higher-order derivatives, resulting in a significant computational and memory burden and potentially encountering gradient disappearance. These limitations hinder the learning of tasks that involve multi-step inner loop optimization. To tackle these issues, Nichol et al. [11] proposed Reptile, a first-order approximation meta-learning method to avoid solving high-order derivatives. However, Reptile has not been widely used in meta-reinforcement learning, and is only effective for few-shot classification problems. Subsequently, the implicit differentiation-based MAML (iMAML) [12] approach significantly increases computational efficiency by eliminating the requirement of backpropagation across the entire inner loop. However, iMAML assumes that the model has already converged in the inner loop, which limits its practical applicability. In the field of few-shot classification, the UNICORN-MAML [13] approach outperforms many contemporary few-shot classification algorithms without sacrificing the simplicity of MAML. Furthermore, by incorporating evolutionary strategies with MAML, meta-reinforcement learning produces more flexible and effective algorithms that remain competitive with current approaches [14,15]. Although these methods have demonstrated success in their respective fields, they lack the generality to simultaneously excel in both few-shot learning and in meta-reinforcement learning similar to MAML while achieving good performance.
To address these limitations, we propose Evolving MAML (Evo-MAML), an efficient meta-reinforcement learning framework with evolving gradient. Specifically, Evo-MAML utilizes an inner-loop evolutionary update in the initial model to estimate the meta-gradient. Our approach leverages first-order gradient, thereby avoiding the need to extend the computational graph for Hessian-free updates, as evolution does not rely on gradient. Our experimental results demonstrate that Evo-MAML achieves competitive performance in typical few-shot learning and meta-reinforcement learning environments, surpassing existing first-order approximate meta-learning algorithms. Additionally, Evo-MAML with evolving gradient significantly reduces computational resource requirements by eliminating the computation of second-order derivatives, resulting in a lightweight and highly efficient framework.
Our contributions:
- We present Evolving MAML (Evo-MAML), a novel meta-learning method that incorporates evolving gradient. Evo-MAML addresses the challenges of low computational efficiency and eliminates the need to compute second-order derivatives.
- Theoretical analysis and empirical experiments demonstrate that Evo-MAML exhibits lower computational complexity, memory usage, and time requirements compared to MAML. These improvements make Evo-MAML more practical and efficient for meta-learning tasks.
- We evaluate the performance of Evo-MAML in both the few-shot learning and meta-reinforcement learning domains. Our results show that Evo-MAML competes favorably with current first-order approximation methods, highlighting its generality and effectiveness across different application areas.
The rest of the paper is structured as follows. Section 2 presents an overview of current research on meta-learning and meta-reinforcement learning along with corresponding considerations. Section 3 formulates the issue of meta-learning and meta-reinforcement learning and presents the implementation of our method Evo-MAML, emphasizing the utilization of the evolving method for meta-learning. Section 4 provides performance demonstrations of the effectiveness and efficiency of our proposed approach, followed by Section 5, which examines the strengths and limitations of our approach. Finally, Section 6 concludes the work.
2. Related Works
Meta-learning, which enables agents to quickly adapt to new tasks based on previously accumulated knowledge, has gained significant attention in recent years [16]. By performing meta-learning on a set of related tasks, agents can extract common information as meta-knowledge. The meta-training process equips the agent with the ability to rapidly resolve new tasks with only a small number of samples, avoiding the need to start learning from scratch. The goal of meta-learning is to train a good initial model that can efficiently adapt to new tasks.
Recently, meta-learning has been embodied in several ways, including metrics [17,18], neural network-based approaches [19,20,21], and Bayesian approaches [22,23,24]. Another branch uses optimization-based architectures [12,25,26] or attempts to learn the whole system, either by initializing parameters [27] or via evolution [7,14,28]. In this work, we primarily focus on optimization-based meta-learning, with a particular emphasis on MAML [3], which is one of the most popular algorithms in this category. MAML learns an effective model initialization through outer loop optimization and quickly adapts to new tasks through the inner loop, demonstrating good performance in few-shot learning scenarios. However, Antoniou et al. [8] highlighted the challenges associated with stabilizing MAML training and achieving high generalization, namely, that it requires meticulous hyperparameter searching and incurs substantial training and inference costs. Additionally, Alireza et al. [29] analyzed the issues arising from the computation of Hessian-vector products required by MAML. In light of these concerns, our work aims to develop a computationally efficient first-order approximation method for MAML. Leveraging the evolutionary method, which avoids the estimation of second-order derivatives and does not require backpropagation, we propose a novel approach to estimate the second-order derivative of MAML.
In meta-reinforcement learning, MAML can be combined with reinforcement learning. The meta-policy can quickly adapt to new tasks through a few gradient descent updates. However, meta-reinforcement learning with MAML presents challenges such as high computational complexity and memory consumption. To address this, Nichol et al. [11] introduced Reptile, a first-order approximation method that significantly improves computational efficiency. Nevertheless, Reptile is primarily suitable for few-shot learning and exhibits subpar performance in meta-reinforcement learning settings. Addressing the difficulties associated with estimating the second derivative, Song et al. [14] proposed the Evolution Strategies MAML (ES-MAML) algorithm, which replaces the gradient descent process of the inner loop with the evolutionary method; their approach has demonstrated promising results in meta-reinforcement learning. Our work similarly tackles the problem of second-order derivative estimation. Differing from ES-MAML, we leverage evolving gradient solely in the final step of the inner loop, eliminating the need for backpropagation. Our method achieves competitive performance in both few-shot learning and meta-reinforcement learning, offering simplicity, efficiency, and ease of implementation.
3. Proposed Method
In this section, we elaborate on the problem formulation and propose a meta-learning method that incorporates evolving gradient.
3.1. Problem Formulation
We aim to find a well-initialized that will lead to a good adaptation of on the unseen new task after a few gradient descent steps. As a representative optimization meta-learning method, MAML [3] leverages few-shot samples to learn new tasks. The primary objective is to minimize the expected loss across all tasks, i.e.,
where the loss function quantifies the performance of the initial model on task , is the inner loop step size, p is the probability distribution over tasks , and denotes the set of all tasks. To address the computational cost associated with computing exact gradient for each task, MAML employs the stochastic gradient descent (SGD) method. During each gradient step, a batch size of tasks is selected; the update process involves optimization within the inner and outer loops. The inner loop leverages a support set of examples for each task , which facilitates inner loop updates. Conversely, the outer loop employs a query set of examples for outer loop updates.
In the inner loop, the stochastic gradient is used to compute a model corresponding to each task through a single step of SGD:
We then define the meta-gradient as
In the outer loop, the meta-model is computed using the updated models for all tasks in . We compute the meta-model by performing the update
where denotes the outer loop step size. Additionally, the gradient is evaluated using the query set .
In the case of meta-reinforcement learning, the task can be formulated as a Markov Decision Process (MDP), denoted by the tuple . In this tuple, represents the specific task, corresponds to the state space of the agent, and is a function that determines the action based on the current state. The probability distribution of the initial state is denoted by , while represents the conditional probability of transitioning from state s to state given action a. The reward function is , which captures the immediate reward associated with the current state and action.
The objective in meta-reinforcement learning is to find a meta-policy that can rapidly adapt to solve an unseen task through a single gradient step with respect to T. The optimization goal can be defined as follows:
where the meta-policy with a step size . Here, denotes the distribution over trajectories, which is dependent on the policy and the given task . The process of obtaining the gradient solution for the meta-reinforcement learning objective function is as follows:
with and with denoting the derivation of the meta-policy.
3.2. Evolving MAML Algorithm
Our objective is to address the optimization-based meta-learning problem described in Equation (1) by employing an iterative gradient-based algorithm of the form . The gradient descent update can be expanded using the chain rule, as illustrated by
In practice, the gradient can be easily obtained through automatic differentiation. However, the primary challenge lies in computing the Hessian , which is defined as an optimization problem. To tackle this update problem, estimating the meta-gradient in Equation (3) poses significant computational and memory burdens due to the involvement of a gradient in the inner loop in a backwards order [3]. This becomes particularly challenging when a large number of gradient steps are required.
To overcome these difficulties, we propose the utilization of an evolutionary method [7] to estimate the meta-gradient, eliminating the need for calculating the second-order gradient or storing a longer calculation graph, significantly improving efficiency.
Specifically, we first consider an approximate solution to the inner optimization problem, which can be obtained by performing k steps of gradient descent, then perform evolutionary learning. We apply random perturbations to the model to generate P variants of the current model, denoted as . We then calculate the training losses of these P variants. Next, we determine the evolutionary model using the following formula
where the weights are denoted as . The temperature factor rescales the losses to adjust the scale of weight changes. The evolving gradient is defined as
Finally, we compute the meta-gradient of the test loss and evaluate the evolutionary updated model on a minibatch drawn from the query set . The evolutionary gradient algorithm [7] is particularly well-suited for solving this problem, as it eliminates the need for second-order gradient in the inner loop and avoids the explicit formation or storage of the Hessian matrix. This stands in contrast to typical methods that employ gradient-based updates in the inner loop, perform differentiation through it (in forward mode or reverse mode), or even apply the implicit function theorem [12]. The overall framework of Evo-MAML is shown in Figure 1. Algorithm 1 provides a comprehensive practical algorithm for our approach.
| Algorithm 1: Evolving Model-Agnostic Meta-Learning (Evo-MAML) |
 |
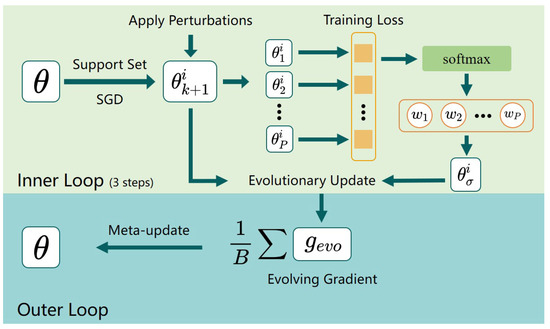
Figure 1.
An overview of our Evolving MAML approach. Our method is based on a bi-level loop. In the inner loop, the model undergoes three steps of SGD followed by the application of perturbations, resulting in P perturbed models. Subsequently, an evolutionary update is performed to obtain an evolutionary model denoted as and the evolving gradient is computed. The yellow box in the figure indicates the training loss of the corresponding model. The outer loop is responsible for learning the evolutionary gradient across tasks, which enables the redirection of learning in the inner loop.
Notably, our approach differs significantly from ES-MAML [14] in the way that agents are updated. While ES-MAML utilizes the evolutionary gradient as the update method for the inner loop, we only employ the evolutionary gradient in the final update step of the inner loop. Moreover, the evolutionary method [7] that we employ is completely distinct from ES-MAML. Furthermore, our method exhibits better generality in the field of few-shot classification and meta-reinforcement learning. In Section 4, we compare our Evo-MAML method with existing first-order approximate meta-learning methods.
3.3. Theoretical Analysis
We conducted an analysis to illustrate how the evolving gradient can effectively reduce the memory and time costs, as demonstrated in Formula (10):
In this formula, the first term is obtained through backpropagation, represents the randomly sampled perturbations, and the last term is derived from the softmax derivatives and training losses of the P perturbation models . Compared to MAML, which computes higher-order gradient using backpropagation, our Evo-MAML method eliminates this step, resulting in a shortened computational map and reduced memory cost.
In Table 1, we compare Evo-MAML to MAML, which is the most relevant and widely-used method [3]. MAML necessitates the computation of higher-order gradient and the associated longer computational graphs due to its requirement for backpropagation through gradient nodes. Consequently, MAML incurs increased memory and time costs. In contrast, Evo-MAML eliminates the need for higher-order gradient, avoids large matrices, and significantly reduces the expansion of the computational graph. While current techniques [3] rely on longer computational graphs, Evo-MAML effectively shortens the graph and reduces memory costs by circumventing this requirement.

Table 1.
Comparison of meta-gradient approximation of Evo-MAML and MAML.
4. Experiments and Results
In our experimental evaluation, we aim to empirically answer the following research questions (RQs):
- RQ1: Does Evo-MAML yield better results in few-shot learning problems compared to MAML?
- RQ2: Does Evo-MAML exhibit improved performance in meta-reinforcement learning tasks?
- RQ3: How do the computational and memory requirements of Evo-MAML compare to those of MAML?
To address RQ1 and RQ2, we utilize the Omniglot [30] and MiniImagenet [31] datasets, which are widely used in few-shot meta-learning. Additionally, we employ standard meta-reinforcement learning tasks. Regarding RQ3, we provide an answer through a theoretical analysis. To further validate our findings, we conduct numerical simulations.
4.1. Experimental Settings
In this section, we present the practical setup of Evo-MAML for evaluating two types of meta-learning experiments. First, Section 4.1.1 provides details on the comparison algorithms employed in the few-shot learning experiments, along with our model architecture and hyperparameter configurations. Subsequently, Section 4.1.2 elaborates on our model architecture and hyperparameter settings for the meta-reinforcement learning problem.
4.1.1. Few-Shot Learning Settings
In few-shot learning challenges, we put the following methods to the test:
- MAML [3]: the standard model-agnostic meta learning.
- First-Order MAML [3]: first-order approximation version of MAML.
- Reptile [11]: update using only the first derivative.
- iMAML [12]: using implicit differential to solve the meta-gradient.
We employed the same four-layer CNN architecture as MAML to perform meta-training with a complete sample batch size (e.g., twenty for twenty-way one-shot) on the meta-training dataset. Subsequently, the model was evaluated using the meta-test dataset. In the Omniglot experiment, we set the inner and outer loop learning rates to 0.4 and 0.001, respectively. For the twenty-way problem, we sampled 32 tasks in batches, while for the five-way problem we sampled 16 tasks in batches. The perturbation parameter and temperature coefficient were both set to 0.01. In the MiniImagenet experiment, we set the inner and outer loop learning rates to 0.05 and 0.002, respectively. We trained Evo-MAML with 15 inner loop steps in both meta-training and meta-testing. For the five-way one-shot setting, we used four tasks for batch sampling and two tasks for five-way one-shot batch sampling.
4.1.2. Meta-Reinforcement Learning Settings
We utilized the same model architecture as in the original paper [3]: a two-layer MLP with 100 hidden units in each layer. The adapted batch size was set to 10, the meta-batch size was 20, and we performed three inner loop update steps with an inner learning rate of 0.1. Additionally, we conducted twenty trajectories for inner loop adaptation. Evo-MAML was trained with three different random seeds, and the mean and standard deviation of the results were reported.
We followed the same process as for MAML to construct the experimental tasks. In evolutionary learning, we uniformly set the number of perturbation models to for all tasks. For the few-shot learning tasks, the perturbation parameter and temperature parameter were set to 0.001 and 0.5, respectively. In the meta-reinforcement learning tasks, they were set to 0.01 and 0.05, respectively. All experiments were performed using a PyTorch implementation, and the models were trained on a single NVIDIA Titan RTX GPU.
4.2. Results
In this section, we conduct a comparative evaluation of our proposed method and analyze its computational efficiency and memory consumption in the context of few-shot learning problems and meta-reinforcement learning problems. Section 4.2.1 evaluates the performance of our proposed method on few-shot classification problems and compares it with previous first-order approximate meta-learning algorithms. Then, Section 4.2.2 examines the performance of Evo-MAML on a meta-reinforcement learning problem and compares it to other evolution-based meta-reinforcement learning methods. Finally, Section 4.2.3 demonstrates the efficiency of Evo-MAML through computational time and memory consumption experiments.
4.2.1. Performance on Few-Shot Learning
To investigate RQ1, we evaluated our method on two popular few-shot classification datasets: Omniglot [30] and MiniImagenet [31]. Table 2 presents the baseline performance of standard MAML [3], first-order MAML [3], Reptile [11], MAML with implicit gradient [12], and Evo-MAML. The results demonstrate that Evo-MAML achieves significantly improved accuracy compared to the original MAML method while remaining competitive with other first-order approximation methods. Furthermore, the performance of MAML, First-Order MAML, and Reptile is quite similar across all tasks. Implicit MAML [12] performs slightly better on Omniglot compared to other methods, and performs similarly to Reptile on MiniImagenet. For a fair comparison, we employed the same convolution architecture as in the cited works. However, it is worth noting that architecture tuning can lead to improved results for all algorithms [13]. Therefore, our method has the potential to achieve higher accuracy on few-shot classification tasks.

Table 2.
Few-shot classification meta-learning with Omniglot and MiniImagenet characters. The results obtained by Evo-MAML are competitive with existing meta-learning models. Confidence intervals for tasks are displayed at . For the five-way and twenty-way tasks, Evo-MAML used 15 and 20 SGD steps, respectively.
4.2.2. Performance on Meta-Reinforcement Learning
To evaluate the proposed Evo-MAML method and address RQ2, we conducted experiments on continuous control tasks in the Navigation2D and MuJoCo environments [32], which serve as common benchmarks for meta-reinforcement learning algorithms [33].
In the Navigation2D exploration environment, the agent is represented as a point on a 2D square and receives a reward equal to its distance from a set goal point on the square at each time step. In our evaluation, we compare the adaptation of the meta-policy to an entirely new position with up to three steps of gradient updating, with 20 samples per update. Figure 2 depicts the various exploration policies learned by MAML and Evo-MAML. The results reveal that after the three-step update, the meta-policy learned by Evo-MAML is more exploratory in all directions and can adapt to the new task faster.
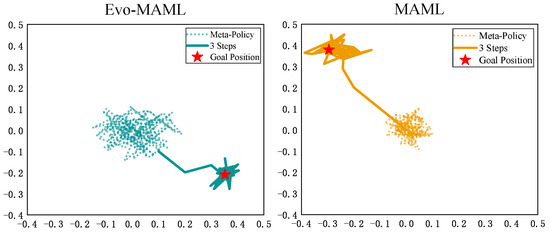
Figure 2.
Comparison of the Navigation2D task exploration behaviors of MAML and Evo-MAML. After three-step updating, Evo-MAML can be adapted to new tasks more quickly.
Next, we compare the average returns of Evo-MAML and three other optimization-based meta-learning algorithms in three MuJoCo environments. The reward functions for these settings (the walking direction for Ant-Fwd-Back and Walker-Fwd-Back and the target velocity for Walker-Vel) all differ from each other. We compare Evo-MAML with three representative meta-reinforcement learning algorithms: ES-MAML [14], based on an evolutionary strategy; E-MAML [28], another method that tries to circumvent the problem of meta-gradient estimation in MAML using evolutionary methods; and standard MAML [3]. To create a fair comparison, the maximum episode duration for all tasks was set to 200, the same as MAML.
Figure 3 illustrates that Evo-MAML outperforms the current first-order approximation meta-reinforcement learning approaches in all three environments in terms of average returns. Our Evo-MAML approach achieves comparable performance to the other algorithms, although its performance declines somewhat in the Walker-Vel environment. This decline may be attributed to the increased number of tasks and their similarity, which could lead to weakened meta-learning ability and slower policy convergence. The average returns obtained using evolving gradient are significantly better than MAML, with the asymptotic performance of Evo-MAML reaching approximately 2.23 and 1.37 times that of MAML in the Ant-Fwd-Back and Walker-Fwd-Back environments, respectively, although they are only slightly improved in the Walker-Vel environment. In summary, our method is more suitable for tasks with low similarity, such as navigating in completely opposite directions.
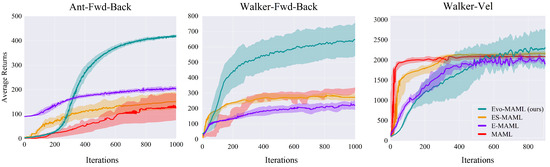
Figure 3.
The meta-learning curves corresponding to different first-order approximation methods combined with MAML. The final asymptotic performance of the proposed Evo-MAML approach consistently outperforms other methods.
4.2.3. Performance on Computation and Memory
For RQ3, we compared the computational efficiency and memory usage of Evo-MAML with the standard MAML in both few-shot classification problems and continuous control problems. To ensure a fair comparison, the same number of training steps were set for each period of the algorithm. The experimental results depicted in Figure 4 demonstrate the compute and memory trade-offs for MAML and Evo-MAML on four types of classification tasks using the Omniglot dataset, as well as on three control tasks in meta-reinforcement learning environments. The results indicate that our approach significantly reduces memory and time costs, realizing savings of at least on memory usage and improving runtime by over . When calculating higher-order gradient, MAML expands the computational graph for backpropagation, which directly increases both memory and time costs. In contrast, Evo-MAML only utilizes a set of weights for implementation, leading to a significant improvement in computational efficiency. Overall, these experiments confirm that Evo-MAML is suitable for meta-learning in various domains, including few-shot classification and meta-reinforcement learning, while providing significantly reduced memory and time consumption.
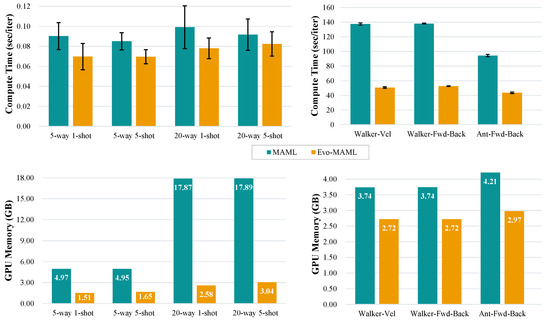
Figure 4.
Comparison of the computation and memory of MAML and Evo-MAML in meta-learning and meta-reinforcement learning. The mean and standard deviation are reported across experiments with different test datasets. Evo-MAML is significantly more efficient in terms of both memory usage and time per iteration.
5. Discussion
Table 1 and Figure 4 theoretically and experimentally illustrate the superior efficiency of the proposed method in terms of both computation time and memory compared to MAML. Additionally, Table 2 demonstrates that Evo-MAML achieves higher classification precision in few-shot classification problems, particularly on the MiniImagenet dataset. Furthermore, Figure 2 and Figure 3 show that Evo-MAML exhibits improved asymptotic performance in meta-reinforcement learning problems, indicating its technical superiority. However, it is important to acknowledge that Evo-MAML does have certain limitations in terms of learning. For instance, in meta-reinforcement learning problems Evo-MAML exhibits subpar sample efficiency during the early stages of training. Specifically, while Evo-MAML displays superior performance only after approximately 300 training iterations in the case of the Ant-Fwd-Back tasks, achieving comparable performance in the Walker-Vel environment requires around 600 iterations.
6. Conclusions
In this paper, we have presented a novel meta-learning framework utilizing evolving gradient which is able to effectively tackle the challenge of estimating second-order derivatives in optimization-based meta-learning. By employing the evolutionary update method, our proposed approach is able to estimate meta-gradient without the need to calculate higher-order derivatives. Notably, our approach avoids the expansion of computation graphs, resulting in enhanced computational efficiency and reduced memory burden. Our findings demonstrate that the proposed method achieves competitive performance in the domains of few-shot learning and meta-reinforcement learning. Moreover, across all experiments we consistently observed significant improvements in time and memory efficiency. Future research directions include extending our proposed framework to multi-agent meta-reinforcement learning environments. In high-dimensional multi-agent scenarios, where the dynamics may be unknown or too complex to model, the light weight and good efficiency of Evo-MAML could provide more flexible performance. Furthermore, upgrading the evolutionary update method in the inner loop using a state-of-the-art evolutionary strategy may lead to better gradient estimation and further improve on our results. Additionally, we anticipate further exploration of the optimization-based meta-learning framework on larger models and problem domains. By addressing these avenues, we aim to enhance the applicability and effectiveness of the proposed approach in real-world scenarios.
Author Contributions
Conceptualization, Z.H. and P.L.; Methodology, W.Y.; Writing—original draft, J.C.; Supervision, S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grants 61806212 and 62376280.
Data Availability Statement
The datasets used in the few-shot learning experiments are publicly available from Torchmeta https://github.com/tristandeleu/pytorch-meta. The meta-reinforcement learning environment code is adapted from https://github.com/cbfinn/maml_rl/tree/9c8e2ebd741cb0c7b8bf2d040c4caeeb8e06cc95/rllab/envs/mujoco (accessed on 10 September 2023).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MAML | Model-Agnostic Meta-Learning |
| Evo-MAML | Evolving MAML |
| ES-MAML | Evolution Strategies MAML |
| iMAML | Implicit MAML |
| SGD | Stochastic Gradient Descent |
References
- Schmidhuber, J.; Zhao, J.; Wiering, M. Simple principles of metalearning. Tech. Rep. IDSIA 1996, 69, 1–23. [Google Scholar]
- Russell, S.; Wefald, E. Principles of metareasoning. Artif. Intell. 1991, 49, 361–395. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Zhang, Z.; Wu, Z.; Zhang, H.; Wang, J. Meta-Learning-Based Deep Reinforcement Learning for Multiobjective Optimization Problems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Grigsby, J.; Sekhon, A.; Qi, Y. ST-MAML: A stochastic-task based method for task-heterogeneous meta-learning. In Proceedings of the Conference on Uncertainty in Artificial Intelligence, Online, 1–5 August 2022; pp. 2066–2074. Available online: https://proceedings.mlr.press/v180/wang22c.html (accessed on 10 September 2023).
- Abbas, M.; Xiao, Q.; Chen, L.; Chen, P.Y.; Chen, T. Sharp-MAML: Sharpness-Aware Model-Agnostic Meta Learning. In Proceedings of the 39th International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; Volume 162, pp. 10–32. [Google Scholar] [CrossRef]
- Bohdal, O.; Yang, Y.; Hospedales, T. EvoGrad: Efficient Gradient-Based Meta-Learning and Hyperparameter Optimization. Adv. Neural Inf. Process. Syst. 2021, 34, 22234–22246. [Google Scholar]
- Antoniou, A.; Edwards, H.; Storkey, A. How to Train Your MAML. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Li, Z.; Zhou, F.; Chen, F.; Li, H. Meta-SGD: Learning to Learn Quickly for Few-Shot Learning. arXiv 2017, arXiv:1707.09835. [Google Scholar]
- Yu, T.; Quillen, D.; He, Z.; Julian, R.; Narayan, A.; Shively, H.; Adithya, B.; Hausman, K.; Finn, C.; Levine, S. Meta-World: A Benchmark and Evaluation for Multi-Task and Meta Reinforcement Learning. In Proceedings of the Conference on Robot Learning, PMLR, Virtual, 16–18 November 2020; pp. 1094–1100. [Google Scholar] [CrossRef]
- Nichol, A.; Achiam, J.; Schulman, J. On First-Order Meta-Learning Algorithms. arXiv 2018, arXiv:1803.02999. [Google Scholar]
- Rajeswaran, A.; Finn, C.; Kakade, S.M.; Levine, S. Meta-learning with implicit gradients. In Proceedings of the Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. Available online: https://api.semanticscholar.org/CorpusID:202542766 (accessed on 10 September 2023).
- Ye, H.J.; Chao, W.L. How to Train Your MAML to Excel in Few-Shot Classification. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022; Available online: https://openreview.net/forum?id=49h_IkpJtaE (accessed on 10 September 2023).
- Song, X.; Gao, W.; Yang, Y.; Choromanski, K.; Pacchiano, A.; Tang, Y. ES-MAML: Simple Hessian-Free Meta Learning. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2020. [Google Scholar]
- Houthooft, R.; Chen, R.Y.; Isola, P.; Stadie, B.C.; Wolski, F.; Ho, J.; Abbeel, P. Evolved Policy Gradients. In Proceedings of the Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 2–8 December 2018; Volume 31. [Google Scholar]
- Thrun, S.; Pratt, L. Learning to learn: Introduction and overview. In Learning to Learn; Springer: Berlin/Heidelberg, Germany, 1998; pp. 3–17. [Google Scholar]
- Xi, B.; Li, J.; Li, Y.; Song, R.; Hong, D.; Chanussot, J. Few-Shot Learning With Class-Covariance Metric for Hyperspectral Image Classification. IEEE Trans. Image Process. 2022, 31, 5079–5092. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Cai, L.; Yang, Z.; Song, S.; Wu, C. Multi-distance metric network for few-shot learning. Int. J. Mach. Learn. Cybern. 2022, 13, 2495–2506. [Google Scholar] [CrossRef]
- Mishra, N.; Rohaninejad, M.; Chen, X.; Abbeel, P. A Simple Neural Attentive Meta-Learner. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Munkhdalai, T.; Yuan, X.; Mehri, S.; Trischler, A. Rapid adaptation with conditionally shifted neurons. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 3664–3673. [Google Scholar]
- Qiao, S.; Liu, C.; Shen, W.; Yuille, A.L. Few-shot image recognition by predicting parameters from activations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7229–7238. [Google Scholar]
- Yoon, J.; Kim, T.; Dia, O.; Kim, S.; Bengio, Y.; Ahn, S. Bayesian model-agnostic meta-learning. In Proceedings of the Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 2–8 December 2018; Volume 31. [Google Scholar]
- Rakelly, K.; Zhou, A.; Finn, C.; Levine, S.; Quillen, D. Efficient off-policy meta-reinforcement learning via probabilistic context variables. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 10–15 June 2019; pp. 5331–5340. [Google Scholar]
- Zintgraf, L.; Shiarlis, K.; Igl, M.; Schulze, S.; Gal, Y.; Hofmann, K.; Whiteson, S. VariBAD: A very good method for Bayes-adaptive deep RL via meta-learning. In Proceedings of the International Conference on Learning Representations, Virtual, 26 April–1 May 2020. [Google Scholar]
- Khodak, M.; Balcan, M.F.F.; Talwalkar, A.S. Adaptive gradient-based meta-learning methods. In Proceedings of the Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Raghu, A.; Raghu, M.; Bengio, S.; Vinyals, O. Rapid Learning or Feature Reuse? Towards Understanding the Effectiveness of MAML. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Lee, Y.; Choi, S. Gradient-based meta-learning with learned layerwise metric and subspace. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 2927–2936. [Google Scholar]
- Stadie, B.; Yang, G.; Houthooft, R.; Chen, X.; Duan, Y.; Wu, Y.; Abbeel, P.; Sutskever, I. Some Considerations on Learning to Explore via Meta-Reinforcement Learning. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Fallah, A.; Mokhtari, A.; Ozdaglar, A. On the Convergence Theory of Gradient-Based Model-Agnostic Meta-Learning Algorithms. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Okinawa, Japan, 16–18 April 2019. [Google Scholar]
- Lake, B.M.; Salakhutdinov, R.; Gross, J.; Tenenbaum, J.B. One shot learning of simple visual concepts. Cogn. Sci. 2011, 33, 2568–2573. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.P.; Kavukcuoglu, K.; Wierstra, D. Matching Networks for One Shot Learning. In Proceedings of the Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Todorov, E.; Erez, T.; Tassa, Y. MuJoCo: A physics engine for model-based control. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 5026–5033. [Google Scholar] [CrossRef]
- Duan, Y.; Chen, X.; Houthooft, R.; Schulman, J.; Abbeel, P. Benchmarking Deep Reinforcement Learning for Continuous Control. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).