Abstract
Virtual power plants are a useful tool for integrating distributed resources such as renewable generation, electric vehicles, manageable loads, and energy storage systems under a coordinated management system to obtain economic advantages and provide ancillary services to the grid. This study proposes a management system for a residential virtual power plant that includes household loads, photovoltaic generation, energy storage systems, and electric vehicles. With the proposed management system, the virtual power plant is economically optimized (as in commercial virtual power plants) while providing ancillary services (as in technical virtual power plants) to the distribution grid. A genetic algorithm with appropriate constraints is designed and tested to manage the energy storage system and the charge/discharge of electric vehicles, with several economic and technical objectives. Single-objective optimization techniques are compared to multi-objective ones to show that the former perform better in the studied scenarios. A deterministic gradient-based optimization method is also used to validate the performance of the genetic algorithm. The results show that these technical targets (usually reserved for larger virtual power plants) and economic targets can be easily managed in restricted-sized virtual power plants.
1. Introduction
Current power systems present two important challenges: the need to reduce dependence on fossil fuels and greenhouse gas emissions and the increase in power demand, which is accelerated by the proliferation of electric vehicles (EVs) and fast charging systems. In this situation, virtual power plants (VPPs) arise as a means to better integrate uncertain renewable energy into the power system, as well as to improve the control of distributed energy resources and help with grid support [1,2,3]. A VPP can be defined as the aggregation and coordination of resources (renewable/non-renewable generation, controllable loads, energy storage systems, and/or EV) with economic and/or technical objectives. Very recent literature reveals the research community’s active interest in the development of VPPs as a means for better integrating and managing renewable energy systems and other resources, valuing their economic and technical impact on power systems [4,5,6]. VPPs are classified into commercial (CVPP) and technical (TVPP) depending on their main objective: CVPPs aim to reduce costs or improve profits, while TVPPs aim to support the grid [2]. However, according to the authors’ opinion, these objectives are complementary, and they should coexist in order for VPPs to be attractive to resource owners and useful for the power system.
Previous works in the literature explore the optimal schedule of different resources included in a VPP or an energy community with different targets. Ref. [7] proposes a mixed integer linear programming (MILP) method to schedule photovoltaic (PV) resources, a fuel cell, a central energy storage system (ESS), and a customer-owned ESS, looking for a zero net energy community. Ref. [8] optimizes demand-side management (DSM) services in an urban microgrid with the aim of reducing electricity prices by participating in flexibility markets. Ref. [9] describes a pilot project of a residential VPP developed in Ireland, where ESS scheduling is addressed with different objective functions, like improving individual or common self-consumption, reducing electricity bills, or providing peak-shaving services. A recently published model [10] adds an extra optimization layer to modify the previous schedule of resources based on economic objectives in order to fulfill the constraints of the distribution grid. Notably, none of these works include the EV charging/discharging schedule. Meanwhile, ref. [11] includes EV among the resources of a VPP to study the impact of VPP management on grid performance. However, the same cost is assumed to charge and discharge the EVs, so they do not participate in economic optimization. No other ESS is considered in [8]. Therefore, the optimization problem is different from the one proposed in this paper. Ref. [12] optimizes renewable energy resources along with battery-based ESSs and EVs in a smart home. However, ESSs and EVs are considered only as backup resources during peak hours when renewable sources are not available. EVs are also managed [13] within a VPP to optimize bidding for the day-ahead market and secondary reserve. However, no constraints are considered regarding the time of EV use, and no other ESS is included. The same optimization targets are used in [14] to jointly schedule the energy resources of two neighbor VPPs with energy interchange between them, but the case does not consider any network constraints. Similarly, a very recent paper [15] presents a home energy management system using model predictive control (MPC), including EV among the resources to be scheduled, but again without considering network constraints. Other works, like [16], manage EV charge/discharge to better exploit renewable generation, but they do not perform any optimal daily scheduling based on economic targets. An interesting approach can be found in [17], which coordinates a home energy management system (EMS), including appliances, renewable sources, ESSs, and EVs. In this case, however, the optimization system decides the state of both the ESS and EVs from three options: charge at maximum power, discharge at maximum power, or idle. No modulation in power is performed, and an oscillating state of charge (SoC) is obtained due to alternating states.
Another aspect studied in this literature is the provision of ancillary services (ASs) to help support the distribution network. According to [18], ASs oriented to the distribution network can be classified into four categories: voltage regulation, voltage unbalance mitigation, congestion management, and power smoothing. The proposed technique intends to contribute to congestion prevention via peak shaving. Additionally, this study also discusses the potential participation of the ESS in other ASs (such as congestion management and power smoothing).
Optimization processes are used in power system planning and management regarding electricity market operation, planning, optimal dispatch, and dynamic safety [19]. Traditional optimization methods like linear, non-linear, mixed integer, and quadratic programming are mathematically rigorous. However, when the problem to be solved is complex or large-scale, convergence may be missed depending on initial conditions [16]. In contrast, an adequate process of mutation and crossover of the genetic algorithm (GA) population has proven to have a good ability to find a global solution within a large range of possible values [20]. GAs have been used for optimization purposes for power network reconfiguration [21], fault diagnosis [22], volt/VAR optimization [20], economic load dispatch [23], renewable resource allocation and sizing [24], and demand response [25], among others. In the field of energy communities, buildings, and microgrids, GAs have been tested to shift the connection of appliances in a home energy management system [26], to size energy resources [27], and also for EMS [28,29,30]. The authors in [28] optimize the use of energy resources from several home agents to perform decentralized management of demand, renewable generation, and storage. However, EVs are not included among these resources. They prefer GA to other optimization techniques due to its flexibility and ability to find near-optimal solutions. Previous research [29] proposes a GA to improve the performance of a MILP technique to schedule the ESS and EV of an individual, minimizing energy costs. No AS is considered in [29]. More recently, Ref. [30] compares GA and multi-objective particle swarm optimization (MOPSO) for managing diverse distributed generation technologies, as well as ESS and demand response in a microgrid, with very similar results. Second-life batteries, previously deployed in EVs, are used as ESSs to perform a home EMS with GA [31]. However, EVs are not considered resources in this approach. Other works, like [32], use a GA to decide which EVs are excluded from charging in a charging facility when not enough energy is available. Afterward, an allocation process, including vehicle-to-grid (V2G), is performed only during overloaded hours.
Finally, previous works by this research team have proposed a GA to schedule the battery management of microgrids for prosumers [33,34]. However, those papers did not manage EVs, and they did not foresee AS provisions.
Other heuristic/meta-heuristic optimization methods may be used to solve an optimization problem in EMS. Some of them, like particle swarm optimization (PSO) or grey wolf optimization (GWO), have been previously used for similar purposes. PSO iteratively tries to improve a candidate solution (expressed as particle positions) by moving these particles around the search space based on their own best-known position and velocity and the entire swarm’s best-known position. Previous work [30] showed very similar results as GAs in a problem like the one proposed in this paper. However, the performance of PSO is very sensitive to an adequate selection of parameters, as discussed in [35], adding some difficulty to the method formulation. GWO is a population-based meta-heuristic algorithm that simulates the leadership hierarchy and hunting mechanism of grey wolves in nature. The paper [17] uses GWO in a home EMS with promising results, although without modulating the power of the different resources. Other interesting optimization tools to be explored are the gravitational search algorithm (GSA) and inclined plane system (IPS) optimization, which are inspired by gravitational and movement laws. The GSA has been used recently for ship EMS [36], although an improvement of the method is required due to its slow convergence speed. In this work, the GA is preferred to other heuristic and meta-heuristic methods because it has already demonstrated proper performance in solving similar problems. Exploring other optimization tools is assumed to be a future line of research.
Table 1 shows a comparison of optimization techniques and energy resources considered in the cited works more closely related to the purpose of this paper. As can be observed, none of them use the same method with the same objectives and resources as the current paper.

Table 1.
Comparative literature review on optimization for EMS.
To sum up, the recent literature offers a wide range of proposals for power system optimization and EMS. However, the use of GA for optimization and the inclusion of both ESSs and EVs have not received such high attention. Moreover, AS provision is hardly considered in these kinds of works.
In light of this state-of-the-art study, the main contributions of this paper are as follows:
- A novel method based on GA has been designed, formulated, and tested for the EMS of a residential VPP that includes loads, renewable generation, ESS, and EVs. The proposed model is suitable for VPPs with limited resources.
- Although the reduction in the electricity bill is the main objective, technical support for the distribution grid is also considered. The literature has hardly examined AS provision from VPPs and energy communities to the distribution grid, even though this is an important challenge under the current energy transition circumstances.
- EVs are considered storage systems with a V2G strategy, respecting the time restriction and the availability of stored energy for mobility purposes. The previous literature has not examined the use of EVs as an EMS resource along with other ESSs to optimize energy costs and provide ASs at a residential level.
- Both single-objective and multi-objective methods are used and compared to combine economic and technical targets.
2. Case Study
The VPP under study encompasses a set of households, a communitarian PV power plant, a battery-based ESS, and EVs (see Figure 1).
Figure 1.
Elements of the VPP under study.
Eight households were included in this study. Their hourly demand profiles throughout the day were supposed to have been forecasted, responding to demand profiles proposed in published works: four houses were modeled for a household with a medium level of annual electricity use in Denmark [37], two houses responded to a high-demand profile [33], and the remaining two houses had low-demand profiles [33].
A communitarian PV power plant rated at a 15 kW peak was supposed to follow a forecasted generation profile proportional to that studied in [33]. This sizing was consistent with Spanish self-consumption habits, which usually limit peak generation power to avoid a high contracted power due to a high power component of network tariffs (an optimum peak power for average dwellings in Spain was estimated at 1.5–2 kW in [38]).
The ESS was considered a set of Li-ion batteries controlled by power electronic converters and centrally managed. The total capacity of the system (Cnom) was 24 kWh, with a maximum charge/discharge power of ±6 kW and a SoC range of 20–100%. The ESS sizing was limited in accordance with Spanish self-consumption remuneration as well. Batteries represent a high percentage of the investment required for self-consumption. Indeed, if only economic advantages were pursued, some studies discourage investment in storage systems until costs decrease [39].
Four EVs, each with a battery capacity of 50 kWh and an average consumption of 20 kWh/100 km, completed the set of resources included in the VPP. Charger plugs were limited to a standard single-phase rating of 230 V 32A, suitable for residential applications. Although EVs are probably plugged in at any hour in the previous evening, it is usual in some countries that a network tariff system encourages consumers to shift some controllable loads to off-peak hours for extra savings. This is the case in Spain, where time-of-use network tariffs have a component due to contracted power that is almost 20 times lower from 0 to 8 h than in the rest of the working day [40]. As this tariff scheme strongly influences the consumers’ habits, it has been assumed that they would prefer charging their EVs during this off-peak time slot.
Accumulated demand and generation within the VPP, excluding the storage system, are depicted in Figure 2a. In this initial situation, EVs were supposed to be charging at maximum power from the moment the charging process started (at 0 h) until they were fully charged. In this base case, the self-consumption rate (SC, percentage of the generation that is self-consumed) and the self-sufficiency rate (SS, percentage of the demand supplied by the own generation) were 59.87% and 33.89%, respectively. Figure 2b shows the power interchanged between the whole VPP and the power grid in this initial situation. It is obvious that maximum demand for power occurs when the EVs are charging (the well-known rebound effect produced by time-of-use tariffs), followed by high-demand hours in the late evening, as is usual in household consumption profiles. Meanwhile, the power injected into the grid reaches its highest values at midday, when the PV plant’s production is at its maximum.
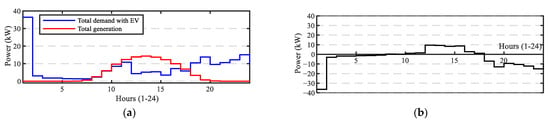
Figure 2.
(a) Initial accumulated demand and generation, excluding the ESS; (b) Power interchange with the distribution grid in the initial situation.
The power profiles of ESSs and EVs will be obtained as a result of the optimization algorithm described in Section 3.
Besides technical data, economic data regarding the purchase or sale of electrical energy are vital to performing an EMS. The reduction in the electricity bill or the increase in profits derived from surplus energy sales constitutes the most important motivation for consumers, prosumers, producers, and other stakeholders to participate in aggregating initiatives. The price of the purchased/sold energy varies with the kind of stakeholders and local regulations in the country. In liberalized market scenarios, prices vary according to a bidding process depending on offer/demand in each scheduled period. In contrast, the commercial offers of retailers to small consumers can be flat or time-of-use tariffs. In any case, the cost of the bought electric energy is usually higher than the price of the sold energy because consumers pay for other power system costs in addition to the energy consumed. In Spain, based on the Iberian electricity market MIBEL coordinated by Spain and Portugal, there are regulated prices that follow the day-ahead market prices for small prosumers who prefer this option to retailers’ offers. These prices are different for purchased energy and sold energy, and the difference is based on general power system costs. Figure 3 shows a daily profile for these prices in Spain, published in the information system of the Spanish System Operator [41] for 1 February. The prices in Figure 3 have been used in the objective functions in this work. A daily bill of EUR 23.47/day for the whole VPP is obtained as the base case when prices in Figure 3 are applied to power values in Figure 2b.
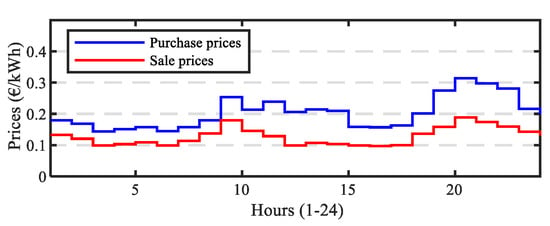
Figure 3.
Prices of energy for prosumers according to the Spanish-regulated frame on 1 February (elaborated from [41]).
3. Optimal Day-Ahead Schedule of Storage and Electric Vehicles
Optimization of the ESS power and the EV power during the time they were connected to the grid was performed using a GA with different objective functions and constraints. An hourly time resolution was applied, as was usual when prices were considered [7,9].
The GA was inspired by evolutionary theories to find a solution for an optimization problem emulating a natural selection process. A random initial population was created as a set of possible solutions (chromosomes). Then, the GA sequentially created new populations by selecting the best individuals according to their fitness values after crossover and mutation operations. After a sufficient number of generations, the GA aimed to find a solution for the optimization problem. The GA was considered to provide powerful search characteristics for large, complex search spaces without requiring full knowledge of the problem domain [20]. Its flexibility and ability to find near-optimal solutions encouraged its use in EMS optimization procedures [28]. Using crossover and mutation operations, a parallel search was performed by GA from the initial population. Thus, it has the ability to avoid being trapped in local optimal solutions, unlike traditional methods that search from a single point. The augmented Lagrangian genetic algorithm constraint solver provided by Matlab® was used to handle constraints in this paper. Figure 4 presents a flow chart of the GA used.
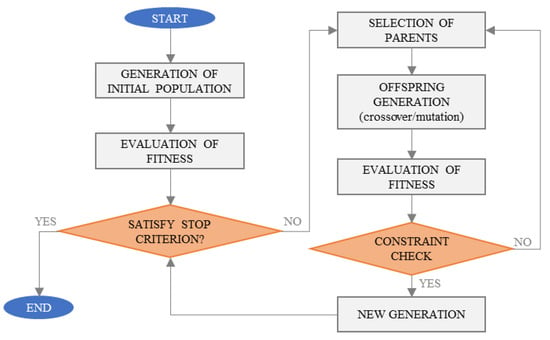
Figure 4.
Flow chart of the genetic algorithm.
The number of variables in the system was determined by the hourly power of the ESS and EVs. It was expressed as 24+nhEV, where nhEV represented the number of hours any EV was connected to the grid and available for charging. Only a time slot during the night was considered for EV scheduling. Other papers open the EV schedule to other time slots during the day [11]. However, this situation may not be realistic in residential environments, as users are usually at home during the night, and both energy prices and network tariffs are usually lower during these hours. Accordingly, it is difficult to motivate EV owners to plug in their EVs at home during the day to participate in VPP management.
The VPP power balance is defined in (1). Starting from (1), the objective functions are shown in (2) and (3).
Objective function f1 in (2) aims to minimize the power interchanged with the grid. It is useful to maximize SC and SS without considering prices, for example, in a TVPP devoted to supporting the distribution grid. A CVPP requires economic incentives for final users to be motivated to participate in the VPP. In this kind of VPP, objective function f2 in (3) is more appropriate, as it aims to minimize the VPP electricity bill. Constraints for the ESS are shown in (4)–(6).
where
The constraint in (4) delimits the allowed range of power of the ESS. The maximum power of the associated power converter PESSmax is considered, and both positive (charge) and negative (discharge) power values are allowed. Meanwhile, (5) delimits the allowed SoC range according to manufacturer recommendations, and (6) guarantees that the difference in SoC between the beginning and the end of the day is lower than 10%. Other works [8] propose equal values for these SoC values in order to complete a daily charge/discharge cycle. However, this constraint reduces the flexibility of the model. A maximum difference of 10% prevents the ESS from being completely charged or discharged at the beginning of the next day, with a certain degree of flexibility. The ESS SoC is calculated as in (7), considering both charge and discharge efficiency rates.
The constraints for EV power are shown in (8)–(10).
There is a time restriction for EVs: they can only be charged/discharged during the time slot in which they are connected to the grid and available for charging/discharging. During these hours, the maximum power is limited to that of individual chargers multiplied by the number of connected vehicles, as in (8). For the remaining hours, the power for the EVs is zero (9). The constraint in (10) guarantees that at the end of the time slot in which the EVs are connected to the grid, the whole energy amount necessary to fully charge all the EVs has been charged, i.e., the SoC for every EV must be 100%.
Finally, to provide support to the distribution grid, a constraint is also included for Pgrid to perform peak shaving as a means of grid congestion prevention (11).
4. Results and Discussion of the Optimization
Four cases have been studied to test the proposed energy management method. The first one intends to minimize the power interchanged with the grid in order to prevent distribution grid congestion. The second one is aligned with most papers in the literature; it aims to optimize the electricity bill. To combine economic and technical targets, the third case minimizes the electricity price subjected to grid congestion constraints via peak shaving. Finally, a multi-objective function optimization is performed in the fourth case. A maximum number of 500 generations and a tolerance of 1 × 10−12 have been programmed for the GA as the stop criterion. The default values suggested by Matlab® support have been selected for the remaining GA parameters.
The parameters used for constraints are the following (discussed in Section 2):
- PESSmax = 6 kW
- SoClo = 20%; SoChi = 100%
- SoCin = 50%
- ηch = ηdi = 0.95
- PEVmax = 7.4 kW
- nEV = 4
- nhEV = 8 (0–8 h)
- EEVtotal = 30 kWh
- Ppeak = 10 kW
- Case 1: Minimization of Power Interchanged with the Grid
This first case corresponds to a situation in which the energy management system is devoted to avoiding network congestion, although peak-shaving AS cannot be provided because limited peak power is not guaranteed. It can be compared to previous works in the literature that intend to minimize the peak-to-average rate. The objective function f1 in (2) and the constraints (4)–(6) and (8)–(10) are used.
- Case 2: Minimization of the Electricity Bill
This case only intends to minimize the electricity bill, and it is in line with the purpose of most works previously published in the literature, as can be inferred from the introduction section. Indeed, AS provision at the distribution level is not usually considered in previous works. The reason may be found in the lack of regulation of AS markets at this level, although it has been identified as a forthcoming challenge. In this case, the objective function f2 in (3) and constraints (4)–(6) and (8)–(10) are used.
- Case 3: Minimization of the Electricity Bill Subjected to Grid Congestion Constraints
This third case corresponds to a trade-off between economic and technical targets, which is what the authors propose as the best solution for the energy scheduling method designed. The same objective function and constraints as in Case 2 are used, and the peak-shaving constraint (11) is added in this case.
- Case 4: Multi-Objective Optimization
As a double target is pursued, a fourth case was studied for comparison, which combines both economic and technical targets in a multi-objective optimization process with a GA. The objective functions f1 (2) and f2 (3) and the constraints of Cases 1 and 2 are used. Figure 5 shows the Pareto front obtained in the process. Each point in the Pareto front represents one possible solution for the problem. The fitness value of both objective functions for each solution is depicted. The marked point of the Pareto front is considered a good trade-off solution, as it provides a low fitness value for both objective functions without prioritizing either of them.
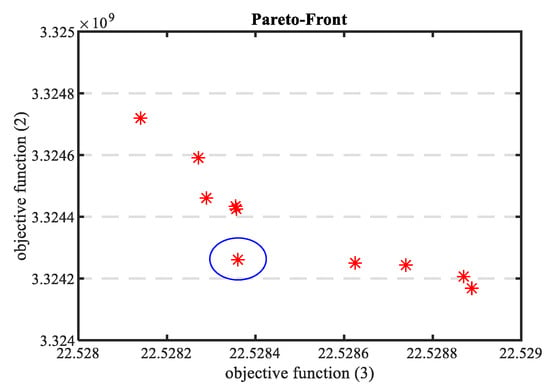
Figure 5.
Pareto front for multi-objective optimization.
Figure 6, Figure 7, Figure 8 and Figure 9 show the results obtained by the GA in each of the described cases.
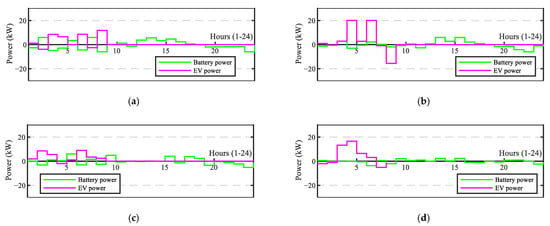
Figure 6.
Power scheduled for the ESS and EVs: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
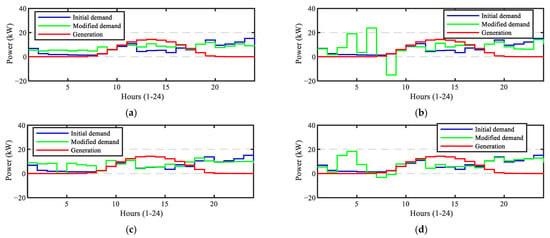
Figure 7.
Accumulated demand and generation after scheduling: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
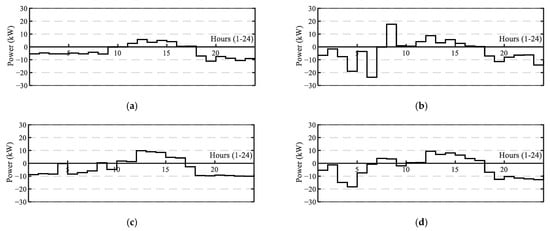
Figure 8.
Power interchange with the distribution grid: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
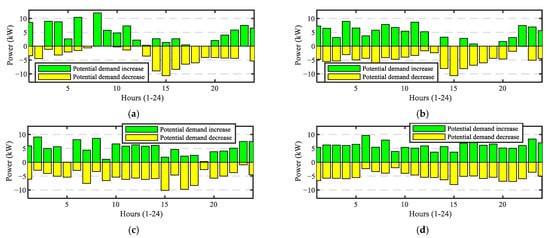
Figure 9.
Potential increase/decrease in ESS power for ASs: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
Figure 6 depicts the scheduled power values for the ESS and EVs at each hour. In these curves, positive values of ESS and EV power correspond to charging, and negative values correspond to discharging. EVs are charging or discharging during the available time slot (0–8 h). In Case 1 (Figure 6a), the ESS is mainly devoted to counteracting the impact of EVs on the power interchanged with the grid during this time slot. During the rest of the day, the ESS shifts energy demanded in the evening to midday hours for a higher self-consumption rate. Figure 6b verifies that the EV charging/discharging at each night hour is sharper in Case 2 than in Case 1, adapting to different prices at each hour without peak-shaving purposes. The operation of the EV chargers is smoother again in Case 3 (Figure 6c), while the participation of the ESS in management is quite lower in Case 4 (Figure 6d).
Figure 7 shows the modified demand along with the power produced and demanded by the households (without EVs). The modified demand includes the initial demand, the ESS, and the EVs. In Case 1 (Figure 7a), the best values of SC (79.10%) and SS (53.30%) are reached. Lower values are reached in Case 2 (SC is 58.16% and SS is 39.19%), Case 3 (SC is 62.88% and SS is 42.36%, which outperform those obtained in Case 2), and Case 4 (SC is 57.75% and SS is 38.91%).
Figure 8 depicts the power interchanged with the grid. The high peak charging power initially present at 0 h has been mitigated in every case because charging/discharging of EVs have been distributed among eight valley hours. The rest of the day, power values are also softer compared to the base case. The bill after scheduling in Case 1 is EUR 20.58/day (a reduction of 12.3% is obtained compared to the base case). Observation of Case 1 leads to the conclusion that, although no economic factors have been considered for energy scheduling, savings are obtained in the electricity bill as a result. Indeed, the energy interchanged with the grid is minimized in this first case—both the sold and the purchased energy (Figure 8a). As the net balance in this case study results in net energy bought for the grid, the higher prices for purchased energy explain the reduction in the final bill: the bought energy decreases. In Case 2, the operation of the ESS is devoted to avoiding buying high amounts of energy at the highest price hours. Therefore, the interchange of power with the grid has higher peaks than in Case 1 (compare Figure 8b to Figure 8a). The highest peaks for bought energy coincide with low-priced hours (the middle of the night and the last hour). It is interesting to highlight that during the last hour of the day, the ESS has not provided most of the energy demanded by storing more energy produced by the PV during the midday. This is because the price for the purchased energy at the end of the day is similar to that of the midday hours, whereas extra PV production can be sold at these central hours. In Case 2, the final bill is EUR 19.95/day (a reduction of 15% from the base case). This bill is the lowest among the studied cases and is detrimental to SC and SS rates. Both the EVs and ESS are coordinated in Case 3 to avoid power peaks higher than 10 kW while economic optimization is performed. Despite this constraint being very strict, assuming that the VPP encompasses eight dwellings and four EVs with a limited PV plant size and ESS, Figure 8c proves that it has been fulfilled. In this case, the obtained SC and SS outperform those obtained in Case 2, which is detrimental to the final bill (EUR 21.94/day), which is higher than before—as was expected—because of the grid constraint. The difference between bill values in Cases 2 and 3 demonstrates the need for economic compensation from the distribution system operator (DSO) due to the AS provision. Observation of Figure 8d leads to the conclusion that the multi-objective optimization process reduces the contribution of the ESS to the whole purpose. Consequently, neither the peak values of interchanged power nor the final bill (EUR 22.53/day) outperform those obtained with a single-objective optimization.
Figure 9 shows the potential for increasing or decreasing the ESS power at each hour. It is labeled as a demand because positive values of ESS power correspond to charging power values. These values are constrained by the maximum charging/discharging power PESSmax and the distance to the extreme values of the SoC. As an ESS converter is a fully controllable bidirectional device, the power range at each hour can be used to face uncertainty in generation or demand forecasting and to provide other ASs to the distribution grid. For example, the DSO might send a power setpoint to the VPP to avoid network congestion in high-demand hours or to smooth power, with the aim of better exploiting the grid capacity and managing grid losses. In Case 1, the ESS is well exploited for the optimization process; thus, low or even no power is available for ASs during some hours (Figure 9a). In Case 2, the potential ranges of ESS power increase/decrease (Figure 9b) suffer from high variability, as in Case 1, although they outperform those of Case 1 during the morning. The use of the ESS in Case 3 is not as strong as in other cases. As a result, the potential increase/decrease in ESS power for providing other ASs is generally higher in this case than in previous ones (Figure 9c). Therefore, this technique is the only one capable of providing peak shaving AS, and it is the best suited for other AS provisions among the techniques studied. Finally, the higher range of power change observed in Case 4 (Figure 9d) is due to the lower participation of the ESS in the optimization process.
These results entail a novel contribution to the research topic. Moreover, as discussed in the introduction, there is a lack of previous works that economically optimize the daily energy scheduling of VPPs or energy communities at a residential level, which involve EVs as another EMS resource and provide ASs to the grid as well.
Table 2 presents a comparison of the different results for the four cases studied (the best results are bolded) and the base case. Although the highest cost discount is reached in Case 2 (minimum cost), peak power is not guaranteed. On the other hand, although Case 1 provides a high-cost saving as well as the best SC and SS rates, if peak shaving is committed as an AS to prevent network congestion, only Case 3 guarantees its commitment, which is detrimental to the final bill and should be compensated via AS payment.

Table 2.
Comparative analysis of results.
For the sake of comparison, constrained non-linear programming (NLP) has also been used with the same objective function and constraints as in Case 3. It is well known that classic gradient-based optimization methods, often used in the literature for problems similar to the one proposed here, are liable to fall into local minima. The obtained result can be summarized in SC and SS values of 59.02% and 39.77%, respectively, and an electricity bill of EUR 22.15/day, while the peak power is restricted to 10 kW. Figure 10 compares the obtained results with the cases in Table 2. In this figure, the best option proposed (Case 3) is highlighted in blue. Light grey represents the base case (without either ESS or optimization), dark grey is related to NLP, and other colors were selected for the remaining cases. NLP provides worse results than Case 3 in terms of both SC and SS, as well as in terms of savings. This result confirms the initial assumption that the GA outperforms traditional optimization methods in this kind of problem, with a large search space and scarce initial information about the optimal solution.
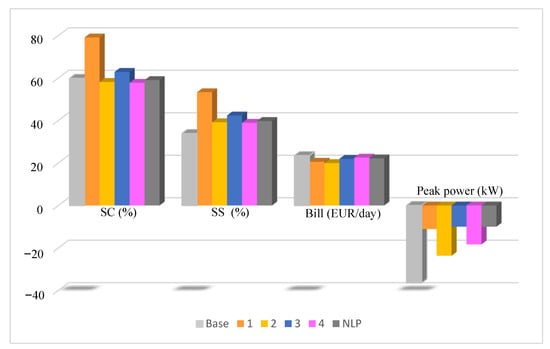
Figure 10.
Comparative results of different cases.
5. Conclusions
This paper proposes a GA-based optimization method to manage a residential VPP with the double objective of reducing the electricity cost and providing ASs related to the prevention of network congestion. The charging/discharging power profiles of an ESS (during the whole day) and the available EVs (during several night hours) were obtained as the result of the optimization process. Different objective functions and constraints were tested. The best result is obtained when a single-objective function based on purchase/sale prices is minimized and a peak-shaving constraint is added to regular constraints related to the different energy resources. This technique guarantees a limited peak power interchanged with the distribution grid, and it minimizes the electricity bill of the whole VPP subject to network constraints—outperforming even a multi-objective optimization technique and traditional deterministic optimization methods as well.
The proposed daily energy scheduling procedure entails a novel contribution to the research topic. As mentioned in the introduction, a research gap has been found in the literature regarding the use of EVs as an EMS resource along with other ESSs to optimize energy costs and provide ASs at a residential level.
According to the obtained results, the GA proved to have the proper performance to manage, in a coordinated way, both ESSs and EV charging/discharging in residential VPPs, even with a reduced number of available EVs. In addition, the proposed technique guarantees the capability of the VPP to provide ASs to the distribution grid, even with limited energy resources. This method may be used for any other VPP with different generation and/or demand profiles, only adapting the initial population range according to the managed data. Due to the flexibility of the GA and its ability to find optimal solutions across wide ranges of values, new proposals, such as adding a DSM purpose to the management systems, may be studied as a future extension of this work. Additional future research directions may be:
- Optimally sizing energy resources (PV power plants, ESSs, and EV clusters) to maximize economic advantages
- Considering uncertainties regarding PV generation and EV users’ habits within the optimization model
- Updating the energy scheduling during the day as far as information and estimations are better known
- Adapting constraints to the AS market at the distribution level, as far as they are developed in the regulations of different countries
- Designing a framework of peer-to-peer or aggregator-to-stakeholder contracts to optimally allocate economic benefits and savings
- Proposing similar management procedures for industrial/commercial VPPs, adapting assumptions and constraints
- Coordinating the daily energy scheduling of different VPPs to increase the capability of the aggregated resources to participate in electricity markets
- Exploring other heuristic and meta-heuristic optimization tools
Author Contributions
Conceptualization, E.G.-R. and E.R.-C.; methodology, E.G.-R.; software, C.R.-C.; validation, E.R.-C., C.R.-C. and F.B.-G.; formal analysis, E.G.-R. and A.-A.A.; resources, M.-I.M.-M.; writing—original draft preparation, E.G.-R.; writing—review and editing, A.-A.A.; supervision, F.B.-G. and M.-I.M.-M.; project administration, E.R.-C.; funding acquisition, E.R.-C. and C.R.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This project has received funding from the European Union’s Horizon 2020 research and innovation program under Marie Skłodowska-Curie grant agreement No. 955614. The work was also co-supported by the Junta de Extremadura, with the project under grant IB20165.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.esios.ree.es/en.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, the collection, analyses, and interpretation of data, the writing of the manuscript, or the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ACRONYMS | |
| CVPP | Commercial virtual power plant |
| DSM | Demand side management |
| DSO | Distribution system operator |
| EMS | Energy management system |
| ESS | Energy storage system |
| EV | Electric vehicle |
| GA | Genetic algorithm |
| GSA | Gravitational search algorithm |
| GWO | Grey wolf optimization |
| IPS | Inclined planes system |
| MILP | Mixed integer linear programming |
| MOPSO | Multi-objective particle swarm optimization |
| MPC | Model predictive control |
| NLP | Non-linear programming |
| OPF | Optimal power flow |
| PSO | Particle swarm optimization |
| PV | Photovoltaic |
| SC | Self-consumption rate |
| SS | Self-sufficiency rate |
| TVPP | Technical virtual power plant |
| VPP | Virtual power plant |
| V2G | Vehicle-to-grid |
| VARIABLES | |
| Cnom | Nominal capacity of ESS, kWh |
| EEVtotal | Energy required for full EV charge, kWh |
| IESSch(h) | Binary index, 1 when PESS(h) > 0 |
| IESSdi(h) | Binary index, 1 when PESS(h) ≤ 0 |
| Ipur(h) | Binary index, 1 when Pgrid(h) ≤ 0 |
| Isel(h) | Binary index, 1 when Pgrid(h) > 0 |
| hEV | Hour at which any EV is grid-connected |
| nEV(h) | Number of EVs connected at hour h |
| nhEV | Number of hours with any EV connected |
| PESS(h) | ESS power at hour h (positive when charging), kW |
| PESSmax | Maximum ESS power, kW |
| PEV(h) | EV power at hour h (positive when charging), kW |
| PEVmax | Maximum power of an individual EV charger, kW |
| Pgrid(h) | Power interchanged with the grid at hour h (positive when injecting), kW |
| PLD(h) | Load demand power at hour h, kW |
| Ppeak | Peak value allowed for peak shaving, kW |
| PPV(h) | PV generation power at hour h, kW |
| ppur(h) | Price for purchased energy at hour h, EUR/kWh |
| psel(h) | Price for sold energy at hour h, EUR/kWh |
| SoC(h) | State of charge of ESS at hour h, % |
| SoCin | Initial value of SoC at hour h = 0, % |
| SoClo | Lower value of SoC recommended by manufacturer, % |
| SoCup | Upper value of SoC recommended by manufacturer, % |
| ηch | Charging efficiency of ESS, pu |
| ηdi | Discharging efficiency of ESS, pu |
References
- Nikonowicz, L.; Milewski, J. Virtual power plants-general review: Structure, application and optimization. J. Power Technol. 2012, 2, 135–149. [Google Scholar]
- Zhang, W.; He, C.; Qian, H.; Lin, Z.; Li, Y.; Zhao, X.; Shu, C. Virtual Power Plant Integration with Smart Grids: A Review. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; pp. 4755–4759. [Google Scholar]
- Bhuiyan, E.A.; Hossain, M.Z.; Muyeen, S.M.; Fahim, S.R.; Sarker, S.K.; Das, S.K. Towards next generation virtual power plant: Technology review and frameworks. Renew. Sustain. Energy Rev. 2021, 150, 111358. [Google Scholar] [CrossRef]
- Borisoot, K.; Liemthong, R.; Srithapon, C.; Chatthaworn, R. Optimal Energy Management for Virtual Power Plant Considering Operation and Degradation Costs of Energy Storage System and Generators. Energies 2023, 16, 2862. [Google Scholar] [CrossRef]
- Liu, J.; Hu, H.; Yu, S.S.; Trinh, H. Virtual Power Plant with Renewable Energy Sources and Energy Storage Systems for Sustainable Power Grid-Formation, Control Techniques and Demand Response. Energies 2023, 16, 3705. [Google Scholar] [CrossRef]
- Ahmadian, A.; Ponnambalam, K.; Almansoori, A.; Elkamel, A. Optimal Management of a Virtual Power Plant Consisting of Renewable Energy Resources and Electric Vehicles Using Mixed-Integer Linear Programming and Deep Learning. Energies 2023, 16, 1000. [Google Scholar] [CrossRef]
- Jo, H.-C.; Byeon, G.; Kim, J.-Y.; Kim, S.-K. Optimal scheduling for a zero net energy community microgrid with customer-owned energy storage systems. IEEE Trans. Power Syst. 2021, 36, 2273–2280. [Google Scholar] [CrossRef]
- Arkhangelski, J.; Abdou-Tankari, M.; Lefebvre, G. Day-Ahead optimal power flow for efficient energy management of urban microgrid. IEEE Trans. Ind. Applicat. 2021, 57, 1285–1293. [Google Scholar] [CrossRef]
- Bahloul, M.; Breathnach, L.; Cotter, J.; Daoud, M.; Saif, A.; Khadem, S. Role of aggregator in coordinating residential virtual power plant in “StoreNet”: A pilot project case study. IEEE Trans. Sustain. Energy 2022, 13, 2148–2158. [Google Scholar] [CrossRef]
- Rocha, R.; Silva, R.; Mello, J.; Faria, S.; Retorta, F.; Gouveia, C.; Villar, J. A three-stage model to manage energy communities, share benefits and provide local grid services. Energies 2023, 16, 1143. [Google Scholar] [CrossRef]
- Gough, M.; Santos, S.F.; Lotfi, M.; Javadi, M.S.; Osório, G.J.; Ashraf, P.; Castro, R.; Catalão, J.P. Operation of a technical virtual power plant considering diverse distributed energy resources. IEEE Trans. Ind. Applicat. 2022, 58, 2547–2558. [Google Scholar] [CrossRef]
- Rehman, A.U.; Wadud, Z.; Elavarasan, R.M.; Hafeez, G.; Khan, I.; Shafiq, Z.; Alhelou, H.H. An optimal power usage scheduling in smart grid integrated with renewable energy sources for energy management. IEEE Access 2021, 9, 84619–84638. [Google Scholar] [CrossRef]
- Iria, J.; Scott, P.; Attarha, A. Network-constrained bidding optimization strategy for aggregators of prosumers. Energy 2020, 207, 11826. [Google Scholar] [CrossRef]
- Dehghanniri, M.F.; Golkar, M.A.; Olanlari, F.G. Power exchanging of a VPP with its neighboring VPPs and participating in day-ahead and spinning reserve markets. In Proceedings of the 2022 30th International Conference on Electrical Engineering (ICEE), Tehran, Iran, 17–19 May 2022; pp. 336–340. [Google Scholar]
- Seal, S.; Boulet, B.; Dehkordi, V.R.; Bouffard, F.; Joos, G. Centralized MPC for Home Energy Management with EV as Mobile Energy Storage Unit. IEEE Trans. Sustain. Energy 2023, 14, 1425–1435. [Google Scholar] [CrossRef]
- Terada, L.Z.; López, J.C.; Guzmán, C.P.; Rider, M.J.; Da Silva, L.C.P. An IoT-based smart charging algorithm considering local distributed energy resources and V2G technology. In Proceedings of the 2022 International Conference on Smart Energy Systems and Technologies (SEST), Eindhoven, The Netherlands, 5–7 September 2022; pp. 1–6. [Google Scholar]
- Mohammad, A.; Zuhaib, M.; Ashraf, I. An optimal home energy management system with integration of renewable energy and energy storage with home to grid capability. Int. J. Energy Res. 2022, 46, 8352–8366. [Google Scholar] [CrossRef]
- Kryonidis, G.C.; Kontis, E.O.; Papadopoulos, T.A.; Pippi, K.D.; Nousdilis, A.I.; Barzegkar-Ntovom, G.A.; Boubaris, A.D.; Papanikolaou, N.P. Ancillary services in active distribution networks: A review of technological trends from operational and online analysis perspective. Renew. Sustain. Energy Rev. 2021, 147, 111198. [Google Scholar] [CrossRef]
- Vijay, A.; Afzal, W.; Tariq, M.; Mustafa, A.; Shahzad, A. Review of power generation optimization algorithms: Challenges and its applications. In Proceedings of the 2022 International Conference on Augmented Intelligence and Sustainable Systems (ICAISS), Trichy, India, 23–25 August 2022; pp. 1391–1397. [Google Scholar]
- Mataifa, H.; Krishnamurthy, S.; Kriger, C. Volt/VAR optimization: A survey of classical and heuristic optimization methods. IEEE Access 2022, 10, 13379–13399. [Google Scholar] [CrossRef]
- Mahdavi, M.; Alhelou, H.H.; Hatziargyriou, N.D.; Jurado, F. Reconfiguration of electric power distribution systems: Comprehensive review and classification. IEEE Access 2021, 9, 118502–118527. [Google Scholar] [CrossRef]
- Furse, C.M.; Kafal, M.; Razzaghi, R.; Shin, Y.-J. Fault diagnosis for electrical systems and power networks: A review. IEEE Sens. J. 2021, 21, 888–906. [Google Scholar] [CrossRef]
- Sharma, R.; Sharma, K.K. Review of economic load dispatch problems by intelligence based optimization. In Proceedings of the 2022 2nd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), Greater Noida, India, 28–29 April 2022; pp. 1646–1650. [Google Scholar]
- Rahman, Y.A.; Manjang, S.; Ilham, A.A. An empirical metaheuristic assessment for solving of multi-type distributed generation allocation problem. In Proceedings of the 2018 International Seminar on Research of Information Technology and Intelligent Systems (ISRITI), Yogyakarta, Indonesia, 21–22 November 2018; pp. 699–702. [Google Scholar]
- Latif, A.; Paul, M.; Das, D.C.; Hussain, S.M.S.; Ustun, T.S. Price Based Demand Response for Optimal Frequency Stabilization in ORC Solar Thermal Based Isolated Hybrid Microgrid under Salp Swarm Technique. Electronics 2020, 9, 2209. [Google Scholar] [CrossRef]
- Qayyum, N.; Amin, A.; Jamil, U.; Mahmood, A. Optimization techniques for home energy management: A review. In Proceedings of the 2019 2nd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 30–31 January 2019; pp. 1–7. [Google Scholar]
- Tsioumas, E.; Jabbour, N.; Koseoglou, M.; Papagiannis, D.; Mademlis, C. Enhanced sizing methodology for the renewable energy sources and the battery storage system in a nearly zero energy building. IEEE Trans. Power Electron. 2021, 36, 10142–10156. [Google Scholar] [CrossRef]
- Celik, B.; Roche, R.; Bouquain, D.; Miraoui, A. Decentralized neighborhood energy management with coordinated smart home energy sharing. IEEE Trans. Smart Grid 2018, 9, 6387–6397. [Google Scholar] [CrossRef]
- Lin, C.-C.; Deng, D.-J.; Kuo, C.-C.; Liang, Y.-L. Optimal charging control of energy storage and electric vehicle of an individual in the internet of energy with energy trading. IEEE Trans. Ind. Inform. 2018, 14, 2570–2578. [Google Scholar] [CrossRef]
- Tabrizi, A.R. Energy management system optimization for grid connected microgrids in presence of energy storage. In Proceedings of the 2022 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 9–11 June 2022; pp. 1–7. [Google Scholar]
- Deng, Y.; Zhang, Y.; Luo, F.; Ranzi, G. Many-objective HEMS based on multi-scale occupant satisfaction modelling and second-life BESS utilization. IEEE Trans. Sustain. Energy 2022, 13, 934–947. [Google Scholar] [CrossRef]
- Abdullah-Al-Nahid, S.; Ahmed Khan, T.; Taseen, M.A.; Jamal, T.; Aziz, T. A novel consumer-friendly electric vehicle charging scheme with vehicle to grid provision supported by genetic algorithm based optimization. J. Energy Storage 2022, 50, 104655. [Google Scholar] [CrossRef]
- Ruiz-Cortes, M.; González-Romera, E.; Amaral-Lopes, R.; Romero-Cadaval, E.; Martins, J.; Milanes-Montero, M.I.; Barrero-Gonzalez, F. Optimal charge/discharge scheduling of batteries in microgrids of prosumers. IEEE Trans. Energy Convers. 2019, 34, 468–477. [Google Scholar] [CrossRef]
- González-Romera, E.; Ruiz-Cortés, M.; Milanés-Montero, M.I.; Barrero-González, F.; Romero-Cadaval, E.; Lopes, R.A.; Martins, J. Advantages of minimizing energy exchange instead of energy cost in prosumer microgrids. Energies 2019, 12, 719. [Google Scholar] [CrossRef]
- Taherkhani, M.; Safabakhsh, R. A novel stability-based adaptive inertia weight for particle swarm optimization. Appl. Soft Comput. 2016, 38, 281–295. [Google Scholar] [CrossRef]
- Li, G.; Wang, Y.; Yu, Y.; Zhu, D.; Chen, H. Ship Energy Management Strategy Based on Improved Gravitational Search Algorithm. In Proceedings of the 2022 5th International Conference on Intelligent Autonomous Systems (ICoIAS), Dalian, China, 23–25 September 2022; pp. 273–279. [Google Scholar]
- Marszal-Pomianowska, A.; Heiselberg, P.; Larsen, O.K. Household electricity demand profiles—A high-resolution load model to facilitate modelling of energy flexible buildings. Energy 2016, 103, 487–501. [Google Scholar] [CrossRef]
- Roldán Fernández, J.M.; Burgos Payán, M.; Riquelme Santos, J.M. Profitability of household photovoltaic self-consumption in Spain. J. Clean. Prod. 2021, 279, 123439. [Google Scholar] [CrossRef]
- Gallego-Castillo, C.; Heleno, M.; Victoria, M. Self-consumption for energy communities in Spain: A regional analysis under the new legal framework. Energy Policy 2021, 150, 112144. [Google Scholar] [CrossRef]
- BOE no. 306, 22 Dec. 2022. Resolución de 15 de Diciembre de 2022, de la Comisión Nacional de los Mercados y la Competencia, por la Que se Establecen los Valores de los Peajes de Acceso a las Redes de Transporte y Distribución de Electricidad de Aplicación a Partir del 1 de Enero de 2023 (Resolution of 15 Dec. 2022, of CNMC, that Approves Transmission and Distribution Tariffs, from 1 Jan. 2023). Available online: https://www.boe.es/diario_boe/txt.php?id=BOE-A-2022-21799 (accessed on 15 June 2023).
- REE-ESIOS, 1 February 2023. Market and Prices. Available online: https://www.esios.ree.es/en (accessed on 10 February 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).