Solid-State-LiDAR-Inertial-Visual Odometry and Mapping via Quadratic Motion Model and Reflectivity Information
Abstract
:1. Introduction
- In the SSLIO subsystem, in-frame motion compensation is performed by using a quadratic motion model (i.e., a variable angular velocity and variable linear acceleration model), and the experimental results prove that this method can effectively handle drastic changes in acceleration and angular velocity.
- A weight function that ensures geometric and reflectivity consistency is designed for each LiDAR feature point when calculating the LiDAR measurement residuals in the ESIKF framework of the SSLIO subsystem. All extrinsic parameters (e.g., extrinsic parameters between camera and IMU) are not estimated online, saving system computational resources. In addition, the colorful point cloud maps obtained by our algorithm, which show the texture of the environment, can be further applied to VR, game development, and other industries.
- A variety of indoor and outdoor field experiments were conducted using a crawler robot (see Figure 1) to validate the robustness and accuracy of the system. Some field experiment results obtained are shown in Figure 2; regarding the roads surrounding the buildings, the algorithm proposed by us shows high accuracy in mapping, so it can meet the requirements of the navigation tasks of mobile robots.
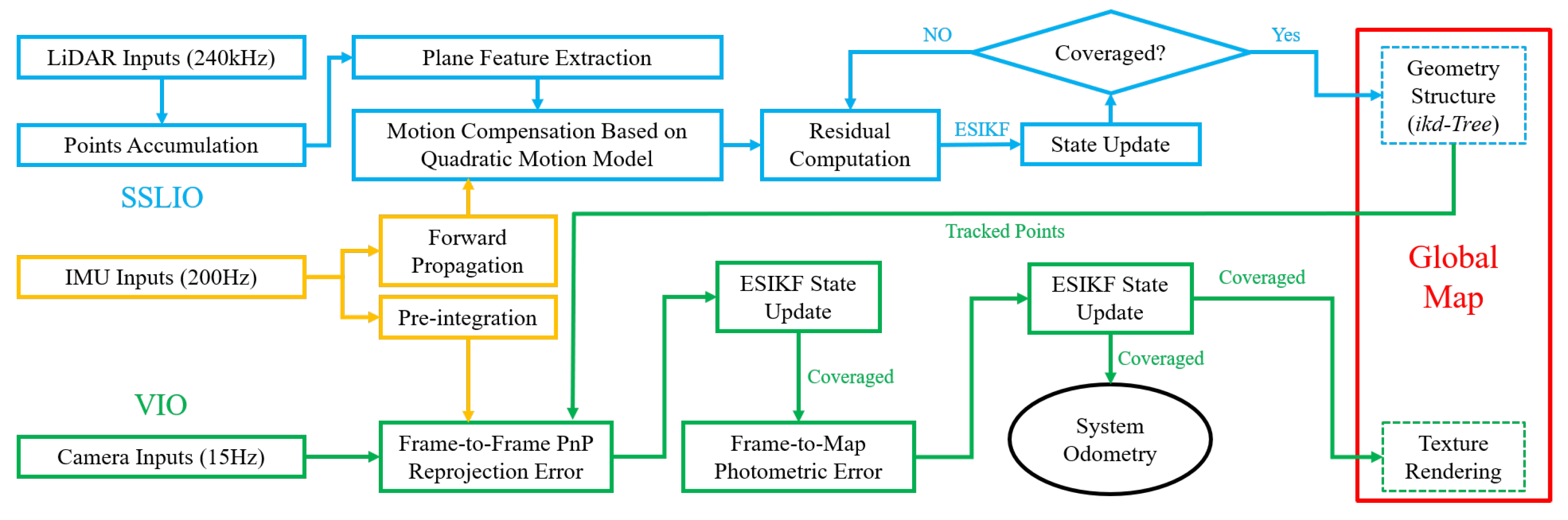
2. Framework Overview
2.1. System Pipeline
2.2. Nomenclature and Full State Vector
2.3. Extrinsic Calibration between Sensors
3. Solid-State-LiDAR-Inertial Odometry Subsystem
3.1. IMU State Transition Model
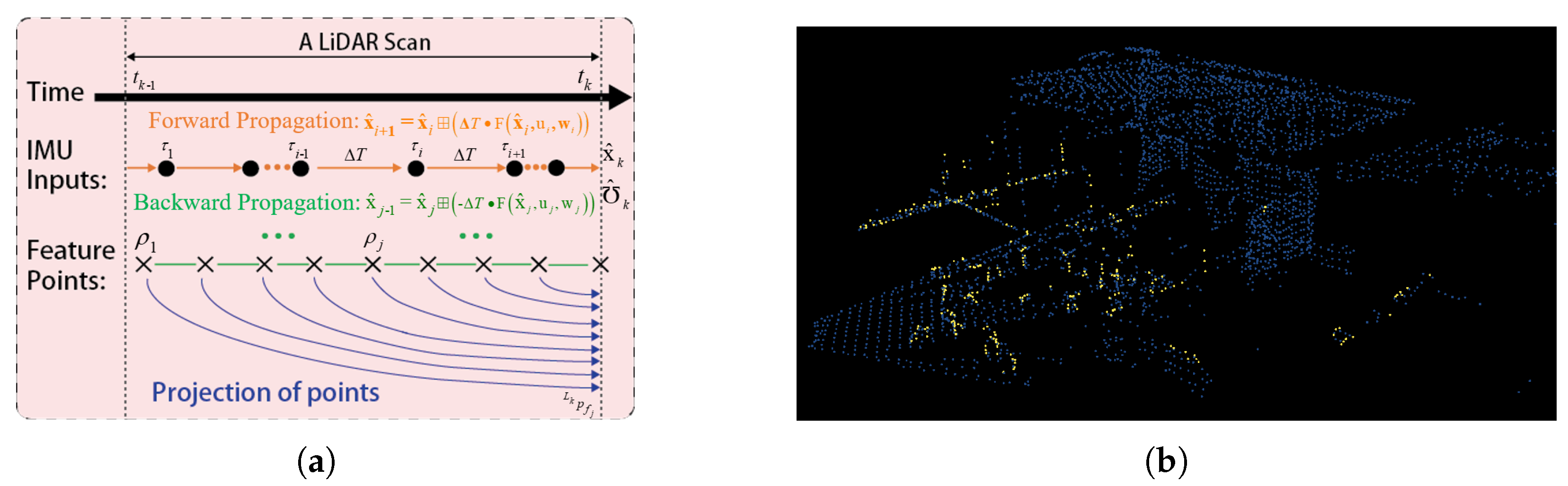
3.2. Preprocessing of Raw LiDAR Points and Forward Propagation
3.3. Motion Distortion Compensation Based on the Quadratic Motion Model
3.4. Point-to-Plane Residual Computation
3.5. ESIKF Update
4. Field Experiments and Evaluation Results
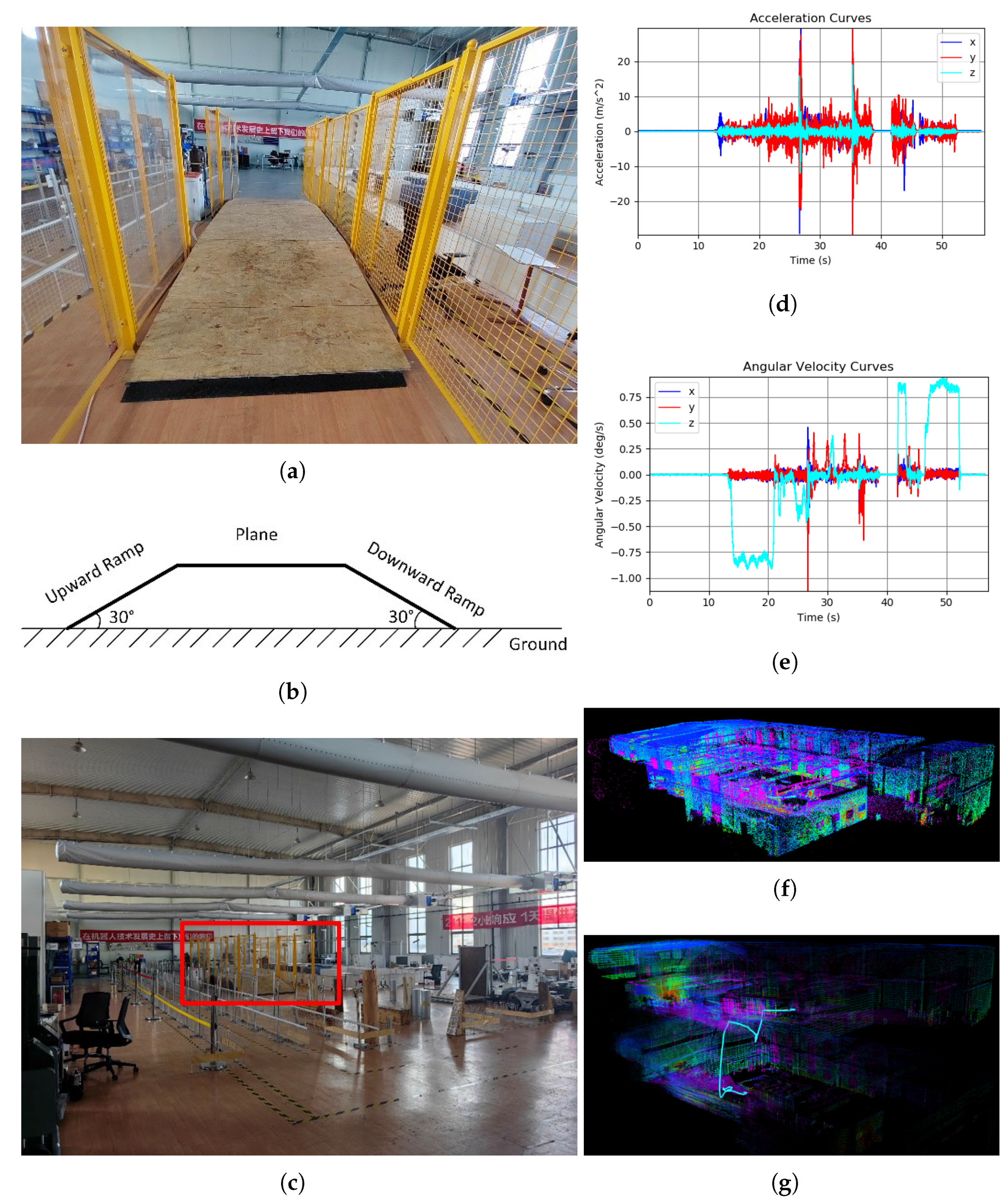
4.1. Experimental Platform
4.2. Extrinsic Calibration between Camera and IMU
4.3. Experiment-1: Experimental Verification of the Validity of Quadratic Motion Model and Weight Function
4.3.1. Experiment-1.1: Public Dataset Experiment
4.3.2. Experiment-1.2: Fast Crossing of the Steep Ramp Experiment Test
4.3.3. Experiment-1.3: Validation Experiment on the Validity of Weighting Function
4.4. Experiment-2: Quantitative Evaluation of Localization Accuracy Using GNSS RTK
4.5. Experiment-3: Outdoor Large-Scale Challenging Factory Environment Mapping
4.6. Run-Time Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SLAM | Simultaneous localization and mapping |
| ESIKF | Error-state iterated Kalman filter |
| SSLIO | Solid-state-LiDAR-inertial odometry |
| VIO | Visual-inertial odometry |
References
- Chen, N.; Kong, F.; Xu, W.; Cai, Y.; Li, H.; He, D.; Qin, Y.; Zhang, F. A self-rotating, single-actuated UAV with extended sensor field of view for autonomous navigation. Sci. Robot. 2023, 8, eade4538. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Wang, Y.; Chen, H.; Liu, Y. EIL-SLAM: Depth-enhanced edge-based infrared-LiDAR SLAM. J. Field Robot. 2022, 39, 117–130. [Google Scholar] [CrossRef]
- Wang, J.; Chen, F.; Huang, Y.; McConnell, J.; Shan, T.; Englot, B. Virtual Maps for Autonomous Exploration of Cluttered Underwater Environments. IEEE J. Ocean. Eng. 2022, 47, 916–935. [Google Scholar] [CrossRef]
- Sousa, R.B.; Sobreira, H.M.; Moreira, A.P. A systematic literature review on long-term localization and mapping for mobile robots. J. Field Robot. 2023, 40, 1245–1322. [Google Scholar] [CrossRef]
- Chen, W.; Zhou, C.; Shang, G.; Wang, X.; Li, Z.; Xu, C.; Hu, K. SLAM Overview: From Single Sensor to Heterogeneous Fusion. Remote Sens. 2022, 14, 6033. [Google Scholar] [CrossRef]
- Elhashash, M.; Albanwan, H.; Qin, R. A Review of Mobile Mapping Systems: From Sensors to Applications. Sensors 2022, 22, 4262. [Google Scholar] [CrossRef] [PubMed]
- Lopac, N.; Jurdana, I.; Brnelić, A.; Krljan, T. Application of Laser Systems for Detection and Ranging in the Modern Road Transportation and Maritime Sector. Sensors 2022, 22, 5946. [Google Scholar] [CrossRef]
- Robosense Laser Beam Solid-State Lidar Priced At 1898. Available online: https://lidarnews.com/ (accessed on 15 June 2023).
- Van Nam, D.; Gon-Woo, K. Solid-State LiDAR based-SLAM: A Concise Review and Application. In Proceedings of the IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju Island, Republic of Korea, 17–20 January 2021. [Google Scholar]
- Lin, J.; Zhang, F. Loam_ livox: A fast, robust, high-precision LiDAR odometry and mapping package for LiDARs of small FoV. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–15 June 2020. [Google Scholar]
- Yuan, C.; Xu, W.; Liu, X.; Hong, X.; Zhang, F. Efficient and Probabilistic Adaptive Voxel Mapping for Accurate Online LiDAR Odometry. IEEE Robot. Autom. Lett. 2022, 7, 8518–8525. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Xie, L.H. Lightweight 3-D Localization and Mapping for Solid-State LiDAR. IEEE Robot. Autom. Lett. 2021, 6, 1801–1807. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, F. FAST-LIO: A Fast, Robust LiDAR-Inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter. IEEE Robot. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- Xu, W.; Cai, Y.; He, D.; Lin, J.; Zhang, F. FAST-LIO2: Fast Direct LiDAR-Inertial Odometry. IEEE Trans. Robot. 2022, 38, 2053–2073. [Google Scholar] [CrossRef]
- Cai, Y.; Xu, W.; Zhang, F. Ikd-tree: An incremental kd tree for robotic applications. arXiv 2021, arXiv:2102.10808. [Google Scholar]
- He, D.; Xu, W.; Chen, N.; Kong, F.; Yuan, C.; Zhang, F. Point-LIO: Robust High-Bandwidth Light Detection and Ranging Inertial Odometry. Adv. Intell. Syst. 2023. [Google Scholar] [CrossRef]
- Bai, C.; Xiao, T.; Chen, Y.; Wang, H.; Zhang, F.; Gao, X. Faster-LIO: Lightweight Tightly Coupled Lidar-Inertial odometry Using Parallel Sparse Incremental Voxels. IEEE Robot. Autom. Lett. 2022, 7, 4861–4868. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the 10th Robotics: Science and Systems, RSS 2014, Berkeley, CA, USA, 12–16 July 2014. [Google Scholar]
- Li, K.L.; Li, M.; Hanebeck, U.D. Towards High-Performance Solid-State-LiDAR-Inertial Odometry and Mapping. IEEE Robot. Autom. Lett. 2021, 6, 5167–5174. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Xie, L. Intensity Scan Context: Coding Intensity and Geometry Relations for Loop Closure Detection. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–15 June 2020. [Google Scholar]
- Zhang, Y.; Tian, Y.; Wang, W.; Yang, G.; Li, Z.; Jing, F.; Tan, M. RI-LIO: Reflectivity Image Assisted Tightly-Coupled LiDAR-Inertial Odometry. IEEE Robot. Autom. Lett. 2023, 8, 1802–1809. [Google Scholar] [CrossRef]
- Liu, K.; Ma, H.; Wang, Z. A Tightly Coupled LiDAR-IMU Odometry through Iterated Point-Level Undistortion. arXiv 2022, arXiv:2209.12249. [Google Scholar]
- Ma, X.; Yao, X.; Ding, L.; Zhu, T.; Yang, G. Variable Motion Model for Lidar Motion Distortion Correction. In Proceedings of the Conference on AOPC—Optical Sensing and Imaging Technology, Beijing, China, 20–22 June 2021. [Google Scholar]
- Lin, J.; Zheng, C.; Xu, W.; Zhang, F. R (2) LIVE: A Robust, Real-Time, LiDAR-Inertial-Visual Tightly-Coupled State Estimator and Mapping. IEEE Robot. Autom. Lett. 2021, 6, 7469–7476. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, F. R3LIVE: A Robust, Real-time, RGB-colored, LiDAR-Inertial-Visual tightly-coupled state Estimation and mapping package. In Proceedings of the 39th IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 23–27 May 2022. [Google Scholar]
- Zheng, C.; Zhu, Q.; Xu, W.; Liu, X.; Guo, Q.; Zhang, F. FAST-LIVO: Fast and Tightly-coupled Sparse-Direct LiDAR-Inertial-Visual Odometry. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022. [Google Scholar]
- Shan, T.; Englot, B.; Ratti, C.; Rus, D. LVI-SAM: Tightly-coupled Lidar-Visual-Inertial Odometry via Smoothing and Mapping. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Qin, T.; Li, P.L.; Shen, S.J. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2020. [Google Scholar]
- Qin, T.; Shen, S.J. Online Temporal Calibration for Monocular Visual-Inertial Systems. In Proceedings of the 25th IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Yuan, C.; Liu, X.; Hong, X.; Zhang, F. Pixel-Level Extrinsic Self Calibration of High Resolution LiDAR and Camera in Targetless Environments. IEEE Robot. Autom. Lett. 2021, 6, 7517–7524. [Google Scholar] [CrossRef]
- Mishra, S.; Pandey, G.; Saripalli, S. Target-free Extrinsic Calibration of a 3D-Lidar and an IMU. In Proceedings of the IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Karlsruhe, Germany, 23–25 September 2021. [Google Scholar]
- Sola, J. Quaternion kinematics for the error-state Kalman filter. arXiv 2017, arXiv:1711.02508. [Google Scholar]
- He, D.; Xu, W.; Zhang, F. Kalman filters on differentiable manifolds. arXiv 2021, arXiv:2102.03804. [Google Scholar]
- Yuan, Z.; Lang, F.; Xu, T.; Yang, X. LIW-OAM: Lidar-Inertial-Wheel Odometry and Mapping. arXiv 2023, arXiv:2302.14298. [Google Scholar]
- Neuhaus, F.; Koc, T.; Kohnen, R.; Paulus, D. MC2SLAM: Real-Time Inertial Lidar Odometry Using Two-Scan Motion Compensation. In Proceedings of the 40th German Conference on Pattern Recognition, Stuttgart, Germany, 9–12 October 2018. [Google Scholar]
- Esfandiari, R.S. Numerical Methods for Engineers and Scientists Using MATLAB, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 160–248. [Google Scholar]
- Rabbath, C.A.; Corriveau, D. A comparison of piecewise cubic Hermite interpolating polynomials, cubic splines and piecewise linear functions for the approximation of projectile aerodynamics. Def. Technol. 2019, 15, 741–757. [Google Scholar] [CrossRef]
- Tibebu, H.; Roche, J.; De Silva, V.; Kondoz, A. LiDAR-Based Glass Detection for Improved Occupancy Grid Mapping. Sensors 2021, 21, 2263. [Google Scholar] [CrossRef] [PubMed]
- Galvez-Lopez, D.; Tardos, J.D. Bags of Binary Words for Fast Place Recognition in Image Sequences. IEEE Trans. Robot. 2012, 28, 1188–1197. [Google Scholar] [CrossRef]
- Yuan, C.; Lin, J.; Zou, Z.; Hong, X.; Zhang, F. STD: Stable Triangle Descriptor for 3D place recognition. arXiv 2022, arXiv:2209.12435. [Google Scholar]









| Symbols | Meanings |
|---|---|
| Component of the state in global frame. | |
| Component of the state in LiDAR frame. | |
| Extrinsic for transformation between LiDAR frame to IMU frame(the extrinsic parameter includes the rotation matrix and the translation vector , i.e., , the same below). | |
| Extrinsic for transformation between camera frame to IMU frame. | |
| Ground-truth state, propagation state, and ESIKF update state, respectively. | |
| Error-state (i.e., the difference between the ground-truth and its corresponding estimation ). |
| Ground Truth | Proposed | LiLiOM | VINS-Mono | |
|---|---|---|---|---|
| Length of | 851.671 | 856.067 | 882.419 | 1136.503 |
| trajectory (m) | ||||
| Rotation error (rad) | × | 0.0108 | 0.0380 | × |
| B1B3_seq | A1A2A3_seq | B1B3B4_seq | |
|---|---|---|---|
| Length of reference trajectory (m) | 586.931 | 655.166 | 709.091 |
| RMSE (m) | 0.524 | 1.449 | 1.529 |
| B1B3_seq | A1A2A3_seq | B1B3B4_seq | |
|---|---|---|---|
| SSLIO per-frame cost time (ms) | 27.15 | 26.97 | 27.23 |
| LIO per-frame cost time (ms) | 19.35 | 19.94 | 20.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, T.; Yao, J.; Lu, Y.; Na, C. Solid-State-LiDAR-Inertial-Visual Odometry and Mapping via Quadratic Motion Model and Reflectivity Information. Electronics 2023, 12, 3633. https://doi.org/10.3390/electronics12173633
Yin T, Yao J, Lu Y, Na C. Solid-State-LiDAR-Inertial-Visual Odometry and Mapping via Quadratic Motion Model and Reflectivity Information. Electronics. 2023; 12(17):3633. https://doi.org/10.3390/electronics12173633
Chicago/Turabian StyleYin, Tao, Jingzheng Yao, Yan Lu, and Chunrui Na. 2023. "Solid-State-LiDAR-Inertial-Visual Odometry and Mapping via Quadratic Motion Model and Reflectivity Information" Electronics 12, no. 17: 3633. https://doi.org/10.3390/electronics12173633
APA StyleYin, T., Yao, J., Lu, Y., & Na, C. (2023). Solid-State-LiDAR-Inertial-Visual Odometry and Mapping via Quadratic Motion Model and Reflectivity Information. Electronics, 12(17), 3633. https://doi.org/10.3390/electronics12173633






