Image Formation Algorithms for Low-Cost Freehand Ultrasound Scanner Based on Ego-Motion Estimation and Unsupervised Clustering

Abstract

This paper describes the application of unsupervised learning techniques to improve ego-motion estimation for a low-cost freehand ultrasound probe. Echo decorrelation measurements, which are used to estimate the lateral velocity of a scanning probe as it is passed over the skin, are found to be sensitive to varying tissue types and echogenicity in the imaged scene, and this can impact the geometric accuracy of the generated images. Here, we investigate algorithms to cluster the collated 1D echo data into regions of different echogenicity by applying a Gaussian mixture model (GMM), spatial fuzzy c-means (SFCM) or k-means clustering techniques, after which the decorrelation measurements can focus on the regions that yield the most accurate velocity estimates. A specially designed mechanical rig is used to provide the ground truth for the quantitative analysis of probe position estimation on phantom and in vivo data using different clustering techniques. It is concluded that the GMM is the most effective in classifying regions of echo data, leading to the reconstruction of the most geometrically correct 2D B-mode ultrasound image.

1. Introduction

According to the World Health Organization (WHO) maternal mortality report (2000–2017) [1], about every 2 min, a woman dies because of preventable complications due to childbirth or pregnancy. The maternal mortality ratio (MMR) in the world’s least developed countries is high, estimated at 415 maternal deaths per 100,000 live births, which is more than 40 times higher than the MMR in Europe and almost 60 times higher than in Australia and New Zealand. The target of reducing the maternal mortality ratio worldwide to less than 70 per 100,000 live births by 2030 has been set by the United Nations (sustainable development goal 3.1) [2]. This crucially depends on ensuring that women have access to basic healthcare services before, during and after childbirth. Maternal mortality risk factors could be detected by using ultrasound imaging, but these devices are very expensive, and thus not affordable for healthcare providers in developing countries.

Furthermore, there is heightened public concern over the healthcare costs and research to miniaturize ultrasound scanners, and making them low-cost devices has been an area of active research over the years [3,4,5]. The 2020 report shows that the global expenditures on healthcare in 190 countries from 2000 to 2018 continually rose and reached USD 8.3 trillion or 10% of the global GDP [6]. Further, the National Health Service (NHS) in the UK performs over 45 million imaging procedures involving 10.5 million ultrasound scans each year [7]. The global ultrasound equipment market is projected to grow from USD 7.80 billion in 2021 to USD 12.93 billion in 2028 at a CAGR of 7.5% in the forecast period (2021–2028) [8]. The growth of healthcare costs worldwide, coupled with the desire for access to care in the developing world, is driving the need for low-cost, high-quality imaging services.

Conventional ultrasound devices use multi-element piezoelectric transducer arrays to produce 2D or 3D images, while only a single-element piezoelectric transducer was used in the proposed ultrasound scanner. Some of the concepts used to minimize hardware complexity in the prototype probe can be found in previous work conducted by our research team [9]. The transducer has a diameter of 15 mm, a thickness ($E_T$) of 0.5 mm and a centre frequency ($f_c$) of approximately 4 MHz and is a type II PZT disc. Operating frequencies of 2–5 MHz are typical for ultrasound abdominal probes, as they represent the best trade-off between resolution and penetration depth. The bandwidth, $\Delta f$, of the transducer is 2 MHz, with a focused beam optimised for 4–15 cm penetration depth and a focal depth of 7 cm. The axial resolution is determined by the bandwidth, $\Delta f$, whereas the lateral and elevation beam widths are determined by the size and geometry of the transducer aperture, and the centre frequency, $f_c$. It takes 2.5 ms to obtain one scan line, which results in a frame rate of 400 frames per second (400 Hz). The sampling frequency, $f_s$, is 25 MHz, and 716 samples are obtained per scan line. This probe design greatly reduces the hardware complexity, power consumption and beamforming computational load, thus bringing the manufacturing cost down to less than USD 100. This will make the device affordable for developing countries. The cost comparison of commercially available portable ultrasound machines is as follows:

• Philips Lumify—200 USD/month per probe + 75 USD/month warranty.
• Sonosite IVIZ—USD 10,000.
• GE VSAN Extend—starts at USD 2995.
• Clarius—starts at USD 6900.
• Butterfly IQ—USD 1999 + 420 USD/year for cloud user license.

There are many companies (such as GE Healthcare; Koninklijke Philips N.V.; Canon Inc.; Hitachi; Siemens Healthcare; Samsung Medison Co., Ltd.; and Esaote) that are constantly focusing on introducing new ultrasound systems with advanced technologies in the market. GE Healthcare dominated the ultrasound industry and accounted for the largest market share in 2020 [8]. Many of the big companies are also shifting their focus towards making portable ultrasound devices that can be carried by a single person from one place to another. On 15 November 2021, TELEMED Medical Systems presented MicrUs Pro Handheld USB Ultrasound, its latest PC-based ultrasound diagnostic system, at the 2021 edition of MEDICA [10].

The mechanical sensors traditionally used to track the ultrasound probe’s position make the device bulky and hard to operate. Therefore, those sensors were not used in this probe. Hence, the formation of a high-quality, geometrically correct ultrasound image at a reduced cost depends upon the utilization of advanced signal processing algorithms. This article provides a detailed description of the proposed image formation algorithms required to generate a geometrically correct, 2D, B-mode ultrasound image with a simple ultrasound probe. However, it does not include in-depth information on the probe’s hardware design. Please refer to [9] for understanding some of the concepts used to minimise hardware complexity in the prototype probe. The ego-motion estimation techniques proposed in the previous work [11], along with advanced signal processing algorithms explained in the presented work, are used to track the probe’s linear motion. The probe’s position estimates help construct a geometrically correct, 2D, B-mode ultrasound image.

A novel ego-motion estimation algorithm that works by finding the decorrelation measurements between series of successive scan-line echo data (1D data) is proposed. This gives information about the lateral velocity of the probe in a linear scan as it is passed over the skin. These velocity estimates help map the image into a set of pixels that are geometrically correct.

The ego-motion estimation algorithm is dependent on the focal parameters of the transducer, the texture or speckle detail, and the echogenicity of the tissue. The very top layer of the human body consists of static tissues that produce a constant speckle pattern over time. The echogenicity is also similar in the top layer, which makes it the optimal region to be considered in motion calculations. However, it is far from the focal point of the transducer. The speckle detail and echogenicity of the tissue start becoming dynamic with an increase in the distance of travel of ultrasound wave in the axial direction (depth). Although these regions are near the focal point of the transducer, they consist of different types of tissues and organs, which creates a dynamic speckle pattern. This would affect the information about the probe’s motion gathered from the echo data, which can eventually impact the geometric accuracy of generated images. Therefore, choosing the optimal region depending on the layers of the human body is crucial. Therefore, the work presented using clustering techniques is needed to optimise the position estimation algorithm to be robust in more complex scenes and variable tissue properties in human scans. This will make the algorithm independent of the scanned region.

For the first time, the Gaussian mixture model (GMM), spatial fuzzy c-means (SFCM) and k-means clustering techniques have been exploited on 1D raw echo data. These techniques have been traditionally used for medical image segmentation on 2D images. But a novel approach has been presented that applies these techniques on the 1D raw ultrasound echo data that helps towards tracking the probe’s velocity. That eventually helps in creating a geometrically correct 2D ultrasound image. These clustering techniques extract the appropriate data from the raw echo scan line data by clustering them into anechoic, hyperechoic, and hypoechoic regions. Only the clustered data in the hypoechoic region is used to estimate the probe’s position with the help of the ego-motion estimation algorithm. A specially designed mechanical rig controls the probe’s motion and measures its real-time position values. Quantitative analysis for estimating the probe’s position using different clustering techniques was carried out using phantom and in vivo experiments, which were compared with the measured probe’s position. The contributions of this article are:

• Optimisation of the decorrelation-based velocity estimation technique for linear scans and application of the unscented Kalman filter (UKF) to filter out the effects of noisy velocity estimates to improve trajectory estimates.
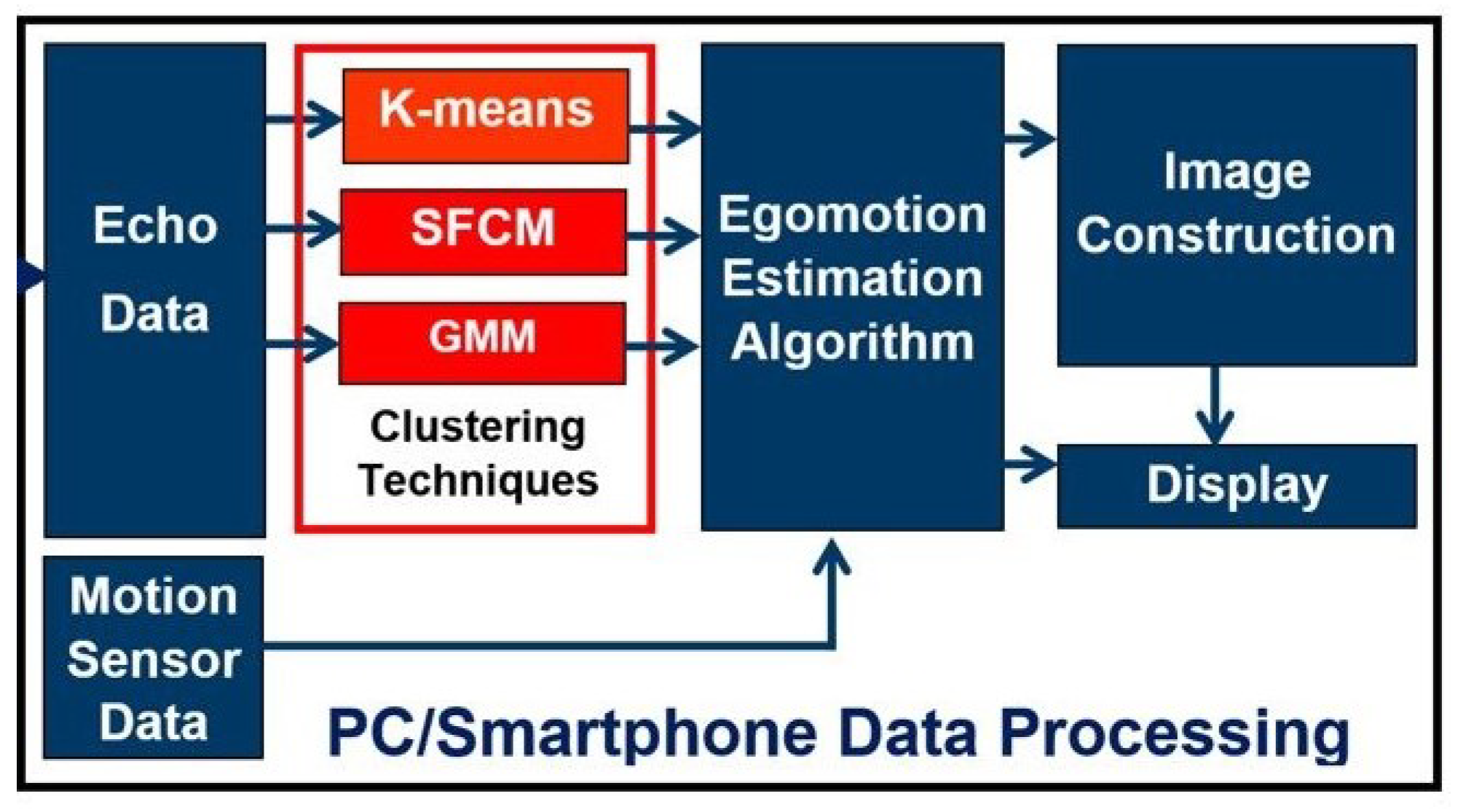
• First-time exploitation of unsupervised clustering (K-means, SFCM and GMM) on the 1D raw ultrasound imaging data.
• Reconstruction of geometrically correct 2D ultrasound images of phantom and in vivo data from the single-element transducer.

The rest of this article is organized as follows. In Section 2, the research related to these image formation algorithms and the clustering techniques is presented. Section 3 presents the proposed ultrasound scanner design and the proposed image formation algorithms: data pre-processing techniques, ego-motion estimation algorithm and the clustering methods. Section 4 presents the experimental setup and the results and discussions. Finally, Section 5 concludes this article.

2. Related Research

Several design parameters need to be addressed to reduce the manufacturing cost of the ultrasound probe and to make the device portable and smaller in size. Many researchers have shown interest in developing ultrasound probes by reducing the number of piezoelectric elements in the transducer. Lokesh B and A.K Thittai presented the design of a low-cost ultrasound system by integrating only 8 or 16 active elements in the transducer [12]. Whereas, M.Fuller et al. presented a system prototype of a future compact, low-cost medical ultrasound device that consists of a 32 × 32 elements, fully sampled 2D transducer array [13,14]. The proposed ultrasound probe consists of only a single-element transducer without the use of any position tracking sensor such as; optical sensors or electromagnetic sensors.

K. Owen et al. have first shown the use of optical sensors to track the transducer’s motion in their initial work [15] and then in [16] combining motion estimates from optical tracking and ultrasound decorrelation measurements, to produce an improved composite estimate of probe’s motion. Q. Cai et al. have recently demonstrated the design and prototype of an ultrasound probe’s tracking system based on a low-cost camera [17]. These sensors make the device bulky in size and difficult to operate. Their cost also adds up to the final manufacturing cost of the low-cost ultrasound scanner. Therefore, the formation of a high-quality ultrasound image at a reduced cost depends upon the utilization of advanced signal processing algorithms with minimal use of hardware.

Several authors have shown the use of decorrelation to track transducer’s motion [18,19,20,21]. J. F. Chen et al., in [18], have calculated decorrelation measurements from the underlying speckle pattern as the transducer moves across the elevation focus to determine the transducer’s motion in the elevation plane. A. Krupa et al. have also presented the direct use of speckle information contained in the images to track both out-of-plane and in-plane motions [19]. A. H. Gee et al. have demonstrated the use of speckle information to acquire freehand 3D ultrasound [20]. R. F. Cheng et al., have also proposed speckle decorrelation techniques for performing freehand 3D ultrasound imaging without the need for a position sensor to provide the location of the ultrasound probe [21].

All these researchers have used decorrelation techniques by first dividing the image obtained with the ultrasound probe into several patches and then finding the correlation between corresponding patches of 2D, B-mode scans/images. They found an approximation of the speckle correlation function as a function of the orthogonal distance between two B-mode scans. However, this requires that the B-scans contain significant amounts of fully developed speckle. This condition is rarely satisfied in scans of real tissue, which instead exhibit fairly ubiquitous coherent scattering [20]; whereas, in our research, a completely novel technique of using correlation-based tracking is presented, which looks directly at the grey level intensity values provided by the ultrasound imaging probe. The correlation between the decorrelation measurements (obtained between the successive scanlines at a certain depth) and the motion of the probe is presented in detail in Section 3.

Machine learning algorithms allow systems to learn from data, identify patterns and predict outcomes without being explicitly programmed, thus having minimal human intervention. Diagnosis and detection with the help of a computer while applying machine learning algorithms can help physicians interpret medical images and reduce interpretation times [22]. There have been various applications of machine learning in the medical field such as; mammography, colonoscopy, MR imaging and CT pulmonary angiography for the detection and diagnosis of breast cancer [23], colon cancer [24,25], neurologic diseases (e.g., Alzheimer) [26,27,28] and pulmonary embolism [29,30], respectively.

Y. Ueno et al. have compared the diagnostic efficiency of endometrial carcinoma among postmenopausal women with an endometrial width of 5 mm with irregular vaginal bleeding. The study was based on three different AI-based approaches such as logistic regression (LR), artificial neural network (ANN), and classification and regression tree (CART). The mathematical model has obtained promising preliminary results, but they must be interpreted with caution until they are validated with an independent data set [31]. The automatic segmentation and detection of an irregular region in the cervical image to diagnose cervical cancer have been proposed by L. Sherin et al. The cervical tissue is differentiated from the normal tissue by implementing an ANN system based on a spectral database [32]. J. Ogasawara et al. proposed a newly constructed deep neural network model (CTG-net) to detect compromised fetal status. It is a quantitative and automated diagnostic aid system that enables early intervention for putatively abnormal fetuses, resulting in a reduction in the number of cases of hypoxic injury [33].

J. Abrantes et al. have presented a study for external validation of a deep learning model for breast density classification based on convolutional neural networks. The mammographic breast density was evaluated using an open-source density evaluation model. This model was developed using a deep convolutional neural network called ResNet-18. The results of this study suggest that while the tool demonstrates a relatively high level of accuracy compared to the original radiologist’s density assessment in distinguishing between dense and non-dense breasts, it may have limitations in accurately classifying the specific BI-RADS density categories [34]. F. M. Calisto et al. has proposed a novel perspective to the design of adaptive communication between intelligent agents (AI) and clinicians using a human-centric AI assistant. This can reduce medical errors by helping clinicians in medical image classification and increase satisfaction by personalizing assertiveness according to the professional experience of each clinician [35,36]. All this has led to an increased interest in the application of machine learning in the field of medicine.

The proposed intelligent feature extraction/segmentation in this article will reduce the effects of anechoic and hyperechoic regions on the velocity estimates calculated from the position algorithm based on decorrelation. This will make the position estimation algorithm independent of the texture or speckle detail of scanned tissue and will lead to improved geometric accuracy on complex image scenes. Much work has been carried out by different researchers to facilitate medical image segmentation by using unsupervised machine learning algorithms (Kmeans, SFCM and GMM clustering or their modified/enhanced versions).

M. Ray et al. have recently (2023) proposed an uncertainty parameter weighted entropy-based fuzzy c-means clustering algorithm for noisy volumetric (3D) brain MR image segmentation. This uses complemented global and spatially constrained local membership functions. The acquired MR images produce blurry tissue boundaries due to inherent noise and intensity inhomogeneity that causes uncertainty while labelling a pixel into its proper tissue region. The proposed framework allows the algorithm to utilize the spatial intensity distribution both locally and globally within the image domain and produce more accurate cluster prototypes [37]. R. E. Pregitha et al. have shown the fetal ultrasound image segmentation using the spatial fuzzy c-mean clustering method. The feature vectors are developed for each pixel of the fetal images used as inputs for the clustering method. The clustering methods segment the fetal image based on spatial information. Experimental results indicate that the Spatial Fuzzy C-Means clustering method can be applied with promising results [38]. The use of kernel-based Fuzzy C-means clustering technique for early prediction of congenital abnormalities and to estimate the delivery date is shown by S. Meenakshi et al. in their work [39]. W. A. Kissara and B. F. Hassan have applied the fuzzy c-means algorithm on the fetal anatomy parameters to determine the fetal sex. The study proved that the features extracted from the images give good results in determining the sex of the fetus [40].

Bing et al. [41] proposed the enhanced FCM algorithm with spatial information (SFCM) to approximate the boundaries of interest. A multi-scale fuzzy c-means method integrated with particle swarm optimization (MsFCM-PSO) has been used for ultrasound image segmentation by Zhang et al. [42]. Yan [43] also proposed the use of fuzzy c-means (FCM) clustering while incorporating spatial information based on image decomposition. All these methods were validated on both simulated and clinical ultrasound images. Sombutkaew et al. [44] have proposed the use of fuzzy c-mean clustering to achieve higher encoding efficiency for medical image data.

The k-means grouping algorithm was initially proposed by MacQueen in 1967 and later enhanced by Hartigan and Wong. Ciklacandir et al. [45] studied the application of the k-means clustering technique for early diagnosis of breast cancer. K-means clustering has been applied for renal calculi detection and on three-dimensional synthetic ultrasound breast images by Upadhyay et al. [46] and Yang et al. [47], respectively. EM-MPM performs significantly better, especially in the cases of high density, which means EM-MPM could greatly help with the dense proportion—cancer risk. Meanwhile, Mandwe and Anjum [48] have proposed a computer-aided system for brain MR image segmentation for the detection of tumour location using an advanced k-means clustering algorithm and fuzzy c-means algorithm. A design approach for performance analysis of infant’s abnormality has been proposed by R. Agrawal et al., using k-means clustering. The parameters like head diameter and abdomen circumference are used to incorporate feature extraction and following that the k-means clustering algorithm is used to classify abnormalities in infants. The proposed system gives promising results for detecting the abnormalities of fetuses and the accuracy is coming out to be 83.76% by using the k-means clustering algorithm [49]. A. A. Hussain et al. have shown the use of k-means clustering or hybrid clustering that combines k-means clustering with a feed-forward neural network (FFNN) to accurately determine the fetal biometry [50].

The expectation maximization (EM) algorithm was introduced by Dempster (1977) for maximization likelihood functions with missing data. Khanna et al. [51] studied the segmentation of ultrasound images based on the conventional expectation maximization (EM) algorithm applied to texture features extracted by a bank of Gabor filters. The segmentation results were compared with the work accomplished using K-means clustering. It was concluded that K-means being a basic technique, results in over-segmentation and converges in local minima. Huang et al. [52] have shown the use of an improved expectation maximization (EM) algorithm to incorporate neutrosophic logic to diagnose breast cancer. S.Belciug et al. proposed a medical decision-making framework designed as a merger between deep learning algorithms and Gaussian Mixture Modelling clustering (GMM) to prevent pregnancy complications and maternal deaths [53]. Ravindraiah and Tejaswini [54] studied the comparison of three segmentation algorithms, K-means clustering, fuzzy c-means (FCM) clustering, and expectation maximization (EM) on intravascular ultrasound images. Experiment results show that the new algorithm (GMM-EM) yields better segmentation results. Furthermore, E. Nsugbe et al. have presented the investigation of combining datasets, using physiological signals such as uterine contractions and foetal and maternal heart rate signals, with various forms of prediction machines. This study is based on predicting premature births in Hispanic labour patients. The results have shown the use of two effective unsupervised learning methods, that is, GMM and K-means, towards the self-sorting of data samples based on the acquired physiological signals [55].

All the papers describe the use of clustering techniques in the field of medical imaging for image segmentation. A novel approach has been presented that applies these techniques on the 1D raw echo data, collected from a simple probe to create a geometrically correct 2D ultrasound image.

3. Material and Methods

This section briefly presents the design of the proposed ultrasound scanner and an extensive overview of the proposed image formation algorithms.

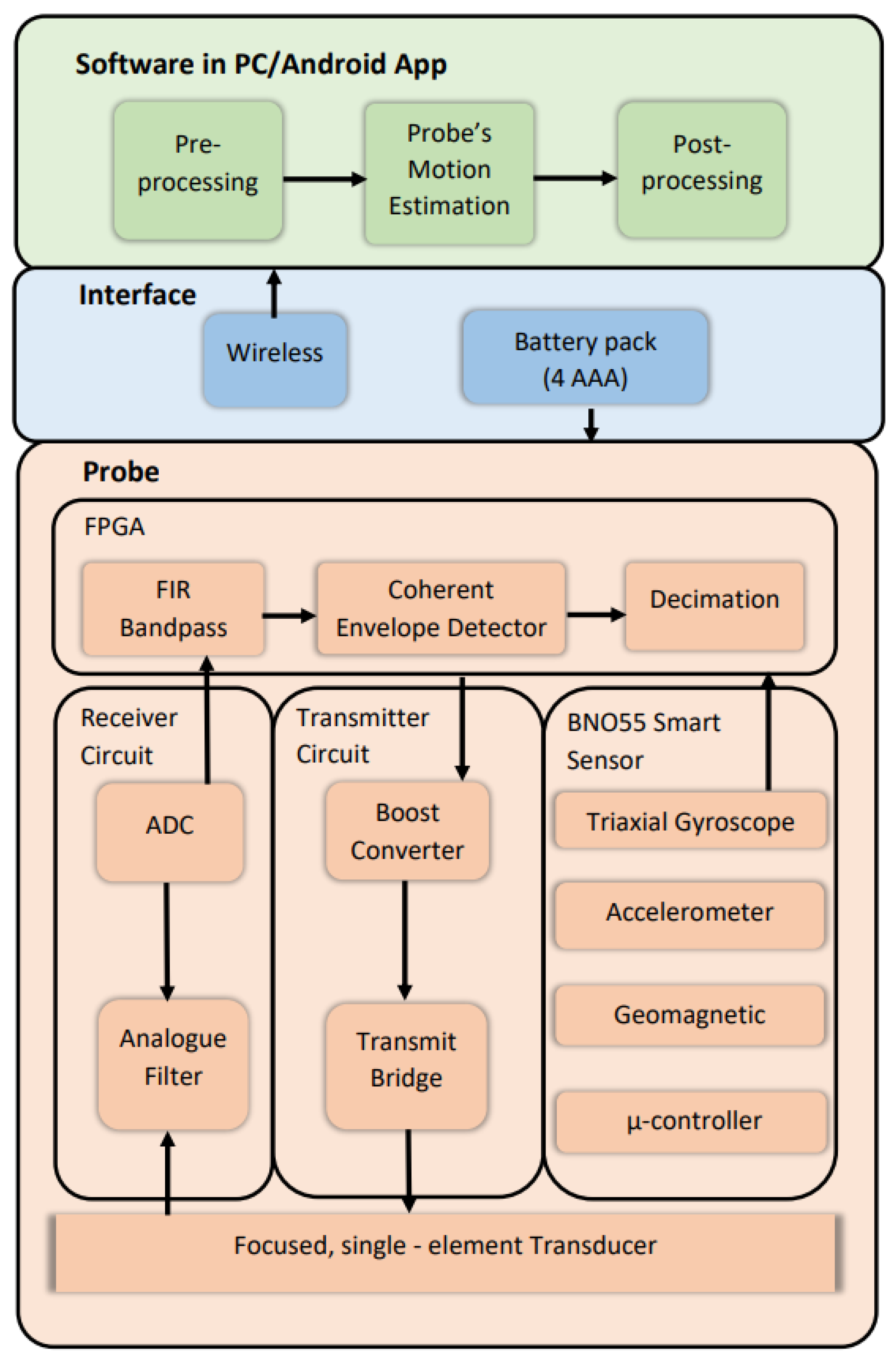
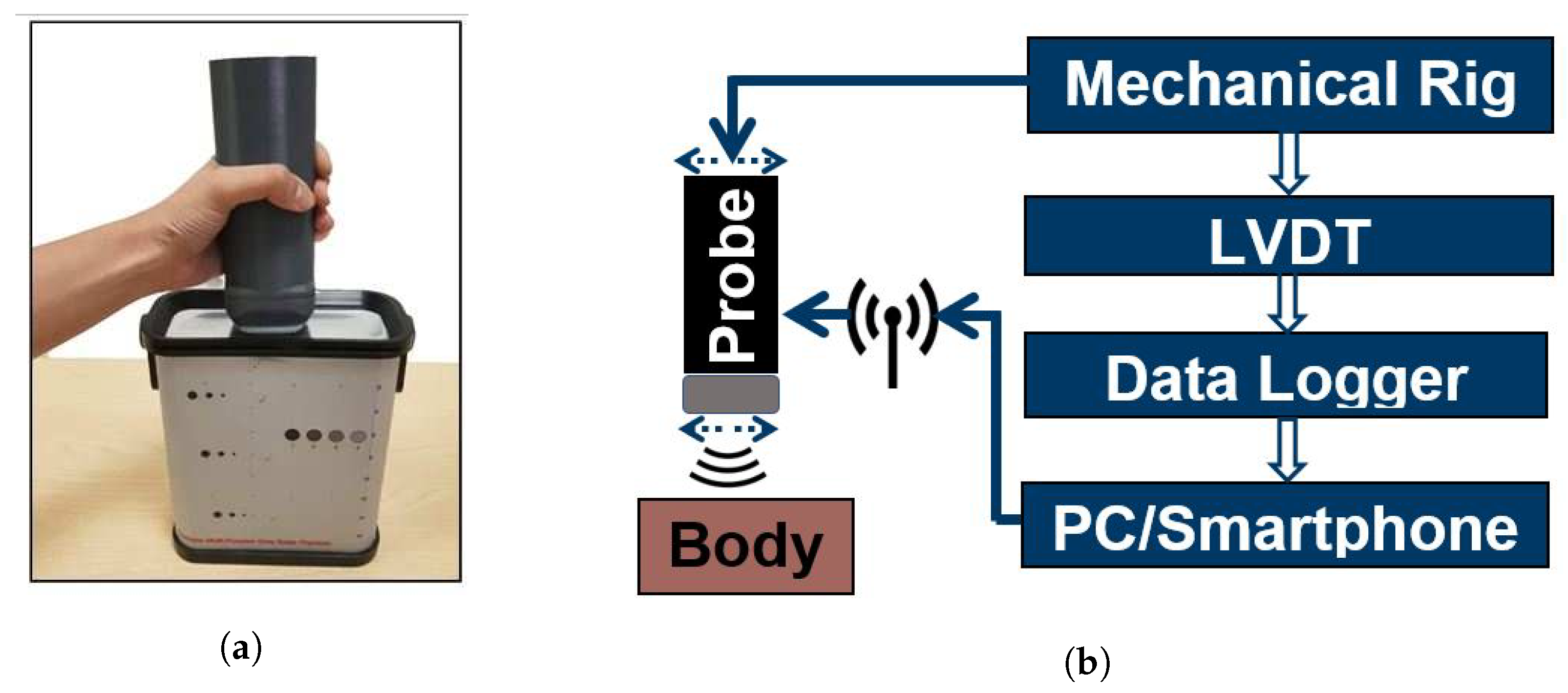
3.1. Proposed Ultrasound Scanner Design

Conventional ultrasound devices use a multi-element piezoelectric transducer array to produce a 2D or a 3D image, while only a single piezoelectric element transducer has been used in the proposed ultrasound scanner. The block diagram for the scanner can be seen in Figure 1. The transducer has a diameter of 15 mm; a thickness, $E_T$, of 0.5 mm; a centre frequency, $f_c$, of approximately 4 MHz; and is a type II PZT disc. Operating frequencies of 2–5 MHz are typical for ultrasound abdominal probes as this represents the best trade-off between resolution and penetration depth. The bandwidth, $\Delta f$, of the transducer is 2 MHz with a focused beam optimised for 4–15 cm penetration depth and a focal depth of 7 cm. The axial resolution is determined by the bandwidth, $\Delta f$, whereas the lateral and elevation beam width is determined by the size and geometry of the transducer aperture and the centre frequency, $f_c$. It takes 2.5 ms to obtain one scan line, which results in a frame rate of 400 frames per second (400 Hz). The sampling frequency, $f_s$, is 25 MHz and 716 samples are obtained per scanline. The summary of all the parameters related to the probe’s design can be seen in

Table 1. Low-cost ultrasound scanner parameters.

Parameter	Symbol	Value
Centre Frequency	$f_c$	4.2 MHz
Bandwidth	$\Delta f$	2 MHz
Range	R	0.15 m
Sampling Frequency	$f_s$	25 MHz
Speed of Sound in tissues	c	1540 ms−1
Element Width	$E_W$	2 mm
Element Length	$E_L$	7 mm
Element Thickness	$E_T$	0.5 mm
Frame/s	$F_R$	400

and related to the imaging resolution can be seen in

Table 2. Low-cost ultrasound scanner parameters related to resolution.

Parameter	Value
Elevation Focus (mm)	50.5
Slice thickness at elevation focus	1.2
Axial Resolution in focus (mm)	0.37 ± 0.05
Axial Resolution averaged over depth (mm)	0.55 ± 0.13
Lateral Resolution in focus (mm)	1.25 ± 0.06
Lateral Resolution averaged over depth (mm)	2.71 ± 1.40
Axial spatial conformity (%)	2 ± 0.06
Dynamic Range (dB)	98 mm
Contrast sensitivity	2.19

. This article does not include in-depth information on the probe’s hardware design. Some of the concepts used to minimise hardware complexity in the prototype probe can be seen in previous work carried out by our research team [9]. This probe design greatly reduces the hardware complexity, power consumption and beamforming computational load, hence bringing the manufacturing cost down to less than $100. This will make the device affordable to the developing countries.

3.2. Pre-Processing the Echo Data

The 1D raw echo data passes through various steps to calculate the probe’s position, which are explained below: The sound wave’s intensity diminishes as it travels through a medium and therefore a time-variant gain (TVG) was applied on the echo data depending upon the distance travelled by the wave. The normalisation process is then applied to the echo data to optimize the information obtained from these data about the probe’s position.

The reliability of the probe’s motion information obtained from the echo intensity’s values depends upon the penetration depth of ultrasound waves. Variation of the mean of absolute differences (MAD) values with respect to the depth of the scanned object was investigated and shown in Figures 5 and 6. The results are obtained by scanning the acoustic phantom with the proposed ultrasound probe, while keeping the orientation near constant. The total number of samples taken across the depth for one scan line was 716. For Figure 5, the range of the data was kept at 100 samples and the comparison was made by moving in steps of 100 in the axial direction (depth). Whereas, for the results in Figure 6, the decorrelation measurements were obtained from the top and bottom half of the scanned region. The top half (1 till 358) of samples correlate with the actual probe’s motion and the bottom half (358 till 716) of samples is highly dominated by noise.

Hence, it is crucial to select the appropriate region from the echo data that will be used to calculate the probe’s position estimate. The distance covered by the wave as it travelled inside the medium ($d_t$) is calculated by the following equation:

$$d_t\left(\mathrm{cm}\right)=S\times \frac{c\times D_f}{2\times S_R}\times 100$$

(1)

where, S is the number of samples at a particular depth per scanline, c is the speed of sound, which is 1540 ms⁻¹, $D_f$ is the decimation factor, which is 6, and $S_R$ is the sampling rate, which is equal to 25 MHz.

The signal-to-noise ratio (SNR) of the reflected echo decreases as the depth increases. This is because the sound waves become attenuated when the distance travelled increases in the medium. The intensity of the reflected sound wave depends upon the following parameters:

$$I_r=I_o{e}^{-\mu d_t}$$

(2)

where, $I_r$ is the intensity of the reflected beam (Wm⁻²), $I_o$ is the intensity of the incident beam (Wm⁻²), $\mu$ is the absorption coefficient (mm⁻¹) and $d_t$ is the distance travelled by the sound wave in the medium.

Overall, 20 controlled ultrasound scans were performed on acoustic phantom [56] and 50 in vivo scans were collected with the help of a mechanical rig. The percentage error between the actual and calculated probe’s position (using the ego-motion estimation algorithm explained later on in this section) has been calculated to obtain the best region for the position algorithm. Each percentage error value is the average error value of all the collected scans. Two experiments have been carried out by either changing the centre of the collected data samples while keeping the range constant or changing the range while keeping the centre constant. The experiments conclude that the number of samples from 1 till 450 (centre at 225 samples) should be used in the position estimation algorithm to give accurate results.

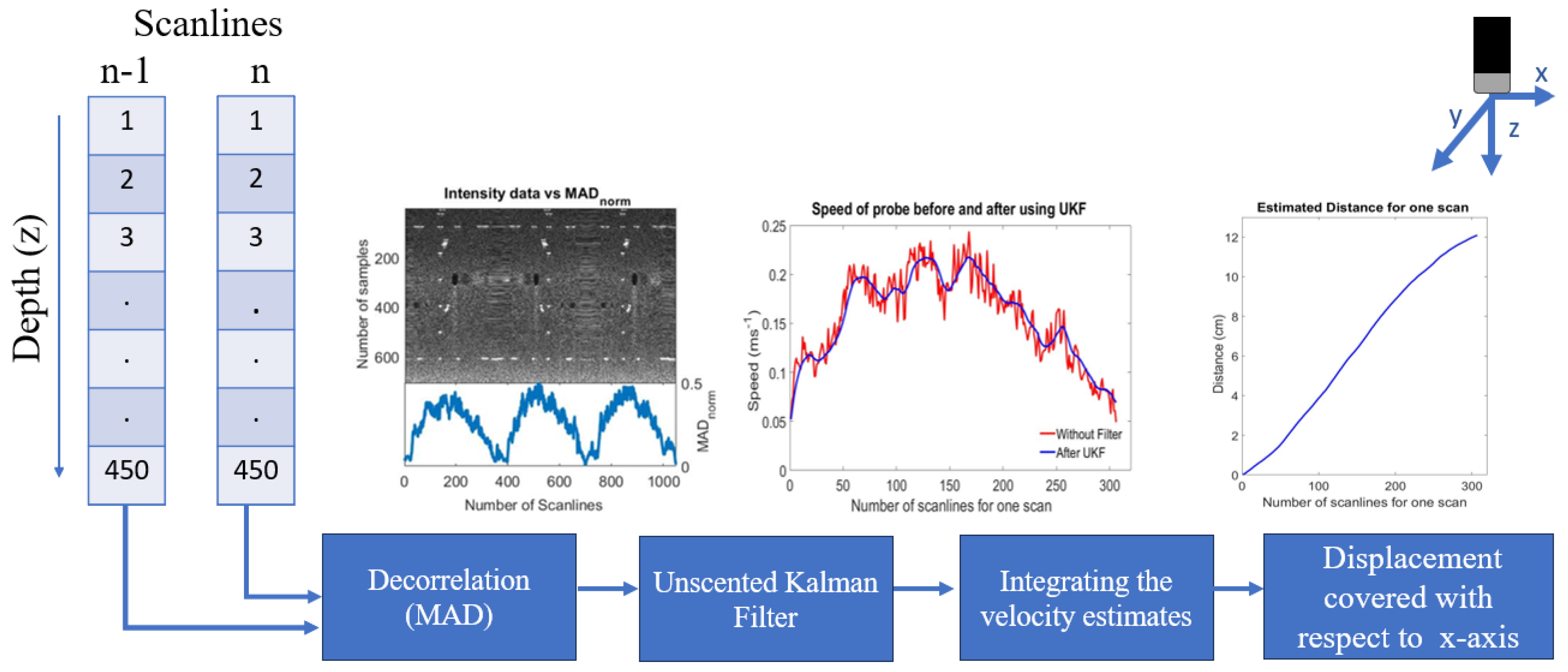
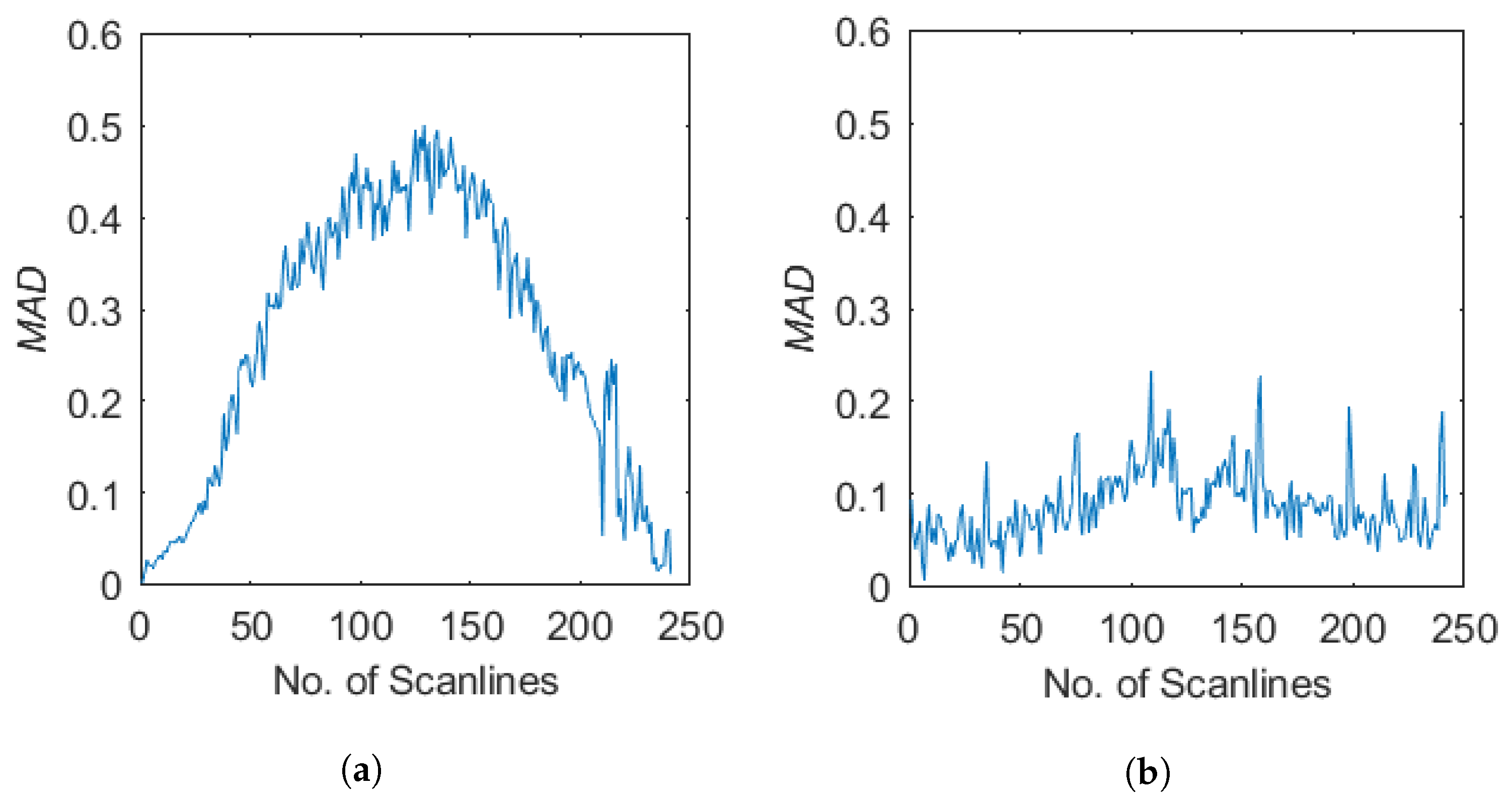
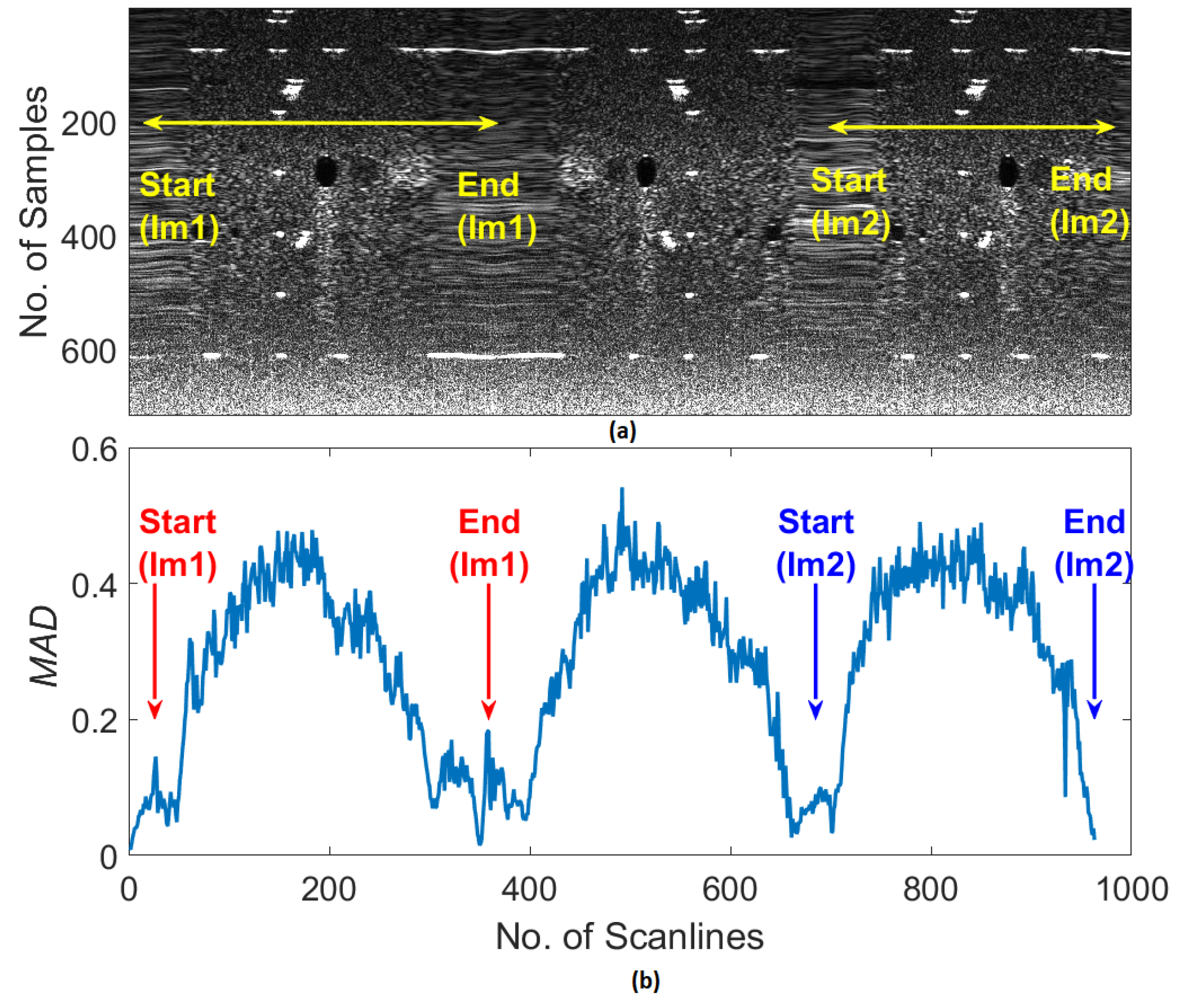
3.3. Ultrasound Decorrelation Measurements

The block diagram for the processing unit of the proposed probe can be seen in Figure 2.

There are two motions that could be associated with an ultrasound image sequence; the motion of the transducer or the tissue that is being scanned. The probe was manually scanned across the subject body (phantom or human skin) linearly while keeping the orientation near constant. Ego-motion estimation techniques are used to estimate the transducer’s motion relative to a static scene inside the subject body. The decorrelation measurements (MAD) between consecutive scanlines are obtained that will correlate with the motion of the probe. For instance, if the scanner moved at a higher speed, the MAD values would be higher and if a probe would have moved at a low speed, the MAD values would be low. The unscented Kalman filter (UKF) is also utilized to filter out the effects of noisy velocity estimates to improve trajectory estimates. These filtered velocity estimates are then integrated across many pings to give the position values. These position estimates are used to scale/stretch the echo data to form a geometrically correct image. The methods are explained in detail below. Decorrelation measurements have been obtained by calculating the mean of absolute differences values ($MAD$) between consecutive scanlines. This is accomplished through the following steps:

(1)

The absolute differences between the echo signal intensities of each consecutive scan line were calculated.

(2)

The mean of the absolute differences was calculated.

(3)

Steps 1 and 2 were repeated for all the other scan lines by moving successively through all the data.

$$MAD=E\left[\left|y_n-y_{n-1}\right|\right]$$

(3)

where $y_n$ and $y_{n-1}$ represent the value of echo signal intensities for consecutive scanlines at a fixed depth and $1\le n\le N$. N represents the total number of samples in the echo data.

3.3.1. Velocity Calculation for the Ultrasound Probe

Velocity was calculated after normalising the $MAD$ values using the formula given below:

$$MA{D}_{norm}=\frac{\frac{1}{N}\sum \left(y_n-y_{n-1}\right)}{\frac{1}{2N}\left(\sum y_n+\sum y_{n-1}\right)}$$

(4)

where, N represents the number of samples, $\frac{1}{N}\sum (y_n-y_{n-1})$ is the mean of absolute differences $\left(MAD\right)$ and $MA{D}_{norm}$ are the normalised $MAD$. These values are directly proportional to the velocity of the probe.

The distance covered by the probe in one direction was calculated by integrating MAD values for one curve. This was compared with the measured distance (with the data logger) to find the constant of proportionality, w, for this particular transducer geometry. This constant was used to calculate the estimated velocity of the probe:

$$V_{estimate}=\frac{MA{D}_{norm}}{w}$$

(5)

where, $V_{estimate}$ represents the estimated velocity of the probe.

3.3.2. Unscented Kalman Filter

Unscented Kalman filter (UKF) is used to estimate the state of this non-linear system. It calculates the optimised value for the velocity by filtering out the effects of the noisy velocity estimates calculated from the decorrelation measurements as shown in Figure 3. This is then integrated to give the estimates of the distance covered by the probe. The estimated distance travelled by the probe is used to create the geometrically correct image of the phantom. Figure 3 shows the overview of the egomotion estimation algorithm.

As explained earlier, the signal-to-noise ratio (SNR) of the reflected echo decreases as the depth increases. This is because the sound waves become attenuated with the travelled distance. Therefore, 1 till 450 samples, along the depth, out of the total 716 samples have been chosen to be used for position estimation.

The ego-motion estimation algorithm is also dependent on the focal parameters of the transducer, the texture or speckle detail and the echogenicity of the tissue. The very top layer of the human body consists of static tissues that produce a constant speckle pattern over time. The echogenicity is also similar in the top layer, which makes it the optimal region to be considered in motion calculations. However, it is far from the focal point of the transducer. The speckle detail and echogenicity of the tissue start becoming dynamic with an increase in the distance of travel of ultrasound wave in the axial direction (depth). Although these regions are near the focal point of the transducer, they consist of different types of tissues and organs, which creates a dynamic speckle pattern. This would affect the information about the probe’s motion, gathered from the echo data. Therefore, choosing the optimal region depending on the layers of the human body is crucial. Hence, the work using unsupervised clustering, presented below is needed to optimise the position estimation algorithm to be robust in more complex scenes and variable tissue properties in human scans. This will make the ego-motion estimation algorithm be independent of the scanned region.

The collected raw-scanline data are classified into three regions: anechoic (air, fat, or fluid), hyperechoic (hard tissue, e.g., bone) and hypoechoic region (soft tissues). The data in the anechoic region contains only noise because sound passes through fluids with almost zero back-scatter, thus reflecting almost no echo. The hyperechoic region does not contain any information about the motion of the probe because this region reflects almost all the incident ultrasound waves. Therefore, the decorrelation between these constant bright targets will show a false indication of the probe being stationary. Hence, the echo data in the hypoechoic region should be separated from the other two regions and will be used in the position algorithm. The collected echo data are classified into three clusters using the proposed algorithms; soft clustering (Gaussian mixture model (GMM) and spatial fuzzy c-means (SFCM) ) or hard clustering techniques (k-means). These clustering techniques are explained in detail below:

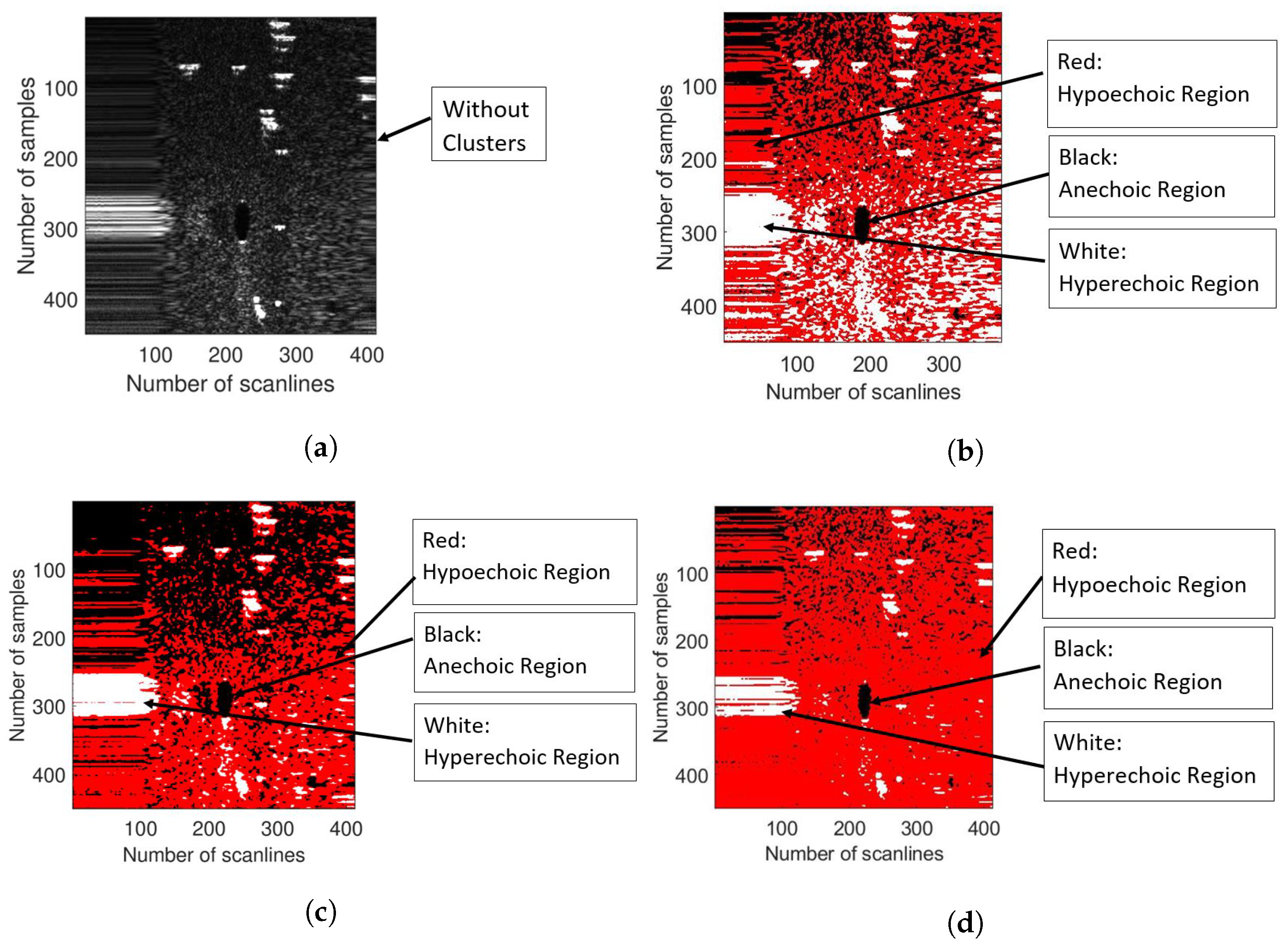
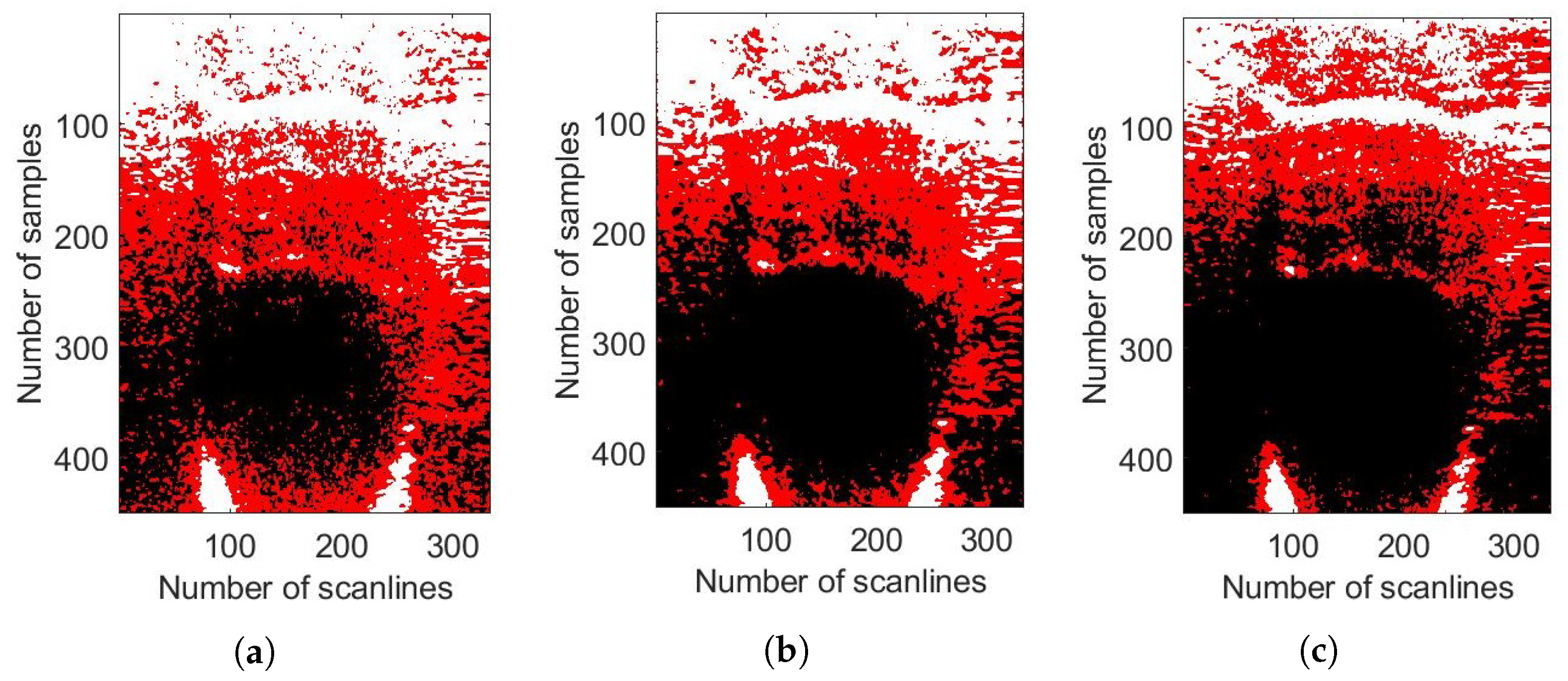
3.4. K-Means Clustering

K-means clustering computes, C, centroids and takes every point from the echo data, y, and group them in the cluster that has a nearby centroid. Euclidean distance is used to compute the nearest centroid distance [57]. It is a repetitive algorithm and aims to minimise the distance of each point from the cluster centroid. Once the cluster is created, the centroid of each cluster is recomputed and thus the new distance is calculated between every centre and the data point built on the centroid and the points with minimum distance are allocated to that cluster.

Let y = {$y_1$,…,$y_N$} be the echo intensity values data set and C = {$c_1$,…,$c_K$}, $c_k$ is the centroid of the $k^{}$th cluster and 1 ≤ k ≤ K.

The pseudocode of the algorithm is summarised in Algorithm 1 and the implementation steps are as follows [58,59]:

• The number of clusters, K, is given as a priori and it has been chosen to be equal to 3 in this project. This is because echo data needs to be clustered in three clusters, i.e., hyperechoic, anechoic and hypoechoic.
• Cluster centres are chosen randomly by the algorithm.
• The distance d between echo data, $y_n$, and the cluster centre, $c_k$, is calculated using the Euclidean distance formula as follows:

  $$d=∥y_n-c_k∥$$

  (6)
• The membership function, $\Lambda$, is computed in which ${\Lambda }_{nk}$ denote the membership degree of the $k^{}$th data point to the $k^{}$th cluster, ${\Lambda }_{nk}$∈ [0,1].

  $$\Lambda =\left(\begin{array}{ccc}{\Lambda }_{11}& \dots & {\Lambda }_{1k}\\ ⋮& \ddots & ⋮\\ {\Lambda }_{n1}& \dots & {\Lambda }_{nk}\end{array}\right)$$

  (7)

  where, k = 3 because echo data need to be clustered in three clusters, i.e., hyperechoic, anechoic and hypoechoic.

Algorithm 1: Kmeans clustering pseudocode.

5.

Then, the k-means objective function is calculated as follows:

$$J(\Lambda ,C)=\sum _{k=1}^K\sum _{n=1}^N{\Lambda }_{nk}{\left|\left|y_n-c_k\right|\right|}^2.$$

(8)

$J(\Lambda ,C)$ is minimized by iterating the k-means algorithm.

6.

The cluster centres, $c_k$, and membership function, $\Lambda$, are updated using the equations shown below:

$$c_k=\frac{{\sum }_{n=1}^N{\Lambda }_{nk}{y}_n}{{\sum }_{n=1}^N{\Lambda }_{nk}}$$

(9)

$${\Lambda }_{nk}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}k=arg\underset{1\le k\le K}{min}{∥y_n-c_k∥}^2\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(10)

3.5. SFCM Clustering

Fuzzy c-means (FCM) clustering is an unsupervised machine learning algorithm and referred as soft clustering or soft k-means [41]. Every data point is classified by its membership values, which indicates the likelihood of that point belonging to that cluster [60].

The pseudocode of the SFCM algorithm is summarised in Algorithm 2 and the implementation steps are as follows [41,61]:

• Set values for K, l and $\beta$. Where,
  K = number of clusters = 3.
  l = is the weighting exponent (>1) on each fuzzy membership that controls the fuzziness of resultant segmentation.
  $\beta$ = termination criterion between [0,1].
• Initialise the fuzzy membership function matrix ${\Lambda }_{nk}$ whereas, the membership functions are subject to the following constraints:

  $$\sum _{n=1}^K{\Lambda }_{nk}=1;0\le {\Lambda }_{nk}\le 1;\sum _{n=1}^N{\Lambda }_{nk}>0;$$

  (11)
• Calculate the cluster centres as follows:

  $$c_k=\frac{{\sum }_{n=1}^n{\Lambda }_{nk}^l{y}_n}{{\sum }_{n=1}^N{\Lambda }_{nk}^l}$$

  (12)

Algorithm 2: SFCM clustering pseudocode.

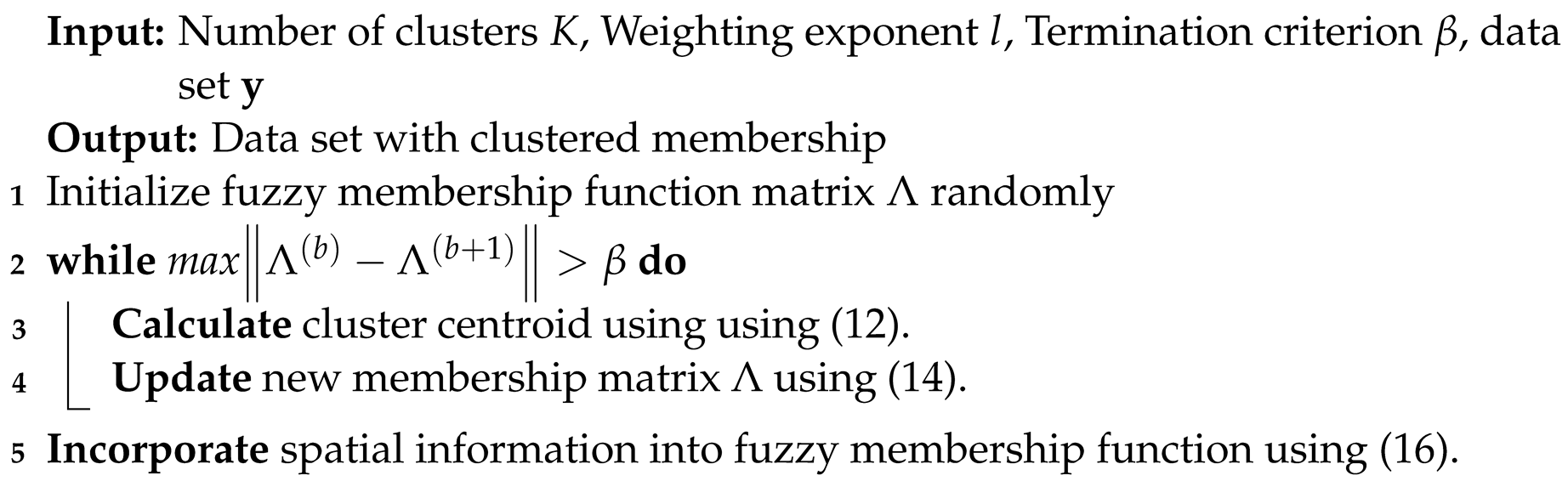4.

Compute the membership function $\Lambda$. For ($n=1,\dots ,N$), calculate the following:

$$I_n=k\mid 1\le k\le K,∥y_n-c_k∥=0,/I$$

(13)

for the $n^{}$th column of the matrix, compute new membership values:

• if $I_k$ = ø then

  $${\Lambda }_{nk}=\frac{{∥y_n-c_k∥}^{-2/(l-1)}}{{\sum }_{k=1}^K{∥y_n-c_k∥}^{-2/(l-1)}}$$

  (14)
• Otherwise, ${\Lambda }_{nk}$ = 0 for all $k\notin$I and ${\sum }_{n\in I_n}{\Lambda }_{nk}=1$;

5.

If $∥{\Lambda }^b-{\Lambda }^{b-1}∥<\beta$, stop; otherwise, keep incrementing the loop and repeat step 3, 4 and 5. Where ($b=1,\dots$ number of iterations = 100).

The cost function $J(\Lambda ,C)$ is calculated after carrying out the iterative steps explained above by using the equation below:

$$\mathit{J}(\Lambda ,C)=\sum _{k=1}^K\sum _{n=1}^N{\Lambda }_{nk}^l{\left|\left|y_n-c_k\right|\right|}^2$$

(15)

Spatial fuzzy clustering (SFCM) is a type of fuzzy c-means clustering in which spatial information is incorporated into fuzzy membership functions [62]. Physiological tissues are usually not homogenous and therefore computing the degree of membership of echo data to the clusters makes the clustering more justifiable for medical images. Spatial information is incorporated into fuzzy membership functions directly using [62]:

$${\Lambda }_{nk}^s=\frac{{\Lambda }_{nk}^p{h}_{nk}^q}{{\sum }_{k=1}^K{\Lambda }_{nk}^p{h}_{nk}^q}$$

(16)

where p and q are two parameters controlling the respective contribution. The variable $h_{nk}$ includes spatial information by

$$h_{nk}=\sum _{k\in W_N}^k{\Lambda }_{nk}$$

(17)

where $W_N$ denotes a local window centred around the input data.

3.6. GMM Clustering

GMM divides the data set into ‘K’ number of ellipsoidal shaped clusters, taking the parameters like probability, mean and variance of each cluster into account by using the expectation maximization (EM) algorithm [63]. This algorithm is used to fit the GMM to the dataset by identifying the parameters of the Gaussian distribution for each cluster.

The pseudocode of the algorithm is summarised in Algorithm 3 and the stages of the proposed EM algorithm and the GMM clustering algorithm are as follows [64,65]:

• K-means clustering for a reduced number of iterations using a random parameter initialization.
• GMM-EM clustering using the parameter initialization is given by the results of the previous K-means clustering phase. Assuming expectation maximization for a Gaussian mixture model (GMM-EM), the goal is to maximize the likelihood function with respect to the parameters (comprising the means and covariances of the components and the mixing coefficients). The steps of the EM clustering are further presented:

  (a)

  Compute the means ${\mu }_k$, covariance matrices ${\Sigma }_k$ and mixing coefficients ${\pi }_K$ (where $k=1,\dots ,K$) as a result of the previous phase of K-means clustering, by considering them as initialization parameters for the present GMM-EM phase and evaluate the initial value of the log-likelihood.

  (b)

  E step. Evaluate the responsibilities using the current parameter values.

  $$\gamma \left(z_{nk}\right)=\frac{{\pi }_{k}N(y_n\mid {\mu }_k,{\sum }_k)}{{\sum }_{k=1}^K{\pi }_{k}N(y_n\mid {\mu }_k,{\sum }_k)}$$

  (18)

  (c)

  M step. Re-estimate the parameters using the current responsibilities.

  $${\mu }_k=\frac{1}{N_k}\sum _{n=1}^N\gamma \left(z_{nk}\right)y_n$$

  (19)

  $$\sum _k=\frac{1}{N_k}\sum _{i=1}^N\gamma \left(z_{nk}\right)(y_n-{\mu }_k){(y_n-{\mu }_k)}^T$$

  (20)

  $${\pi }_k=\frac{N_k}{N}$$

  (21)

  where,

  $$\sum _{n=1}^N\gamma \left(z_{n}k\right)=N_k$$

  (22)

  (d)

  Evaluate the log-likelihood.

  $$lnp(Y\mid \pi ,\mu ,\Sigma )=\sum _{n=1}^{N}ln\sum _{k=1}^K{\pi }_{k}N(y\mid {\mu }_k,\sum _k))$$

  (23)

  (e)

  Check for convergence of either the parameters or the log-likelihood. If the convergence criterion is not satisfied, return to Step B.

Algorithm 3: GMM clustering pseudocode.

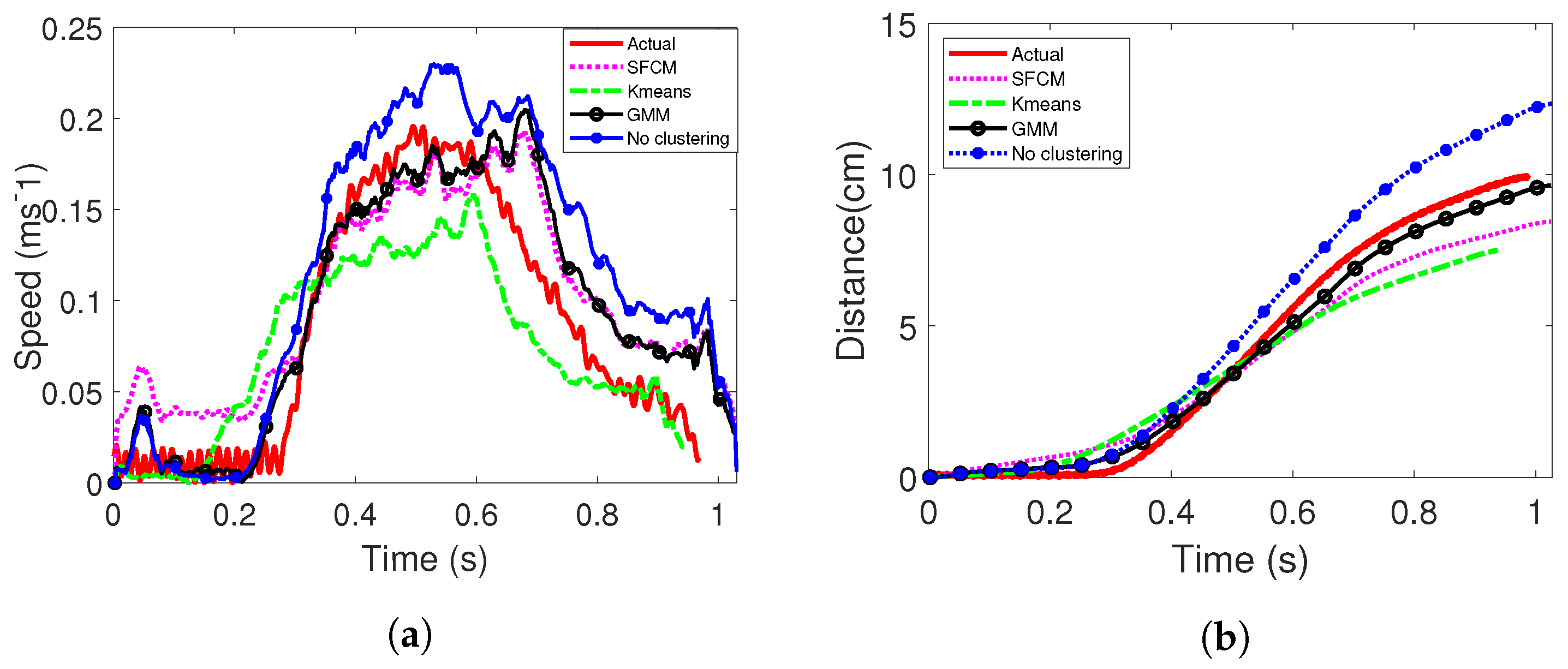
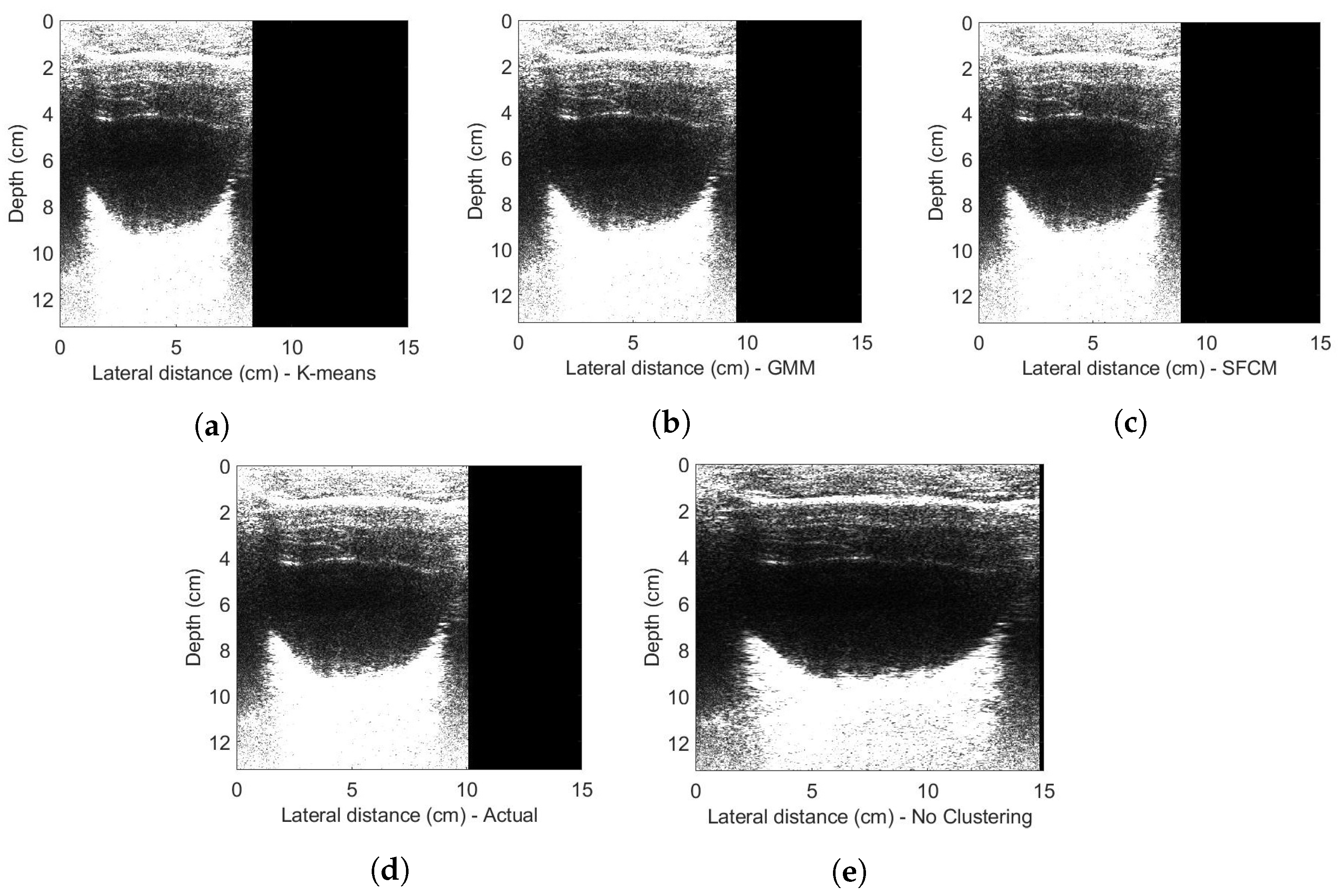
4. Experimental Evaluations

In this section, the experimental setup and the proposed methods are evaluated on phantom and in vivo datasets.

4.1. Set-Up for Scanning

The proposed ultrasound probe is a freehand scanner and the setup for scanning the probe manually across the acoustic phantom (linearly) while keeping the orientation near constant can be seen in Figure 4a.

A mechanical rig has been designed to control the probe’s motion to compare the probe’s real motion with the calculated motion. The cylinder, which was the key part of the rig, was designed by using the Autodesk inventor software and printed by a 3D printer. It was designed to perform a rotation of 180°, resulting in the probe’s linear motion of 10 cm in one direction. A length of 10 cm was used in accordance with the dimensions of the phantom. This motion pattern was chosen by considering the natural motion pattern for any free-hand ultrasound probe used by a person.

The probe will be stationary at the start of the scanned object and the speed will increase gradually by reaching the maximum value somewhere in the middle of the object. The speed would go to zero when reaching the other end of the scanned object, thus giving half a sine curve motion. The motion would be the same but in the opposite direction when coming back to the point from where the probe would have started scanning thus, completing a sine wave. The schematic diagram showing the experimental set-up for scanning with the help of a mechanical rig can be seen in Figure 4b.

A linear variable differential transducer (LVDT) is used to convert the linear movement of the ultrasound probe to the equivalent electrical signal. It works on the transformer principle and is used to measure the probe’s displacement. LVDT has been mounted next to the horizontal bar, which moves the probe horizontally. A data logger has been used to record the displacement of the ultrasound’s probe over time.

The above-mentioned clustering techniques have been evaluated on the data that were obtained by scanning the ultrasound probe over the precision multi-purpose grey scale phantom and the human body. The motion of the scanner was controlled with the mechanical rig that gives the real motion information with the help of a data logger. The distance moved by the scanner, every millisecond, was measured and compared with the distance calculated using the clustering techniques and ego-motion estimation algorithm.

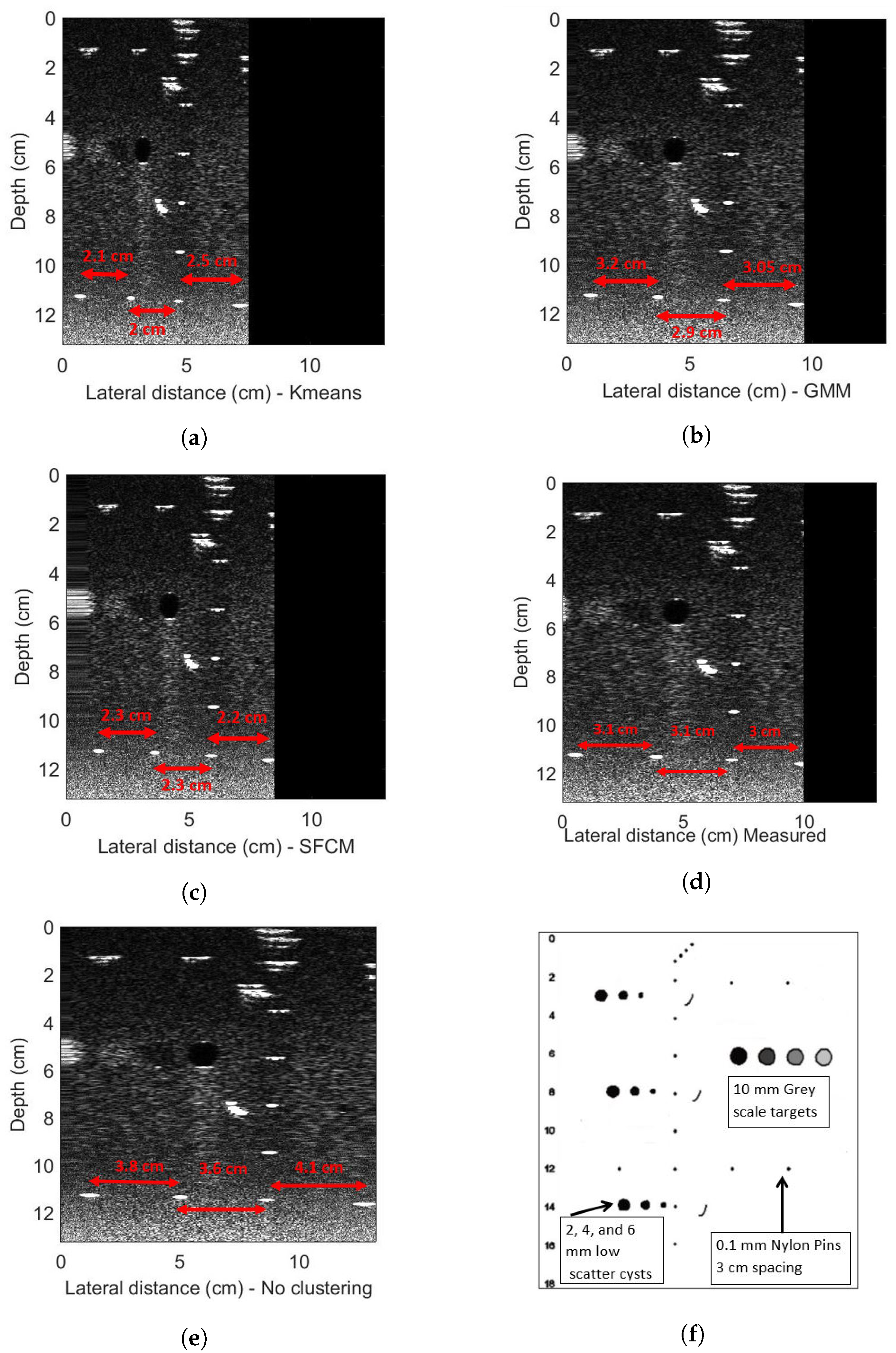
4.2. Phantom Experiments

The probe was manually scanned across the phantom (linearly), while keeping the orientation near constant. Variation of the mean of absolute differences (MAD) values with respect to depth of the scanned object was investigated as shown in Figure 5. It could be observed that the signal-to-noise ratio (SNR) decreased as the depth was increased. This is because the sound waves become attenuated with the distance travelled in the medium. The $MAD$ values from 1 till 100 samples and 100 till 200 samples are calculated from the near field of the transducer where a complex constructive and destructive interference pattern happens. This region is far from the focal region of the transducer and it could be seen that the $MAD$ values are affected by the interference pattern. The ultrasound probe has a focused beam optimised for 4–15 cm penetration depth and a maximum lateral resolution of 0.2 mm at the focal depth of 5 cm. The $MAD$ values in the 200 till 300 samples and 300 till 400 samples are comparable with the actual probe’s motion as it falls in the focal region of the transducer. The $MAD$ values calculated from the deeper layers (500 till 600 and 600 till 700) of the body are highly dominated by noise due to signal attenuation.

Figure 6 shows the decorrelation measurements obtained by the top and bottom half of the scanned region. The top half (1 till 358) of the samples correlate with the actual probe’s motion and the bottom half (358 till 716) of samples is highly dominated by noise. Hence, it is really crucial to select the appropriate region to give the optimum probe’s position estimate. The experiment to compare the decorrelation measurements with respect to depth that was explained in Section 3 concludes that the number of samples from 1 till 450 (centre at 225 samples) should be used in the position estimation algorithm to give accurate results.

Figure 7a shows the image when the scan line data were plotted consecutively. The data were collected by scanning over the phantom, with the help of the mechanical rig. The probe moves back and forth to perform a linear scan while the rotational angles are kept constant. It can be observed in Figure 7a that the image has been stretched from the start and the end because of the probe moving at the lowest speed. Figure 7b shows the mean of absolute differences (MAD) values for the echo data. It could be observed that the (MAD) values increase gradually until it reaches a maximum value and then start decreasing, for one full scan in one direction. This is related to the movement of the probe because as the probe starts scanning from one corner to the other corner of the phantom, its speed follows a similar pattern. The start and end of a scan in Figure 7a can be correlated with the minimum value of (MAD) in Figure 7b.

Figure 8a shows the top half section of the phantom, which is considered for clustering. Figure 8b–d shows all three clusters obtained using k-means, SFCM and GMM clustering, respectively. The data points in black indicate the anechoic cluster, the white colour indicates the points in the hyperechoic cluster and the points in red are in the hypoechoic cluster. It can be observed that these different types of clustering algorithms classify the same data points differently.

Figure 8b shows the clusters obtained by using k-means clustering that uses standard Euclidean distance metric to create clusters, which is usually insufficient for image clustering. It manages to create three clusters, but classify most of the intensity values into a hyperechoic cluster rather than in the hypoechoic region. In the case of in vivo scans, K-means will inaccurately classify the soft tissues into the hyperechoic cluster. The crucial information about the motion of the probe that could be obtained from the soft tissues will not be included. This will affect the accuracy of speed’s estimates calculated by measuring the decorrelation between successive scanlines.

Figure 8c shows the clusters obtained by using spatial fuzzy c-means clustering (SFCM) that classifies every data point by its membership values, which indicates the likelihood of that point belonging to that cluster. The spatial relationship of neighbouring pixels has also been considered while creating these clusters. However, it is inaccurately classifying most of the top layered data points into anechoic regions (noise), thus leaving fewer points to be considered for speed calculation. The drawback of SFCM is that it is sensitive to noise. Hence in the above results, it can be observed that the result seems to be affected by noise at the top layer of the phantom.

A Gaussian mixture model using expectation maximization (GMM-EM) has been evaluated and the clusters obtained can be seen in Figure 8d. SFCM clustering is truly concentrated on updating new centroids and then the membership function. Whereas, GMM-EM includes the necessary information on the mean and variance of the individual regions to obtain optimum results. From the above result, it can be observed that this method is choosing the correct data points for each cluster and not classifying data points inaccurately in either anechoic or hyperechoic regions. This will classify the data points containing soft tissues in the hypoechoic cluster accurately.

Figure 9a shows the estimated speed values of the probe using different clustering algorithms along with the measured (actual) speed values. The speed values were calculated using the ego-motion estimation (mean of absolute differences between successive scanlines) algorithm and Kalman filter on the clustered echo data. Probe’s position as shown in Figure 9b is estimated by integrating the speed values. These values are then compared with the actual position values. The graph in red shows the measured speed and distance values, blue shows the estimates without using any clustering techniques, pink shows the result of SFCM, green shows K-means and black shows the speed and distance estimates calculated using GMM. This is the result of one of the phantom’s scans.

The phantom that has been used has grey-scale targets for monitoring the contrast and temporal resolution as shown in Figure 10f. The 0.1 mm vertical pins have 3 cm spacing between each other and are used to measure horizontal distance accuracy. It can be seen in Figure 10e where no clustering technique has been used that the vertical pins are not spaced equally and have spacing distances of 3.8 cm, 3.6 cm and 4.1 cm, respectively. GMM in Figure 10b makes the vertical pins almost equidistant from each other, and the distances are 3.2 cm, 2.9 cm and 3.05 cm. Greyscale targets are supposed to be round and 10 mm in diameter. By comparing these targets, when no clustering technique is used, targets are being stretched, whereas K-means (Figure 10a) and SFCM (Figure 10c) are shrinking them. GMM makes it appear like a circle, thus correcting the image geometry.

The probe’s position estimates calculated using these different techniques have been compared by using the quality parameters such as mean percentage error, maximum percentage error, min percentage error, mean square error, RMS error and computational time. The equations to calculate these metrics are presented below. Mean percentage error is the error calculated by taking the mean of 50 phantom images and 30 bladder images. The mean percentage error $\left(PE\right)$ for not using any clustering technique is 28.7%, K-means is 12.3%, SFCM is 14.99% and GMM is 4.2% as shown in

Table 3. Quantitative analysis of clustering techniques for estimating probe’s position.

Quantitative Metrics	Without Clustering	K-Means	SFCM	GMM
Mean PE (%)	28.7	12.3	14.9	4.2
Max PE (%)	57.2	59.1	18.8	20.9
Min PE (%)	22.4	0.011	0.017	0.001
MSE (10${}^{-5}$)	37	5.5	15	2.1
RMSE (10${}^{-2}$)	1.94	0.74	1.22	0.46
Time (s)	0	2.72	5.7	291

. The root mean square error $\left(RMSE\right)$ for not using any clustering technique is $1.94\times {10}^{-2}$, K-means is $0.74\times {10}^{-2}$, SFCM is $1.22\times {10}^{-2}$ and GMM is $0.46\times {10}^{-2}$.

Where Mean PE is the mean percentage error, Max PE is the maximum percentage error, Min PE is the minimum percentage error, MSE is the mean square error and RMSE is the root mean square error.

The equations to calculate these errors are presented below:

$$P.E=\frac{\left|D_{estimated}-D_{actual}\right|}{D_{actual}}\times 100$$

(24)

Whereas, $D_{estimated}$ is the distance covered by the probe for one complete scan in one direction, which was calculated using the ego-motion estimation algorithm and $D_{actual}$ is the distance measured with the picolog.

$$MSE=\frac{1}{n}\sum _{i=1}^n{(D_{estimated}-D_{actual})}^2$$

(25)

where, n is the number of scans used to quantitatively analyse the estimation algorithm, which is equal to 50 scans in this case.

$$RMSE=\sqrt{MSE}$$

(26)

GMM outperforms in all these quality parameters except the computational time, as it takes 291 s therefore making it computationally expensive as compared to other given clustering techniques. Thus, from Table 3, GMM gives the better segmentation result, but is a computationally expensive algorithm to implement.

4.3. In Vivo Experiments

Figure 11 shows the clusters obtained by using each type of clustering technique on bladder data obtained by using the low-cost ultrasound scanner.

The final image obtained using the ego-motion estimation algorithm on different types of clustered data can be seen in Figure 12 where Figure 12d shows the actual bladder image considering the probe’s position readings measured with the data logger. Figure 12e shows the bladder image obtained by using the unclustered data to calculate the probe’s position with the help of the ego-motion estimation algorithm. It can be observed that the geometry of the image is not accurately estimated as it is stretching the image. Figure 12a–c shows the result by using K-means, GMM and SFCM clustering techniques. There is an improvement in the position estimates by using the clustering technique as compared to not using any technique. GMM works the best in correcting the image geometry.

The use of clustering algorithms has substantially improved the quality of the egomotion estimation algorithm and hence the geometric accuracy of the images produced by the freehand scanner. These clustering methods have reduced its sensitivity to non-ideal operator behaviour and variation in tissue types.

The work presented in this paper has shown promising results by reconstructing a geometrically correct 2D, B-mode ultrasound image of the raw echo data collected from a simple, single-element ultrasound probe. The use of the proposed novel signal processing algorithm has enabled the system to produce high-quality ultrasound images at a fraction of the cost of traditional systems. The current ultrasonic parameters (frequency band, beam shape) are the best estimate of what is suited to abdominal imaging. However, there are numerous directions for future investigation to enhance the imaging performance of such a scanner, optimise for different imaging applications and assess the clinical potential of such a device. These are explained in detail in the Section 5 below.

5. Conclusions and Future Work

The production cost of the very low-cost medical ultrasound imaging system was reduced to approximately USD 100 by replacing a multi-element piezoelectric transducer array with a single piezoelectric element. This probe design greatly reduces the hardware complexity, power consumption and beamforming computational load. Raw echo data were gathered by scanning the transducer over the phantom or the skin in a freehand linear/polar motion or with the help of a specially designed mechanical rig. These data were transmitted to the computer via Wi-Fi for further processing.

The research presented in this article describes the design and implementation of image formation techniques for a linear scan. In the free-hand linear scan, the probe is manually scanned over the desired region of interest (ROI), by translating it from one direction to the other while keeping the orientation near constant. A novel position estimation algorithm is proposed, which measures the decorrelation between successive scanlines to estimate the probe’s velocity. With the aid of an unscented Kalman filter (UKF), this is used to estimate the probe’s position. Clustering is used to make the position estimation algorithm be robust in more complex scenes and variable tissue properties in human scans. For the first time, the Gaussian mixture model (GMM), spatial fuzzy c-means (SFCM) and k-means clustering techniques have been exploited on a 1D raw echo data.

Quantitative analysis for estimating probe’s position was carried out, and it is observed that the Gaussian mixture model (GMM) works the best in classifying the desired data points in the correct cluster and reduces the mean percentage error, for estimating a probe’s position, from 28.7% to 4.2% and mean square error from 37 × 10${}^{-5}$ to 2.1 × 10${}^{-5}$ cm². Although, this method is computationally expensive as compared to other presented techniques: SFCM and K-means. The reason that the other two clustering methods do not give the best result is because k-means uses a standard Euclidean distance metric to create clusters which is usually insufficient for image clustering. Also, SFCM clustering is truly concentrated on updating new centroids and then the membership function. Whereas, GMM includes the necessary information on the mean and variance of the individual regions to obtain optimum results. It could be concluded that the clustering algorithms have substantially improved the quality of egomotion estimation and hence the geometric accuracy of the images produced by the freehand scanner. These clustering methods have reduced its sensitivity to non-ideal operator behaviour and variation in tissue types. Initial in vivo experiments have shown promising results for clinical diagnosis, and with further work this technique has the potential to deliver a very low-cost ultrasound probe design for use in the developing world.

Future Work

The feasibility of a freehand scanner based on ego-motion estimation has been demonstrated, making use of unsupervised learning techniques to improve geometric accuracy. The implementation of these algorithms was based on the condition that the ultrasound probe would have moved in a linear manner (having only translation and almost no rotation in any of the axes). The ultimate goal of this project is to design the image formation algorithms for a single-element, free-hand ultrasound scanner. And indeed, the free-hand motion includes multiple and time-variant rotations on different axes. Therefore, future work is required to enable the algorithms to work in the case of combined motions (translation and rotation) by using the clustering techniques and ego-motion algorithm together with the motion sensor data.

The current ultrasonic parameters (frequency band, beam shape) are the best estimate of what is suited to abdominal imaging. However, there are numerous directions for future investigation to enhance the imaging performance of such a scanner, optimise for different imaging applications and assess the clinical potential of such a device:

• Physical beam shape—in a fixed focus ultrasonic design, it is clear that the beam width and depth of focus have a strong influence on the backscattered signals and hence both the image resolution and the performance of correlation-based ego-motion estimation. More investigation is required to understand this relationship and to determine the optimum parameters for different applications.
• Synthetic focusing—a fixed focus design places constraints on lateral resolution vs. depth. It is interesting to consider whether monostatic synthetic aperture concepts as in [9] could be applied to the freehand scanner. This is very challenging, however, due to the requirement for precise tracking/control of the transducer trajectory and orientation.
• Frequency band—the frequency band considered in this paper (fc = 4.2 MHz, B = 2 MHz) was chosen for abdominal imaging with penetration up to 15 cm. Other possible applications aimed at imaging more superficial structures (e.g., muscles, vascular, breast) would favour a higher frequency design and the scalability of the proposed scanner design and the algorithms needs to be investigated.
• Front end—the ultrasound front end design in these experiments is sub-optimal in terms of noise performance and this limits both the image SNR and the depth range, which can be effectively utilised for correlation. A review of the front-end amplifier and impedance matching arrangements has significant potential to improve on this.

Clinical applications— Once the design has been optimised, close collaboration with clinicians is needed in the future to assess the diagnostic potential of such a device in low-resource settings. The authors limited research on this suggests that the most promising applications are in basic obstetric monitoring in developing nations, bladder imaging for self-management of urological conditions and early detection of aortic aneurysms. Larger scale studies are required to compare images with “ground truth” obtained from high-end ultrasound scanners over a wide range of patients.