A Novel JSF-Based Fast Implementation Method for Multiple-Point Multiplication

Abstract

ECC is a popular public-key cryptographic algorithm, but it lacks an effective solution to multiple-point multiplication. This paper proposes a novel JSF-based fast implementation method for multiple-point multiplication. The proposed method requires a small storage space and has high performance, making it suitable for resource-constrained IoT application scenarios. This method stores and encodes the required coordinates in the pre-computation phase and uses table lookup operations to eliminate the conditional judgment operations in JSF-5, which improves the efficiency by about 70% compared to the conventional JSF-5 in generating the sparse form. This paper utilizes Co-Z combined with safegcd to achieve low computational complexity for curve coordinate pre-computation, which further reduces the complexity of multiple-point multiplication in the execution phase of the algorithm. The experiments were performed with two short Weierstrass elliptic curves, nistp256r1 and SM2. In comparison to the various CPU architectures used in the experiments, our proposed method showed an improvement of about 3% over 5-NAF.

1. Introduction

1.1. Related Work

Elliptic curve cryptography (ECC) is a public-key cryptography algorithm, which has been a rapidly developing branch of cryptography in recent years, based on elliptic curve theory from number theory. The method constructs a public-key cryptosystem on an elliptic curve’s finite group of domain points. Compared to ElGamal [1] and RSA [2], the key length required for ECC to achieve equivalent security is shorter, making it suitable for the IoT [3,4,5,6]. Blockchain [7] is widely used in [8]. Single-point multiplication is the most critical operation in ECC and is denoted as $kP$, where $P\in E\left({\mathbb{F}}_p\right)$ is a point on the elliptic curve $E/F_q$, and k is a scalar. $kP$ indicates that the points P on the elliptic curve are summed k times. Multiple-point multiplication is the most important operation in the elliptic curve digital signature algorithm [9] (ECDSA) and it is denoted $kP+lQ$.

In recent years, optimizing the single-point multiplication in elliptic curve cryptography (ECC) has been an important research direction for many scholars. Currently, the mainstream algorithms include the binary double-and-add method [10], non-adjacent form (NAF) [11,12], and windowed non-adjacent form [13]. The core idea of these algorithms is to reduce the average Hamming weight of the scalar to decrease the extra computation in ECC. However, some algorithms may introduce additional pre-computation [14,15]. The ECDSA requires more optimization for multiple-point multiplication, and to achieve this, joint sparse form (JSF) was proposed in [12], but the complexity of computing JSF coefficients is high. The joint Hamming weight of the scalar generated by JSF has no advantage over NAF. Based on JSF, Li et al. [16] extended the character set to a five-element joint sparse form, JSF-5, which can reduce the average joint Hamming weight from $0.5l$ to $0.38l$, where l is the length of data. Then, Wang et al. [17] proposed a new JSF-5 algorithm based on this, which can further reduce the average joint Hamming weight to $l/3$. Although JSF has been continuously improved to reduce the average joint Hamming weight, the difficulty of computing the joint sparse form of multiple points has yet to be addressed. In this paper, we propose an improved method to generate JSF-5.

For optimizing multiple-point multiplication, Ref. [18] proposed a bucket set construction that can be utilized in the context of Pippenger’s bucket method to speed up MSM over fixed points with the help of pre-computation. Ref. [19] proposed Topgun, a novel and high-performance hardware architecture for point multiplication over Curve25519. Ref. [20] presented a novel crypto-accelerator architecture for a resource-constrained embedded system that utilizes ECC.

In recent years, there have been numerous studies on optimizing single-point multiplication but relatively few studies on optimizing multiple-point multiplication. Research on multiple-point multiplication has mainly focused on optimizing hardware circuit designs. Some studies have proposed excellent optimization algorithms but they still follow the original computational approach, where the coordinates of the points involved in the execution phase are still in the Jacobian coordinate system.

Safegcd is a fast, constant-time inversion algorithm; traditional binary Euclidean inversion takes over 13,000 clock cycles. In [21], safegcd required 8543 clock cycles on the Intel Kaby Lake architecture, and the researchers have continued to optimize it. On the official safegcd website [22], researchers have implemented an optimized version that requires only 3816 clock cycles on the Intel Kaby Lake architecture. The superiority of safegcd has also provided new solution approaches for other algorithms. In [23], researchers proposed three polynomial multiplication methods based on NTT and implemented them on Cortex-M4 microcontrollers using safegcd. Similarly, researchers [24] have studied public key compression capabilities using safegcd.

In the standard method for the ECDSA, we input a point like $(x,y)$ as the affine coordinates and then transform the point into Jacobian coordinates like $(X,Y,Z)$ to compute the result. However, in the end, we need the final result for the point in affine coordinates. This transformation needs many inversion operations, and points in Jacobian coordinates require the computation of the Z coordinate. This is a rather time-consuming operation. We need the fastest way to invert the coordinates of the points. Safegcd has brought new ideas for the further optimization of multiple-point multiplication. We can use safegcd to restore the pre-computed coordinates $(X,Y,Z)$ required for ECC to $(x,y)$. We can significantly reduce the data length and lower the computational overhead during the ECC execution phase.

In the ECDSA, summing refers to point addition. Point addition is not the same as the usual addition. This depends on the operation rules in ECC. We can use the Co-Z formula to improve the speed of point addition. The Co-Z formula [25] is a point addition algorithm that allows for very efficient point addition with minimal overhead and is explicitly designed for projected points that share the same Z coordinates. The Co-Z formula also has advantages over left-to-right [26] binary methods. Based on this, researchers [27] have proposed an improved Co-Z addition formula and optimized register allocation to adapt to different point additions on Weierstrass [28] elliptic curves. In addition, scholars [29,30] have proposed several improved Montgomery algorithms.

The Co-Z formula has been widely used in compact hardware implementations of elliptic curve cryptography, especially on binary fields. In particular, in [31], the Co-Z formula was applied to radio frequency identification and successfully reduced the required number of registers from nine to six while balancing compactness and security [32]. Additionally, Ref. [33] proposed a compact Montgomery elliptic curve scalar multiplier structure that saves hardware resources by introducing the Co-Z formula.

However, the efficiency of the Co-Z formula implementation depends on the length of the Euclidean addition chain. To address this issue, Refs. [34,35] considered the conjugate point addition algorithm [36], which inherits the previous security properties and can naturally resist SPA-type attacks [37] and security error attacks [38,39]. Due to the efficiency of Co-Z, Ref. [40] proposed an improved ECC multiplier processor structure based on Co-Z. The modular arithmetic components in the processor structure were highly optimized at the architectural and circuit levels. Then, Ref. [41] proposed an improved Montgomery multiplication processor structure based on RSD [42]. Ref. [43] proposed a set of Montgomery scalar multiplication operations based on Co-Z. On general, short Weierstrass curves with characteristics greater than three, each scalar bit requires only 12 field multiplications using eight or nine registers. Co-Z was initially proposed to optimize point operations, but now researchers focus more on saving hardware resources [44,45,46], and there is relatively little research on multiple-point multiplication in ECC.

We can change our method to assembly form to obtain more significant optimization. BMI2 instructions are one of the extensions to the bit-manipulation instruction set provided by Intel and AMD processors, and they are also an essential part of the x86-64 instruction set. On a 64-bit platform, we need four 64-bit registers to perform a 256-bit data operation that involves handling carry flags. However, the operations of the BMI2 instruction set only affect specific carry flags and support ternary instructions, making them more efficient and flexible. The BMI2 instruction set allows us to perform up to four large-number operations simultaneously.

1.2. Objectives and Contribution

The focus of this paper is on optimizing the multiple-point multiplication operation. The contribution of this paper is its study of the optimized implementation of the NIST P-256 curve (nistp256r1) [47] and the SM2 [48] curve based on related research [49,50,51,52,53].

We propose the new idea of utilizing the safegcd algorithm for coordinate transformation during the pre-computation phase. Based on this idea, we optimized and improved the computations in each stage. We were able to introduce the Co-Z algorithm for optimizing the double-point operations thanks to our idea. We re-encode and store the results after pre-computation, making subsequent calculations easier.

We propose an improved encoding method that enhances JSF-5, optimizing the internal memory encoding method and solving the problem of using many conditionals in the operation process. When the improved method was run, we observed that the length of data involved in each round of computations affected efficiency. To address this issue, we improved the method and introduced the new encoding JSF-5 segmentation method.

Finally, the optimization was implemented at the assembly level, leveraging the BMI2 instruction set. We report the experimental results using four CPU architectures and validate our theory. Our research has promising applications in the fields of information encryption, information communication security, blockchain and the IoT. It offers a new method to optimizing ECC, providing novel solutions.

Our improved JSF-5 method differs significantly from the original JSF-5 algorithm. Firstly, our approach leverages the advantages of the BMI2 instruction sets, eliminating the overhead of conditional checks during runtime. This trade-off allows us to significantly improve performance while sacrificing only a small portion of the storage space. Additionally, thanks to the segmented data processing, our method exhibits decreasing time complexity with each round. Furthermore, we encode the generated sparse form by storing the bilinear scalar information in an array.

We still want to emphasize that our method may not be the best, but we hope our research can inspire other researchers and receive positive feedback so that we can improve together.

This article is organized as follows. Section 2 describes elliptic, nistp256r1, and SM2 curves and provides some basic arithmetic definitions. Section 3 discusses the relevant optimizations in our proposed method for the pre-computed phase. Accordingly, for the optimization of the execution phase of the algorithm, we present the relevant optimization methods in Section 4. In Section 5, we compare the performance of the proposed method through experiments. Finally, we provide a conclusion drawn from this research in Section 6.

2. Preliminaries

2.1. Basic Operation

An elliptic curve $E:y^2=x^3+ax+b$ refers to a set of points defined over the prime field ${\mathbb{F}}_p$, where $p>3$, $a,b\in {\mathbb{F}}_p$, and $4a^3+27b^2\ne 0$. This condition is imposed to ensure that the curve does not contain singular points. This equation is known as the Weierstrass standard form of the elliptic curve. Adding $P+Q$ between any two points P and Q on the curve is defined as a fundamental operation. If $P\ne Q$, $P+Q$ is called point addition, and if $P=Q$, $P+Q=2P$ is called point doubling. The scalar multiplication $k·P$ on the curve indicates multiplying a point by a scalar, where k is a non-negative integer.

The performance of various field operations is what primarily determines the efficiency of ECC. The cost associated with the described point operations is measured by the number of operations performed on the finite field where the elliptic curve is defined. These operations include field multiplication (M), field squaring (S), and inversion (I) and are commonly referred to as large-number operations. However, thanks to continuous hardware advancements and iterations, modern computers have reached a point where the efficiency of field multiplication and squaring is nearly comparable to that of field addition (A). As a result, when evaluating the complexity of algorithms, it has become necessary to account for the cost of field addition.

To increase the computational efficiency of ECC, we can transform the elliptic curve in affine coordinates (denoted as $\mathcal{A}$) into Jacobian coordinates (denoted as $\mathcal{J}$) for operations. The point coordinates in the affine coordinate system are represented as $(x,y)$, and the point coordinates in the Jacobian coordinate system are represented as $(X,Y,Z)$. The conversion between them is given by $x=X/Z^2$ and $y=Y/Z^3$, with a modulo operation concerning the order of the prime field. Let P and Q be points in Jacobian coordinates and t be the computation time. Suppose $P=(X_1,Y_1,Z_1)$ and $Q=(X_2,Y_2,Z_2)$. We want to compute $P+Q$ and $2P=(X_3,Y_3,Z_3)$, as shown in Table 1.

Table 1. Basic operation.

Calculate $\mathit{P}+\mathit{Q}$, ${\mathit{Z}}_2\ne 1$

$A=X_1{Z}_1^2,B=X_2{Z}_1^2,C=Y_1{Z}_2^3,D=Y_2{Z}_1^3$

$E=B-A,F=D-C$

$X_3=-E^3-2A{E}^2+F^2,Y_3=-C{E}^3+F(A{E}^2-X_3),Z_3=Z_1{Z}_{2}E$

Calculate $2P$.

If $a=-3$, the arithmetic cost can be reduced to $4M+4S+10A$

$S=4X_1{Y}_1^2,M=3X_1^2+a{Z}_1^4$

$X_3=M^2-2S,Y_3=M(S-X_3)-8Y_1^4,Z_3=2Y_1{Z}_1$

t($2\mathcal{J}$) = $4M+6S+9A$

Calculate $P+Q$, $Z_2\ne 1$

$C=Y_1{Z}_2^3,E=X_2-X_1,F=Y_2-Y_1$

$X_3=-E^3-2X_1{E}^2+F^2,Y_3=-C{E}^3+F(X_1{E}^2-X_3)$

$Z_3=Z_{2}E$

t($\mathcal{J}+\mathcal{J}$) = $8M+3S+7A$

After the entire computation process, the ECC must convert the result in Jacobian coordinates to a point in affine coordinates, which requires a modular inverse operation.

2.2. 256-Bit Curve

This article is based on the short Weierstrass elliptic curve $E:y^2=x^3-3x+b$.

The National Institute of Standards and Technology (NIST) [47] is a non-regulatory federal agency within the Technology Administration of the U.S. Department of Commerce. Its mission includes the development of federal information processing standards related to security. NIST curves are cryptographic protocol standards published by the NIST. These curves have predictable mathematical properties and security and are widely used for digital signatures, key exchange, and authentication. The most commonly used curves are the NIST p-256 and p-384 curves, whose names are derived from the bit lengths of the prime number p used in the curve equation. The nistp256r1 curve is defined on $y^2=x^3-3x+b$, and the results presented in this article are related to optimizing the nistp256r1 curve. The parameters of the nistp256r1 curve are given in Table A1.

SM2 [48] is an elliptic curve cryptography algorithm developed in China and published by the Chinese State Cryptography Administration. It has been widely used in various network communication systems and e-government systems. The official curve used by the SM2 algorithm is $y^2=x^3-3x+b$, and it is recommended to use a prime field with 256 bits of data and fixed parameters, as shown in Table A2.

2.3. Other Operations

In some algorithms, we need to compute and store the triple point during the execution of ECC. The traditional standard implementation uses the two operations of multiple-point multiplication $2P$ and point addition $2P+P$. Some scholars [54,55,56] have studied how to compute triple points efficiently. Ref. [57] presented an optimized algorithm for calculating triple points, which is called Tripling. In Table A3, we show the computational complexity of Tripling. In a common analysis process, the time complexity of an algorithm is measured based on the number of different operations. In Section 2.1, we present the definitions of M, S, A, and I. These symbols denote various basic operations in all figures and tables.

The safegcd algorithm is a fast, constant-time modular inverse algorithm used for computing point coordinate recovery in elliptic curve cryptography. In this paper, the safegcd algorithm is used to recover the coordinates of points on elliptic curves. Our test data are shown in Table 2.

Table 2. Clock cycles required by safegcd algorithm for modular inversion with Curve25519 on different CPU architectures.

Raptor Lake	Comet Lake	Coffee Lake	Zen 4
2975	2876	2970	2818

An improved $2P+Q$ algorithm was proposed in [56,58] to replace the traditional double-and-add algorithm that can effectively reduce the number of doubling operations. Then, the authors of [59,60] improved the original $2P+Q$ algorithm by combining it with Co-Z. $2P+Q$ is more suitable for single-array operations. As shown in Table A4, if the Q point involved in the operation has a Z-coordinate of one, the complexity of point addition after processing can be reduced from $12M+4S+7A$ to $8M+3S+7A$, which improves the efficiency of the original $2P+Q$ algorithm.

This section mainly describes and theoretically analyzes the related algorithms for scalar multiplication $kP$ and various sparse forms. In this section, we learn that the efficiency of multiple-point multiplication directly affects the overall efficiency of ECC execution.

In the multiple-point multiplication $kP+lQ$, P and Q are points on the elliptic curve, and assuming that the order of this elliptic curve is n, then $k,l\in [1,n-1]$. If the point is $P=(x,y)$, then $-P=(x,-y)$. After converting the scalar into a sparse form, there are two approaches to performing the calculation: from left-to-right and from right-to-left [61]. We use the left-to-right approach in our calculation.

If the scalars k and l are converted to binary sparse form $k=\sum k_i{2}^i,l=\sum l_i{2}^i$, then the general idea of left-to-right binary multiple-point multiplication can be seen, as in Algorithm A1.

The sparse forms generated by different scalar transformation methods for scalars k and l vary in efficiency and may require some pre-computation to store repeatedly used points.

2.4. Sparse Form

2.4.1. NAF

Unlike conventional binary representation, the NAF uses signed numbers to represent the scalar k. The w-NAF form is a low-average-Hamming-weight $\mathcal{D}$ character representation form, where w is the base of the number system and is denoted as w-NAF for convenience. The Hamming weight of the generated sparse form strongly depends on w, and the average Hamming weight of the generated single scalar is $1/w+1$.

Table 3 shows the average Hamming weight from different NAF documents. The larger the window size, the more points need to be pre-computed and the higher the overall computational cost will be. Algorithm A3 implements the w-NAF method.

Table 3. Average Hamming weight recorded in NAF documents for different character sets, where l is the corresponding NAF length.

w	${\mathcal{D}}_{\mathit{w}}$	Hamming Weight
2	$0,\pm 1$	$l/3$
3	$0,\pm 1,\pm 3$	$l/4$
4	$0,\pm 1,\pm 3,\pm 5,\pm 7$	$l/5$
5	$0,\pm 1,\pm 3,\pm 5,\pm 7,\pm 9,\pm 11,\pm 13,\pm 15$	$l/6$

2.4.2. JSF

JSF is an algorithm for two scalars that considers the bit values of two scalars at the same position during the generation process, thereby reducing the number of generation calculations. In comparison, the NAF algorithm for two scalars requires two-generation calculations. By computing the JSF of multiple scalars, the corresponding sparse form can be obtained with only one computation, giving the NAF algorithm a significant advantage.

When the character set size is 3, the JSF form uses a character set of $\{0,\pm 1\}$, and the points to pre-compute are $P+Q$ and $P-Q$, a total of two points. When the character set size is 5, we refer to JSF-5, which requires pre-computing $3Q,P+Q,P-Q,3P+Q,3P-Q,$$P+3Q,P-3Q,3P+3P$, and $3P-3Q$ for a total of nine points. Algorithm A4 describes the flow of the JSF-5 algorithm as presented in the literature. Table 4 compares two different JSF algorithms.

Table 4. Comparison of different JSF algorithms, where l is the length of the data.

Algorithm	Hamming Weight	Number of Point Additions
JSF	$l/2$	$l/2$
JSF-5	$l/3$	$l/3$

To be consistent with the actual situation, we generated one million sets of random data using the Intel random number generator, transformed them into different sparse forms, and then reconstructed their joint Hamming weight distribution to facilitate the subsequent theoretical analysis, as shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6.

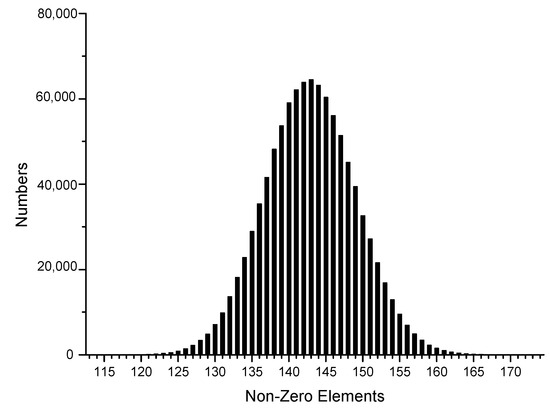
Figure 1. NAF.

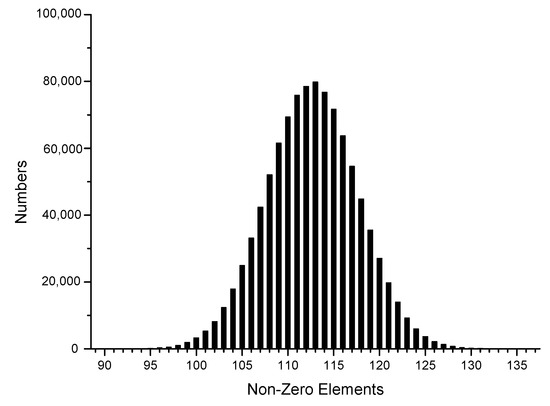
Figure 2. 3-NAF.

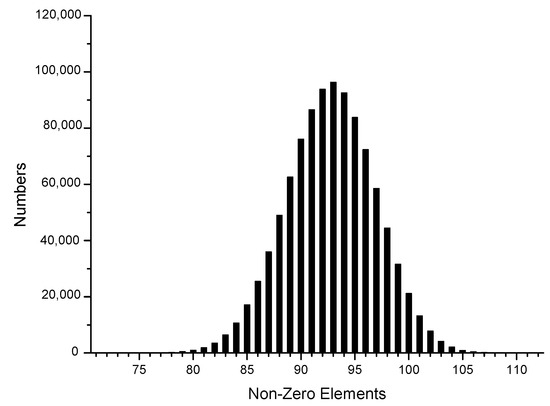
Figure 3. 4-NAF.

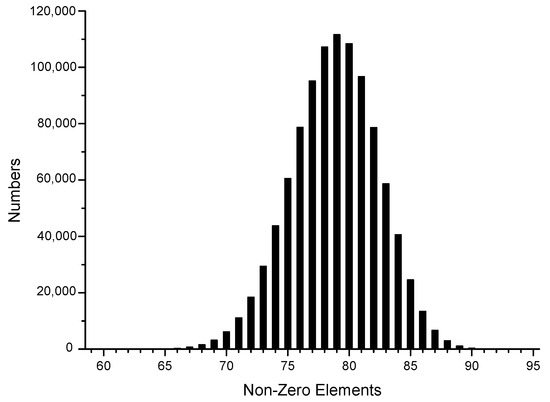
Figure 4. 5-NAF.

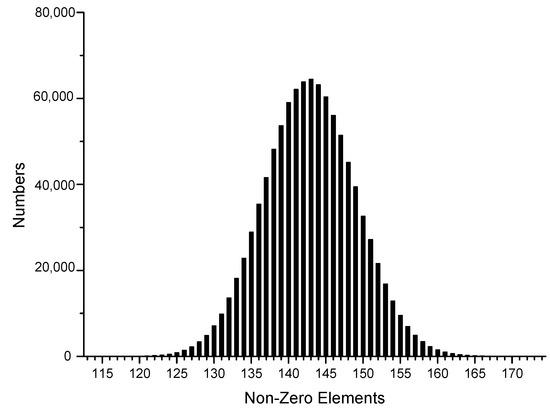
Figure 5. JSF.

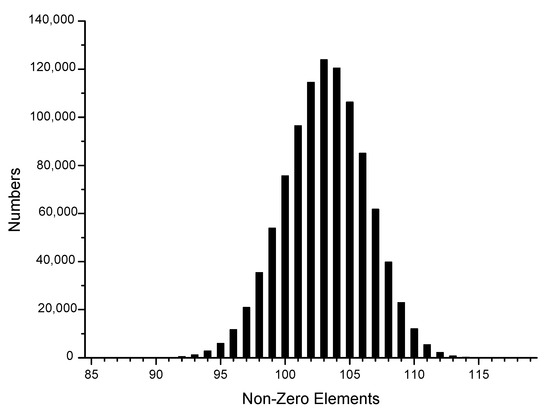
Figure 6. JSF-5.

The x-axis in the figures represents the number of non-zero elements in sparse form, and the y-axis represents the number of corresponding data elements among one million datasets. It can be observed that the window size chosen in the sparse form algorithm significantly affected the proportion of non-zero elements in the sparse form. In the case of the NAF algorithm, most of the joint sparse forms generated had 143 non-zero elements, with 3-NAF having the highest proportion of 114 non-zero elements. Similarly, we organized the results for other sparse forms, as shown in Table A5.

3. Using Coordinate Inversion for Pre-Computed Data

In this section, we discuss and propose an optimization scheme for multiple-point multiplication and analyze the algorithm based on the various optimization algorithms introduced in the previous section.

3.1. Pre-Computed Complexity Analysis

Due to the high efficiency of safegcd, we can reduce the coordinates of the pre-computed points $(X,Y,Z)$ in various JSFs back to $(x,y)$ using modulo inverse operations, where the reduced Z coordinate is 1 by default. The concern at this point is whether the overhead of the execution phase saved by using two coordinate inversions is more than the additional time overhead consumed in the NAF. Table 5 compares our proposed method based on optimization ideas. Next, we analyzed each algorithm execution phase based on the data in Section 2, as shown in Table 6.

Table 5. Sums of different basic operations in theory for pre-computation phase.

Algorithm	Sum of Basic Operation	Case One	Case Two	Case Three
NAF	0	0	0	0
3-NAF	$12M+7S+17A$	$21M$	$22.7M$	$26.1M$
4-NAF	$36M+15S+31A$	$54.2M$	$57.3M$	$63.5M$
5-NAF	$84A+31S+59A$	$120.6M$	$126.5M$	$138.3M$
JSF	$10M+4S+11A+I$	$95.4M$	$86.5M$	$78.7M$
Proposed method	$67M+22S+56A+I$	$175.8M$	$171.4M$	$172.6M$

Table 6. Sums of different basic operations in theory for execution phase.

Algorithm	Sum of Basic Operation	Case One	Case Two	Case Three
NAF	$2396M+1536S+3754A+I$	$4455.6M$	$4821M$	$5561.8M$
3-NAF	$2320M+1475S+3460A+I$	$4272M$	$4608M$	$5290M$
4-NAF	$2060M+1391S+3278A+I$	$3908.4M$	$4226.2M$	$4871.8M$
5-NAF	$1880M+1321S+3152A+I$	$3647.2M$	$3952.4M$	$4572.8M$
JSF	$2311M+1167S+3132A+I$	$3951M$	$4254.2M$	$4870.6M$
Proposed JSF-5	$1951M+1127S+2972A+I$	$3527M$	$3814.2M$	$4398.6M$

Table 7 shows the statistics for the combined overhead for different algorithms in the pre-computation and execution phases. It can be seen that the pre-computed, coordinate-reduced JSF-5 algorithm had a minor computational overhead and a low joint Hamming weight. However, the computational complexity of the coefficients generated with the JSF-5 algorithm and how we can reduce the difficulty of JSF-5 coefficient computation are the challenges we had to solve. Next, we solved this problem by first optimizing the implementation of the pre-computed data storage code.

Table 7. The total sums of different basic operations in theory for pre-computation and execution phases (excluding the sparse form generation cost).

Algorithm	Sum of Basic Operation	Case One	Case Two	Case Three
NAF	$2396M+1536S+3754A+I$	$4455.6M$	$4821M$	$5561.8M$
3-NAF	$2332M+1482S+3477A+I$	$4476.6M$	$4843.7M$	$5587.9M$
4-NAF	$2096M+1406S+3309A+I$	$3962.6M$	$4283.5$	$4935.3M$
5-NAF	$1964M+1352S+3211A+1I$	$3767.8M$	$4078.9M$	$4711.1M$
JSF	$2321M+1171S+3143A+2I$	$4046.4M$	$4340.7M$	$4949.3M$
Proposed JSF-5	$2018M+1149S+3028A+2I$	$3702.8M$	$3985.6M$	$4571.2M$

3.2. Pre-Computed Storage Table Encoding

Storing the pre-computed data with the appropriate encoding can reduce the evaluation overhead in the fetch operation. Table 8 shows the encoding of the data when we set $P=1$ and $Q=5$.

Table 8. Encoding when $P=1$ and $Q=5$.

Operation	Encoding	Operation	Encoding
P	1	Q	5
$Q-P$	4	$P+Q$	6
$3P$	3	$3Q$	15
$3Q+P$	16	$3Q-P$	14
$Q+3P$	8	$Q-3P$	2
$3Q-3P$	12	$3P+3Q$	18

The calculation shows that the encoding is not continuous. Furthermore, to reduce the data range, the encoding is corrected, and the new encoding after correction is shown in Table 9.

Table 9. Encoding for storing pre-computed coordinates.

Operation	Encoding	Operation	Encoding
P	1	Q	5
$Q-P$	4	$P+Q$	6
$3P$	2	$3Q$	10
$3Q+P$	11	$3Q-P$	9
$Q+3P$	7	$Q-3P$	3
$3Q-3P$	8	$3P+3Q$	12

Due to how the coordinate system works, $Q+P$ has the same Z coordinate as $Q-P$, and $Q+3P$ has the same Z coordinate as $Q-3P$. There are four different Z-coordinates in the data to be calculated.

We first define Algorithm 1, named function $XYZ(OA,OS,tZ,i,o)$, where $i,o$ is the input point, the point coordinates are in the form $(x,y)$, OA stores the output of $i+o$, $OS$ stores the output of $i-o$, and $tZ$ is the Z-coordinate of the two outputs. We then define the Algorithm 2, named function $XYZ1(OA,OS,tZ,i,o)$, which differs from function $XYZ$ in that the Z coordinate of the point involved in the operation is 1. Using a 64-bit integer array to store the data, the input coordinate length of function $XYZ1$ is 512 bits, occupying 8 array spaces; the input coordinate length of function $XYZ$ is 768 bits, occupying 12 array spaces. Algorithm 3 shows the process of pre-computing coordinates and storing them in encoding. Algorithm A5 shows the method of reducing coordinates during pre-computation.

Algorithm 1 Function $XYZ(OA,OS,tZ,i,o)$

Require: Point $i=(X_1,Y_1,Z_1),o=(X_2,Y_2,Z_2)$ Ensure: $tZ,OA=(X_a,Y_a,Z_a),OS=(X_s,Y_s,Z_s)$ 1: $ZZ\leftarrow Z_1^2$;      $ZZZ\leftarrow Z_1·ZZ$;      $X_2\leftarrow X_2·ZZ$; 2: $Y_2\leftarrow Y_2·ZZZ$;      $T\leftarrow X_2-X_1$;      $A\leftarrow T^2$; 3: $B\leftarrow X_1·A$;      $C\leftarrow X_2·A$;      $T_2\leftarrow Y_2-Y_1$; 4: $F_0\leftarrow Y_2+Y_1$;      $F\leftarrow F_0^2$;      $D\leftarrow T_2^2$; 5: $A\leftarrow C-B$;       $T_3\leftarrow C+B$;      $E\leftarrow Y_1·A$; 6: $X_a\leftarrow D-T_3$;      $X_s\leftarrow F-T_3$;      $T_3\leftarrow B-X_a$; 7: $Y_a\leftarrow T_3-E$;      $T_3\leftarrow X_s-B$;      $tZ\leftarrow Z_1·T$; 8: $T_3\leftarrow F_0·T_3$;      $Y_s\leftarrow T_3-E$;      $X_1\leftarrow B$; 9: $Y_1\leftarrow E$;      $Z_1\leftarrow tZ;$ 10: return $tZ,X_a,Y_a,X_s,Y_s$

Algorithm 2 Function $XYZ1(OA,OS,tZ,i,o)$

Require: Point $i=(X_1,Y_1),o=(X_2,Y_2)$ Ensure: $tZ,OA=(X_a,Y_a),OS=(X_s,Y_s)$ 1: $tZ\leftarrow X_2-X_1$;      $A\leftarrow t{Z}^2$;      $B\leftarrow X_1·A$ 2: $C\leftarrow X_2·A$;      $T_2\leftarrow Y_2-Y_1$;      $F_0\leftarrow Y_2+Y_1$; 3: $F\leftarrow F_0^2$;      $D\leftarrow T_2^2$;      $A\leftarrow C-B$; 4: $T_3\leftarrow C+B$;      $E\leftarrow Y_1·A$;      $X_a\leftarrow D-T_3$; 5: $X_s\leftarrow F-T_3$;      $T_3\leftarrow B-X_a$;      $T_3\leftarrow T_2·T_3$; 6: $Y_a\leftarrow T_3-E$;      $T_3\leftarrow X_s-B$;      $T_3\leftarrow F_0·T_3$; 7: $Y_s\leftarrow T_3-E$; 8: return $tZ,X_a,Y_a,X_s,Y_s$

Algorithm 3 Pre-computation

Require: Q-point coordinates Ensure: Pre-computed array $Pix[12\times 8]$ 1: $Pix[1\times 8]\leftarrow P$;      $Pix[5\times 8]\leftarrow Q$; 2: $Pix[2\times 8]\leftarrow P$;      $3Q\leftarrow Tripling\left[Q\right]$; 3: $Pix[10\times 8]\leftarrow 3Q$ 4: $XYZ1\left(Pix\right[6\times 8],Pix[4\times 8],Z1,Q,P)$ 5: $XYZ1\left(Pix\right[7\times 8],Pix[3\times 8],Z2,Q,3P)$ 6: $XYZ\left(Pix\right[11\times 8],Pix[9\times 8],Z3,3Q,P)$ 7: $XYZ\left(Pix\right[12\times 8],Pix[8\times 8],Z4,3Q,3P)$

4. Improving the Operational Efficiency of the Method Execution Phase

In the previous section, we encoded and implemented a single-array representation of the JSF by pre-computing the data; next, we need to optimize the data fetch in the execution phase.

4.1. JSF-5 Encoding Method and Table Look-Up Method

By encoding, we can combine the two arrays generated by the JSF-5 algorithm into one while making the stored data and the pre-computed storage table correspond, thus eliminating the evaluation parts of these operations and reducing the overall overhead of the execution phase. First, we developed a new JSF-5 single-array method that combines the two arrays it generates into one. We show the details of this method in Algorithm A2.

The JSF-5 single-array algorithm changes the values of $x_j$ and $y_j$ based on the parity of the scalars involved in each round and computes the result for the current bit based on these two values. This process requires a large number of evaluation operations. Therefore, we improved the algorithm by looking up the table operation to directly take out the corresponding values, thus eliminating the judgment and related operations. By analyzing the algorithm, we can eliminate the $\overline{mod}8$ operation in the algorithm and directly build the corresponding statistics table using the result for $mod8$ as an intermediate variable. As the output value of each round of operations is determined by the last three digits of the scalar, we first analyze the output in different cases based on the algorithmic operation logic while preserving the last three digits of the scalar:

• If the scalars involved in the operation are all even, then the current bit of the JSF-5 result is 0; the output results are shown in Table 10;
  Table 10. Both scalars are even, and $x_j=xmod8$ and $y_j=ymod8$.

  ${\mathit{x}}_{\mathit{j}}$	${\mathit{y}}_{\mathit{j}}$	Output	${\mathit{x}}_{\mathit{j}}$	${\mathit{y}}_{\mathit{j}}$	Output
  6	6	0	6	2	0
  6	4	0	6	0	0
  4	4	0	4	6	0
  4	2	0	4	0	0
  2	6	0	2	4	0
  2	2	0	2	0	0
  0	6	0	0	0	0
  0	2	0	0	4	0

• If the scalars are all odd, according to the algorithm, the expected output result will correspond to the storage code; the output results are shown in Table 11;
  Table 11. Both scalars are odd.

  ${\mathit{x}}_{\mathit{j}}$	${\mathit{y}}_{\mathit{j}}$	Output	${\mathit{x}}_{\mathit{j}}$	${\mathit{y}}_{\mathit{j}}$	Output
  7	7	−6	7	5	−11
  7	3	9	7	1	4
  5	7	−11	5	5	−12
  5	3	8	5	1	−9
  3	3	12	3	1	7
  3	5	−8	3	7	−3
  1	7	−4	1	1	6
  1	3	11	1	5	−9

• If one the scalars involved in the operation is odd and one even, the result is counted; the output results are shown Table 12.
  Table 12. One of the scalars is odd and one is even.

  ${\mathit{x}}_{\mathit{j}}$	${\mathit{y}}_{\mathit{j}}$	Output	${\mathit{x}}_{\mathit{j}}$	${\mathit{y}}_{\mathit{j}}$	Output
  7	6	1	7	4	−1
  7	2	1	7	0	−1
  5	6	−1	5	4	1
  5	2	−1	5	0	1
  3	6	1	3	4	−1
  3	2	1	3	0	−1
  1	6	−1	1	4	1
  1	2	−1	1	0	1
  6	7	5	6	5	−5
  6	3	5	6	1	−5
  4	7	−5	4	5	5
  4	3	−5	4	1	5
  2	7	5	2	5	−5
  2	3	5	2	1	−5
  0	7	−5	0	5	5
  0	3	−5	0	1	5

According to the output analysis, encoding can eliminate large-number operations. We use the following formula to prevent duplicate encoding from calculating the encoding storage location as $Loc$.

$$Loc=xmod8\times 8+ymod8$$

We combine the intermediate variables $x_j$ and $y_j$ with the encoding results as a dataset. To facilitate the search and subsequent optimization, we add a 0 variable to each set of data, and each set of data consists of {$x_j,y_j$, $correspondingencoding$, 0} a total of four elements. The calculation formula is:

$$\begin{array}{c}Loc=(xmod8\times 8+ymod8)\times 4\\ x_j=Tbl\left[Loc\right]\\ y_j=Tbl[Loc+1]\\ Encoding=Tbl[Loc+2]\end{array}$$

We present the final encoding table results obtained using this method in Table 13, and Algorithm 4 shows our concrete implementation of this method.

Algorithm 4 New encoding JSF-5 method

Require: Non-negative integer pairs $x,y$ Ensure: New encoding array $u\left[l\right]$ of $x,y$ 1: j ← 0; 2: while $x\ne 0$ or $y\ne 0$ do 3:    $x_j\leftarrow xmod8;y_j\leftarrow ymod8$; 4:    $Location=x_j\times 32+y_j\times 4$; 5:    $x_j=TBL\left[Loc\right]$; 6:    $y_j=TBL[Loc+1]$; 7:    $u\left[j\right]=TBL[Loc+2]$; 8:    $x\leftarrow (x-x_j)/2,y\leftarrow (y-y_j)/2$; 9:    $j\leftarrow j+1$; 10: end while

Table 13. JSF-5 encoding table results with a total of 256 elements containing 64 groups of data.

Array Position	JSF-5 TBL Table
0–31	0, 0, 0, 0	0, 1, 5, 0	0, 0, 0, 0	0, −1, −5, 0	0, 0, 0, 0	0, 1, 5, 0	0, 0, 0, 0	0, −1, −5, 0
32–63	1, 0, 1, 0	1, 1, 6, 0	−1, 0, −1, 0	1, 3, 11, 0	1, 0, 1, 0	1, −3, −9, 0	−1, 0, −1, 0	1, −1, −4, 0
64–95	0, 0, 0, 0	0, −1, −5, 0	0, 0, 0, 0	0, 1, 5, 0	0, 0, 0, 0	0, −1, −5, 0	0, 0, 0, 0	0, 1, 5, 0
96–127	−1, 0, −1, 0	3, 1, 7, 0	1, 0, 1, 0	3, 3, 12, 0	−1, 0, −1, 0	3, −3, −8, 0	1, 0, 1, 0	3, −1, −3, 0
128–159	0, 0, 0, 0	0, 1, 5, 0	0, 0, 0, 0	0, −1, −5, 0	0, 0, 0, 0	0, 1, 5, 0	0, 0, 0, 0	0, −1, −5, 0
160–191	1, 0, 1, 0	−3, 1, 3, 0	−1, 0, −1, 0	−3, 3, 8, 0	1, 0, 1, 0	−3, −3, −12, 0	−1, 0, −1, 0	−3, −1, −7, 0
192–223	0, 0, 0, 0	0, −1, −5, 0	0, 0, 0, 0	0, 1, 5, 0	0, 0, 0, 0	0, −1, −5, 0	0, 0, 0, 0	0, 1, 5, 0
224–255	−1, 0, −1, 0	−1, 1, 4, 0	1, 0, 1, 0	−1, 3, 9, 0	−1, 0, −1, 0	−1, −3, −11, 0	1, 0, 1, 0	−1, −1, −6, 0

4.2. Segmentation Method for New Encoding JSF-5

In the concrete implementation, the actual parameters involved in the operation are 256-bit integers, and the computation of $x-x_j$ and $x/2$ is performed with the 256-bit integers as a whole. We reduce the number of operations per segment by segmenting the 256-bit integers so that, when the higher segment is finished, there is no need to participate in subsequent computations, as shown in Figure 7.

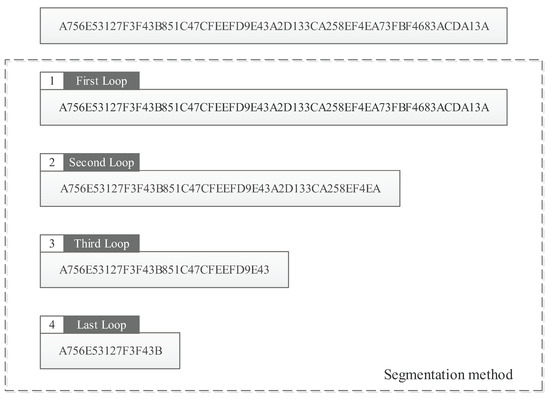
Figure 7. Data segmentation.

After segmentation, each segment of the while function processes 64 bits less than the previous segment. Compared with the previous 256-bit data computation, the data processing overhead after segmentation is lower. We propose a data segmentation method based on the new encoding JSF-5, and Algorithm A6 shows the implementation details for this method.

4.3. Assembly Implementation of the New Encoding JSF-5 Segmentation Method

In the previous sections, our proposed method was implemented in C. To cope with more complex runtime environments, we implemented our proposed method in assembly.

Our proposed method was implemented in assembly to optimize the flow of the algorithm further. After the segmentation process, for the original C code’s second, third, and fourth loops, the stack is no longer needed to store temporary data because the data length is short and the number of available registers is increased. We use the sarx instruction in the BMI2 instruction set to extend the sign bits to get $-1$ and 0 for our accumulation calculation, and we use the combination of adox, adcx, shlx, shrx, and lea instructions to implement two addition chains and 256-bit division operations simultaneously, eliminating the conditional evaluation in the original C code and improving performance, as shown in Algorithm A7.

The proposed method in C cannot directly call the relevant instructions in the BMI2 instruction set; so, to take advantage of the characteristics of the BMI2 instruction set, the proposed method uses the assembly language when generating sparse forms.

Based on the theoretical analysis, the basic algorithmic workflow of this paper is shown in Figure 8.

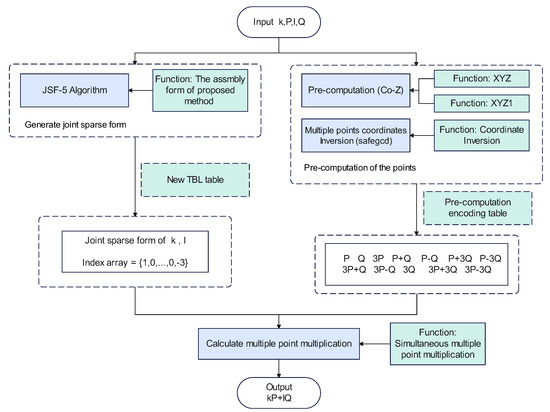
Figure 8. Workflow of the proposed method.

We combine the functions $XYZ$ and $XYZ1$ to generate the pre-computation data. We invert the pre-computation multiple points with safegcd. At the same time, we use our proposed method to generate the sparse form of the input coefficients. Lastly, we calculate the result using the standard method.

5. Experiment

Our experiments used various CPU architectures to verify the generality of the algorithm; namely, Comet Lake, Coffee Lake, Raptor Lake, and Zen 4. We conducted experimental tests in the experimental environments of these architectures. The random numbers used in the experiments were generated by the CPU’s internal random number generator.

5.1. Experimental Preparation

5.1.1. Experimental Environment

We list the CPU architectures and the corresponding experimental environments below. All experiments were conducted using the same software environment, test program, and compiler. Our compilation options were “-march=native -O2 -m64 -mrdrnd”.

• Comet Lake: Intel Core i7-10700@2.9 GHz with a single channel of DDR4 16 GB 2933 MHz memory (Intel Corporation, Santa Clara, CA, USA);
• Coffee Lake: Intel Core i9-9900K@3.6 GHz with four channels of DDR4 32 GB 3200 MHz memory;
• Raptor Lake: Intel Core i7-13700K@3.4 GHz with dual-channel DDR5 32 GB 4800 MHz memory;
• Zen 4: AMD Ryzen 7 7700X@4.5GHz with dual-channel DDR5 32 GB 4800 MHz memory (AMD, Santa Clara, CA, USA).

5.1.2. Relevant Data Test

Operation A is a collective term referring to more specific operations. In the specific algorithm, the addition, subtraction, and doubling of pairs of large integers are all part of operation A. Therefore, we counted the numbers of various types of these operations in the execution phase of the algorithm to determine the precise number of clock cycles consumed for operation A, as shown in Table 14.

Table 14. The numbers of different operations comprising operation A: ADD means calculating the sum of two numbers, SUB means calculating the difference between two numbers, 2X means calculating two times X, 3X means calculating three times X, 4X means calculating four times X, and 8X means calculating eight times X.

Operation	ADD	SUB	2X	3X	4X	8X
Numbers	418.5	1706.5	407	151	151	151

We generated 10 million random datasets to test the basic large-number operations. We counted the median number of clock cycles required by the basic large-number operations during the execution phase of the proposed method to facilitate a more accurate analysis of the execution overhead of the algorithm, as shown in Table 15.

Table 15. Clock cycles required for different operations in operation A with different CPU architectures.

Architecture	Curve	ADD	SUB	2X	3X	4X	8X
Comet Lake	nistp256r1	24.50	31.32	20.08	20.89	19.93	19.69
	SM2	25.03	31.52	20.64	21.70	20.42	20.25
Coffee Lake	nistp256r1	18.91	27.57	15.50	16.80	15.35	15.44
	SM2	21.44	28.46	16.40	16.66	15.96	16.12
Raptor Lake	nistp256r1	6.15	6.41	12.86	15.24	12.20	12.42
	SM2	7.67	6.10	12.46	15.16	12.13	12.63
Zen 4	nistp256r1	11.05	11.15	12.25	13.40	11.55	10.80
	SM2 curve	10.7	10.29	11.25	13.30	11.10	11.00

Next, we generalized the time overheads of simple operations to a simple unified operation, operation A, based on the proportion of each type of simple operation in the actual case combined with the clock cycle overhead in the actual case. In Table 16, we list the overheads of the basic large-number operations with different architectures.

Table 16. Clock cycles required for operation A with different architectures.

Architecture	Curve	Clock Cycles Consumed
Comet Lake	nistp256r1	27.14
	SM2	27.50
Coffee Lake	nistp256r1	22.93
	SM2	23.98
Raptor Lake	nistp256r1	8.30
	SM2	8.28
Zen 4	nistp256r1	11.40
	SM2	10.71

Fifty million datasets were randomly generated for testing. Moreover, the median generation times for different sparse forms were compared, as shown in Table 17.

Table 17. Clock cycles required by sparse-form generating functions with different architectures.

Algorithm	Comet Lake	Coffee Lake	Raptor Lake	Zen 4
NAF	7403.95	7137.10	7822.61	6352.62
3-NAF	6044.00	5821.92	6419.55	5164.59
4-NAF	5213.45	5024.53	5530.54	4452.62
5-NAF	4682.22	4507.97	4945.97	3960.53
JSF	14,281.36	13,675.65	13,213.60	12,394.62
JSF-5	12,743.82	12,254.46	12,657.90	11,822.74
Proposed method	6650.02	6453.95	6200.18	5598.06
Proposed method in assembly	3585.34	3447.29	5866.41	3748.62

The advantages of the proposed method can be seen from the data in the table. Our proposed method in C was, on average, 50% faster than the original JSF-5 algorithm with different architectures. 5-NAF is one of the mainstream sparse forms, and it was also implemented in assembly in this study. The proposed method in assembly was ahead of most algorithms.

5.1.3. Experimental Theoretical Results

Using the previous experimental preparation, we also performed statistical tests on other regular large-number operations, and the final results are shown in Table 18.

Table 18. The clock cycle cost for large-number operations with different architectures.

Architecture	Curve	A	M	S	I
Comet Lake	nistp256r1	27.14	75.46	60.45	4287.60
	SM2	27.50	69.96	56.48	4211.25
Coffee Lake	nistp256r1	22.93	66.86	52.96	4133.13
	SM2	23.98	63.23	50.40	4067.77
Raptor Lake	nistp256r1	8.30	59.54	58.05	4880.29
	SM2	8.28	59.79	49.26	4873.46
Zen 4	nistp256r1	11.40	58.64	57.10	3557.01
	SM2	10.71	56.70	44.10	3556.65

Based on the data in Table 7, Table 17 and Table 18, the theoretical values for the clock cycles required for each algorithm were calculated based on different large-number conversion ratios, and the results are displayed in Table A6.

According to Table A6, the proposed method required about 3% fewer clock cycles on average than the 5-NAF algorithm in the same assembly form. The proposed method took up less pre-computed space.

With different CPU architectures, the clock cycles required for large-number operations varied significantly from one architecture to another due to the architectures’ underlying scheduling logic, the operation frequency, turbo boost technology, and the significant differences in the random datasets generated using true random number generators. Therefore, in terms of actual operation, our theoretical results may also have errors compared to the actual results, which is inevitable. We tested whether our method significantly improves over the current mainstream 5-NAF algorithms with different architectures to verify the feasibility of our method.

5.2. Experimental Results

Thirty million datasets of random numbers were generated under different architectures. Statistics on the running effects of various algorithms were obtained to build histograms for comparison, and the results are shown in Figure 9, Figure 10, Figure 11 and Figure 12.

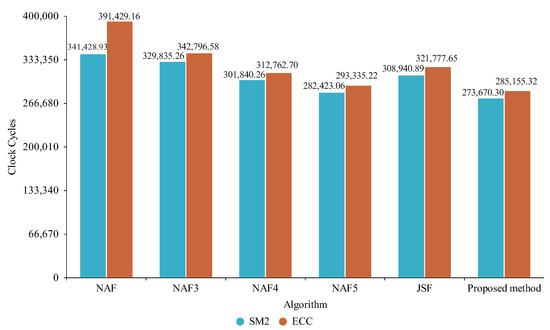
Figure 9. Comparison between nistp256r1 and SM2 for Comet Lake.

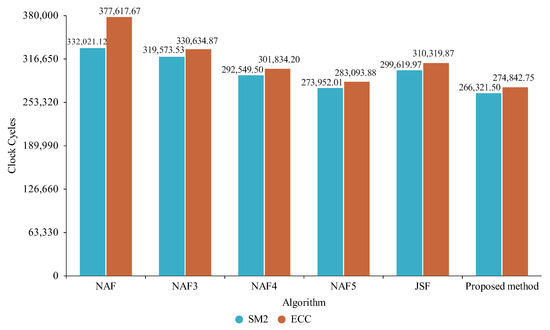
Figure 10. Comparison between nistp256r1 and SM2 for Coffee Lake.

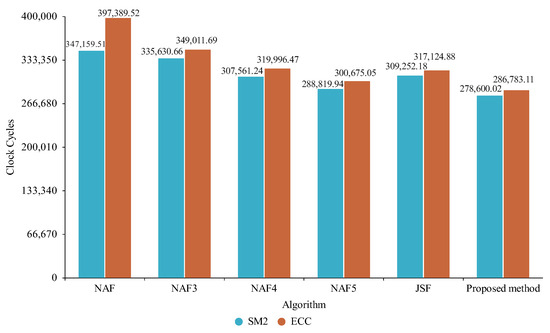
Figure 11. Comparison between nistp256r1 and SM2 for Raptor Lake.

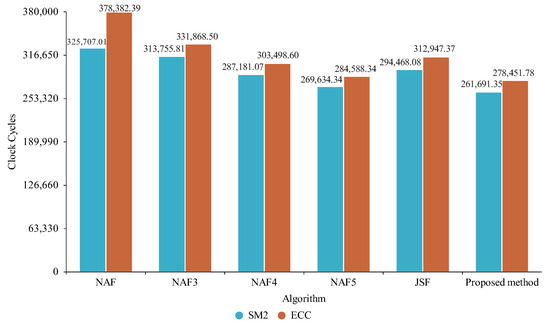
Figure 12. Comparison between nistp256r1 and SM2 for Zen 4.

6. Results

6.1. Analysis and Discussion

We can see that the proposed method required the lowest numbers of clock cycles with the nistp256r1 and SM2 curves in all our experimental environments.

With the Comet Lake architecture, the actual clock cycles required for the proposed method with the nistp256r1 curve differed from the theoretical number by about 0.76%, which was close to the theoretical result for case one; the actual clock cycles required for the proposed method with the SM2 curve were about 3.1% less than the theoretical value, which was closer to the theoretical result for case two.

With the Coffee Lake architecture, the actual clock cycles required for the proposed method with the nistp256r1 curve differed from the theoretical number by about 1.82%, which was close to the theoretical result for case two; the actual clock cycles required for the proposed method with the SM2 curve differed from the theoretical value by about 4.25%, which was closer to the theoretical result for case two.

With the Raptor Lake architecture, the actual clock cycles required for the proposed method with the nistp256r1 curve differed from the theoretical number by about 3.15%, which was close to the theoretical result for case three; the actual clock cycles required for the proposed method with the SM2 curve were about 0.21% less than the theoretical value, which was closer to the theoretical result for case three.

With the Zen 4 architecture, the actual clock cycles required for the proposed method with the nistp256r1 curve differed from the theoretical number by about 2.45%, which was close to the theoretical result for case three; the actual clock cycles required for the proposed method with the SM2 curve were about 0.47% less than the theoretical value, which was closer to the theoretical result for case three.

Indeed, due to varying proportions of different types of operations across various architectures, there may be slight discrepancies between the results and the theoretical expectations. These variations can contribute to minor errors in the results. The experimental results with different architectures verified our theoretical analysis. In Table 19, we summarize the improvement rates for the proposed method compared to other algorithms.

Table 19. Comparison of the lift rate for the proposed method with other algorithms.

Architecture	Curve	NAF	3-NAF	4-NAF	5-NAF	JSF
Comet Lake	nistp256r1	27.15%	16.82%	8.83%	2.79%	11.38%
	SM2	19.85%	17.03%	9.33%	3.10%	11.42%
Coffee Lake	nistp256r1	27.22%	16.87%	8.94%	2.91%	11.43%
	SM2	19.79%	16.66%	8.97%	2.79%	11.11%
Raptor Lake	nistp256r1	27.83%	17.83%	10.38%	4.62%	9.57%
	SM2	19.75%	16.99%	9.42%	3.54%	9.91%
Zen 4	nistp256r1	26.41%	16.10%	8.25%	2.16%	11.02%
	SM2	19.65%	16.59%	8.88%	2.95%	11.13%

According to Table 19, the average improvement with the proposed method compared to 5-NAF was around 3%. With the Zen 4 architecture, the clock cycles required for the proposed method differed significantly from the results for this method with the experimental environments of the other Intel CPUs because AMD CPUs use an entirely different processor architecture, and factors such as CPU instruction branch prediction affect the actual operation. However, with the Zen 4 architecture, the proposed method also showed a stable improvement, which validated the correctness of the proposed method.

6.2. Conclusions

In this paper, we proposed an improved fast JSF-based method. We utilized Co-Z combined with safegcd to achieve low computational complexity for curve coordinate pre-computation. By encoding the data, we reduced the unnecessary operational overhead. We tested the clock cycles required for various algorithms to generate sparse forms and the overall performance of the algorithms across various architectures.

Based on our experiments, it was observed that our proposed JSF-5 method could improve the efficiency of sparse form generation by approximately 70% compared to the original JSF-5. In the case of the nistp256 curve, our method achieved an overall efficiency improvement of approximately 27% compared to NAF across the different CPU architectures. It also demonstrated efficiency improvements of approximately 16.9% compared to 3-NAF, 9% compared to 4-NAF, 3.12% compared to 5-NAF, and 10.85% compared to JSF. In the case of the SM2 curve, our method achieved an overall efficiency improvement of approximately 19.76% compared to NAF across the different CPU architectures. It also demonstrated efficiency improvements of approximately 16.8% compared to 3-NAF, 9.15% compared to 4-NAF, 3% compared to 5-NAF, and 10.89% compared to JSF.

The theory of the proposed method was verified by our experiments, which demonstrated a reduction in resource costs and enhancement of computational efficiency. This method has potential applications in the field of information security, privacy protection, and cryptocurrencies.