HEBCS: A High-Efficiency Binary Code Search Method
Abstract
:1. Introduction
- Our method addresses the challenge of cross-architecture binary code comparison, accommodating the diverse types of closed-source binary files. We extract architecture-independent features to enable similarity analysis across multiple architectures;
- Furthermore, we propose a novel approach that accurately represents functions through multi-dimensional feature hashing, making it well suited for analyzing massive amounts of data. By integrating various features, we significantly reduce the storage space required for storing the generated hashes;
- To improve detection accuracy, we assign targeted weights to different features based on their relevance in similarity comparison. This approach enhances the precision of our detection process while efficiently handling functions;
- In terms of storage and querying, we utilize a pigeonhole principle, which optimizes the storage and retrieval of hashes. This strategy minimizes the indexing time of binary files and significantly reduces the time complexity of queries, thereby improving the overall query speed of the system.
2. Related Work
3. Background
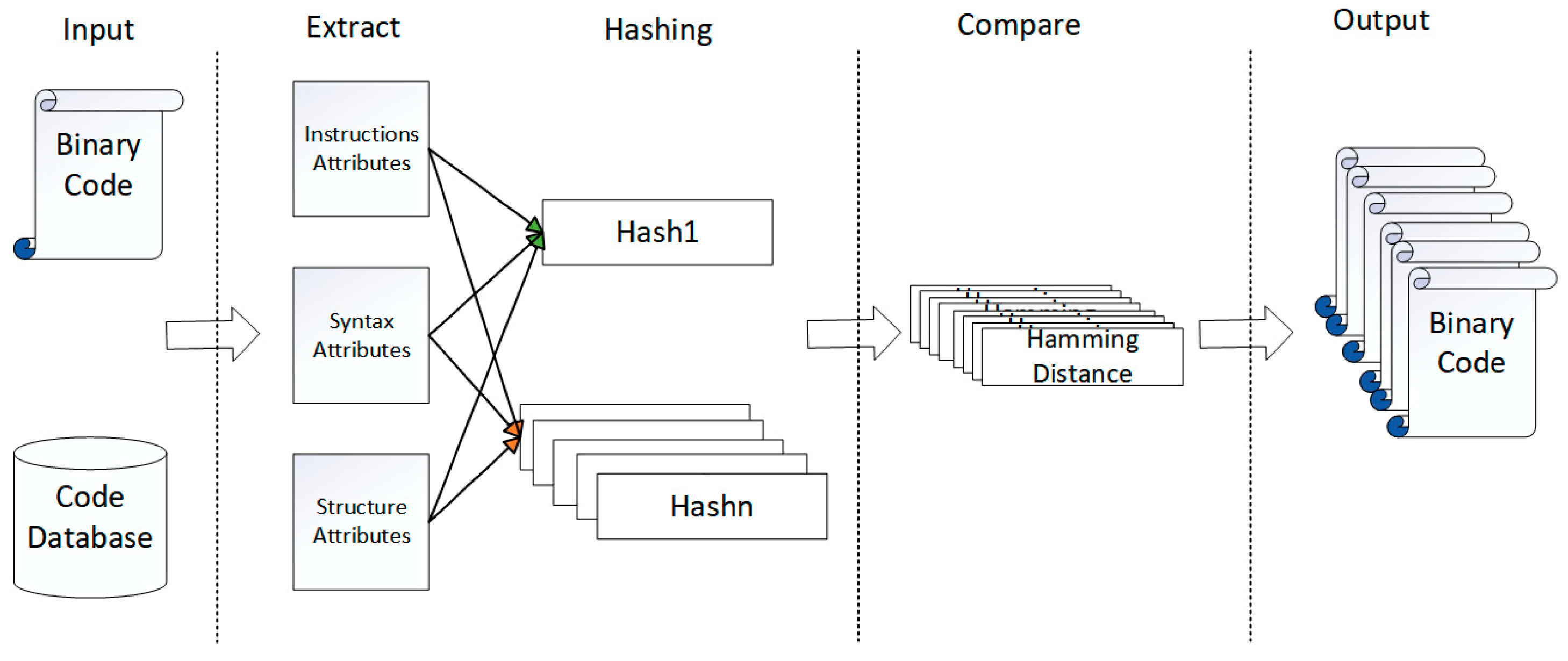
4. Methods
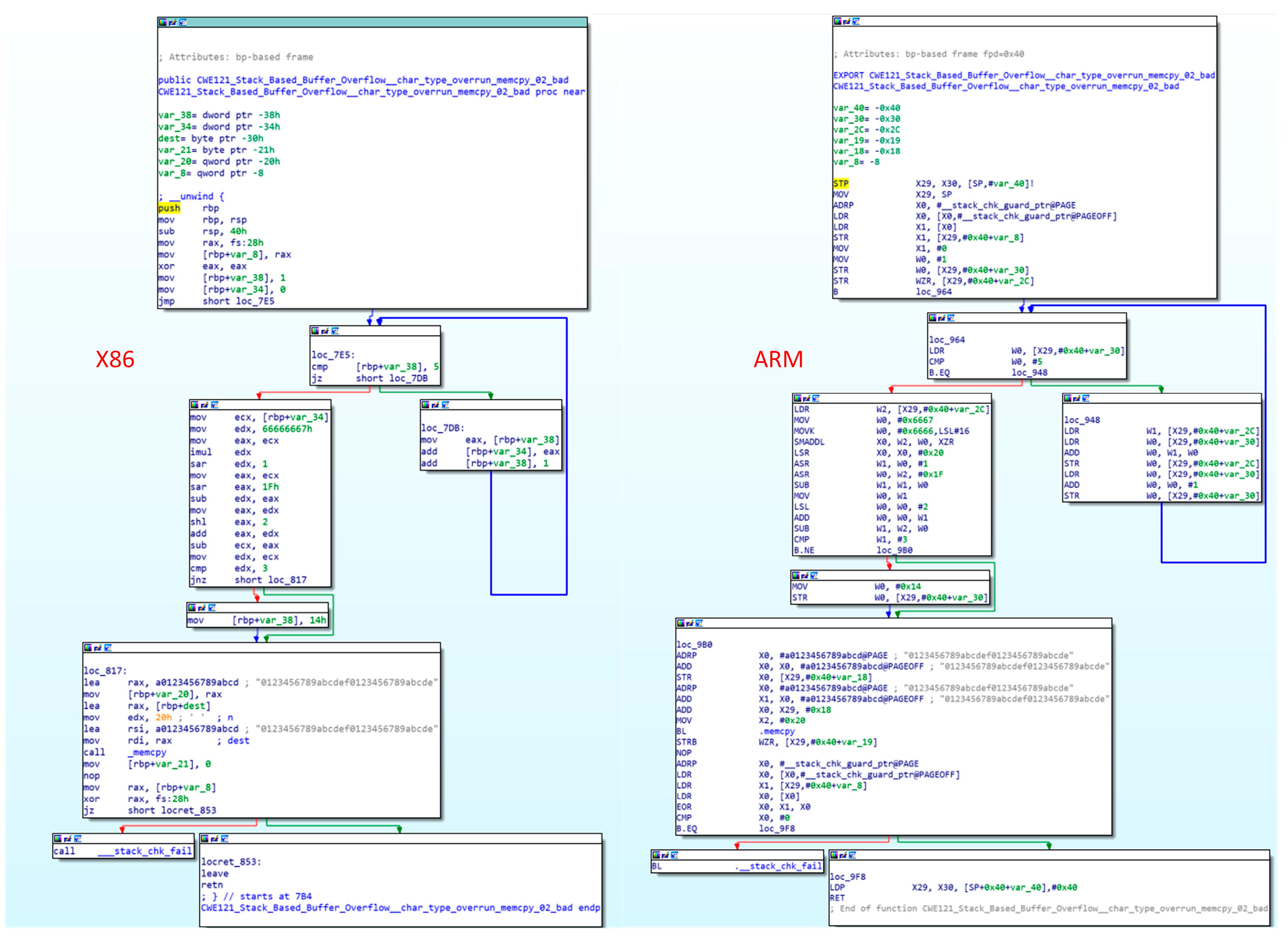
4.1. Feature Selection
4.2. Function Hashing
4.2.1. Numerical Hashing
| Algorithm 1 Numerical similarity processing algorithm |
| Input: is the number to be converted, is the number of bits in the hash Output: is the obtained hash if then for to do end for for to do end for else end for return |
4.2.2. String Hashing
- First, we extract all the strings in the binary function and combine them into one string and then segment the string combination to get all the words in the string;
- Then, the hash function is used to convert each word after the first word segmentation into a fixed-length hash value so that each word has a unique hash value;
- The next step involves weighting the words extracted in the first step, assigning different weights to different words based on the position of the string they belong to in the code. Words that exist in print-related statements should be given greater weights. Afterwards, the hash obtained in the second step is weighted, and the weighting process is shown in Formula (3). If the hash value obtained in the second step has a bit value of 1, the weight is multiplied by 1. If the value of a bit is 0, the weight is multiplied by -1, and the weighted hash obtained is replaced by the hash calculated in the second step. This hash is the weighted hash value of different words.
- 4.
- The hash value results of different words in a string are accumulated so that the string sequence of each function has only a unique string of hash values;
- 5.
- Finally, the result of each hash string is judged. All hash bits are traversed, and if the bit is greater than 0, it is set to 1; otherwise, it is set to 0. Finally, the bit stream sequence is the SimHash value of the string.
4.2.3. CFG Hashing
- Initialization: Set each node of the original graph as an independent initial label. Labels can be objects of any type, such as numbers, strings or tuples;
- Iteration: For each iteration, traverse each node in the graph, combine the labels of its neighbors and its own nodes through a hash function and generate a new label;
- Update: Assign the generated new label to the node;
- Judge: Compare whether the label sequences of nodes in two graphs are completely equal after several iterations. If they are equal, the two graphs are isomorphic and vice versa.
4.2.4. Feature Weight Assignment
4.3. Similarity Search
- Set the Hamming distance threshold as N;
- Assuming that the hash value of the function to be compared is M bits, divide it into N + 1 segments and make the hash bits in each segment except the last segment
- 3.
- The hash value is stored in the form of a dictionary. Different stores set the hashes of the segmented segments as Key and the remaining segments as Value; that is, will be indexed N + 1 times according to different segments:
- 4.
- During the similarity comparison, query the hash segment with the same index key as the target function. Since the function has N + 1 indexes, there can be N + 1 queries at most;
- 5.
- If the same index segment is found, the value corresponding to the index segment is traversed to calculate whether the Hamming distance is greater than N. The maximum number of queries required to traverse the value corresponding to the key is .
5. Experiment Setup
5.1. Dataset
5.2. Evaluation Metrics
5.3. Baselines
5.4. Supporting Tools
6. Evaluation
6.1. Research Questions
6.2. RQ1: Effectiveness of Feature Selection
6.3. RQ2: Effectiveness of Weight Training
6.4. RQ3: Selection of Hamming Distance
6.5. RQ4: Effectiveness of HEBCS
6.6. RQ5: Real-World Performance
7. Conclusions and Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, J.; Fu, C.; Liu, X.-Y.; Yin, H.; Zhou, P. Codee: A Tensor Embedding Scheme for Binary Code Search. IEEE Trans. Softw. Eng. 2022, 48, 2224–2244. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, Y.; Li, J.; Wang, H.; Li, B.; Gu, D. BinMatch: A Semantics-Based Hybrid Approach on Binary Code Clone Analysis. In Proceedings of the 2018 IEEE International Conference on Software Maintenance and Evolution (ICSME), Madrid, Spain, 23–29 September 2018; pp. 104–114. [Google Scholar]
- Gao, J.; Yang, X.; Fu, Y.; Jiang, Y.; Sun, J. VulSeeker: A Semantic Learning Based Vulnerability Seeker for Cross-Platform Binary. In Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, Montpellier, France, 3–7 September 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 896–899. [Google Scholar]
- Duan, Y.; Li, X.; Wang, J.; Yin, H. DeepBinDiff: Learning Program-Wide Code Representations for Binary Diffing. In Proceedings of the Proceedings 2020 Network and Distributed System Security Symposium, San Diego, CA, USA, 23–26 February 2020; Internet Society: San Diego, CA, USA, 2020. [Google Scholar]
- Whale, G. Plague: Plagiarism Detection Using Program Structure; University of New South Wales: Sydney, Australia, 1988. [Google Scholar]
- Eschweiler, S.; Yakdan, K.; Gerhards-Padilla, E. DiscovRE: Efficient Cross-Architecture Identification of Bugs in Binary Code. In Proceedings of the Network and Distributed System Security Symposium, San Diego, CA, USA, 21–24 February 2016. [Google Scholar]
- Zuo, F.; Li, X.; Young, P.; Luo, L.; Zeng, Q.; Zhang, Z. Neural Machine Translation Inspired Binary Code Similarity Comparison beyond Function Pairs. In Proceedings of the Proceedings 2019 Network and Distributed System Security Symposium, San Diego, CA, USA, 24–27 February 2019; Internet Society: San Diego, CA, USA, 2019. [Google Scholar]
- Mengin, E.; Rossi, F. Binary Diffing as a Network Alignment Problem via Belief Propagation. In Proceedings of the 2021 36th IEEE/ACM International Conference on Automated Software Engineering (ASE), Melbourne, Australia, 15–19 November 2021; IEEE: Melbourne, Australia, 2021; pp. 967–978. [Google Scholar]
- Ahmadi, M.; Farkhani, R.M.; Williams, R.R.; Lu, L. Finding Bugs Using Your Own Code: Detecting Functionally-Similar yet Inconsistent Code. In Proceedings of the USENIX Security Symposium, Virtual, 11–13 August 2021. [Google Scholar]
- Zhang, X.; Sun, W.; Pang, J.; Liu, F.; Ma, Z. Similarity Metric Method for Binary Basic Blocks of Cross-Instruction Set Architecture. In Proceedings of the P2020 Workshop on Binary Analysis Research, San Diego, CA, USA, 23 February 2020; Internet Society: San Diego, CA, USA, 2020. [Google Scholar]
- Li, X.; Yu, Q.; Yin, H. PalmTree: Learning an Assembly Language Model for Instruction Embedding. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, 15–19 November 2021; pp. 3236–3251. [Google Scholar]
- Ullah, S.; Oh, H. BinDiffNN: Learning Distributed Representation of Assembly for Robust Binary Diffing Against Semantic Differences. IIEEE Trans. Softw. Eng. 2022, 48, 3442–3466. [Google Scholar] [CrossRef]
- Ahn, S.; Ahn, S.; Koo, H.; Paek, Y. Practical Binary Code Similarity Detection with BERT-Based Transferable Similarity Learning. In Proceedings of the 38th Annual Computer Security Applications Conference, San Juan, PR, USA, 9–13 December 2022; ACM: Austin, TX, USA, 5 December 2022; pp. 361–374. [Google Scholar]
- Feng, Q.; Zhou, R.; Xu, C.; Cheng, Y.; Testa, B.; Yin, H. Scalable Graph-Based Bug Search for Firmware Images. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016. [Google Scholar]
- Xu, X.; Liu, C.; Feng, Q.; Yin, H.; Song, L.; Song, D. Neural Network-Based Graph Embedding for Cross-Platform Binary Code Similarity Detection. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; ACM: Dallas, TX, USA, 2017; pp. 363–376. [Google Scholar]
- Dai, H.; Dai, B.; Song, L. Discriminative Embeddings of Latent Variable Models for Structured Data. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; JMLR.org: New York, NY, USA, 2016; Volume 48, pp. 2702–2711. [Google Scholar]
- FunctionSimSearch 2023. Available online: https://github.com/googleprojectzero/functionsimsearch (accessed on 1 August 2023).
- Pei, K.; Xuan, Z.; Yang, J.; Jana, S.S.; Ray, B. Trex: Learning Execution Semantics from Micro-Traces for Binary Similarity. arXiv 2020, arXiv:2012.08680. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar]
- Wang, H.; Qu, W.; Katz, G.; Zhu, W.; Gao, Z.; Qiu, H.; Zhuge, J.; Zhang, C. JTrans: Jump-Aware Transformer for Binary Code Similarity Detection. In Proceedings of the 31st ACM SIGSOFT International Symposium on Software Testing and Analysis, Virtual, 18–22 July 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 1–13. [Google Scholar]
- Liu, Z. Binary Code Similarity Detection. In Proceedings of the 36th IEEE/ACM International Conference on Automated Software Engineering, Melbourne, Australia, 15–19 November 2021; IEEE Press: Melbourne, Australia, 2022; pp. 1056–1060. [Google Scholar]
- Redmond, K.; Luo, L.; Zeng, Q. A Cross-Architecture Instruction Embedding Model for Natural Language Processing-Inspired Binary Code Analysis. arXiv 2018, arXiv:1812.09652. [Google Scholar]
- Kim, D.; Kim, E.; Cha, S.K.; Son, S.; Kim, Y. Revisiting Binary Code Similarity Analysis Using Interpretable Feature Engineering and Lessons Learned. IEEE Trans. Softw. Eng. 2023, 49, 1661–1682. [Google Scholar] [CrossRef]
- Indyk, P.; Motwani, R. Approximate Nearest Neighbors: Towards Removing the Curse of Dimensionality. In Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing, Dallas, TX, USA, 24–26 May 1998; Association for Computing Machinery: New York, NY, USA, 1998; pp. 604–613. [Google Scholar]
- Manku, G.S.; Jain, A.; Sarma, A.D. Detecting Near-Duplicates for Web Crawling. In Proceedings of the the Web Conference, Banff, AB, Canada, 8–12 May 2007. [Google Scholar]
- Massarelli, L.; Luna, G.A.D.; Petroni, F.; Querzoni, L.; Baldoni, R. Investigating Graph Embedding Neural Networks with Unsupervised Features Extraction for Binary Analysis. In Proceedings of the 2019 Workshop on Binary Analysis Research, San Diego, CA, USA, 21–24 February 2016. [Google Scholar]
- Massarelli, L.; Luna, G.A.D.; Petroni, F.; Querzoni, L.; Baldoni, R. SAFE: Self-Attentive Function Embeddings for Binary Similarity. arXiv 2018, arXiv:1811.05296. [Google Scholar]
- Yu, Z.; Zheng, W.; Wang, J.; Tang, Q.; Nie, S.; Wu, S. CodeCMR: Cross-Modal Retrieval For Function-Level Binary Source Code Matching. In Proceedings of the Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar]
- Marcelli, A.; Graziano, M.; Ugarte-Pedrero, X.; Fratantonio, Y.; Mansouri, M.; Balzarotti, D. How Machine Learning Is Solving the Binary Function Similarity Problem. In Proceedings of the 31st USENIX Security Symposium (USENIX Security 22), Boston, MA, USA, 10–12 August 2022; USENIX Association: Boston, MA, USA, 2022; pp. 2099–2116. [Google Scholar]
- Marastoni, N.; Giacobazzi, R.; Dalla Preda, M. A Deep Learning Approach to Program Similarity. In Proceedings of the 1st International Workshop on Machine Learning and Software Engineering in Symbiosis, Montpellier, France, 3 September 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 26–35. [Google Scholar]
- David, Y.; Partush, N.; Yahav, E. FirmUp: Precise Static Detection of Common Vulnerabilities in Firmware. In Proceedings of the Twenty-Third International Conference on Architectural Support for Programming Languages and Operating Systems, Williamsburg, VA, USA, 24–28 March 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 392–404. [Google Scholar]
- Sun, P.; Garcia, L.; Salles-Loustau, G.; Zonouz, S. Hybrid Firmware Analysis for Known Mobile and IoT Security Vulnerabilities. In Proceedings of the 2020 50th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), Valencia, Spain, 29 June–2 July 2020; pp. 373–384. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.S.; Dean, J. Efficient Estimation of Word Representations in Vector Space. In Proceedings of the International Conference on Learning Representations, Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Li, Y.; Gu, C.; Dullien, T.; Vinyals, O.; Kohli, P. Graph Matching Networks for Learning the Similarity of Graph Structured Objects. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- GitHub—ReFirmLabs/Binwalk: Firmware Analysis Tool. Available online: https://github.com/ReFirmLabs/binwalk (accessed on 5 August 2023).







| Category | Features | Count |
|---|---|---|
| Instruction Attributes | Total number of instructions | 4 |
| Number of arithmetic instructions | ||
| Number of transfer instructions | ||
| Number of logic instructions | ||
| Syntax Attributes | Number of call instructions | 2 |
| String constant | ||
| Structure Attributes | Number of incoming calls | 4 |
| Number of edges in CFG | ||
| Number of basic blocks | ||
| Weisfeiler–Lehman test of isomorphism | ||
| Total | 10 | |
| Method | Time (Functions/Seconds) |
|---|---|
| Gemini | 69 |
| Trex | 734 |
| HEBCS | 3186 |
| X86 vs. ARM | ARM vs. MIPS | MIPS vs. X86 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| P | R | F1 | P | R | F1 | P | R | F1 | |
| Gemini | 0.912 | 0.972 | 0.941 | 0.910 | 0.958 | 0.933 | 0.912 | 0.950 | 0.931 |
| Trex | 0.943 | 0.957 | 0.950 | 0.950 | 0.967 | 0.958 | 0.943 | 0.952 | 0.947 |
| HEBCS | 0.928 | 0.949 | 0.938 | 0.939 | 0.936 | 0.958 | 0.947 | 0.945 | 0.945 |
| CVE List | Suspicious Firmware in the Firmware Dataset | Whether There Exists a Real Vulnerability |
|---|---|---|
| CVE-2020-27867 (NETGEAR R6800) | NETGEAR R6080 | Yes |
| NETGEAR R6120 | Yes | |
| NETGEAR R6220 | Yes | |
| NETGEAR R6700V2 | Yes | |
| NETGEAR R7450 | Yes | |
| NETGEAR WNR2020 | Yes | |
| Nighthawk AC2100 | Yes | |
| CVE-2018-16333 (US_AC15V1.0BR_V15.03.05.19_multi_TD01) | Tenda AC7 V15.03.06.44_CN Tenda AC9 V15.03.05.19(6318)_CN | Yes |
| Yes | ||
| Tenda AC10 V15.03.06.23_CN | Yes | |
| Tenda AC15 V15.03.05.19_CN | Yes | |
| Tenda AC18 V15.03.05.19(6318)_CN | Yes | |
| CVE-2021-33514 (NETGEAR GS110TPP_V7.0.1.16) | NETGEAR GC108PP_V1.0.7.2 | Yes |
| NETGEAR GC108PP_V1.0.7.1 | Yes | |
| NETGEAR GS110TPv3_7.0.6.3 | Yes | |
| NETGEAR GS110TUP_1.0.4.3 | Yes | |
| NETGEAR GS710TUP_1.0.4.2 | No | |
| NETGEAR GS710TUP_1.0.4.5 | Yes | |
| NETGEAR GS724TPP_2.0.4.3 | Yes | |
| NETGEAR GS724TPV2_6.0.6.3 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Wei, Q.; Du, J.; Wang, Y. HEBCS: A High-Efficiency Binary Code Search Method. Electronics 2023, 12, 3464. https://doi.org/10.3390/electronics12163464
Sun X, Wei Q, Du J, Wang Y. HEBCS: A High-Efficiency Binary Code Search Method. Electronics. 2023; 12(16):3464. https://doi.org/10.3390/electronics12163464
Chicago/Turabian StyleSun, Xiangjie, Qiang Wei, Jiang Du, and Yisen Wang. 2023. "HEBCS: A High-Efficiency Binary Code Search Method" Electronics 12, no. 16: 3464. https://doi.org/10.3390/electronics12163464
APA StyleSun, X., Wei, Q., Du, J., & Wang, Y. (2023). HEBCS: A High-Efficiency Binary Code Search Method. Electronics, 12(16), 3464. https://doi.org/10.3390/electronics12163464





