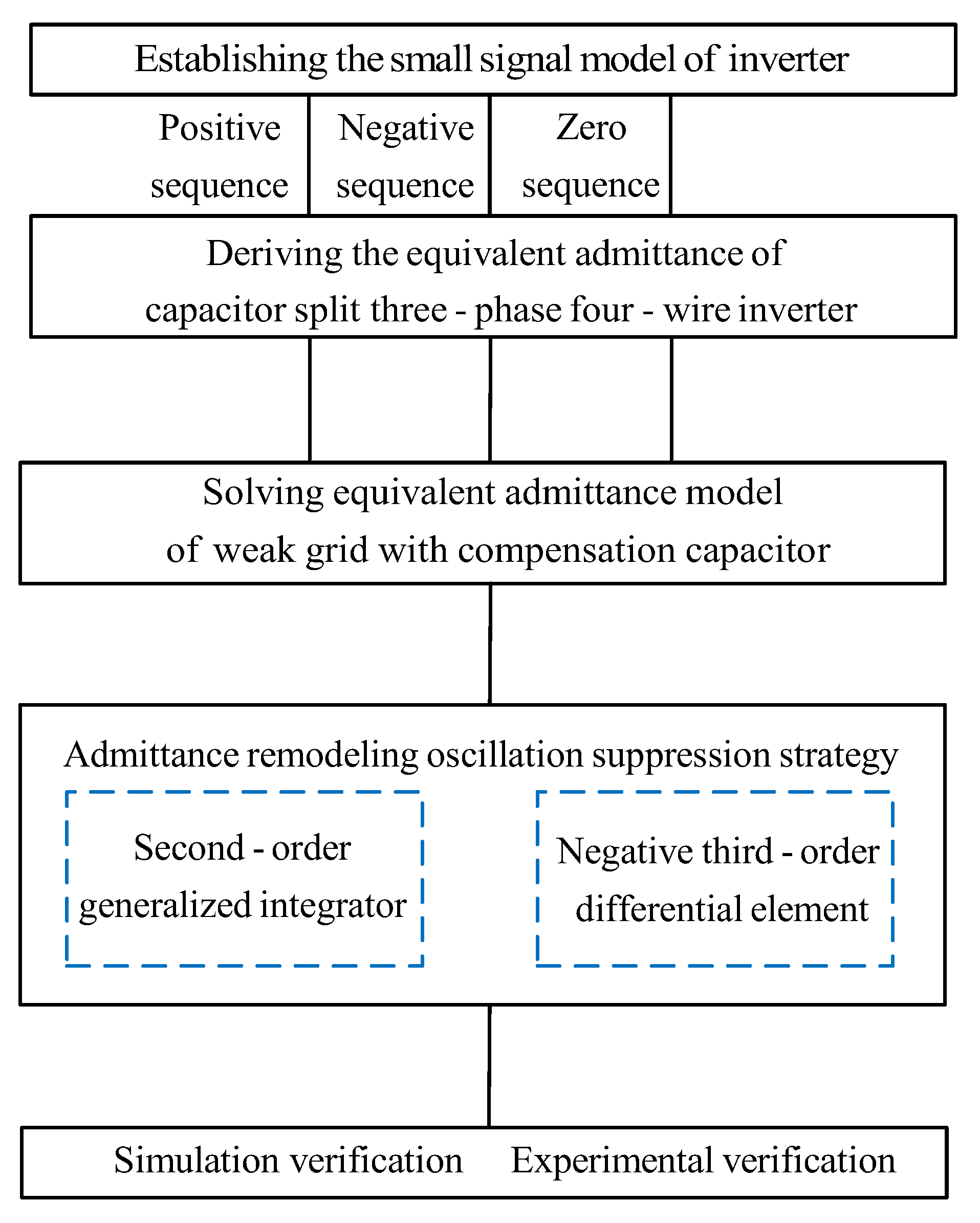
Oscillation Suppression Strategy of Three-Phase Four-Wire Grid-Connected Inverter in Weak Power Grid
Abstract
:1. Introduction
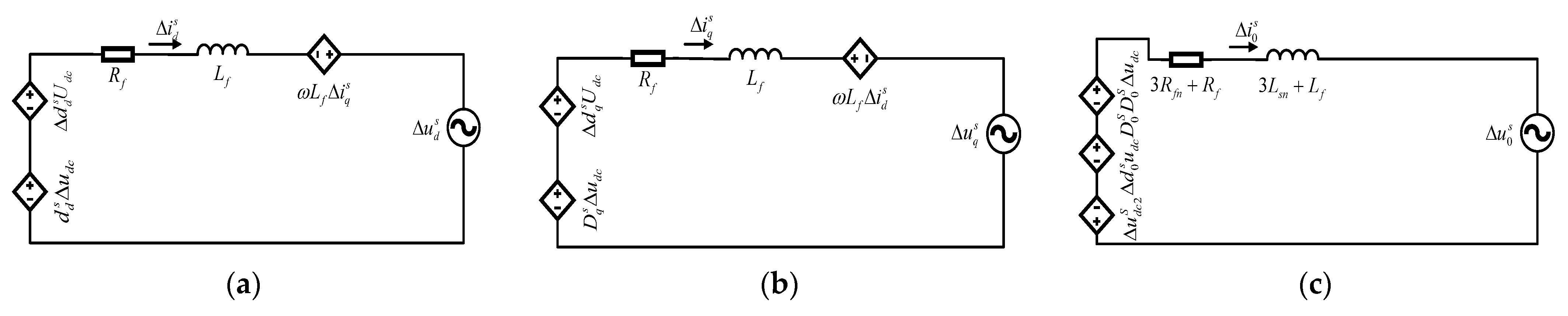
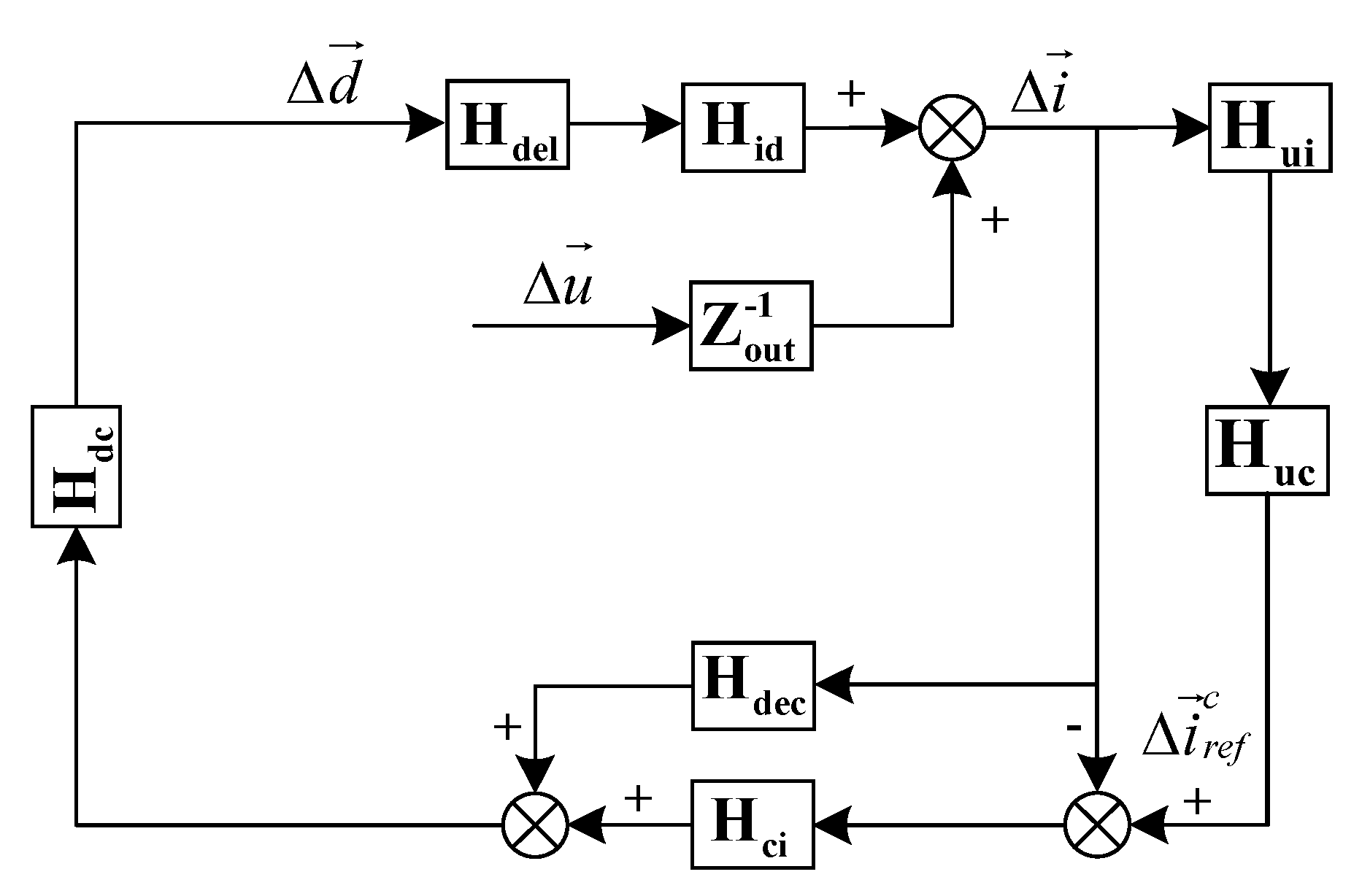
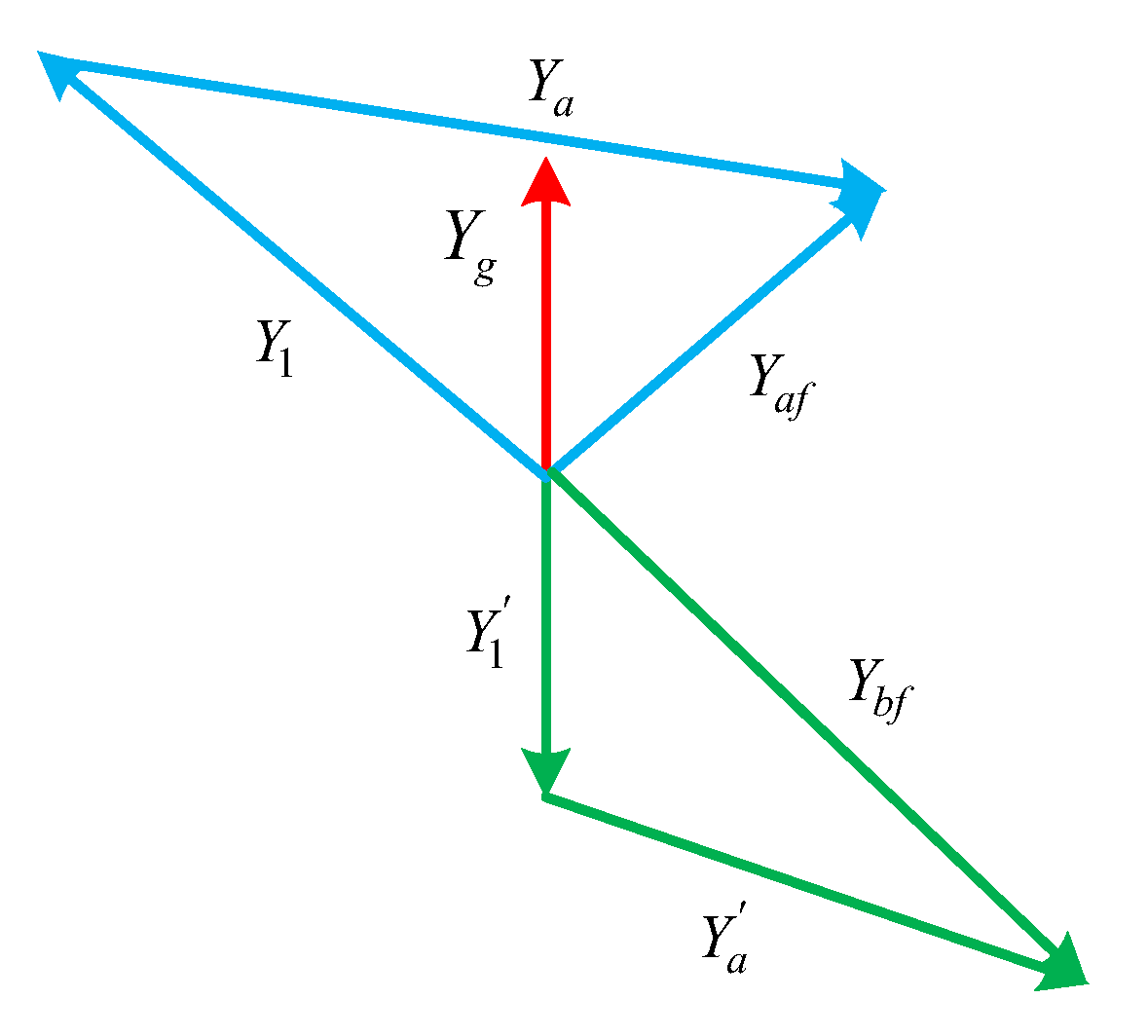
2. Research on the Admittance Model of Three-Phase Four-Wire Grid-Connected Inverter
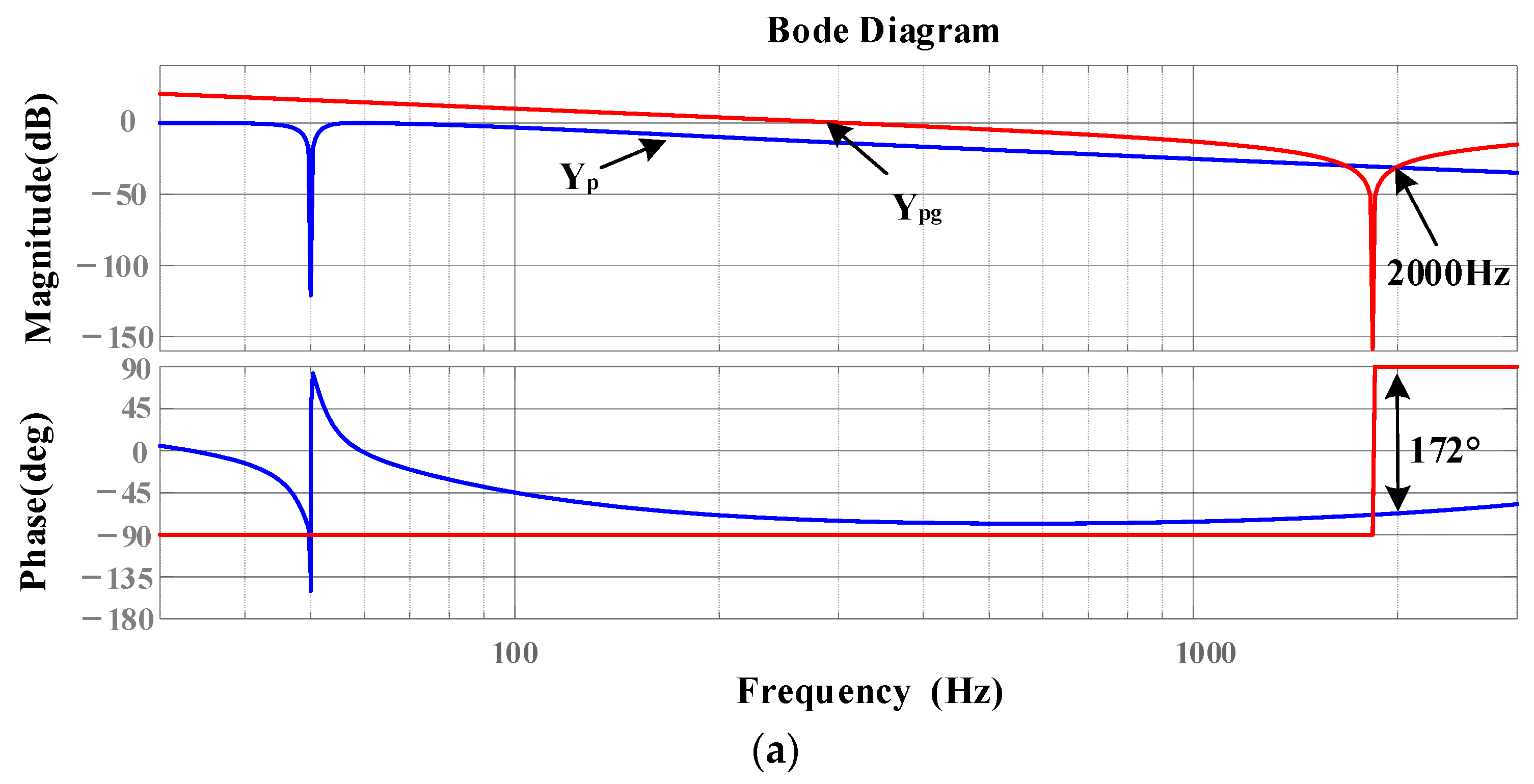
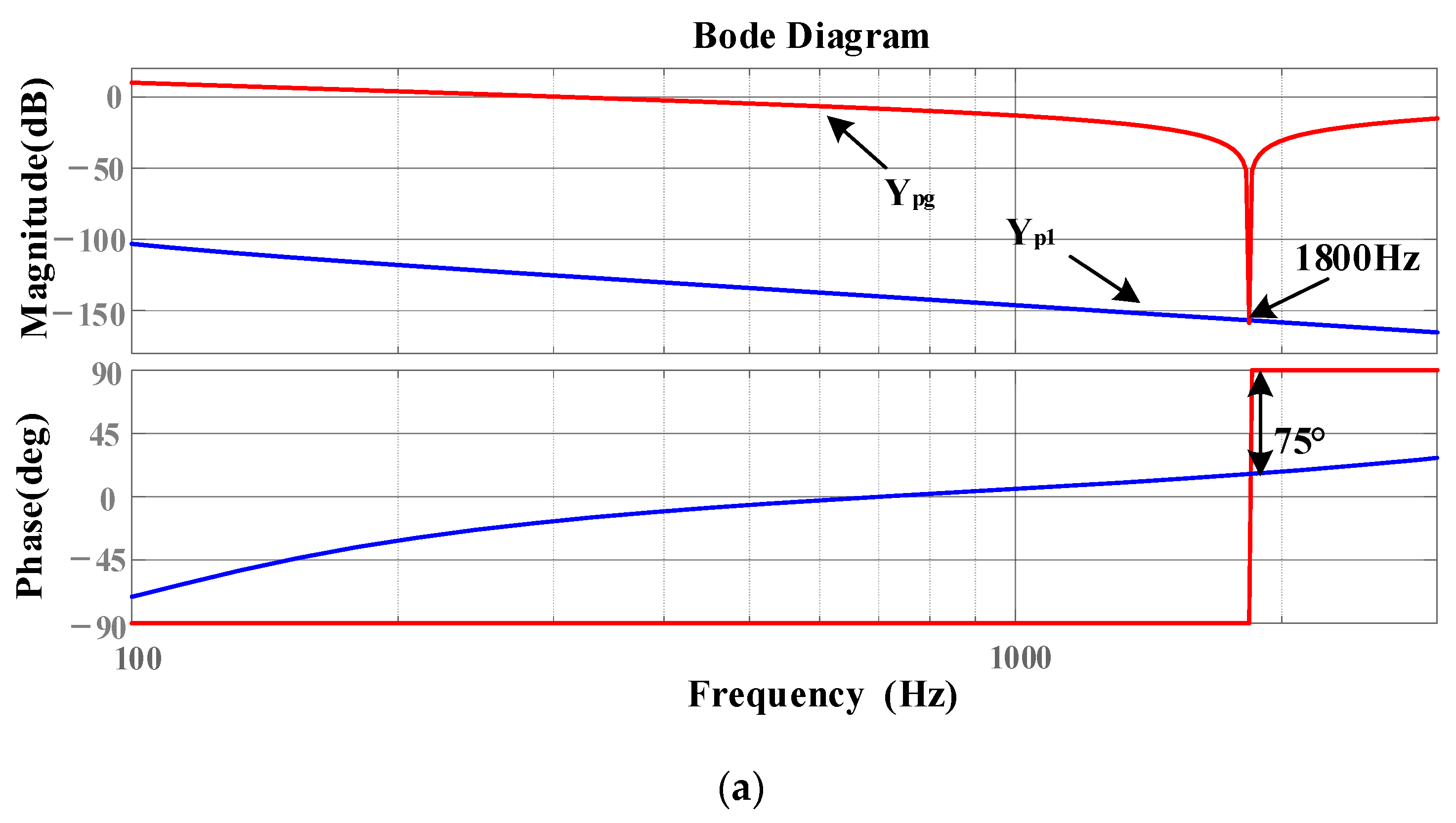
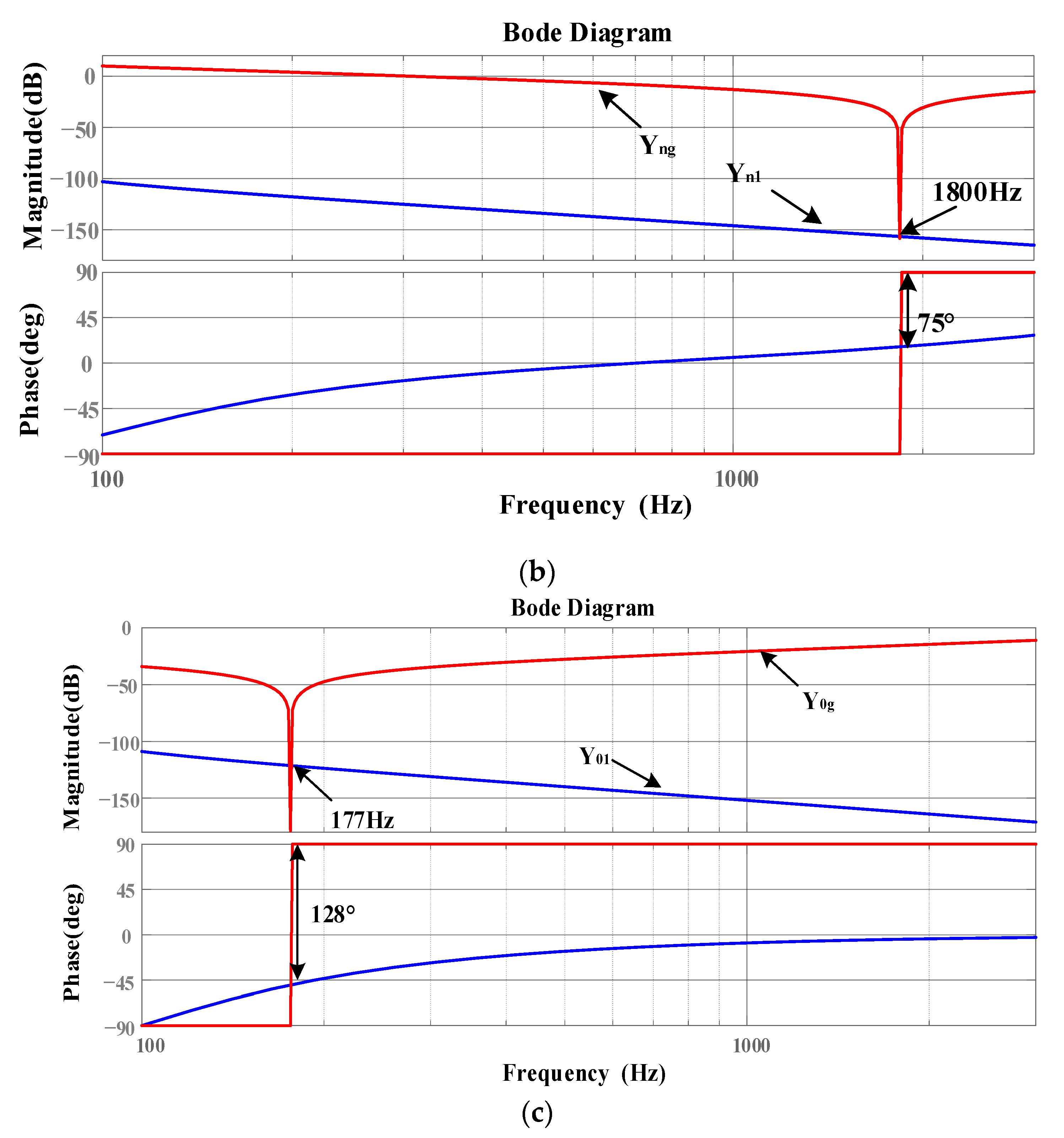
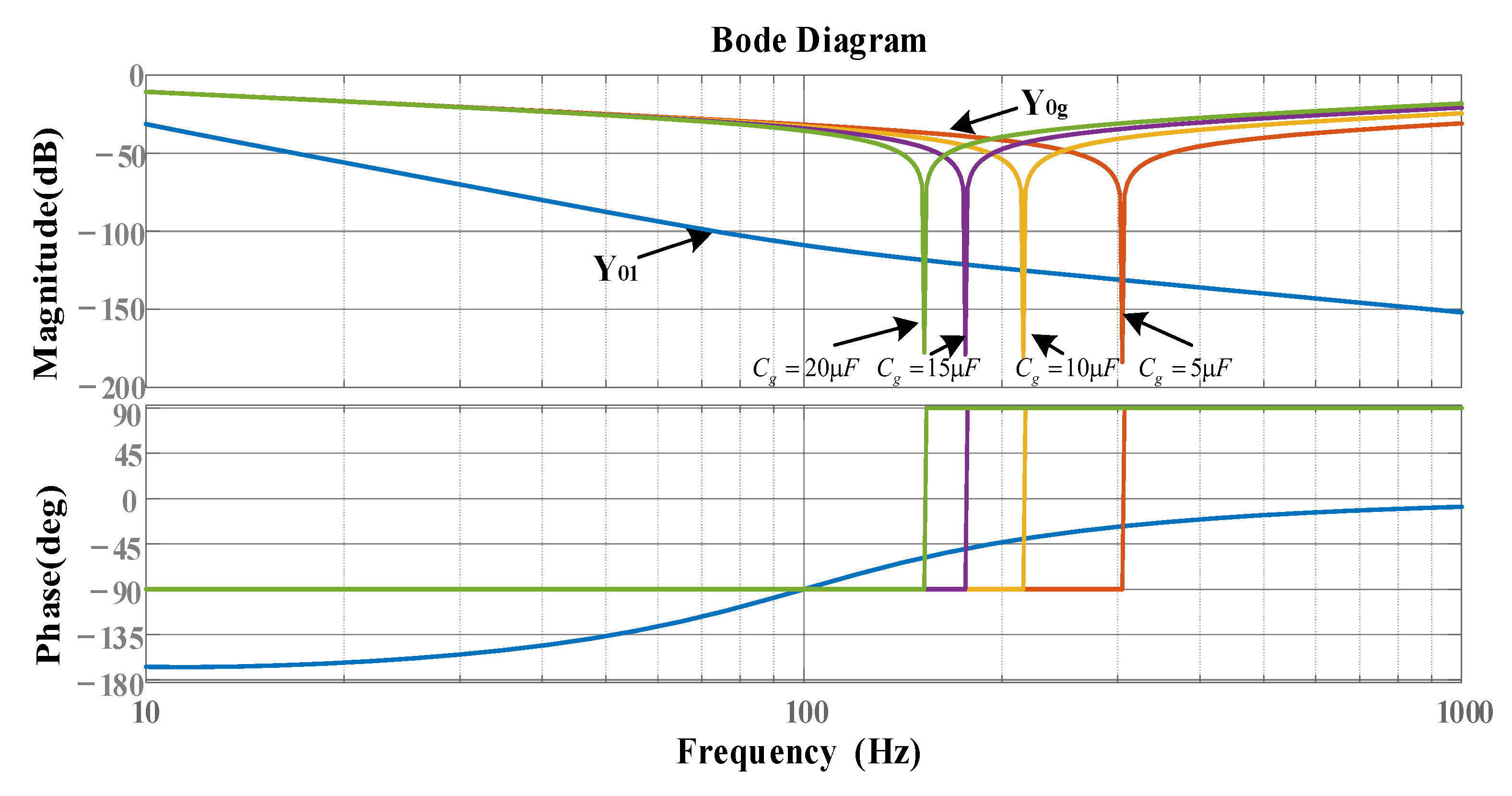
3. Stability Analysis of Three-Phase Four-Wire Grid-Connected Inverter with Shunt Capacitor in Weak Grid
4. Research on High Frequency Oscillation Suppression Strategy of Three-Phase Four-Wire Grid-Connected Inverter
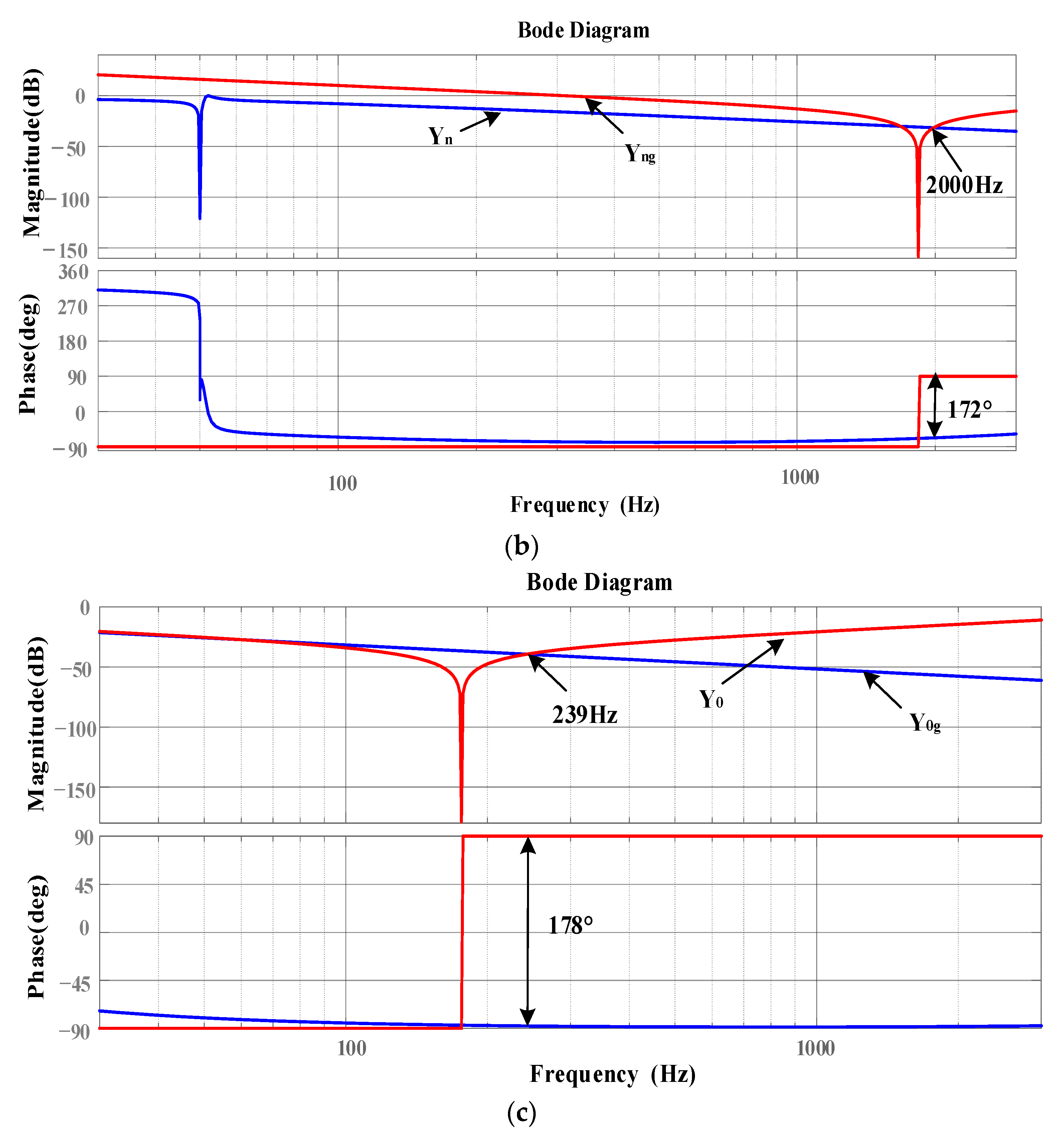
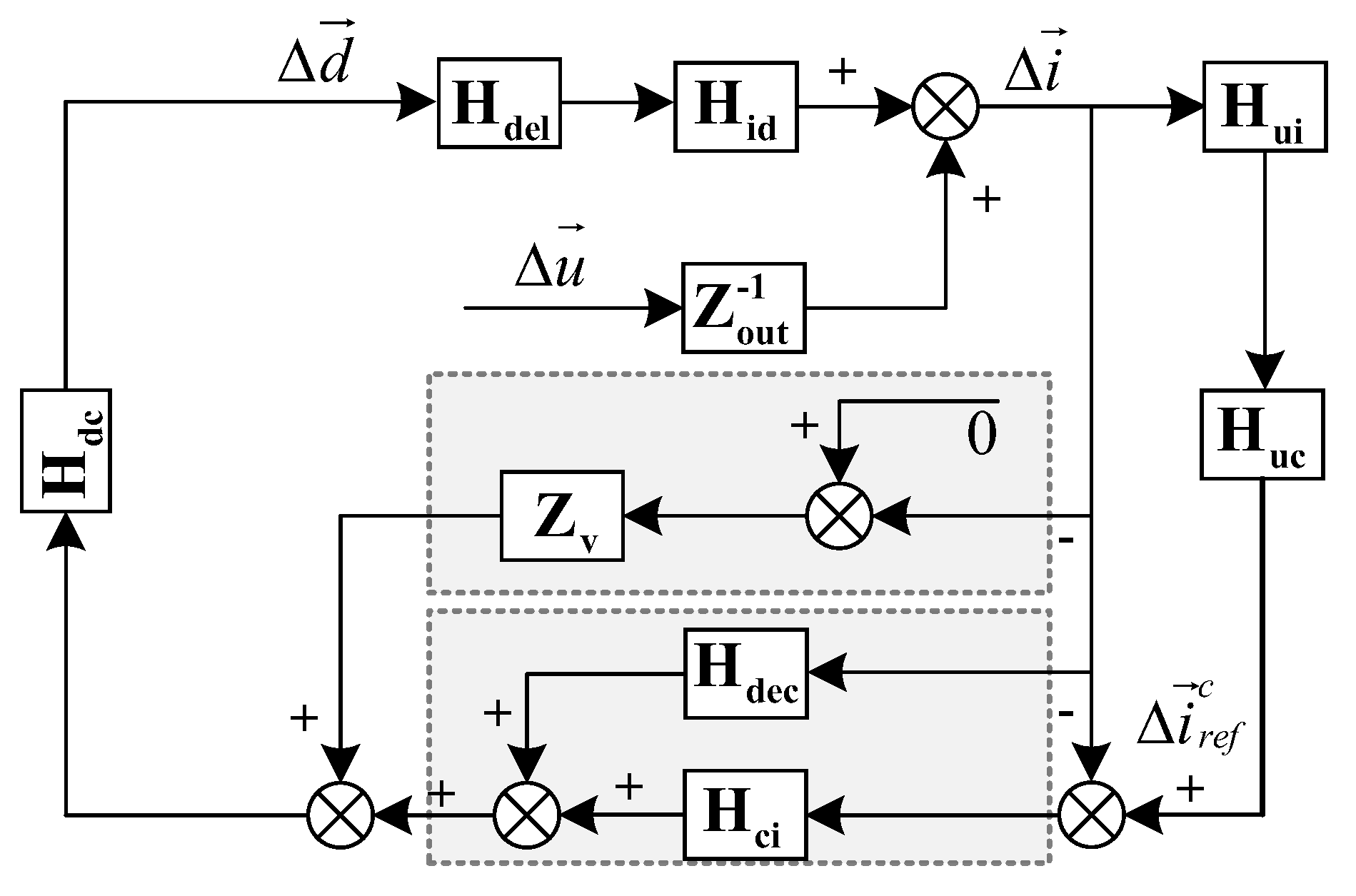
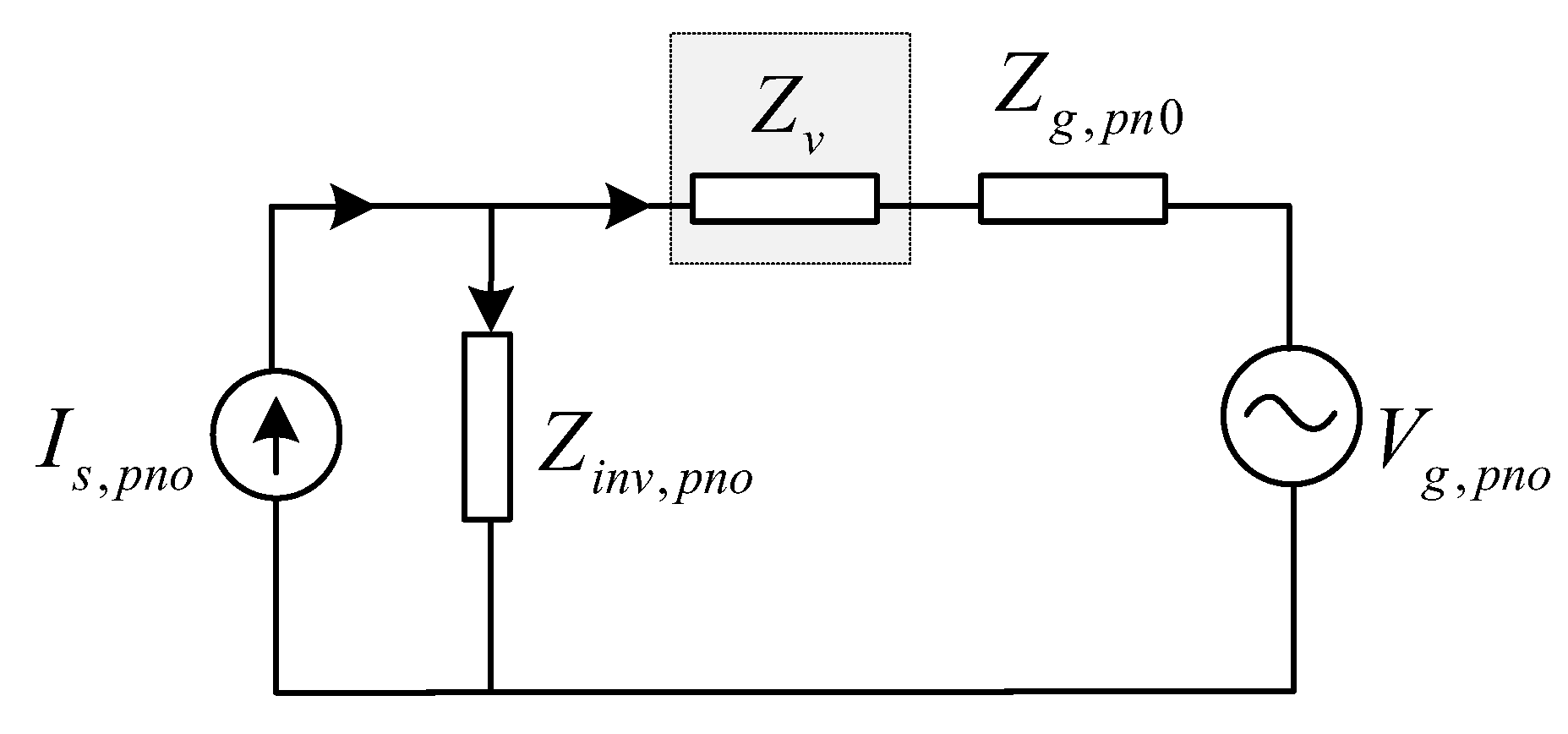
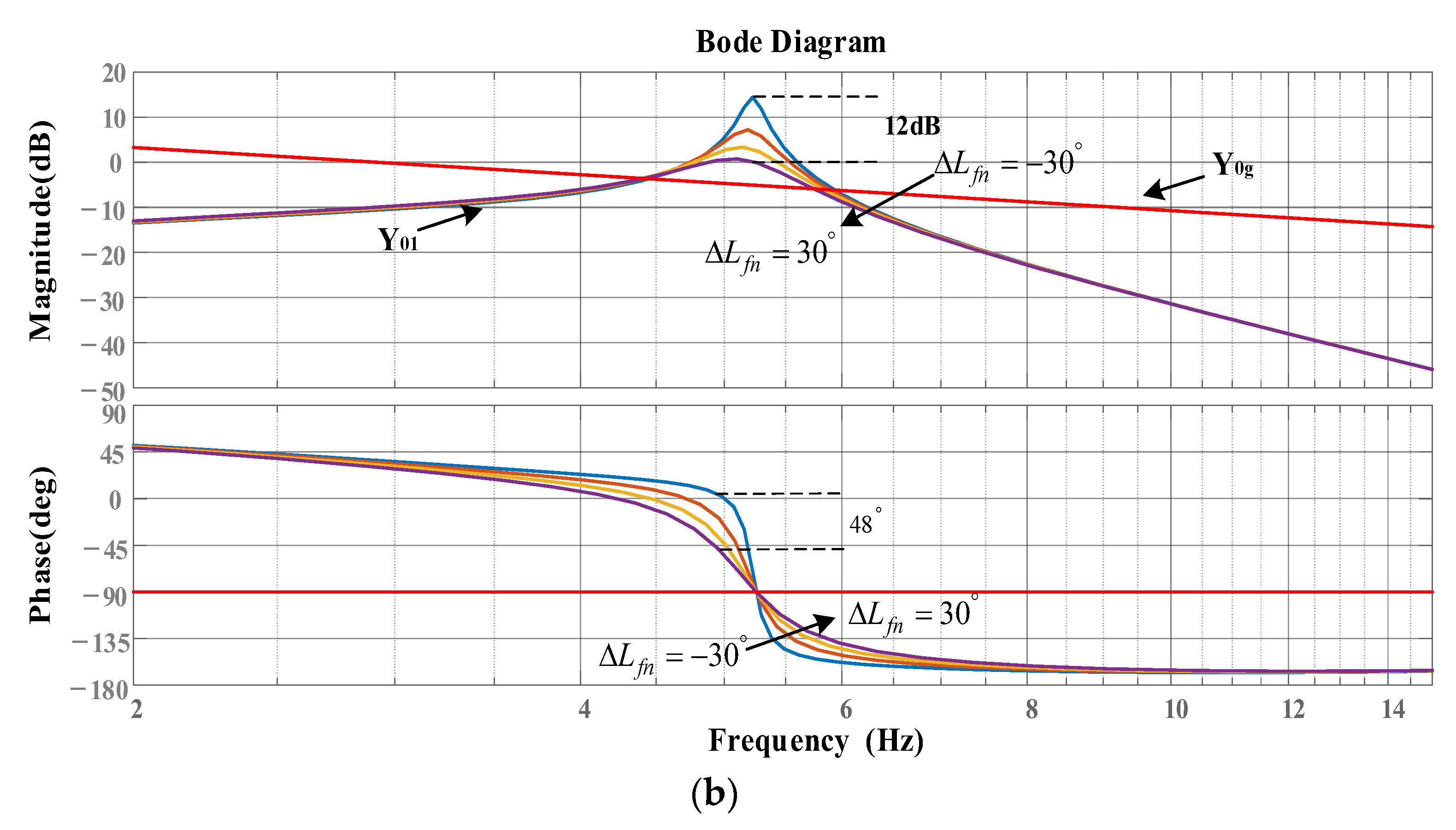
4.1. Research on Impedance Remodeling Strategy Based on Improved Damping Controller
- (1)
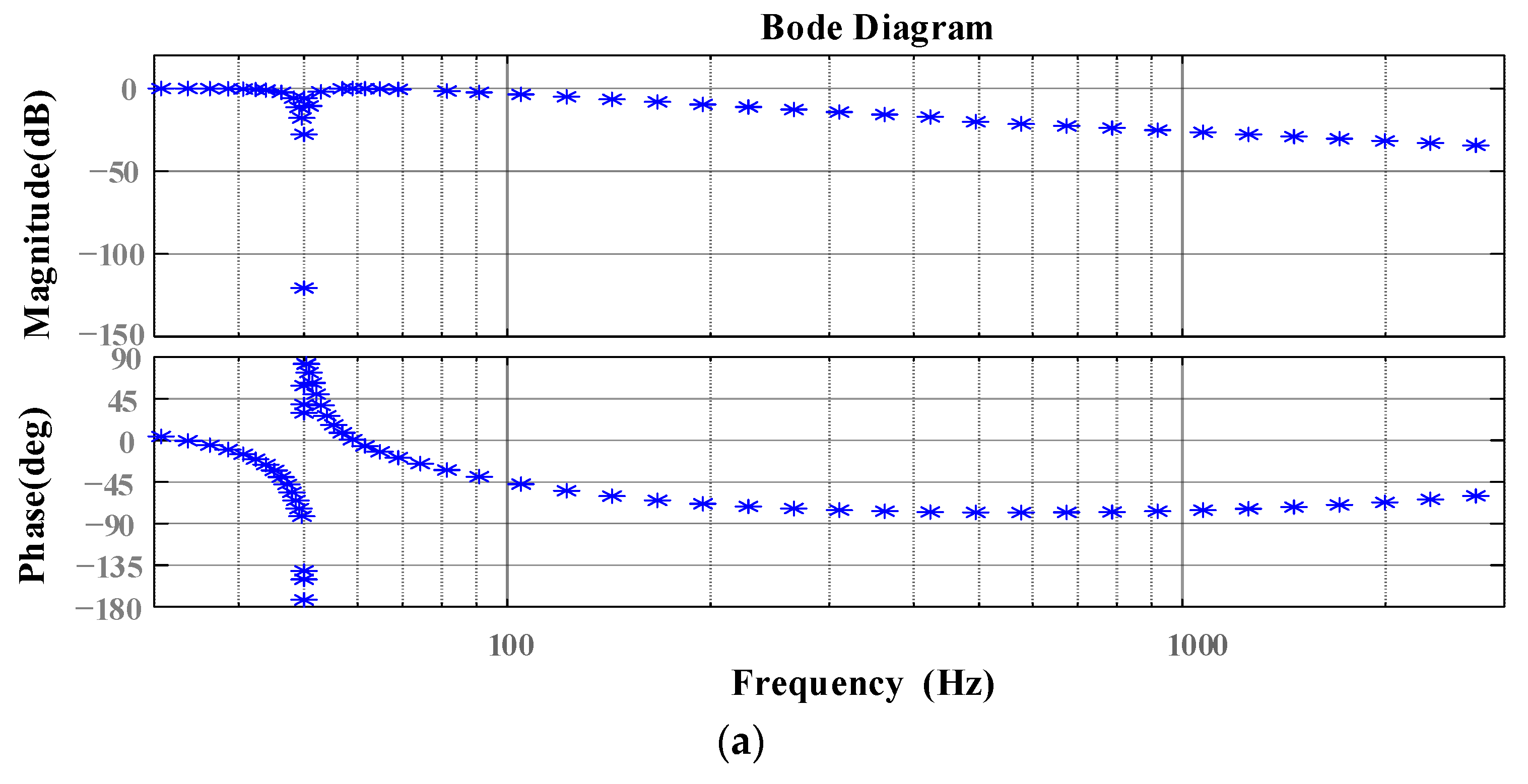
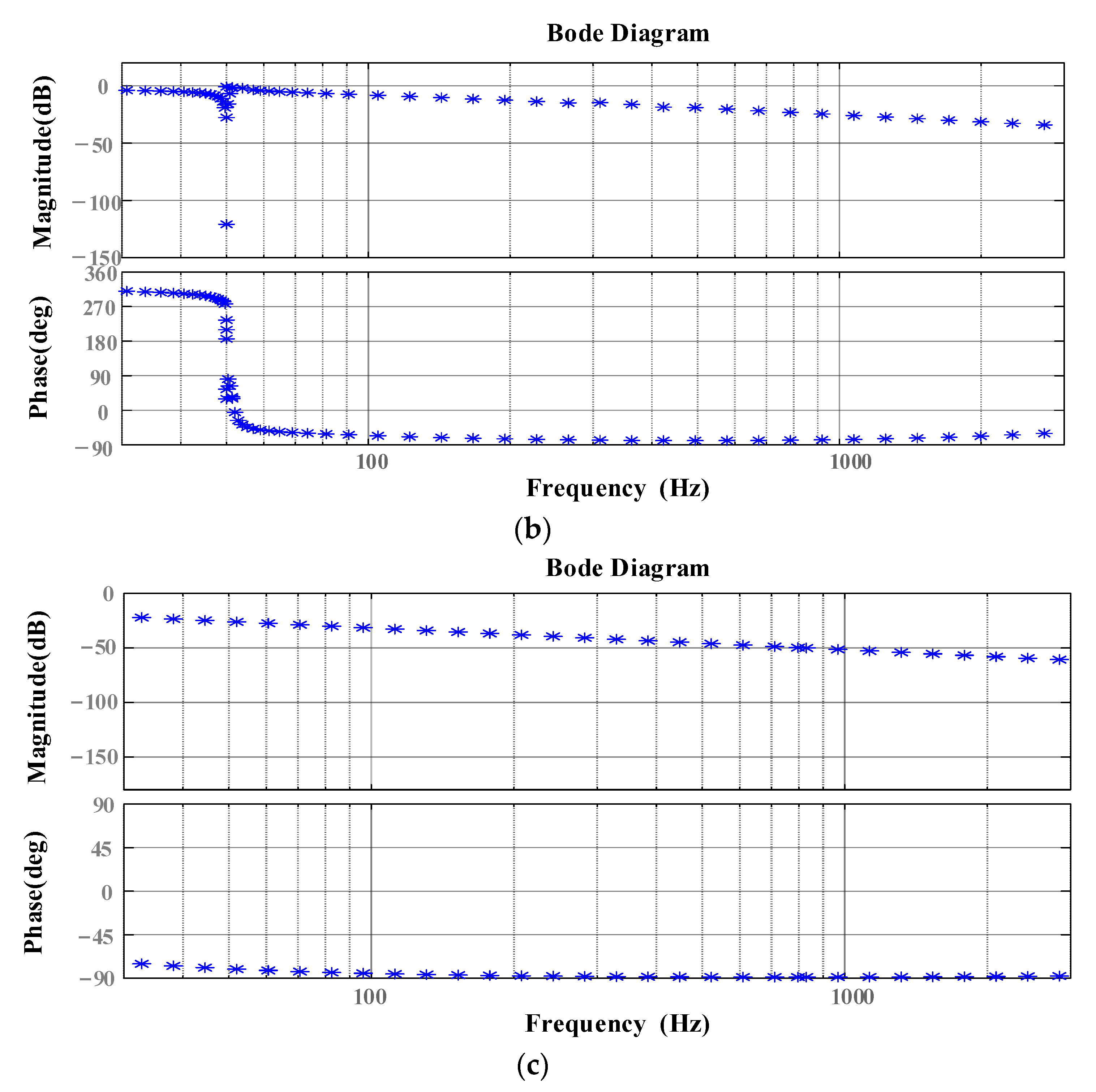
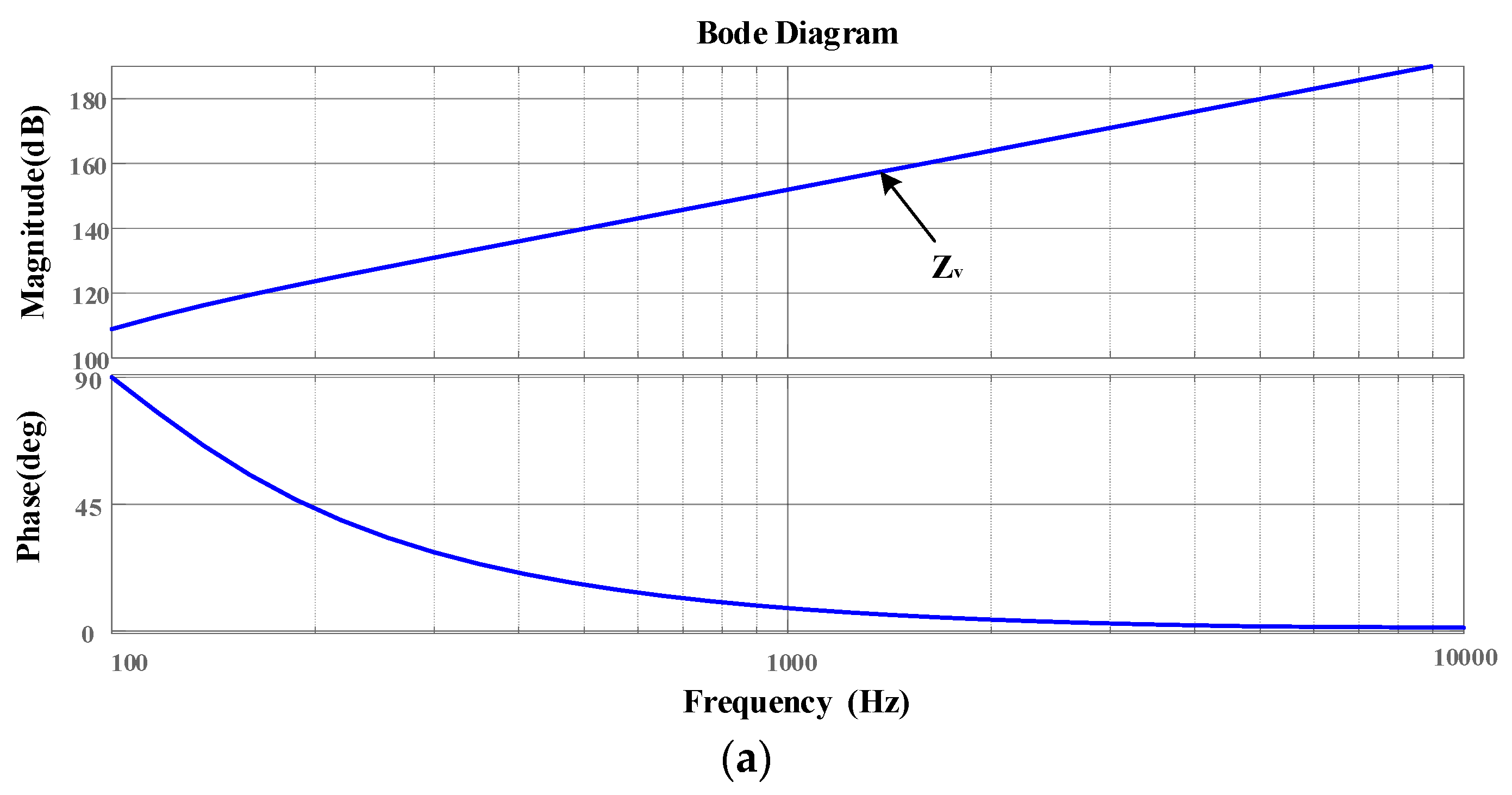
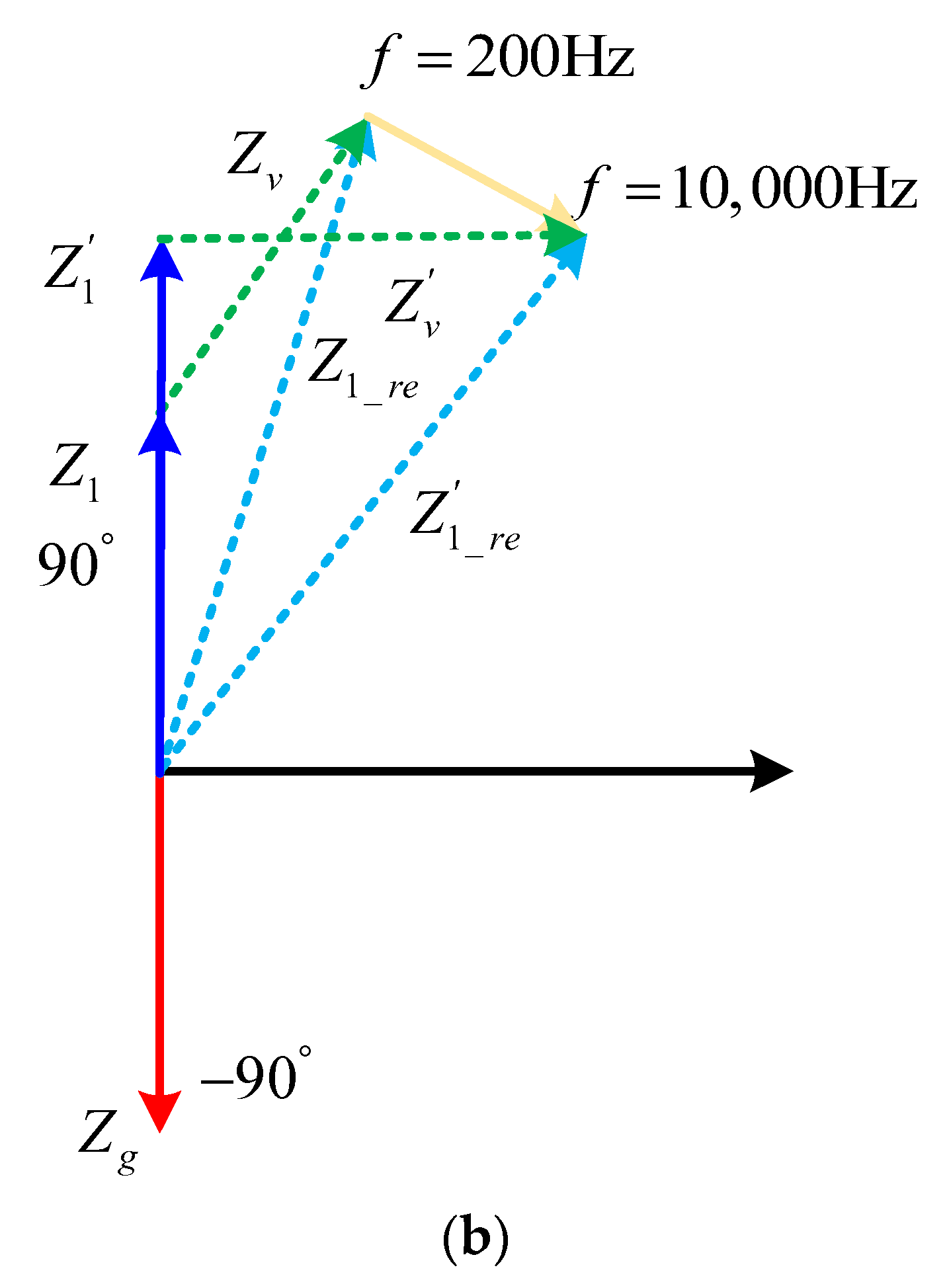
- The amplitude of the inverter system at high frequency is high, so that the intersection frequency of the amplitude-frequency characteristics of the inverter and the grid admittance with shunt capacitor is located on the right side of the grid admittance phase 180° jump, thus introducing high-frequency instability frequency points into the system.
- (2)
- The admittance phase of the inverter at the frequency band near the intersection of the admittance amplitude-frequency characteristics of the inverter at high frequency and the grid with a shunt capacitor is low. Based on the admittance stability theory, the stability region of the system at high frequency is small.
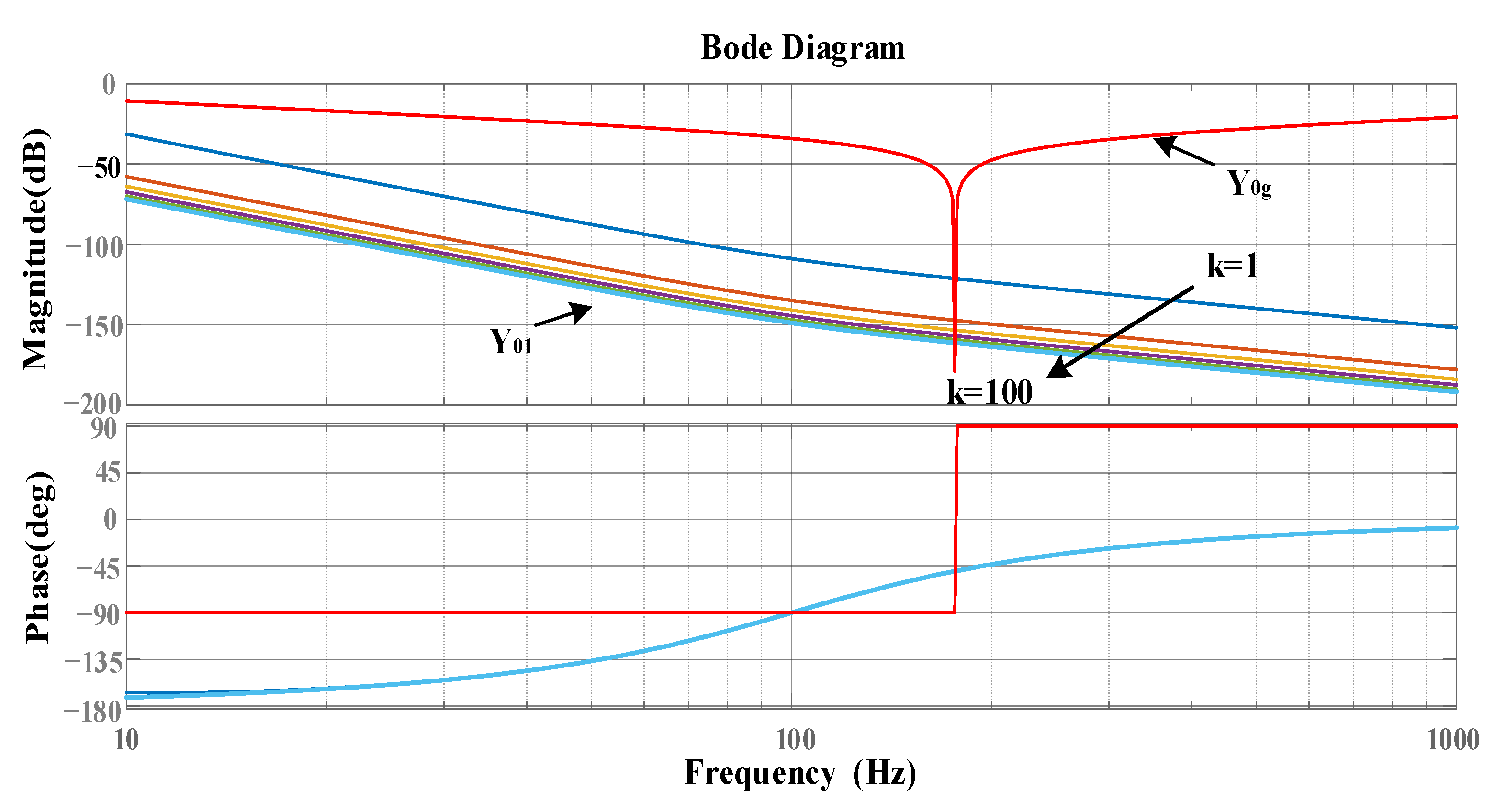
4.2. Parameter Analysis of High Frequency Oscillation Controller
5. Simulation and Experimental
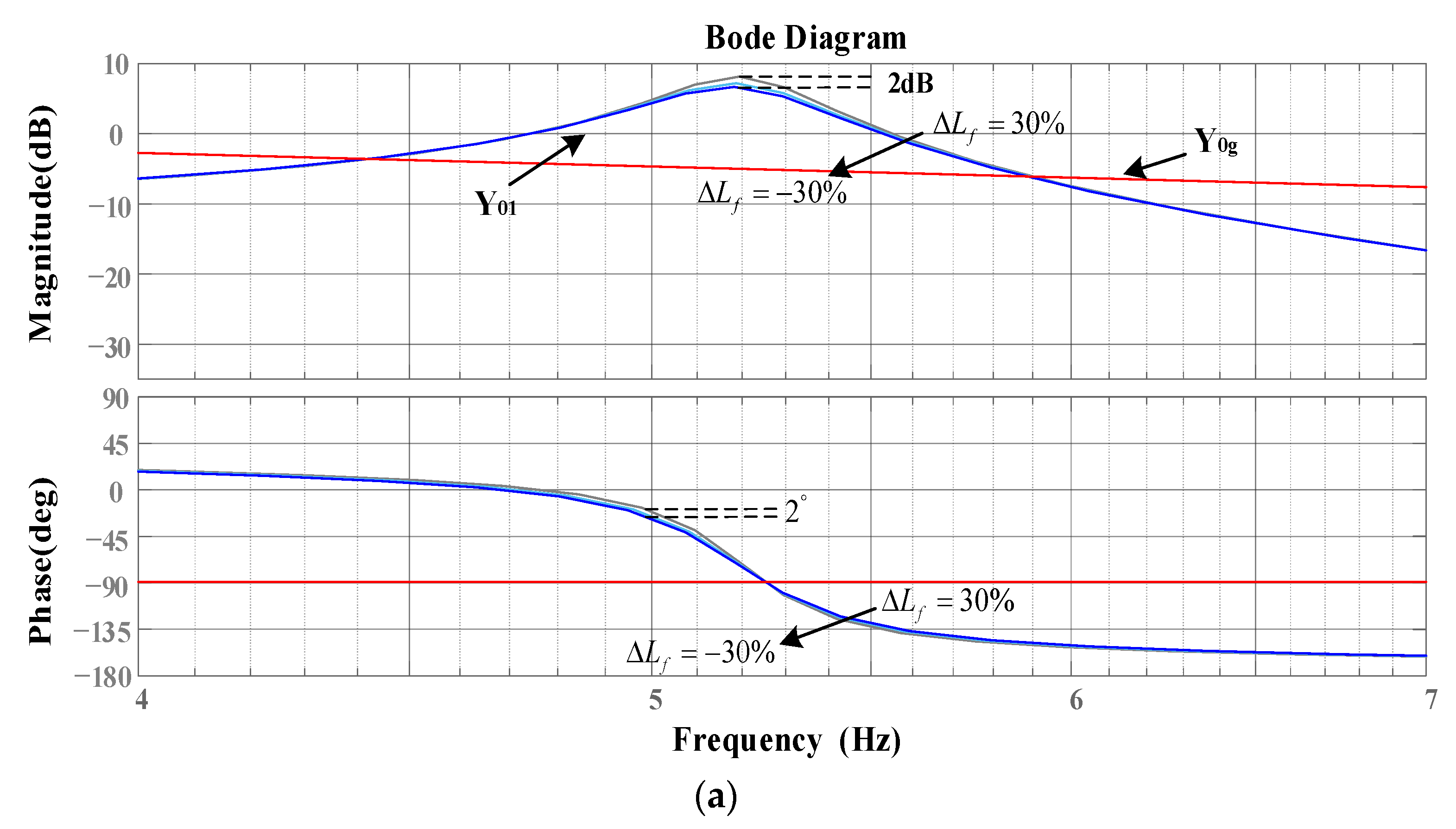
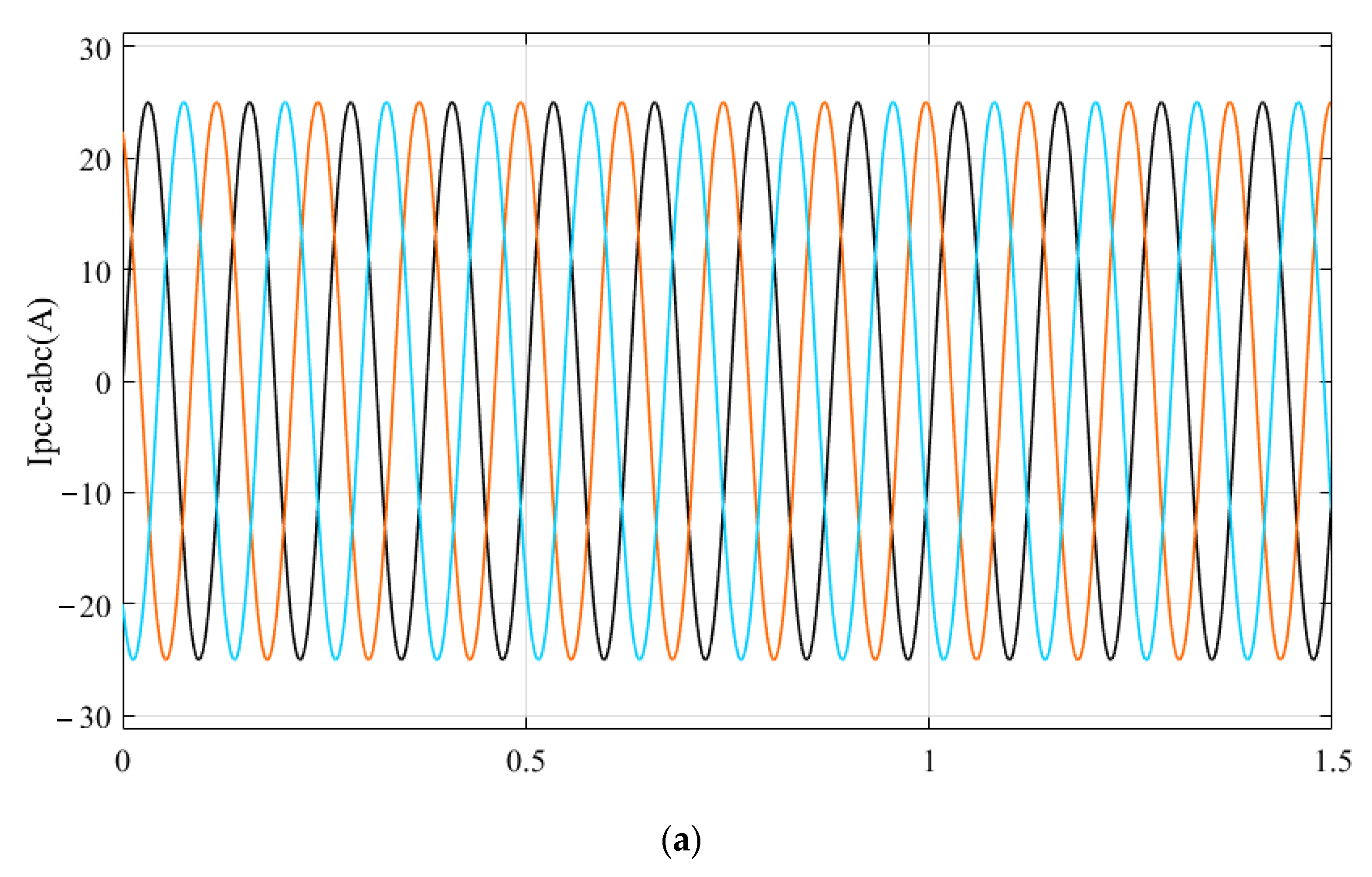
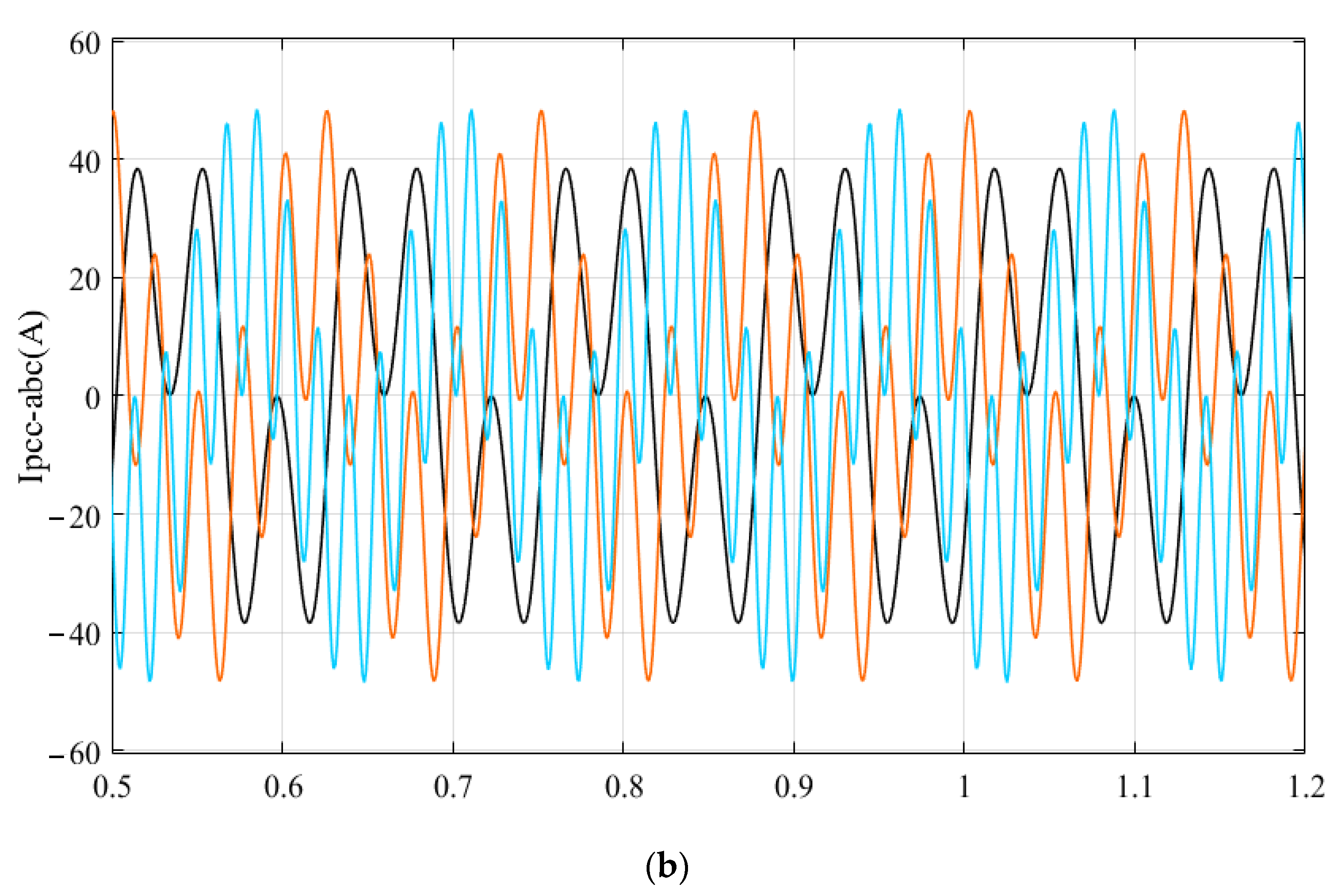
5.1. Simulation Verification
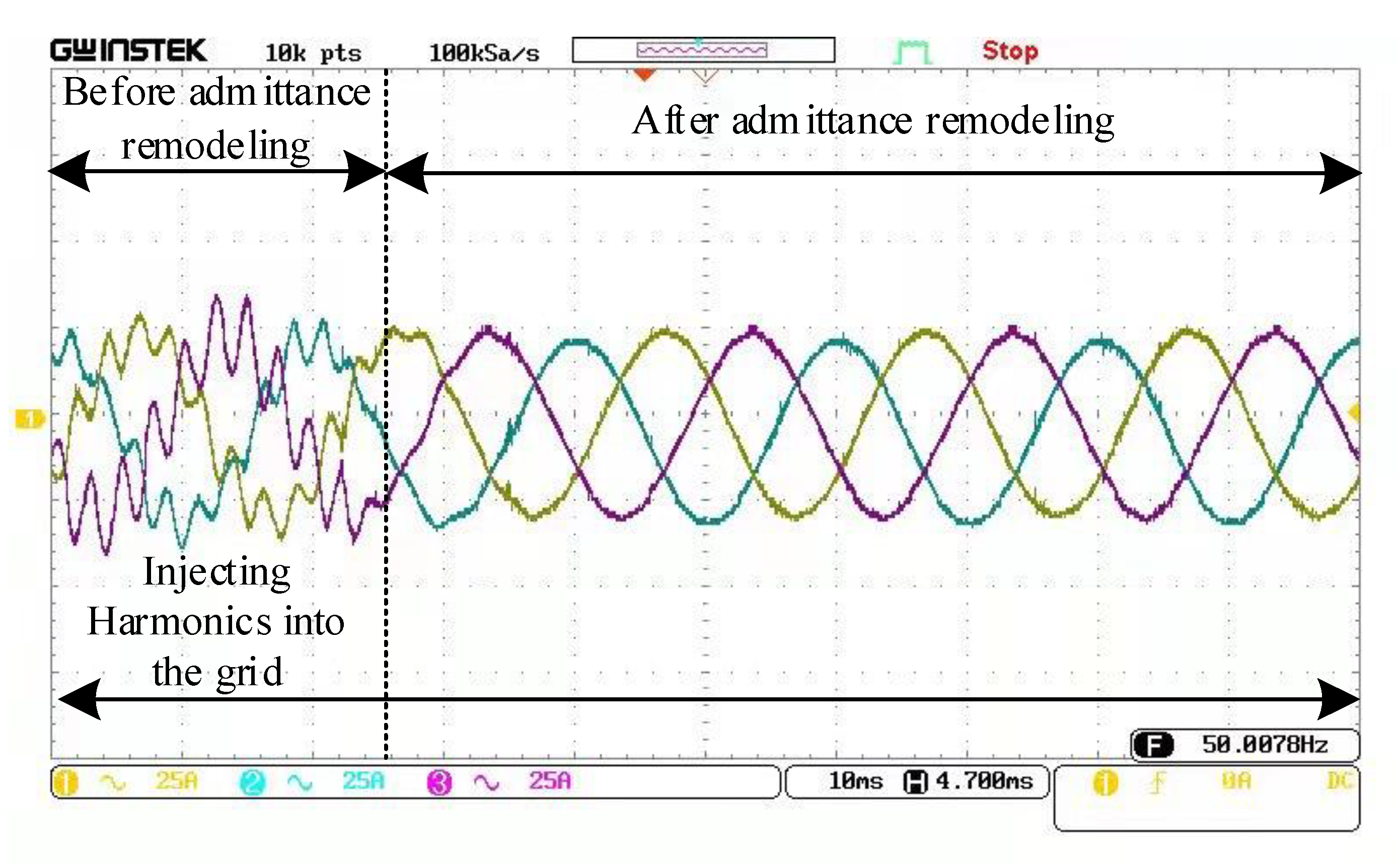
5.2. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Tu, C.; Gao, J.; Zhao, J.; Guo, Q. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid. Trans. China Electrotech. Soc. 2020, 35, 1327–1335. [Google Scholar]
- Zhou, X.; Chen, S.; Lu, Z.; Huang, Y.; Ma, S.; Zhao, Q. Technology features of the new generation power system in China. Proc. CSEE 2018, 38, 1893–1904. [Google Scholar]
- Zhou, L.; Luo, A.; Chen, Y.; Chen, Z.Y. A single-phase grid-connected power control and active damping optimization strategy with LCL filter. Trans. China Electrotech. Soc. 2016, 31, 144–154. [Google Scholar]
- Xie, Z.; Wu, W.; Chen, Y.; Cao, S.; Xu, Y. Sequence-Admittance Measurement Method of Grid-Connected Inverter With Its Control System Disturbance. IEEE Trans. Ind. Electron. 2023, 70, 8598–8602. [Google Scholar] [CrossRef]
- Sun, H.; Zhai, H.; Wu, X. Research and application of multi-energy coordinated control of generation, network, load and storage. Trans. China Electrotech. Soc. 2021, 36, 3264–3271. [Google Scholar]
- Wu, X.; Wang, J.; Liu, J.; Zhao, Y.; Liu, F.; Zhao, Z.; Zhang, X. Three-phase four-wire power supply method for three-phase three-leg inverter using low-voltage neutral point regulator. Power Syst. Technol. 2019, 43, 4209–4217. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Wang, Y.; Gong, C. Impedance-phased dynamic control method of grid-connected inverters under weak grid condition. Trans. China Electrotech. Soc. 2017, 32, 97–106. [Google Scholar]
- Xu, H.; Wu, H.; Li, Z. Several key issues on stability study of DFIG-based wind turbines with negative sequence control during low short-circuit ratio power grids. Trans. China Electrotech. Soc. 2021, 36, 4688–4702. [Google Scholar]
- Nian, H.; Pang, B.; Xu, G. Reshaping strategy of wide frequency impedance for DFIG system to suppress high frequency resonance under parallel compensation grid. Autom. Electr. Power Syst. 2018, 42, 48–56. [Google Scholar]
- Muhammad, T.; Khan, A.U.; Abid, Y.; Khan, M.H.; Ullah, N.; Blazek, V.; Prokop, L.; Misák, S. An Adaptive Hybrid Control of Reduced Switch Multilevel Grid Connected Inverter for Weak Grid Applications. IEEE Access 2023, 11, 28103–28118. [Google Scholar] [CrossRef]
- Xie, Z.; Chen, Y.; Wu, W. A global high-frequency oscillation suppression method for multi-inverter grid-connected system in weak grid. Trans. China Electrotech. Soc. 2020, 35, 885–895. [Google Scholar]
- Huang, Y.; Yuan, X.; Hu, J.; Zhou, P.; Wang, D. DC-Bus voltage control stability affected by AC-bus voltage control in VSCs connected to weak AC grids. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 445–457. [Google Scholar] [CrossRef]
- Xiong, L.; Zhou, F.; Wang, F.; Liu, X.; Chen, Y.; Zhu, M.; Yi, H. Static synchronous generator model: A new perspective to investigate dynamic characteristics and stability issues of grid-tied PWM inverter. IEEE Trans. Power Electron. 2016, 31, 6264–6280. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, X.; Hu, J.; Zhou, P. Modeling of VSC connected to weak grid for stability analysis of DC-link voltage control. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1193–1204. [Google Scholar] [CrossRef]
- Wang, C.; Sun, J.; Gong, J.; Zha, X. Mechanism and damping strategy of interactive instability between grid-connected inverter and grid impedance. Trans. China Electrotech. Soc. 2020, 35, 503–511. [Google Scholar]
- Yang, D.; Ruan, X.; Wu, H. Impedance shaping of the grid-connected inverter with LCL filter to improve its adaptability to the weak grid condition. IEEE Trans. Power Electron. 2014, 29, 5795–5805. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, D.; Wu, H. The active damping method for improving the stability of DC microgrid. Trans. China Electrotech. Soc. 2018, 33, 370–379. [Google Scholar]
- Liu, J.; Chen, Y.; Wu, W. Sequence impedance modeling and high-frequency oscillation suppression method for Island microgrid. Trans. China Electrotech. Soc. 2020, 35, 1538–1552. [Google Scholar]
- Liu, H.; Xie, X.; Li, Y.; Liu, H.; Hu, Y. Mitigation of SSR by embedding subsynchronous notch filters into DFIG converter controllers. IET Gener. Transm. Distrib. 2017, 11, 2888–2896. [Google Scholar] [CrossRef]
- Nian, H.; Hu, B.; Chen, L.; Xu, Y. Impedance modeling and stability analysis of direct power controlled doubly fed induction generator system without phase-locked loop. Proc. CSEE 2020, 40, 951–962. [Google Scholar]
- Hu, B.; Nian, H.; Li, M.; Xu, Y. Impedance characteristic analysis and reshaping method of DFIG system based on DPC without PLL. IEEE Trans. Ind. Electron. 2021, 68, 9767–9777. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, M.; Yang, X.; Yan, M.; Sun, Q.; Sun, J. Grid-connected inverter stabilization method based on adaptive composite admittance correction. High Volt. Eng. 2022, 48, 2088–2097. [Google Scholar]
- Wang, X.; Qin, K.; Ruan, X.; Pan, D.; He, Y.; Liu, F. A robust grid-voltage feedforward scheme to improve adaptability of grid-connected inverter to weak grid condition. IEEE Trans. Power Electron. 2021, 36, 2384–2395. [Google Scholar] [CrossRef]
- Li, W.; Ruan, X.; Pan, D.; Wang, X. Full-feedforward schemes of grid voltages for a three-phase LCL-type grid-connected inverter. IEEE Trans. Ind. Electron. 2013, 60, 2237–2250. [Google Scholar] [CrossRef]



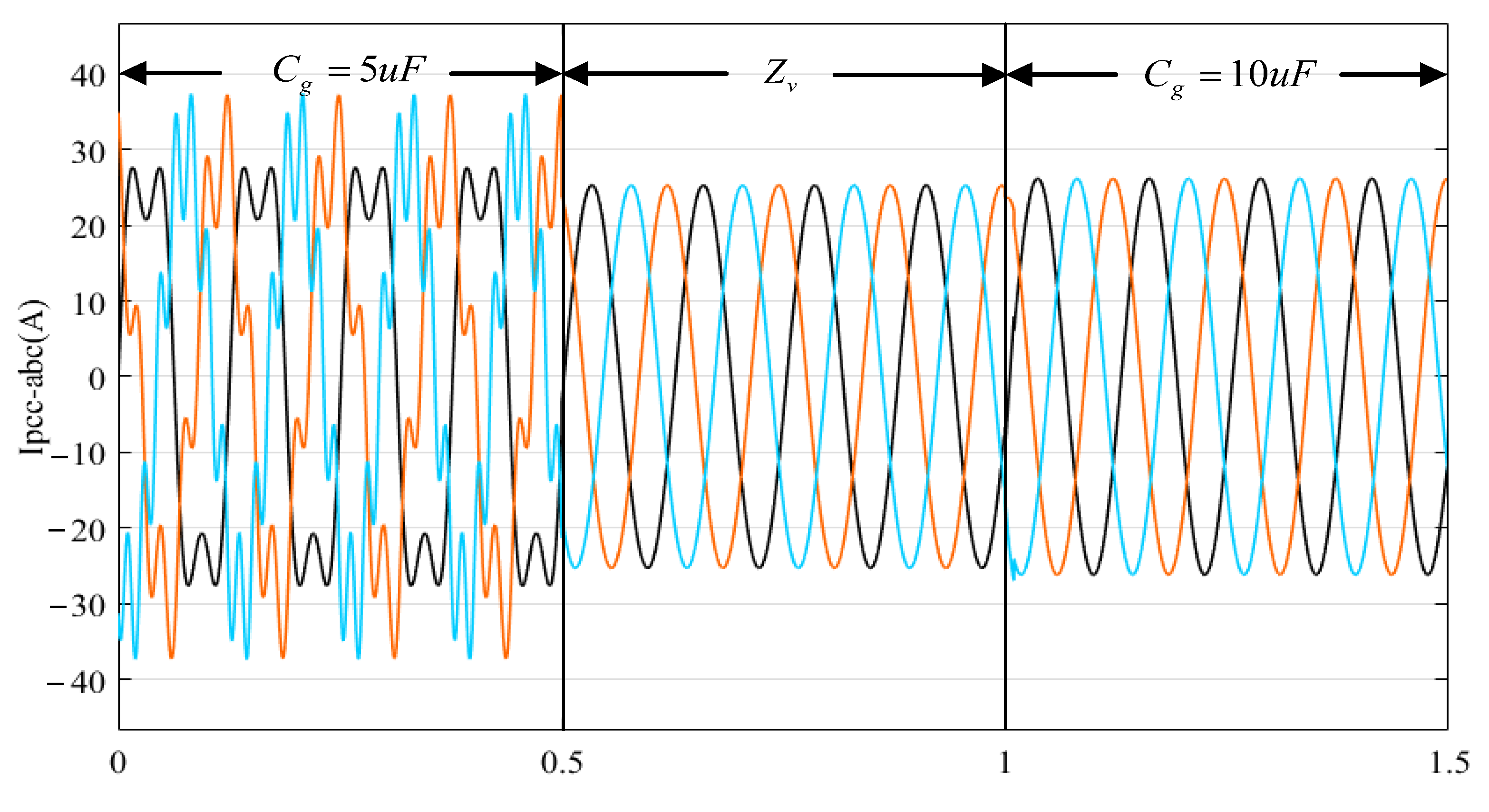
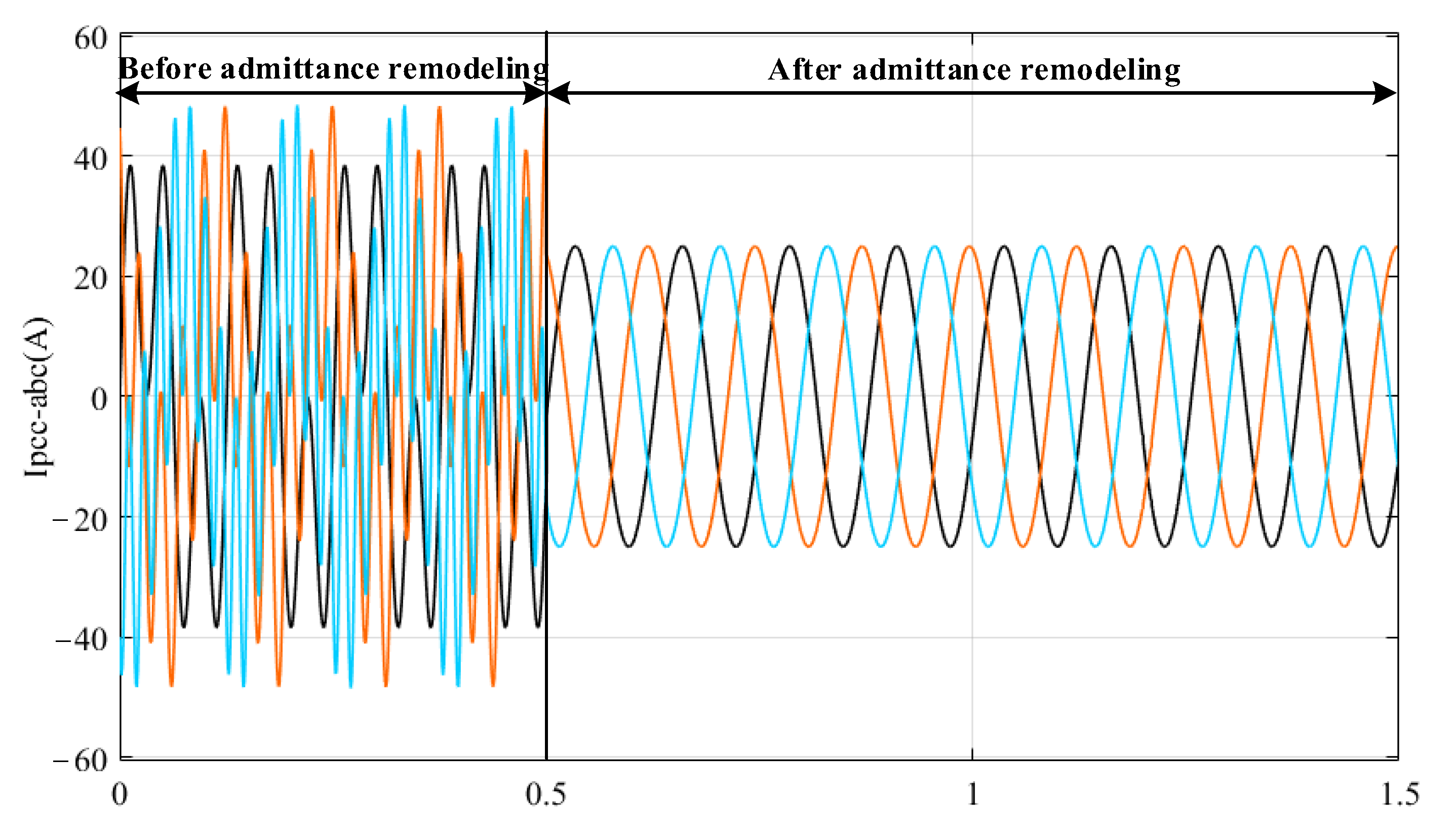


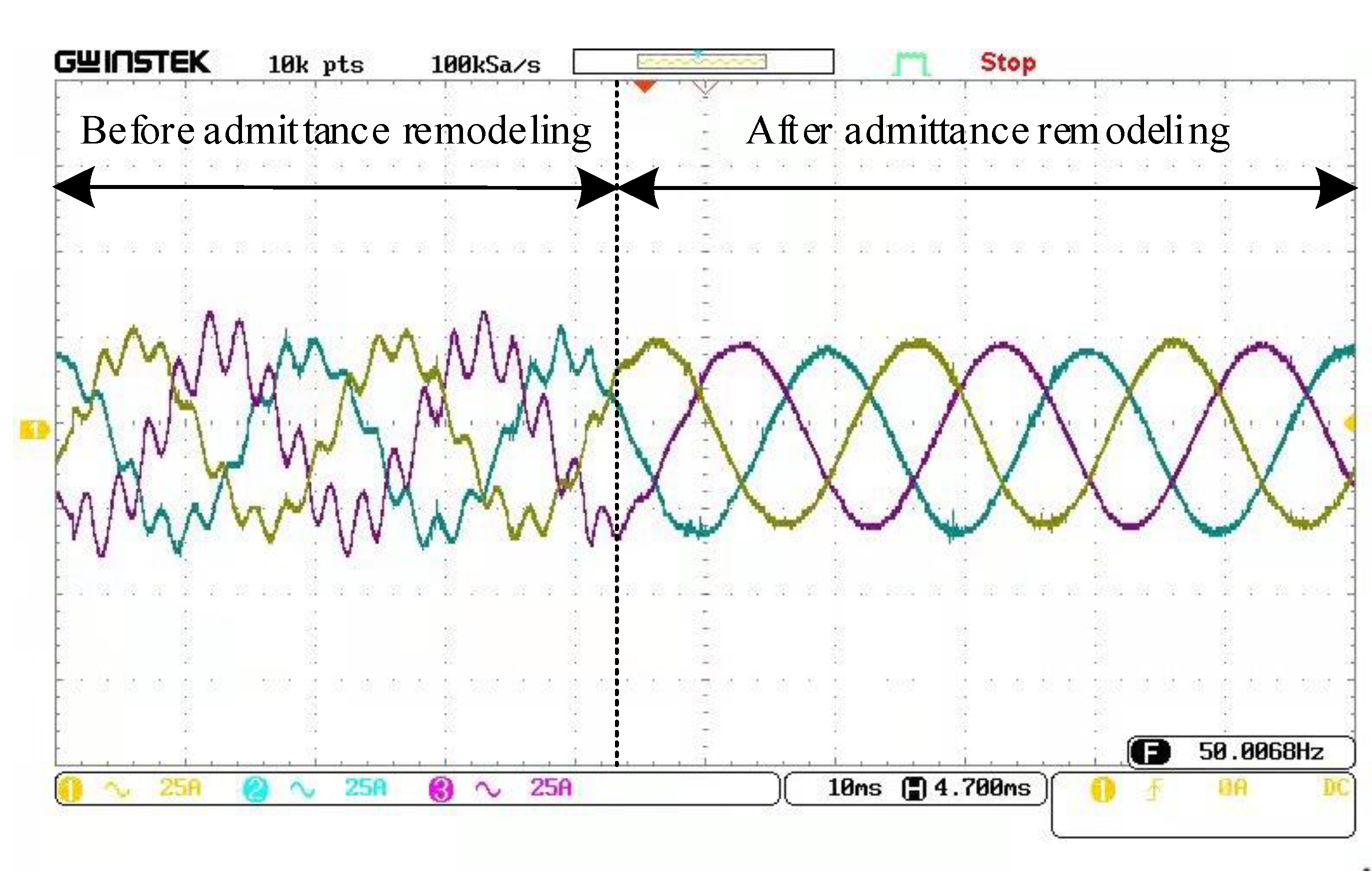
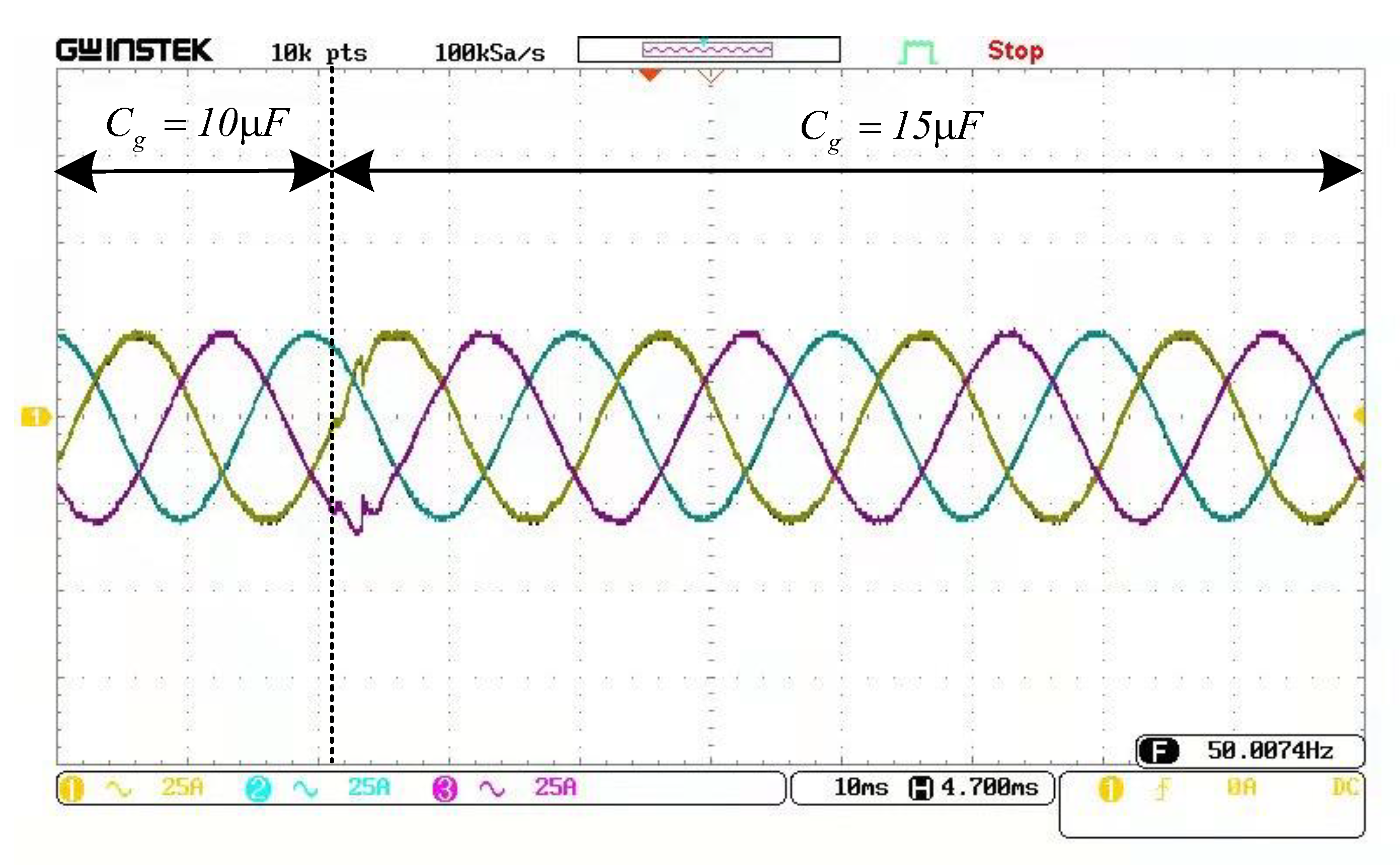
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| DC voltage Udc | 800 V | Integral coefficient of PLL controller kpi | 0.25 |
| Grid phase voltage Ug | 220 V | Proportion coefficient of d-axis current controller kdip | 1 |
| nominal power Po | 11 kW | Integral coefficient of q-axis current controller kdii | 18 |
| switching frequency fs | 5 kHz | Proportion coefficient of d-axis current controller kqip | 1 |
| fundamental frequency f1 | 50 Hz | Integral coefficient of q-axis current controller kqii | 18 |
| Inverter side inductance Lf | 3 mH | 0 axis current controller proportional coefficient k0ip | 3 |
| Carrier wave amplitude Vtri | 1 V | 0 axis current controller integral coefficient k0ii | 54 |
| grid inductance Lg | 2 mH | Proportional coefficient of DC side voltage balance PI controller kdcp | 2.1 |
| Proportion coefficient of PLL controller kpp | 0.16 | Integral coefficient of DC voltage balance PI controller kdci | 4.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, G.; Ye, Z.; Xia, Y.; Nian, H.; Jiang, Y. Oscillation Suppression Strategy of Three-Phase Four-Wire Grid-Connected Inverter in Weak Power Grid. Electronics 2023, 12, 3105. https://doi.org/10.3390/electronics12143105
Feng G, Ye Z, Xia Y, Nian H, Jiang Y. Oscillation Suppression Strategy of Three-Phase Four-Wire Grid-Connected Inverter in Weak Power Grid. Electronics. 2023; 12(14):3105. https://doi.org/10.3390/electronics12143105
Chicago/Turabian StyleFeng, Guoli, Zhihao Ye, Yihui Xia, Heng Nian, and Yunxiang Jiang. 2023. "Oscillation Suppression Strategy of Three-Phase Four-Wire Grid-Connected Inverter in Weak Power Grid" Electronics 12, no. 14: 3105. https://doi.org/10.3390/electronics12143105
APA StyleFeng, G., Ye, Z., Xia, Y., Nian, H., & Jiang, Y. (2023). Oscillation Suppression Strategy of Three-Phase Four-Wire Grid-Connected Inverter in Weak Power Grid. Electronics, 12(14), 3105. https://doi.org/10.3390/electronics12143105







