A New PSO Technique Used for the Optimization of Multiobjective Economic Emission Dispatch

Abstract

Most power is generated using fossil fuels like coal, natural gas, and diesel. The contribution of coal to power generation is very high compared to other sources. Almost all thermal power plants use coal as a fuel for power generation. Such sources of fossil fuels are limited and thus the cost of power generation increases. At the same time, the induced toxic gases due to these fossil fuels pollute the environment. The objective of this work is to solve the economic emission dispatch problem. Economic emission dispatch helps to find out how to operate power plants at the minimum cost and induce the minimum emissions at a thermal power plant. Economic emission dispatch with constraints is a nonlinear optimization problem. For the solution of such nonlinear economic emission load dispatch problems, this work considers a new particle swarm optimization technique. The proposed new PSO gives the best solution for economic emission load dispatch and handles the constraints. For the testing of the proposed new PSO algorithm, this work considered a case study of a system of six generating units, and it was tested for load demands of 700 MW, 800 MW, and 1000 MW. The results of the new PSO for the three load demands considered give the minimum generation cost, minimum emission, and minimum total cost compared to other optimization algorithms. The proposed techniques are effective, and they can help obtain the minimum generation cost and minimize emissions.

1. Introduction

Everyone is concerned about the growing number of environmental challenges throughout the world. There are several factors that either directly or indirectly impact the environment; 78% of the carbon dioxide in the environment is released by some of the primary culprits, including factories and cars. Since electricity is the lifeblood of every country, demand for it has risen as a result of economic expansion in all areas. The majority of nations rely on thermal power plants to provide their electricity. Numerous techniques exist and are regularly applied to the emissions challenge. This study reports on a novel particle swarm optimization (PSO) method for balancing the economic emission dispatch model. The technique reported here incorporates costs and emissions (with COx and NOx), and it is tested against systems of six generating units for various loads. The outcomes of the proposed PSO method have been compared in terms of minimizing costs and emissions. The unique contribution this study makes is the optimization technique, which has not yet been discussed in the literature studied thus far. The proposed PSO is a new variant of the PSO algorithm, and it has many advantages over classical PSO, such as the following.

• In classical PSO, the velocity needs to be updated after every iteration in order to update the particle positions. In this PSO, if some particles move away from the search area, they cannot come back and do not participate in the search for a global solution, but they continuously move their position away from the search area. Therefore, it is possible in classical PSO for particles to be used for local solutions. In the new PSO, the focus is to update the particle positions in such a way that they cannot stop before obtaining the neither solution nor move away from the search area.
• In classical PSO, constriction factors C1 and C2 are taken as constant values (C1 = C2 = 2.1), as shown in Equations (10) and (11). Therefore, a constant value is not very effective, and hence it cannot help the particles to come back if they move away from the search area. In the new PSO, the values of C1 and C2 are defined in such a way that they help to move the particles into the search area towards the global solution of the problem and cannot allow them to move away from the search area. The values of C1 and C2 are shown in Equations (12) and (13).
• In classical PSO, the weight of inertia is considered, which depends on the number of iterations and the minimum and maximum values of the inertia weight. In the new PSO, inertia weight is defined between the particle position mean and minimum value; this helps particles move continuously until they obtain the global solution to the problem.

Therefore, the proposed new PSO always provides a fast and effective global solution to the problem. That is the main motive for selecting this new PSO in this work for the solution of economic emission dispatch.

The rest of this paper is divided as follows: Section 2 outlines the literature in the PSO domain; Section 3 describes the underlying mathematical model of the economic emission problem; Section 4 presents the optimization techniques of the novel PSO; Section 5 discusses assumptions for obtaining the results, the importance of the novel PSO with ELD formulation, and the comparative results of different techniques with the proposed new PSO. Finally, Section 6 concludes this study.

2. PSO in the Literature

Some of the major causes of environmental pollution are large industries, thermal power plants, and diesel and gasoline vehicles. They emit around 82% carbon dioxide and carbon monoxide into the environment. Coal is used as fuel at thermal power plants, and it is the main source of carbon dioxide and sulphur dioxide in the environment. Due to sulphur dioxide, acid rain arises, which affects lung function and also has adverse effects on the eye. Similarly, carbon dioxide produces greenhouse gases and induces many health issues such as difficulty breathing, headaches, high blood pressure, and asphyxia.

An innovative water evaporation optimization technique was put forth to address the economic load dispatch problem with emission constraints. The goal was to produce a product at the lowest possible cost with the fewest emissions. The suggested water evaporation optimization technique was based on molecular dynamics simulations of the evaporation of a small number of water molecules on solid surfaces with various degrees of wet ability [1,2].

A combined economic emission dispatch (CEED) model for the microgrid system was proposed for obtaining the optimal generation cost. A novel improved Mayfly algorithm incorporating Levy flight cost and emission was examined for the case study of the Island microgrid model. The results obtained by the proposed methods were compared to those obtained by thermal-powered, solar-powered, and wind-powered generating units [3].

An economic emission model with line flow constraints for obtaining the minimum cost of generation and emissions was proposed. For the solution of the proposed model of 14 IEEE-bus systems, a classical technique was suggested [4].

Article [5] used deterministic and stochastic economic load dispatch models and optimized them with improved particle swarm optimization (PSO) to deal with the economic load dispatch and environmental impact. Results obtained by the proposed method were compared with those obtained by the other PSO variants, a cultural algorithm, simulated annealing, and Tabu search algorithms for analyzing the economic load dispatch. Two cases of data from 10 generators and 13 generator systems were considered [6].

Economic load dispatch with renewable energy sources was optimized by a hybrid model of particle swarm optimization and the bat algorithm [7]. A new PSO technique was very effective in finding the optimum solution for the random data set [8]. Moreover, its value does not differ if the data set values increase. Various PSO variants for optimization of economic load dispatch were considered in different case studies and compared the results obtained by different PSO techniques [9].

An improved PSO technique for the solution of a multiobjective microgrid dispatch model for the development of microgrids included PV systems, wind turbines, microturbines, and electric vehicles. Mobile distributed energy storage devices were considered the batteries of electric vehicles [10].

A combined economic emission dispatch problem to obtain the optimal cost of the system was considered. The proposed objective model was used for obtaining the minimum cost of generation and emission values. For the optimization of the proposed ELD model, a new interior search algorithm was suggested. Four cases were solved without solar and wind energy sources [11].

A multiobjective model, including electric vehicles as load-optimized for the analysis of the economy and the environmental protection of a microgrid system, was considered. For the optimization of the proposed model, the simulated annealing particle swarm optimization algorithm (ASAPSO) was suggested. A linear weighting method was used, which was based on the theory of a two-person zero-sum game for the full consumption of renewable energy [12].

A new particle swarm optimization algorithm was proposed for the solution for handling the economic load dispatch with emissions, along with power balance and generation limits [13]. The authors of [14] solved the grid-connected microgrid system by using an improved bee colony. Differential evolution and quantum particle swarm optimization techniques were also used to solve the microgrid model of economic load dispatch [15]. A deep analysis of environmental emissions due to carbon dioxide, nitrogen oxide, and greenhouse gases was performed [16]; CO₂ emissions, global warming, and its resultant climate change were shown, which induce serious environmental problems and affect human beings. Methods were also suggested to reduce the CO₂, SO₂, and greenhouse gases induced by all sectors of human activity, including power generation [17].

To reduce the cost of generation and environmental emissions, a three-echelon supply chain system with multi-level trade credit and single-setup, multiple-delivery policies was suggested. This system was used to quantify the effects of the environmental regulations and trade credit period [18].

A quasi-oppositional search-based political optimizer was used to solve the non-convex-single- and bi-objective economic and emission load dispatch problems. The proposed bi-objective EELDP problem was solved with constraints such as the valve-point loading effect and generator limits [19].

The multi-area economic load dispatch problem was solved by convergent particle swarm optimization [20]. A hybrid dynamic model of economic emission dispatch was solved by the moth–flame optimization algorithm, including a renewable energy generation system [21]. The dynamic programming technique suggested for the solution of the economic and emission dispatch problems [22]. The economic emission dispatch problem is optimised by the grasshopper algorithm with power flow constraints [23]. An adaptive multi population-based differential evolutionary technique was proposed that improves ELD global solutions [24]. A hybrid generation system can help reduce the cost of power generation as well as carbon emissions [25].

A multiobjective ELD problem was formulated using a wind energy system and a distributed generation system [26]. Foraging optimization based on the spiral foraging approach given for solving the ELD problem improves global search capability and convergence velocity [27]. To address the complex economic load dispatch issue, a new hybrid grey wolf optimization method with a strong learning mechanism was developed [28].

An optimization algorithm based on the theory of demand and supply was used to optimize the ELD model. The proposed algorithm efficiently moves the particles in the search space between local and global searches [29]. The authors of [30] considered class-topping optimization techniques that are based on human intelligence. They solved ELD as well as CEED using four different case studies. Two test cases of 10 and 15 generating units were taken and optimized for the ELD problem by PPSO [31].

The bat algorithm was used for optimization of multiobjective problems. This work considered economic emission dispatch as a multiobjective problem and found the overall generation cost of the plant [32]. A contemporary search-and-rescue optimization approach that is motivated by the behavior of humans during search-and-rescue operations was used for the combined solution of emissions and economic dispatch [33].

To overcome ELD difficulties, enhanced arithmetic optimization was suggested. Two crucial variables in the original AOA were math optimizer acceleration and math optimizer probability [34]. For optimization of multi-objective ELDs, data mining technology was used. The proposed techniques give the best decision for the sample test data [35].

Harris hawks optimization techniques were used to address the issues of economic load dispatch. The Harris hawks optimizer was used for finding the number of possible solutions in the search space, and each of these regions can be thoroughly searched for the local best solution via adaptive hill climbing [36].

The chameleon swarm algorithm was proposed for the minimization of emissions as well as the generation costs of the power plant [37]. A novel evolutionary optimization approach was proposed to resolve the economic load dispatch issue. The standard harmony search random selection process was replaced with a mutation process based on wavelet theory to increase the performance of the suggested strategy [38].

3. Economic Emission Load Dispatch Model

This section considers the mathematical model of economic dispatch, first as a single objective given in Equation (1). The minimization of the generation cost ($/h) of the thermal power plant for the T^th generating system [3] is given as

$${\mathrm{F}}_{\mathrm{T}}=\mathrm{m}\mathrm{i}\mathrm{n}{\sum }_{\mathrm{i}=1}^{\mathrm{T}}{(\mathrm{a}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}^2+{\mathrm{b}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}+{\mathrm{c}}_{\mathrm{i}}\left)\right(\$/\mathrm{h})$$

(1)

where a_i, b_i, and c_i are the cost coefficients included during the generation, P_i is the generated power, and F_T is the total generation cost.

This is subject to following constraints.

3.1. Real Power Balance

Power generated at the power plant that is consumed by the consumer is called load demand, and some power is lost during the transmission of power from the generating plant to consumers. The real power balance is defined as

$$\sum _{\mathrm{i}=1}^{\mathrm{T}}{\mathrm{P}}_{\mathrm{i}}-{\mathrm{P}}_{\mathrm{L}}={\mathrm{P}}_{\mathrm{D}}$$

(2)

where P_D is the load demand and P_L is the losses in the transmission line.

3.2. Generation Capacity Limits

All plants generate power between the lower and upper limits so that it can be loaded into the grid.

$${{\mathrm{P}}_{\mathrm{i}}^{\mathrm{M}\mathrm{i}\mathrm{n}}\le \mathrm{P}}_{\mathrm{i}}\le {\mathrm{P}}_{\mathrm{i}}^{\mathrm{M}\mathrm{a}\mathrm{x}}$$

(3)

where ${\mathrm{P}}_{\mathrm{i}}^{\mathrm{M}\mathrm{i}\mathrm{n}}$ and ${\mathrm{P}}_{\mathrm{i}}^{\mathrm{M}\mathrm{a}\mathrm{x}}$ are the lower and upper limits of power generated at power plant.

Then, include one more objective called environmental emission, which is induced when fossil fuel combustion occurs at thermal power plants (SOx, NOx, and COx are emitted and pollute the environment). Emissions from the thermal power plant due to these toxic gases are considered a second objective and are given as Equation (4) for T^th generating units. The emission is calculated in tons per hour as a function of the generated power [3]. So, as power generation increases, emissions into the environment also increase.

$${\mathrm{E}}_{\mathrm{T}}=\mathrm{m}\mathrm{i}\mathrm{n}{\sum }_{\mathrm{i}=1}^{\mathrm{T}}{(\mathrm{d}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}^2+{\mathrm{e}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}+{\mathrm{f}}_{\mathrm{i}}\left)\right(\mathrm{T}/\mathrm{h})$$

(4)

where d_i, e_i, and f_i are the emission coefficients and E_T is the total emission (tons/h).

3.3. Combined Economic Emission Dispatch (CEED)

The main objective of the combined economic emission dispatch model is to reduce the cost of power generation; at the same time, emission levels should also be mitigated without violating the considered constraints. The combined economic emission function is given as Equation (5).

$${\mathrm{T}}_{\mathrm{c}}=\mathrm{M}\mathrm{i}\mathrm{n}\sum _{\mathrm{i}=1}^{\mathrm{T}}\{{\mathrm{F}}_{\mathrm{T}}\left({\mathrm{P}}_{\mathrm{i}}\right),{\mathrm{E}}_{\mathrm{T}}\left({\mathrm{P}}_{\mathrm{i}}\right)\}$$

(5)

The first objective (ELD) is given in Equation (1) in $/h, and the second objective (minimizing emissions) is given in Equation (4) in tons/h. For obtaining multiobjective economic emission dispatch, Equations (1) and (4) are combined by using the price penalty factor h ($/ton), as given in Equation (6). The penalty factor is defined as the ratio of power produced by the plant to the actual power requirement of the load being satisfied after line loss.

$$\mathrm{h}=\frac{{\mathrm{F}}_{\mathrm{T}}\left({\mathrm{P}}_{\mathrm{i}}^{\mathrm{M}\mathrm{a}\mathrm{x}}\right)}{{\mathrm{E}}_{\mathrm{T}}\left({\mathrm{P}}_{\mathrm{i}}^{\mathrm{M}\mathrm{a}\mathrm{x}}\right)}=\frac{{(\mathrm{a}}_{\mathrm{i}}{(\mathrm{P}}_{\mathrm{i}}^{\mathrm{M}\mathrm{a}\mathrm{x}})^2+{\mathrm{b}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}^{\mathrm{M}\mathrm{a}\mathrm{x}}+{\mathrm{c}}_{\mathrm{i}})}{{(\mathrm{d}}_{\mathrm{i}}{(\mathrm{P}}_{\mathrm{i}}^{\mathrm{M}\mathrm{a}\mathrm{x}})^2+\mathrm{e}{\mathrm{P}}_{\mathrm{i}}^{\mathrm{M}\mathrm{a}\mathrm{x}}+{\mathrm{f}}_{\mathrm{i}})}$$

(6)

Therefore, combined economic emission function is given as

$${\mathrm{T}}_{\mathrm{c}}=\sum _{\mathrm{i}=1}^{\mathrm{T}}{(\mathrm{a}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}^2+{\mathrm{b}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}+{\mathrm{c}}_{\mathrm{i}})+\mathrm{h}\ast (\sum _{\mathrm{i}=1}^{\mathrm{T}}{(\mathrm{d}}_{\mathrm{i}}{\mathrm{P}}_{\mathrm{i}}^2+\mathrm{e}{\mathrm{P}}_{\mathrm{i}}+{\mathrm{f}}_{\mathrm{i}})$$

(7)

where ${\mathrm{T}}_{\mathrm{c}}$ is the total cost of economic emission dispatch, F_T and E_T are the functions of fuel cost and emission, respectively, and h is the penalty factor used for the combination of fuel cost and emission function. Since fuel costs are represented in $/h and emissions are represented in tons/h, the direct combination of both objectives is not possible without the use of a penalty factor. Therefore, the penalty factor as given in Equation (6) is used to combine the two objectives into a single objective (producing a multiobjective model).

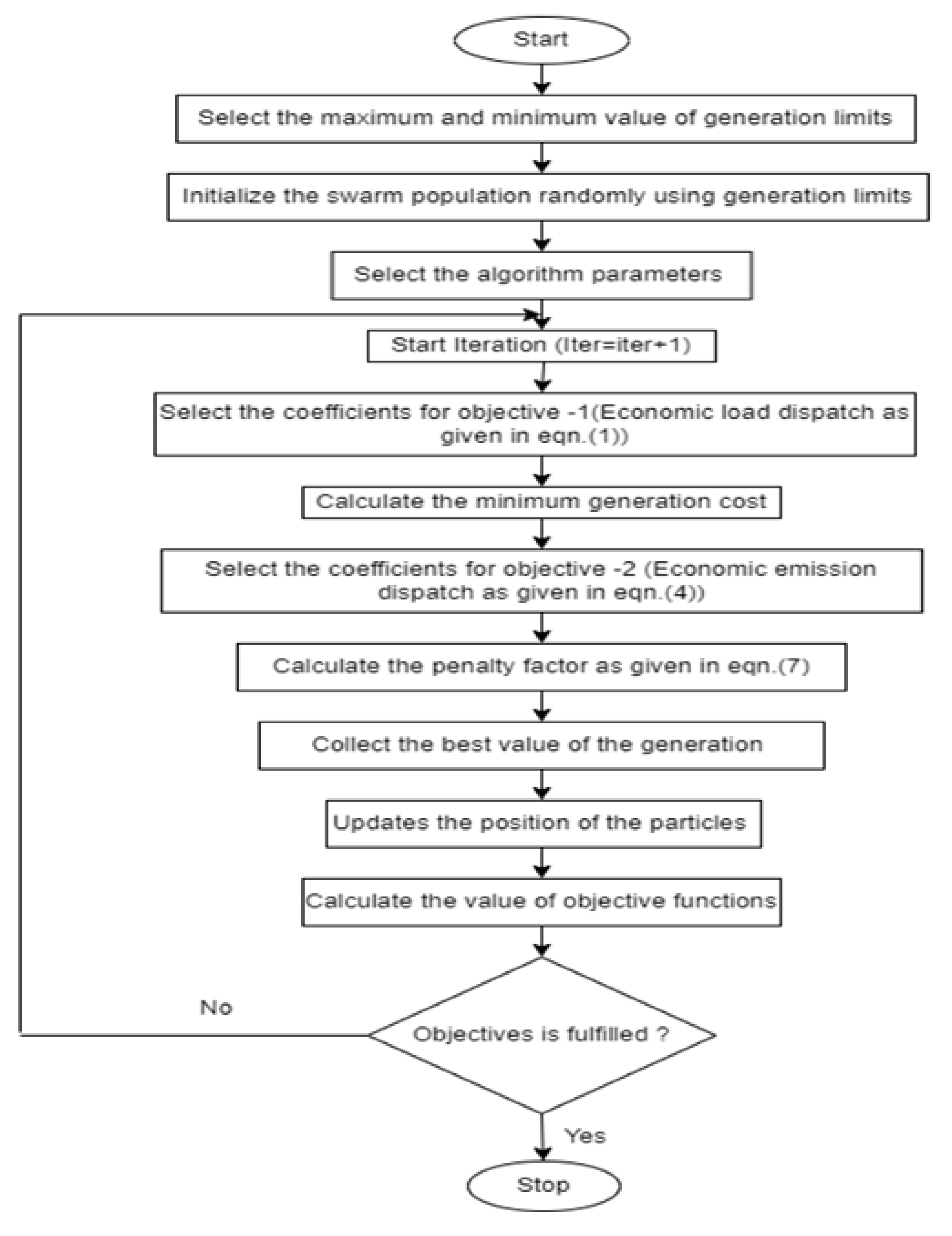
4. Modified PSO (Modified Particle Swarm Optimization)

This is a modified new PSO; it is better than the classical model in terms of providing an effective and efficient solution. For the development of algorithms in MATLAB, the following steps are followed.

• First, initiate the particle positions with the help of the maximum and minimum limits of generated power, as given in Equation (8).

$${\mathrm{S}}_{\mathrm{i}}^{\mathrm{K}}={\mathrm{P}}_{\mathrm{m}\mathrm{i}\mathrm{n}}+\left({\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{P}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\right)\ast \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}$$

(8)

where P_max and P_min are the set of generated power limits and rand is the random value between zero and one generated by MATLAB during the optimization.

2

Take the set of data cost coefficients (a, b, and c) and emission coefficients (c, d, e, and f) from

Table 1. Test data for six generating units with economic emission dispatch coefficients.

Gen. Unit	${\mathbf{a}}_{\mathbf{i}}$	${\mathbf{b}}_{\mathbf{i}}$	${\mathbf{c}}_{\mathbf{i}}$	${\mathbf{d}}_{\mathbf{i}}$	${\mathbf{e}}_{\mathbf{i}}$	${\mathbf{f}}_{\mathbf{i}}$	${\mathbf{P}}_{\mathbf{i}}^{\mathbf{m}\mathbf{i}\mathbf{n}}$	${\mathbf{P}}_{\mathbf{i}}^{\mathbf{m}\mathbf{a}\mathbf{x}}$
1	0.1525	38.54	756.8	0.0042	0.33	13.86	10	125
2	0.106	46.16	451.32	0.004	0.33	13.86	10	150
3	0.0208	40.159	1049.99	0.00683	−0.5455	40.27	35	225
4	0.0355	38.31	1234.5	0.0068	−0.5455	40.27	35	210
5	0.0211	36.328	1658.6	0.0046	−0.5112	42.7	130	325
6	0.0179	38.27	1356.7	0.0042	−0.5112	42.7	125	315

.

3

Then, initiate the velocity of the particles using the particle positions, as given by Equation (9).

$${\mathrm{V}}_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}\left({\mathrm{V}}_{\mathrm{i}}^{\mathrm{k}}\right)={\mathrm{V}}_{\mathrm{m}\mathrm{i}\mathrm{n}}+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\ast ({\mathrm{V}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{V}}_{\mathrm{m}\mathrm{i}\mathrm{n}})$$

(9)

where ${\mathrm{V}}_{\mathrm{m}\mathrm{i}\mathrm{n}}=-\frac{{\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{P}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{u}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{s}}$ and ${\mathrm{V}}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{{\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{P}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{u}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{s}}$.

V_min is the minimum speed of the particles required to move in the search area, V_max is the maximum speed of the particles, and rand is a real number generated by MATLAB between zero and one. If the speed increases beyond V_max, particles may move away from the search space, and hence the final results may differ from the optimum value.

4.

Set the number of iterations (iteration = 1 + maximum iteration).

5.

Define the initial particle best and global best values.

6.

After completion of iterations, select the Pbest and Gbest from the swarm. Then, the updating of the position of the particle is given as in Equation (11) when rand () ≥ α:

$${\mathrm{S}}_{\mathrm{i}}^{(\mathrm{K}+1)}={\mathrm{W}}_{\mathrm{n}\mathrm{e}\mathrm{w}}\ast {\mathrm{S}}_{\mathrm{i}}^{\mathrm{K}}+{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}_1{\mathrm{C}}_1\left({\mathrm{P}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}-{\mathrm{S}}_{\mathrm{i}}^{\mathrm{K}}\right)+{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}_2{\mathrm{C}}_2\left({\mathrm{g}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}-{\mathrm{S}}_{\mathrm{i}}^{\mathrm{K}}\right)$$

(10)

When rand () ≤ α position of the particles is updated as given in Equation (11):

$${\mathrm{S}}_{\mathrm{i}}^{(\mathrm{K}+1)}={\mathrm{W}}_{\mathrm{n}\mathrm{e}\mathrm{w}}\ast {\mathrm{S}}_{\mathrm{i}}^{\mathrm{K}}+{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}_1{\mathrm{C}}_1\left({\mathrm{P}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}-{\mathrm{S}}_{\mathrm{i}}^{\mathrm{K}}\right)+{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}_2{\mathrm{C}}_2\left({\mathrm{g}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}-{\mathrm{S}}_{\mathrm{i}}^{\mathrm{K}}\right)+{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}_3{\mathrm{C}}_3\left({\mathrm{n}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}-{\mathrm{S}}_{\mathrm{i}}^{\mathrm{K}}\right)$$

(11)

where α is the certain probability in each iteration of evaluation, ${\mathrm{n}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}$-present optimal particles, and ${\mathrm{C}}_1,{\mathrm{C}}_2,\mathrm{a}\mathrm{n}\mathrm{d} {\mathrm{C}}_3$ are the acceleration coefficients given as

$${\mathrm{C}}_1={\mathrm{C}}_3=0.5+2\cos \left[\frac{\mathsf{\pi }\left(\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}-1\right)}{2\left(\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m} \mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}-1\right)}\right]$$

(12)

$${\mathrm{C}}_2=0.5+2\sin \left[\frac{\mathsf{\pi }(\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}-1)}{2(\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m} \mathrm{i}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}-1)}\right]$$

(13)

7.

Select the weight of inertia, which helps the movement of particles until they reach the solution. In this new PSO, a modified inertia weight is used, as given in Equation (14). Here, the inertia weight does not depend on the number of iterations, and its value always follows the position of the particles. Therefore, it always tries to move the particles in such a way that they can reach the solution as soon as possible and cannot move away from the search space.

$${\mathrm{W}}_{\mathrm{n}\mathrm{e}\mathrm{w}}={\mathrm{W}}_{\mathrm{m}\mathrm{i}\mathrm{n}}-\frac{\left({\mathrm{W}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{W}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\right)({\mathrm{S}}_{\mathrm{i}}^{\mathrm{k}}-{\mathrm{S}}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{k}})}{{\mathrm{S}}_{\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}^{\mathrm{k}}-{\mathrm{S}}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{k}}}$$

(14)

where ${\mathrm{W}}_{\mathrm{m}\mathrm{a}\mathrm{x}}=$ 0.9, and ${\mathrm{W}}_{\mathrm{m}\mathrm{i}\mathrm{n}}=$0.4.

The procedure used for the optimization of the economic emission dispatch is shown as a flow chart in Figure 1. It shows the execution of the new PSO algorithm using MATLAB. For the execution of the new PSO algorithm, it is necessary to select all parameters related to the problem formulation, such as the economic load dispatch given in Equation (1), which needs maximum and minimum power generation limits along with cost coefficients. Similarly, for the calculation of economic emissions given in Equation (4), it is necessary to select power generation limits along with emissions coefficients. The new PSO algorithm is initiated with the selection of the swarm size and number of iterations. The pseudocode of the new PSO is shown in Figure 2.

The convergence characteristic of the new PSO is shown in Figure 3. It shows the minimization of the objective function with respect to maximum iterations. The objective of the proposed work is to find out the minimum generation cost and minimum environmental emissions at a thermal power plant in relation to a particular load demand. Therefore, when load demand is fulfilled at a particular generation point, it is taken as an economic generating point. Figure 3 shows that the proposed new PSO effectively obtained the objective within the selected iteration limits and could not be diverted from the search space until it achieved the optimum global solution to the proposed objective.

5. Results and Discussion

This section considers a case study of a thermal power plant with six generating units. Test data are given in Table 1, taken from [22], which contain the cost coefficients, emission coefficients, and limits of power generation of the thermal power plant.

These test data tested the load demand of 700 MW in the first case, 800 MW in the second case, and 1000 MW in the third case.

5.1. Case 1

This case considered the generation cost and emission generation parameters of six generating units and calculated the optimum economic load dispatch using Equation (1), the minimum induced emission using Equation (4), and the total economic emission dispatch given in Equation (7). To find out the optimum solution and check the effectiveness of the proposed novel PSO, different techniques were applied, and their results are shown in

Table 2. Results obtained for six generating units for a load demand of 700 MW.

Output Power	WEO [2]	FA [18]	BA [18]	DE [22]	GOA [23]	PSO [9]	New PSO
P1 (MW)	62.0893	62.1127	62.1032	43.446	56.24	62.0205	41.43
P2 (MW)	61.6638	61.6689	61.6698	42.426	58.57	61.62	43.65
P3 (MW)	119.9716	119.9746	119.9712	123.758	151.72	120.48	121.511
P4 (MW)	119.4758	119.4606	119.4756	117.855	136.97	119.67	119.12
P5 (MW)	178.1915	178.1913	178.1929	189.36	171.50	178.16	185.73
P6 (MW)	175.6549	175.6480	175.6432	183.148	125.00	175.57	188.56
Power output (MW)	700	700	700	700	700	700	700
Fuel cost ($/h)	37,500.17	37,500.93	37,500.84	36,313.9	36,837.05	37,500	36,144.84
Emission (tons/h)	439.60	439.61	439.61	434.38	443.11	439.635	424.242
Total EED cost ($/h)	57,189.11	57,190.01	57,190.01	57,128.3	57,127.33	57,190	56,534.84
Computation time(s)	11.4	7.14	4.7	2.01	5.47	1.838	1.710

for the same objective problem and same data set. A new PSO algorithm was developed using MATLAB 2022 and runs on a HP Intel Core I5 processor (8 GB RAM/512 GB SSD) on Windows 10. The algorithm used 100 iterations and 100 trials during the conversion. It was observed that the same values were yielded for more than 100 iterations, so only 100 iterations were considered.

Economic fuel cost, emission, and total generation cost for the water evaporation algorithm [2], PSO [9], firefly algorithm [18], bat algorithm [18], DE [22], grasshopper optimization algorithm [23], and novel PSO are shown in Table 2.

From Table 2, it is observed that the novel PSO results in terms of fuel cost, emission, and total cost are better than the other techniques such as WHO [2], PSO [9], FA [18], BA [18], DP [22], and the grasshopper optimization algorithm [23]. The minimum fuel cost obtained by the new PSO is 36,144.84 $/h, the minimum environmental emission obtained is 424.242 tons/h, and the total minimum generation cost (combined economic emission dispatch) is 56,534.84 $/h. Therefore, when observing the results given in Table 2, it is found that the proposed novel PSO algorithm is effective and efficient in finding out the economic emission dispatch. The price penalty factor calculation for six generating units using Equation (6) is shown in

Table 3. Price penalty factor for six generating units using Equation (6).

Gen. Units	Price Penalty Factor (h) Using Equation (6)
1	65.95
2	61.85
3	42.47
4	47.89
5	43.27
6	44.93

.

5.2. Case 2

In this case, we considered the same test data and evaluated solutions for the load demand of 800 MW. The results obtained by the proposed new PSO along with WEO [2], FA [18], BA [18], DP [22], PSO [22] and the grasshopper optimization algorithm [23] are shown in

Table 4. Results for the load demand of 800 MW.

Output Power	WEO [2]	FA [18]	BA [18]	DE [22]	GOA [23]	PSO [22]	New PSO
P1 (MW)	76.5712	76.5733	76.5756	55.170	55.17	55.17	52.53
P2 (MW)	79.2635	79.2629	79.2678	56.189	56.19	56.89	55.22
P3 (MW)	135.2372	135.2268	135.225	139.112	139.11	139.52	142.11
P4 (MW)	134.1532	134.1554	134.153	131.751	131.76	131.751	131.51
P5 (MW)	199.7063	199.7071	199.710	212.225	212.22	212.225	210.78
P6 (MW)	197.2528	197.2628	197.256	205.552	205.55	205.52	207.85
Power output	800 MW	800 MW	800 MW	800 MW	800 MW	800 MW	800 MW
Fuel cost ($/h)	42,784.22	42,784.41	42,784.52	41,152.6	41,147.85	41,160.3	40,932
Emission (ton/h)	557.19	557.20	557.20	547.802	547.78	547.844	526.226
Total EED cost ($/h) Equation (7)	67,739.85	67,740.26	67,740.26	67,064.47	67,389.75	67,412.23	66,773.2

. Table 4 clearly shows that the proposed new PSO results are given a minimum fuel cost of 40,932 $/h, a minimum emission of 526.226, and a total minimum combined economic emission dispatch cost of 66,773.2 $/h. Therefore, for 800 MW, the proposed method is effective and gives the best solution compared to other techniques.

5.3. Case 3

The third case considered the same six generating units shown in Table 1 and tested for a load demand of 1000 MW. This test case also considered 100 iterations and 100 trials. The optimized results of the proposed new PSO are shown in

Table 5. Results for the load demand of 1000 MW.

Output Power	WEO [2]	FA [18]	BA [18]	PSO [22]	DE [22]	Grasshopper Optimization Algorithm [23]	New PSO
P1 (MW)	107.1622	107.1685	107.1631	78.45	78.617	82.53	81.2
P2 (MW)	116.5485	116.5498	116.5483	83.97	83.716	97.40	92.93
P3 (MW)	165.6537	165.6550	165.6599	169.32	169.820	206.35	171.4
P4 (MW)	163.4009	163.4014	163.4001	159.74	159.542	181.20	161.84
P5 (MW)	242.0415	242.0380	242.0355	257.744	257.944	219.08	239.26
P6 (MW)	239.7982	239.7979	239.8036	250.56	250.361	213.44	253.37
Power output	1000 MW	1000 MW	1000 MW	1000 MW	1000 MW	1000 MW	1000 MW
Fuel cost ($/h)	54,123.83	54,124.28	54,124.12	51,269.6	51,264.5	51,833.81	51,225.22
Emission (tons/h)	851.52	851.53	851.53	828.863	828.715	834.79	785.136
Total EED cost ($/h)	94,845.59	94,846.36	94,846.36	91,285.4	91,271.05	90,934.41	90,204.88

. Again, the results of the new PSO compared with the water evaporation algorithm (WEO) [2], firefly algorithm (FA) [18], bat algorithm (BA) [18], differential evaluation (DE) [18], PSO [22], and grasshopper optimization algorithm (GOA) [23] show that the performance of the new PSO is best in all areas, such as minimum fuel cost, minimum emission, and minimum total cost for the used data set.

The results of the new PSO show that the minimum fuel cost is 51,225.22 $/h, the minimum emission is 785.136 tons/h, and the total minimum combined economic emission dispatch cost is 90,204.88 $/h.

6. Conclusions

The economic emission dispatch problem was used to find out the minimum generation cost as well as the minimum emission at the thermal power plant. This work demonstrates the proposed objective using three different cases. The thermal power plant uses the optimum economic emission model so that the plant can be operated at a lower cost and also emits low emissions into the environment. This article discusses the economic emission dispatch problem and tries to give the best solution for the data set of six generating units using a novel PSO. The proposed PSO is a new variant of PSO, and it is effective and efficient in solving the multiobjective nonlinear problem very easily. The uniqueness of this work is in the proposed PSO techniques, which can handle the nonlinear optimization data set as well as constraints. This study demonstrates the effectiveness of the novel PSO for the optimization of economic emission dispatch. It was tested for 700 MW, 800 MW, and 1000 MW, and in all cases, it gives the best performance compared to other techniques. In all cases, fuel cost, emission, and combined economic emission dispatch cost yielded minimal values compared to other optimization techniques. Therefore, the proposed techniques’ results are validated and give the best solution for the selected test data set.

Limitations and future work: this work considered data from six generating units from classical power generation systems for analysis of economic emission dispatch. Future work could consider the economics of emission dispatch integrated with renewable energy systems. Some countries have already started working on such an integration. Therefore, when considering renewable integrated systems along with classical power generation systems (thermal plants), the costs of generation and emission generation will decrease.