Unconditionally Stable System Incorporated Factorization-Splitting Algorithm for Blackout Re-Entry Vehicle
Abstract
1. Introduction
2. Formulation
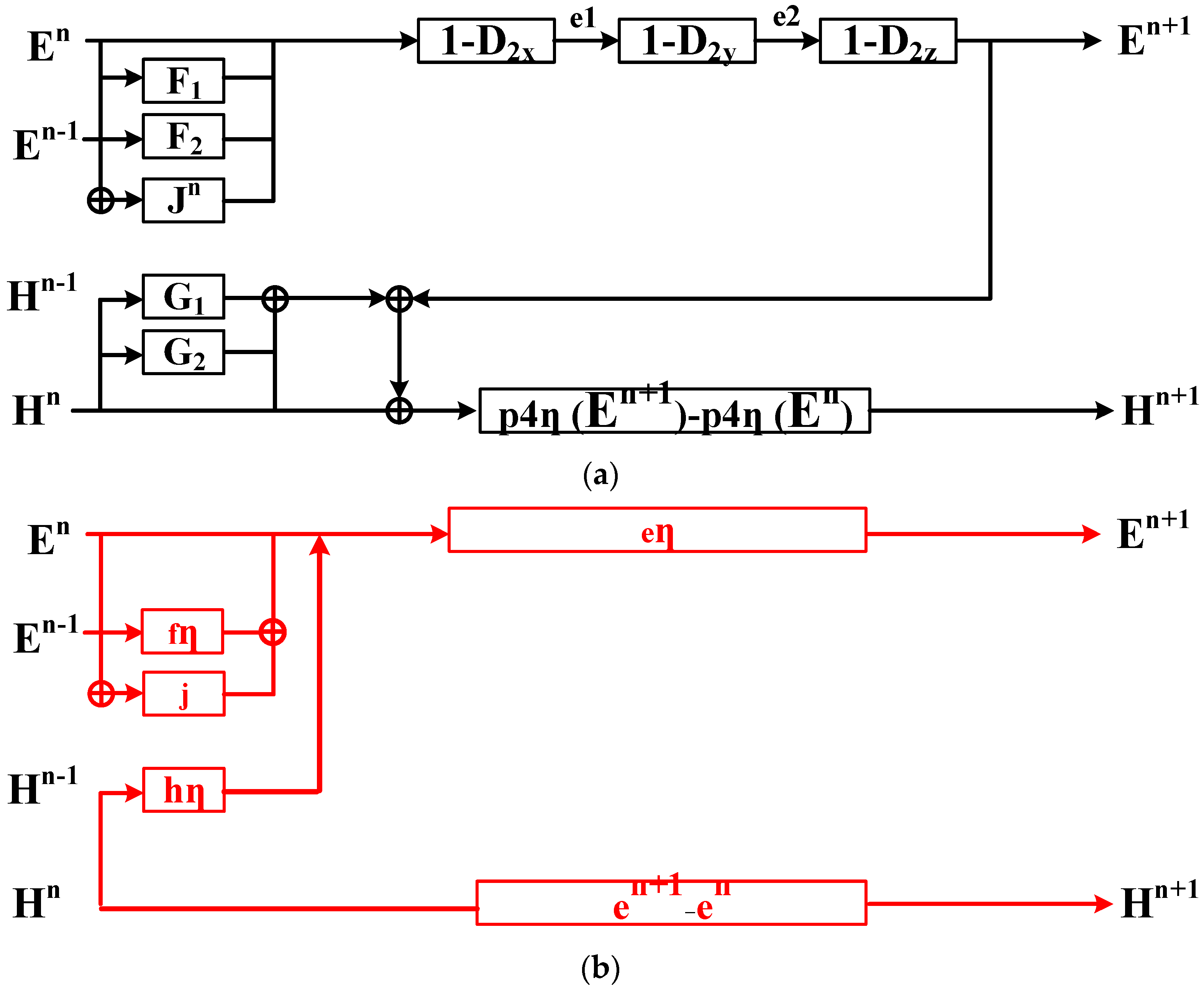
2.1. Modified ADE Algorithm for Unconditionally Stable SI Scheme
2.2. consumption, simulation duration, and time CPML Formulation
3. Numerical Results and Discussion
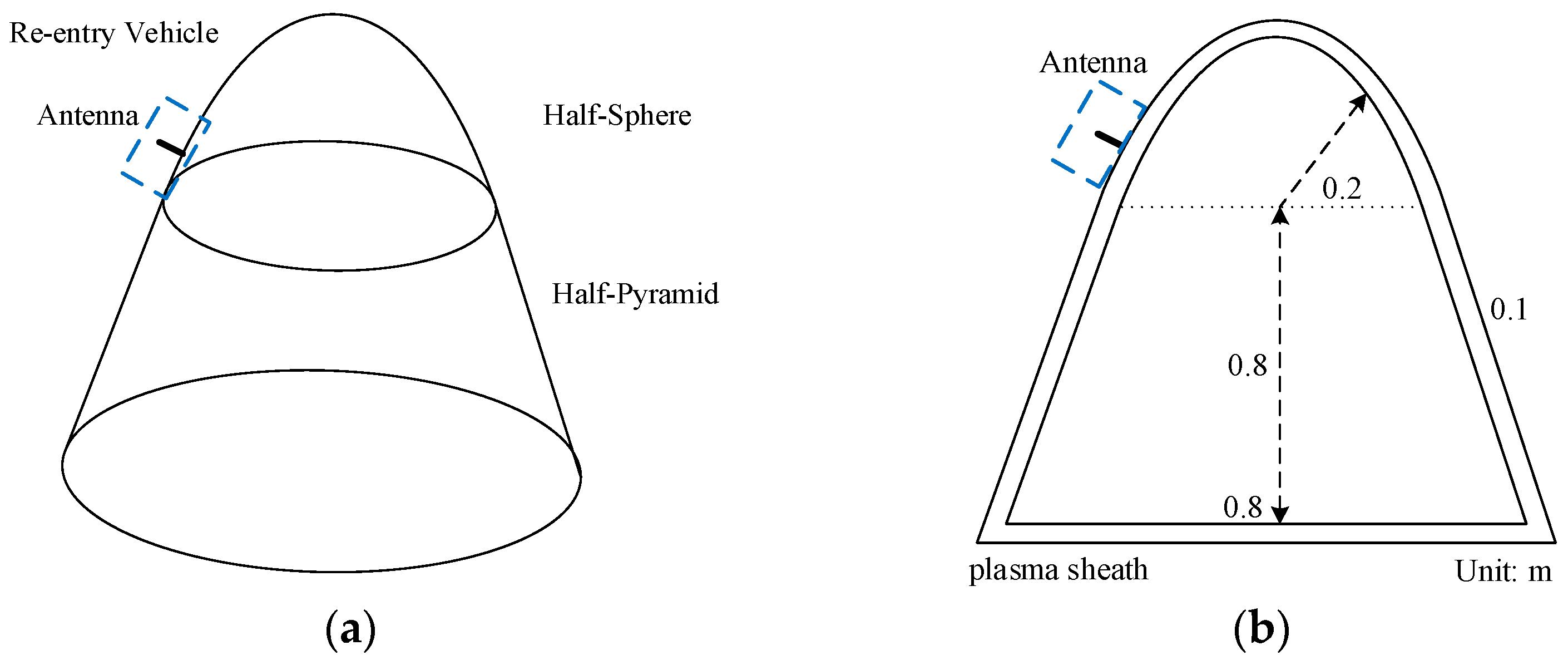
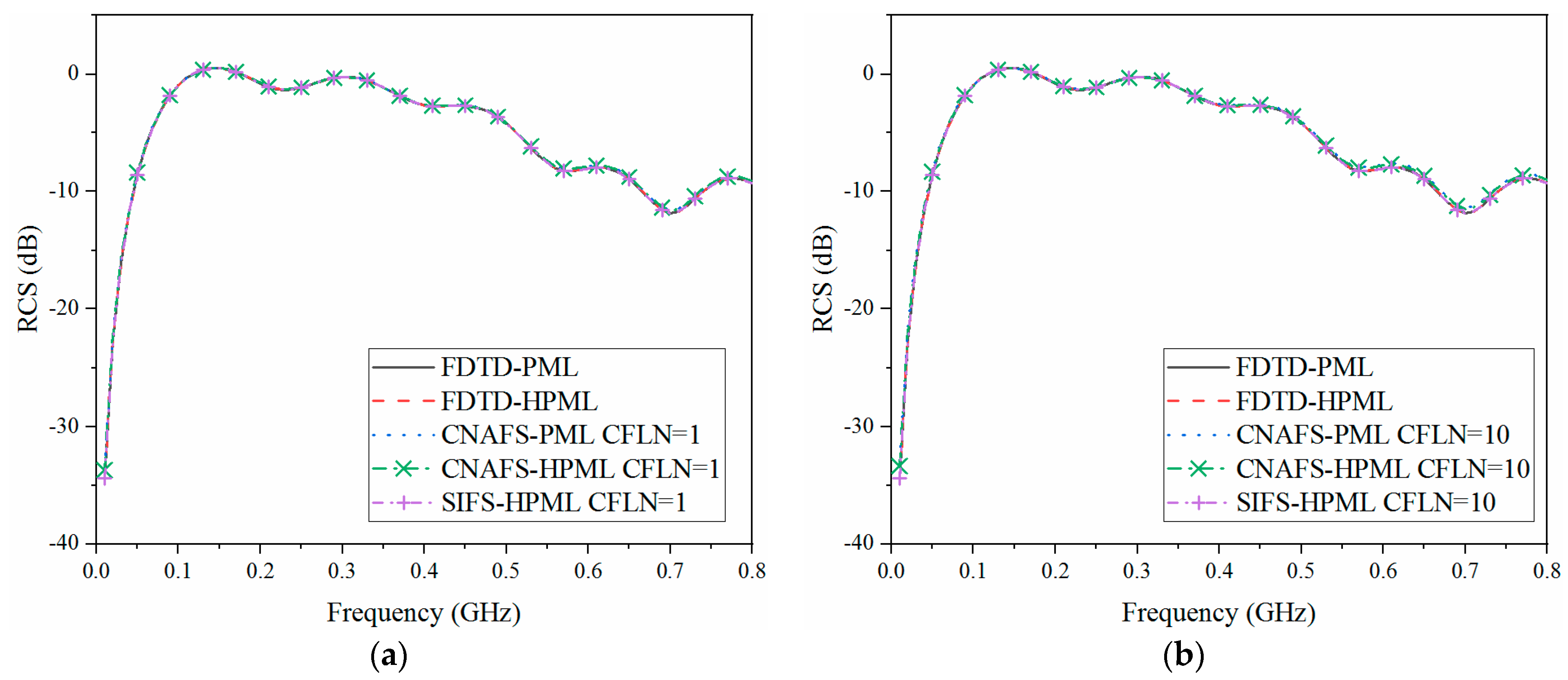
3.1. Target Characteristic Problem: Radar Echo Wave of the Blackout Re-Entry Vehicle
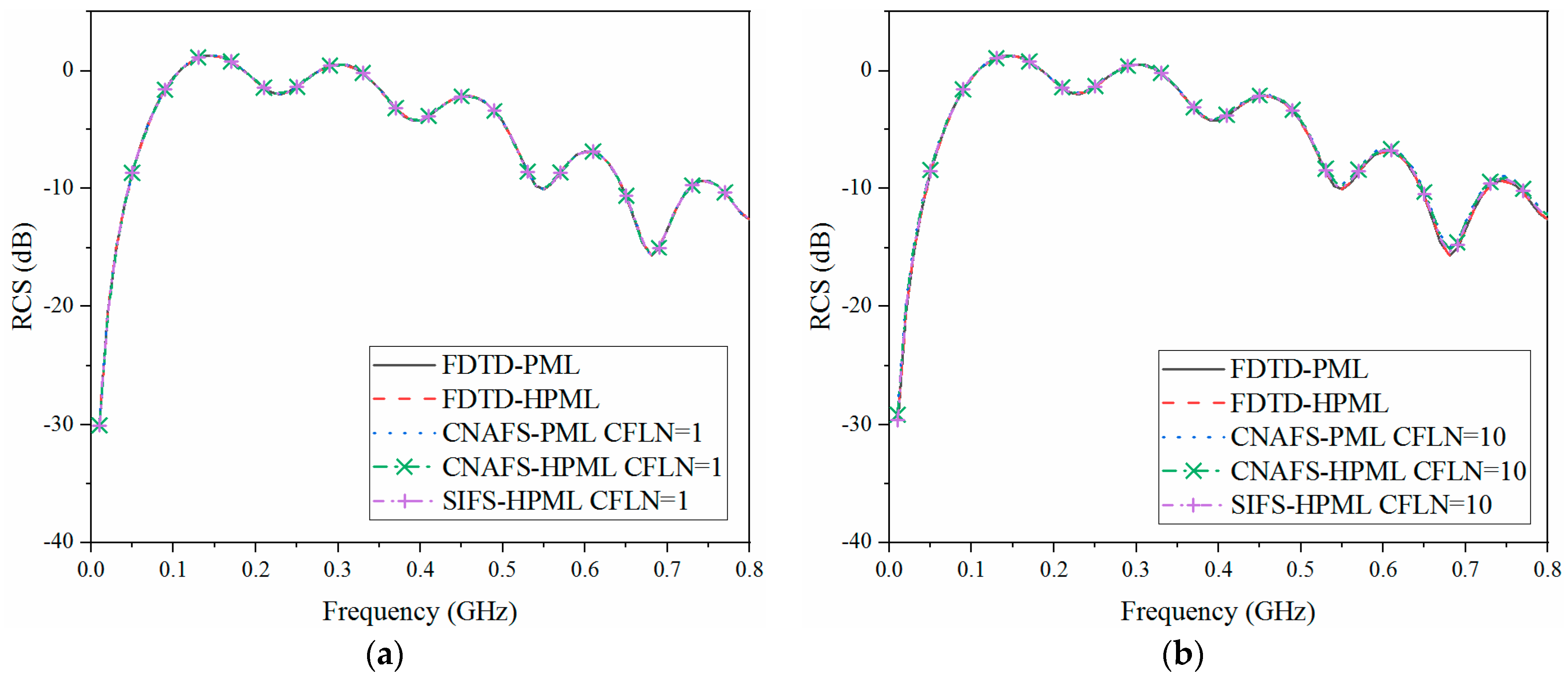
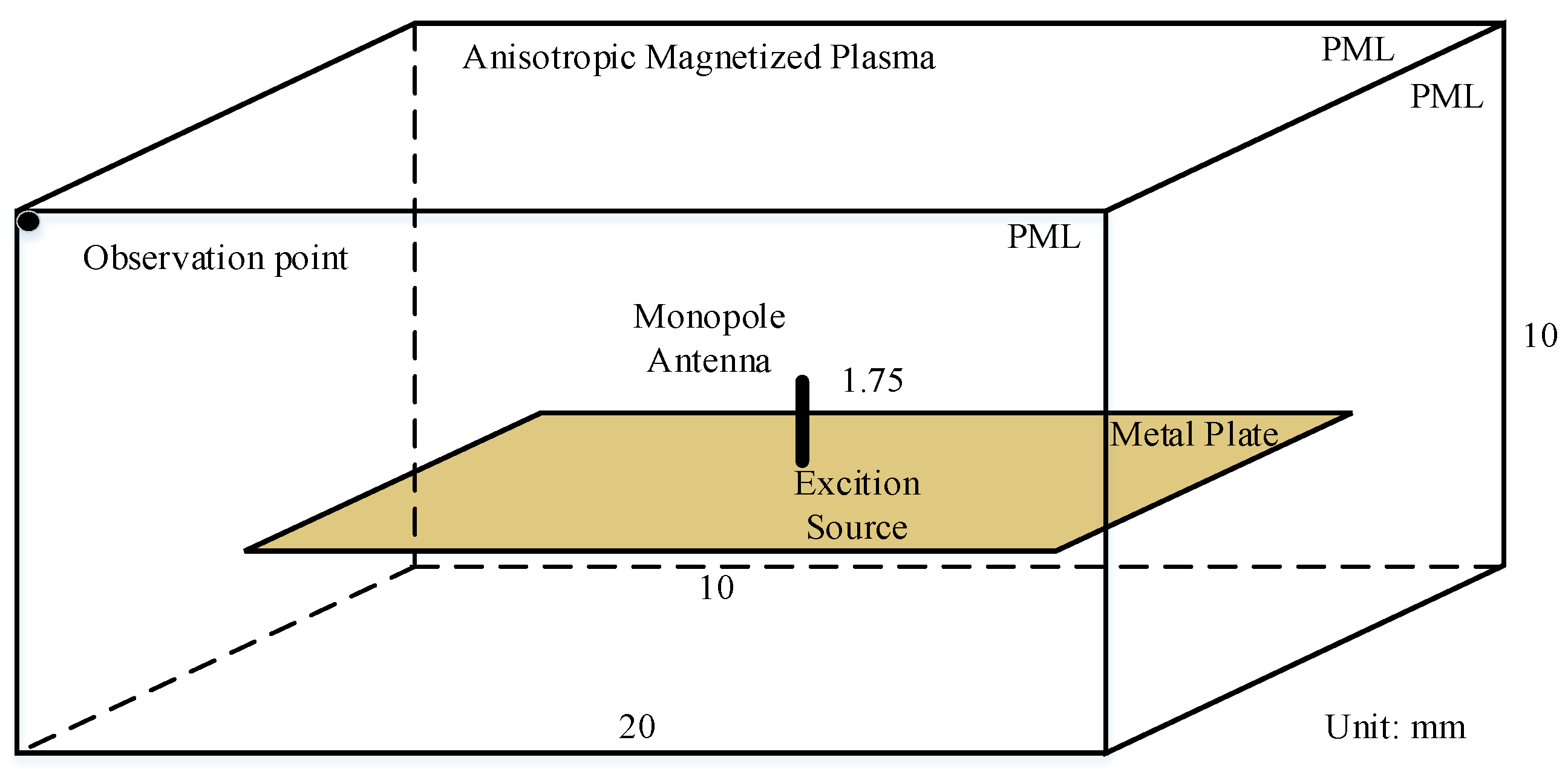
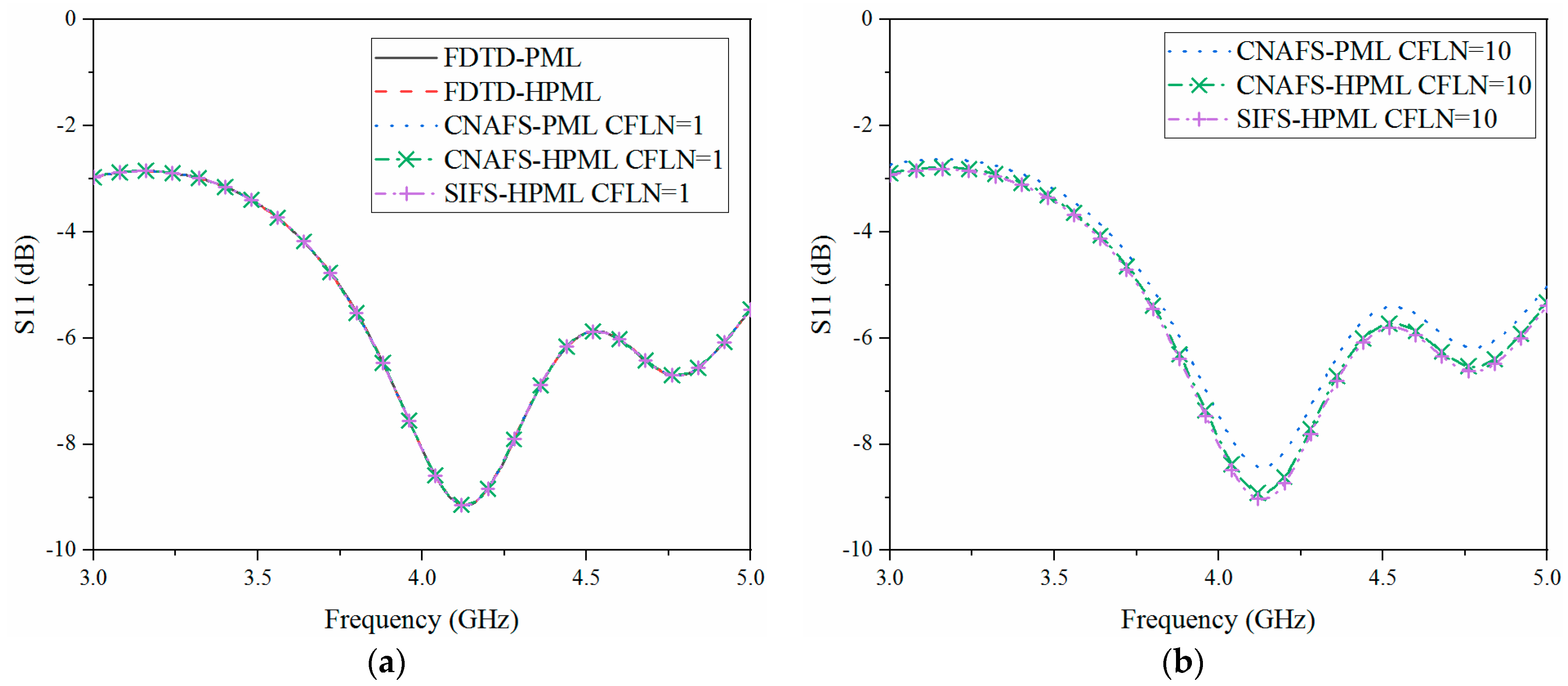
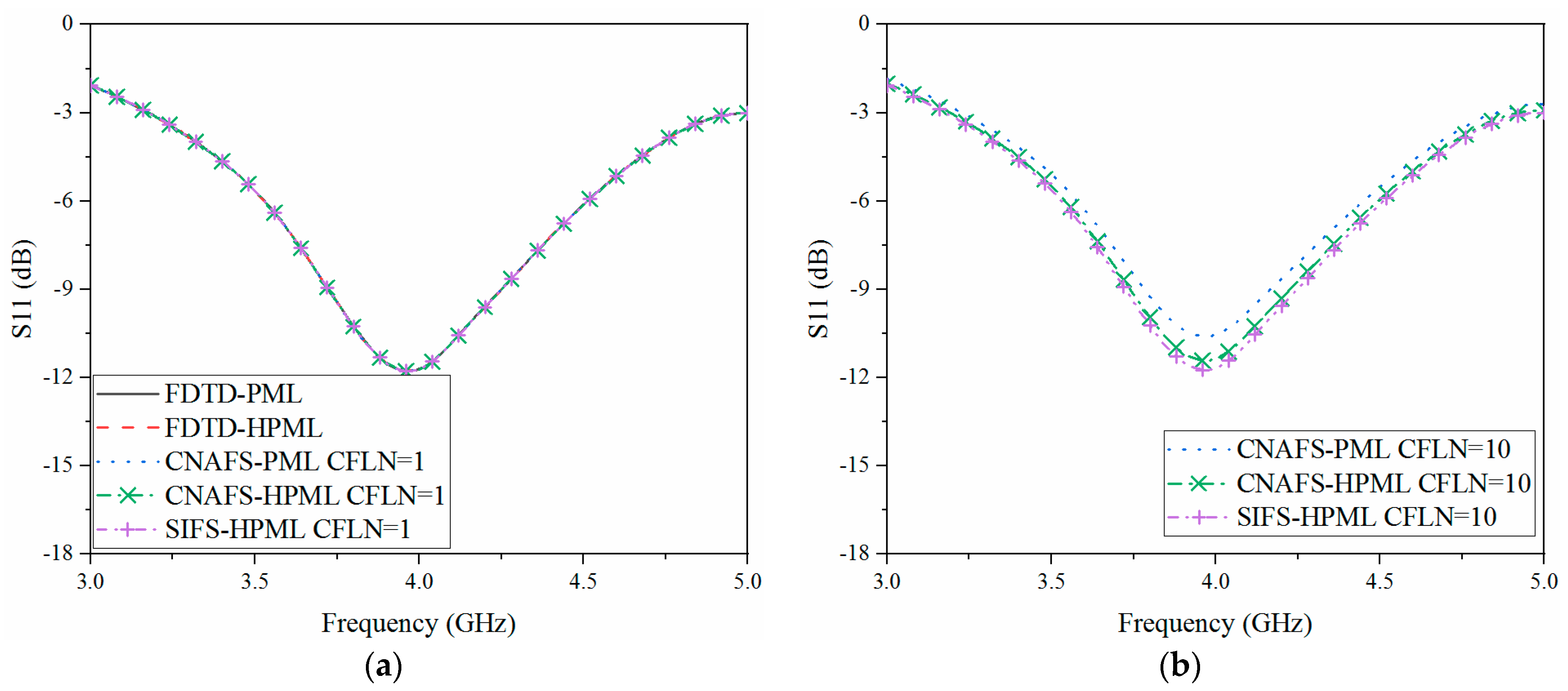
3.2. Wave Radiation Problem: Antenna Communication in the Plasma Sheath on the Surface of the Blackout Re-Entry Vehicle
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- Takahashi, Y.; Nakasato, R.; Oshima, N. Analysis of Radio Frequency Blackout for a Blunt-Body Capsule in Atmospheric Reentry Missions. Aerospace 2016, 3, 2. [Google Scholar] [CrossRef]
- Webb, B.A.; Ziolkowski, R.W. A Metamaterial-Inspired Approach to Mitigating Radio Frequency Blackout When a Plasma Forms Around a Reentry Vehicle. Photonics 2020, 7, 88. [Google Scholar] [CrossRef]
- Yu, M.; Qiu, Z.; Lv, B.; Takahashi, Y. Multiphysics Mathematical Modeling and Flow Field Analysis of an Inflatable Membrane Aeroshell in Suborbital Reentry. Mathematics 2022, 10, 832. [Google Scholar] [CrossRef]
- Niu, G.; Liu, Y.; Bai, B.; Ding, Y.; Song, L.; Li, X. Polarization Scattering Characteristic of Plasma-Sheath-Covered Hypersonic Vehicle. IEEE Trans. Plasma Sci. 2023, 51, 641–648. [Google Scholar] [CrossRef]
- Wang, S.; Guo, L.-X.; Yu, Z.-F.; Wang, J.; Chen, J. Method of 2-D Range-Doppler Imaging for Plasma Wake Based on Range Walk Correction. IEEE Trans. Plasma Sci. 2023, 51, 1076–1084. [Google Scholar] [CrossRef]
- Ding, Y.; Bai, B.; Li, X.; Niu, G.; Liu, Y. Research on EM Shielding Mechanism of the Plasma-Sheath-Covered Target. IEEE Trans. Plasma Sci. 2023, 51, 632–640. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Song, Z.; Ma, J.; Jiang, T. Fast Analysis of the Electromagnetic Scattering of Targets Coated with Plasma Sheath Based on IBC. IEEE Antennas Wirel. Propag. Lett. 2021, 21, 491–495. [Google Scholar] [CrossRef]
- Liu, S.-H.; Guo, L.-X. Analyzing the Electromagnetic Scattering Characteristics for 3-D Inhomogeneous Plasma Sheath Based on PO Method. IEEE Trans. Plasma Sci. 2016, 44, 2838–2843. [Google Scholar] [CrossRef]
- Yee, K.S. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time Domain Method, 3rd ed.; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Namiki, T. 3-D ADI-FDTD method-unconditionally stable time-domain algorithm for solving full vector Maxwell’s equations. IEEE Trans. Microw. Theory Tech. 2000, 48, 1743–1748. [Google Scholar] [CrossRef]
- Shibayama, J.; Nomura, A.; Ando, R.; Yamauchi, J.; Nakano, H. A Frequency-Dependent LOD-FDTD Method and Its Application to the Analyses of Plasmonic Waveguide Devices. IEEE J. Quantum Electron. 2009, 46, 40–49. [Google Scholar] [CrossRef]
- Chu, Q.; Kong, Y.-D. Three New Unconditionally-Stable FDTD Methods with High-Order Accuracy. IEEE Trans Antennas Propag. 2009, 57, 2675–2682. [Google Scholar]
- Chen, J.; Wang, J. A Three-Dimensional Semi-Implicit FDTD Scheme for Calculation of Shielding Effectiveness of Enclosure with Thin Slots. IEEE Trans. Electromagn. Compat. 2007, 49, 354–360. [Google Scholar] [CrossRef]
- Tan, E.L. From Time-Collocated to Leapfrog Fundamental Schemes for ADI and CDI FDTD Methods. Axioms 2022, 11, 23. [Google Scholar] [CrossRef]
- Pereda, J.A.; Serroukh, A.; Grande, A.; Vegas, A. Implementation of Absorbing Boundary Conditions Based on the Second-Order One-Way Wave Equation in the LOD- and the ADI-FDTD Methods. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 981–983. [Google Scholar] [CrossRef]
- Tan, E.L. Fundamental Leapfrog ADI and CDI FDTD Methods. In Proceedings of the 2021 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (APS/URSI), Singapore, 4–10 December 2021; pp. 643–644. [Google Scholar]
- Wang, X.-H.; Yin, W.-Y.; Chen, Z.D. One-step leapfrog ADI-FDTD method for anisotropic magnetized plasma. In Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest (MTT), Seattle, WA, USA, 2–7 June 2013; pp. 1–4. [Google Scholar]
- Li, Y.; Wang, N.; Lei, J.; Wang, F.; Li, C. Modeling GPR Wave Propagation in Complex Underground Structures Using Conformal ADI-FDTD Algorithm. Appl. Sci. 2022, 12, 5219. [Google Scholar] [CrossRef]
- Liu, S.; Tan, E.L.; Zou, B.; Zhang, L. Higher Order CPML for Leapfrog Complying-Divergence Implicit FDTD Method and Its Numerical Properties. IEEE Trans. Microw. Theory Tech. 2022, 71, 522–535. [Google Scholar] [CrossRef]
- Sun, G.; Trueman, C.W. Approximate Crank-Nicolson scheme for the 2-D finite-difference time-domain method for TEz waves. IEEE Trans. Antennas Propag. 2004, 52, 2963–2972. [Google Scholar] [CrossRef]
- Sun, G.; Trueman, C.W. Unconditionally stable Crank-Nicolson scheme for solving two-dimensional Maxwell’s equations. Electron. Lett. 2003, 39, 595–597. [Google Scholar] [CrossRef]
- Wu, P.; Xie, Y.; Jiang, H.; Niu, L. Higher-Order Approximate CN-PML Theory for Magnetized Ferrite Simulations. Adv. Theory Simul. 2020, 3, 1900221. [Google Scholar] [CrossRef]
- Sun, G.; Trueman, C. Unconditionally-stable FDTD method based on Crank-Nicolson scheme for solving three-dimensional Maxwell equations. Electron. Lett. 2004, 40, 589–590. [Google Scholar] [CrossRef]
- Sun, G.; Trueman, C. Efficient implementations of the Crank-Nicolson scheme for the finite-difference time-domain method. IEEE Trans. Microw. Theory Tech. 2006, 54, 2275–2284. [Google Scholar] [CrossRef]
- Wu, P.; Wang, J.; Chen, J.; Jiang, H.; Xie, Y.; Natsuki, T. System incorporated direct-splitting algorithm for periodic nonuniform metamaterial design in open regions. Optik 2022, 271, 169812. [Google Scholar] [CrossRef]
- Wu, P.; Xie, Y.; Jiang, H.; Natsuki, T. Complex Envelope Approximate CN-PML Algorithm with Improved Absorption. IEEE Ante. Wirel. Propagat. Lett. 2020, 19, 1521–1525. [Google Scholar] [CrossRef]
- Wu, P.; Xie, Y.; Jiang, H.; Di, H.; Natsuki, T. Implicit Approximate Crank–Nicolson Theory for Anisotropic Ferrite Structure Simulation with Enhanced Absorption. Adv. Theory Simul. 2021, 4, 2000309. [Google Scholar] [CrossRef]
- Rezaee, M.R.; Niknam, A.; Ghomi, H.; Latifi, H. Magnetized plasma sheath dynamics in plasma source ion implantation. In Proceedings of the 2008 IEEE 35th International Conference on Plasma Science, Karlsruhe, Germany, 15–19 June 2008; p. 1. [Google Scholar] [CrossRef]
- Fang, Y.; Xi, X.-L.; Liu, J.-F.; Pu, Y.-R.; Zhang, J.-S. An Iterative WLP-FDTD Method for Wave Propagation in Magnetized Plasma. IEEE Trans. Plasma Sci. 2017, 45, 2215–2219. [Google Scholar] [CrossRef]
- Liu, S.; Liu, S. Runge-Kutta exponential time differencing FDTD method for anisotropic magnetized plasma. IEEE Antennas Wirel. Propag. Lett. 2008, 7, 306–309. [Google Scholar]
- Xu, L.; Yuan, N. JEC-FDTD for 2-D conducting cylinder coated by anisotropic magnetized plasma. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 892–894. [Google Scholar] [CrossRef]
- Samimi, A.; Simpson, J.J. An Efficient 3-D FDTD Model of Electromagnetic Wave Propagation in Magnetized Plasma. IEEE Trans. Antennas Propag. 2015, 63, 269–279. [Google Scholar] [CrossRef]
- Berenger, J.P. A perfectly matched layer for the absorption of electromagnetic waves. J. Com. Phys. 1994, 11, 185–200. [Google Scholar] [CrossRef]
- Chew, W.C.; Weedon, W.H. A 3D perfectly matched medium from modified maxwell’s equations with stretched coordinates. Microw. Opt. Technol. Lett. 1994, 7, 599–604. [Google Scholar] [CrossRef]
- Kuzuoglu, M.; Mittra, R. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers. IEEE Microw. Guid. Wave Lett. 1996, 6, 447–449. [Google Scholar] [CrossRef]
- Gedney, S.; Liu, G.; Roden, J.; Zhu, A. Perfectly matched layer media with CFS for an unconditionally stable ADI-FDTD method. IEEE Trans. Antennas Propag. 2001, 49, 1554–1559. [Google Scholar] [CrossRef]
- Correia, D.; Jin, J.-M. Performance of regular PML, CFS-PML, and second-order PML for waveguide problems. Microw. Opt. Technol. Lett. 2006, 48, 2121–2126. [Google Scholar] [CrossRef]
- Berenger, J.P. Perfectly Matched Layer (PML) for Computational Electromagnetics; Morgan & Claypool: San Rafael, CA, USA, 2007. [Google Scholar]
- Giannopoulos, A. Higher-Order Convolution PML (CPML) for FDTD Electromagnetic Modeling. IEEE Trans. Antennas Propag. 2020, 68, 6226–6231. [Google Scholar] [CrossRef]
- Wu, S.; Sun, Y.; Chi, M.; Chen, X. Performance enhanced absorbing boundary condition for electromagnetic modelling and simulation. Int. J. Numer. Model. Electron. Netw. Devices Fields 2020, 33, e2760. [Google Scholar] [CrossRef]
- Wu, P.; Xie, Y.; Jiang, H.; Niu, L. Different implementations of material independent multi-order nearly perfectly matched layers for EM simulations. Microw. Opt. Technol. Lett. 2020, 62, 3485–3498. [Google Scholar] [CrossRef]
- Wu, P.; Wang, X.; Xie, Y.; Jiang, H.; Natsuki, T. Hybrid Implicit-Explicit Procedure With Improved Absorption for Anisotropic Magnetized Plasma in Bandpass Problem. IEEE J. Multiscale Multiphysics Comput. Tech. 2021, 6, 229–238. [Google Scholar] [CrossRef]
- Wu, P.Y.; Jiang, H.L.; Xie, Y.J.; Niu, L.Q. Three-Dimensional Higher Order PML Based on Alternating Direction Implicit Algorithm. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2592–2596. [Google Scholar] [CrossRef]
- Yu, Y.; Li, Q.; Liu, E.; Png, C.E.; Su, X. Simulation of dispersive plasmas using implicit and explicit ADE-FDTD schemes. In Proceedings of the 2015 IEEE 4th Asia-Pacific Conference on Antennas and Propagation (APCAP), Bali, Indonesia, 30 June–3 July 2015; pp. 128–129. [Google Scholar] [CrossRef]
- Wu, P.; Xie, Y.; Jiang, H.; Zhang, J.; Chen, J.; Natsuki, T. Complex Envelope Weaker HIE with Higher Order PML Algorithm for FDTD Simulation. IEEE Microw. Wirel. Technol. Lett. 2023, 33, 251–254. [Google Scholar] [CrossRef]
- Teixeira, M.; Rodriguez, D. A novel derivation of the Agarwal-Cooley fast cyclic convolution algorithm based on the Good-Thomas Prime Factor algorithm. In Proceedings of the 38th Midwest Symposium on Circuits and Systems, Rio de Janeiro, Brazil, 13–16 August 1995; Volume 1, pp. 89–91. [Google Scholar]
- Jiang, H.L.; Wu, L.T.; Zhang, X.G.; Wang, Q.; Wu, P.Y.; Liu, C.; Cui, T.J. Computationally Efficient CN-PML for EM Simulations. IEEE Trans. Microw. Theory Tech. 2019, 67, 4646–4655. [Google Scholar] [CrossRef]
- Wu, P.; Xie, Y.; Jiang, H.; Natsuki, T. Performance Enhanced Crank-Nicolson Boundary Conditions for EM Problems. IEEE Trans. Antennas Propag. 2020, 69, 1513–1527. [Google Scholar] [CrossRef]
- Haolin, J.; Yongjun, X.; Peiyu, W.; Jianfeng, Z.; Liqiang, N. Unsplit-field higher-order nearly PML for arbitrary media in EM simulation. J. Syst. Eng. Electron. 2021, 32, 1–6. [Google Scholar] [CrossRef]
- Li, J.; Yang, Q.; Niu, P.; Feng, N. An efficient implementation of the higher-order PML based on the Z-transform method. In Proceedings of the 2011 IEEE International Conference on Microwave Technology & Computational Electromagnetics, Beijing, China, 22–25 May 2011; pp. 414–417. [Google Scholar] [CrossRef]
- Jiang, H.L.; Cui, T.J. Efficient PML Implementation for Approximate CN-FDTD Method. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 698–701. [Google Scholar] [CrossRef]
- Niu, L.; Xie, Y.; Gao, J.; Wu, P.; Jiang, H. Approximate Crank–Nicolson Algorithm with Higher-Order PML Implementation for Plasma Simulation in Open Region Problems. Int. J. Antennas Propag. 2021, 2021, 6618492. [Google Scholar] [CrossRef]


| Algorithms | CFLN | Steps | Memory (G) | Time (min) | Reduction (%) |
|---|---|---|---|---|---|
| FDTD-PML | 1 | 32768 | 27.5 | 43.4 | - |
| FDTD-HPML | 1 | 32768 | 35.9 | 91.7 | −111.3 |
| CNAFS-PML | 1 | 32768 | 40.4 | 372.3 | −757.8 |
| CNAFS-HPML | 1 | 32768 | 53.1 | 440.1 | −1006.2 |
| SIFS-HPML | 1 | 32768 | 47.3 | 389.5 | −785.9 |
| CNAFS-PML | 10 | 3277 | 40.4 | 21.9 | 49.5 |
| CNAFS-HPML | 10 | 3277 | 53.1 | 26.4 | 39.2 |
| SIFS-HPML | 10 | 3277 | 47.3 | 22.1 | 49.1 |
| Algorithms | CFLN | Steps | Memory (G) | Time (min) | Reduction (%) |
|---|---|---|---|---|---|
| FDTD-PML | 1 | 32768 | 1.1 | 4.7 | - |
| FDTD-HPML | 1 | 32768 | 1.9 | 22.3 | −377.5 |
| CNAFS-PML | 1 | 32768 | 2.5 | 75.1 | −1497.9 |
| CNAFS-HPML | 1 | 32768 | 3.0 | 90.4 | −1823.4 |
| SIFS-HPML | 1 | 32768 | 2.6 | 81.6 | −1636.2 |
| CNAFS-PML | 10 | 3277 | 2.5 | 2.6 | 44.7 |
| CNAFS-HPML | 10 | 3277 | 3.0 | 4.1 | 12.8 |
| SIFS-HPML | 10 | 3277 | 2.3 | 3.3 | 29.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, Y.; Wang, J.; Xu, H. Unconditionally Stable System Incorporated Factorization-Splitting Algorithm for Blackout Re-Entry Vehicle. Electronics 2023, 12, 2892. https://doi.org/10.3390/electronics12132892
Wen Y, Wang J, Xu H. Unconditionally Stable System Incorporated Factorization-Splitting Algorithm for Blackout Re-Entry Vehicle. Electronics. 2023; 12(13):2892. https://doi.org/10.3390/electronics12132892
Chicago/Turabian StyleWen, Yi, Junxiang Wang, and Hongbing Xu. 2023. "Unconditionally Stable System Incorporated Factorization-Splitting Algorithm for Blackout Re-Entry Vehicle" Electronics 12, no. 13: 2892. https://doi.org/10.3390/electronics12132892
APA StyleWen, Y., Wang, J., & Xu, H. (2023). Unconditionally Stable System Incorporated Factorization-Splitting Algorithm for Blackout Re-Entry Vehicle. Electronics, 12(13), 2892. https://doi.org/10.3390/electronics12132892





