MSWOA: A Mixed-Strategy-Based Improved Whale Optimization Algorithm for Multilevel Thresholding Image Segmentation

Abstract

Multilevel thresholding image segmentation is one of the most widely used segmentation methods in the field of image segmentation. This paper proposes a multilevel thresholding image segmentation technique based on an improved whale optimization algorithm. The WOA has been applied to many complex optimization problems because of its excellent performance; however, it easily falls into local optimization. Therefore, firstly, a mixed-strategy-based improved whale optimization algorithm (MSWOA) is proposed using the k-point initialization algorithm, the nonlinear convergence factor, and the adaptive weight coefficient to improve the optimization ability of the algorithm. Then, the MSWOA is combined with the Otsu method and Kapur entropy to search for the optimal thresholds for multilevel thresholding gray image segmentation, respectively. The results of algorithm performance evaluation experiments on benchmark functions demonstrate that the MSWOA has higher search accuracy and faster convergence speed than other comparative algorithms and that it can effectively jump out of the local optimum. In addition, the image segmentation experimental results on benchmark images show that the MSWOA–Kapur image segmentation technique can effectively and accurately search multilevel thresholds.

1. Introduction

With the rapid development of computer technology, computer vision has gradually formed its own scientific system. Computer vision usually involves the evaluation of images or videos, including image classification, object detection [1], image segmentation, image enhancement [2], and other subtasks. In recent years, deep learning technology has been applied to almost every field of computer vision. Researchers have proposed various network optimization models for different tasks and achieved a series of remarkable research results [3].

Image segmentation, one of the computer vision research hotspots, is a fundamental stage in image processing, visual analysis, and pattern recognition. At present, image segmentation has been applied in a variety of fields, including medical image processing and analysis [4], traffic images [5], remote sensing images [6], and satellite images [7]. Image segmentation makes an image easier to analyze by simplifying or changing the representation of it. The most classical method for image segmentation is binarization. Shaikh et al. [8] discussed the method of image segmentation using binarization. The numerous image segmentation methods [9] can be broadly categorized into thresholding segmentation, image edge detection, region growth-based segmentation, feature space-based clustering segmentation, and morphology-based image segmentation. Among these methods, thresholding segmentation has become the most widely used segmentation method in image segmentation due to its stable performance, simple algorithm, easy implementation, and high efficiency. It has been a hot research point in the field of image segmentation.

Histogram-based thresholding segmentation is one of the most studied image segmentation techniques. The most famous threshold selection criteria include the Otsu method [10] and Kapur entropy [11]. These segmentation methods usually use a specific objective function to find the optimal threshold using an analytic formula under certain conditions. Due to the discrete characteristics of image pixels, these multilevel thresholding segmentation methods based on objective functions are essentially solved using exhaustive search. However, as there are more thresholds, using an analytical formula to solve the threshold has the drawbacks of large search space, high computational complexity, large amount of calculation, and high time consumption. Therefore, it is challenging to employ the conventional exhaustive method for multilevel thresholding segmentation when the number of thresholds to be selected is huge. How to increase real-time performance without lowering search accuracy is a hot issue in research on this kind of algorithm.

Swarm intelligence (SI)-based optimization algorithms have gained popularity in recent years as some of the standard methods for multilevel thresholding image segmentation due to their ability to significantly increase the speed and stability of the optimization process. Segmentation methods based on swarm intelligence optimization algorithms often use some unique computing techniques to improve algorithm performance, and the objective function often uses the Otsu method or some entropy functions such as Kapur, Tsallis, or Minimum Cross Entropy (MCE). Swarm intelligence optimization algorithms have become a popular topic in research in the optimization sector, mainly because they can find a more workable solution with a very low calculation cost, which can reduce operation time and improve solution accuracy. They have the advantages of simple and effective computing, fast operation speed, high precision, and being suitable for large-scale parallel solutions. Common swarm intelligence optimization algorithms include particle swarm optimization (PSO) [12], the artificial bee colony algorithm (ABC) [13], the firefly algorithm (FA), the bat algorithm (BA) [14], moth–flame optimization (MFO) [15], cuckoo search (CS) [16], the bacterial foraging optimization algorithm (BFO) [17], gray wolf optimizer (GWO) [18], etc. Until now, these new optimization algorithms have been applied to the field of image segmentation. Wu Peng applied the firefly algorithm (FA) combined with maximum entropy for image segmentation. The experimental results demonstrate that the method can quickly and accurately find the optimal thresholds and improve accuracy and anti-noise performance. Chao Yuan et al. [19] proposed a multilevel thresholding image segmentation method based on the generalized inverse particle swarm optimization and gravity search hybrid algorithm (GOPSOGSA) by combining PSO and the gravitational search algorithm (GSA). The experimental results indicate that the proposed method is better than the GSA in segmentation accuracy but needs more computing time. Pare et al. [16] proposed ELR-CS (Egg Laying Radius) on the basis of CS (cuckoo search) and extended the energy curve of gray-scale images into color images. The experimental results prove that the color image segmentation method using the CS–Kapur energy curve can obtain higher segmentation accuracy. Prateek Agarwal [20] applied histograms based on bimodal and multimodal thresholds, and the social spider algorithm (SSA) to the multilevel thresholding segmentation of gray-scale images, effectively improving computing time and realizing the optimization of the optimal threshold. Hao Gao et al. [13] applied a modified artificial bee colony algorithm to multilevel thresholding image segmentation to solve the problems of large amount of computation and long computing time. A gray image segmentation method [21] using Kapur entropy based on the month swarm algorithm (MSA) was proposed; it effectively solves the issue of large amount of computation in multilevel thresholding segmentation. Ashish Kumar Bhandari [22] proposed a multilevel thresholding segmentation method named Energy-Masi-MSA based on Masi entropy. Compared with other meta heuristic algorithms, the MSA has better performance in threshold evaluation index and reducing computational complexity. Abdul Kayom et al. [12] used GWO to identify the best threshold of gray images under the conditions of Kapur entropy and Otsu. According to the experimental results, the suggested method has higher convergence precision and is more stable than PSO and BFO. In the same year, Shubham Kapoor [23] applied the GWO algorithm to satellite image segmentation and achieved advantages in computational efficiency and accuracy. K.P. Baby Resma et al. [24] applied the krill herd optimization algorithm (KHO) to gray-scale image segmentation; Lifang He [25] proposed an efficient krill herd algorithm (EKH) for color image segmentation. Comparative experiments on Otsu, Kapur entropy and Tsallis entropy showed that EKH–Kapur entropy is more effective in color image segmentation and is more accurate and robust. GuoShen Ding et al. [26] improved the fruit fly optimization algorithm (FOA). The experimental results demonstrate that the suggested method outperforms other algorithms in terms of segmentation efficiency and global convergence. Pankaj Upadhyay et al. [27] proposed a multilevel thresholding segmentation method for gray images based on the crow search algorithm (CSA) and Kapur entropy. The experimental findings prove that the suggested approach has superior accuracy in solution and segmentation effect when comparing PSNR, SSIM, FSIM, and computation time. Zhikai Xing [28] improved emperor penguin optimization (EPO) by introducing strategies such as Levy flight, Gaussian mutation, and opposition-based learning into the algorithm to improve the search ability of it. Moreover, improved EPO is applied to the segmentation of various types of color images. Erick Rodríguez-Esparza [29], Aneesh Wunnava [30], and Mohamed Abd Elaziz [31] applied Harris Hawks Optimization (HHO) and improved HHO to multilevel thresholding image segmentation and achieved good results. A modified remora optimization algorithm (MROA) [32] was proposed for global optimization and image segmentation tasks. The experimental results prove that it is a promising method for global optimization problems and image segmentation. As intelligent optimization algorithms quickly advance, more and more academics are starting to apply them to multilevel thresholding image segmentation, which can partially address the issue of operating efficiency. These research results also demonstrate the viability and efficiency of intelligent optimization methods for multilevel thresholding image segmentation.

The whale optimization algorithm (WOA) [33] is a brand-new swarm intelligence optimization algorithm that simulates the behavior of whale predation. Compared with other classical intelligent optimization algorithms, such as PSO and the GSA, it has the advantages of straightforward structure, fewer parameters, and strong optimization capacity. The WOA has attracted the attention of numerous academics and has been used to address a variety of real-world issues, such as constrained engineering design problems [34], forecasting water resource demand [35], multiobjective optimization problems [36], large-scale global optimization problems and high-dimensional global optimization problems [37,38], optimal single mobile robot scheduling [39], real-time task scheduling in multiprocessor systems [40], talent stability prediction [41], and multilevel thresholding image segmentation [42]. Similar to other swarm intelligence optimization algorithms, the WOA also has some problems, such as being premature and easily falling into local optimization. Numerous scholars have attempted to modify it to overcome these shortcomings and boost performance by mostly concentrating on three aspects, where the first is to improve population initialization. For example, Zhang Yong et al. [43] used piecewise logistic chaotic maps to generate a chaotic sequence to initialize the population position, so as to maintain the diversity of the initial population in the global search. Secondly, the search strategy and search process are improved to balance the local search and global search. Third, other optimization algorithms or strategies are used to improve the original algorithm. For example, Seyed et al. [44] introduced differential evolution (DE) into the search process of the whale optimization algorithm to obtain better solutions; this obtains better experimental results, but it also makes the algorithm more complex.

The main work and contribution of this paper are as follows:

• The definitions of k-point and k-point-based initialization algorithm are proposed.
• The mixed-strategy whale optimization algorithm (MSWOA) is proposed using the k-point-based initialization strategy, the nonlinear convergence factor, and the adaptive weight coefficient to improve the optimization ability.
• The proposed algorithm was applied to the multilevel thresholding segmentation of gray images using the Otsu method and Kapur entropy, respectively. PSNR, SSIM, FISM, and CPU time were chosen to measure it.

The rest of the paper is arranged as follows: In Section 2, the mathematical description of the multilevel thresholding segmentation of gray images and the mathematical formulas of the Otsu method and Kapur entropy are described. In Section 3, a mixed-strategy whale optimization algorithm is proposed and applied to gray image multilevel thresholding segmentation. In Section 4, the performance of the MSWOA is discussed using experiments based on benchmark functions. Section 5 presents the comparative experiment and analysis of image segmentation. Finally, Section 6 presents the conclusion and future research directions.

2. System Model and Definitions

In this work, the type of image we discuss is gray images. Assuming that there are L gray levels in the given gray image, I, and the gray range is {0,1,2,…,($L-$1)}, then m thresholds divide the image into $m+1$ classes, which can be described as follows:

$$\begin{array}{c}{C}_0=\{g(i,j)\in I\mid 0\le g(i,j)\le t_1-1\},\hfill \\ C_1=\{g(i,j)\in I\mid t_1\le g(i,j)\le t_2-1\},\hfill \\ C_2=\{g(i,j)\in I\mid t_2\le g(i,j)\le t_3-1\},\hfill \\ ...\hfill \\ C_m=\{g(i,j)\in I\mid t_m\le g(i,j)\le L-1\},\hfill \end{array}$$

(1)

where $t_i(i=1,2,...,m)$ is the ith threshold, $C_i$ is the ith pixel set of image I, and $g(i,j)$ is the gray level of image I at pixel $(i,j)$. When $m=1$, there is only one threshold, also known as single-level thresholding, while if $m\ge 2$, it is called multilevel thresholding. In this study, we mainly discuss multilevel thresholding image segmentation.

Assuming that $f(t_1,t_2,...,t_m)$ is an objective function of a set of thresholds $\{t_1,t_2,...,t_m\}$$(t_1<t_2<...<t_m)$ of image I, the goal of multilevel thresholding segmentation is to find a set of optimal thresholds $\{{\displaystyle t_1^{*}},{\displaystyle t_2^{*}},...,{\displaystyle t_m^{*}}\}$ to maximize objective function $f(t_1,t_2,...,t_m)$ under the condition of a given threshold number, m, which can be described as follows:

$${\displaystyle t_1^{*}},{\displaystyle t_2^{*}},...,{\displaystyle t_m^{*}}=arg\underset{t_1,t_2,...,t_m}{max}f(t_1,t_2,...,t_m).$$

(2)

In this paper, among the common multilevel thresholding image segmentation methods, the Otsu method and Kapur entropy are selected and combined with the MSWOA to achieve image segmentation. The Otsu method and Kapur entropy are detailed below.

2.1. Otsu Method

The Otsu method [10] was proposed by Japanese scholar Nobuyuki Otsu in 1979. Its basic idea is to use the one-dimensional probability histogram of the image gray level to select the segmentation threshold when the between-class variance of the image reaches the maximum. The best threshold divides the image into sections with the largest between-class variance. The Otsu method considers that the image segmentation effect is the best under this condition.

Assuming that image I has N pixels, probability $p_i$ of the ith gray level can be expressed as shown in Equation (3):

$$p_i=\frac{h_i}{N},0\le i\le (L-1),$$

(3)

where $h_i$ represents the sum of the number of the ith gray levels and ${\displaystyle \sum _{i=0}^{L-1}}{p}_i=1$. Threshold set $\{t_1,t_2,...,t_m\}$ divides the image into $m+1$ parts. If the probability of the ith part is ${\omega }_i$ and the average gray level of the ith part is ${\mu }_i$, then the function of the between-class variance of image I can be expressed as shown in Equation (4):

$$f_{Otsu}(t_1,t_2,...,t_m)={\displaystyle {\sigma }_0^2}+{\displaystyle {\sigma }_1^2}+{\displaystyle {\sigma }_2^2}+...+{\displaystyle {\sigma }_m^2},$$

(4)

where

$$\begin{array}{c}{\displaystyle {\sigma }_0^2}={\omega }_0{({\mu }_0-{\mu }_T)}^2,{\omega }_0={\displaystyle \sum _{i=0}^{t_1-1}}{p}_i,{\mu }_0={\displaystyle \sum _{i=0}^{t_1-1}}\frac{i{p}_i}{{\omega }_0},\hfill \\ {\displaystyle {\sigma }_1^2}={\omega }_1{({\mu }_1-{\mu }_T)}^2,{\omega }_1={\displaystyle \sum _{i=t_1}^{t_2-1}}{p}_i,{\mu }_1={\displaystyle \sum _{i=t_1}^{t_2-1}}\frac{i{p}_i}{{\omega }_1},\hfill \\ {\displaystyle {\sigma }_2^2}={\omega }_2{({\mu }_2-{\mu }_T)}^2,{\omega }_2={\displaystyle \sum _{i=t_2}^{t_3-1}}{p}_i,{\mu }_2={\displaystyle \sum _{i=t_2}^{t_3-1}}\frac{i{p}_i}{{\omega }_2},\hfill \\ ...\hfill \\ {\displaystyle {\sigma }_m^2}={\omega }_m{({\mu }_m-{\mu }_T)}^2,{\omega }_m={\displaystyle \sum _{i=t_m}^{L-1}}{p}_i,{\mu }_m={\displaystyle \sum _{i=t_m}^{L-1}}\frac{i{p}_i}{{\omega }_m}.\hfill \end{array}$$

In Equation (4), ${\mu }_T={\displaystyle \sum _{i=0}^{L-1}}i{p}_i$ represents the average gray level of the whole image, and ${\omega }_0{\mu }_0+{\omega }_1{\mu }_1+{\omega }_2{\mu }_2+...+{\omega }_m{\mu }_m={\mu }_T$.

2.2. Kapur Entropy

Kapur entropy [11], also known as the maximum entropy method, was proposed by Kapur in 1985. Its basic idea is to divide the gray histogram of an image into independent classes with several thresholds, so as to maximize the sum of the entropy values. The function of Kapur entropy of image I can be expressed as shown in Equation (5):

$$f_{Kapur}(t_1,t_2,...,t_m)=H_0+H_1+H_2+...+H_m,$$

(5)

where

$$\begin{array}{c}{H}_0=-{\displaystyle \sum _{i=0}^{t_1-1}}\frac{p_i}{{\omega }_0}ln\frac{p_i}{{\omega }_0},{\omega }_0={\displaystyle \sum _{i=0}^{t_1-1}}{p}_i,\hfill \\ H_1=-{\displaystyle \sum _{i=t_1}^{t_2-1}}\frac{p_i}{{\omega }_1}ln\frac{p_i}{{\omega }_1},{\omega }_1={\displaystyle \sum _{i=t_1}^{t_2-1}}{p}_i,\hfill \\ H_2=-{\displaystyle \sum _{i=t_2}^{t_3-1}}\frac{p_i}{{\omega }_2}ln\frac{p_i}{{\omega }_2},{\omega }_2={\displaystyle \sum _{i=t_2}^{t_3-1}}{p}_i,\hfill \\ ...\hfill \\ H_m=-{\displaystyle \sum _{i=t_m}^{L-1}}\frac{p_i}{{\omega }_m}ln\frac{p_i}{{\omega }_m},{\omega }_m={\displaystyle \sum _{i=t_m}^{L-1}}{p}_i.\hfill \end{array}$$

3. Our Proposed MSWOA Scheme

This section first introduces the basic whale optimization algorithm. Then, a mixed-strategy-based improved whale optimization algorithm (MSWOA) is proposed. Finally, the proposed algorithm is applied to the multilevel thresholding segmentation of gray images. As mentioned above, the Otsu method and Kapur entropy are combined with the MSWOA to achieve image segmentation. When the function of between-class variance or the Kapur entropy function obtains the maximum value, image segmentation works best. In this work, a gray image segmentation task is proposed as shown in Equation (6):

$$max{f}_{Otsu}(t_1,t_2,...,t_m)or{f}_{Kapur}(t_1,t_2,...,t_m),$$

(6)

where the mathematical expressions of the objective functions are shown in Equations (4) and (5).

3.1. Whale Optimization Algorithm

The whale optimization algorithm is a meta heuristic optimization algorithm simulating the behavior of whales in the ocean. It includes three main stages: prey encircling, bubble hunting, and prey searching. In the whale optimization algorithm, assuming that the size of the whale population is N and the dimension of the solution space is D, the corresponding position of the ith whale in the D-dimensional space is $X_i=({\displaystyle x_i^1},{\displaystyle x_i^2},...,{\displaystyle x_i^D}),i=1,2,3,...,N$, and the position of the optimal whale (prey) corresponds to the global optimal solution.

Prey encircling: The whale locates prey and surrounds it throughout the predation phase. Other members of the group move to the best position, which is assumed to be where the prey is currently, and the position is updated using the formula below:

$$D=\mid C·X^{*}\left(t\right)-X\left(t\right)\mid ,$$

(7)

$$X(t+1)=X^{*}\left(t\right)-A·D,$$

(8)

where t indicates the current iteration; $X^{*}\left(t\right)$ represent the optimal whale position in the tth iteration; $X\left(t\right)$ is the position of the individual whale in the tth iteration; and A and C are coefficients calculated with the following equations:

$$A=2a·r-a,$$

(9)

$$C=2·r,$$

(10)

where r is a random number in [0, 1] and a decreases linearly from 2 to 0 during iteration.

Bubble hunting: In the WOA, whale predation behavior is classified as shrinking encircling and spiral updating. Of these, shrinking encircling is realized according to Equation (9), where convergence factor a decreases linearly with iterations and A is a random value in $[-a,a]$. If $\left|A\right| \le 1$, the individual whale updates its position as it approaches prey and completes the contraction of prey in accordance with Equation (8). Individual whales in spiral updating must first calculate how far apart they are from prey and then prey on the prey in a spiral form. The following is the mathematical expression of this behavior:

$$D^{\prime }=\mid X^{*}\left(t\right)-A\left(t\right)\mid ,$$

(11)

$$X(t+1)=D^{\prime }·e^{bl}·cos\left(2\pi l\right)+X^{*}\left(t\right),$$

(12)

where Equation (11) indicates the distance between the ith whale and its prey, l is a random number in $[-1,1]$, and b is a constant that defines the shape of the spiral.

In the whale predation process, spiral updating is carried out at the same time as shrinking encircling. To simulate this synchronization process, the WOA assumes that probability p of performing these two predation behaviors is 50%. The mathematical model is as follows:

$$\begin{array}{c}\hfill X(t+1)=\left\{\begin{array}{c}{X}^{*}\left(t\right)-A·Dp<0.5\hfill \\ D^{\prime }·e^{bl}·cos\left(2\pi l\right)+X^{*}\left(t\right)p\ge 0.5.\hfill \end{array}\right.\end{array}$$

(13)

Prey searching: When $\mid A\mid \ge 1$, a member of the population is randomly chosen as prey for the global search to avoid falling into the local optimum. The mathematical model is shown as follows:

$$D=\mid C·X_{rand}-X\mid ,$$

(14)

$$X(t+1)=X_{rand}-A·D,$$

(15)

where $X_{rand}$ indicates the position of a random whale (or prey) in the current population.

3.2. Mixed-Strategy-Based Improved Whale Optimization Algorithm

A mixed-strategy-based improved whale optimization algorithm (MSWOA) is presented using the k-point initialization algorithm, the nonlinear convergence factor, and the adaptive weight coefficient to enhance the search ability of the WOA. In addition, the MSWOA is applied to multilevel thresholding gray image segmentation combined with the Otsu method and Kapur entropy, respectively.

3.2.1. Population Initialization Based on k-Point Search Strategy

Haupt et al. [45] and Gondro et al. [46] pointed out that the accuracy and convergence speed of swarm intelligent optimization algorithms depend on the quality of the initial population. A better initial solution can accelerate the convergence speed of the algorithm and help to find the global optimal solution. However, the global optimal solution of the problem to be optimized is usually unknown. Without any prior knowledge, swarm intelligence optimization algorithms, including the WOA, usually use random methods to generate initial population individuals. The search accuracy and efficiency of an algorithm is somewhat impacted by the variety of the initial population, which cannot be guaranteed using the random initialization method.

In this work, inspired by the idea of the opposition-based learning strategy [47] and the binary search strategy, we propose a new search strategy called k-point and apply it to the algorithm for population initialization.

Definition of k-point: If there is a real number x in interval $[lb,ub]$, the left binary point of x is defined as $x^l=(lb+x)/k$, and the right binary point is defined as $x^r=(x+ub)/k$. The definition is extended to d-dimensional space. Let $p=(x_1,x_2,...,x_d)$ be a point in d-dimensional space, where $x_i\in [l{b}_i,u{b}_i],i=1,2,...,d$; the left binary point of p is defined as $p^l=({\displaystyle x_1^l},{\displaystyle x_2^l},...,{\displaystyle x_d^l})$, where ${\displaystyle x_i^l}=(l{b}_i+x_i)/k$, and the right binary point of p is defined as $p^r=({\displaystyle x_1^r},{\displaystyle x_2^r},...,{\displaystyle x_d^r})$, where ${\displaystyle x_i^r}=(x_i+u{b}_i)/k$. k is an integer larger than 1.

According to the above definition, the specific steps for generating the initial population using the k-point search strategy are shown in Algorithm 1.

Algorithm 1: Population initialization based on k-point search strategy.

Set population size N for $i=1$ to N do       for $j=1$ to d do             ${\displaystyle X_i^j}=l{\displaystyle b_i^j}+rand(0,1)·(u{\displaystyle b_i^j}-l{\displaystyle b_i^j})$       end for end for for $i=1$ to N do       for $j=1$ to d do             $L{\displaystyle X_i^j}=(l{\displaystyle b_i^j}+{\displaystyle X_i^j})/k$             $R{\displaystyle X_i^j}=({\displaystyle X_i^j}+u{\displaystyle b_i^j})/k$       end for end for merge $\left\{X\right(N)\cup LX(N)\cup RX(N\left)\right\}$, select N individuals with the best fitness as the initial population.

3.2.2. Nonlinear Convergence Factor and Adaptive Weight Coefficient

Similar to other swarm intelligence optimization algorithms, the basic WOA suffers from imbalance between global and local search capabilities when trying to identify the optimal solution. How to coordinate its exploration and development abilities is very important. Exploration ability means that the group needs to explore a wider search area to prevent the algorithm from falling into the local optimum; exploitation ability primarily uses the existing information of the group to search for some neighborhood of the solution space, which has a significant impact on the convergence speed of the algorithm. In the basic WOA, Equation (9) is used to control the global search or local search. When $A\ge 1$, the algorithm conducts a random global search with a probability of 0.5. When $A<1$, the algorithm performs a local search, and the value of A is mostly determined by convergence factor a. Therefore, in order to discover the best solution, the change in convergence factor a is crucial. Convergence factor a in the basic WOA decreases linearly with the increase in the number of iterations, which makes the algorithm’s convergence speed excessively slow.

In the initial stage of iteration, the algorithm is better able to escape the local extremum if a is larger; in the middle stage of iteration, in order to ensure faster convergence speed, a should be rapidly reduced to a smaller value with the increase in the number of iterations; while the search range of the optimal solution is basically determined in the later stage, a smaller a should be selected to improve the convergence accuracy of the algorithm. In order to accelerate the convergence speed while maintaining the algorithm’s potential for both global exploration and local exploitation, we introduce a nonlinear adjustment strategy without altering the changing trend of the original convergence factor. The specific formula is as follows:

$$a=2-2·{(2^{\frac{t}{T_{max}}}-1)}^u,$$

(16)

where u is a constant coefficient, which is used to adjust the attenuation degree of convergence factor a; and the value range of u is greater than 0; t is the number of iterations; and $T_{max}$ is the maximum number of iterations. When $T_{max}=500$, the curve of a changing with u is shown in Figure 1.

As shown in Figure 1, when the attenuation degree of convergence factor a changes from slow to rapid, compared with the basic WOA, $A\ge 1$ accounts for a larger proportion of iterations, and the random global exploration ability of the algorithm is enhanced, while the local development ability is weakened; on the contrary, when the attenuation degree of convergence factor a changes from fast to slow, $A\ge 1$ takes up a smaller proportion of iterations, and the local development ability of the algorithm is enhanced, while the random global exploration ability is weakened. In this paper, $u=0.4$ was selected to enhance the local development ability of the algorithm and improve the convergence speed and accuracy of the algorithm.

In the basic WOA, the position of prey is the location of the optimal solution. However, in the process of algorithm execution, the location of prey $X^{*}\left(t\right)$ in Equations (8), (13) and (15) is not fully utilized. In this paper, the adaptive weight coefficient is presented to make use of the optimal solution to increase the accuracy of the algorithm. The adaptive weight coefficient, $\omega$, is defined as follows:

$$\omega \left(t\right)=1-\frac{2}{\pi }arccos\left(\frac{t}{T_{max}}\right),$$

(17)

$$X(t+1)=\omega \left(t\right)·X^{*}\left(t\right)-A·D\mid A\mid <1,p<0.5,$$

(18)

$$X(t+1)=\omega \left(t\right)·X_{rand}-A·D\mid A\mid \ge 1,p<0.5,$$

(19)

$$X(t+1)=D^{\prime }·e^{bl}·cos\left(2\pi l\right)+[1-\omega \left(t\right)]X^{*}\left(t\right)p\ge 0.5,$$

(20)

where t is the number of iterations and $T_{max}$ is the maximum number of iterations. It is obvious that the value of $\omega$ is increased from 0 to 1. In Equations (18)–(20), adaptive weight coefficient $\omega$ increases with the number of iterations, which means that after each iteration, the position of prey is closer to the theoretical optimal solution, so as to improve the optimization accuracy of the algorithm; in the spiral update, the whale continues to approach its prey as the number of iterations rises. To enhance the local search capability of the algorithm, a smaller weight is introduced, which can make it possible to discover whether there is a better solution near the prey while updating the location.

3.2.3. Multilevel Thresholding Using MSWOA

In this work, the proposed MSWOA was applied to the threshold segmentation of gray images to obtain the optimal threshold and realize the segmentation of images. The task of image segmentation is described in Equation (6). The basic idea of using the MSWOA to search for the optimal threshold is to transform the threshold search into the minimum or maximum search of the objective function using the Otsu or Kapur method. In this process, a group of thresholds can be regarded as the position values of individual whales in the search space. Therefore, the continuous adjustment of the whale position means that the threshold is searched for continuously until convergence accuracy is reached or the stop condition of the optimization algorithm is satisfied. The flow chart is shown in Figure 2.

4. Performance Evaluation

In order to test the performance of the proposed algorithm, especially in terms of solution accuracy and convergence speed, 13 benchmark functions [33] (as shown in

Table 1. 13 Benchmark functions.

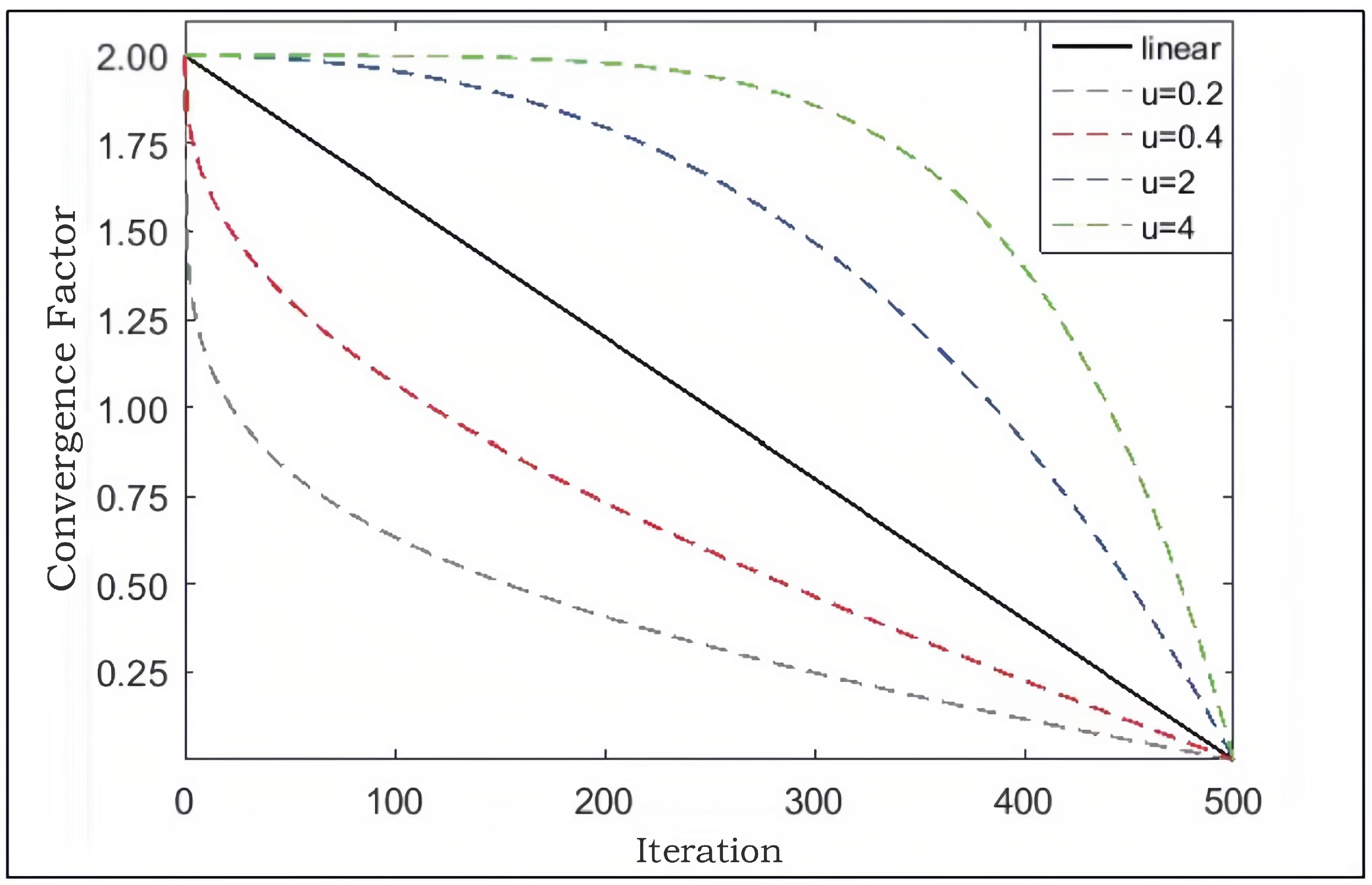
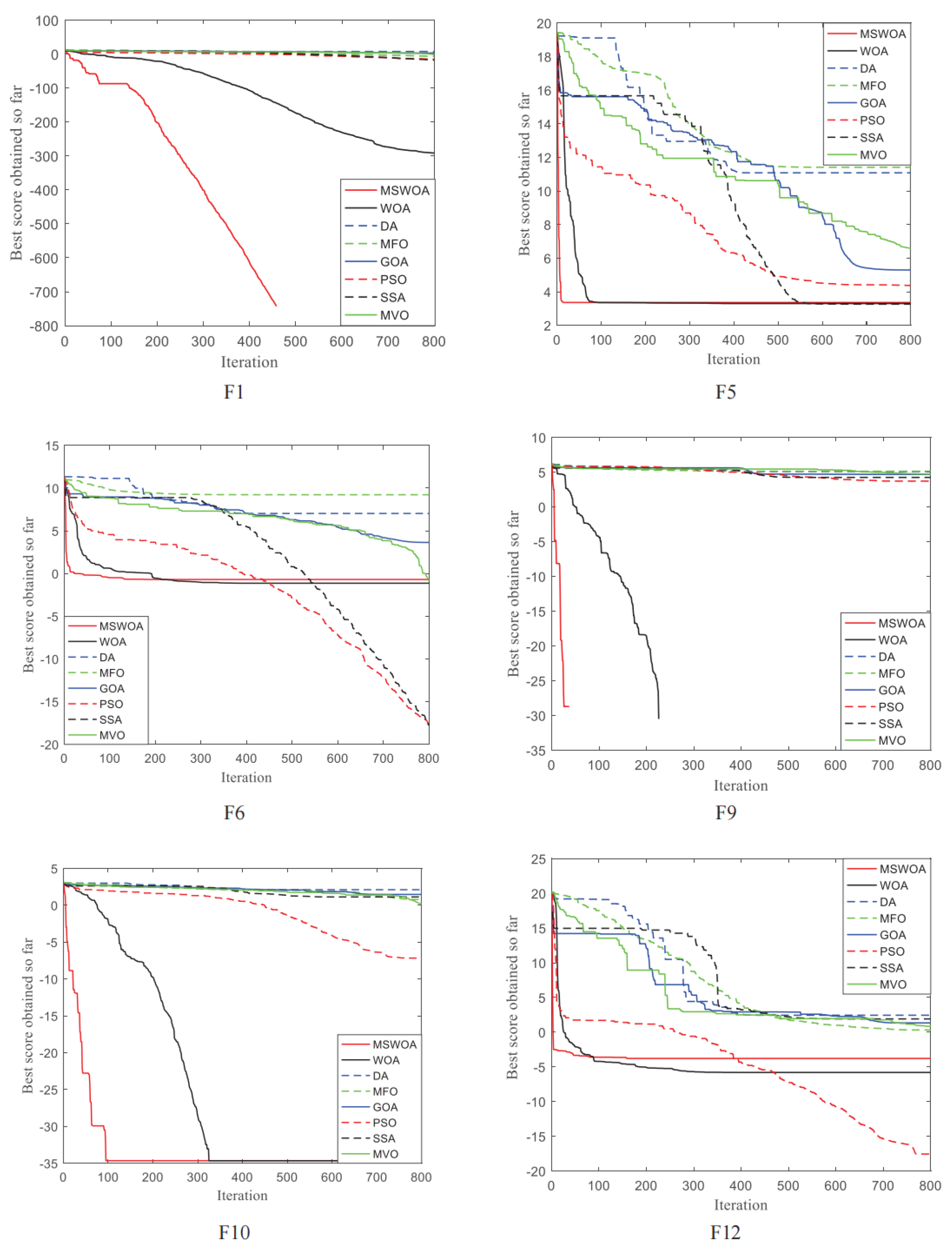
Function	Dim	Range	${\mathit{f}}_{\mathit{min}}$	Type
$F_1\left(x\right)={\displaystyle {\sum }_{i=1}^n}{\displaystyle x_i^2}$	30	[−100, 100]	0	Unimodal
$F_2\left(x\right)={\displaystyle {\sum }_{i=1}^n}\mid x_i\mid +{\displaystyle {\prod }_{i=1}^n}\mid x_i\mid$	30	[−10, 10]	0	Unimodal
$F_3\left(x\right)={\displaystyle {\sum }_{i=1}^n}{\left({\displaystyle {\sum }_{j=1}^n}{x}_j\right)}^2$	30	[−100, 100]	0	Unimodal
$F_4\left(x\right)=ma{x}_i\{\mid x_i\mid ,1\le i\le n\}$	30	[−100, 100]	0	Unimodal
$F_5\left(x\right)={\displaystyle {\sum }_{i=1}^{n-1}}[100{(x_{i+1}-{\displaystyle x_i^2})}^2+{(x_i-1)}^2]$	30	[−30, 30]	0	Unimodal
$F_6\left(x\right)={\displaystyle {\sum }_{i=1}^n}{\left([x_i+0.5]\right)}^2$	30	[−100, 100]	0	Unimodal
$F_7\left(x\right)={\displaystyle {\sum }_{i=1}^n}i{\displaystyle x_i^4}+random[0,1)$	30	[−1.28, 1.28]	0	Unimodal
$F_8\left(x\right)={\displaystyle {\sum }_{i=1}^n}-x_i\sin \left(\sqrt{\mid x_i\mid }\right)$	30	[−500, 500]	$-418.98295$	Multimodal
$F_9\left(x\right)={\displaystyle {\sum }_{i=1}^n}[{\displaystyle x_i^2}-10cos\left(2\pi x_i\right)+10]$	30	[−5.12, 5.12]	0	Multimodal
$F_{10}\left(x\right)=-20exp(-0.2\sqrt{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n}{\displaystyle x_i^2}})-exp\left(\frac{1}{n}{\displaystyle {\sum }_{i=1}^n}\cos \left(2\pi x_i\right)\right)+20+e$	30	[−32, 32]	0	Multimodal
$F_{11}\left(x\right)=\frac{1}{4000}{\displaystyle {\sum }_{i=1}^n}{\displaystyle x_i^2}-{\displaystyle {\prod }_{i=1}^n}cos\left(\frac{x_i}{\sqrt{i}}\right)+1$	30	[−600, 600]	0	Multimodal
$F_{12}\left(x\right)=\frac{\pi }{n}\{10sin\left(\pi y_1\right)+{\displaystyle {\sum }_{i=1}^{n-1}}{(y_i-1)}^2[1+10{sin}_2\left(\pi y_{i+1}\right)]+{(y_n-1)}^2\}+{\displaystyle {\sum }_{i=1}^n}u(x_i,10,100,4)$
$y_i=1+\frac{x_i+1}{4}u(x_i,a,k,m)=\left\{\begin{array}{c}k{(x_i-a)}^m{x}_i>a\hfill \\ 0-a<x_i<a\hfill \\ k{(-x_i-a)}^m{x}_i<-a\hfill \end{array}\right.$	30	[−50, 50]	0	Multimodal
$F_{13}\left(x\right)=0.1{\sin }^2\left(3\pi x_1\right)+[1+{\displaystyle {\sum }_{i=1}^n}{(x_i-1)}^2{\sin }^2(3\pi x_i+1)]+{(x_n-1)}^2[1+{\sin }^2\left(2\pi x_n\right)]$
$+{\displaystyle {\sum }_{i=1}^n}u(x_i,5,100,4)$	30	[−50, 50]	0	Multimodal

) were selected for experiments. The benchmark functions in Table 1 included seven unimodal functions and six multimodal functions. We compared the proposed algorithm with the WOA, PSO, the SSA [48], the GOA [49], MFO [15], MVO [50], and the DA [51] to prove its effectiveness. The simulation experiments in this paper were conducted using Intel(R) Core (TM) i7-8700 CPU, 3.20 GHz, 16 GB RAM, and Windows 10 (64-bit) operating system, and the programming software was MATLAB R2016b.

4.1. Parameter Settings

The population size ($PopSize$) of all algorithms in this section was set to 30. Each algorithm was run independently for each function 30 times to obtain the average value and standard deviation. Due to the slow convergence speed of some algorithms (e.g., MFO and DA), more iterations were needed to achieve a certain convergence accuracy, so 500 and 800 were set as the maximum iteration ($Max\_Iter$) numbers for independent experiments and compared. The core parameter settings and their values involved in all algorithms are shown in

Table 2. Parameter settings.

Algorithm	Parameter	Value
MSWOA	u	0.4
	$\omega$	$[0,1]$
WOA	Convergence factor a	$[0,2]$
	l	$[-1,1]$
	b	1
PSO	Cognitive and social constants	$c_1=c_2=2$
	Inertial weigh $\omega$	Linearly decreases from 0.9 to 0.2
SSA	$c_1$	nonlinearly decreases from 2 to 0
	$c_2$	$[0,1]$
	$c_3$	$[0,1]$
GOA	cmax	1
	cmin	0.00004
MFO	b	1
	l	$[-1,1]$
	a	Linearly decreases from $-1$ to $-2$
MVO	$WE{P}_{Max}$	1
	$WE{P}_{Min}$	0.2
DA	f	$[0,2]$

. Other parameters and their values not listed in the table were set according to the original paper.

4.2. Experimental Results and Analysis

Table 3. Comparison of optimization results obtained on benchmark functions ($PopSize=30$; $Max\_Iter=500$).

F	MSWOA		WOA		PSO		SSA		GOA		MFO		MVO		DA
	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.
F1	0.00E+00	0.00E+00	5.68E-74	2.47E-73	1.14E-04	1.28E-04	1.94E-07	2.44E-07	3.88E+01	2.54E+01	2.68E+03	5.83E+03	2.68E+03	5.83E+03	2.73E+03	1.39E+03
F2	2.18E-219	1.58E-219	2.85E-51	7.99E-51	7.31E-02	1.61E-01	1.71E+00	1.32E+00	1.82E+01	1.95E+01	2.91E+01	2.02E+01	2.91E+01	2.02E+01	1.65E+01	6.19E+00
F3	0.00E+00	0.00E+00	4.32E+04	1.05E+04	7.36E+01	2.74E+01	2.14E+03	1.21E+03	3.36E+03	1.71E+03	1.57E+04	9.57E+03	1.57E+04	9.57E+03	1.32E+04	7.45E+03
F4	2.48E-205	0.00E+00	4.89E+01	3.08E+01	1.11E+00	2.42E-01	1.22E+01	3.35E+00	1.39E+01	4.07E+00	6.81E+01	8.40E+00	6.81E+01	8.40E+00	3.14E+01	1.08E+01
F5	2.76E+01	5.08E+00	2.79E+01	4.07E-01	9.62E+01	6.65E+01	2.59E+02	4.92E+02	6.60E+03	9.31E+03	1.42E+04	3.33E+04	1.42E+04	3.33E+04	2.46E+05	2.36E+05
F6	4.04E-01	1.38E-01	4.40E-01	2.30E-01	2.01E-04	2.50E-04	9.92E-08	8.94E-08	3.73E+01	2.33E+01	3.68E+03	6.67E+03	3.68E+03	6.67E+03	2.42E+03	1.60E+03
F7	6.88E-05	6.47E-05	3.51E-03	5.05E-03	1.61E-01	6.37E-02	1.99E-01	9.15E-02	5.08E-02	2.13E-02	2.07E+00	4.19E+00	2.07E+00	4.19E+00	6.89E-01	7.28E-01
F8	−1.25E+04	1.17E+02	−9.89E+03	1.63E+03	−4.82E+03	1.22E+03	−7.47E+03	5.49E+02	−7.30E+03	5.12E+02	−8.66E+03	8.76E+02	−8.66E+03	8.76E+02	−5.35E+03	6.50E+02
F9	0.00E+00	0.00E+00	0.00E+00	0.00E+00	5.53E+01	1.53E+01	6.08E+01	2.00E+01	1.03E+02	5.22E+01	1.62E+02	4.43E+01	1.62E+02	4.43E+01	1.69E+02	4.61E+01
F10	8.88E-16	0.00E+00	5.03E-15	2.48E-15	2.29E-01	4.55E-01	2.70E+00	8.49E-01	5.65E+00	1.53E+00	1.43E+01	7.18E+00	1.43E+01	7.18E+00	1.01E+01	1.97E+00
F11	0.00E+00	0.00E+00	2.02E-02	6.48E-02	8.05E-03	9.65E-03	2.02E-02	1.50E-02	1.15E+00	7.73E-02	1.13E+00	1.09E+00	1.13E+00	1.09E+00	1.73E+01	7.20E+00
F12	2.19E-02	1.47E-02	2.12E-02	1.15E-02	3.12E-06	4.67E-06	9.04E+00	5.79E+00	1.11E+01	6.63E+00	8.59E+00	9.46E+00	8.59E+00	9.46E+00	3.06E+04	1.53E+05
F13	3.01E-01	1.51E-01	4.67E-01	2.42E-01	7.38E-03	1.27E-02	1.83E+01	1.51E+01	4.15E+01	2.43E+01	1.37E+07	7.49E+07	1.37E+07	7.49E+07	2.75E+05	4.14E+05

The bolded part is the algorithm that performs best on the benchmark functions (Avg or Std metrics).

and

Table 4. Comparison of optimization results obtained on benchmark functions ($PopSize=30$; $Max\_Iter=800$).

F	MSWOA		WOA		PSO		SSA		GOA		MFO		MVO		DA
	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.	Avg.	Std.
F1	0.00E+00	0.00E+00	8.88E-120	4.54E-119	3.20E-06	1.21E-05	1.53E-08	3.79E-09	1.36E+01	1.15E+01	3.33E+02	1.83E+03	3.33E+02	1.83E+03	1.38E+03	7.31E+02
F2	0.00E+00	0.00E+00	1.77E-83	5.71E-83	1.45E-03	1.76E-03	1.53E+00	1.34E+00	1.62E+01	2.58E+01	3.70E+01	1.88E+01	3.70E+01	1.88E+01	1.73E+01	7.80E+00
F3	0.00E+00	0.00E+00	3.01E+04	1.31E+04	2.61E+01	9.84E+00	6.41E+02	4.62E+02	2.72E+03	1.47E+03	2.25E+04	1.78E+04	2.25E+04	1.78E+04	1.07E+04	6.00E+03
F4	0.00E+00	0.00E+00	3.77E+01	3.16E+01	7.26E-01	2.09E-01	9.20E+00	4.01E+00	1.38E+01	3.81E+00	6.54E+01	9.36E+00	6.54E+01	9.36E+00	2.77E+01	9.06E+00
F5	2.74E+01	5.07E+00	2.77E+01	5.08E-01	5.65E+01	4.64E+01	9.81E+01	1.26E+02	2.83E+03	4.98E+03	1.28E+04	3.09E+04	1.28E+04	3.09E+04	2.69E+05	3.48E+05
F6	2.83E-01	1.15E-01	1.65E-01	1.21E-01	1.71E-06	8.05E-06	1.81E-08	5.81E-09	1.17E+01	8.30E+00	2.34E+03	4.32E+03	2.34E+03	4.32E+03	1.38E+03	7.37E+02
F7	3.86E-05	3.29E-05	2.06E-03	3.69E-03	1.03E-01	4.20E-02	1.13E-01	3.82E-02	2.67E-02	1.21E-02	4.81E+00	6.84E+00	4.81E+00	6.84E+00	3.92E-01	2.74E-01
F8	−1.26E+04	1.14E+00	−1.07E+04	1.75E+03	−5.95E+03	1.31E+03	−7.36E+03	8.10E+02	−7.52E+03	7.54E+02	−8.67E+03	9.27E+02	−8.67E+03	9.27E+02	−5.47E+03	6.24E+02
F9	0.00E+00	0.00E+00	0.00E+00	0.00E+00	4.82E+01	1.27E+01	5.62E+01	1.60E+01	1.02E+02	3.64E+01	1.55E+02	4.04E+01	1.55E+02	4.04E+01	1.62E+02	3.29E+01
F10	8.88E-16	0.00E+00	3.61E-15	2.41E-15	1.37E-01	4.26E-01	2.35E+00	4.92E-01	4.55E+00	1.13E+00	1.41E+01	7.19E+00	1.41E+01	7.19E+00	9.16E+00	1.70E+00
F11	0.00E+00	0.00E+00	1.79E-02	5.81E-02	1.55E-01	8.85E-03	8.04E-03	8.04E-03	8.77E-01	1.55E-01	1.51E+01	4.15E+01	1.51E+01	4.15E+01	1.32E+01	5.95E+00
F12	1.59E-02	1.06E-02	1.38E-02	1.88E-02	6.99E-09	1.66E-08	5.03E+00	2.90E+00	8.22E+00	5.74E+00	1.47E+00	1.49E+00	1.47E+00	1.49E+00	5.44E+01	1.28E+02
F13	2.30E-01	9.58E-02	3.17E-01	2.25E-01	2.93E-03	4.94E-03	7.53E+00	1.57E+01	2.76E+01	1.57E+01	4.24E+00	6.60E+00	4.24E+00	6.60E+00	1.15E+05	2.62E+05

The bolded part is the algorithm that performs best on the benchmark functions (Avg or Std metrics).

show the running results of eight optimization algorithms on 13 benchmark functions in Table 1. Among them, Table 3 shows the results of 500 iterations after running the algorithms independently 30 times; Table 4 shows the results of 800 iterations after running the algorithms independently 30 times. It can be seen from Table 3 that compared with the WOA, except for F12, the MSWOA had better solution accuracy; especially, it could converge to the theoretical minimum value of 0 of F1, F3, F9, and F11. Compared with other six algorithms, PSO had more advantages in solving F6, F12, and F13; the SSA had more advantages in solving F6; and the MSWOA performed better in other benchmark functions. Similarly, it can be seen from Table 4 that compared with the WOA, the MSWOA only performed slightly worse in the results of F6 and F12, but the order of magnitude was the same, and there was no significant difference in numerical value. Similar to the results in Table 3, in Table 4, compared with other six algorithms, the solution accuracy of the MSWOA for F6, F12, and F13 was not as good as that of PSO and the SSA, and there were many differences in the order of magnitude, but it was the best in solving other functions. In general, the accuracy of the MSWOA was obviously better than that of the other seven optimization algorithms.

In order to reflect the speed of convergence and the capability to jump out of the local optimum of the MSWOA intuitively, we selected six typical function convergence curves when the maximum iteration number was 800, as shown in Figure 3. The solution accuracy of the ordinate in the figure was logarithmized based on 10. It can be seen from Figure 2 that the curves of the MSWOA have the fastest descent and convergence speed. Among them, the convergence curves of F1 and F9 are interrupted when the number of iterations is less than 500, which indicates that the algorithm jumped and converged to 0 (logarithm cannot be taken as 0), which is consistent with the values shown in Table 4. The convergence curves of F5 and F10 show that the convergence accuracy of the MSWOA and that of the WOA in these two functions are similar, but the convergence speed of the MSWOA is obviously faster than that of the WOA. Combined with the data in Table 3 and Table 4, it can be concluded that the MSWOA and the WOA generally converge within 500 iterations. When the number of iterations increases from 500 to 800, there is little room for further improvement in solution accuracy, while for other algorithms, especially the GOA and the DA, more iterations (more than 500) are needed to achieve similar convergence accuracy. The convergence curves of F6 and F12 show that the MSWOA and the WOA have faster convergence speed (less than 100 iterations) than other algorithms, but they are not as accurate as PSO and the SSA. Generally speaking, the MSWOA has faster convergence speed than other algorithms in Table 3 and Table 4, and the decline range has mutation, which can effectively jump out of the local optimum.

5. Multilevel Image Thresholding Based on MSWOA

5.1. Benchmark Images

In this work, we selected eight common images for a multilevel thresholding segmentation experiment based on histograms. These images were from Berkeley Segmentation Dataset and the Benchmarks 500 (BSDS500) dataset. The color images were grayed. Figure 4 shows the original images of the benchmark images: (a) Lena, (b) Baboon, (c) Starfish, (d) Couple, (e) Cameraman, (f) Pepper, (g) Tree, and (h) Building, where the size of Lena and Baboon was 512 × 512, the size of Cameraman and Pepper was 256 × 256, and the size of other images was 481 × 321. Figure 5 shows the histogram curve corresponding to each image in Figure 4.

5.2. Experimental Settings

In this experiment, we used m to represent the multiple threshold levels of images. We mainly considered four different threshold levels: 2-threshold level, 3-threshold level, 5-threshold level, and 8-threshold level (

Table 5. Comparison of PSNR computed with eight algorithms using the Otsu and Kapur methods with m of 2, 3, 5, and 8.

Image	m	MSWOA		WOA		PSO		SSA		GOA		MFO		MVO		DA
		Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur
Lena	2	11.9025	14.4845	11.9025	14.3883	11.9025	14.3883	11.9025	14.3883	11.9025	14.3883	11.9025	14.3883	11.9025	14.3883	11.9025	14.3883
	3	14.1027	16.9552	14.1027	16.8255	14.1027	16.8255	14.1027	16.8255	13.7579	16.3516	14.1027	16.8481	14.1027	16.8255	14.1027	16.8255
	5	19.2113	19.8729	19.1614	19.7923	16.9648	19.7923	16.9648	19.7923	18.9844	19.7882	17.2025	19.8662	16.9648	19.7923	16.9648	19.8662
	8	22.5797	24.9741	20.5756	21.8269	19.9752	22.7018	20.7126	22.7093	20.3216	22.7085	20.3667	22.5234	20.3368	22.7083	20.4286	22.9321
Baboon	2	11.5837	12.3381	11.5837	12.3381	11.5837	12.3381	11.5837	12.3381	11.5837	12.3381	11.5837	12.3381	11.5837	12.3381	11.5837	12.3381
	3	13.6321	14.3441	13.5413	14.3441	13.5413	14.3441	13.5413	14.3441	13.3099	14.275	13.5413	14.3441	13.5413	14.3441	13.5413	14.3441
	5	17.1771	22.9336	17.2723	22.859	16.1728	22.8544	16.1728	22.8544	17.1589	21.6078	16.1728	22.859	16.1728	22.8544	16.1728	22.859
	8	20.3869	30.3807	20.018	30.3609	18.3586	30.2933	18.5683	30.2947	18.7169	30.3341	18.6087	30.3259	18.5668	30.3063	19.9064	30.3144
Starfish	2	12.697	15.1602	12.6237	15.1602	12.6237	15.1602	12.6237	15.1602	12.6237	15.1602	12.6237	15.1602	12.6237	15.1602	12.6237	15.1602
	3	15.2587	18.1574	15.2587	18.1574	15.2587	18.1574	15.2587	18.1574	14.4788	17.7476	15.3654	18.1574	15.2587	18.1574	15.2691	18.1574
	5	19.59	22.2217	19.0518	22.0858	19.0518	21.971	19.0518	21.971	19.1947	22.1121	19.0518	22.0858	19.0518	21.971	19.0518	21.9724
	8	25.2279	28.3071	23.1711	25.2777	22.2434	25.3942	22.7858	25.3805	22.5893	25.4139	22.2528	25.7199	22.2434	25.1868	22.7135	25.3236
Couple	2	12.1121	14.2889	12.1121	14.2889	12.1121	14.2889	12.1121	14.2889	12.1121	14.2889	12.1121	14.2889	12.1121	14.2889	12.1121	14.2889
	3	14.2726	16.9785	14.2726	16.9265	14.2726	16.9265	14.2726	16.9265	17.5171	18.1743	14.2726	16.9265	14.2726	16.9265	14.2726	16.9265
	5	18.1173	20.7261	16.8914	20.5302	16.8914	20.4364	16.8914	20.4364	19.8416	21.9673	17.6576	20.4364	16.5569	20.4364	16.7982	20.5302
	8	25.3153	28.1138	20.7382	22.0762	19.919	22.0762	21.7495	22.0762	20.5679	22.0482	20.7138	22.0762	21.4869	22.0762	21.4539	22.241
Cameraman	2	12.231	14.9016	12.231	14.729	12.231	14.729	12.231	14.729	12.231	14.729	12.231	14.729	12.231	14.729	12.231	14.729
	3	15.7204	21.7574	14.5472	21.2833	14.5472	21.2833	14.5472	21.2833	13.7709	21.0183	14.5472	21.418	14.5472	21.2833	14.5472	21.2833
	5	18.6227	26.0676	18.6207	25.683	17.6339	25.8299	18.5595	25.6675	18.5093	25.3852	17.8744	25.8332	18.4315	25.6675	18.5271	25.6894
	8	20.993	29.1303	20.8943	29.0543	20.6932	29.0267	20.81	29.0267	20.8285	29.0265	20.6976	29.0454	20.8618	28.9892	23.9218	29.0309
Pepper	2	12.2981	13.211	12.2981	13.211	12.2981	13.211	12.2981	13.211	12.2981	13.211	12.2981	13.211	12.2981	13.211	12.2981	13.211
	3	14.4837	15.4188	14.4082	15.4188	14.4082	15.4188	14.4082	15.4188	14.4124	13.6771	14.4082	15.4188	14.4082	15.4188	14.4082	15.4188
	5	19.5722	23.561	18.0195	23.3721	16.7909	23.2099	16.8888	23.2099	18.3362	21.7569	17.1978	23.3058	17.1978	23.2099	17.1978	23.2954
	8	22.7276	29.5103	22.3483	29.3608	20.1303	27.5703	21.9444	28.5212	20.4323	28.6622	20.1355	28.8707	20.2841	28.5367	20.1161	29.0532
Tree	2	13.9934	16.5731	13.9934	16.4114	13.9934	16.4114	13.9934	16.4114	13.9934	16.4114	13.9934	16.4114	13.9934	16.4114	13.9934	16.4114
	3	16.7393	19.8968	16.5091	19.7753	16.5091	19.7753	16.5091	19.7753	15.968	20.5578	16.5091	19.7753	16.5091	19.7753	16.5091	19.8155
	5	21.3783	22.5034	20.0391	22.1753	19.8873	22.4102	19.9665	22.141	20.1136	21.6881	20.0394	22.4102	20.0075	22.141	19.9486	22.2266
	8	25.4625	28.3796	25.0236	26.0232	23.5182	25.5521	24.418	25.5543	24.3086	25.5089	24.233	25.5654	24.437	25.3931	25.5159	25.6348
Building	2	12.0557	12.1508	12.0557	12.1508	12.0557	12.1508	12.0557	12.1508	12.0557	12.1508	12.0557	12.1508	12.0557	12.1508	12.0557	12.1508
	3	14.0772	13.4318	13.9276	13.4318	13.9276	13.4318	13.9276	13.4318	13.6812	12.7967	13.9276	13.4318	13.9276	13.4318	13.9276	13.4318
	5	18.4052	19.2348	17.7485	19.2325	16.5801	19.2325	16.5801	19.2325	18.3092	22.1147	16.5801	19.2325	16.5801	19.2325	17.3635	19.2325
	8	20.9671	30.3721	20.8138	29.8267	18.2647	28.1713	20.1842	28.1738	18.5888	28.3911	18.466	28.1801	18.2695	28.1713	19.6706	28.7902

The bolded part is the algorithm that performs best in PSNR metrics at the threshold level (m = 2, 3, 5, 8).

,

Table 6. Comparison of SSIM computed with eight algorithms using the Otsu and Kapur methods with m of 2, 3, 5, and 8.

Image	m	MSWOA		WOA		PSO		SSA		GOA		MFO		MVO		DA
		Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur
Lena	2	0.38469	0.48354	0.38469	0.47856	0.38469	0.47856	0.38469	0.47856	0.38469	0.47856	0.38469	0.47856	0.38469	0.47856	0.38469	0.47856
	3	0.46863	0.57261	0.46863	0.5661	0.46863	0.5661	0.46863	0.5661	0.53953	0.5747	0.46863	0.56327	0.46863	0.5661	0.46863	0.5661
	5	0.70299	0.64855	0.69893	0.65079	0.5953	0.65079	0.5953	0.65079	0.65574	0.64961	0.61027	0.65061	0.5953	0.65079	0.5953	0.65061
	8	0.80157	0.78909	0.72308	0.72653	0.70873	0.72556	0.72737	0.725	0.71318	0.72993	0.71964	0.72535	0.71622	0.72484	0.7153	0.7316
Baboon	2	0.44418	0.51738	0.44418	0.51738	0.44418	0.51738	0.44418	0.51738	0.44418	0.51738	0.44418	0.51738	0.44418	0.51738	0.44418	0.51738
	3	0.52143	0.62295	0.52115	0.62295	0.52115	0.62295	0.52115	0.62295	0.56317	0.61809	0.52115	0.62295	0.52115	0.62295	0.52115	0.62295
	5	0.70501	0.79125	0.71025	0.79012	0.64116	0.78958	0.64116	0.78958	0.67826	0.77005	0.64116	0.79012	0.64116	0.78958	0.64116	0.79012
	8	0.80349	0.90719	0.80074	0.90603	0.7261	0.90579	0.73494	0.90583	0.73576	0.90605	0.72769	0.90644	0.7349	0.90598	0.75196	0.90688
Starfish	2	0.32402	0.37677	0.31997	0.37677	0.31997	0.37677	0.31997	0.37677	0.31997	0.37677	0.31997	0.37677	0.31997	0.37677	0.31997	0.37677
	3	0.44135	0.50411	0.44135	0.50411	0.44135	0.50411	0.44135	0.50411	0.44856	0.53117	0.44372	0.50411	0.44135	0.50411	0.43892	0.50411
	5	0.6384	0.65176	0.61666	0.65019	0.61666	0.64842	0.61666	0.64842	0.6172	0.6669	0.61666	0.65019	0.61666	0.64842	0.61666	0.64841
	8	0.85447	0.84501	0.75891	0.76051	0.73528	0.76604	0.74951	0.76902	0.75064	0.76787	0.73579	0.77422	0.73528	0.76435	0.72405	0.76448
Couple	2	0.42424	0.48148	0.42424	0.48148	0.42424	0.48148	0.42424	0.48148	0.42424	0.48148	0.42424	0.48148	0.42424	0.48148	0.42424	0.48148
	3	0.5046	0.57505	0.5046	0.57523	0.5046	0.57523	0.5046	0.57523	0.63914	0.60493	0.5046	0.57523	0.5046	0.57523	0.5046	0.57523
	5	0.65832	0.69971	0.62697	0.69618	0.62697	0.69469	0.62697	0.69469	0.68041	0.71734	0.64438	0.69469	0.61397	0.69469	0.62153	0.69618
	8	0.83363	0.85812	0.74142	0.77094	0.73274	0.77094	0.756	0.77094	0.74062	0.76977	0.74641	0.77094	0.75415	0.77094	0.75271	0.77335
Cameraman	2	0.4337	0.54566	0.4337	0.54219	0.4337	0.54219	0.4337	0.54219	0.4337	0.54219	0.4337	0.54219	0.4337	0.54219	0.4337	0.54219
	3	0.52401	0.65435	0.48218	0.67089	0.48218	0.67089	0.48218	0.67089	0.58483	0.66203	0.48218	0.67177	0.48218	0.67089	0.48218	0.67089
	5	0.61409	0.72728	0.61366	0.7218	0.5838	0.72222	0.61256	0.72073	0.63054	0.72917	0.58382	0.72226	0.61194	0.72073	0.61261	0.7224
	8	0.67576	0.75398	0.6727	0.75446	0.66587	0.7536	0.66945	0.7536	0.66986	0.75109	0.6663	0.75356	0.67207	0.75146	0.72546	0.75374
Pepper	2	0.37259	0.52509	0.37259	0.52509	0.37259	0.52509	0.37259	0.52509	0.37259	0.52509	0.37259	0.52509	0.37259	0.52509	0.37259	0.52509
	3	0.47407	0.60368	0.4709	0.60368	0.4709	0.60368	0.4709	0.60368	0.54324	0.55867	0.4709	0.60368	0.4709	0.60368	0.4709	0.60368
	5	0.66539	0.73477	0.61695	0.72891	0.56822	0.7254	0.5663	0.7254	0.62583	0.67435	0.5894	0.7272	0.5894	0.7254	0.5894	0.72665
	8	0.76063	0.82785	0.76389	0.82146	0.6947	0.81031	0.74605	0.80994	0.69994	0.81331	0.69496	0.81627	0.69825	0.80977	0.69047	0.82057
Tree	2	0.49566	0.51668	0.49566	0.51024	0.49566	0.51024	0.49566	0.51024	0.49566	0.51024	0.49566	0.51024	0.49566	0.51024	0.49566	0.51024
	3	0.54613	0.63348	0.51989	0.62626	0.51989	0.62626	0.51989	0.62626	0.66417	0.70363	0.51989	0.62626	0.51989	0.62626	0.51989	0.62858
	5	0.67056	0.66774	0.64365	0.65768	0.62807	0.66891	0.64419	0.65534	0.65817	0.66971	0.63699	0.66891	0.64396	0.65534	0.6329	0.66488
	8	0.814	0.84406	0.79544	0.75482	0.73269	0.74323	0.74858	0.74279	0.73825	0.74241	0.75644	0.74248	0.79721	0.73817	0.75012	0.74028
Building	2	0.35267	0.573	0.35267	0.573	0.35267	0.573	0.35267	0.573	0.35267	0.573	0.35267	0.573	0.35267	0.573	0.35267	0.573
	3	0.47778	0.6141	0.4602	0.6141	0.4602	0.6141	0.4602	0.6141	0.46291	0.61332	0.4602	0.6141	0.4602	0.6141	0.4602	0.6141
	5	0.698	0.72373	0.68839	0.72254	0.59742	0.72254	0.59742	0.72254	0.68095	0.78525	0.59742	0.72254	0.59742	0.72254	0.62213	0.72254
	8	0.76008	0.91042	0.75812	0.89699	0.66833	0.88193	0.74163	0.88185	0.68433	0.88479	0.67421	0.87996	0.66962	0.88193	0.71373	0.88609

The bolded part is the algorithm that performs best in SSIM metrics at the threshold level (m = 2, 3, 5, 8).

,

Table 7. Comparison of FSIM computed with eight algorithms using the Otsu and Kapur methods with m of 2, 3, 5, and 8.

Image	m	MSWOA		WOA		PSO		SSA		GOA		MFO		MVO		DA
		Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur
Lena	2	0.66709	0.68502	0.66709	0.68355	0.66709	0.68355	0.66709	0.68355	0.66709	0.68355	0.66709	0.68355	0.66709	0.68355	0.66709	0.68355
	3	0.71461	0.75583	0.71461	0.75424	0.71461	0.75424	0.71461	0.75424	0.73591	0.74224	0.71461	0.75245	0.71461	0.75424	0.71461	0.75424
	5	0.80462	0.84361	0.80161	0.84327	0.8061	0.84327	0.8061	0.84327	0.8027	0.84442	0.81027	0.84135	0.8061	0.84327	0.8061	0.84135
	8	0.90754	0.90661	0.87568	0.88462	0.8802	0.89071	0.87403	0.89137	0.87887	0.89146	0.88062	0.8951	0.87778	0.89179	0.87737	0.88891
Baboon	2	0.688	0.73346	0.688	0.73346	0.688	0.73346	0.688	0.73346	0.688	0.73346	0.688	0.73346	0.688	0.73346	0.688	0.73346
	3	0.75093	0.79605	0.75005	0.79605	0.75005	0.79605	0.75005	0.79605	0.76046	0.79347	0.75005	0.79605	0.75005	0.79605	0.75005	0.79605
	5	0.81479	0.89807	0.8179	0.89676	0.80484	0.89663	0.80484	0.89663	0.82366	0.89796	0.80484	0.89676	0.80484	0.89663	0.80484	0.89676
	8	0.86657	0.97901	0.86399	0.97865	0.84049	0.97836	0.84382	0.97833	0.84615	0.97879	0.84562	0.97819	0.84386	0.97826	0.8932	0.97857
Starfish	2	0.55442	0.57051	0.55295	0.57051	0.55295	0.57051	0.55295	0.57051	0.55295	0.57051	0.55295	0.57051	0.55295	0.57051	0.55295	0.57051
	3	0.64086	0.66335	0.64086	0.66335	0.64086	0.66335	0.64086	0.66335	0.63624	0.66263	0.64228	0.66335	0.64086	0.66335	0.64022	0.66335
	5	0.77469	0.77491	0.76794	0.77584	0.76794	0.77618	0.76794	0.77618	0.76785	0.77394	0.76794	0.77584	0.76794	0.77618	0.76794	0.77644
	8	0.86523	0.86684	0.85618	0.85909	0.85164	0.86286	0.85582	0.86549	0.84919	0.8643	0.85235	0.86668	0.85164	0.86291	0.83965	0.86261
Couple	2	0.62621	0.64581	0.62621	0.64581	0.62621	0.64581	0.62621	0.64581	0.62621	0.64581	0.62621	0.64581	0.62621	0.64581	0.62621	0.64581
	3	0.69087	0.72318	0.69087	0.72336	0.69087	0.72336	0.69087	0.72336	0.68601	0.66714	0.69087	0.72336	0.69087	0.72336	0.69087	0.72336
	5	0.7896	0.81238	0.76813	0.81234	0.76813	0.8127	0.76813	0.8127	0.78228	0.77021	0.78754	0.8127	0.7604	0.8127	0.7648	0.81234
	8	0.8412	0.89005	0.84638	0.86496	0.84603	0.86496	0.83553	0.86496	0.84271	0.86409	0.84774	0.86496	0.83688	0.86496	0.83935	0.86422
Cameraman	2	0.62811	0.65634	0.62811	0.65467	0.62811	0.65467	0.62811	0.65467	0.62811	0.65467	0.62811	0.65467	0.62811	0.65467	0.62811	0.65467
	3	0.71029	0.78483	0.67558	0.79562	0.67558	0.79562	0.67558	0.79562	0.76263	0.79189	0.67558	0.79546	0.67558	0.79562	0.67558	0.79562
	5	0.79243	0.86897	0.79129	0.85491	0.7614	0.86627	0.78938	0.85596	0.80823	0.87304	0.75929	0.86623	0.78603	0.85596	0.78782	0.8592
	8	0.83747	0.90969	0.83611	0.91034	0.82432	0.9093	0.83093	0.9093	0.83006	0.90818	0.8259	0.90933	0.83586	0.90783	0.81813	0.90993
Pepper	2	0.61103	0.64532	0.61103	0.64532	0.61103	0.64532	0.61103	0.64532	0.61103	0.64532	0.61103	0.64532	0.61103	0.64532	0.61103	0.64532
	3	0.66632	0.7008	0.6662	0.7008	0.6662	0.7008	0.6662	0.7008	0.67632	0.68421	0.6662	0.7008	0.6662	0.7008	0.6662	0.7008
	5	0.77134	0.78993	0.75042	0.788	0.72792	0.78884	0.72539	0.78884	0.74203	0.76781	0.7357	0.78881	0.7357	0.78884	0.7357	0.78903
	8	0.81246	0.85776	0.80773	0.85752	0.79761	0.87135	0.82421	0.86303	0.79961	0.86398	0.7979	0.86285	0.79801	0.86332	0.79446	0.85741
Tree	2	0.6901	0.69492	0.6901	0.6925	0.6901	0.6925	0.6901	0.6925	0.6901	0.6925	0.6901	0.6925	0.6901	0.6925	0.6901	0.6925
	3	0.71442	0.7664	0.70264	0.7647	0.70264	0.7647	0.70264	0.7647	0.75091	0.78328	0.70264	0.7647	0.70264	0.7647	0.70264	0.76547
	5	0.79345	0.79837	0.77636	0.79379	0.77316	0.79648	0.77406	0.79364	0.7712	0.79678	0.77638	0.79648	0.77542	0.79364	0.77363	0.79743
	8	0.84685	0.86426	0.83214	0.85264	0.82945	0.84984	0.83514	0.84984	0.83549	0.8495	0.84328	0.84994	0.83332	0.84886	0.83778	0.84956
Building	2	0.62024	0.60693	0.62024	0.60693	0.62024	0.60693	0.62024	0.60693	0.62024	0.60693	0.62024	0.60693	0.62024	0.60693	0.62024	0.60693
	3	0.6793	0.65926	0.67837	0.65926	0.67837	0.65926	0.67837	0.65926	0.64477	0.64741	0.67837	0.65926	0.67837	0.65926	0.67837	0.65926
	5	0.74698	0.76923	0.73842	0.76816	0.73181	0.76816	0.73181	0.76816	0.76116	0.79763	0.73181	0.76816	0.73181	0.76816	0.77878	0.76816
	8	0.81805	0.90462	0.79738	0.90365	0.77242	0.90049	0.80183	0.90036	0.77753	0.9008	0.77692	0.90017	0.77327	0.90049	0.81865	0.90051

The bolded part is the algorithm that performs best in FSIM metrics at the threshold level (m = 2, 3, 5, 8).

and

Table 8. Comparison of CPU time computed with eight algorithms using the Otsu and Kapur methods with m of 2, 3, 5, and 8.

Image	m	MSWOA		WOA		PSO		SSA		GOA		MFO		MVO		DA
		Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur	Otsu	Kapur
Lena	2	1.751	2.528	1.673	2.492	1.273	1.851	1.833	2.311	8.245	9.094	1.383	1.961	1.583	2.059	15.753	15.838
	3	1.789	2.567	1.723	2.607	1.337	1.916	1.933	2.400	13.619	14.511	1.425	2.021	1.628	2.141	17.074	17.197
	5	1.891	2.678	1.857	2.692	1.439	2.025	1.969	2.489	18.832	20.081	1.536	2.115	1.714	2.267	17.594	20.126
	8	1.973	2.886	1.973	2.894	1.525	2.219	2.067	2.507	23.850	24.907	1.609	2.285	1.780	2.468	19.037	21.626
Baboon	2	1.747	2.577	1.724	2.497	1.291	1.870	1.871	2.289	8.305	9.162	1.368	1.975	1.546	2.105	14.499	14.509
	3	1.785	2.609	1.733	2.565	1.364	1.983	1.925	2.349	13.539	14.470	1.461	2.076	1.573	2.219	15.973	18.692
	5	1.847	2.681	1.832	2.654	1.416	2.058	1.980	2.481	18.541	19.824	1.545	2.129	1.707	2.308	17.627	19.636
	8	1.989	2.895	1.969	2.830	1.528	2.172	2.064	2.542	24.009	24.903	1.643	2.239	1.736	2.430	18.617	21.149
Starfish	2	2.048	2.840	2.076	2.851	1.723	2.183	2.124	2.637	8.579	9.631	1.653	2.306	1.802	2.402	13.983	14.644
	3	2.209	2.907	2.137	2.981	1.827	2.243	2.377	2.733	13.865	14.679	1.741	2.416	1.958	2.488	14.433	17.130
	5	2.251	3.119	2.165	3.055	1.844	2.327	2.361	2.808	19.008	19.975	1.884	2.537	2.093	2.659	16.493	19.225
	8	2.272	3.220	2.236	3.227	1.914	2.490	2.415	2.872	24.082	25.464	2.033	2.610	2.168	2.771	19.150	22.101
Couple	2	2.024	2.835	2.014	2.812	1.619	2.139	2.195	2.648	8.601	9.382	1.690	2.262	1.799	2.382	16.990	18.928
	3	2.132	2.919	2.028	2.888	1.696	2.275	2.218	2.725	13.762	14.850	1.738	2.347	1.921	2.452	17.766	19.570
	5	2.237	3.029	2.158	3.094	1.798	2.422	2.331	2.875	19.014	20.280	1.887	2.584	1.967	2.549	18.218	20.176
	8	2.289	3.229	2.333	3.262	1.853	2.534	2.383	3.033	24.019	25.234	1.985	2.614	2.054	2.687	19.394	21.061
Cameraman	2	1.686	2.586	1.648	2.511	1.241	1.859	1.819	2.282	8.268	9.020	1.378	1.951	1.457	2.090	16.552	17.429
	3	1.774	2.617	1.726	2.588	1.351	1.955	1.897	2.418	13.525	14.307	1.402	2.068	1.529	2.153	17.065	19.041
	5	1.870	2.709	1.782	2.676	1.396	2.032	1.966	2.496	18.532	19.806	1.485	2.143	1.599	2.313	17.675	20.150
	8	1.870	2.889	1.908	2.870	1.554	2.106	2.019	2.543	23.576	24.741	1.587	2.244	1.723	2.416	18.679	23.891
Pepper	2	1.870	2.484	1.639	2.516	1.296	1.843	1.835	2.281	8.357	9.110	1.357	1.984	1.449	2.074	12.879	14.165
	3	1.763	2.585	1.707	2.608	1.332	1.974	1.846	2.381	13.528	14.497	1.429	2.057	1.507	2.140	13.741	15.968
	5	1.834	2.684	1.761	2.689	1.439	2.009	1.900	2.402	18.417	19.695	1.515	2.162	1.634	2.304	16.078	17.843
	8	1.917	2.871	1.963	2.885	1.488	2.131	1.986	2.577	23.565	24.961	1.620	2.317	1.769	2.456	18.578	19.317
Tree	2	2.006	2.873	2.029	2.797	1.653	2.180	2.095	2.679	8.549	9.478	1.690	2.356	1.855	2.452	16.561	18.706
	3	2.172	2.948	2.105	2.908	1.778	2.387	2.184	2.778	13.838	14.803	1.739	2.446	1.998	2.537	17.565	19.387
	5	2.201	3.161	2.193	3.044	1.822	2.420	2.328	2.813	18.776	20.021	1.882	2.556	2.023	2.759	18.089	20.541
	8	2.242	3.239	2.271	3.255	1.924	2.522	2.536	2.922	24.152	25.566	1.933	2.639	2.207	2.819	19.121	22.506
Building	2	2.079	2.819	2.042	2.798	1.574	2.150	2.155	2.634	8.570	9.416	1.704	2.349	1.852	2.396	13.706	14.570
	3	2.124	2.937	2.088	2.898	1.696	2.293	2.234	2.739	13.731	14.719	1.848	2.349	1.908	2.495	15.166	17.454
	5	2.226	3.090	2.104	2.967	1.707	2.301	2.320	2.883	18.786	20.156	1.950	2.561	1.941	2.584	17.881	20.206
	8	2.357	3.253	2.247	3.208	1.835	2.433	2.474	2.935	24.118	25.250	2.013	2.634	2.163	2.725	18.916	21.613

The bolded part is the algorithm that performs best in CPU time metrics at the threshold level (m = 2, 3, 5, 8).

). In particular, the 10-threshold level, 15-threshold level, 20-threshold level, 25-threshold level, and 30-threshold level were also considered for the proposed algorithm (

Table 9. Quality metrics using MSWOA with m of 10, 15, 20, 25, and 30.

Image	m	MSWOA–Otsu				MSWOA–Kapur
		PSNR	SSIM	FSIM	CPU Time	PSNR	SSIM	FSIM	CPU Time
Lena	10	24.4184	0.82938	0.92279	2.087	29.2312	0.82569	0.93433	2.957
	15	26.4413	0.8489	0.92419	2.239	34.9205	0.89644	0.97552	3.250
	20	29.1939	0.90849	0.96019	2.348	37.3848	0.92921	0.98806	3.372
	25	29.4113	0.9203	0.96336	2.479	39.524	0.95595	0.99283	3.583
	30	30.0487	0.93176	0.966	2.646	40.8332	0.9651	0.9959	3.833
Baboon	10	21.4973	0.84181	0.8908	2.111	32.2484	0.93157	0.98597	2.984
	15	23.0685	0.88173	0.91105	2.193	35.7915	0.96434	0.99435	3.225
	20	24.1548	0.89982	0.9228	2.355	38.2818	0.97834	0.99687	3.429
	25	24.204	0.90305	0.9248	2.465	40.0448	0.98568	0.998	3.648
	30	25.6349	0.92119	0.93523	2.650	41.493	0.98992	0.99848	3.895
Starfish	10	27.3784	0.8874	0.89176	2.548	30.2351	0.88828	0.90864	3.464
	15	30.4003	0.9303	0.93793	2.705	34.3505	0.93709	0.95418	3.651
	20	32.2543	0.94946	0.95344	2.834	36.8757	0.96021	0.97281	3.902
	25	34.2589	0.95466	0.95788	2.908	39.0146	0.97414	0.98361	4.380
	30	35.2437	0.96846	0.96848	3.070	40.0975	0.97948	0.98779	4.806
Couple	10	27.5822	0.86965	0.87914	2.580	31.3583	0.90111	0.92346	3.430
	15	30.6577	0.91347	0.9203	2.681	35.1567	0.9371	0.95049	3.716
	20	33.0988	0.94778	0.94782	2.809	37.8	0.96125	0.97169	3.922
	25	33.8256	0.94957	0.95569	2.936	39.4134	0.97072	0.97952	4.147
	30	34.0727	0.9524	0.96171	3.037	41.2076	0.97959	0.98637	4.238
Cameraman	10	21.7303	0.76076	0.84978	2.070	30.3116	0.7792	0.93556	2.970
	15	24.872	0.81106	0.8802	2.218	31.6061	0.80175	0.95446	3.179
	20	25.0229	0.851	0.88759	2.295	32.5066	0.82242	0.96354	3.377
	25	25.289	0.89029	0.90829	2.426	38.0123	0.94764	0.97557	3.724
	30	26.6468	0.91999	0.92832	2.534	40.4888	0.96649	0.9856	3.818
Pepper	10	23.0539	0.79687	0.8315	2.048	31.0602	0.84417	0.88818	2.968
	15	24.5456	0.83395	0.87439	2.273	34.3132	0.90889	0.93283	3.156
	20	25.7144	0.89303	0.90093	2.290	37.2635	0.94199	0.96404	3.387
	25	26.5311	0.89389	0.90447	2.475	39.1598	0.96048	0.97767	3.600
	30	27.9315	0.93563	0.93786	2.560	40.7748	0.97119	0.98638	3.924
Tree	10	25.4787	0.84004	0.85797	2.576	28.1936	0.79808	0.87612	3.494
	15	27.6307	0.89688	0.90849	2.738	34.2033	0.90838	0.93295	3.752
	20	28.6342	0.89984	0.91491	2.824	37.0525	0.93887	0.95831	4.139
	25	31.0213	0.93606	0.94288	2.936	38.5149	0.9525	0.97065	4.439
	30	32.2795	0.94655	0.95309	3.025	40.0247	0.96254	0.97842	4.512
Building	10	21.4909	0.78388	0.81508	2.564	31.7135	0.91946	0.93261	3.562
	15	23.1007	0.81757	0.84871	2.699	35.7692	0.94988	0.96582	3.644
	20	24.509	0.84078	0.86457	2.826	37.7051	0.96485	0.97479	3.832
	25	25.5752	0.88356	0.8924	2.915	37.79	0.96457	0.98052	4.078
	30	26.2617	0.90559	0.90474	3.118	40.0328	0.9744	0.98708	4.268

The bolded part is the algorithm that performs best in quality metrics (PSNR, SSIM, FSIM, CPU time) at the threshold level (m = 10, 15, 20, 25, 30).

). Since this work focused on gray images, gray level L was 255, that is, the value range of each pixel was $[0,255]$. Therefore, for the m-level optimization problem, the search space was ${[0,255]}^m$.

In order to compare the image segmentation effect, we compared the MSWOA, and the WOA, PSO, the SSA, the GOA, MFO, MVO, and the DA to prove the effectiveness of the proposed algorithm in image segmentation. The parameter settings of each algorithm are shown in Table 2. The population size of all algorithms was 30, and the maximum iteration number was 800. The experimental environment was the same as that in Section 4.

5.3. Segmented Image Quality Metrics

In order to evaluate the segmentation effect of the eight algorithms, the commonly used peak signal-to-noise ratio (PSNR ), structural similarity (SSIM), feature similarity (FSIM), and CPU time were selected as the evaluation criteria of the quality of image segmentation [16]. As a common image evaluation standard in image segmentation, PSNR is used to compare the signal-to-noise ratio between the original image and the segmented image and is calculated using the following equation:

$$PSNR=20lo{g}_{10}\left(\frac{255}{\sqrt{MSE}}\right),$$

(21)

where MSE is the mean square error, which is defined as follows:

$$MSE=\frac{1}{MN}{\displaystyle \sum _{I=1}^M}{\displaystyle \sum _{j=1}^N}{[I(i,j)-\tilde{I}(i,j)]}^2,$$

(22)

where M and N are the sizes of image I, I is the original image, and I is the segmented image.

SSIM is a metric used to measure the similarity between two images [52]. Assuming that there are image x and image y, the structural similarity of the two images can be calculated using the following equation:

$$SSIM(x,y)=\frac{(2{\mu }_x{\mu }_y+c_1)(2{\sigma }_{xy}+c_2)}{({\displaystyle {\mu }_x^2}+{\displaystyle {\mu }_y^2}+c_1)({\displaystyle {\sigma }_x^2}+{\displaystyle {\sigma }_y^2}+c_2)},$$

(23)

where ${\mu }_x$ is the average value of image x, ${\mu }_y$ is the average value of image y, ${\displaystyle {\sigma }_x^2}$ is the variance of image x, ${\displaystyle {\sigma }_y^2}$ is the variance of image y, ${\sigma }_{xy}$ is the covariance of image x and image y, and $c_1$ and $c_2$ are used to maintain a stable constant in order to avoid the case where the denominator is 0. The value range of SSIM is $[0,1]$, and the larger the value is, the more similar the structures of the two images are. When two images are the same, the value of SSIM is equal to 1.

FSIM is a variant of SSIM whose principle is that all pixels in an image are not of the same importance. Some special pixels, such as those on the edge of objects, are more important in defining the structure of objects than those of other background areas. Therefore, more weight should be given to these pixels in calculation to highlight the important features of an image. The definition of FSIM is shown as follows [53]:

$$FSIM=\frac{{\sum }_{x\in \omega }{S}_L\left(x\right)P{C}_m\left(x\right)}{{\sum }_{x\in \omega }P{C}_m\left(x\right)},$$

(24)

where $\omega$ represents the entire image and $S_L\left(x\right)$ indicates the similarity between the segmented image and the original image.

5.4. Experimental Results and Analysis

5.4.1. Analysis of Otsu and Kapur Methods

According to the PSNR, SSIM, and FSIM results with m = 2, 3, 5, and 8 (as shown in Table 5, Table 6 and Table 7), the method based on Kapur entropy could obtain better data values under the same number of thresholds, and image segmentation quality and accuracy increased, showing a better segmentation effect. Figure 6 shows bar charts for Baboon with MSWOA–Otsu and MSWOA–Kapur with m = 2, 3, 5, and 8. It is obvious that the values of the Otsu-based method were smaller than those of the Kapur entropy-based method. Figure 7 and Figure 8 show the segmentation effects of MSWOA-Otsu and MSWOA-Kapur with m = 2, 3, 5 and 8, respectively. And the segmentation effect in Figure 7 is clearer than that in Figure 8. In terms of CPU time, as shown in Table 8, Kapur took a little longer than Otsu, that is to say, the Otsu-based method took less time, but the difference between them was not significant, and the value was in the same order of magnitude. The segmentation results of MSWOA–Otsu and MSWOA–Kapur with m = 10, 15, 20, 25, and 30 are given in Table 9, which further shows that the segmentation effect of Kapur was still better in high dimensions (with more thresholds), and the numerical difference was significant. Figure 9 shows line charts of PSNR, SSIM, FSIM, and CPU time for Lena with MSWOA–Otsu and MSWOA–Kapur with m = 10, 15, 20, 25, and 30. Generally speaking, for the same optimization algorithm, the method based on Kapur entropy was significantly better than the Otsu-based method in the given segmentation image and the same number of thresholds, m.

5.4.2. Analysis of MSWOA and Other Seven Optimization Algorithms

With the Kapur entropy-based method, when the number of thresholds was small (e.g., m = 2 and 3), the segmentation results of each algorithm were almost the same. When the number of thresholds was large (e.g., m = 5 and 8), the numerical difference in the segmentation results was obvious. By comparing the results of eight optimization algorithms based on the Kapur entropy-based method in Table 5, Table 6, Table 7 and Table 8, it is not difficult to find that the segmentation results of the MSWOA were the best among all algorithms except for individual singular values. Figure 10, Figure 11, Figure 12 and Figure 13 show images segmented with different segmentation methods. In terms of program time consumption (CPU time), except for the GOA and the DA, the time consumption of the other six optimization algorithms was not significantly different, all of which were on the same data level. The reason is that although the solution time of intelligent optimization algorithms increases with the increase in solution space, it is not a positive-proportion (or exponential) growth. Therefore, compared with the traditional exhaustive method, the multilevel thresholding segmentation method based on an intelligent optimization algorithm is much faster, especially in the case of high dimensions (many thresholds). In terms of PSNR, SSIM, and FSIM, their overall numerical trend is also consistent, and the value based on the MSWOA shows the majority of advantages. For the Otsu-based method, the conclusion is similar to that of the Kapur entropy-based method. Generally speaking, the segmentation effect of the MSWOA was the best among the eight algorithms, whether using the Otsu or Kapur method.

5.4.3. Statistical Analysis with Wilcoxon Rank Sum Test

Wilcoxon rank sum test [18] is a kind of nonparametric test. In this paper, it was used to test whether there was a significant difference in the overall distribution of sequence data obtained with two groups of different algorithms at the 5% significance level. The null hypothesis indicated that there was no significant difference among the algorithms, while the alternative hypothesis indicated significant difference among the algorithms. In this work, the MSWOA proposed in this paper was compared with other seven algorithms in terms of the PSNR value of segmented images. The objective functions were Otsu and Kapur. Each algorithm ran 100 times for each of the cases, with m = 5 and 8, and the experimental results are shown in

Table 10. Wilcoxon rank sum test results based on multilevel thresholding methods using the Otsu method.

Image	m	MSWOA vs.
		WOA		PSO		SSA		GOA		MFO		MVO		DA
		p	h	p	h	p	h	p	h	p	h	p	h	p	h
Lena	5	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	>0.05${}^{\#}$	0	>0.05${}^{\#}$	0	>0.05${}^{\#}$	0	<0.05${}^{+}$	0	>0.05${}^{\#}$	0	>0.05${}^{\#}$	0	<0.05${}^{+}$	1
Baboon	5	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	>0.05${}^{\#}$	0
Starfish	5	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	>0.05${}^{\#}$	0	<0.05${}^{+}$	1
	8	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	>0.05${}^{\#}$	0
Couple	5	<0.05${}^{+}$	1	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
Cameraman	5	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
Pepper	5	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
Tree	5	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
Building	5	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1

‘+’ indicates that the MSWOA performed better than the other algorithms. ‘#’ indicates that MSWOA performance was similar to or worse than that of the other algorithms.

and

Table 11. Wilcoxon rank sum test results based on multilevel thresholding methods using Kapur entropy.

Image	m	MSWOA vs.
		WOA		PSO		SSA		GOA		MFO		MVO		DA
		p	h	p	h	p	h	p	h	p	h	p	h	p	h
Lena	5	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
Baboon	5	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
Starfish	5	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
Couple	5	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
Cameraman	5	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
Pepper	5	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	>0.05${}^{\#}$	0
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
Tree	5	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	>0.05${}^{\#}$	0	>0.05${}^{\#}$	0
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
Building	5	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1
	8	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	<0.05${}^{+}$	1	>0.05${}^{\#}$	0	<0.05${}^{+}$	1	<0.05${}^{+}$	1

‘+’ indicates that the MSWOA performed better than the other algorithms. ‘#’ indicates that MSWOA performance was similar to or worse than that of the other algorithms.

. Among them, a p-value less than 0.05 (or h = 1) means that the null hypothesis could be rejected at the 5% significance level, indicating that there were obvious differences between algorithms; on the contrary, a p-value greater than 0.05 (or h = 0) indicates that the null hypothesis was accepted, that is to say, there was no obvious difference among the algorithms. Superscript ’+’ indicates a significant difference at the level of p-value < 0.05, which means that the MSWOA performed better than the other algorithms, while ’#’ indicates that MSWOA performance was similar to or worse than that of the other algorithms. As can be seen from Table 10 (Otsu-based), the numbers of instances of p-value<0.05 (or h = 1) were 12 (MSWOA vs. WOA), 13 (MSWOA vs. PSO), 14 (MSWOA vs. SSA), 13 (MSWOA vs. GOA), 13 (MSWOA vs. MFO), 14 (MSWOA vs. MVO), and 14 (MSWOA vs. DA), respectively. Similarly, in Table 11 (Kapur-based), the numbers of instances of p-value < 0.05 (or h = 1) were 13 (MSWOA vs. WOA), 16 (MSWOA vs. PSO), 15 (MSWOA vs. SSA), 14 (MSWOA vs. GOA), 14 (MSWOA vs. MFO), 14 (MSWOA vs. MVO), and 14 (MSWOA vs. DA). The results show that there were significant differences between the MSWOA and the other seven algorithms. Therefore, in most cases, the multilevel thresholding segmentation effect of the MSWOA was better than that of the other seven algorithms.

Based on all the above analysis, we can consider that the MSWOA–Kapur multilevel thresholding image segmentation method proposed in this paper can quickly and accurately find the best thresholds of the image and is better than other algorithms compared in the paper in terms of segmentation effect and statistical analysis.

6. Conclusions and Future Work

To address the issues of extensive calculation and time consumption in multilevel thresholding image segmentation, a new intelligent optimization algorithm called WOA is introduced, which has the advantages of simple structure, few parameters, and fast solving speed. It can effectively handle the high-dimensional space optimization problem, yet it also has some drawbacks, such as easily falling into the local optimum. Firstly, the MSWOA was designed by improving the basic WOA in terms of initialization, nonlinear convergence factor, and adaptive weight, especially proposing a new initialization strategy named k-point. Using 13 benchmark functions, the effectiveness of the MSWOA was proved. Then, the MSWOA was applied to the multilevel thresholding segmentation of gray images. We chose the Otsu method and Kapur entropy as the objective functions and selected PSO, the SSA, the GOA, MFO, MVO, and the DA as the comparative algorithms to perform a series of experiments. According to PSNR, SSIM, FSIM, CPU time, and other evaluation criteria, and statistical analysis (Wilcoxon rank sum test), we believe that the MSWOA–Kapur multilevel thresholding image segmentation proposed in this paper is a better method that can effectively reduce the amount of calculation, improve the operation efficiency, and obtain relatively good thresholds. In general, the main work of this paper is to propose the MSWOA and prove its effectiveness and advantages from the two aspects of algorithm performance and multilevel thresholding image segmentation.

This paper is based on histogram gray image segmentation; as a further study, we will try to improve the histogram, take some spatial properties (e.g., energy curve) [53,54] into consideration to improve the quality of image segmentation, and apply it to color image segmentation. Meanwhile, we are going to apply more intelligent optimization algorithms (e.g., Seagull Optimization Algorithm (SOA)) [55] and segmentation methods (e.g., Tsalli entropy and Reny entropy) to multilevel thresholding image segmentation.