Multi-Objective Optimization for EE-SE Tradeoff in Space-Air-Ground Internet of Things Networks

Abstract

The Internet of Things (IoT) has become increasingly popular, and its communication requirements have grown beyond what traditional ground networks can handle. The space–air–ground (SAG) integrated network has been proposed as a potential solution, where unmanned aerial vehicles (UAVs) collect data from IoT devices and transmit them to satellites. However, the limited energy of UAVs is one of the key factors restricting communication performance, so it is necessary to consider communication energy efficiency (EE). In addition, the improvement of EE will bring about the decline of spectral efficiency (SE). Therefore we consider the tradeoff between EE and SE. Considering a SAG-IoT network, the focus of the paper is to optimize sub-channel selection, power control, and UAV position deployment to maximize EE and SE of the network, which is a multi-objective optimization (MOO) problem. On this premise, we try to improve the data throughput between IoT devices and UAVs. To solve this MOO problem, we use the $ϵ$-constraint to convert it into a single-objective optimization problem. We then employ various optimization algorithms such as the Dinkelbach algorithm, successive convex approximation algorithm, Lagrange dual algorithm, and block coordinate descent algorithm to solve the mixed integer non-convex problem. Simulation results show that the proposed algorithm converges to at least one sub-optimal solution.

1. Introduction

1.1. Problem Statement

In recent years, the Internet of Things (IoT) has received widespread attention because of its ability to enhance communication between people and things, and between things and things, which can help improve the quality of life and promote economic development [1]. At present, the Internet of Things has been applied in many fields such as industry, medical care, agriculture, and transportation, and the density of the physical objects connected to the IoT network increases significantly [2]. According to research by Markus Rothmuller and Sam Barker, IoT devices will continue to soar, with the total number of devices expected to reach 83 billion by 2024, more than doubling from 35 billion in 2020 [3]. With the significant rise in the number of access devices and growing demand for communication capabilities, traditional ground-based communication methods are becoming insufficient, necessitating the expansion of communication infrastructure to include space-based communication. The space–air–ground integrated network (SAGIN), which builds upon the existing ground-based network and is supplemented and extended by the air-based network and the space-based network, has received extensive attention. SAGIN boasts wide coverage, high throughput, and flexible deployment, making it an ideal solution for meeting the demands of smart connections across large areas and providing global seamless access. Its ultimate aim is to provide uninterrupted and consistent information services to people all over the world. At present, many organizations have started research on SAGIN, such as SpaceX [4]. The SAGIN network offers extensive coverage and high communication capacity through its use of satellites, enabling it to provide services to remote areas such as deserts and rural regions. The air segment network complements satellite communications, enhancing the overall quality of communication services. Meanwhile, the densely deployed ground segment system can support high data rate access [5]. Therefore, relying on SAGIN, the connectivity, capacity, and energy efficiency of IoT networks can be significantly improved.

With the rapid development of unmanned aerial vehicle (UAV) technology, UAVs are playing an increasingly important role in communication. Due to their high mobility, high line-of-sight (LoS) probability, flexible deployment, and low cost, UAVs have become the main information carrier of the SAGIN air segment network and have been extensively studied [6,7]. Since UAVs have limited energy, their duration has been a key constraint on communication performance [8]. Therefore, we consider improving the throughput of the system at the same energy consumption, that is, the energy efficiency (EE). However, while considering the energy efficiency of the system, we should also focus on the spectral efficiency (SE) of the system. Due to the large distance between the UAV and the satellite, the communication link requires a substantial allocation of bandwidth for data transmission, which occupies a considerable amount of limited spectrum resources. Thus, it is essential to comprehensively consider both SE and EE of the system for a compromise optimization approach.

This paper focuses on the SAG-IoT network, and solves the problem of balancing the EE and SE of the system by optimizing the transmission power of UAVs and IoT devices, sub-channel selection, and UAV position deployment.

1.2. Related Works

At present, many experts and scholars have carried out research on resource optimization in SAG-IoT network. Wang et al. [9] proposed a resource allocation strategy for UAV networks within the context of a space–air–ground heterogeneous communication system. They investigated a two-stage joint hovering height and power control scheme to maximize system throughput. The feasible deployment scheme of UAV was given by Lagrangian dual decomposition and concave–convex process method. The authors in [10] studied the computation task scheduling problem in the SAGIN and designed a reinforcement learning algorithm based on deep deterministic policy gradient. By jointly optimizing task scheduling and UAVs trajectories, the algorithm minimizes task processing delays. A space–air–ground remote Internet of Things (SAG-IoRT) framework in which UAVs acted as relay stations was proposed in [11]. The joint optimization problem of smart device connection scheduling, power control, and UAV trajectory was solved to maximize system capacity by variable substitution, continuous convex optimization, and block coordinate descent algorithms.

In addition to improving system throughput, system energy consumption has also attracted more and more attention, and improving energy efficiency has gradually become a research hotspot. An Internet of Things system with limited airborne energy was studied in [12]. The study considered the probability of the line-of-sight channel and planned the trajectory of a UAV to optimize the transmission scheduling between ground equipment and the UAV. Ouamri et al. proposed a double deep Q-network-based RA framework, which can improve energy efficiency while ensuring a certain throughput in UAV-assisted terrestrial networks in [13]. And Liu et al. proposed a novel multi-UAV-assisted multi-access MEC model, which can effectively reduce the energy consumption of users and UAVs in [14]. They jointly optimized the bit allocation, transmit power, CPU frequency, bandwidth allocation and UAVs’ trajectories to minimize the weighted sum energy consumption of UAVs and users. Ma et al. [15] proposed a layered SAG-IoRT network design, which maximized data capacity at the IoT-UAV layer, and considered data collection and energy consumption at the UAV-satellite layer. A approach based on block coordinate descent (BCD) algorithm was used to optimize bandwidth allocation, UAV power, trajectory, and satellite selection to solve the two-level optimization problem.

The distance between UAVs and satellites is very large, so a large amount of bandwidth needs to be allocated to communication links for data transmission, which occupies a significant portion of limited spectrum resources. With the goal of maximizing the spectral efficiency of the system, Shi et al. [16] focused on cross-layer data transmission in SAGIN. The joint optimization of gateway selection, resource allocation, and UAV deployment was achieved using Dinkelbach, simulated annealing, and successive convex approximation (SCA) methods. In fact, improving the spectral efficiency of the system could potentially reduce the energy efficiency of the system. Thus, it is essential to comprehensively consider both SE and EE of the system for a compromise optimization approach [17].

At present, most of the existing papers related to the space–air–ground network only consider optimizing one aspect of performance, but there are also a few papers that focus on multi-objective optimization. For example. Cui et al. [18] provided a multi-objective optimization framework for SAG networks, and provided simple examples with total throughput and total latency as objective functions. A series of future research challenges were identified and a potential solution was emphasized in the paper. The authors focused on the tradeoff between energy efficiency and spectral efficiency in [19]. However, their model was intelligent reflecting-surface-assisted cognitive radio networks with non-orthogonal multiple access. In addition, most papers consider the channel between UAVs and IoT devices as a line of sight channel. However, due to obstacles such as buildings, it is highly likely that there is a non-line-of-sight connection between UAVs and IoT devices [20], so non line of sight channels will be considered. In this paper, we consider probabilistic LoS channels, with energy efficiency and spectral efficiency as objective functions. We compare our work with several related works, as shown in

Table 1. Comparison between this paper and related works.

Reference	Model	Objective	Variables	Method
T. Ma et al. [15]	Multiple users, UAVs and satellites; line of sight channels	Penalty function constructed from throughput and energy consumption	Bandwidth allocation; UAV trajectory; UAV power; indicator variable about UAV and satellite	BCD algorithm; SCA algorithm
Y. Shi et al. [16]	Multiple users, UAVs, one or more satellites; probabilistic LoS channel	Spectral efficiency	gateway selection; bandwidth allocation; UAV deployment	Dinkelbach method; simulated annealing algorithm; SCA algorithm
J. Cui et al. [18]	3D integrated SAG networks with multiple vertical layers	Data rate; latency; reliability; energy efficiency and so on	Only a framework was provided without specific explanation	NSGA-II; no specific steps provided
Y. Wu et al. [19]	IRS-assisted CRNs with NOMA; perfect and imperfect CSI	Energy efficiency; spectral efficiency	the phase shift matrix of IRS; beamforming vector	BCD algorithm; $ϵ$-constraint method; $\mathcal{S}$-procedure method; introduce auxiliary variables
This paper	Multiple users, UAVs, one satellite probabilistic LoS channel	Energy efficiency; spectral efficiency	IoT device power; UAV power; sub-channel selection; UAV deployment	BCD algorithm; SCA algorithm; Dinkelbach method; $ϵ$-constraint method; introduce slack variables

.

1.3. Main Contribution

Combining the above content, this paper focuses on the SAG-IoT network architecture, considering the multi-objective optimization problem of energy efficiency and spectrum efficiency of the system. Analyzing the uplink, UAVs collect data from IoT devices on the ground and transmit them to the satellite. The main contributions of this paper are as follows:

• This paper formulates a multi-objective optimization (MOO) problem problem for SAG-IoT network, which maximizes the energy efficiency and spectrum efficiency of the system by optimizing the power of IoT devices, sub-channel selection, UAV power and UAV position deployment.
• We take into account non-line-of-sight (NLOS) channels between UAVs and IoT devices, which deviates from the common practice in most articles that only consider line-of-sight channels. This approach is more aligned with real-world scenarios, where obstacles such as buildings and trees can obstruct the direct path between the transmitter and receiver in wireless communication, although it makes UAV position deploymen sub-problem more complex. We solve this sub-problem by introducing relaxation variables and SCA algorithm.
• With the help of the $ϵ$-constraint method, we transform the multi-objective problem into a single-objective optimization (SOO) problem. Then we decompose the complex single-objective optimization problem into three sub-problems. The matching algorithm is used to solve the sub-channel selection sub-problem, Dinkelbach algorithm, SCA algorithm, and Lagrange dual algorithm are used to solve the power optimization sub-problem, and the UAV position deployment sub-problem is solved by introducing relaxation variables and SCA algorithm. Finally, the solution of the original problem is obtained by solving the three sub-problems alternately.
• Simulation results show the proposed algorithm converges to at least one sub-optimal solution, and the influence of each variable on the result is simulated.

The rest of the paper is organized as follows: Section 2 introduces the system model and formulates the problem of maximizing the EE and SE of the system. Section 3 presents the solution to the proposed problem and gives a detailed derivation process. Section 4 conducts numerical simulation, gives the simulation results, and analyzes them. Section 5 summarizes this paper, and gives the shortcomings and future research directions.

2. System Model and Problem Formulation

In this paper, we consider a three-tier space–air–ground network as shown in Figure 1. We assume there are I IoT devices on the ground, denoted by $\mathcal{I}$ = {1, 2, …, I}, and a satellite with an orbital altitude of $h_s$ provides the full coverage to all these devices. In our setup, U UAVs, denoted by $\mathcal{U}$ = {1, 2, …, U}, are deployed to collect data from IoT devices and transmit them to the satellite. The Cartesian coordinate system is introduced, so the coordinate of IoT device i is denoted by $(x_i^{\mathrm{I}},y_i^{\mathrm{I}},0)$. The coordinates of UAV u are denoted by $(x_u^{\mathrm{U}},y_u^{\mathrm{U}},h_{\mathrm{U}})$, where $h_{\mathrm{U}}$ is the fixed flight altitude. In order to support communication with a large number of IoT devices at the same time, OFDMA is adopted, which has the advantages of flexible bandwidth and power allocation over users [21]. We assume that the total bandwidth available to IoT devices is equally divided into I resource blocks, and each IoT device is allocated a resource block. Meanwhile, we assume that each UAV can only communicate with K IoT devices simultaneously. This means each channel between UAVs and IoT devices is divided into K sub-channels and there is no interference between different sub-channels. Assume the sub-channel bandwidth between each UAV and IoT devices is B and there is no interference between different channels. For convenience of discussion, let $I=UK$. Similarly, it is assumed that the channel bandwidth between each UAV and the satellite is W, and there is no interference between different channels.

2.1. IoT-UAV Data Gathering

Considering there may be occlusion between UAVs and devices, according to [22,23], the average path-loss between IoT device i and UAV u can be expressed as

$$L_{iu}=20lg\left(\frac{4\pi f_{\mathrm{c}}{d}_{iu}}{v}\right)+P_{iu}{\eta }_{\mathrm{LOS}}+(1-P_{iu}){\eta }_{\mathrm{NLOS}},$$

(1)

where $f_{\mathrm{c}}$ (Hz) is the carrier frequency, v (m/s) is the velocity of light in a vacuum, ${\eta }_{\mathrm{LOS}}$ and ${\eta }_{\mathrm{NLOS}}$ (dB) are the average additive losses caused by the free space path-loss for LOS and NLOS links, respectively, $d_{iu}=\sqrt{{(x_u^{\mathrm{U}}-x_i^{\mathrm{I}})}^2+{(y_u^{\mathrm{U}}-y_i^{\mathrm{I}})}^2+h_{\mathrm{U}}^2}$ is the distance between IoT device i and UAV u, and $P_{iu}$ is the LOS probability, which can be expressed as

$$P_{iu}=\frac{1}{1+\varphi e^{-\phi ({\theta }_{iu}-\varphi )}},$$

(2)

where $\varphi$ and $\phi$ are constants greater than zero determined by the environment. ${\theta }_{iu}$ is the elevation angle between IoT device i and UAV u. It can be seen that the probability of the line-of-sight link is closely related to the elevation angle. The higher the elevation angle, the greater the probability of line-of-sight link, and the greater the channel gain. The expression for elevation angle ${\theta }_{iu}$ is

$${\theta }_{iu}=arctan\left(\frac{h_{\mathrm{U}}}{\sqrt{{(x_u^U-x_i^I)}^2+{(y_u^U-y_i^I)}^2}}\right).$$

(3)

Therefore, the channel gain $g_{iu}$ between IoT device i and UAV u can be expressed as

$$g_{iu}={10}^{\frac{-L_{iu}}{10}}.$$

(4)

Suppose that an IoT device can only communicate with one UAV at the same time. The rate at which IoT device i transmits data to UAV u can be expressed as

$$r_{iu}=a_{iu}B{log}_2\left(1+\frac{p_i{g}_{iu}}{B{N}_0}\right),$$

(5)

where $p_i$ is the transmit power of IoT device i. $N_0$ is the additive white Gaussian noise (AWGN) power spectral density at the UAV receiver. $a_{iu}$ is 0, 1 binary variable. $a_{iu}=1$ indicates that there is communication between device i and UAV u, and $a_{iu}=0$ is the opposite.

2.2. UAV–Satellite Data Transmission

Because there are few obstacles between UAVs and the satellite, the propagation loss follows the free space loss model. Taking antenna pattern into account, the radio propagation loss between UAVs and the satellite can be expressed as

$$L_{us}=\frac{v\sqrt{G_{tx}{G}_{rx}}}{4\pi f_{\mathrm{c}}{d}_{us}},$$

(6)

where $G_{tx}$ and $G_{rx}$ are the antenna gain of UAV and satellite, respectively. $d_{us}$ is the distance between UAV u and the satellite, which is approximately equal to satellite orbital height $h_{\mathrm{S}}$. So the gain between UAVs and the satellite can be expressed as

$$g_{us}=L_{us}^2.$$

(7)

Similarly, the data transmission rate between UAV u and the satellite can be expressed as

$$r_{us}=W{log}_2\left(1+\frac{p_u{g}_{us}}{W{N}_1}\right),$$

(8)

where $N_1$ is the noise power spectral density and $p_u$ is the transmit power of UAV u.

2.3. Problem Formulation

Firstly, we provide expressions for energy efficiency and spectral efficiency, and construct the objective function for the optimization problem. Energy efficiency ${\eta }_{\mathrm{EE}}$ is the ratio of effective information transmission rate to power. Since the data rate of the system depends on the communication rate between UAVs and the satellite, the EE can be expressesd as

$${\eta }_{\mathrm{EE}}=\frac{{\sum }_u{r}_{us}}{{\sum }_i{p}_i+{\sum }_u{p}_u+U{p}_{\mathrm{h}}},$$

(9)

where $p_{\mathrm{h}}$ is the power required for each UAV to maintain levitation.

The spectrum efficiency ${\eta }_{\mathrm{SE}}$ is defined as the information rate divided by the bandwidth of the communication channel, which can be expressed as

$${\eta }_{\mathrm{SE}}=\frac{{\sum }_u{r}_{us}}{U(W+BK)}=\frac{{\sum }_{u}W{log}_2\left(1+\frac{p_u{g}_{us}}{W{N}_1}\right)}{U(W+BK)}.$$

(10)

For notational convenience, the horizontal and vertical coordinates of IoT device i and UAV u are denoted as ${\mathbf{d}}_i^{\mathrm{I}}=(x_i^{\mathrm{I}},y_i^{\mathrm{I}})$ and ${\mathbf{d}}_u^{\mathrm{U}}=(x_u^{\mathrm{U}},y_u^{\mathrm{U}})$. Letting $\mathbf{D}=\left\{{\mathbf{d}}_u^{\mathrm{U}}\right\}$, $\mathbf{A}=\left\{a_{iu}\right\}$, ${\mathbf{P}}_I=\left\{p_i\right\}$ and ${\mathbf{P}}_U=\left\{p_u\right\}$, the problem can be described as

$$\begin{array}{cc}\hfill {\mathcal{P}}_1:& \underset{\mathbf{A},{\mathbf{P}}_I,{\mathbf{P}}_U,\mathbf{D}}{max}{\eta }_{\mathrm{EE}},{\eta }_{\mathrm{SE}}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& C1:a_{iu}\in \{0,1\},\forall i,u,\hfill \\ \hfill & C2:\sum _i{a}_{iu}=K,\forall u,\hfill \\ \hfill & C3:\sum _u{a}_{iu}\le 1,\forall i,\hfill \\ \hfill & C4:0\le p_i\le p_{\mathrm{imax}},\forall i,\hfill \\ \hfill & C5:0\le p_u\le p_{\mathrm{umax}},\forall u,\hfill \\ \hfill & C6:r_{iu}\ge r_{\min },\forall i,\hfill \\ \hfill & C7:\sum _i{r}_{iu}\ge r_{us},\forall u,\hfill \\ \hfill & C8:\left|\right|{\mathbf{d}}_m^{\mathrm{U}}-{\mathbf{d}}_n^{\mathrm{U}}{\left|\right|}^2\ge d_{\min },\forall m,n\in \mathcal{U},m\ne n,\hfill \end{array}$$

(11)

where $r_{\min }$ represents the minimum rate requirement for IoT devices to transmit data. $p_{\mathrm{imax}}$ and $p_{\mathrm{umax}}$ represent the maximum transmitting power of IoT devices and UAVs respectively. $d_{\min }$ represents the minimum distance between two UAVs.

In problem ${\mathcal{P}}_1$, constraint $C1$ stipulates that $a_{iu}$ is a binary variable. $a=1$ means there is communication between the UAV and the IoT device, otherwise $a=0$. Constraints $C2$ and $C3$ limit the number of communication devices. They ensure that each UAV can communicate with K IoT devices and each IoT device can communicate with at most one UAV respectively. Constraints $C4$ and $C5$ indicate that the transmission power of IoT devices and UAVs cannot exceed the specified maximum transmission power. Constraint $C6$ guarantees the rate at which each IoT device transmits data is greater than the minimum rate required to meet the requirements of service quality. Constraint $C7$ means the rate at which the IoT device transmits data to the UAV is greater than the rate at which the UAV transmits data to the satellite. Furthermore, constraint $C8$ guarantees that there is adequate safety distance between two UAVs. This ensures that any UAVs will not collide with each other.

3. Problem Solution

Problem ${\mathcal{P}}_1$ has two objective functions, including energy efficiency and spectral efficiency. According to [24], because the two objective functions conflict with each other, the MOO problem is hard to solve. The authors in [25] introduced a multi-objective optimization framework for optimizing URLLC design in the presence of decoding complexity constraints. They solved the proposed multi-objective optimization problem through two scalarization methods. The purpose of scalarization is to transform the objective into a single objective function and simplify the problem into a constrained single objective optimization problem. We apply this method to the SAG-IoT network, using the $ϵ$-constraint method to convert multi-objective optimization functions into single objective optimization functions. We retained energy efficiency as the objective function, transformed spectral efficiency into constraint conditions. Therefore, we obtain a single objective optimization problem, which can be described as

$$\begin{array}{cc}\hfill {\mathcal{P}}_2:& \underset{\mathbf{A},{\mathbf{P}}_I,{\mathbf{P}}_U,\mathbf{D}}{max}\frac{{\sum }_u{r}_{us}}{{\sum }_i{p}_i+{\sum }_u{p}_u+U{p}_{\mathrm{h}}}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& C1:a_{iu}\in \{0,1\},\forall i,u,\hfill \\ \hfill & C2:\sum _i{a}_{iu}=K,\forall u,\hfill \\ \hfill & C3:\sum _u{a}_{iu}\le 1,\forall i,\hfill \\ \hfill & C4:0\le p_i\le p_{\mathrm{imax}},\forall i,\hfill \\ \hfill & C5:0\le p_u\le p_{\mathrm{umax}},\forall u,\hfill \\ \hfill & C6:r_{iu}\ge r_{\min },\forall i,\hfill \\ \hfill & C7:\sum _i{r}_{iu}\ge r_{us},\forall u,\hfill \\ \hfill & C8:\left|\right|{\mathbf{d}}_m^{\mathrm{U}}-{\mathbf{d}}_n^{\mathrm{U}}\left|\right|\ge d_{\min },\forall m,n\in \mathcal{U},m\ne n,\hfill \\ \hfill & C9:\frac{{\sum }_{u}W{log}_2\left(1+\frac{p_u{g}_{us}}{W{N}_1}\right)}{U(W+BK)}\ge ϵ,\hfill \end{array}$$

(12)

where $ϵ$ represents the coefficient of trade off between SE and EE.

Although converted into a SOO problem, the problem is still difficult to solve because of the non-convex function in fractional form containing integer variables. To solve problem ${\mathcal{P}}_2$, we can divide the problem into three sub-problems.

3.1. Sub-Problem 1: Sub-Channel Selection

First, we consider the establishment of communication between IoT devices and UAVs. Appropriate sub-channels need to be selected, so the first sub-problem is called sub-channel selection, which is related to the integer variable $\mathbf{A}$. We fix the variable $\mathbf{D}$, ${\mathbf{P}}_I$, and ${\mathbf{P}}_U$, the problem can be described as

$$\begin{array}{cc}\hfill {\mathcal{SP}}_1:& \underset{\mathbf{A}}{max}\frac{{\sum }_u{r}_{us}}{{\sum }_i{p}_i+{\sum }_u{p}_u+U{p}_{\mathrm{h}}}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& C1,C2,C3,C6,C7.\hfill \end{array}$$

(13)

Observing ${\mathcal{SP}}_1$, we can see that the value of the objective function is fixed for any $\mathbf{A}$ that meets the constraint conditions. Therefore, when meeting the constraints, we consider optimizing the throughput of the IoT devices, which can be described as

$$\begin{array}{cc}\hfill {\mathcal{SP}}_2:& \underset{\mathbf{A}}{max}\sum _i{r}_{iu}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& C1,C2,C3,C6,C7.\hfill \end{array}$$

(14)

Due to the presence of integer variables, the problem is complex to solve. A matching algorithm is used to solve ${\mathcal{SP}}_2$, as shown in Algorithm 1. IoT devices and UAVs construct preference lists based on descending communication rate between IoT devices and UAVs, respectively. Taking the selection of the UAV sub-channel by IoT device $I_1$ as an example. Assume the preference list of $I_1$ is $\{r_{12},r_{13},\dots \}$, where $r_{12}$ means the communication rate between IoT device $I_1$ and UAV $U_2$. $I_1$ first selects $U_2$ and calculates the number of devices $N_2$ that have communicated with $U_2$. If $N_2$ is less than K, the match is successful. Otherwise, look at the preference list of $U_2$, and assume the list is $\{r_{12},r_{32},r_{22},r_{42},\dots \}$. Based on the preference list of $U_2$, compare the lowest priority of the K devices $I_2$ that already match $U_2$ to $I_1$. If $I_1$ has a higher priority, match $I_1$ with $U_2$. Meanwhile, delete $U_2$ from the preference list of $I_2$ and rematch $I_2$. If $I_1$ has a lower priority, delete $U_2$ from the preference list of $I_1$ and rematch $I_1$. If there is communication between UAV u and IoT device i, $a_{iu}=1$, otherwise $a_{iu}=0$. According to the matching algorithm, we can obtain $\mathbf{A}$.

Algorithm 1 A matching algorithm for solving subchannel selection.

1: Input: Power allocation ${\mathbf{P}}_I$ and ${\mathbf{P}}_U$, UAVs positon $\mathbf{D}$. 2: Let the set of IoT devices to be matched be $\mathcal{I}$ and the set of devices that have been matched UAV u be ${\mathcal{U}}_u$. 3: Initial all $a_{iu}$ to be zero. 4: Calculate $r_{iu}$. Construct preference lists of IoT devices $P{L}_i$ and UAVs $P{L}_u$. 5: while$\mathcal{I}\ne \varnothing$do 6:    for IoT device i⊆$\mathcal{I}$ do 7:      if $P{L}_i\ne \varnothing$ then 8:         Select the most preferred UAV $u\in P{L}_i$. 9:         Count the number of devices that have been matched to UAV u, denoted as $N_u$. 10:         if $N_u=K$ then 11:           Select the worst matched IoT $i^{\prime }$ in ${\mathcal{U}}_u$. 12:           if i has a higher priority than $i^{\prime }$ in $P{L}_u$ then 13:              Replace $i^{\prime }$ with i in ${\mathcal{U}}_u$ and $\mathcal{I}$, then delete u from $P{L}_{i^{\prime }}$. 14:              Swap $a_{i^{\prime }u}$ and $a_{iu}$. 15:           else 16:              Delete u from $P{L}_i$. 17:           end if 18:         else 19:           Add i into ${\mathcal{U}}_u$, and delete i from $\mathcal{I}$. 20:           $a_{iu}=1$, $N_u=N_u+1$. 21:         end if 22:      end if 23:    end for 24: end while 25: Output: Subchannel selection $\mathbf{A}$.

3.2. Sub-Problem 2: Power Allocation

The second sub-problem is power allocation, including transmit power of IoT devices and UAVs. For the given $\mathbf{D}$ and $\mathbf{A}$, power allocation sub-problem can be described as

$$\begin{array}{cc}\hfill {\mathcal{SP}}_3:& \underset{{\mathbf{P}}_I,{\mathbf{P}}_U}{max}\frac{{\sum }_u{r}_{us}}{{\sum }_i{p}_i+{\sum }_u{p}_u+U{p}_{\mathrm{h}}}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& C4,C5,C6,C7,C9.\hfill \end{array}$$

(15)

This is a non-convex problem because objective function and constraint $C7$ are non-convex. For $C7$, $r_{us}$ is a concave function of $p_u$, so we can obtain its upper bounder at $p_u^0$ through first-order Taylor expansion

$$r_{us}\le Wlo{g}_2\left(1+\frac{p_u^0{g}_{us}}{W{N}_1}\right)+\frac{N_{1}W}{\left(N_{1}W+p_u^0\right)ln2}\left(p_u-p_u^0\right).$$

(16)

Denote the upper bounder as ${\overline{r}}_{us}$, which is linear respect to $p_u$. Constraint $C7$ can be described as

$$C{7}^{\prime }:\sum _i{r}_{iu}\ge {\overline{r}}_{us},\forall u,$$

(17)

which is convex. For the objective function, which is in fractional form, Dinkelbach algorithm is adopted. Introduce a non-negative parameter $\lambda$, which is

$$\lambda =\frac{{\sum }_u{r}_{us}}{{\sum }_i{p}_i+{\sum }_u{p}_u+U{p}_{\mathrm{h}}}.$$

(18)

The objective function can be transformed into a parametric subtractive form as

$$\begin{array}{cc}\hfill F\left(\lambda \right)& =\underset{{\mathbf{P}}_I,{\mathbf{P}}_U}{max}\sum _u{r}_{us}-\lambda (\sum _i{p}_i+\sum _u{p}_u+U{p}_{\mathrm{h}})\hfill \\ \hfill & =\underset{{\mathbf{P}}_I,{\mathbf{P}}_U}{max}R-\lambda P,\hfill \end{array}$$

(19)

which is continuous and strictly monotonic decreasing in $\lambda$ and has an unique root. Denote ${\lambda }^{*}$ is the the root of $F\left(\lambda \right)$, which can be derived using the Dinkelbach method. Substituting (19) for the objective function of ${\mathcal{SP}}_3$, the optimal solution set of the problem is the same as that of ${\mathcal{SP}}_3$ with $\lambda ={\lambda }^{*}$.

According to the above derivation, the transformed sub-problem can be obtained as

$$\begin{array}{cc}\hfill {\mathcal{SP}}_4:& \underset{{\mathbf{P}}_I,{\mathbf{P}}_U}{max}R-\lambda P\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& C4,C5,C6,C{7}^{\prime },C9.\hfill \end{array}$$

(20)

Containing two variables, problem ${\mathcal{SP}}_4$ can be solved by Lagrange dual algorithm because it is a convex problem. The Lagrange function of (20) can be described as

$$\begin{array}{cc}\hfill & \mathcal{L}({\mathbf{P}}_I,{\mathbf{P}}_U,\mathbf{\mu },\mathbf{\upsilon },\mathbf{\omega },\mathbf{\epsilon },\mathbf{\tau })\hfill \\ \hfill & =R-\lambda P+\sum _i{\mu }_i\left(p_{\mathrm{imax}}-p_i\right)\hfill \\ \hfill & +\sum _u{\upsilon }_u\left(p_{\mathrm{umax}}-p_u\right)\hfill \\ \hfill & +\sum _u{\omega }_u\left(r_{us}-r_{\min }\right)\hfill \\ \hfill & +\sum _u{\epsilon }_u\left(\sum _i{r}_{iu}-{\overline{r}}_{us}\right)\hfill \\ \hfill & +\tau \left(\frac{{\sum }_{u}W{log}_2\left(1+\frac{p_u{g}_{us}}{W{N}_1}\right)}{U(W+BK)}-ϵ\right),\hfill \end{array}$$

(21)

where $\mathbf{\mu },\mathbf{\upsilon },\mathbf{\omega },\mathbf{\epsilon },\mathbf{\tau }$ are Lagrangian multipliers related to the constraints.

The Lagrangian dual expression is

$$\begin{array}{cc}\hfill & \mathcal{G}(\mathbf{\mu },\mathbf{\upsilon },\mathbf{\omega },\mathbf{\epsilon },\mathbf{\tau })\hfill \\ \hfill & =\underset{{\mathbf{P}}_I,{\mathbf{P}}_U}{sup}\mathcal{L}({\mathbf{P}}_I,{\mathbf{P}}_U,\mathbf{\mu },\mathbf{\upsilon },\mathbf{\omega },\mathbf{\epsilon },\mathbf{\tau }).\hfill \end{array}$$

(22)

Therefore, the Lagrangian dual problem can be described as

$$\begin{array}{cc}\hfill {\mathcal{SP}}_5:& \underset{(\mathbf{\mu },\mathbf{\upsilon },\mathbf{\omega },\mathbf{\epsilon },\mathbf{\tau })}{min}\mathcal{G}(\mathbf{\mu },\mathbf{\upsilon },\mathbf{\omega },\mathbf{\epsilon },\mathbf{\tau })\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \mathbf{\mu },\mathbf{\upsilon },\mathbf{\omega },\mathbf{\epsilon },\mathbf{\tau }⪰0.\hfill \end{array}$$

(23)

Next, we derive the optimal solution with given $\mathbf{\mu }$, $\mathbf{\upsilon }$, $\mathbf{\omega }$, $\mathbf{\epsilon }$, $\mathbf{\tau }$. Due to $C4$, the optimal solution $p_i^{*}$ should satisfy the condition

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\left.\frac{\partial \mathcal{L}}{\partial p_i}\right|}_{p_i=0}<0,p_i^{*}=0,\hfill \\ {\left.\frac{\partial \mathcal{L}}{\partial p_i}\right|}_{p_i=p_i^{*}}=0,p_i^{*}>0.\hfill \end{array}\right.\end{array}$$

(24)

Similarly, the optimal solution $p_u^{*}$ should satisfy the condition

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\left.\frac{\partial \mathcal{L}}{\partial p_u}\right|}_{p_u=0}<0,p_u^{*}=0,\hfill \\ {\left.\frac{\partial \mathcal{L}}{\partial p_u}\right|}_{p_u=p_u^{*}}=0,p_u^{*}>0.\hfill \end{array}\right.\end{array}$$

(25)

Because the Lagrangian dual function in (20) may be non-differentiable, the subgradient method is used to update the Lagrangian multipliers. We can update the Lagrangian multipliers $\mathbf{\mu }$, $\mathbf{\upsilon }$, $\mathbf{\omega }$, $\mathbf{\epsilon }$, $\mathbf{\tau }$ as follows

$$\begin{array}{c}\hfill {\mu }_i^{n+1}={\left[{\mu }_i^n-{\gamma }_1^n\left(p_{\mathrm{imax}}-p_i\right)\right]}^{+},\end{array}$$

(26)

$$\begin{array}{c}\hfill {\upsilon }_u^{n+1}={\left[{\upsilon }_u^n-{\gamma }_2^n\left(p_{\mathrm{umax}}-p_u\right)\right]}^{+},\end{array}$$

(27)

$$\begin{array}{c}\hfill {\omega }_u^{n+1}={\left[{\omega }_u^n-{\gamma }_3^n\left(r_{us}-r_{\min }\right)\right]}^{+},\end{array}$$

(28)

$$\begin{array}{c}\hfill {\epsilon }_u^{n+1}={\left[{\epsilon }_u^n-{\gamma }_4^n\left(\sum _i{r}_{iu}-{\overline{r}}_{us}\right)\right]}^{+},\end{array}$$

(29)

$$\begin{array}{c}\hfill {\tau }^{n+1}={\left[{\tau }^n-{\gamma }_5^n\left(\frac{{\sum }_{u}W{log}_2\left(1+\frac{p_u{g}_{us}}{W{N}_1}\right)}{U(W+BK)}-ϵ\right)\right]}^{+},\end{array}$$

(30)

where n is the iterative index, $\gamma$ is the step length, and ${[·]}^{+}=max\{0,·\}$.

We adopt the adaptive step size shown below

$$\begin{array}{c}\hfill {\gamma }_i^n=\frac{1}{\sqrt{n}},i=1,2,3,4,5.\end{array}$$

(31)

In summary, Algorithm 2 gives the solution process of the power allocation sub-problem.

Algorithm 2 Dinkelbach algorithm based on Lagrangian duality.

1: Input: Subchannel selection $\mathbf{A}$, UAVs positon $\mathbf{D}$, tradeoff coefficient $ϵ$, and the maximum number of iterations N. 2: Initialize Lagrangian multipliers $\mathbf{\mu }$, $\mathbf{\upsilon }$, $\mathbf{\omega }$, $\mathbf{\epsilon }$, $\mathbf{\tau }$, variable $\lambda$, and tolerance ${\Delta }_1$, ${\Delta }_2$. 3: while$|F\left({\lambda }_k\right)|>{\Delta }_1$ and $k\le N$ do 4:    while $|{\Phi }^n|>{\Delta }_2$ and $n\le N$ do 5:      Use (24) and (25) to obtain the optimal power ${\mathbf{P}}_I^{n+1}$ and ${\mathbf{P}}_U^{n+1}$. 6:      Use (26)∼(31) to obtain update multipliers ${\mathbf{\mu }}^{n+1}$, ${\mathbf{\upsilon }}^{n+1}$, ${\mathbf{\omega }}^{n+1}$, ${\mathbf{\epsilon }}^{n+1}$, ${\mathbf{\tau }}^{n+1}$. 7:      Calculate the difference ${\Phi }^n=\frac{\parallel {\mathbf{\mu }}^{n+1}-{\mathbf{\mu }}^n\parallel }{\parallel {\mathbf{\mu }}^n\parallel }-\frac{\parallel {\mathbf{\upsilon }}^{n+1}-{\mathbf{\upsilon }}^n\parallel }{\parallel {\mathbf{\upsilon }}^n\parallel }-\frac{\parallel {\mathbf{\omega }}^{n+1}-{\mathbf{\omega }}^n\parallel }{\parallel {\mathbf{\omega }}^n\parallel }-\frac{\parallel {\mathbf{\epsilon }}^{n+1}-{\mathbf{\epsilon }}^n\parallel }{\parallel {\mathbf{\epsilon }}^n\parallel }-\frac{\parallel {\mathbf{\tau }}^{n+1}-{\mathbf{\tau }}^n\parallel }{\parallel {\mathbf{\tau }}^n\parallel }$. 8:      $n=n+1$. 9:    end while 10:    ${\lambda }_{k+1}\leftarrow \frac{R}{P}$ with ${\mathbf{P}}_I^k$ and ${\mathbf{P}}_U^k$. 11:    $k=k+1$. 12: end while 13: Onput: Power allocation ${\mathbf{P}}_I$ and ${\mathbf{P}}_U$.

3.3. Sub-Problem 3: UAV Position Deployment

After solving the sub-channel selection and power control, we need to consider the UAV position deployment sub-problem. According to sub-problems 1 and 2, we have $\mathbf{A}$, ${\mathbf{P}}_I$, and ${\mathbf{P}}_U$. On this basis, the objective function of ${\mathcal{P}}_2$ has been fixed. Like sub-problem 1, we consider maximizing the device transmission rate, so the UAV position deployment sub-problem can be described as

$$\begin{array}{cc}\hfill {\mathcal{SP}}_6:& \underset{\mathbf{D}}{max}\sum _i{r}_{iu}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& C6,C7,C8.\hfill \end{array}$$

(32)

Obviously, ${\mathcal{SP}}_6$ is a non-convex problem. In order to solve this problem, we introduce a new variable $\Theta =\left\{{\theta }_{iu}\right\}$. ${\mathcal{SP}}_6$ can be redescribed as

$$\begin{array}{cc}\hfill {\mathcal{SP}}_7:& \underset{\mathbf{D},\Theta }{max}\sum _i{r}_{iu}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& C6,C7,C8,\hfill \\ \hfill & C10:{\theta }_{iu}=arctan\left(\frac{h_{\mathrm{U}}}{\parallel {\mathbf{d}}_u^{\mathrm{U}}-{\mathbf{d}}_i^{\mathrm{I}}\parallel }\right),\forall i,u.\hfill \end{array}$$

(33)

Then, to address the non-affine constraint $C9$ [26], we can relax the problem into

$$\begin{array}{cc}\hfill {\mathcal{SP}}_8:& \underset{\mathbf{D},\Theta }{max}\sum _i{r}_{iu}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& C6,C7,C8,\hfill \\ \hfill & C{10}^{\prime }:{\theta }_{iu}\le arctan\left(\frac{h_{\mathrm{U}}}{\parallel {\mathbf{d}}_u^{\mathrm{U}}-{\mathbf{d}}_i^{\mathrm{I}}\parallel }\right),\forall i,u,\hfill \end{array}$$

(34)

where $C6$, $C7$, $C8$, $C{9}^{\prime }$ and objective function are non-convex.

Using SCA algorithm for constraint $C8$, the lower bounder of ${\parallel {\mathbf{d}}_m^{\mathrm{U}}-{\mathbf{d}}_n^{\mathrm{U}}\parallel }^2$ at ${\mathbf{d}}_m^{\mathrm{U}0}$ and ${\mathbf{d}}_n^{\mathrm{U}0}$ can be expressed as

$$\begin{array}{cc}\hfill \parallel {\mathbf{d}}_m^{\mathrm{U}}-{\mathbf{d}}_n^{\mathrm{U}}{\parallel }^2& \ge -\parallel {\mathbf{d}}_m^{\mathrm{U}0}-{\mathbf{d}}_n^{\mathrm{U}0}{\parallel }^2\hfill \\ \hfill & +2{\left({\mathbf{d}}_m^{\mathrm{U}0}-{\mathbf{d}}_n^{\mathrm{U}0}\right)}^T\left({\mathbf{d}}_m^{\mathrm{U}}-{\mathbf{d}}_n^{\mathrm{U}}\right).\hfill \end{array}$$

(35)

In addition, it is also necessary to convert non-convex constraints $C6$, $C7$ and objective function into convex constraints. Denote $\sqrt{\parallel {\mathbf{d}}_u^{\mathrm{U}}-{\mathbf{d}}_i^{\mathrm{I}}{\parallel }^2+h_{\mathrm{U}}^2}$ as x and $(1+\varphi e^{-\phi ({\theta }_{iu}-\varphi )})$ as y. We can konw that $C6$ and $C7$ are convex for variables x and y, as shown below.

Proof. 

Obviously, both x and y are greater than 0. Under normal circumstances, ${\eta }_{\mathrm{NLOS}}$ is much larger than ${\eta }_{\mathrm{LOS}}$. Therefore, $g_{iu}$ can be expressed as

$$\begin{array}{cc}\hfill g_{iu}& ={10}^{-2log\left(\frac{4\pi f_c{d}_{iu}}{v}\right)+\frac{P_{iu}\left({\eta }_{\mathrm{NLOS}}-{\eta }_{\mathrm{LOS}}\right)}{10}-\frac{{\eta }_{\mathrm{NLOS}}}{10}}\hfill \\ \hfill & =A_1\frac{A_2}{x^2}{10}^{\frac{A_3}{y}},\hfill \end{array}$$

(36)

where $A_1$, $A_2$, and $A_3$ are constants greater than 0.

Therefore, $r_{iu}$ can be expressed as

$$\begin{array}{cc}\hfill r_{iu}& =a_{iu}B{log}_2\left(1+\frac{p_i{g}_{iu}}{B{N}_0}\right)\hfill \\ \hfill & =a_{iu}B{log}_2\left(1+\frac{p_i{A}_1\frac{A_2}{x^2}{10}^{\frac{A_3}{y}}}{B{N}_0}\right)\hfill \\ \hfill & =a_{iu}B{log}_2\left(1+\frac{C_1}{x^2}{10}^{\frac{C_2}{y}}\right),\hfill \end{array}$$

(37)

where $C_1$ and $C_2$ are constants greater than 0.

Then, calculate the Hessian matrix $\mathbf{H}$ of data transmission rate $r_{iu}$

$$\mathbf{H}=\left[\begin{array}{cc}\frac{{\partial }^2{r}_{iu}}{\partial x^2}& \frac{{\partial }^2{r}_{iu}}{\partial x\partial y}\\ \frac{{\partial }^2{r}_{iu}}{\partial y\partial x}& \frac{{\partial }^2{r}_{iu}}{\partial y^2}\end{array}\right]$$

(38)

For any $\mathbf{t}={[t_1,t_2]}^T$, the following formula can be obtained

$$\begin{array}{cc}\hfill {\mathbf{t}}^T\mathbf{H}\mathbf{t}& =\frac{a_{iu}B}{x^4{y}^{4}ln2\left(C_1{10}^{\frac{C_2}{y}}+x^2\right)}\hfill \\ \hfill & \times \left[\left(2C_1^2{10}^{\frac{2C_2}{y}}{y}^4+6C_1{10}^{\frac{C_2}{y}}{x}^2{y}^4\right)t_1^2\right.\hfill \\ \hfill & +\left(C_1{C}_2^2{10}^{\frac{C_2}{y}}{ln}^{2}10x^4+2C_1^2{C}_2{10}^{\frac{2C_2}{y}}ln10x^{2}y\right.\hfill \\ \hfill & \left.+2C_1{C}_2{10}^{\frac{C_2}{y}}ln10x^{4}y\right)t_2^2\hfill \\ \hfill & \left.+4C_1{C}_2{10}^{\frac{C_2}{y}}{ln}^{2}10x^3{y}^2{t}_1{t}_2\right]\hfill \\ \hfill & \ge \frac{a_{iu}B}{x^4{y}^{4}ln2\left(C_1{10}^{\frac{C_2}{y}}+x^2\right)}\hfill \\ \hfill & ·\left[\left(2C_1^2{10}^{\frac{2C_2}{y}}{y}^4+2C_1{10}^{\frac{C_2}{y}}{x}^2{y}^4\right)t_1^2\right.\hfill \\ \hfill & +\left(2C_1^2{C}_2{10}^{\frac{2C_2}{y}}ln10x^{2}y+2C_1{C}_2{10}^{\frac{C_2}{y}}ln10x^{4}y\right)t_2^2\hfill \\ \hfill & \left.+{\left(2\sqrt{C_1{10}^{\frac{C_2}{y}}}x{y}^2{t}_1+\sqrt{C_1{10}^{\frac{C_2}{y}}}{C}_{2}ln10x^2{t}_2\right)}^2\right]\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

(39)

According to (39), $r_{iu}$ is a convex function of x, y. □

Therefore, according to the Taylor expansion, $r_{iu}$ at point $x^0$, $y^0$ can be lower-bounded by

$$\begin{array}{cc}\hfill r_{iu}& \ge r_{iu}(x^0,y^0)+\Psi (x^0,y^0)(x-x^0)+\Omega (x^0,y^0)(y-y^0)\hfill \\ \hfill & =r_{iu}\left({\mathbf{d}}_u^{\mathrm{U}0},{\theta }_{iu}^0\right)+\Psi \left({\mathbf{d}}_u^{\mathrm{U}0},{\theta }_{iu}^0\right)\hfill \\ \hfill & \times \left(\varphi e^{-\phi ({\theta }_{iu}-\varphi )}-\varphi e^{-\phi ({\theta }_{iu}^0-\varphi )}\right)+\Omega \left({\mathbf{d}}_u^{\mathrm{U}0},{\theta }_{iu}^0\right)\hfill \\ \hfill & \times \left(\sqrt{\parallel {\mathbf{d}}_u^{\mathrm{U}}-{\mathbf{d}}_i^{\mathrm{I}}{\parallel }^2+h_{\mathrm{U}}^2}-\sqrt{\parallel {\mathbf{d}}_u^{\mathrm{U}0}-{\mathbf{d}}_i^{\mathrm{I}}{\parallel }^2+h_{\mathrm{U}}^2}\right)\hfill \\ \hfill & ={\overline{r}}_{iu},\forall i,u,\hfill \end{array}$$

(40)

where $\Psi$ and $\Omega$ are the partial derivatives of $r_{iu}$ against x and y, respectively, which can be expressed as

$$\Psi =\frac{\partial r_{iu}}{\partial x}=-\frac{2a_{iu}B{C}_1{10}^{\frac{C_2}{y}}}{xln2(C_1{10}^{\frac{C_2}{y}}+x^2)},$$

(41)

$$\Omega =\frac{\partial r_{iu}}{\partial y}=-\frac{a_{iu}B{C}_1{C}_2{10}^{\frac{C_2}{y}}ln10}{y^{2}ln2(C_1{10}^{\frac{C_2}{y}}+x^2)}.$$

(42)

For the non-convex constraints $C{9}^{\prime }$, we can know it is a convex function of $\parallel {\mathbf{d}}_u-{\mathbf{d}}_i\parallel$. Therefore, ${\theta }_{i}u$ at point ${\mathbf{d}}_u^0$ can be lower-bounded by

$$\begin{array}{cc}\hfill {\theta }_{iu}& \ge arctan\left(\frac{h_{\mathrm{U}}}{\parallel {\mathbf{d}}_u^{\mathrm{U}0}-{\mathbf{d}}_i^{\mathrm{I}}\parallel }\right)\hfill \\ \hfill & +\Phi \left({\mathbf{d}}_u^{\mathrm{U}0}\right)\left(\parallel {\mathbf{d}}_u^{\mathrm{U}}-{\mathbf{d}}_i^{\mathrm{I}}\parallel -\parallel {\mathbf{d}}_u^{\mathrm{U}0}-{\mathbf{d}}_i^{\mathrm{I}}\parallel \right)\hfill \\ \hfill & ={\overline{\theta }}_{iu},\forall i,u,\hfill \end{array}$$

(43)

where

$$\Phi =\frac{\partial {\theta }_{iu}}{\partial \parallel {\mathbf{d}}_u^{\mathrm{U}}-{\mathbf{d}}_i^{\mathrm{I}}\parallel }=-\frac{h_{\mathrm{U}}}{\parallel {\mathbf{d}}_u^{\mathrm{U}}-{\mathbf{d}}_i^{\mathrm{I}}{\parallel }^2+h_{\mathrm{U}}^2}.$$

(44)

According to (35), (40), and (43), the problem can be described as

$$\begin{array}{cc}\hfill {\mathcal{SP}}_9:& \underset{\mathbf{D},\Theta }{max}\sum _i{\overline{r}}_{iu}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& C{6}^{\prime }:{\overline{r}}_{iu}\ge r_{\min },\forall i,\hfill \\ \hfill & C{7}^{\prime \prime }:\sum _i{\overline{r}}_{iu}\ge r_{us},\forall u,\hfill \\ \hfill & C{8}^{\prime }:-{\parallel {\mathbf{d}}_m^{\mathrm{U}0}-{\mathbf{d}}_n^{\mathrm{U}0}\parallel }^2+2{\left({\mathbf{d}}_m^{\mathrm{U}0}-{\mathbf{d}}_n^{\mathrm{U}0}\right)}^T\left({\mathbf{d}}_m^{\mathrm{U}}-{\mathbf{d}}_n^{\mathrm{U}}\right)\hfill \\ \hfill & \ge d_{\min },\forall m,n\in \mathcal{U},m\ne n,\hfill \\ \hfill & C{10}^{\prime \prime }:{\theta }_{iu}\le {\overline{\theta }}_{iu},\forall i,u,\hfill \end{array}$$

(45)

which is a convex optimization problem.

So far, we have obtained the solutions of the three sub-problems. On this basis, we jointly optimize the sub-channel selection, power allocation, and UAV position deployment through the BCD process. First, for a given suitable ${\mathbf{D}}^0$, ${\mathbf{P}}_I^0$, and ${\mathbf{P}}_U^0$, solve sub-problem 1 to obtain ${\mathbf{A}}^1$. Then, according to the obtained ${\mathbf{A}}^1$ and fixed ${\mathbf{D}}^0$, solve sub-problem 2 to obtain ${\mathbf{P}}_I^1$ and ${\mathbf{P}}_U^1$, and then solve sub-problem 3 to obtain ${\mathbf{D}}^1$. According to ${\mathbf{D}}^1$, ${\mathbf{P}}_I^1$, and ${\mathbf{P}}_U^1$, solve sub-problem 1 to obtain the new ${\mathbf{A}}^2$. Alternately solve the three sub-problems like this until the error tolerance is met.

4. Results

In this section, numerical results are given to demonstrate the performance of our proposed algorithm. We assume IoT devices are randomly distributed in a square area of 1 km × 1 km. Assume that the minimum transmission rate requirement of the IoT device is 15 kbps, and the maximum transmission power is 0.1 W. UAVs collect data from IoT devices and transmit them to the low-orbit satellite, which orbital height is 500 km. The antenna array element of UAV is generally considered to be omni-directional, so $G_{tx}=1$, and the antenna gain of the satellite is assumed to be 15 dbi. The minimum safety distance between UAVs is assumed to be 50 m. Bandwidth between each UAV and IoT devices and between each UAV and the satellite are both 1 MHz, and carrier frequency is 5 GHz. Assume the noise power spectral density is −169 dBm/Hz. The values of variables $(\varphi ,\phi ,{\eta }_{\mathrm{LOS}},{\eta }_{\mathrm{NLOS}})$ related to the environment are $(4.88,0.43,0.1,21)$.

First, we verify the convergence of the proposed algorithm. Assuming there are two UAVs, $U=2$, and the number of sub-channels is 4, so there are eight IoT devices, $I=8$. The flight altitude of UAVs is 100 m, and the maximum transmission power is 8 W. Figure 2 illustrates how spectral efficiency (SE) varies with the number of iterations for different values of $ϵ$. As seen in the Figure 2, SE converges as the number of iterations increases. When $ϵ=0.35$, the system achieves maximum energy efficiency (EE), and the SE is greater than 0.35. However, when $ϵ=0.40$ and $ϵ=0.45$, the system’s SE is limited to 0.40 and 0.45, respectively, since the system has to sacrifice some of its energy efficiency to achieve the desired SE.

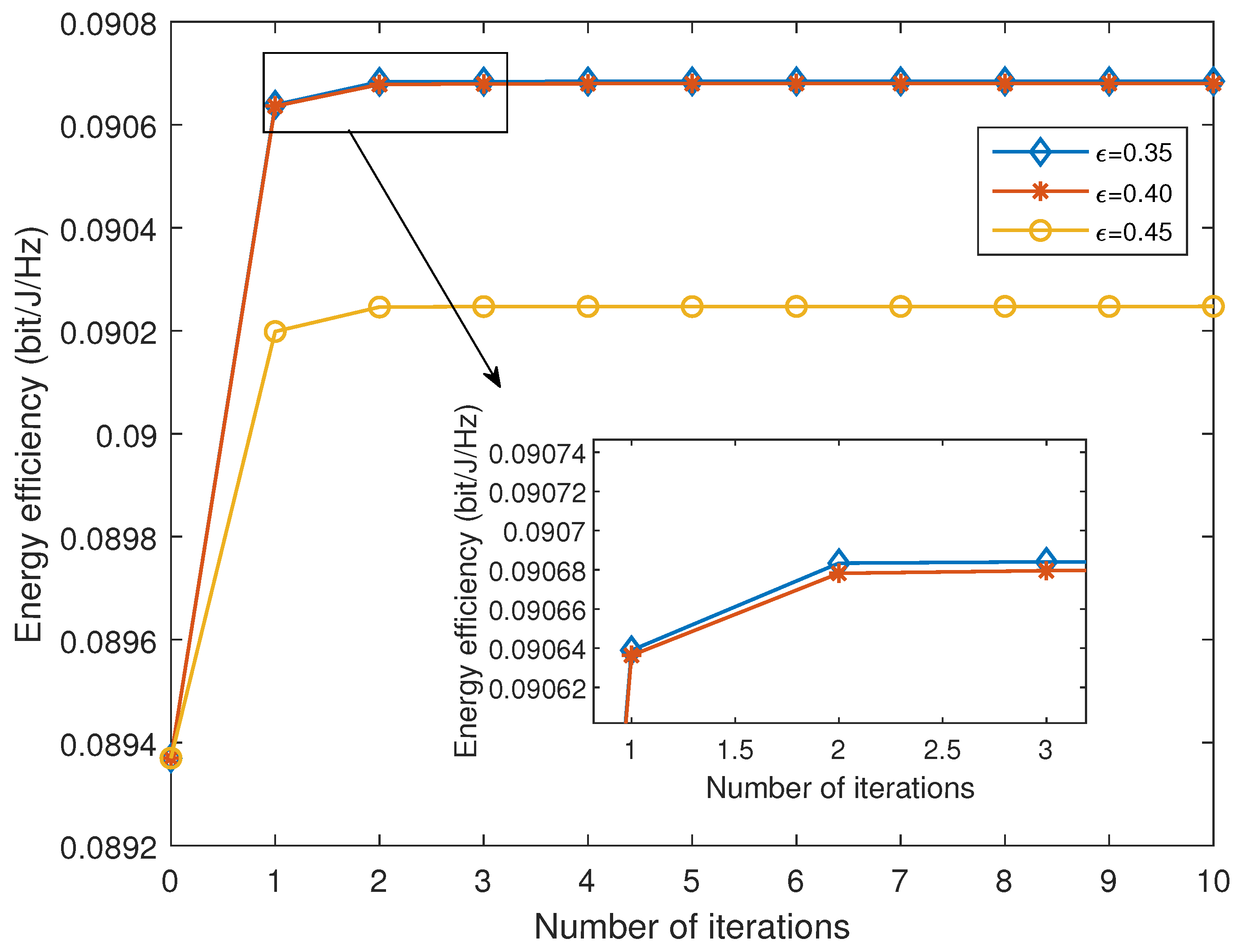
Figure 3 displays the variation of energy efficiency with the number of iterations for different $ϵ$, which shows that EE reaches a stable value as the number of iterations increases, indicating convergence. Moreover, Figure 3 demonstrates that different values of $ϵ$ affect the tradeoff between energy efficiency and spectral efficiency. Specifically, increasing SE may lead to a decrease in EE. The curves for $ϵ=0.35$ and $ϵ=0.40$ in the plot are very similar, suggesting that when $ϵ=0.35$, the system achieves the maximum EE while maintaining an SE greater than 0.35.

Considering the large system bandwidth, although the EE gap is small, it has a greater impact on the total amount of transmitted data in the system. The spectral efficiency is the same. The total transmission rate between IoT devices and UAVs is shown in Figure 4. According to Figure 2 and bandwidth, we can obtain the total transmission rate between UAVs and the satellite, which is close to the transmission rate in Figure 4. Considering the UAV capacity, the transmission quality can be guaranteed.

Then, assuming that the flight altitudes of UAVs are 100 m, 500 m, and 1000 m, we have obtained the curves of the energy efficiency varies with $ϵ$ under three flight altitudes, as shown in Figure 5, and the curves of the spectral efficiency varies with $ϵ$ under three flight altitudes, as shown in Figure 6.

Figure 5 and Figure 6 show the tradeoff between the system energy efficiency and spectral efficiency. As shown in Figure 5, the energy efficiency initially remains constant but then decreases as the tradeoff coefficient $ϵ$ increases. On the other hand, in Figure 6, the spectral efficiency remains constant and then increases to the same level as the tradeoff coefficient increases. There exists a optimal value of the tradeoff coefficient where the energy efficiency and spectral efficiency of the system remain constant, and the maximum energy efficiency can be attained while fulfilling the spectral efficiency requirements. However, beyond this value, increasing the tradeoff coefficient will result in the system sacrificing some energy efficiency to achieve the desired spectral efficiency. Thus, a suitable tradeoff coefficient should be chosen based on the specific requirements of the system.

In addition, Figure 5 shows that the flight altitude of UAVs has an impact on the EE. It can be seen that the higher the flight altitude of the aircraft, the lower the energy efficiency of the system. An increase in aircraft altitude results in a decrease in energy efficiency because an increase in altitude results in a decrease in the channel gain between the IoT devices and the UAVs. IoT devices need to increase its transmission power to maintain a reliable connection, which leads to a decrease in EE. Figure 6 shows the impact of flight altitude on SE. In contrast to the impact on EE, an increase in flight altitude will lead to an increase in SE, which is also consistent with theoretical derivation.

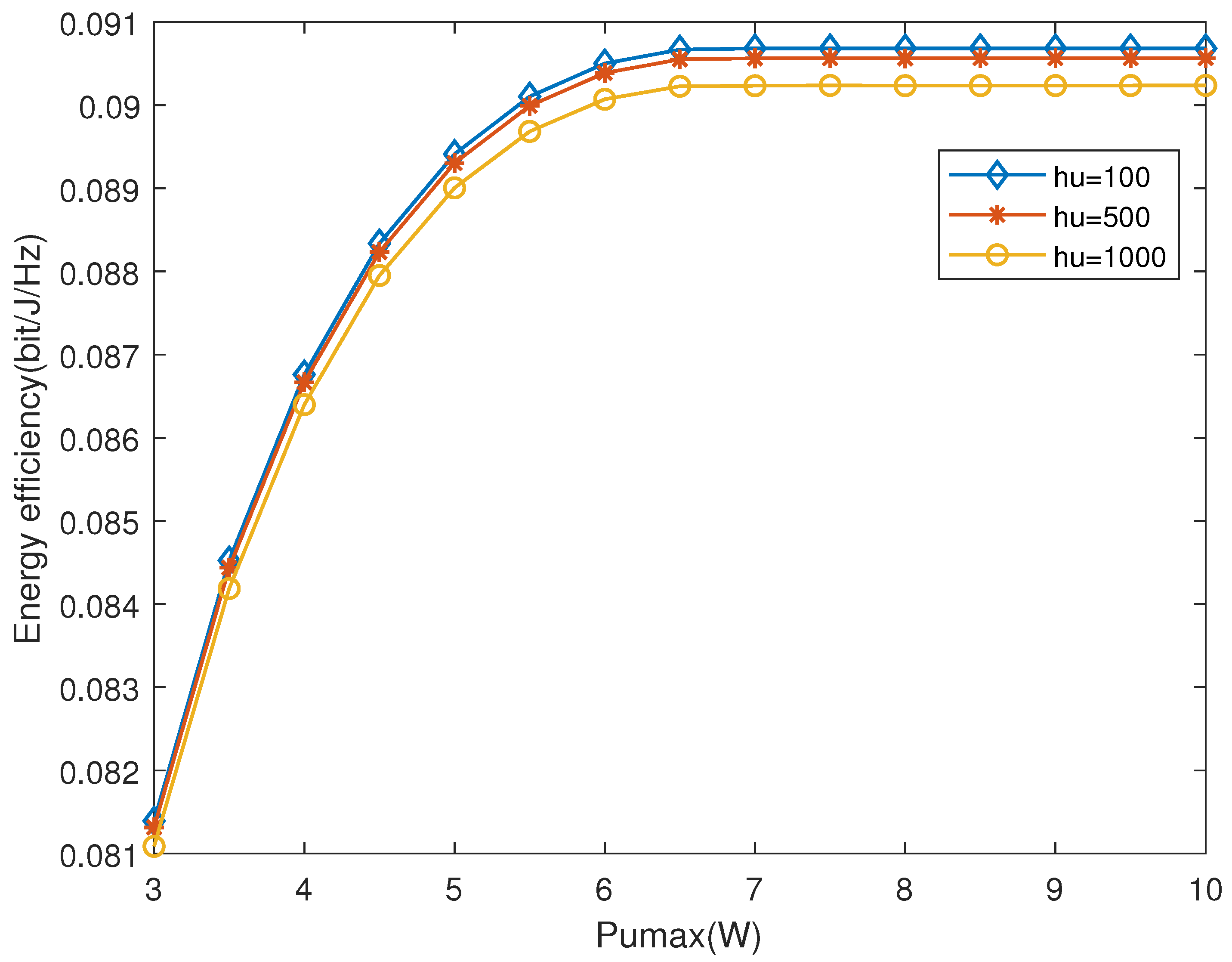
Next, we observe the impact of UAV transmission power limitations on system energy efficiency and spectral efficiency, and assume the power increases from 3 W to 10 W. The curves of the energy efficiency changing with the maximum transmission power of the UAV at different flying heights of the UAV are shown in Figure 7. In addition to the impact of flight altitude on system EE, Figure 7 also shows that the EE first increases and then remains constant as the UAV transmission power increases. This is because there is an optimal UAV transmission power that results in the highest EE. Further increasing the transmission power beyond this optimal point will not bring about any performance improvements in terms of EE.

The curves in Figure 8 illustrate the variation of SE concerning different UAV transmission powers and flying heights. It can be seen that with the increase of the transmission power of the UAV, SE increases until it reaches the optimal value and remains unchanged.

5. Conclusions and Future Works

In this paper, we construct a SAG-IoT model, equating the channel between IoT devices and UAVs to a line of sight channel. Due to the limited energy of drones, we focus on energy efficiency, but an increase in energy efficiency can lead to a decrease in spectral efficiency. Therefore, we consider both energy efficiency and spectral efficiency as objective functions to construct optimization problems. We improve the $ϵ$-constraint to transform the multi-objective optimization problem into a single-objective optimization problem with additional constraints. Additionally, we introduce a BCD-based method to jointly optimize sub-channel selection, IoT device transmission power, UAV transmission power, and UAV location deployment to solve the complex single-objective optimization problem. Simulation results demonstrate the convergence of our proposed algorithm. At the end of the paper, we provide simulations to demonstrate the convergence of the proposed algorithm, analyz the effects of different tradeoff coefficients on the energy efficiency and spectral efficiency of the system, and analyz the effects of factors such as UAV flight altitude and maximum launch power on the algorithm performance. However, our SAG-IoT model only includes one satellite, and we should consider the case of multiple satellites in the future. In addition, we only considered the location deployment of UAVs without considering the trajectory. We will carry out further research on this.