Aggregate Entity Authentication Identifying Invalid Entities with Group Testing

Abstract

It is common to implement challenge-response entity authentication with a MAC function. In such an entity authentication scheme, aggregate MAC is effective when a server needs to authenticate many entities. Aggregate MAC aggregates multiple tags (responses to a challenge) generated by entities into one short aggregate tag so that the entities can be authenticated simultaneously regarding only the aggregate tag. Then, all associated entities are valid if the pair of a challenge and the aggregate tag is valid. However, a drawback of this approach is that invalid entities cannot be identified when they exist. To resolve the drawback, we propose group-testing aggregate entity authentication by incorporating group testing into entity authentication using aggregate MAC. We first formalize the security requirements and present a generic construction. Then, we reduce the security of the generic construction to that of aggregate MAC and group testing. We also enhance the generic construction to instantiate a secure scheme from a simple and practical but weaker aggregate MAC scheme. Finally, we show some results on performance evaluation.

1. Introduction

1.1. Background

A MAC function is one of the most basic symmetric-key primitives for cryptography. Its typical application is challenge-response entity authentication, which assumes that a server and an entity share a secret key. In this scheme, the server first sends a challenge to the entity. Next, the entity computes a tag for the challenge using the MAC function with the shared secret key and returns it to the server. Finally, the server computes the tag in the same way and verifies the received tag.

Entity authentication is often crucial in identifying invalid entities to secure network applications and services. Additionally, a server may need to authenticate many devices simultaneously in an IoT network. In scenarios where an edge device plays the role of an aggregator, as shown in Figure 1, aggregate MAC [1] is suitable for efficient communication between the server and the aggregator for entity authentication. Aggregate MAC allows users to aggregate multiple tags into a tag so that the aggregate tag is as short as each of the multiple tags. In the situation shown in Figure 1, if the aggregator aggregates tags from devices and sends the aggregate tag to the server, then the server can authenticate the devices based only on the aggregate tag. If the aggregate tag is valid, then the server knows that all devices are valid. On the other hand, if the aggregate tag is invalid, then the server only knows that one or more invalid devices are included, which cannot be identified. The problem is if the server can identify invalid devices without knowing individual tags. As far as we know, it has not been addressed for entity authentication.

1.2. Our Contribution

We observe that group testing [2] can be employed to solve the above problem. For group testing, each item is assumed to be positive or negative. Multiple items are assumed to be able to be inspected by a test whose result is positive only if one or more positive items are included. All positive items can be identified with fewer tests than individual tests if the number of positive items is relatively small [3].

We introduce and explore group-testing aggregate authentication. It is a protocol participated in by multiple entities, an aggregator, and a server. Each entity has its own secret key shared with the server. The aggregator broadcasts a challenge from the server to the entities and collects their responses. The server then identifies the invalid entities by verifying the responses with the help of the aggregator.

We first formalizesd the scheme and its security requirements. The security requirements are impersonation resistance, completeness, and soundness. Impersonation resistance represents the notion that adversaries cannot impersonate an entity without knowing its secret key. Completeness requires that a valid response must not be judged invalid. Soundness requires that an invalid response must not be judged valid.

Furthermore, we present a generic construction combining a group-testing scheme and an aggregate MAC scheme. For each test in group testing, it aggregates the tags of entities examined by the test and verifies the aggregate tag. The aggregate tag is valid (negative) if all the involved tags are valid. Thus, invalid entities can be identified with fewer tests than by examining them individually. We also show that the generic construction satisfies impersonation resistance if the underlying aggregate MAC scheme is unforgeable, completeness if the underlying group-testing scheme satisfies completeness, and soundness if the underlying aggregate MAC scheme satisfies soundness. Furthermore, considering that the simple and practical Katz-Lindell aggregate MAC scheme [1] does not satisfy soundness, we enhance the generic construction to instantiate group-testing aggregate entity authentication satisfying soundness by using aggregate MAC not satisfying soundness.

Finally, we evaluate the performance of the proposed construction instantiated with SHA-256 [4] and HMAC [5] by software implementation.

1.3. Related Work

Katz and Lindell [1] introduced and investigated aggregate MAC. They presented a provably secure scheme for generating an aggregate tag by XOR of the associated tags. Eikemeier et al. [6] formalized sequential aggregate MAC and presented provably secure schemes. Sato et al. [7] proposed a sequential aggregate MAC scheme for aggregating tags without using the secret keys of associated users. Ishii and Tada [8] presented an aggregate MAC scheme that aggregates tags following the structure represented by a series-parallel graph.

Goodrich et al. [9] applied group testing to MAC schemes for identifying tampered data items. Along this line of research, Minematsu [10] proposed a computationally efficient scheme of group testing MAC based on PMAC [11]. Minematsu and Kamiya [12] proposed a method for reducing the number of tags.

Hirose and Shikata [13,14] applied group testing to aggregate MAC for identifying invalid messages from multiple senders. They used non-adaptive group testing for a generic construction. Sato and Shikata [15] presented a generic construction using adaptive group testing. Anada and Kamibayashi [16] followed the discussion by Sato and Shikata [17] and discussed the quantum security of aggregate MAC combined with non-adaptive group-testing. Ogawa et al. [18] presented a scheme reducing the number of aggregate tags based on biorthogonal codes.

1.4. Organization

Section 2 defines notations and cryptographic primitives and describes group testing. Section 3 provides the syntax and security requirements of aggregate MAC and its concrete schemes. Section 4 formalizes group-testing aggregate entity authentication and presents its generic construction, combining group-testing and aggregate MAC. Section 5 discusses the security of the generic construction and presents its enhancement. Section 6 shows some results of the performance evaluation by software implementation. Section 7 gives a brief concluding remark.

This article is an extended and improved version of our conference paper [19]. We refine the formalization of security requirements, which are described in Section 4, based on the idea by Bellare and Rogaway [20]. Accordingly, we revise the theorems and proofs, which are given in Section 5. We also add the results on performance evaluation.

2. Preliminaries

2.1. Notation

${\{0,1\}}^l$ is regarded as the set of all binary sequences of length l. Let ${\{0,1\}}^{*}:={\bigcup }_{l\ge 0}{\{0,1\}}^l$. For binary sequences $x,y$, their concatenation is denoted by $x\parallel y$.

Let $\mathcal{S}$ be a set. For $\mathit{v}:=(v_1,\dots ,v_n)\in {\{0,1\}}^n$ and $\mathit{s}:=(s_1,\dots ,s_n)\in {\mathcal{S}}^n$, let $\mathit{v}⊡\mathit{s}:=(s_{j_1},\dots ,s_{j_w})$, where $1\le j_1<\cdots <j_w\le n$ and $v_j=1$ iff $j\in \{j_1,\dots ,j_w\}$. For $\mathit{u},{\mathit{u}}^{\prime }\in {\{0,1\}}^n$, let $\mathit{u}\vee {\mathit{u}}^{\prime }$ be their component-wise disjunction. Let $s\leftarrow \leftarrow \mathcal{S}$ represent that s is sampled uniformly at random from $\mathcal{S}$.

2.2. MAC Function and Pseudorandom Function

Let $f:\mathcal{K}\times \mathcal{X}\to \mathcal{Y}$ be a keyed function with its key space $\mathcal{K}$. $f(K,·)$ is often denoted by $f_K(·)$.

f is called a secure MAC function or unforgeable if it is intractable to predict unknown outputs of $f_K$, where $K\leftarrow \leftarrow \mathcal{K}$. An adversary $\mathbf{A}$ is given a tagging oracle ${\mathsf{T}}_K^f$ and a verification oracle ${\mathsf{V}}_K^f$ and is allowed to make queries adaptively to them. In response to a query $X\in \mathcal{X}$, ${\mathsf{T}}_K^f$ returns $f_K\left(X\right)$. In response to a query $(X,Y)\in \mathcal{X}\times \mathcal{Y}$, ${\mathsf{V}}_K^f$ returns 1 if $f_K\left(X\right)=Y$ and 0 otherwise. $\mathbf{A}$ is not allowed to ask $(X,Y)$ to ${\mathsf{V}}_K^f$ after asking X to ${\mathsf{T}}_K^f$. ${\mathbf{A}}^{{\mathsf{T}}_K^f,{\mathsf{V}}_K^f}$ is successful iff ${\mathsf{V}}_K^f$ returns 1 in response to at least one query. The advantage of $\mathbf{A}$ against f is

$${\mathrm{Adv}}_f^{\mathrm{mac}}\left(\mathbf{A}\right):=Pr\left[{\mathbf{A}}^{{\mathsf{T}}_K^f,{\mathsf{V}}_K^f}\mathrm{is}\mathrm{successful}\right].$$

f is called a secure pseudorandom function (PRF) if it is intractable to distinguish $f_K$ with $K\leftarrow \leftarrow \mathcal{K}$ from a uniform random function $\rho :\mathcal{X}\to \mathcal{Y}$. An adversary $\mathbf{A}$ is given either $f_K$ or $\rho$ as an oracle and is allowed to make adaptive queries in $\mathcal{X}$. $\mathbf{A}$ outputs 0 or 1. The advantage of $\mathbf{A}$ against f is

$${\mathrm{Adv}}_f^{\mathrm{prf}}\left(\mathbf{A}\right):=\left|Pr\left[{\mathbf{A}}^{f_K}=1\right]-Pr\left[{\mathbf{A}}^{\rho }=1\right]\right|,$$

where $\mathbf{A}$ is regarded as a random variable which takes values in $\{0,1\}$. It is easy to see that a secure PRF is a secure MAC function, and that a secure MAC function is not necessarily a secure PRF.

2.3. Cryptographic Hash Function

A cryptographic hash function $H:{\{0,1\}}^{*}\to {\{0,1\}}^{\tau }$ is often simply called a hash function. Among its various security requirements, our work is concerned with the random oracle model and collision resistance.

The random oracle model [21] assumes that H is an ideal function such that, for any $X\in {\{0,1\}}^{*}$, $H\left(X\right)$ is chosen uniformly at random from ${\{0,1\}}^{\tau }$. H is called a random oracle.

H is said to satisfy collision resistance if it is intractable to find a pair of distinct inputs of H mapped to the same output. The advantage of an adversary $\mathbf{A}$ against H is

$${\mathrm{Adv}}_H^{\mathrm{col}}\left(\mathbf{A}\right):=Pr[(X,X^{\prime })\leftarrow \mathbf{A}\left(H\right):X\ne X^{\prime }\wedge H\left(X\right)=H\left(X^{\prime }\right)].$$

Notice that the above definition is not theoretically precise: H should be sampled from a sufficiently large number of hash functions at random.

2.4. Group Testing

Suppose that there exists a set of items, each of which is either positive or negative. It is assumed that a test can inspect multiple items simultaneously and that the result is positive iff one or more positive items exist among them. Then, it may be possible to identify positive items with fewer tests than by inspecting all the items individually.

A group-testing algorithm can be described as a sequence of sets of tests. Suppose that there are n items. Then, each test can be denoted by a vector in ${\{0,1\}}^n$ such that the j-th element equals 1 iff the test examines the j-th item. Let ${\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_u\subseteq {\{0,1\}}^n$ be a sequence of sets of tests, where u is the number of its stages. The sets of tests are conducted in this order, and the order of the tests in each stage is arbitrary. A group-testing algorithm is called non-adaptive if all the tests are determined beforehand. Thus, it has only a single stage. A group-testing algorithm is called adaptive if the tests in the next stage are determined after the tests in the current stage.

Let $\mathcal{G}:={\mathcal{G}}_1\cup {\mathcal{G}}_2\cup \cdots \cup {\mathcal{G}}_u$. It is reasonable to assume that each test examines at least one item and that the whole set of tests examines all items. Namely, $0^n\notin \mathcal{G}$ and ${\bigvee }_{\mathit{g}\in \mathcal{G}}\mathit{g}=1^n$. The group-testing algorithm extracts candidates of positive items in the following way. For $1\le j\le n$, let ${\mathit{id}}_j$ denote the j-th item. For $1\le i\le u$, let ${\mathcal{G}}_i:=\{{\mathit{g}}_{i,1},{\mathit{g}}_{i,2},\dots ,{\mathit{g}}_{i,|{\mathcal{G}}_i|}\}$. Let $\mathcal{O}\left(\mathit{g}\right):=\left\{{\mathit{id}}_j\right|1\le j\le n\mathrm{and}{g}_j=1\}$, where $\mathit{g}:=(g_1,g_2,\dots ,g_n)\in {\{0,1\}}^n$.

(1)

${\mathcal{J}}_0\leftarrow \{{\mathit{id}}_1,{\mathit{id}}_2,\dots ,{\mathit{id}}_n\}$.

(2)

For $1\le i\le u$, do the followings: (a) ${\mathcal{J}}_i\leftarrow {\mathcal{J}}_{i-1}$; (b) For $1\le l\le |{\mathcal{G}}_i|$, if the result of ${\mathit{g}}_{i,l}$ is negative, then ${\mathcal{J}}_i\leftarrow {\mathcal{J}}_i\setminus \mathcal{O}\left({\mathit{g}}_{i,l}\right)$.

(3)

Output ${\mathcal{J}}_u$.

We call the group-testing algorithm complete if ${\mathcal{J}}_u$ does not include any negative elements. We call it sound if ${\mathcal{J}}_u$ includes all the positive elements. It is sound if the results of the tests are always correct. On the other hand, it may not be complete in general.

For non-adaptive group testing, let us see the matrix $\mathit{G}$ whose rows are the vectors in a set $\mathcal{G}$ of tests, which is called a group-testing matrix. We call $\mathit{G}$ d-disjunct if the component-wise disjunction of any d columns in $\mathit{G}$ does not equal the component-wise disjunction of itself and any other single column. Suppose that non-adaptive group testing is represented by a d-disjunct matrix. Then, it is complete if there are at most d positive items. Specifically, all the positive items are identified.

Suppose that there are at most d positive items. For non-adaptive group testing, it is known that there exists a complete algorithm with $O(d^{2}logn)$ tests [3,22,23,24]. In addition, a non-asymptotic lower bound was conjectured as $min\{{(d+1)}^2,n\}$ [25] while it is true for $d\le 5$, and actually derived as $min\left\{\right(d+2\left)\right(d+1)/2,n\}$[26] and $min\{d^2(15+\sqrt{33})/24,n\}$ [27]. For adaptive group testing, it is known that there exists a complete algorithm with $O(dlog(n/d\left)\right)$ tests [3,28,29]. A tight lower bound is shown as $dlog(n/d)+o(dlog(n/d\left)\right)$ [3].

3. Aggregate MAC

3.1. Syntax

A tuple of algorithms $\mathsf{AM}:=(\mathsf{KG},\mathsf{Tag},\mathsf{Agg},\mathsf{Ver})$ formalizes an aggregate MAC scheme. It is associated with an ID space $\mathcal{I}$, a key space $\mathcal{K}$, a message space $\mathcal{M}$, a tag space $\mathcal{T}$, and an aggregate-tag space $\mathcal{A}$.

• $\mathsf{KG}$ is a key-generation algorithm such that $k\leftarrow \mathsf{KG}\left(1^{\kappa }\right)$, where $\kappa$ is a security parameter and $k\in \mathcal{K}$. Each entity is assigned a secret key independently generated by $\mathsf{KG}$.
• $\mathsf{Tag}$ is a tagging algorithm such that $t\leftarrow \mathsf{Tag}(k,m)$, where $(k,m)\in \mathcal{K}\times \mathcal{M}$ and $t\in \mathcal{T}$.
• $\mathsf{Agg}$ is an aggregate algorithm such that $T\leftarrow \mathsf{Agg}(({\mathit{id}}_1,m_1,t_1),\dots ,({\mathit{id}}_p,m_p,t_p)),$ where $({\mathit{id}}_j,m_j,t_j)\in \mathcal{I}\times \mathcal{M}\times \mathcal{T}$ for $1\le j\le p$ and $T\in \mathcal{A}$. $({\mathit{id}}_j,m_j)$’s are required to be distinct from each other. It is often the case that T depends only on $t_1,t_2,\dots ,t_p$.
• $\mathsf{Ver}$ is a verification algorithm such that $d\leftarrow \mathsf{Ver}((({\mathit{id}}_1,k_1),\dots ,({\mathit{id}}_p,k_p)),(({\mathit{id}}_1,m_1),\dots ,({\mathit{id}}_p,m_p)),T)$, where $({\mathit{id}}_j,k_j)\in \mathcal{I}\times \mathcal{K}$ and $({\mathit{id}}_j,m_j)\in \mathcal{I}\times \mathcal{M}$ for $1\le j\le p$, $T\in \mathcal{T}$ if $p=1$ and $T\in \mathcal{A}$ otherwise, and $d\in \{0,1\}$. $({\mathit{id}}_j,m_j)$’s are required to be distinct from each other. With respect to $(({\mathit{id}}_1,k_1),\dots ,({\mathit{id}}_p,k_p))$, the pair $(({\mathit{id}}_1,m_1),\dots ,({\mathit{id}}_p,m_p))$ and T are valid if $d=1$ and invalid otherwise.

$\mathsf{AM}$ satisfies correctness. For $({\mathit{id}}_1,k_1),\dots ,({\mathit{id}}_p,k_p)$ and $({\mathit{id}}_1,m_1),\dots ,({\mathit{id}}_p,m_p)$, let $t_j\leftarrow \mathsf{Tag}(k_j,m_j)$ for $1\le j\le p$ and $T\leftarrow \mathsf{Agg}(({\mathit{id}}_1,m_1,t_1),\dots ,({\mathit{id}}_p,m_p,t_p))$. Then, it holds that $\mathsf{Ver}((({\mathit{id}}_1,k_1),\dots ,({\mathit{id}}_p,k_p)),(({\mathit{id}}_1,m_1),\dots ,({\mathit{id}}_p,m_p)),T)=1.$ In particular, for $p=1$, if $t\leftarrow \mathsf{Tag}(k,m)$, then $\mathsf{Ver}\left(\right(\mathit{id},k),(\mathit{id},m),t)=1$.

3.2. Security Requirement

Unforgeability and soundness are formalized as security requirements for aggregate MAC. Soundness is required for applying group testing to aggregate MAC [14].

3.2.1. Unforgeability

We introduce a game ${\mathcal{G}}_{\mathsf{AM},\mathbf{A}}^{\mathrm{uf}}$ to define unforgeability, where $\mathbf{A}$ is an adversary allowed to make queries adaptively to the oracles $\mathcal{TG}$, $\mathcal{KD}$, and $\mathcal{VR}$.

• $\mathcal{TG}$ is called a tagging oracle. It returns $t\leftarrow \mathsf{Tag}(k_{\mathit{id}},m)$ in response to a query $(\mathit{id},m)$, where $k_{\mathit{id}}$ is the key of the entity $\mathit{id}$.
• $\mathcal{KD}$ is called a key-disclosure oracle. It accepts a query $\mathit{id}$ and returns $k_{\mathit{id}}$.
• $\mathcal{VR}$ is called a verification oracle. It accepts a query $((({\mathit{id}}_1,m_1),\dots ,({\mathit{id}}_p,m_p)),T)$ and returns $d\leftarrow \mathsf{Ver}((({\mathit{id}}_1,k_1),\dots ,({\mathit{id}}_p,k_p)),(({\mathit{id}}_1,m_1),\dots ,({\mathit{id}}_p,m_p)),T).$

For a query $((({\mathit{id}}_1,m_1),\dots ,({\mathit{id}}_p,m_p)),T)$ made by $\mathbf{A}$ to $\mathcal{VR}$, we call $({\mathit{id}}_j,m_j)$ a fresh pair if $\mathbf{A}$ does not ask it to $\mathcal{TG}$ and does not ask ${\mathit{id}}_j$ to $\mathcal{KD}$ prior to the query. $\mathcal{VR}$ does not accept a query with no fresh pair. ${\mathcal{G}}_{\mathsf{AM},\mathbf{A}}^{\mathrm{uf}}$ outputs 1 iff $\mathbf{A}$ gets 1 from $\mathcal{VR}$ for at least one query. The advantage of $\mathbf{A}$ against $\mathsf{AM}$ for unforgeability is defined by

$${\mathrm{Adv}}_{\mathsf{AM}}^{\mathrm{uf}}\left(\mathbf{A}\right):=Pr[{\mathcal{G}}_{\mathsf{AM},\mathbf{A}}^{\mathrm{uf}}=1].$$

It is informally stated that $\mathsf{AM}$ is unforgeable or satisfies unforgeability if, for any efficient $\mathbf{A}$, ${\mathrm{Adv}}_{\mathsf{AM}}^{\mathrm{uf}}\left(\mathbf{A}\right)$ is negligible.

3.2.2. Soundness

To define soundness, we specify a game ${\mathcal{G}}_{\mathsf{AM},\mathbf{A}}^{\mathrm{snd}}$, where $\mathbf{A}$ is an adversary allowed to make queries adaptively to the aggregate-then-verify oracle $\mathcal{AVR}$ in addition to the oracles $\mathcal{TG}$, $\mathcal{KD}$, and $\mathcal{VR}$. $\mathcal{AVR}$ accepts a query $(({\mathit{id}}_1,m_1,t_1),\dots ,({\mathit{id}}_p,m_p,t_p))$ and computes

• $d_j\leftarrow \mathsf{Ver}(({\mathit{id}}_j,k_j),({\mathit{id}}_j,m_j),t_j)$ for $1\le j\le p$,
• $T\leftarrow \mathsf{Agg}(({\mathit{id}}_1,m_1,t_1),\dots ,({\mathit{id}}_p,m_p,t_p))$, and
• $D\leftarrow \mathsf{Ver}((({\mathit{id}}_1,k_1),\dots ,({\mathit{id}}_p,k_p)),(({\mathit{id}}_1,m_1),\dots ,({\mathit{id}}_p,m_p)),T)$.

Then, it returns $D\wedge (\overline{d_1}\vee \overline{d_2}\vee \cdots \vee \overline{d_p})$. ${\mathcal{G}}_{\mathsf{AM},\mathbf{A}}^{\mathrm{snd}}$ outputs 1 iff $\mathbf{A}$ gets 1 from $\mathcal{AVR}$ for at least one query. The advantage of $\mathbf{A}$ against $\mathsf{AM}$ for soundness is defined by

$${\mathrm{Adv}}_{\mathsf{AM}}^{\mathrm{snd}}\left(\mathbf{A}\right):=Pr[{\mathcal{G}}_{\mathsf{AM},\mathbf{A}}^{\mathrm{snd}}=1].$$

It is informally stated that $\mathsf{AM}$ is sound or satisfies soundness if, for any efficient $\mathbf{A}$, ${\mathrm{Adv}}_{\mathsf{AM}}^{\mathrm{snd}}\left(\mathbf{A}\right)$ is negligible.

3.3. Aggregate MAC Scheme by Katz and Lindell

Let $F:\mathcal{K}\times \mathcal{M}\to {\{0,1\}}^{\tau }$ be a MAC function. The Katz-Lindell aggregate MAC scheme [1] using F is specified as follows:

• Each entity $\mathit{id}\in \mathcal{I}$ is given a secret key $k_{\mathit{id}}\leftarrow \leftarrow \mathcal{K}$.
• The tagging algorithm returns a tag $t\leftarrow F_k\left(m\right)$ in response to $(k,m)\in \mathcal{K}\times \mathcal{M}$.
• The aggregate algorithm returns an aggregate tag $T\leftarrow {⨁}_{1\le i\le p}{t}_i$ in response to $({\mathit{id}}_1,m_1,t_1),\dots ,({\mathit{id}}_p,m_p,t_p)\in \mathcal{I}\times \mathcal{M}\times \mathcal{T}$.
• Taking $({\mathit{id}}_1,k_1),\dots ,({\mathit{id}}_p,k_p)$ and $(({\mathit{id}}_1,m_1),\dots ,({\mathit{id}}_p,m_p),T)$ as input, the verification algorithm outputs 1 iff ${⨁}_{1\le i\le p}{F}_{k_i}\left(m_i\right)=T$.

Let ${\mathsf{AM}}_{\mathrm{X}}$ denote the Katz-Lindell aggregate MAC scheme. ${\mathsf{AM}}_{\mathrm{X}}$ is shown to be unforgeable for any efficient adversary asking the verification oracle a single query [1]. It is also shown to be unforgeable even for any efficient adversary asking the verification oracle multiple queries:

Proposition 1 

([14]). Let $\mathbf{A}$ be any adversary against ${\mathsf{AM}}_{\mathrm{X}}$ with ℓ users. Suppose that $\mathbf{A}$ asks the tagging oracle $q_{\mathrm{t}}$ queries and the verification oracle $q_{\mathrm{v}}$ queries. Suppose that each verification query by $\mathbf{A}$ consists of at most p pairs of ID and message. Then, there exists some adversary $\dot{\mathbf{A}}$ satisfying

$${\mathrm{Adv}}_{{\mathsf{AM}}_{\mathrm{X}}}^{\mathrm{uf}}\left(\mathbf{A}\right)\le \ell q_{\mathrm{v}}·{\mathrm{Adv}}_F^{\mathrm{mac}}\left(\dot{\mathbf{A}}\right).$$

$\dot{\mathbf{A}}$ asks the tagging oracle at most $(q_{\mathrm{t}}+p)$ queries and the verification oracle at most one query. $\dot{\mathbf{A}}$’s running time is at most about that of ${\mathcal{G}}_{{\mathsf{AM}}_{\mathrm{X}},\mathbf{A}}^{\mathrm{uf}}$.

It is easy to see that ${\mathsf{AM}}_{\mathrm{X}}$ is not sound. Let $\tilde{\mathbf{A}}$ be an adversary working as follows. $\tilde{\mathbf{A}}$ first asks $({\mathit{id}}_1,m_1)$ and $({\mathit{id}}_2,m_2)$ to the tagging oracle and gets $t_1=F_{k_1}\left(m_1\right)$ and $t_2=F_{k_2}\left(m_2\right)$. Then, $\tilde{\mathbf{A}}$ gets 1 from the aggregate-then-verify oracle by asking $(({\mathit{id}}_1,m_1,{\tilde{t}}_1),({\mathit{id}}_2,m_2,{\tilde{t}}_2))$ such that $({\tilde{t}}_1,{\tilde{t}}_2)\ne (t_1,t_2)$ and ${\tilde{t}}_1\oplus {\tilde{t}}_2=t_1\oplus t_2$.

3.4. Aggregate MAC Scheme Using Hashing

We refer to the aggregate MAC scheme using a hash function $H:{\{0,1\}}^{*}\to {\{0,1\}}^{\tau }$ to aggregate tags [14] as ${\mathsf{AM}}_{\mathrm{H}}$. ${\mathsf{AM}}_{\mathrm{H}}$ is specified as follows:

• The key generation and tagging algorithms are identical to those of ${\mathsf{AM}}_{\mathrm{X}}$.
• For $({\mathit{id}}_1,m_1,t_1),\dots ,({\mathit{id}}_p,m_p,t_p)$, the aggregate algorithm returns $T\leftarrow H(t_1\parallel \cdots \parallel t_p)$. For the uniqueness of the aggregate tag T, $({\mathit{id}}_1,m_1,t_1),\dots ,({\mathit{id}}_p,m_p,t_p)$ are assumed to be ordered in a lexicographic order.
• Taking $({\mathit{id}}_1,k_1),\dots ,({\mathit{id}}_p,k_p)$ and $(({\mathit{id}}_1,m_1),\dots ,({\mathit{id}}_p,m_p),T)$ as input, the verification algorithm outputs 1 if $H(F_{k_1}\left(m_1\right)\parallel \cdots \parallel F_{k_p}\left(m_p\right))=T$ and 0 otherwise.

${\mathsf{AM}}_{\mathrm{H}}$ is shown to be unforgeable if F is unforgeable and H is a random oracle [14]:

Proposition 2. 

Let $\mathbf{A}$ be any adversary against ${\mathsf{AM}}_{\mathrm{H}}$ with ℓ users. Suppose that $\mathbf{A}$ asks the random oracle H $q_{\mathrm{h}}$ queries, the tagging oracle $q_{\mathrm{t}}$ queries, and the verification oracle $q_{\mathrm{v}}$ queries. Suppose that each verification query by $\mathbf{A}$ consists of at most p pairs of ID and message. Then, there exists some adversary $\dot{\mathbf{A}}$ satisfying

$${\mathrm{Adv}}_{{\mathsf{AM}}_{\mathrm{H}}}^{\mathrm{uf}}\left(\mathbf{A}\right)\le \ell q_{\mathrm{v}}·{\mathrm{Adv}}_F^{\mathrm{mac}}\left(\dot{\mathbf{A}}\right)+q_{\mathrm{v}}/2^{\tau }.$$

$\dot{\mathbf{A}}$ asks the random oracle at most $(q_{\mathrm{h}}+q_{\mathrm{v}})$ queries, the tagging oracle at most $(q_{\mathrm{t}}+p)$ queries, and the verification oracle at most one query. $\dot{\mathbf{A}}$’s running time is at most about that of ${\mathcal{G}}_{{\mathsf{AM}}_{\mathrm{H}},\mathbf{A}}^{\mathrm{uf}}$.

The soundness of ${\mathsf{AM}}_{\mathrm{H}}$ is reduced to the collision resistance of H [14]:

Proposition 3. 

For any adversary $\mathbf{A}$ against ${\mathsf{AM}}_{\mathrm{H}}$ concerning soundness, there exists some adversary $\dot{\mathbf{A}}$ satisfying

$${\mathrm{Adv}}_{{\mathsf{AM}}_{\mathrm{H}}}^{\mathrm{snd}}\left(\mathbf{A}\right)\le {\mathrm{Adv}}_H^{\mathrm{col}}\left(\dot{\mathbf{A}}\right).$$

The running time of $\dot{\mathbf{A}}$ is at most about that of ${\mathcal{G}}_{{\mathsf{AM}}_{\mathrm{H}},\mathbf{A}}^{\mathrm{snd}}$.

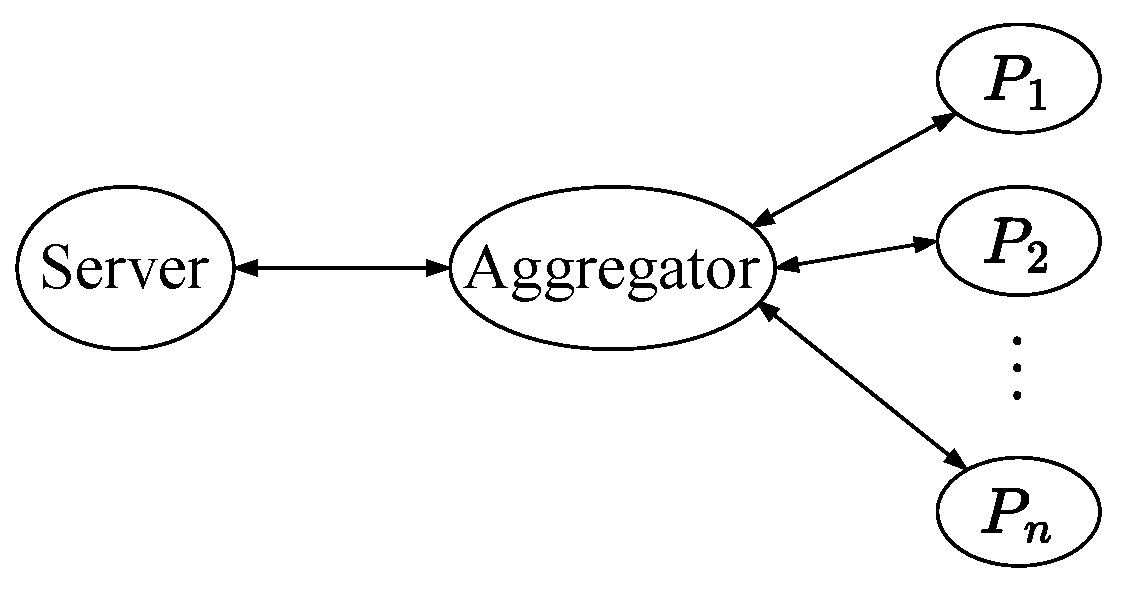
4. Group-Testing Aggregate Entity Authentication

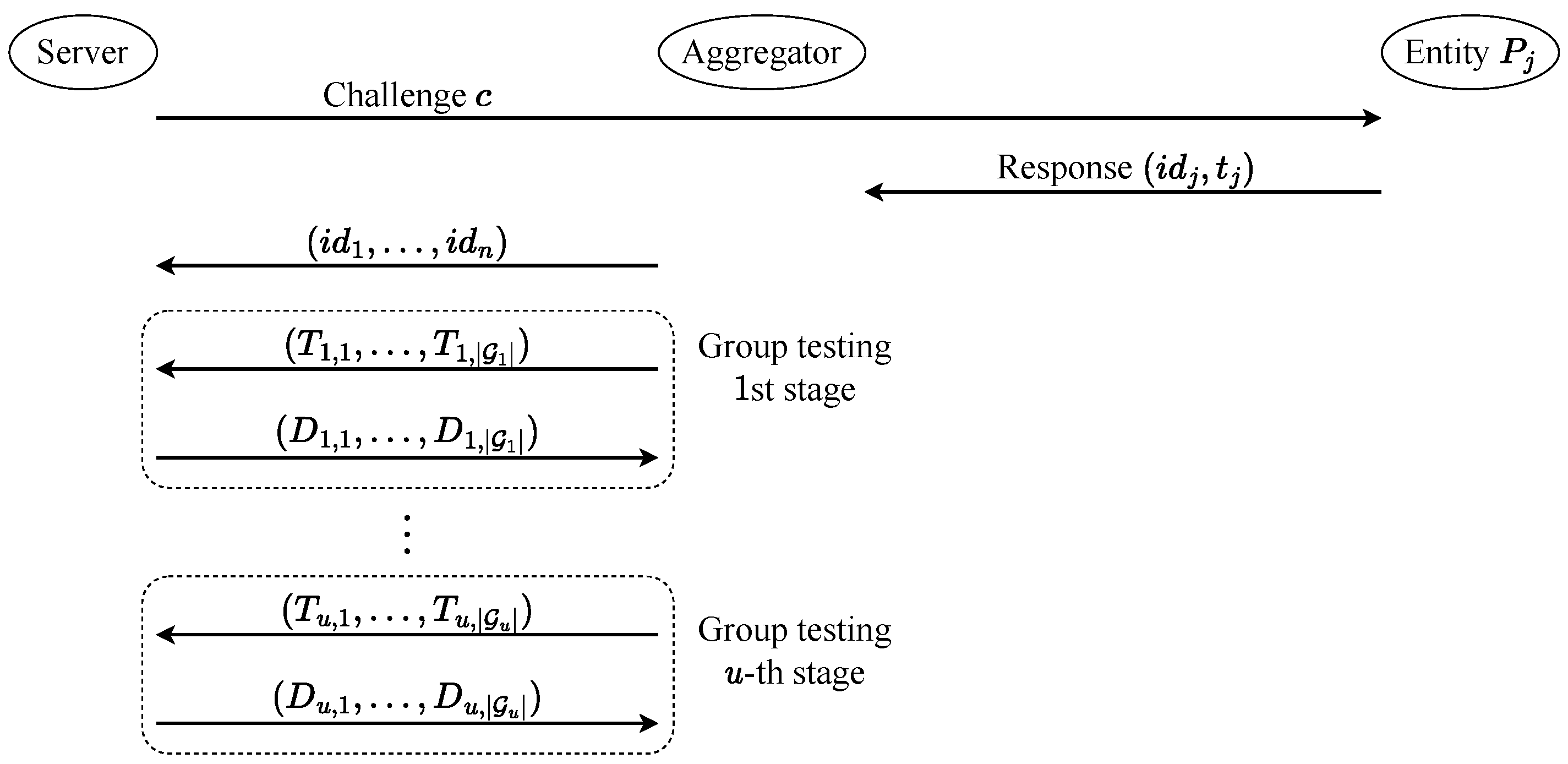
4.1. Scheme

We present a group-testing aggregate entity authentication scheme. It is a challenge-response protocol between a server and a set of entities, and they communicate through an aggregator (Figure 1). It consists of a group-testing algorithm $\mathsf{GT}$ and an aggregate MAC scheme $\mathsf{AM}:=(\mathsf{KG},\mathsf{Tag},\mathsf{Agg},\mathsf{Ver})$ and is denoted by $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$.

Let $\mathcal{P}:=\{P_1,P_2,\dots ,P_n\}$ denote the set of entities. Each $P_j$ has an ID ${\mathit{id}}_j$ and shares a secret key $k_j\leftarrow \mathsf{KG}\left(1^{\kappa }\right)$ with the server. $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ proceeds as follows:

Step 1:

The server sends a challenge $c\leftarrow \leftarrow {\{0,1\}}^{\nu }$ to the aggregator, which broadcasts it to the entities.

Step 2:

In response to c, each entity $P_j$ returns $({\mathit{id}}_j,t_j)$ to the aggregator, where $t_j\leftarrow \mathsf{Tag}(k_j,c)$.

Step 3:

The aggregator sends $({\mathit{id}}_1,{\mathit{id}}_2,\dots ,{\mathit{id}}_n)$ to the server.

Step 4:

With the help of the aggregator, the server identifies the valid entities using $\mathsf{GT}$, $\mathsf{Agg}$, and $\mathsf{Ver}$ in the following way:

1.

${\mathcal{J}}_0\leftarrow \{{\mathit{id}}_1,{\mathit{id}}_2,\dots ,{\mathit{id}}_n\}$.

2.

Let u be the number of stages of $\mathsf{GT}$. For $1\le i\le u$,

(a)

According to $\mathsf{GT}$, both the server and the aggregator determine the set of tests ${\mathcal{G}}_i:=\{{\mathit{g}}_{i,1},\dots ,{\mathit{g}}_{i,|{\mathcal{G}}_i|}\}$.

(b)

The aggregator computes $T_{i,l}\leftarrow \mathsf{Agg}({\mathit{g}}_{i,l}⊡(({\mathit{id}}_1,c,t_1),\dots ,({\mathit{id}}_n,c,t_n)))$ for $1\le l\le |{\mathcal{G}}_i|$ and sends $(T_{i,1},T_{i,2},\dots ,T_{i,|{\mathcal{G}}_i|})$ to the server.

(c)

The server first sets ${\mathcal{J}}_i\leftarrow {\mathcal{J}}_{i-1}$. Then, for $1\le l\le |{\mathcal{G}}_i|$, it computes

$$D_{i,l}\leftarrow \mathsf{Ver}({\mathit{g}}_{i,l}⊡(({\mathit{id}}_1,k_1),\dots ,({\mathit{id}}_n,k_n)),{\mathit{g}}_{i,l}⊡(({\mathit{id}}_1,c),\dots ,({\mathit{id}}_n,c)),T_{i,l})$$

and ${\mathcal{J}}_i\leftarrow {\mathcal{J}}_i\setminus \mathcal{O}\left({\mathit{g}}_{i,l}\right)$ if $D_{i,l}=1$. Finally, it sends $(D_{i,1},D_{i,2},\dots ,D_{i,|{\mathcal{G}}_i|})$ to the aggregator.

3.

Output ${\mathcal{J}}_u$.

The communication among the server, the aggregator, and the entities in $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ is depicted in Figure 2.

For the description above, Step 3 can be merged with the first move of 2(b) in Step 4 if the server knows the number of entities to be authenticated in advance. If $\mathsf{GT}$ is non-adaptive, then $u=1$, and both the server and the aggregator know all the tests in advance. In addition, the server does not have to send the results of the tests to the aggregator in Step 4(c). If $\mathsf{GT}$ is adaptive, then the results of ${\mathcal{G}}_1,\dots ,{\mathcal{G}}_j$ determine ${\mathcal{G}}_{j+1}$. Since the server sends the results of the current tests to the aggregator, the aggregator can also determine the new set of tests.

4.2. Security Requirement

The security requirements of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ are impersonation resistance, completeness, and soundness.

4.2.1. Impersonation Resistance

We introduce a game ${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{im}}$ to formalize impersonation resistance. In this game, the adversary $\mathbf{A}$ is supplied with oracles $\left\{S^{\left(i\right)}\right|i\in \mathbb{N}\}$ working as the server. For the i-th run of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$, $\mathbf{A}$ triggers $S^{\left(i\right)}$, which starts the protocol by returning a challenge $c^{\left(i\right)}$ to $\mathbf{A}$. $\mathbf{A}$ is also supplied with oracles $\left\{P_j^{\left(i\right)}\right|i\in \mathbb{N}\mathrm{and}1\le j\le n\}$ working as entities.

The i-th run of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ proceeds with the communication between $S^{\left(i\right)}$ and $\mathbf{A}$. Multiple runs may proceed concurrently in general. Each $P_j^{\left(i\right)}$ accepts two kinds of queries. For a tagging query $(\mathtt{tag},c)$, $P_j^{\left(i\right)}$ returns $\mathsf{Tag}(k_j,c)$. For a corrupt query $\mathtt{corrupt}$, it returns $k_j$. Once $\mathbf{A}$ gets $c^{\left(i\right)}$, $\mathbf{A}$ is allowed to ask it only to $P_j^{\left(i\right)}$. At the end of the run, $S^{\left(i\right)}$ outputs the set ${\mathcal{J}}^{\left(i\right)}$ of IDs of invalid entities. $S^{\left(i\right)}$ may abort the run if $\mathbf{A}$ does not follow the protocol.

${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{im}}$ outputs 1 iff there exist some $i^{*}$ and $j^{*}$ such that ${\mathit{id}}_{j^{*}}\notin {\mathcal{J}}^{\left(i^{*}\right)}$, $\mathbf{A}$ does not ask $c^{\left(i^{*}\right)}$ to $P_{j^{*}}^{\left(i^{*}\right)}$, and $\mathbf{A}$ does not ask $\mathtt{corrupt}$ to $P_{j^{*}}^{\left(i\right)}$ for any i. The advantage of $\mathbf{A}$ against $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ for impersonation resistance is

$${\mathrm{Adv}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}]}^{\mathrm{im}}\left(\mathbf{A}\right):=Pr[{\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{im}}=1].$$

4.2.2. Completeness and Soundness

Completeness and soundness are security requirements for the identifiability of (in)valid responses to a challenge. We introduce games ${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{cmp}}$ and ${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{snd}}$. In both games, the adversary $\mathbf{A}$ is not allowed to corrupt the server and the aggregator, and the communication channel between them is authenticated. Notice that, if $\mathbf{A}$ is allowed to tamper aggregate tags, then any valid response by an entity can be judged invalid by the server.

In both of the games, the adversary $\mathbf{A}$ is supplied with oracles $\left\{S{A}^{\left(i\right)}\right|i\in \mathbb{N}\}$ playing the roles of the server and the aggregator. $\mathbf{A}$ is also supplied with oracles $\left\{P_j^{\left(i\right)}\right|i\in \mathbb{N},1\le j\le n\}$ working as entities, which are specified in Section 4.2.1. For the i-th run of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$, $\mathbf{A}$ triggers $S{A}^{\left(i\right)}$, which starts the protocol by returning a challenge $c^{\left(i\right)}$ to $\mathbf{A}$. Once $\mathbf{A}$ gets $c^{\left(i\right)}$, $\mathbf{A}$ is allowed to ask it only to $P_j^{\left(i\right)}$. In response to $c^{\left(i\right)}$, $\mathbf{A}$ returns $({\mathit{id}}_1,t_1^{\left(i\right)}),({\mathit{id}}_2,t_2^{\left(i\right)}),\dots ,({\mathit{id}}_n,t_n^{\left(i\right)})$ to $S{A}^{\left(i\right)}$. $S{A}^{\left(i\right)}$ runs the protocol step by step. Each step is triggered by $\mathbf{A}$. $\mathbf{A}$ can also see the messages communicated during the protocol. At the end of the run, $S{A}^{\left(i\right)}$ outputs the set ${\mathcal{J}}^{\left(i\right)}$ of IDs of invalid entities. Multiple runs may proceed concurrently in general.

${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{cmp}}$ outputs 1 iff there exists some $i^{*}$ such that

$${\mathcal{J}}^{\left(i^{*}\right)}\cap \left\{{\mathit{id}}_j\right|t_j^{\left(i^{*}\right)}=\mathsf{Tag}(k_j,c^{\left(i^{*}\right)})\}\ne \varnothing .$$

${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{snd}}$ outputs 1 iff there exists some $i^{*}$ such that

$$\left\{{\mathit{id}}_j\right|t_j^{\left(i^{*}\right)}\ne \mathsf{Tag}(k_j,c^{\left(i^{*}\right)})\}\setminus {\mathcal{J}}^{\left(i^{*}\right)}\ne \varnothing .$$

The advantage of $\mathbf{A}$ for completeness and soundness of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ is

$$\begin{array}{cc}\hfill {\mathrm{Adv}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}]}^{\mathrm{cmp}}\left(\mathbf{A}\right)& :=Pr[{\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{cmp}}=1],\mathrm{and}\hfill \\ \hfill {\mathrm{Adv}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}]}^{\mathrm{snd}}\left(\mathbf{A}\right)& :=Pr[{\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{snd}}=1],\hfill \end{array}$$

respectively.

Remark 1. 

The unforgeability of the tagging algorithm is irrelevant to soundness. This is because, for soundness, $\mathbf{A}$ is allowed to ask $(\mathtt{tag},c^{\left(i\right)})$ and $\mathtt{corrupt}$ to $P_j^{\left(i\right)}$ for any i and j. If the tagging algorithm is unforgeable and $\mathbf{A}$ is not allowed to ask them to $P_j^{\left(i\right)}$, then it cannot return a valid tag to $c^{\left(i\right)}$. Thus, impersonation resistance can be regarded as weak soundness in that

$$\left\{{\mathit{id}}_j\right|t_j^{\left(i\right)}\ne \mathsf{Tag}(k_j,c^{\left(i\right)})\mathrm{and}\mathbf{A}\mathrm{neither}\mathrm{gets}\mathsf{Tag}(k_j,c^{\left(i\right)})\mathrm{nor}\mathrm{corrupts}{P}_j\}\setminus {\mathcal{J}}^{\left(i\right)}=\varnothing .$$

All in all, impersonation resistance is sufficient to identify invalid entities. Soundness is required to achieve the same function as individual verification of each response, that is, to identify invalid responses.

5. Discussion on Security

5.1. Impersonation Resistance

The impersonation resistance of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ is reduced to the unforgeability of $\mathsf{AM}$:

Theorem 1. 

For any adversary $\mathbf{A}$ against $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ for impersonation resistance, triggering at most $q_{\mathrm{r}}$ runs of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ and making at most $q_{\mathrm{t}}$ tagging queries and $q_{\mathrm{c}}$ corrupt queries, there exists some adversary $\dot{\mathbf{A}}$ satisfying

$${\mathrm{Adv}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}]}^{\mathrm{im}}\left(\mathbf{A}\right)\le {\mathrm{Adv}}_{\mathsf{AM}}^{\mathrm{uf}}\left(\dot{\mathbf{A}}\right)+q_{\mathrm{r}}(q_{\mathrm{r}}+2q_{\mathrm{t}})/2^{\nu +1}.$$

The number of queries made by $\dot{\mathbf{A}}$ to $\mathcal{TG}$ is at most $q_{\mathrm{t}}$. The number of queries made by $\dot{\mathbf{A}}$ to $\mathcal{KD}$ is at most $q_{\mathrm{c}}$. The number of queries made by $\dot{\mathbf{A}}$ to $\mathcal{VR}$ is at most the total number of tests completed by $S^{\left(i\right)}$’s in ${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{im}}$. The running time of $\dot{\mathbf{A}}$ is at most about that of ${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{im}}$.

Proof. 

In ${\mathcal{G}}_{\mathsf{AM},\dot{\mathbf{A}}}^{\mathrm{uf}}$, $\dot{\mathbf{A}}$ runs ${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{im}}$. If $\mathbf{A}$ makes a tagging query $(\mathtt{tag},c)$ to $P_j^{\left(i\right)}$, then $\dot{\mathbf{A}}$ asks $({\mathit{id}}_j,c)$ to $\mathcal{TG}$ and gets $t_j\leftarrow \mathsf{Tag}(k_j,c)$, which is returned to $\mathbf{A}$. If $\mathbf{A}$ makes a corrupt query to $P_j^{\left(i\right)}$, then $\dot{\mathbf{A}}$ asks ${\mathit{id}}_j$ to $\mathcal{KD}$ and gets $k_j$, which is returned to $\mathbf{A}$. $\dot{\mathbf{A}}$ simulates $S^{\left(1\right)},S^{\left(2\right)},\dots ,S^{\left(q_{\mathrm{r}}\right)}$ by making use of $\mathcal{VR}$.

Suppose that ${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{im}}$ outputs 1. Then, there are two cases:

• There exists some $i^{*}$ such that the challenge $c^{\left(i^{*}\right)}$ of the $i^{*}$-th run of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ collides with some previous challenge $c^{\left(i^{\prime }\right)}$ ($i^{\prime }<i^{*}$) or c in a previous tagging query.
• There exists some $i^{*}$ and $j^{*}$ such that, for some test $\mathit{g}:=(g_1,\dots ,g_n)\in {\{0,1\}}^n$ with $g_{j^{*}}=1$ during the $i^{*}$-th run of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$, $\mathsf{Ver}(\mathit{g}⊡(({\mathit{id}}_1,k_1),\dots ,({\mathit{id}}_n,k_n)),\mathit{g}⊡(({\mathit{id}}_1,c^{\left(i^{*}\right)}),\dots ,({\mathit{id}}_n,c^{\left(i^{*}\right)})),T^{*})=1$, and $\mathbf{A}$ does not ask $(\mathtt{tag},c^{\left(i^{*}\right)})$ to $P_{j^{*}}^{\left(i^{*}\right)}$ and $\mathtt{corrupt}$ to any $P_{j^{*}}^{\left(i\right)}$.

For the first case, notice that $\mathbf{A}$ triggers at most $q_{\mathrm{r}}$ runs of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ and makes at most $q_{\mathrm{t}}$ tagging queries. Thus, the probability of the first case is at most

$$(q_{\mathrm{r}}(q_{\mathrm{r}}-1)/2)/2^{\nu }+q_{\mathrm{r}}{q}_{\mathrm{t}}/2^{\nu }\le q_{\mathrm{r}}(q_{\mathrm{r}}+2q_{\mathrm{t}})/2^{\nu +1}.$$

For the second case, $\dot{\mathbf{A}}$ gets 1 from $\mathcal{VR}$ in response to the query $(\mathit{g}⊡(({\mathit{id}}_1,c^{\left(i^{*}\right)}),\dots ,({\mathit{id}}_n,c^{\left(i^{*}\right)})),T^{*})$, and $({\mathit{id}}_{j^{*}},c^{\left(i^{*}\right)})$ is a fresh pair. Thus, ${\mathcal{G}}_{\mathsf{AM},\mathbf{A}}^{\mathrm{uf}}$ outputs 1.    □

5.2. Completeness and Soundness

It is easy to see that the completeness of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ is reduced to the completeness of $\mathsf{GT}$ since $\mathsf{AM}$ satisfies correctness:

Theorem 2. 

If $\mathsf{GT}$ satisfies completeness, then, for any adversary $\mathbf{A}$ against $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$,

$${\mathrm{Adv}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}]}^{\mathrm{cmp}}\left(\mathbf{A}\right)=0.$$

Proof. 

Since $\mathsf{GT}$ satisfies completeness, for any valid tag, there exists some test such that it examines the tag and all the other tags it examines are valid. Since $\mathsf{AM}$ satisfies correctness, any aggregate tag generated only from valid tags is judged valid.    □

The soundness of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ is reduced to the soundness of $\mathsf{AM}$:

Theorem 3. 

For any adversary $\mathbf{A}$ against $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ for soundness, triggering at most $q_{\mathrm{r}}$ runs of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ and making at most $q_{\mathrm{t}}$ tagging queries and $q_{\mathrm{c}}$ corrupt queries, there exists some adversary $\dot{\mathbf{A}}$ satisfying

$${\mathrm{Adv}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}]}^{\mathrm{snd}}\left(\mathbf{A}\right)\le {\mathrm{Adv}}_{\mathsf{AM}}^{\mathrm{snd}}\left(\dot{\mathbf{A}}\right).$$

The number of queries made by $\dot{\mathbf{A}}$ to $\mathcal{TG}$ is at most $q_{\mathrm{t}}$. The number of queries made by $\dot{\mathbf{A}}$ to $\mathcal{KD}$ is at most $q_{\mathrm{c}}$. The number of queries made by $\dot{\mathbf{A}}$ to $\mathcal{VR}$ is at most the total number of tests during the runs of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$. The number of queries made by $\dot{\mathbf{A}}$ to $\mathcal{AVR}$ is also at most the total number of tests during the runs of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$. The running time of $\dot{\mathbf{A}}$ is at most about that of ${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{snd}}$.

Proof. 

In ${\mathcal{G}}_{\mathsf{AM},\dot{\mathbf{A}}}^{\mathrm{snd}}$, $\dot{\mathbf{A}}$ runs ${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{snd}}$ in the similar way described in the proof of Theorem 1. $\dot{\mathbf{A}}$ simulates $S{A}^{\left(1\right)},S{A}^{\left(2\right)},\dots ,S{A}^{\left(q_{\mathrm{r}}\right)}$ by making use of $\mathcal{VR}$. Suppose that $\mathbf{A}$ returns $({\mathit{id}}_1,t_1^{\left(i\right)}),({\mathit{id}}_2,t_2^{\left(i\right)}),\dots ,({\mathit{id}}_n,t_n^{\left(i\right)})$ to $S{A}^{\left(i\right)}$ in response to the challenge $c^{\left(i\right)}$. Then, for each test $\mathit{g}:=(g_1,\dots ,g_n)\in {\{0,1\}}^n$ during the i-th run of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$, $\dot{\mathbf{A}}$ also makes a query $\mathit{g}⊡(({\mathit{id}}_1,c^{\left(i\right)},t_1^{\left(i\right)}),\dots ,({\mathit{id}}_n,c^{\left(i\right)}),t_n^{\left(i\right)})$ to $\mathcal{AVR}$.

Suppose that ${\mathcal{G}}_{\mathsf{EA}[\mathsf{GT},\mathsf{AM}],\mathbf{A}}^{\mathrm{snd}}$ outputs 1 in ${\mathcal{G}}_{\mathsf{AM},\dot{\mathbf{A}}}^{\mathrm{snd}}$. Then, there exists some $i^{*}$ and $j^{*}$ such that $\left\{{\mathit{id}}_{j^{*}}\right|t_{j^{*}}^{\left(i^{*}\right)}\ne \mathsf{Tag}(k_{j^{*}},c^{\left(i^{*}\right)})\}\setminus {\mathcal{J}}^{\left(i^{*}\right)}\ne \varnothing$. Thus, during the $i^{*}$-th run of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$, there exists some test ${\mathit{g}}^{*}:=(g_1^{*},\dots ,g_n^{*})$ with $g_{j^{*}}^{*}=1$ such that $\mathsf{Ver}({\mathit{g}}^{*}⊡(({\mathit{id}}_1,k_1),\dots ,({\mathit{id}}_n,k_n)),{\mathit{g}}^{*}⊡(({\mathit{id}}_1,c^{\left(i^{*}\right)}),\dots ,({\mathit{id}}_n,c^{\left(i^{*}\right)})),T^{*})=1$ and $t_{j^{*}}^{\left(i^{*}\right)}\ne \mathsf{Tag}(k_{j^{*}},c^{\left(i^{*}\right)})$, where $T^{*}:=\mathsf{Agg}({\mathit{g}}^{*}⊡(({\mathit{id}}_1,c^{\left(i^{*}\right)},t_1^{\left(i^{*}\right)}),\dots ,({\mathit{id}}_n,c^{\left(i^{*}\right)},t_n^{\left(i^{*}\right)})))$. Thus, $\dot{\mathbf{A}}$ gets 1 from $\mathcal{AVR}$ in response to ${\mathit{g}}^{*}⊡(({\mathit{id}}_1,c^{\left(i^{*}\right)},t_1^{\left(i^{*}\right)}),\dots ,({\mathit{id}}_n,c^{\left(i^{*}\right)},t_n^{\left(i^{*}\right)}))$.    □

5.3. Enhancing the Generic Construction

From the results so far, we confirm that $\mathsf{EA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$ and $\mathsf{EA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{H}}]$ satisfy impersonation resistance and satisfy completeness if $\mathsf{GT}$ satisfies completeness. On the other hand, $\mathsf{EA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$ does not satisfy soundness, while $\mathsf{EA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{H}}]$ satisfies soundness. We enhance the proposed scheme and present $\mathsf{EEA}[\mathsf{GT},\mathsf{AM}]$, which achieves soundness even with ${\mathsf{AM}}_{\mathrm{X}}$.

$\mathsf{EEA}[\mathsf{GT},\mathsf{AM}]$ is equipped with a PRF $R:\mathcal{R}\times \mathcal{I}\times {\{0,1\}}^{\nu +\tau }\to {\{0,1\}}^{\tau }$, where $\mathcal{R}$ is its key space. A shared secret key $r\in \mathcal{R}$ is given to the server and the aggregator. Notice that, for soundness, the communication channel between the server and the aggregator is assumed to be authenticated. Thus, the assumption is not critical that the server and the aggregator share a secret key. $\mathsf{EEA}[\mathsf{GT},\mathsf{AM}]$ is specified as follows:

Steps 1 to 3:

Identical to those of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$.

Step 4:

$t_j\leftarrow R_r({\mathit{id}}_j,c\parallel t_j)$ for $1\le j\le n$.

Step 5:

Identical to Step 4 of $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$.

The sole difference between $\mathsf{EEA}[\mathsf{GT},\mathsf{AM}]$ and $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$ is that the former utilizes R to randomize the tags from the entities. Thus, Theorems 1 and 2 hold for $\mathsf{EEA}[\mathsf{GT},\mathsf{AM}]$ as well as for $\mathsf{EA}[\mathsf{GT},\mathsf{AM}]$. In addition, $\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$ satisfies soundness if R is a secure PRF:

Theorem 4. 

Let $\mathbf{A}$ be any adversary against $\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$ for soundness. Suppose that $\mathbf{A}$ triggers at most $q_{\mathrm{r}}$ runs of $\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$ and makes at most $q_{\mathrm{t}}$ tagging queries. Suppose that the runs of $\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$ conduct at most $q_{\mathrm{v}}$ tests in total and R is called at most $q_{\mathrm{p}}$ times in total. Then, there exists some adversary $\dot{\mathbf{A}}$ such that

$${\mathrm{Adv}}_{\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]}^{\mathrm{snd}}\left(\mathbf{A}\right)\le {\mathrm{Adv}}_R^{\mathrm{prf}}\left(\dot{\mathbf{A}}\right)+q_{\mathrm{r}}^2/2^{\nu +1}+q_{\mathrm{v}}/2^{\tau }.$$

$\dot{\mathbf{A}}$ makes at most $q_{\mathrm{p}}$ queries to its oracle, and its running time is at most about that of ${\mathcal{G}}_{\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}],\mathbf{A}}^{\mathrm{snd}}$.

Proof. 

Let ${\mathsf{EEA}}^{\rho }[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$ be identical to $\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$ except that the former uses $\rho :\mathcal{I}\times {\{0,1\}}^{\nu +\tau }\to {\{0,1\}}^{\tau }$ chosen uniformly at random instead of $R_r$ with $r\leftarrow \leftarrow \mathcal{R}$. The adversary $\dot{\mathbf{A}}$ against R is given access to either $R_r$ or $\rho$. $\dot{\mathbf{A}}$ runs ${\mathcal{G}}_{\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}],\mathbf{A}}^{\mathrm{snd}}$ or ${\mathcal{G}}_{{\mathsf{EEA}}^{\rho }[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}],\mathbf{A}}^{\mathrm{snd}}$ with the use of $R_r$ or $\rho$, respectively. $\dot{\mathbf{A}}$ outputs 1 iff $\mathbf{A}$ is successful for soundness. Then,

$${\mathrm{Adv}}_{\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]}^{\mathrm{snd}}\left(\mathbf{A}\right)\le {\mathrm{Adv}}_{{\mathsf{EEA}}^{\rho }[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]}^{\mathrm{snd}}\left(\mathbf{A}\right)+{\mathrm{Adv}}_R^{\mathrm{prf}}\left(\dot{\mathbf{A}}\right)$$

since

$$\begin{array}{cc}\hfill {\mathrm{Adv}}_R^{\mathrm{prf}}\left(\dot{\mathbf{A}}\right)& =\left|Pr[{\dot{\mathbf{A}}}^{R_r}=1]-Pr[{\dot{\mathbf{A}}}^{\rho }=1]\right|\hfill \\ \hfill & =\left|{\mathrm{Adv}}_{\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]}^{\mathrm{snd}}\left(\mathbf{A}\right)-{\mathrm{Adv}}_{{\mathsf{EEA}}^{\rho }[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]}^{\mathrm{snd}}\left(\mathbf{A}\right)\right|.\hfill \end{array}$$

For ${\mathcal{G}}_{{\mathsf{EEA}}^{\rho }[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}],\mathbf{A}}^{\mathrm{snd}}$, let $\mathtt{Col}$ be the event that there exists a collision among the challenges generated in the runs of ${\mathsf{EEA}}^{\rho }[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$. Then,

$${\mathrm{Adv}}_{{\mathsf{EEA}}^{\rho }[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]}^{\mathrm{snd}}\left(\mathbf{A}\right)\le Pr\left[\mathtt{Col}\right]+Pr[{\mathcal{G}}_{{\mathsf{EEA}}^{\rho }[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}],\mathbf{A}}^{\mathrm{snd}}=1|\overline{\mathtt{Col}}].$$

Since $\mathbf{A}$ triggers at most $q_{\mathrm{r}}$ runs of $\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$,

$$Pr\left[\mathtt{Col}\right]\le (q_{\mathrm{r}}(q_{\mathrm{r}}-1)/2)/2^{\nu }\le q_{\mathrm{r}}^2/2^{\nu +1}.$$

Finally, let us see that

$$Pr[{\mathcal{G}}_{{\mathsf{EEA}}^{\rho }[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}],\mathbf{A}}^{\mathrm{snd}}=1|\overline{\mathtt{Col}}]\le q_{\mathrm{v}}/2^{\tau }.$$

Let $c^{\left(i\right)}$ be the challenge in the i-th run of ${\mathsf{EEA}}^{\rho }[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$ and $t_{i,j}:=F_{k_j}\left(c^{\left(i\right)}\right)$. If $\mathtt{Col}$ does not occur, then $\rho ({\mathit{id}}_j,c^{\left(i\right)}\parallel t_{i,j})$ is chosen uniformly at random. Thus, the probability that the result of a test involving $({\mathit{id}}_j,t_{i,j}^{\prime })$ such that $t_{i,j}^{\prime }\ne t_{i,j}$ happens to be valid is at most $1/2^{\tau }$.    □

6. Performance Evaluation

We implemented the verification algorithms of group-testing aggregate entity authentication for $\mathsf{EA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$, $\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$, and $\mathsf{EA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{H}}]$. We used the MAC function HMAC-SHA-256 for tagging and SHA-256 to aggregate tags for ${\mathsf{AM}}_{\mathrm{H}}$. For $\mathsf{GT}$, we adopted non-adaptive group testing and used d-disjunct matrices generated by the shifted transversal design (STD) [30], where d is the upper bound on the number of invalid entities.

We implemented the algorithms in Python 3.10.9 and utilized the modules hmac and hashlib for SHA-256 and HMAC-SHA-256. We evaluated the performance of our implementations on a MacBook Pro with Apple M1, 16 GB of memory, and macOS Ventura 13.3.1.

The results are summarized in

Table 1. Runtime (milliseconds).

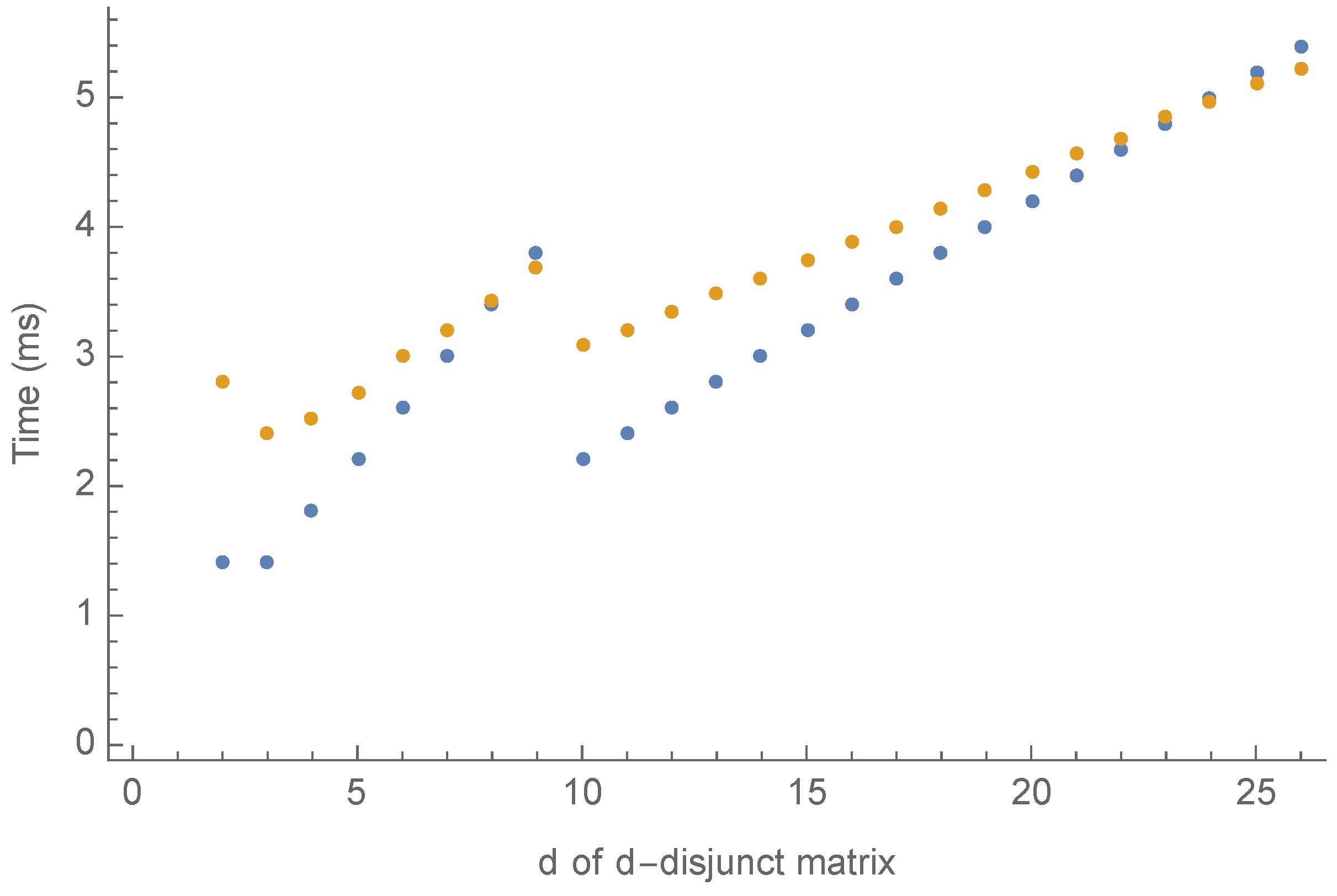
Number of Entities	Tagging	Verification
		$\mathsf{EA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$	$\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$	$\mathsf{EA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{H}}]$
100	$1.37\times {10}^{-1}$	$2.65\times {10}^{-1}$	$4.28\times {10}^{-1}$	$3.05\times {10}^{-1}$
1000	$7.83\times {10}^{-1}$	$3.61$	$4.18$	$3.66$
10,000	$7.31$	$8.88\times {10}^1$	$1.03\times {10}^2$	$1.24\times {10}^2$

. For the numbers of the entities 100, 1000, and 10,000, the sizes of the matrices are $66\times 100$, $666\times 1000$, and $6969\times$ 10,000, respectively. They are 5-, 17-, and 68-disjunct matrices, respectively.

Each time presented in Table 1 is the smallest of ten measurements. The “Tagging” column shows the time required to generate all the tags for the entities. Thus, they almost equal the time to verify all the tags of the entities one by one. For the same number of entities, there is no significant difference in the times required for verification by $\mathsf{EA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$, $\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$, and $\mathsf{EA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{H}}]$. They depend on the numbers of 1’s in the group-testing matrices, which are 600, 18,000, and 690,000 for 100, 1000, and 10,000 entities, respectively.

Figure 3 presents more details on the runtime for verification of $\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$ with 1000 entities and $2\le d\le 26$.

Table 2. The number of rows and the number of 1’s of d-disjunct matrices used for the experiments on Figure 3.

d	2	3	4	5	6	7	8	9	10
# rows	49	77	99	121	169	255	289	361	407
# 1’s	7000	7000	9000	11,000	13,000	15,000	17,000	19,000	11,000
d	11	12	13	14	15	16	17	18	19
# rows	444	481	518	555	592	629	666	703	740
# 1’s	12,000	13,000	14,000	15,000	16,000	17,000	18,000	19,000	20,000
d	20	21	22	23	24	25	26
# rows	777	814	851	888	925	962	999
# 1’s	21,000	22,000	23,000	24,000	25,000	26,000	27,000

presents the number of rows and the number of 1’s in the group-testing matrices used for the experiments. If $d\ge 27$, then $\mathsf{EEA}[\mathsf{GT},{\mathsf{AM}}_{\mathrm{X}}]$ cannot reduce the amount of communication between the server and the aggregator.

In Figure 3, the orange dots represent the times. For reference, we also give the blue dots representing the values of $\left(\mathrm{the}\mathrm{number}\mathrm{of}1’\mathrm{s}\mathrm{in}\mathrm{the}\mathrm{group}-\mathrm{testing}\mathrm{matrix}\right)/5000$. As shown in Table 2, for group-testing matrices based on STD, the number of rows increases with the value of d. On the other hand, this is not necessarily the case for the number of 1’s.

7. Concluding Remark

We have introduced and explored group-testing aggregate authentication. We have first formalized the scheme and security requirements. Then, we have presented a general construction utilizing a group-testing scheme and an aggregate MAC scheme. We have reduced the security properties of the generic construction and its enhancement to those of the underlying group testing and aggregate MAC. Finally, we have shown results on the performance evaluation of the proposed construction instantiated with SHA-256 and HMAC.

The proposed construction can easily be deployed due to its simplicity. In addition, any progress in group testing and aggregate MAC will benefit it. Future work is to improve the performance further. It is interesting to see if the idea of Minematsu and Kamiya [12] is effective for our proposed construction.