TCAD Modeling of GaN HEMT Output Admittance Dispersion through Trap Rate Equation Green’s Functions
Abstract
1. Introduction
2. Trap Dynamic Model Implementation
- Analysis of nonlinear dynamic operation, and in particular large-signal periodic (in our implementation through the Harmonic Balance method);
- Straightforward extension to non-local trap mechanisms;
- Availability of the Green’s Functions of the trap rate equations, that are useful for numerically efficient sensitivity analysis.
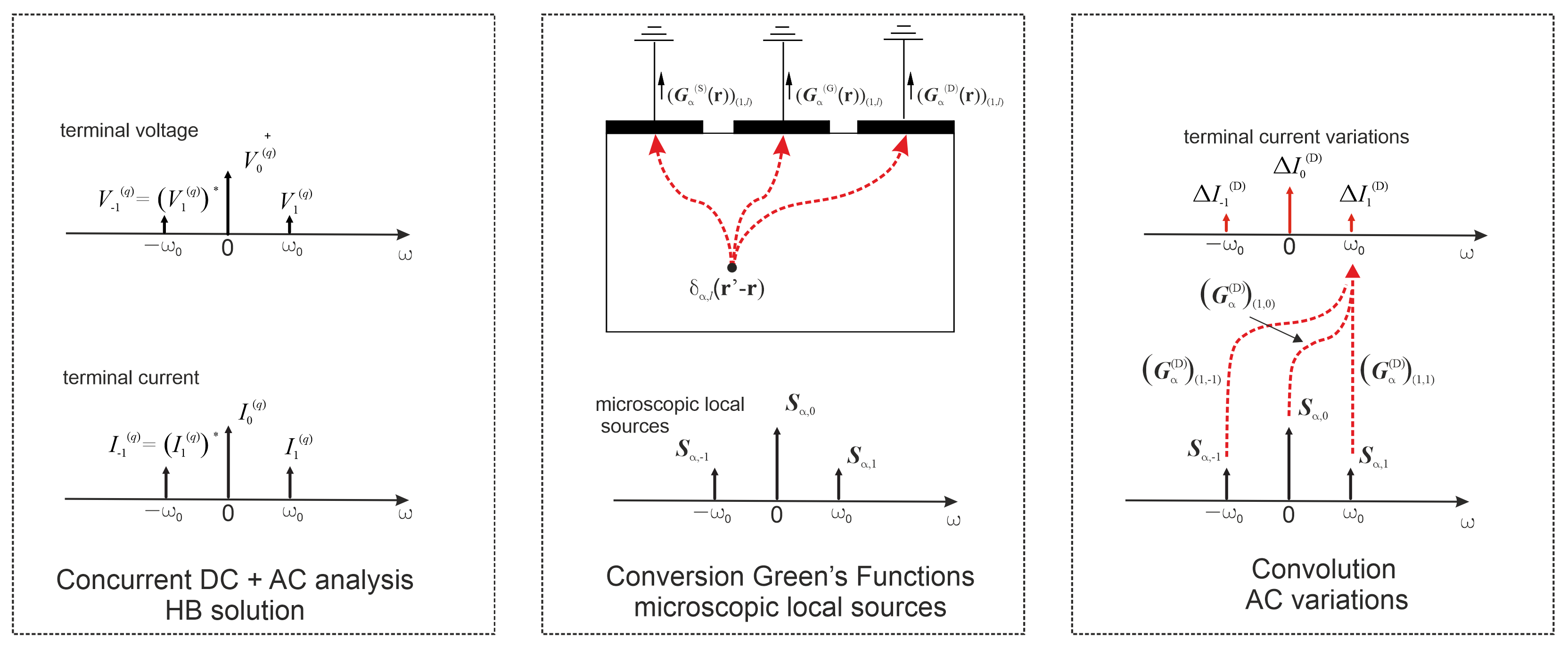
- The system (11) is converted into the frequency domain, yielding the HB system [22]where and are the collection of the harmonic amplitudes of and , respectively. is an operator representing time derivation in the frequency domain, and is the operator implementing the discrete Fourier transform between phasors and time samples. In this contribution, concurrent DC and AC analyses are carried out by applying a DC voltage and a small-amplitude tone to the contacts, and calculating the corresponding phasors of the terminal currents, see Figure 1 (left). The simulation is fast, since the spectrum can be truncated to DC plus the fundamental frequency. The AC Y matrix is then recovered aswhere and are the phasors of voltage at terminal r and of current at terminal q, respectively (see Figure 1, left). Notice that the admittance matrix is not based on any equivalent circuit, but rather directly stems from the solution of the physical model.
- System (12) is linearized and the CGFs are computed with negligible numerical effort using the algorithms detailed in [22,28]. Furthermore, assuming a static parameter variation , the microscopic local sources are computed as the residual of (12) evaluated with the nominal solution and [20]. Since the parameter variation is static, the varied residual is characterized by the same spectrum of the nominal solution, as shown in Figure 1 (middle).
- The variation of the AC terminal currents due to is recovered by the convolution integralwhere is the element of the Conversion Green’s Function.A graphic interpretation of the convolution is sketched in Figure 1 (right), where it is evident that (14) can be split into three individual contributions accounting for the frequency conversion effects towards the fundamental frequency. In particular, the element of the Green’s Function accounts for the conversion from DC.
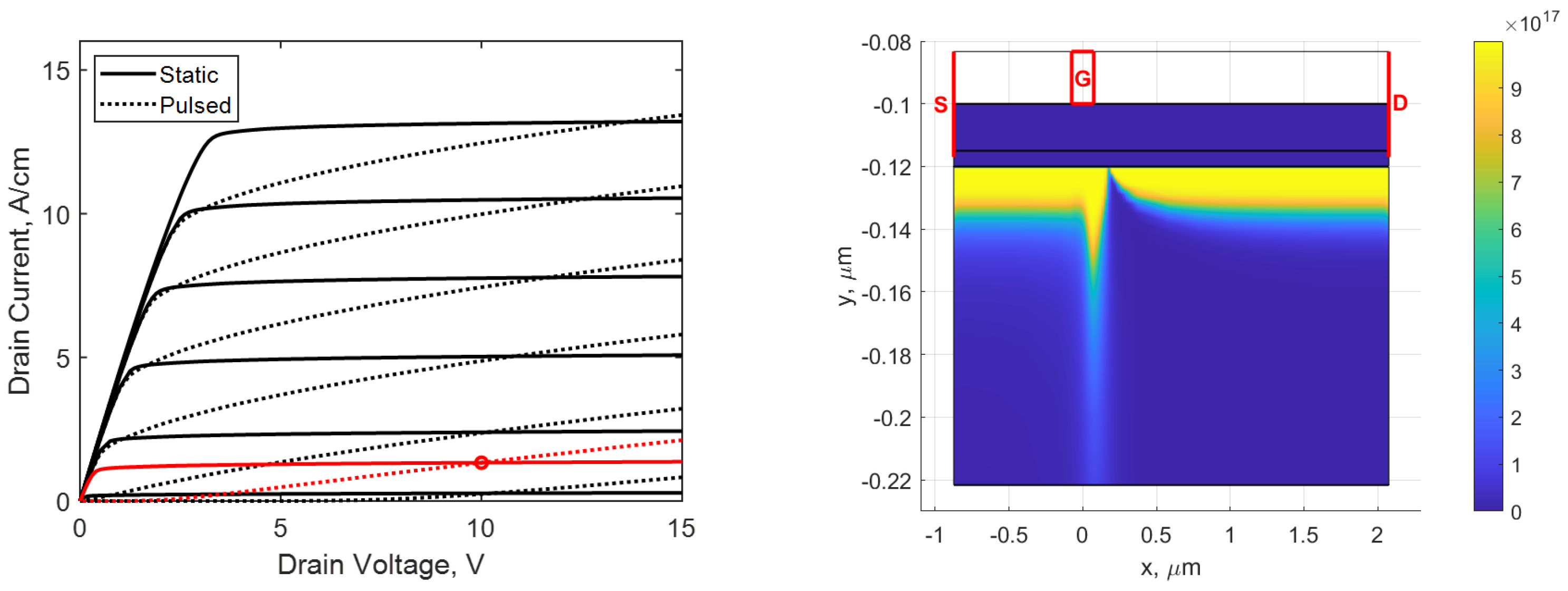
3. HEMT Device Structure
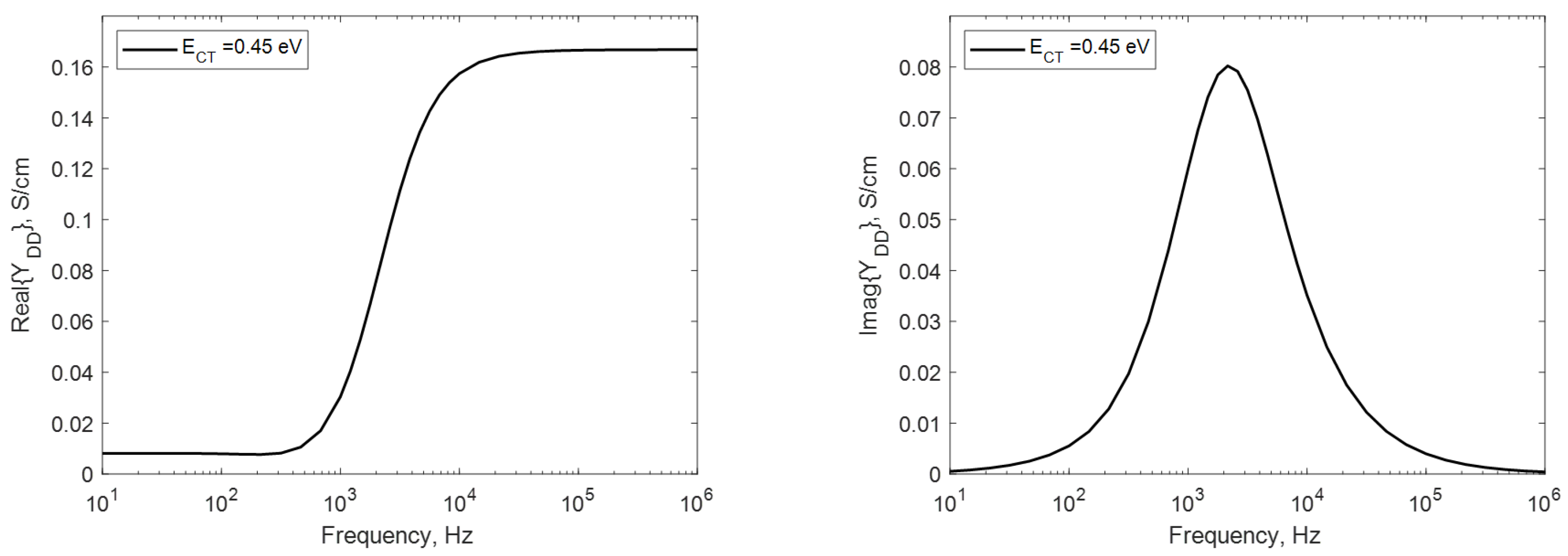
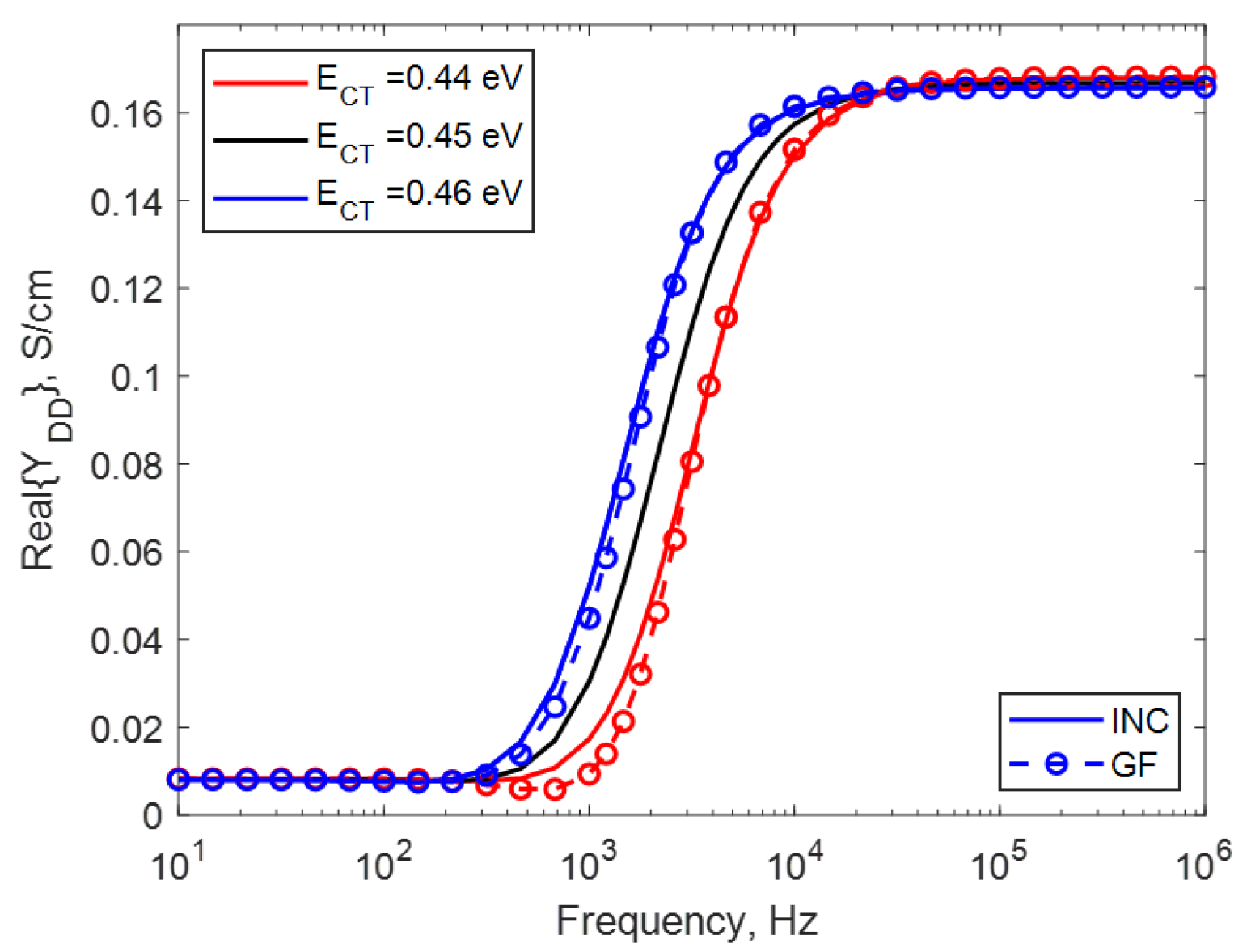
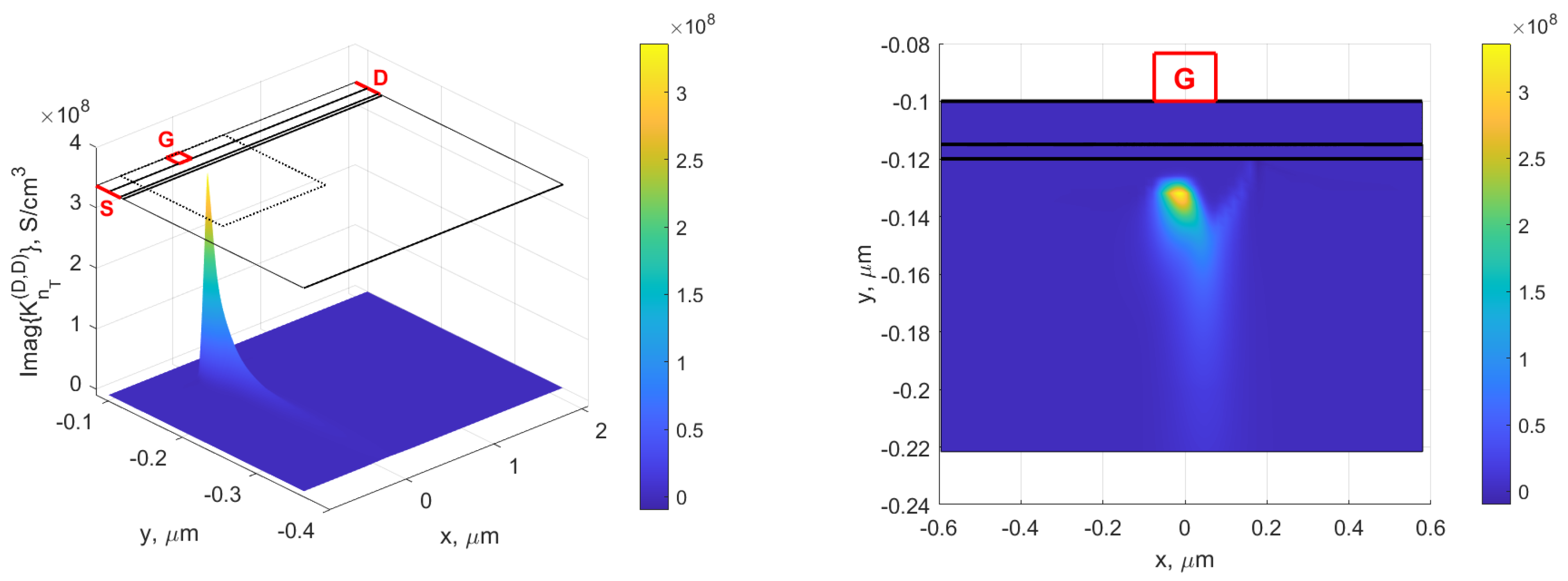
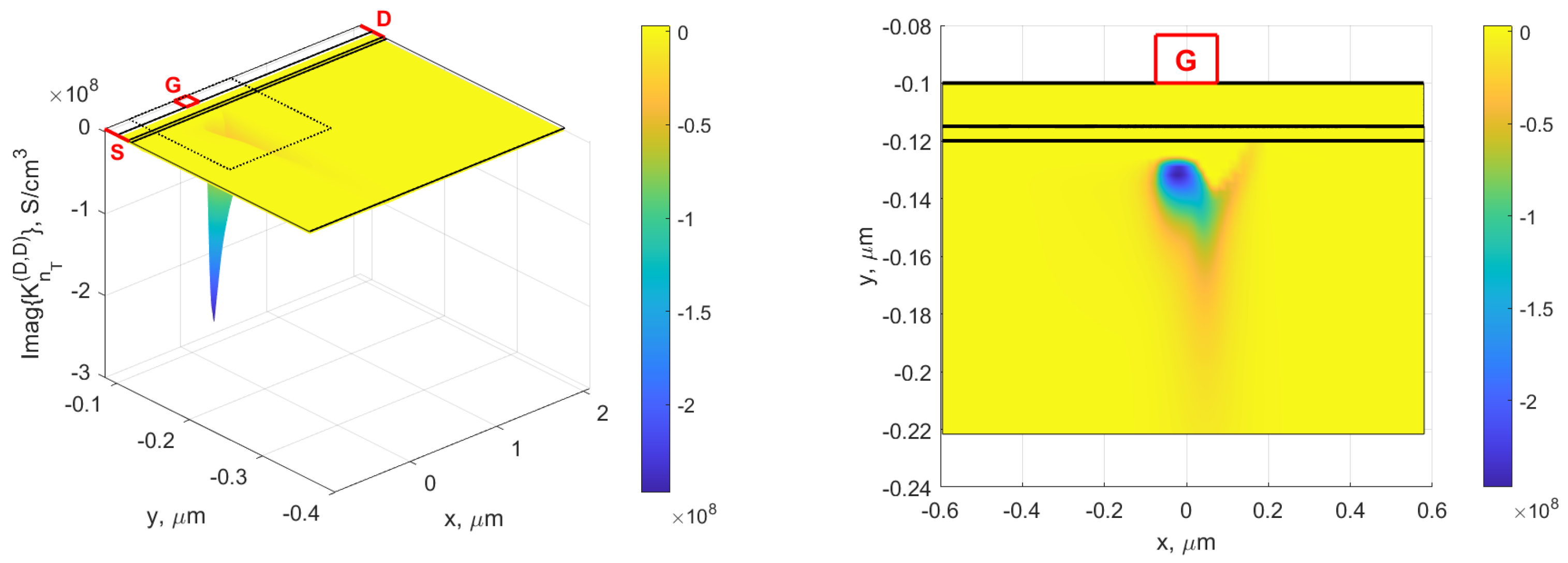
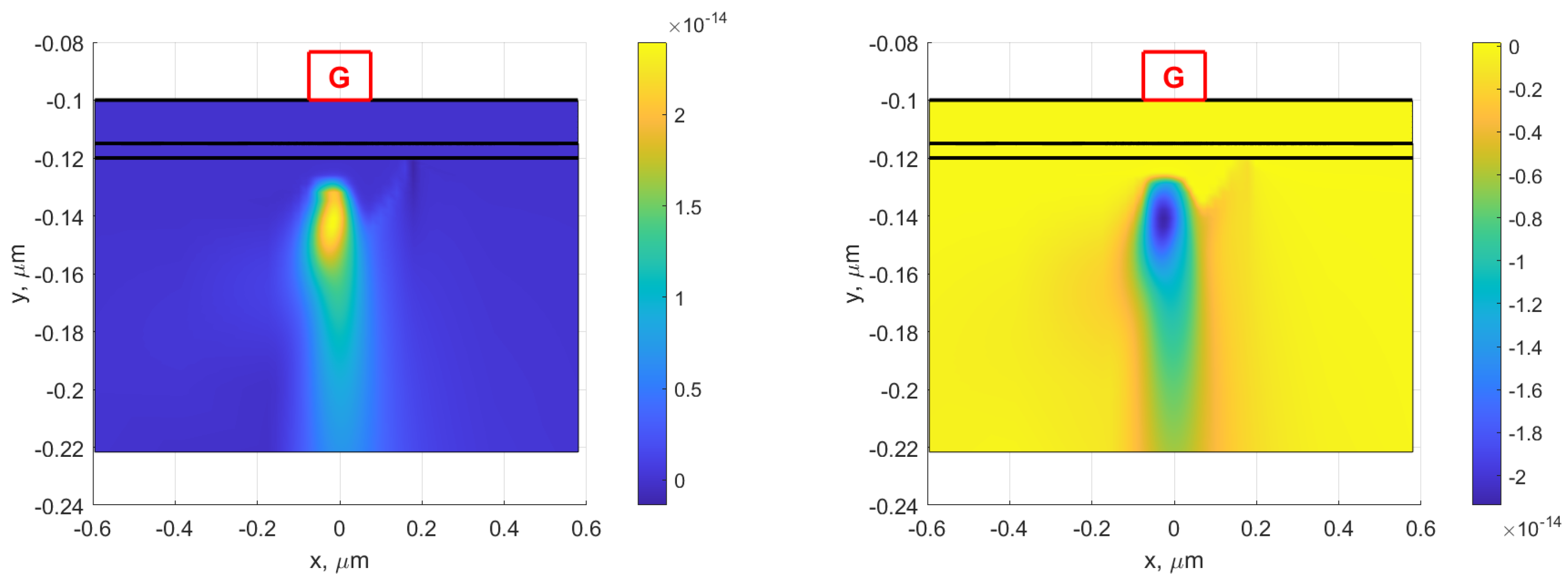
4. Sensitivity of Real
5. Sensitivity of
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mishra, U.; Likun, S.; Kazior, T.; Wu, Y.F. GaN-Based RF Power Devices and Amplifiers. Proc. IEEE 2008, 96, 287–305. [Google Scholar] [CrossRef]
- Meneghesso, G.; Verzellesi, G.; Danesin, F.; Rampazzo, F.; Zanon, F.; Tazzoli, A.; Meneghini, M.; Zanoni, E. Reliability of GaN High-Electron-Mobility Transistors: State of the Art and Perspectives. IEEE Trans. Device Mater. Reliab. 2008, 8, 332–343. [Google Scholar] [CrossRef]
- UMS GaN GH15-10. Available online: https://www.ums-rf.com/ums-gan-gh15-10-technology-is-space-evaluated/ (accessed on 28 May 2023).
- The Qorvo Gan Advantage. Available online: https://www.qorvo.com/innovation/technology/gan (accessed on 28 May 2023).
- MMIC Advanced Technology. Available online: https://www.winfoundry.com/en-US/Tech/tech_advanced (accessed on 28 May 2023).
- III—V Processes. Available online: https://www.ommic.com/iii-v-processes/ (accessed on 28 May 2023).
- Wang, K.; Jiang, H.; Liao, Y.; Xu, Y.; Yan, F.; Ji, X. Degradation Prediction of GaN HEMTs under Hot-Electron Stress Based on ML-TCAD Approach. Electronics 2022, 11, 3582. [Google Scholar] [CrossRef]
- Modolo, N.; Santi, C.D.; Minetto, A.; Sayadi, L.; Prechtl, G.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Trap-state mapping to model GaN transistors dynamic performance. Sci. Rep. 2022, 12, 1755. [Google Scholar] [CrossRef] [PubMed]
- Joshi, V.; Soni, A.; Tiwari, S.P.; Shrivastava, M. A Comprehensive Computational Modeling Approach for AlGaN/GaN HEMTs. IEEE Trans. Nanotechnol. 2016, 15, 947–955. [Google Scholar] [CrossRef]
- Zagni, N.; Verzellesi, G.; Chini, A. Temperature-Independent Current Dispersion in 0.15 μm AlGaN/GaN HEMTs for 5G Applications. Micromachines 2022, 13, 2244. [Google Scholar] [CrossRef] [PubMed]
- Angelotti, A.M.; Gibiino, G.P.; Santarelli, A.; Florian, C. Experimental Characterization of Charge Trapping Dynamics in 100-nm AlN/GaN/AlGaN-on-Si HEMTs by Wideband Transient Measurements. IEEE Trans. Electron Devices 2020, 67, 3069–3074. [Google Scholar] [CrossRef]
- Oishi, T.; Otsuka, T.; Tabuchi, M.; Yamaguchi, Y.; Shinjo, S.; Yamanaka, K. Bias Dependence Model of Peak Frequency of GaN Trap in GaN HEMTs Using Low-Frequency Y22 Parameters. IEEE Trans. Electron Devices 2021, 68, 5565–5571. [Google Scholar] [CrossRef]
- Vertiatchikh, A.; Eastman, L. Effect of the surface and barrier defects on the AlGaN/GaN HEMT low-frequency noise performance. IEEE Electron Device Lett. 2003, 24, 535–537. [Google Scholar] [CrossRef]
- Beleniotis, P.; Schnieder, F.; Chevtchenko, S.; Rudolph, M. Localization of Trapping Effects in GaN HEMTs with Pulsed S-parameters and Compact Models. In Proceedings of the 2022 17th European Microwave Integrated Circuits Conference (EuMIC), Milan, Italy, 26–27 September 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Gomes, J.L.; Nunes, L.C.; Pedro, J.C. Transient Pulsed S-Parameters for Trapping Characterization. In Proceedings of the 2020 International Workshop on Integrated Nonlinear Microwave and Millimetre-Wave Circuits (INMMiC), Cardiff, UK, 16–17 July 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Nicollian, E.H.; Goetzberger, A. MOS Conductance Technique For Measuring Surface State Parameters. Appl. Phys. Lett. 1965, 7, 216–219. [Google Scholar] [CrossRef]
- Nicollian, E.; Goetzberger, A.; Lopez, A. Expedient method of obtaining interface state properties from MIS conductance measurements. Solid-State Electron. 1969, 12, 937–944. [Google Scholar] [CrossRef]
- Subramani, N.K. Physics-Based TCAD Device Simulations and Measurements of GaN HEMT Technology for RF Power Amplifier Applications. Ph.D. Dissertation, University of Limoges, Limoges, France, 2017. Available online: https://tel.archives-ouvertes.fr/tel-01702325 (accessed on 28 May 2023).
- Shanbhag, A.; Sruthi, M.P.; Chakravorty, A.; DasGupta, N.; DasGupta, A. Compact Modeling of Static and Transient Effects of Buffer Traps in GaN HEMTs. IEEE Trans. Electron Devices 2022, 69, 999–1005. [Google Scholar] [CrossRef]
- Donati Guerrieri, S.; Bonani, F.; Bertazzi, F.; Ghione, G. A Unified Approach to the Sensitivity and Variability Physics-Based Modeling of Semiconductor Devices Operated in Dynamic Conditions—Part I: Large-Signal Sensitivity. IEEE Trans. Electron Devices 2016, 63, 1195–1201. [Google Scholar] [CrossRef]
- Donati Guerrieri, S.; Bonani, F.; Bertazzi, F.; Ghione, G. A Unified Approach to the Sensitivity and Variability Physics-Based Modeling of Semiconductor Devices Operated in Dynamic Conditions.—Part II: Small-signal and Conversion Matrix Sensitivity. IEEE Trans. Electron Devices 2016, 63, 1202–1208. [Google Scholar] [CrossRef]
- Bonani, F.; Donati Guerrieri, S.; Ghione, G.; Pirola, M. A TCAD approach to the physics-based modeling of frequency conversion and noise in semiconductor devices under large-signal forced operation. IEEE Trans. Electron Devices 2001, 48, 966–977. [Google Scholar] [CrossRef]
- Raja, P.V.; Subramani, N.K.; Gaillard, F.; Bouslama, M.; Sommet, R.; Nallatamby, J.C. Identification of Buffer and Surface Traps in Fe-Doped AlGaN/GaN HEMTs Using Y21 Frequency Dispersion Properties. Electronics 2021, 10, 3096. [Google Scholar] [CrossRef]
- Potier, C.; Martin, A.; Campovecchio, M.; Laurent, S.; Quere, R.; Jacquet, J.C.; Jardel, O.; Piotrowicz, S.; Delage, S. Trap characterization of microwave GaN HEMTs based on frequency dispersion of the output-admittance. In Proceedings of the 2014 9th European Microwave Integrated Circuit Conference, Rome, Italy, 6–7 October 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Synopsys Sentaurus. Available online: https://www.synopsys.com/silicon/tcad/device-simulation/sentaurus-device.html (accessed on 28 May 2023).
- Bonani, F.; Ghione, G. Noise in Semiconductor Devices; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Troyanovsky, B.; Yu, Z.; Dutton, R.W. Large Signal Frequency Domain Device Analysis Via the Harmonic Balance Technique. In Simulation of Semiconductor Devices and Processes; Springer: Vienna, Austria, 1995; pp. 114–117. [Google Scholar] [CrossRef]
- Donati Guerrieri, S.; Pirola, M.; Bonani, F. Concurrent Efficient Evaluation of Small-Change Parameters and Green’s Functions for TCAD Device Noise and Variability Analysis. IEEE Trans. Electron Devices 2017, 64, 1269–1275. [Google Scholar] [CrossRef]
- Golio, J.; Miller, M.; Maracas, G.; Johnson, D. Frequency-dependent electrical characteristics of GaAs MESFETs. IEEE Trans. Electron Devices 1990, 37, 1217–1227. [Google Scholar] [CrossRef]
- Donati Guerrieri, S.; Ramella, C.; Catoggio, E.; Bonani, F. Bridging the Gap between Physical and Circuit Analysis for Variability-Aware Microwave Design: Modeling Approaches. Electronics 2022, 11, 860. [Google Scholar] [CrossRef]

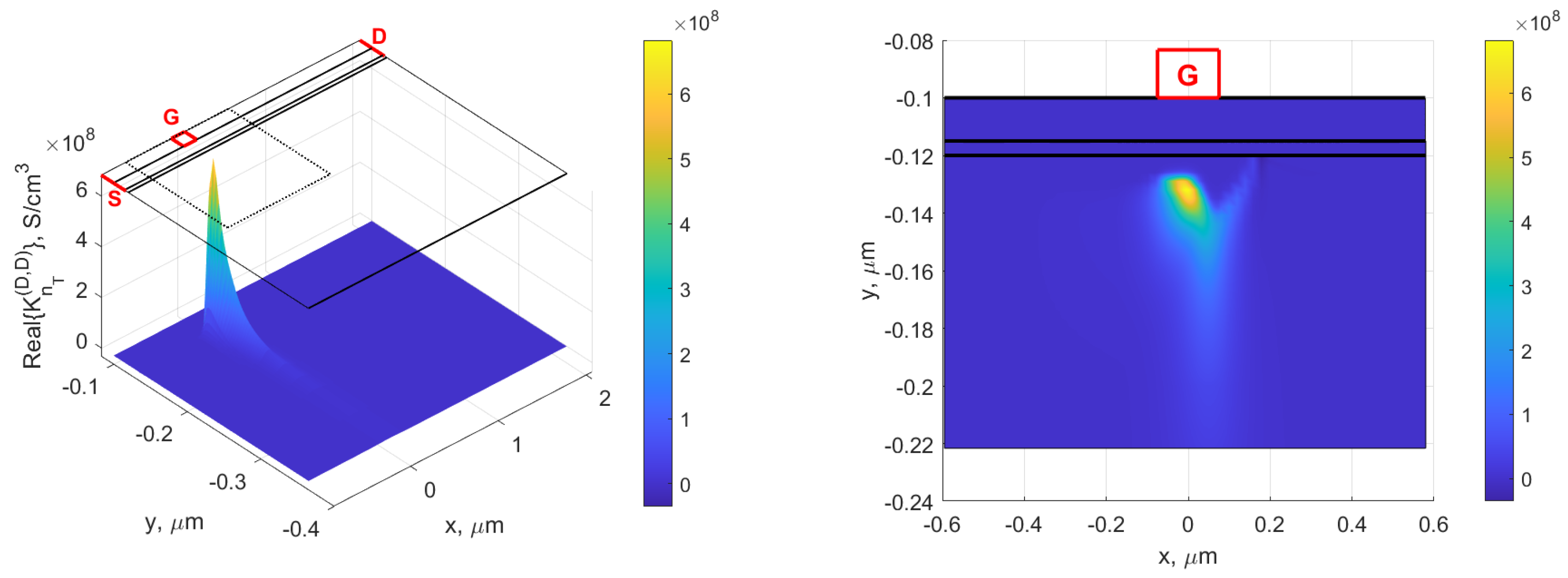
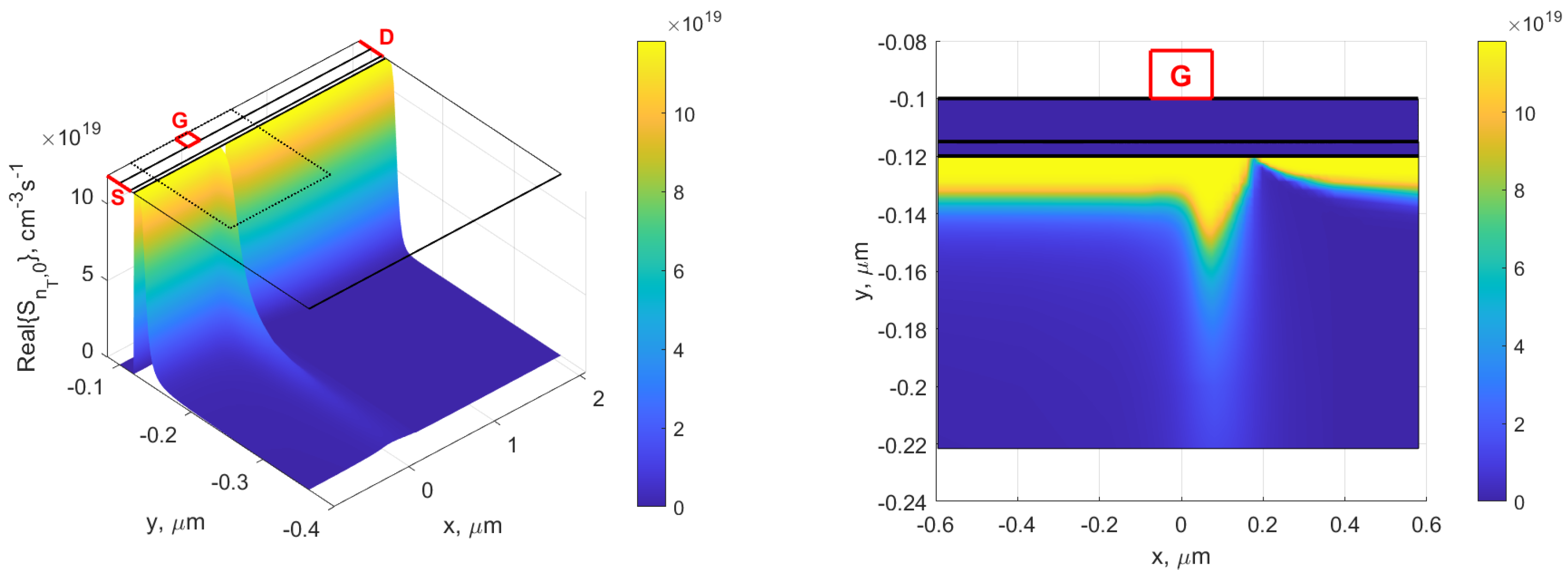
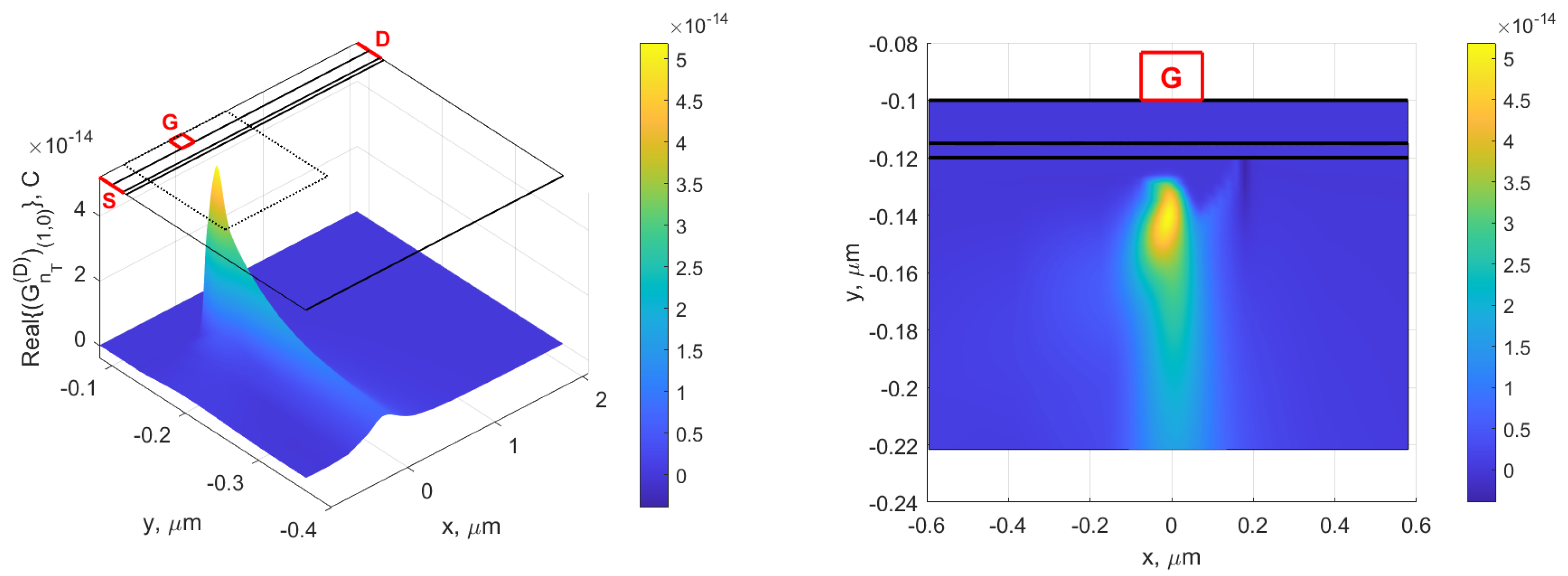
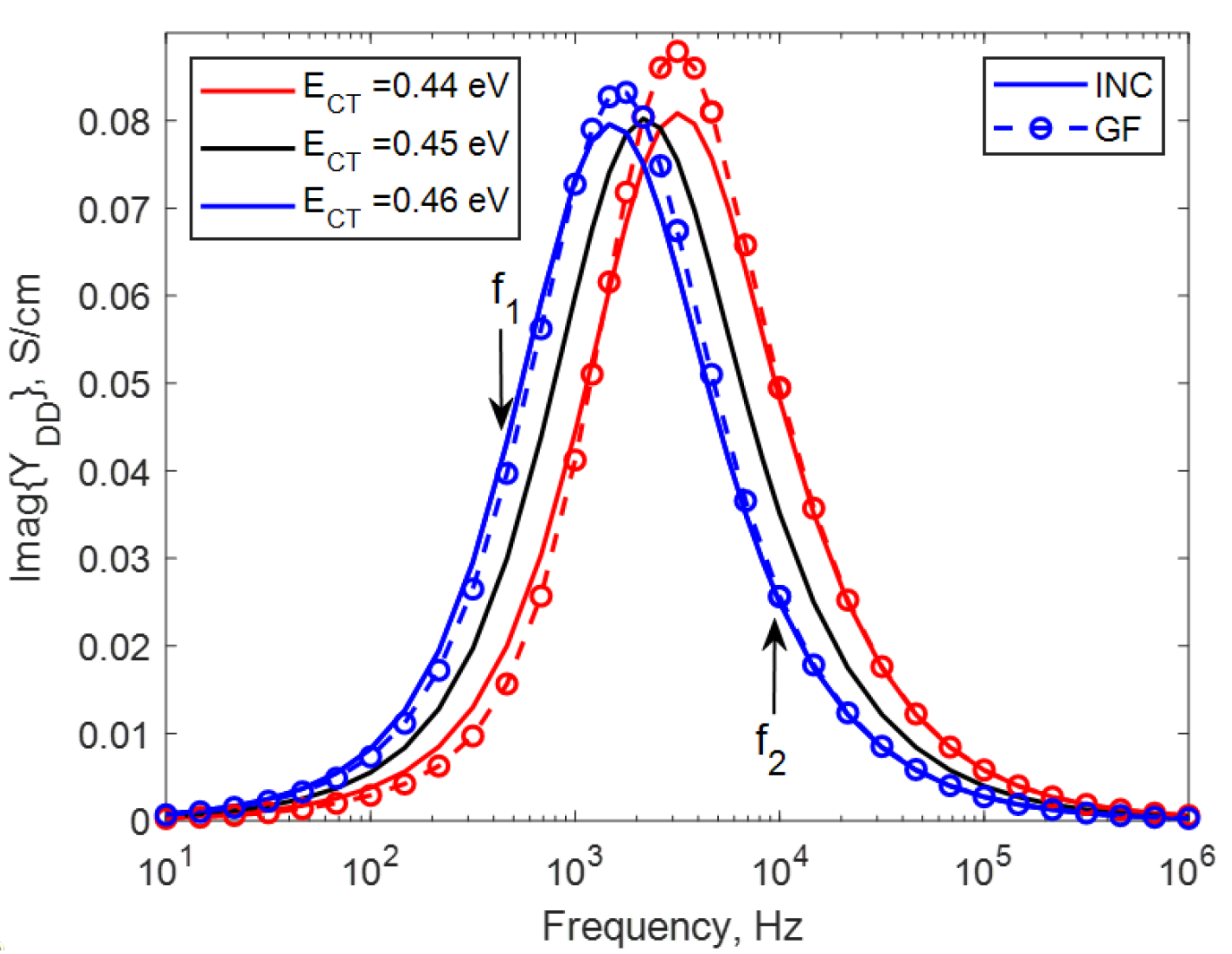
| Real () [S/cm] | [ cm] | |
|---|---|---|
| Static DC | 122 | |
| AC (low frequency) | 124 | |
| Pulsed DC | 0.17 | 6 |
| AC (high frequency) | 0.17 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Catoggio, E.; Donati Guerrieri, S.; Bonani, F. TCAD Modeling of GaN HEMT Output Admittance Dispersion through Trap Rate Equation Green’s Functions. Electronics 2023, 12, 2457. https://doi.org/10.3390/electronics12112457
Catoggio E, Donati Guerrieri S, Bonani F. TCAD Modeling of GaN HEMT Output Admittance Dispersion through Trap Rate Equation Green’s Functions. Electronics. 2023; 12(11):2457. https://doi.org/10.3390/electronics12112457
Chicago/Turabian StyleCatoggio, Eva, Simona Donati Guerrieri, and Fabrizio Bonani. 2023. "TCAD Modeling of GaN HEMT Output Admittance Dispersion through Trap Rate Equation Green’s Functions" Electronics 12, no. 11: 2457. https://doi.org/10.3390/electronics12112457
APA StyleCatoggio, E., Donati Guerrieri, S., & Bonani, F. (2023). TCAD Modeling of GaN HEMT Output Admittance Dispersion through Trap Rate Equation Green’s Functions. Electronics, 12(11), 2457. https://doi.org/10.3390/electronics12112457







