Securely Computing Protocol of Set Intersection under the Malicious Model
Abstract
1. Introduction
- (1)
- This paper proposes an MPC protocol for set intersection under the semi-honest model, based on the Paillier encryption algorithm. It then analyzes potential malicious behaviors that could arise.
- (2)
- Building on the semi-honest model protocol and considering potential malicious behaviors, this paper proposes an MPC protocol for computing set intersection under the malicious model, utilizing cryptographic tools such as cut-and-choose and zero-knowledge proof.
- (3)
- Using the real/ideal model paradigm, the paper proves the security of the proposed protocol under the malicious model and analyzes and compares its efficiency.
- (4)
- The efficacy of the proposed protocols is validated through a range of performance analyses, comparisons, and simulation experiments when compared to existing methodologies.
2. Related Work
3. Preliminary Knowledge
3.1. Paillier Cryptosystem
- (1)
- Public key encryption: The Paillier cryptosystem employs public and private keys for encryption and decryption operations. The public key can be publicly shared, allowing senders to encrypt data using the recipient’s public key and transmitting it through insecure channels. Only the holder of the private key can decrypt the data, ensuring that even if the public key is compromised, attackers cannot access the plaintext. This public key encryption scheme ensures secure transmission.
- (2)
- Randomization: In the Paillier cryptosystem, the encryption process involves the use of random numbers to encrypt the plaintext. Even if the same plaintext is encrypted multiple times, the resulting ciphertext will differ due to the utilization of different random numbers. This randomization feature enhances the security of the cryptosystem by preventing attackers from extracting information about the plaintext by analyzing multiple ciphertexts.
- (3)
- Completeness: The Paillier cryptosystem is complete, enabling encryption and decryption of arbitrary integers without limitations on specific data ranges. This flexibility allows the cryptosystem to handle various types of data, regardless of their size, through encryption and decryption operations.
- (4)
- Resistance to attacks: Extensive cryptographic research and analysis have demonstrated the security and reliability of the Paillier cryptosystem. It withstands many common cryptographic attacks, including chosen plaintext attacks, chosen ciphertext attacks, and active attacks. These attacks attempt to deduce information about the keys or plaintext by obtaining plaintext–ciphertext pairs or manipulating the ciphertext. However, the Paillier cryptosystem effectively thwarts these attacks.
3.2. Zero-Knowledge Proof
- (1)
- Completeness: If the statement being proven is true, the verifier will always accept it.
- (2)
- Soundness: If the statement being proven is false, the verifier will always reject it, and the probability of the prover successfully persuading the verifier is negligible.
- (3)
- Zero-knowledge: During the proof, the verifier does not learn any information about the knowledge or answer being proven by the prover.
- (1)
- Privacy safeguarding: Zero-knowledge proofs enable a prover to validate a statement’s veracity to a verifier without disclosing any specific details about the statement. By solely presenting the essential proof while keeping sensitive data concealed, individual privacy is upheld.
- (2)
- Preservation of confidentiality: Zero-knowledge proofs ensure that the verifier cannot gain access to additional information regarding the statement, apart from verifying its validity. Although the prover can establish the truthfulness of a fact, the verifier cannot extract the specific information underpinning the proof, thereby maintaining confidentiality.
- (3)
- Reliability and verifiability: Zero-knowledge proofs assure that the prover can correctly construct the proof in accordance with predefined rules and protocols, allowing the verifier to verify its validity. This enhances the proof’s dependability and the overall system’s verifiability.
- (4)
- Efficiency: Zero-knowledge proofs can be executed within relatively short timeframes without excessive computational demands. This renders them practical and efficient for real-world applications.
3.3. Cut-and-Choose Method
- (1)
- Security: The cut-and-choose method ensures robust security measures. Participants engage in interactions where one participant (usually the prover) executes the computation and submits evidence, while the other participant (the verifier) randomly selects and verifies a subset of the evidence to establish the correctness of the computation. This mechanism effectively thwarts attacks such as cheating, tampering, and forgery.
- (2)
- Zero-knowledge property: The cut-and-choose method exhibits the zero-knowledge property, enabling the prover to demonstrate the correctness of their computation to the verifier without disclosing any sensitive inputs or computational methods. The verifier solely verifies that the computation’s outcome is correct, without requiring knowledge of the computation’s specifics.
- (3)
- Resilience against attacks: This technique demonstrates robust resistance against various types of attacks. Even if the prover conducts erroneous computations or attempts to deceive by manipulating certain evidence elements, the verifier can effectively identify errors or cheating behaviors through random selection and verification of a portion of the evidence.
- (4)
- Scalability: The cut-and-choose method can be readily scaled to accommodate different application scenarios and computational complexities. Enhancing the precision and reliability of verification can be achieved by increasing the number of evidence elements or selecting a larger number of random samples.
- (5)
- Generality: The cut-and-choose method serves as a versatile zero-knowledge proof protocol applicable across diverse domains and computational tasks. It finds utility in verifying cryptographic protocols, password cracking results, data privacy, and numerous other applications.
3.4. Security under the Malicious Model
3.5. Ranking Method
- (1)
- Participants jointly agree on a complete set , satisfying . Under the complete set , each participant constructs an n-dimension vector according to their own array :where for each , define:
- (2)
- Let , take turns sending the vector to ; construct a new vector according to and :where for each , define:
- (3)
- calculates the sorting position in the following way:
3.6. Coding Method
3.7. Transformation Problem of Set Intersection
4. The MPC Protocol of Set Intersection under the Semi-Honest Model
| Algorithm 1. Computing the set intersection under the semi-honest model. |
| Input: : Alice’s input; : Bob’s input; : public key; : Alice’s private key; : encode with the Coding method 1; : encrypt by the Paillier system; : ciphertexts; : decrypt the ciphertexts. (1) (2) (3) (4) Select and (5) Compute (6) (7) Make (8) If is even and is even then is even; is even; make ; else if is odd then is odd; is odd; make ; else if is odd then make (9) Perform the steps (3)–(8) for and ,, and (10) Obtain the intersection (11) Obtain plain elements of according to the elements in the Output: Intersection of and . |
| Protocol 1. The MPC protocol of set intersection under the semi-honest model. |
| Input: Private set of Alice, private set of Bob. Output: The intersection of and . Preparation: The Paillier cryptosystem’s public and private keys, and respectively, are created by Alice. Following this, Alice transmits the public key to Bob. (1) Alice encodes to and Bob encodes to . Since the following calculations are the same for and , …, , and , the calculation of and are described as an example. In each of the following steps, and , …, , and are calculated at the same time as and . (2) Alice encrypts with the public key to and sends to Bob. (3) Then Bob selects new random numbers ( takes a random odd number) and to calculate , and sends to Alice. (4) Alice gets by decrypting . Alice owns , and makes the set . ① In the case that is an even number, if is an even number (where is a random odd number), according to the properties of odd and even numbers, Alice can conclude that is an even number, since is even, then is even. Then Alice makes . If is an odd number, Alice can conclude that is an odd number, then is odd. Then Alice makes . ② In the case that is an odd number, Alice makes . (5) For and ,, , and , Alice and Bob perform the calculation and judgment in steps (2)–(4) above at the same time. Eventually, Alice obtains the intersection of and . (6) Alice sends to Bob. According to the elements in the intersection , the elements of the corresponding order position (where and ) in Alice and Bob’s respective private sets are the plain elements of the intersection set . The protocol ends. |
5. The MPC Protocol of Set Intersection under the Malicious Model
- (1)
- If Bob is characterized as being semi-honest, Alice may engage in deceitful behavior, such as deliberately conveying an incorrect set to Bob at the conclusion of the protocol, resulting in an inaccurate outcome for Bob. It is inequitable for either party to disclose the computation results to the other.
- (2)
- When Alice is semi-honest, Bob can perform malicious acts such as: Bob does not choose a real random number when calculating . However, as the decryption has eliminated the impact of , Bob cannot get any private information from . If selected by Bob is not a random odd number, but a random even number, then when Alice publishes the value of , Bob will get the correct result, but Alice will not get the correct result.
5.1. Specific Protocol
| Algorithm 2. Computing the set intersection under the malicious model. |
| Input: : Alice’s input; : Bob’s input; : public key generated by Alice; : Public key generated by Bob; : Alice’s private key; : Bob’s private key; : encode with the Coding method 1; : ciphertexts. (1) Compute (2) Compute (3) Exchange and (4) (5) (6) Select odd numbers (7) Select odd numbers (8) (9) (10) Select sets of from sets of (11) Verify If and then continue else terminate (12) Select sets of from sets of (13) Verify If and then continue else terminate (14) Select a group of and from the remaining and (15) Select random numbers and (16) (17) (18) (19) (20) Exchange and (21) Verify If and then continue else terminate (22) Compute to obtain (23) Make (24) If is even and is even then is even; is even; make ; else if is odd then is odd; is odd; make ; else if is odd then make (25) Compute to obtain (26) Perform steps similar to step (24) to make or (27) Perform the steps (6)–(26) above for and ,, , and (28) Obtain and (29) Obtain plain elements of and according to the elements in the and Output: Intersection of and . |
| Protocol 2. The MPC protocol of the set intersection under the malicious model. |
| Input: Private set of Alice; private set of Bob. Output: The intersection of and . Preparation: Alice and Bob each create a public key, and , respectively, for the Paillier cryptosystem, and compute values and . They then exchange values and . (1) Alice encodes to and Bob encodes to . Since the following calculations are the same for and , , , and , the calculation of and are described as an example. In each of the following steps, and , , , and are calculated at the same time as and . (2) For and , Alice and Bob each randomly select odd numbers, denoted as and , respectively, where , and then compute the value of: , , then publish , , respectively. (3) Alice employs the cut-and-choose technique to randomly select sets of from a total of sets of . She then requests Bob to make public the corresponding values of and , which she subsequently validates using and . The protocol proceeds if the verification is successful, otherwise it halts. (4) Bob randomly chooses groups of from a set of groups of , and requests Alice to disclose the corresponding and . Bob then verifies and . If the verification is successful, Bob proceeds with the protocol; otherwise, the protocol terminates. (5) Alice and Bob respectively and randomly select a group of and from the remaining and , and respectively select random numbers and . Alice calculates: , Bob calculates: , and they send the results to each other. (6) Alice calculates , Bob calculates . Next, and exchange one another. (7) In Section 3.2, both parties employ the zero-knowledge proof technique to demonstrate the accuracy of their computation results, thereby verifying and . If one party fails to pass, it is proved to be malicious. (8) If all are proved, Bob has the ability to compute , which enables him to derive , and subsequently acquire . Bob owns , and makes the set . ① In the case that is an even number, if is an even number, according to the properties of odd and even numbers, Bob can conclude that is an even number, so is even. Then Bob makes . If is an odd number, Bob can conclude that is an odd number, then is odd. Then Bob makes . ② In the case that is an odd number, Bob makes . Alice can calculate to obtain , and then obtain . Alice uses similar methods above to make the set or . (9) Alice obtains the set , Bob obtains the set ; the intersection of and , . According to the elements in the intersection , the elements of the corresponding order position (where and ) in Alice and Bob’s respective private sets are the plain elements of the intersection set . The protocol ends. |
5.2. Correctness Analysis
- (1)
- Step (1) in Protocol 2 is for the participants to obtain the coding vectors of their own sets. In this process, Alice converts the elements in her set into random even numbers in the vector , and the elements that do not exist into random odd numbers. In this way, it is avoided to directly use the original data for calculation.
- (2)
- In step (2), Alice publishes , but the published information is encrypted, and Bob cannot obtain any valuable information.
- (3)
- Steps (3)–(5) employ the cut-and-choose technique to ascertain the presence of any malicious behavior among the participants.
- (4)
- In step (7), Alice is required to prove the correctness of the decryption outcome via a zero-knowledge proof. If the in the remaining groups of are also random odd numbers, Bob can calculate and judge the parity of after publishing .
- (5)
- During the implementation of the protocol, the malicious act Alice may successfully perform is that Bob chooses a certain which does not meet the requirements, and does not find it during the verification in step (3). In step (5), Bob mistakenly selects it, leading to an incorrect conclusion. Nevertheless, the information of remains inaccessible to Alice, because is unsolvable for her (there are two unknowns in an equation), so Alice cannot judge the parity of from it.
- (6)
- In steps (7)–(9), the two parties exchanged ciphertext and decrypted it by themselves, avoiding the situation that one party informed the other of the result, which is fair.
5.3. Security Proof
- (1)
- During the execution of the protocol, since is an honest participant, it can be inferred that is also honest, and will replicate the actions of in transmitting the authentic information to the trusted third party (TTP).
- (2)
- During the execution of the protocol, as is acting in a dishonest manner, is also acting dishonestly. The information that they send to TTP is dependent on the policy of , and the policy of aligns with the policy of . Consequently, the input message that transmits to TTP is .
- (3)
- The input information obtained by TTP is , and is calculated.
- (4)
- gets from TTP, uses to get an which is computational, indistinguishable from the obtained by when the protocol is actually implemented, and hands to to get the output of . Subsequently, based on its own input and the protocol outcome, the simulator presumes that the input value of the other party satisfies the outcome, and conducts the protocol execution. In this case, selects to simulate the protocol and generates . The particular steps involved in the implementation process of are as follows:
- ①
- sends the information required in step (2) to ;
- ②
- After publishes the information in step (3), will verify it;
- ③
- In step (4), will publish the information that requires to publish;
- ④
- In step (5), chooses the necessary information from the remaining sets, computes the information, and then publicly discloses it;
- ⑤
- Calculate in step (6) and publish it;
- ⑥
- During step (7), zero-knowledge proof is utilized to authenticate the information, and as a result, acquires the message sequence .
- (1)
- If Alice ignores TTP after getting the information, TTP will send to Bob. Then:
- (2)
- Otherwise, TTP will send to Bob, then:
- (1)
- During the execution of the actual protocol, is acting dishonestly; as a result, is also acting dishonestly. The information transmitted by to TTP is dependent on the policy of , which is the same as the policy of . Then will send to TTP.
- (2)
- During the execution of the actual protocol, as is an honest participant, it can be inferred that is also honest, and it sends TTP the real input information .
- (3)
- The input information obtained by TTP is , and TTP calculates .
- (4)
- uses obtained from TTP to obtain , and should be computationally indistinguishable from obtained from the actual protocol implemented by . The output of is obtained by handing over the execution of the protocol to after . Subsequently, conducts the protocol execution by presuming that the other party’s input satisfies the outcome based on its own input and calculation results, that is, selects to simulate the protocol and makes . The specific implementation process of is as follows:
- ①
- sends the information required in step (2) to ;
- ②
- In step (3), will publish the information that requires to publish;
- ③
- After publishes the information in step (4) of the protocol, will verify it;
- ④
- In step (5), chooses the necessary information from the remaining sets, computes the information, and then publicly discloses it;
- ⑤
- Calculate in step (6) and publish it;
- ⑥
- In step (7), ZKP is used to verify the information and obtains the message sequence .
- (1)
- If ignores TTP after getting the information, then:
- (2)
- Otherwise,
6. Performance and Comparison of Protocols
6.1. Computation Complexity
6.2. Communication Complexity
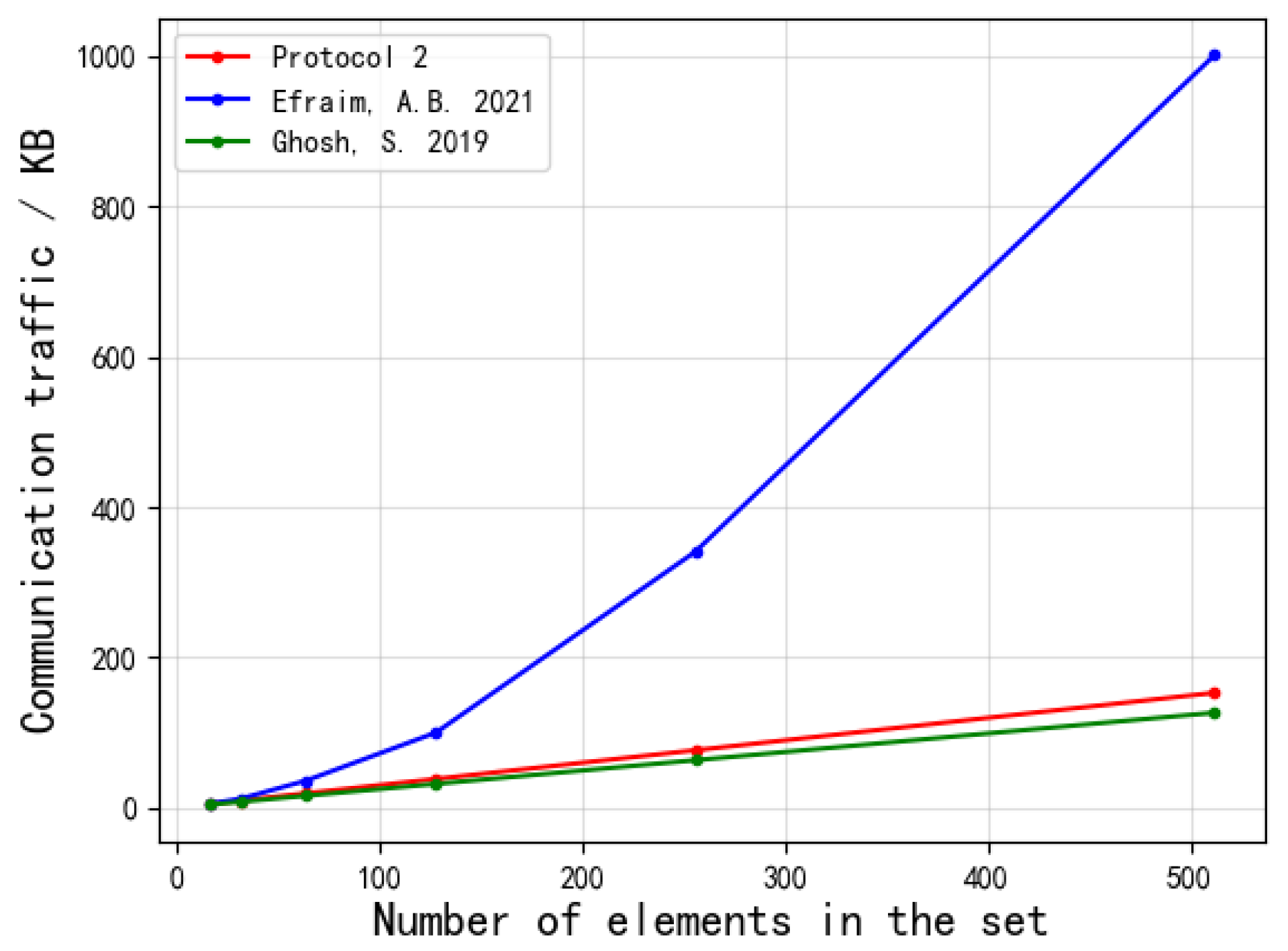
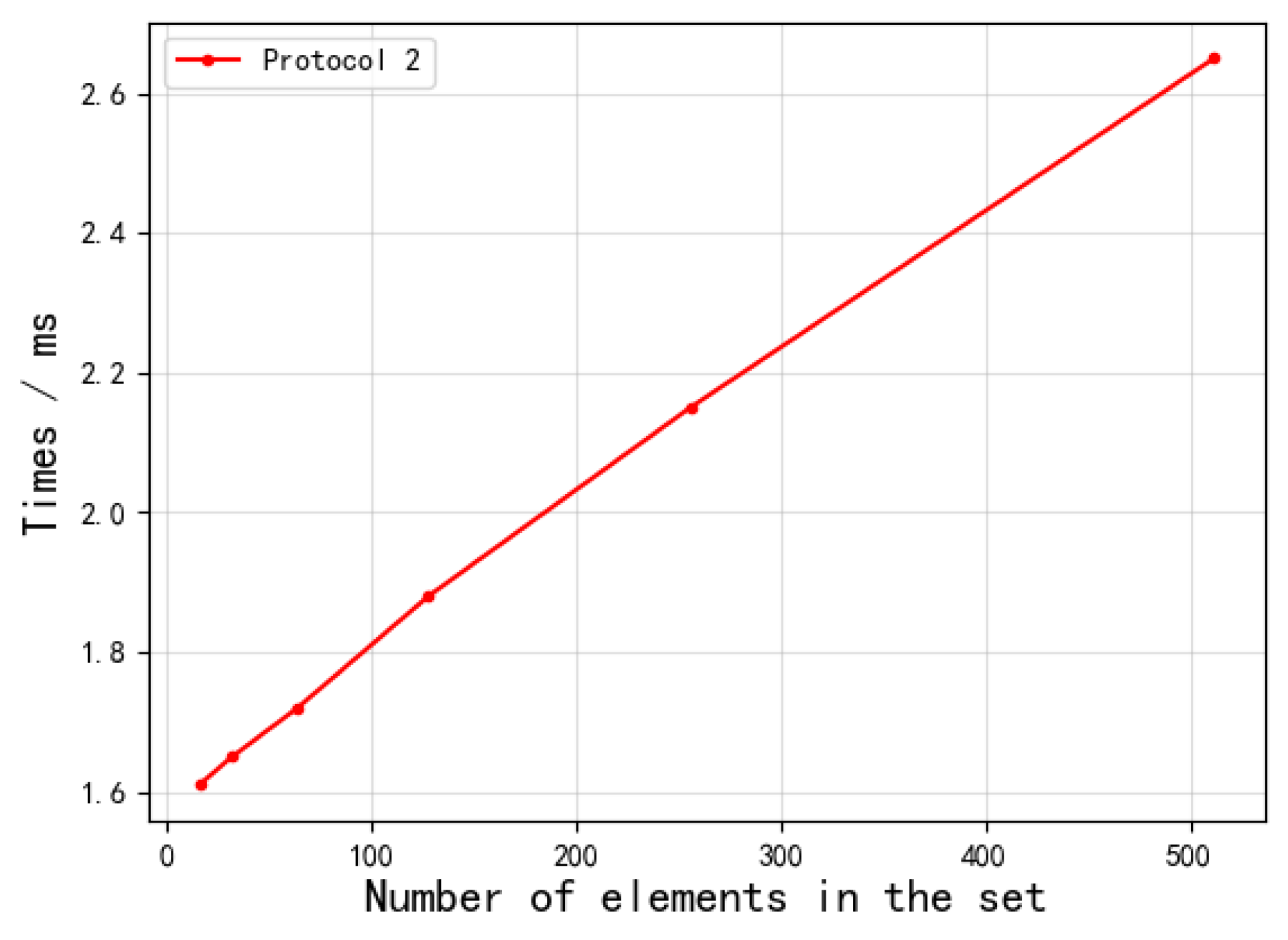
6.3. Simulation Experiment
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Weihong, X.I.E.; Qian, Z. The online website privacy disclosure behavior of users based on concerns-outcomes model. Soft Comput. 2022, 26, 11733–11747. [Google Scholar] [CrossRef]
- Knott, B.; Venkataraman, S.; Hannun, A.; Sengupta, S.; Ibrahim, M.; van der Maaten, L. Crypten: Secure multi-party computation meets machine learning. Adv. Neural Inf. Process. Syst. 2021, 34, 4961–4973. [Google Scholar]
- Zhou, J.; Feng, Y.; Wang, Z.; Guo, D. Using secure multi-party computation to protect privacy on a permissioned blockchain. Sensors 2021, 21, 1540. [Google Scholar] [CrossRef] [PubMed]
- Yao, A.C. Protocols for secure computation. In Proceedings of the 23rd Annual Symposium on Foundation of Computer Science, Chicago, IL, USA, 3–5 November 1982; pp. 160–164. [Google Scholar]
- Goldreich, O. The Fundamental of Crytography: Basic Application; Cambridge University Press: London, UK, 2004. [Google Scholar]
- Cramer, R.; Damgard, I.B.; Nielsen, J.B. Secure Multiparty Compution; Cambridge University Press: London, UK, 2015. [Google Scholar]
- Liu, J.; Tian, Y.; Zhou, Y.; Xiao, Y.; Ansari, N. Privacy preserving distributed data mining based on secure multi-party computation. Comput. Commun. 2020, 153, 208–216. [Google Scholar] [CrossRef]
- Yao, Y.; Xiong, N.; Park, J.H.; Ma, L.; Liu, J. Privacy-preserving max/min query in two-tiered wireless sensor networks. Comput. Math. Appl. 2013, 65, 1318–1325. [Google Scholar] [CrossRef]
- Nevo, O.; Trieu, N.; Yanai, A. Simple, fast malicious multiparty private set intersection. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, Republic of Korea, 15–19 November 2021; pp. 1151–1165. [Google Scholar]
- Fu, A.; Zhang, X.; Xiong, N.; Gao, Y.; Wang, H.; Zhang, J. VFL: A verifiable federated learning with privacy-preserving for big data in industrial IoT. IEEE Trans. Ind. Inform. 2020, 18, 2513–2520. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, R.; Srivastava, G.; Gupta, G.P.; Tripathi, R.; Gadekallu, T.R.; Xiong, N.N. PPSF: A privacy-preserving and secure framework using blockchain-based machine-learning for IoT-driven smart cities. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2326–2341. [Google Scholar] [CrossRef]
- Subramaniyaswamy, V.; Jagadeeswari, V.; Indragandhi, V.; Jhaveri, R.H.; Vijayakumar, V.; Kotecha, K.; Ravi, L. Somewhat homomorphic encryption: Ring learning with error algorithm for faster encryption of iot sensor signal-based edge devices. Secur. Commun. Netw. 2022, 2022, 2793998. [Google Scholar] [CrossRef]
- Sengan, S.; Subramaniyaswamy, V.; Indragandhi, V.; Velayutham, P.; Ravi, L. Detection of false data cyber-attacks for the assessment of security in smart grid using deep learning. Comput. Electr. Eng. 2021, 93, 107211. [Google Scholar] [CrossRef]
- Rosulek, M.; Trieu, N. Compact and malicious private set intersection for small sets. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, Republic of Korea, 15–19 November 2021; pp. 1166–1181. [Google Scholar]
- Efraim, A.B.; Nissenbaum, O.; Omri, E.; Paskin-Cherniavsky, A. Psimple: Practical multiparty maliciously-secure private set intersection. Cryptol. Eprint Arch. 2021, 122. Available online: https://eprint.iacr.org/2021/122 (accessed on 22 May 2023).
- Liu, X.; Zhang, R.L.; Xu, G.; Chen, X.B. Securely determine the inclusion relation of a point and a convex polygon in malicious model. J. Cryptologic Res. 2022, 9, 524–534. [Google Scholar] [CrossRef]
- Ghosh, S.; Nilges, T. An algebraic approach to maliciously secure private set intersection. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, 19–23 May 2019; pp. 154–185. [Google Scholar]
- Rabin, M.O. How to exchange secrets with oblivious transfer. Cryptol. Eprint Arch. 2005, 2005, 187. [Google Scholar]
- Chase, M.; Miao, P. Private set intersection in the internet setting from lightweight oblivious PRF. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2020; pp. 34–63. [Google Scholar]
- Chauhan, A.K.; Kumar, A.; Sanadhya, S.K. Quantum free-start collision attacks on double block length hashing with round-reduced AES-256. IACR Trans. Symmetric Cryptol. 2021, 2021, 316–336. [Google Scholar] [CrossRef]
- Pinkas, B.; Rosulek, M.; Trieu, N.; Yanai, A. PSI from PaXoS: Fast, malicious private set intersection. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; pp. 739–767. [Google Scholar]
- Zhang, E.; Liu, F.H.; Lai, Q.; Jin, G.; Li, Y. Efficient multi-party private set intersection against malicious adversaries. In Proceedings of the 2019 ACM SIGSAC conference on cloud computing security workshop, London, UK, 11 November 2019; pp. 93–104. [Google Scholar]
- Yousefipoor, V.; Eghlidos, T. An efficient, secure and verifiable conjunctive keyword search scheme based on rank metric codes over encrypted outsourced cloud data. Comput. Electr. Eng. 2023, 105, 108523. [Google Scholar] [CrossRef]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; pp. 223–238. [Google Scholar]
- Goldreich, O.; Oren, Y. Definitions and properties of zero-knowledge proof systems. J. Cryptol. 1994, 7, 1–32. [Google Scholar]
- Chaum, D.; Pedersen, T.P. Transferred cash grows in size. In Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques, Gold Coast, Australia, 13–16 December 1992; pp. 390–407. [Google Scholar]
- Lindell, Y. Fast cut-and-choose-based protocols for malicious and covert adversaries. J. Cryptol. 2016, 29, 456–490. [Google Scholar] [CrossRef]
- Goldreich, O. Foundations of Cryptography: Volume 2, Basic Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Li, S.D.; Wang, W.L.; Du, R.M. Protocol for millionaires’ problem in malicious models. Sci. Sin. Inf. 2021, 51, 75–88. [Google Scholar] [CrossRef]
- Li, S.D.; Du, R.M.; Yang, Y.J.; Wei, Q. Secure Multiparty Multi-Data Ranking. Chin. J. Comput. 2020, 43, 1448–1462. [Google Scholar]

| Element | Algorithm | Sorting Position |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 + 1 | 2 |
| 3 | 1 + 1 + 1 | 3 |
| 6 | 1 + 1 + 1 + 0 + 0 + 1 | 4 |
| Protocol | Study [15] | Study [17] | Protocol 2 |
|---|---|---|---|
| Number of participants | 3 | 3 | 2 |
| Security model | Malicious | Malicious | Malicious |
| Communication rounds | 8 | 12 | 5 |
| Communication complexity | |||
| Computation complexity | |||
| Key methods | Garbled Bloom filters | Oblivious Linear Function Evaluation | Paillier cryptosystem; zero-knowledge proof; cut-and-choose |
| Set Size | |||||||
|---|---|---|---|---|---|---|---|
| Traffic (kb)/Runtime (s) | |||||||
| Protocol 2 | 4.720.061 | 9.510.118 | 19.120.210 | 38.190.401 | 76.450.799 | 152.851.589 | |
| Study [15] | 5.030.077 | 12.120.123 | 36.060.219 | 99.950.430 | 340.830.910 | 1001.512.110 | |
| Study [17] | 3.980.073 | 7.920.112 | 15.830.205 | 31.650.411 | 63.190.841 | 126.371.799 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Chen, W.; Xiong, N.; Luo, D.; Xu, G.; Chen, X. Securely Computing Protocol of Set Intersection under the Malicious Model. Electronics 2023, 12, 2410. https://doi.org/10.3390/electronics12112410
Liu X, Chen W, Xiong N, Luo D, Xu G, Chen X. Securely Computing Protocol of Set Intersection under the Malicious Model. Electronics. 2023; 12(11):2410. https://doi.org/10.3390/electronics12112410
Chicago/Turabian StyleLiu, Xin, Weitong Chen, Neal Xiong, Dan Luo, Gang Xu, and Xiubo Chen. 2023. "Securely Computing Protocol of Set Intersection under the Malicious Model" Electronics 12, no. 11: 2410. https://doi.org/10.3390/electronics12112410
APA StyleLiu, X., Chen, W., Xiong, N., Luo, D., Xu, G., & Chen, X. (2023). Securely Computing Protocol of Set Intersection under the Malicious Model. Electronics, 12(11), 2410. https://doi.org/10.3390/electronics12112410






