1. Introduction
With the rapid development of the global economy, according to the survey of the Baltic and International Maritime Council/International Chamber Shipping (BIMCO/ICS), the maritime industry has accounted for 80% of the world’s trade and transportation [
1]. Thus, the safety and efficiency of maritime transportation are of paramount importance. Current issues of maritime transportation include: (1) about 75–96% marine vessel accidents being caused by humans; (2) a severe shortage of seafarers and management personnel; (3) more than 80% of shipping costs being from fuel and labor [
2]. Autonomous navigation is vital to mitigate the above issues for ships in that it can be more vigilant than humans at avoiding accidents by perceptions from heterogeneous sensors such as a camera, laser scanner, and mmWave radar [
3]. Ship autonomy not only saves human labor costs but also utilizes intelligent path planning methods to achieve optimized fuel consumptions.
Realizing autonomous ships requires localization and path planning. Currently, the global positioning system (GPS) and compass have been commonly available to provide reliable location services. In contrast, path planning for ships still poses several challenges. Existing works mainly focus on the path planning for lightweight surface vessels, which are agile and applicable to harbor patrol, marine resource exploration, etc. [
4]. Ships, however, exhibit high inertia and thus a significant delay in motion control. When encountering sudden situations, e.g., encountering a large iceberg, its dynamic nature prevents agile avoidance [
5]. In addition to the “shortest path”, dynamical feasibility is crucial for ship path planning [
6].
Existing ship path planners are typically optimal path searching methods based on A* and its modifications [
7]. Although they provide optimal paths in a given map [
8], the optimality is limited in ideal maps including the occupancy grid map, Voronoi-visibility roadmap [
9], risk contour map [
10], etc. Their path searching is conducted by discretized heading directions without considering the ships’ dynamical constraints, making the planned path dynamically infeasible. More recent works [
11,
12] have taken the dynamical constraints into consideration. However, their iterative methods have high computational complexities, failing to plan in real time to avoid expected sudden risks. Researchers also proposed hybrid approaches that fuse the artificial potential field (APF) algorithm with velocity odometry and path optimization [
13,
14,
15] to achieve real-time obstacle avoidance in complex maritime environments. However, the APF causes oscillations when searching for paths through narrow areas, causing frequent turning and increasing fuel consumptions and navigation risks. In addition to optimization-based methods, researchers incorporate reinforcement learning into path planning [
16,
17]. However, learning-based methods suffer from a trade-off between generality and accuracy. Their stochastic results cannot guarantee the safety and efficiency of ship navigation. In summary, none of the existing path planning methods meet the safety and efficiency needs when considering ship dynamics.
This paper presents ESP, a combinatorial optimized path planning approach that generates a safe, smooth, and dynamically feasible trajectory while minimizing the shipping cost. Realizing such an elegant approach poses several challenges: (1) to quantify the turning cost in optimal and dynamically feasible path searching; (2) to minimize the shipping cost in terms of fuel by formulating a minimum-snap problem, which is non-trivial in combining the dynamic model of ships; (3) to cope with sudden risks, e.g., avoid expected obstacles or enemy vessels, which requires replanning a smooth, safe, feasible and optimized path in real time.
To address the above challenges, ESP consists of three components. First, we propose A-turning, a path searching algorithm that quantifies the turning cost in order to obtain the optimal path with fewer turns. Then, we formulate the minimum-snap optimization problem subject to the dynamic constraints of ships to achieve the minimum shipping cost in terms of fuel. Finally, we propose a real-time path replanning algorithm using quasi-uniform cubic B-spline, achieving millisecond-level path replanning to cope with sudden risks.
In summary, the contributions of this paper include: (1) quantifying the turning cost and incorporating it into an optimal global path search through a modified A* algorithm; (2) formulating a minimum-snap optimization problem to generate a smooth trajectory that consumes the least fuel and satisfies the ship’s dynamic constraints; (3) enabling real-time obstacle avoidance for ships through a B-spline-based local trajectory replanner.
ESP is evaluated in a data-driven simulator implemented by MATLAB and our developed geographic information system (GIS). The simulation results demonstrate the effectiveness of ESP in generating a safe, smooth, and feasible path with minimal turns and fuel consumption. Moreover, ESP enables a quick reaction for ships to smoothly avoid unexpected obstacles by path replanning in less than 48 ms.
The rest of this paper is organized as follows.
Section 2 reviews related works. Then, we elaborate on the design of ESP in
Section 3. The performance evaluation in
Section 4 demonstrates the effectiveness of ESP.
Section 5 concludes this paper.
2. Related Works
Path planning can be divided into two steps: path searching and path optimization. Path searching involves searching for an obstacle-free path from the start to the end. Path optimization involves optimizing the searched path to meet users’ specific objectives, e.g., the shortest sailing distance, minimum fuel consumption, and minimum shipping cost.
Path searching has been well-studied for decades. It can be categorized by graph-search-based and random-sampling-based path searching approaches. Graph-search-based path planning methods follow a set of steps to generate unique navigation paths. The classic algorithm, Dijkstra, expands a large number of irrelevant nodes during searching, which greatly slows down the searching process. In order to improve the searching efficiency, A*-family algorithms have been proposed. They make the searching process more purposeful to the destination by introducing heuristic functions [
18,
19,
20]. These heuristic functions treat vessels as a mass point with unlimited turning and sailing speeds. Their results may have large-angle steers between consecutive path segments. However, to the best of our knowledge, the maximum speed of a ship (displacement > 320 t) is 15 knots, the maximum acceleration is 1, and the turning radius is three times the ship length. Simply considering the ship as a mass point leads to infeasible path planning, making the above heuristic solutions impractical. In addition, Yu et al. [
21] proposed an A* algorithm with velocity variation and global optimization (A*-VVGO), which achieves the purpose of obstacle avoidance by changing the speed of the ship, and combines the artificial potential field method to ensure the smoothness of the path. Sang et al. [
22] proposed a hybrid algorithm of an artificial potential field based on A* and local programming, which is often combined with many algorithms, such as the genetic algorithm (GA) [
23], Fuzzy artificial potential field (FAPF) [
24], etc. These hybrid algorithms contain various advantages. However, these methods do not consider vehicles’ dynamic constraints. Tracking the paths cannot guarantee safety and smoothness. Moreover, graph-search-based methods cannot work efficiently in large environments due to the searching space being exponential to the size of the occupancy grid maps.
To address the searching efficiency problem with respect to the occupancy grid maps, random-sampling-based algorithms have been proposed to incrementally build maps by sampling. They can work in the planning of the ocean. Zhang et al. [
25] proposed the adaptive hybrid dynamic step size and target attractive force–RRT (AHDSTAF–RRT), imposing the dynamic constraints of unmanned surface vehicles (USVs) to allow USVs to navigate complex aquatic environments. Webb et al. [
26] proposed Kinodynamic RRT*, achieving asymptotically optimal motion planning for robots. However, these approaches suffer from slow convergence and inflexible settings of step size. Thus, Strub et al. [
27] designed a heuristic function in the exploitation of random sampling with the aim that the new samples would be more likely to be closer to the destination. Xu et al. [
28] proposed a simplified map-based regional sampling RRT* (SMRS–RRT*) algorithm to achieve path planning in complex environments. Dong et al. [
29] proposed a path planning method based on improved RRT*–Smart, which optimizes the node sampling method by sampling in the polar coordinate system with the origin of USV, improves the search efficiency, and ensures that the navigation path follows the International Regulation for Preventing Collision at Sea. This design does not only improve the convergence speed but also improves the quality of the solution. Nevertheless, random-sampling-based methods cannot provide optimal solutions. Their results are not unique. The searched path usually contains many sharp turns, which is especially evident in open water.
Based on the path searching from graph-search-based and random-sampling-based methods, researchers tried to generate smooth trajectories. A strawman option is to use interpolation. Liang et al. [
30] interpolated the trajectory with the Dobbins curve to ensure the smoothness and reduce the number of sharp turns, but the trajectory curvature was discontinuous. To solve this problem, Candeloro et al. [
31] used the Fermat spiral to connect the straight line segment with the curved segment, generating the trajectory with a continuous curvature. Wang et al. [
32] used B-spline interpolation to construct smooth trajectories with sparse waypoints. It, however, does not impose the vehicle’s dynamic constraints, making trajectories infeasible to be executed. To generate dynamic feasible trajectories, control-space sampling approaches [
5,
6,
33] are simple and effective. However, such approaches lack purpose, so their sampling process could take too much time and fail to plan paths in real time. MahmoudZadeh et al. [
34] combined a novel B-spline data frame and the particle swarm optimization (PSO) algorithm to establish a continuous route planning system to achieve route planning for USV ocean sampling missions. Zheng et al. [
35] proposed a ship collision avoidance decision method based on improved cultural particle swarm to achieve the steering collision avoidance of a ship, but without considering the speed constraint of the ship.
3. Methods
3.1. Problem Formulation
The obstacles considered in this paper are the static obstacles in the chart and the unexpected static obstacles that appear within the detection range of the ship’s radar during the actual navigation of the ship. One primary objective of our path planning is to be collision-free. Additionally, we optimize two more objectives: best stability and minimum fuel consumption. The specific objective function and constraints are given in the following subsections.
3.2. Kinematic Model
The previous studies often ignored the influence of marine environments on the ship’s motion state for the ease of modeling. In order to make the planned path fit the actual sailing situation, this paper establishes the kinematics model of ships considering the ocean current.
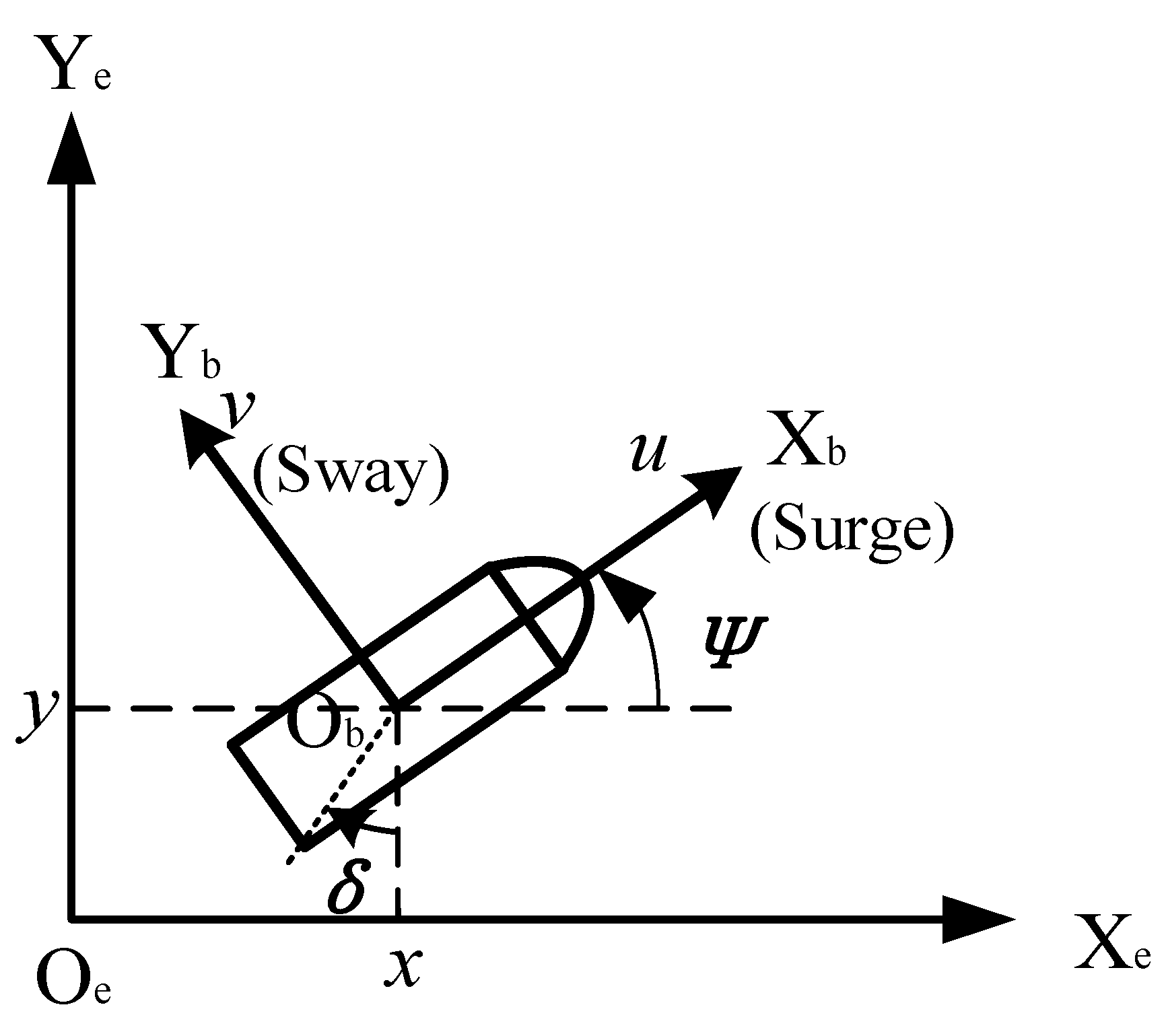
Figure 1 illustrates the kinematic model of a ship.
denotes the world frame, which refers to the coordinate system with respect to the earth. The earth’s gravity points to the positive direction of the z-axis. The x–y–z axes follow the right-hand rule. The origin of the world frame
is the geometrical center’s initial position, the positive direction of the
axis points to east, and the positive direction of
points to north.
denotes the local frame, which refers to the ship’s body frame,
is used as the center of gravity of the ship, the positive direction of the
axis points to the bow, and the positive direction of the
axis points to the port side.
Ψ denotes the yaw angle,
the surge velocity,
the sway velocity, and δ the rudder angle. According to Newton’s second law, considering surge, sway, and yaw, the force at the center of gravity of the ship is
where
denotes the force along the x-axis,
the force along the y-axis,
the position of the ship’s center of gravity in the world frame,
m the mass of the ship,
the force along the z-axis,
the angular acceleration, and
the moment of inertia around the z-axis. As shown in Equation (2), it depends on the volume of the ship
and the mass density
. With the yaw
, we express the transformation between the world frame and the local frame as
Then, the forces on the surge and sway directions can be expressed as
where
denotes the yaw rate, and
and
denote the acceleration on the surge and sway directions, respectively. From Equations (3) and (4), we obtain the kinematic model as follows.
3.3. Dynamic Model
This paper uses the first-order K–T model to represent the hydrodynamic model of the ship, assuming that the port and starboard sides of the ship are symmetrical and the ship mass is uniformly distributed. The hydrodynamic equation can be expressed as:
where
,
where
denotes the inertial mass matrix,
the Coriolis centripetal force matrix, and
the drag coefficient matrix.
and
denote the derivatives for the hydrodynamic,
,
, and
.
denotes the force imposed by the environment and
denotes the thrust of the propeller.
3.4. Ocean Circulation Model
Affected by the environment such as sea wind and ocean currents, a ship easily deviates from its course or even capsizes during sailing, resulting in property damage and even casualties. Therefore, we consider the influence of ocean currents on the ship’s motion state when planning its path.
Ocean currents are formed when seawater flows in a certain direction at a regular, relatively steady speed. It is a large-scale, aperiodic form of seawater movement. According to the characteristics of its location and time, ocean currents can be divided into uniform currents, non-uniform currents, steady currents, and unsteady currents. In offshore or seabed areas with irregular topography, the model of ocean currents is more complicated. To simplify the modeling, we assume that ocean currents are constant and uniform. Let
denote the ocean current speed and
the direction of the current. Then, the velocity of the ocean currents can be expressed as
Affected by ocean currents, the actual velocity of the ship is different from its velocity in still water. At this time , where is the velocity of the ship relative to the ocean current.
3.5. Optimization Objectives
When a ship sails along a trajectory, the collision-free cost function is
where
denotes the minimum distance from a waypoint
to the obstacles, which can be obtained by the Euclidean signed distance field (ESDF) [
36]. The distance will be negative if a waypoint is within an obstacle.
The smoothness is determined by the sum of snaps along the trajectory. The smoothness cost can be defined as
where
denotes the fourth-order derivative, i.e., jerk, at time
t.
The fuel consumption depends on the sailing speed. We use the exponential distribution model proposed in [
37] as follows to describe the relationship between fuel consumption and speed.
where
. Thus, we define the cost function of fuel consumption as
where
denotes the time duration between waypoint
and
and
the fuel consumption per hour between waypoint
and
.
Combining the collision-free cost, the smoothness cost, and the fuel consumption cost, we obtain the overall optimization objective function
subject to
where
,
, and
are the maximum surge velocity, the maximum sway velocity, and the maximum yaw rate, respectively.
3.6. Occupancy Grid Map Construction
In order to apply the environmental information provided by the electronic chart for path planning, it is necessary to process the chart into a binary occupancy grid map as shown in
Figure 2. In this process, we first set an appropriate binarization threshold that converts an RGB image into a binary image. Such a threshold [
38] is vital to constructing an accurate grid map that ensures the feasibility of path planning. If the threshold is inappropriate, as shown in
Figure 2c, then a shoal is identified as a passable area, greatly increasing the navigation risk. Second, the grid size determines the resolution of path planning. Too large a grid cannot capture the subtle details of environments, e.g., small obstacles, resulting in unsafe path searching. On the other hand, too small a grid greatly increases the search space, reducing the computation speed.
Considering the maneuverability of a ship, this paper chooses the minimum turning radius as the criterion to measure the grid size. The ship’s minimum turning radius can be measured through the ship’s maneuverability experiment. The turning radius depends on the sailing speed and water flow velocity. According to [
39], in our simulation, we set the minimum turning radius of the ship as three times the length of the ship. Finally, we map the geographic chart represented in terms of longitude and latitude to the grid map using the following equation:
where
and
denote the longitude and latitude of position
.
and
denote the longitude and latitude at the top-left corner of the selected area.
and
denote the longitude and latitude at the bottom-right corner of the selected area.
and
denote the width and height of the electronic chart.
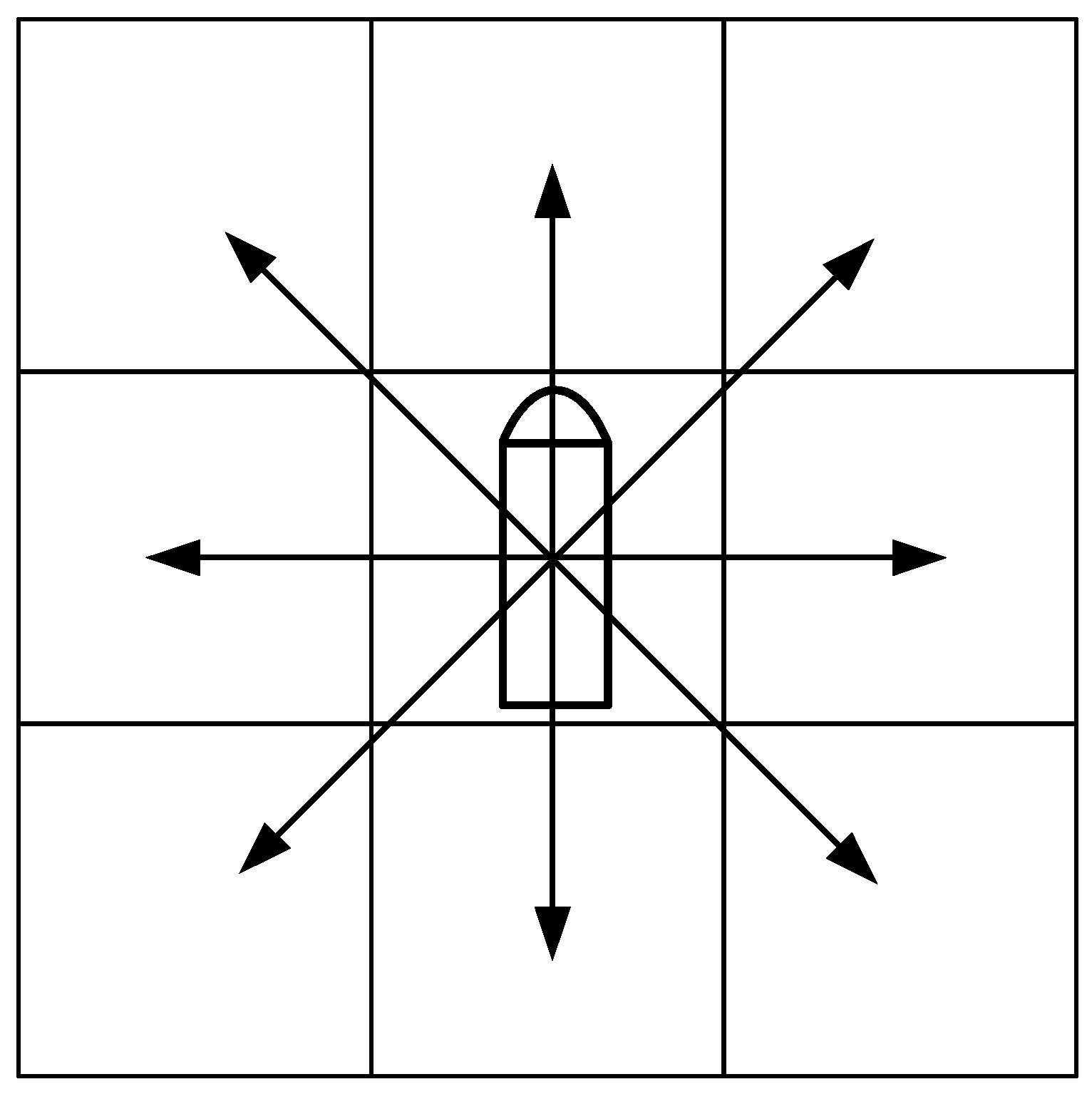
In our simulated forward exploration, we use eight discretized directions in the grid map to search for paths as shown in
Figure 3.
3.7. Quantification of Turning Cost
The A* algorithm uses Equation (18) as the evaluation function to obtain a path with the shortest distance.
where
denotes the estimated cost from the starting point to the target point,
the actual cost from the initial node to node
, and
the estimated cost of the best path from node
to the target node.
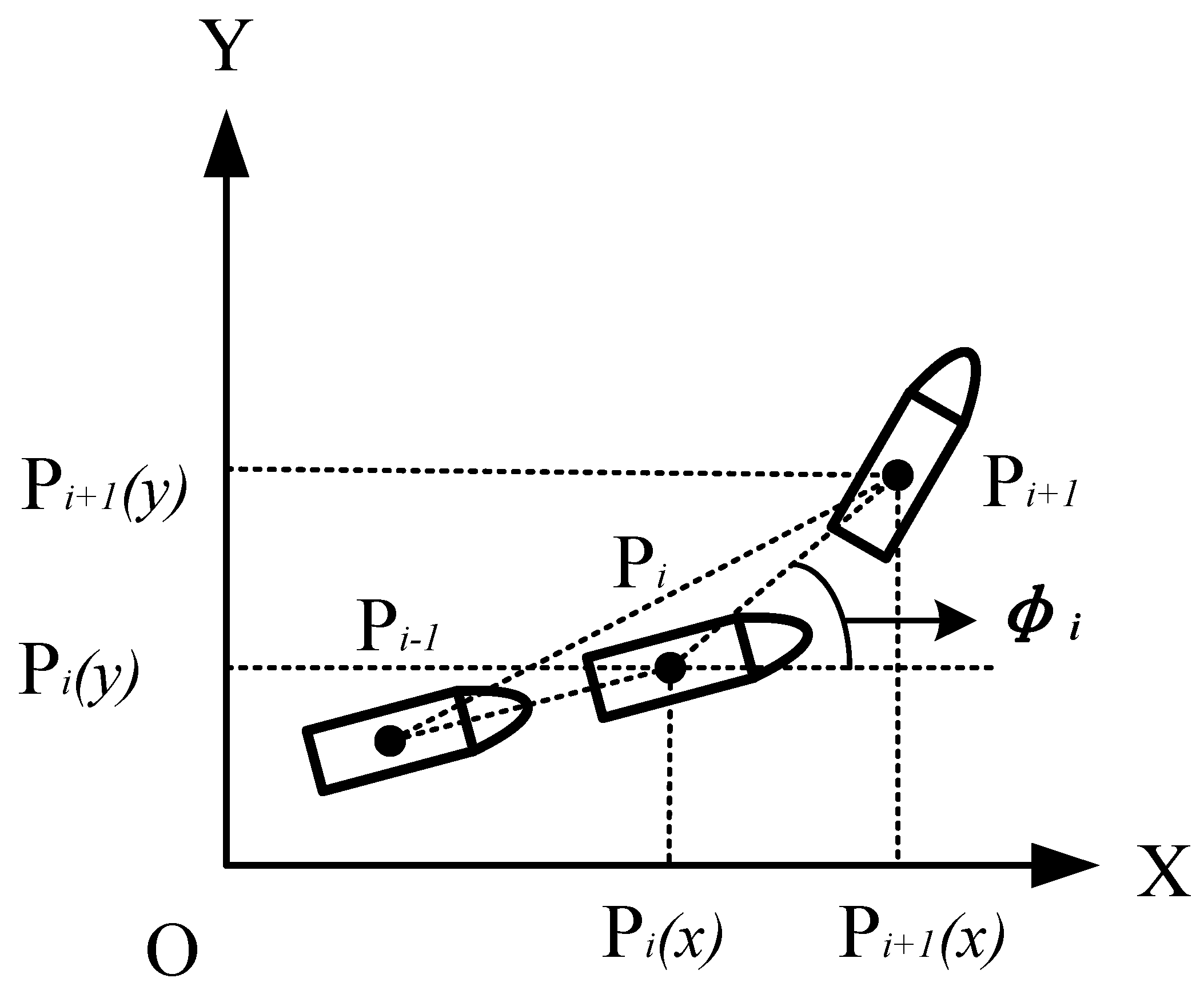
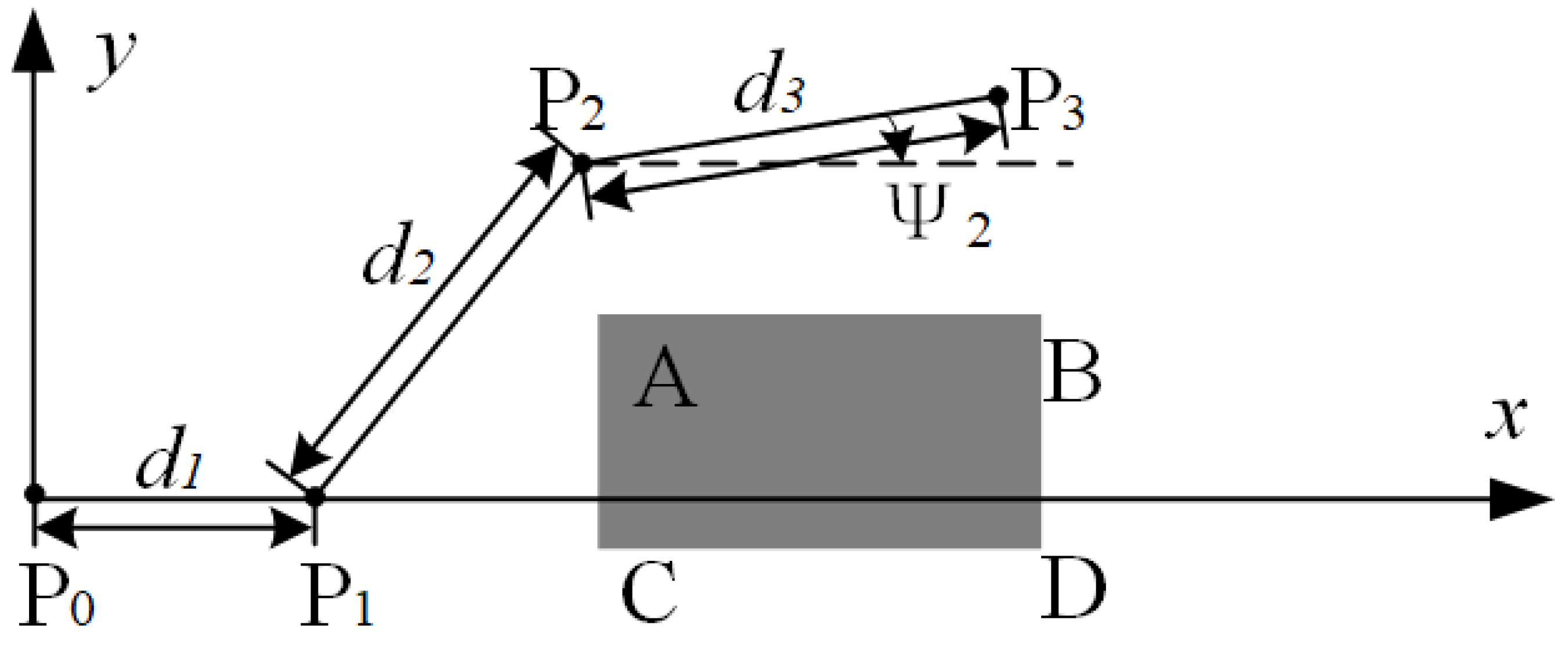
However, in path searching for ships, the turning is much more difficult than for cars or aerial vehicles. Thus, we have to add the cost of turning in order to better evaluate the path. Here we use the diagonal distance to compute the turning cost as shown in
Figure 4.
The yaw
between waypoint
and
can be computed as follows.
where
denote the coordinates of waypoint
,
,
the coordinates of waypoint
,
,
the coordinates of waypoint
. Preventing collisions is still of the highest priority in path planning. Thus, it is not reasonable to simply pursue the minimum turning cost in planning. We add a penalty to the turning cost:
where
is the penalty threshold of the yaw and
the penalty coefficient. Empirically, we set
and
.
is computed as follows.
Finally, the new evaluation function of our path searching algorithm is defined as:
The improved A* algorithm is shown in Algorithm 1.
| Algorithm 1. Improved A* algorithm |
Input: Start node Xstart, end node Xend 1: OPEN_list:= Xstart, where f(Xstart) = h(Xstart) 2: CLOSE_list:={ } 3: while OPEN_list is not empty do 4: current node Xn:= the node in the OPEN_list with the lowest f(X) 5: if Xn = Xend break 6: Remove Xn from OPEN_list and add it to CLOSE_list 7: for each adjacent node, Xi of Xn do 8: if f(Xi) = 0 || Xi ∈ CLOSE_list continue 9: if Xi ∉ OPEN_list 10: add Xi into OPEN_list 11: the parent node of Xi=, Xi > parent = Xn 12: calculate f(Xi), g(Xi), h(Xi) and c(Xi) 13: if Xi ∈ OPEN_list 14: calculate f(Xi) via (25) 15: Resort and keep OPEN_list sorted by f value 16: Xp = Xend 17: Path_list:= Xp 18: while Xp ≠ Xstart do 19: Xp = Xp.parent 20: Path_list = {Path_list, Xp} Return: Path_list
|
3.8. Global Trajectory Optimization
The previous path searching gives us a discrete path with the minimum cost. However, the path does not consider the dynamic feasibility with respect to time, velocity, and acceleration. This part requires a further step to optimize the searched path into a smooth trajectory. The trajectory can be defined as a -order polynomial.
where
are the coefficients of this trajectory. We denote
, and then Equation (23) can be rewritten as
Then, Equation (14) can be expressed as
However, the polynomial expression cannot explicitly control the shape of the trajectory. To gain better control, we choose the Bezier curve using Bernstein polynomials. The
k-th segment of the trajectory can be expressed as
where
,
[0,1]
denotes the control point of the
k-th segment of the Bezier curve.
Since the trajectory must pass through the first and last control points, it can satisfy the positional constraints of the initial and final states. In addition, based on the hodograph of the Bezier curve, we impose constraints on the velocity and acceleration of the trajectory, ensuring the multi-order continuity of the trajectory.
3.9. Real-Time Obstacle Avoidance
In a static chart, a ship can navigate safely along the aforementioned global trajectory. However, the marine environment is complex and changeable. Ships need to deal with unexpected risks when sailing, e.g., avoiding islands and reefs. As shown in
Figure 5, if the ship maintains the planned global trajectory, it will collide with a temporary obstacle. To address this issue, we perform local path planning based on the B-spline curve. The advantage of the B-spline trajectory is that it can change the curve locally by adjusting few control points, while any control point of a Bezier curve will change the shape of the whole trajectory. Moreover, it guarantees that the locally replanned trajectory still satisfies the ship’s kinematic and dynamic constraints. This not only achieves the goal of real-time obstacle avoidance, but also satisfies all optimization objectives.
A B-spline can be expressed as
where
denotes the
-th control point and
is the B-spline basis function of degree
.
is the knot vector. Typically, a three-degree B-spline can ensure the smoothness of accelerations. Thus, we have
Figure 6 illustrates the collision avoidance algorithm. In this figure,
and
are the start and the end of the local planning. The gray area
represents an obstacle.
denotes the yaw at position
.
denotes the distance between
and
. The geometrical relationship among these positions can be expressed as
First, based on random sampling [
40] and collision detection [
41], we obtain
and
(
), and then use the geometric relations in Equations (34) and (35) to solve for the position of
and
. At last, the locally replanned B-spline can be generated by the control points
,
,
, and
.
4. Simulation and Results
We conduct the evaluation of ESP by implementing a data-driven simulator in MATLAB. All simulation experiments are run on a quad-core 2.40 GHz Intel i5-1135G7 processor and 16 GB RAM. We input the data from the database of our developed GIS. The data include image and vector maps, longitude and latitude coordinates, and ship route information. During the simulation, we use environmental data such as shoals and whirlpools that are not currently marked in the GIS database to evaluate the effectiveness of ESP. The simulated settings are listed in
Table 1. Specifically, the ship length is 30 m, the maximum turning radius is 3 times the ship length. The maximum velocity is 7.7 m/s. The maximum acceleration and jerk are 1
and 10
[
42], respectively.
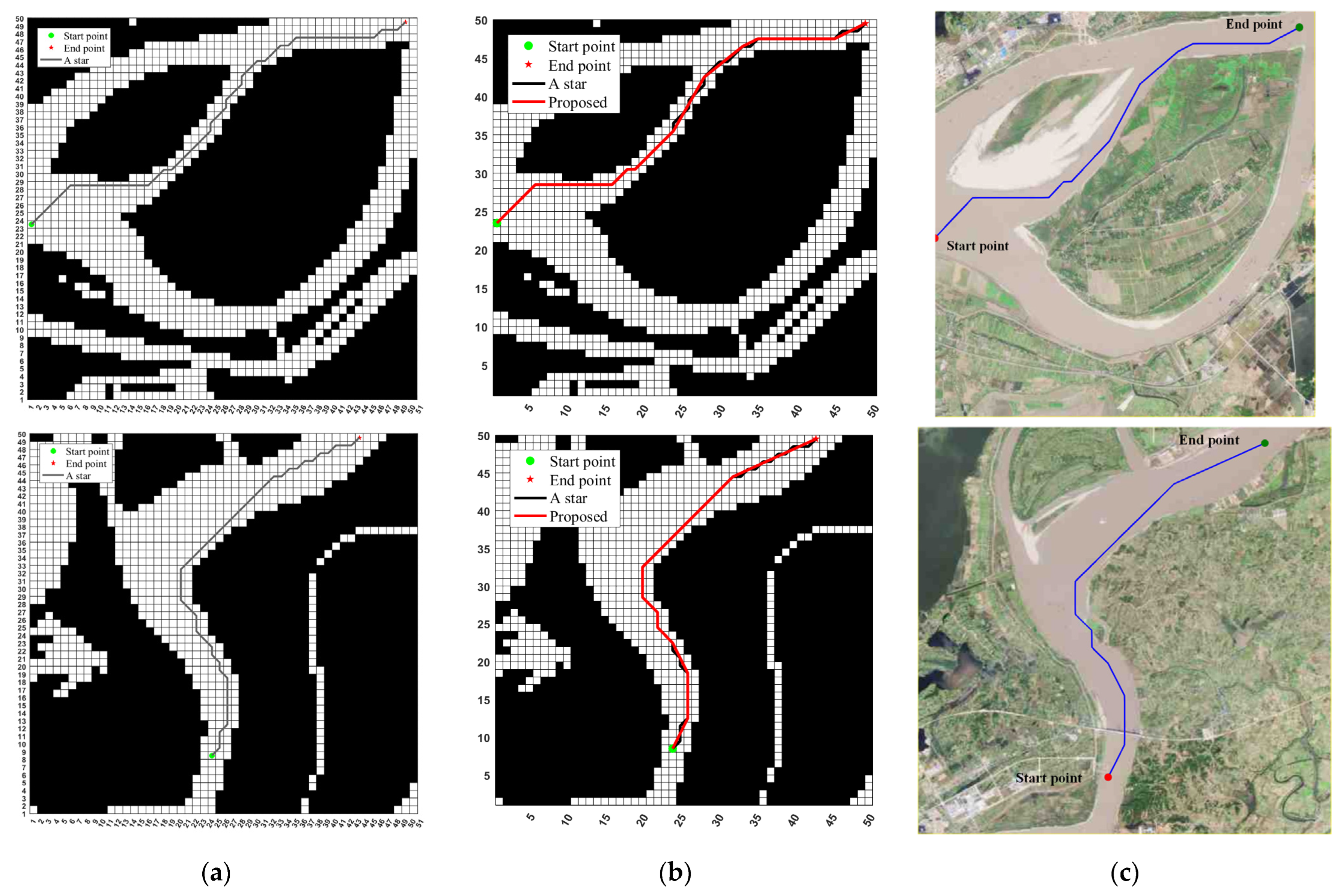
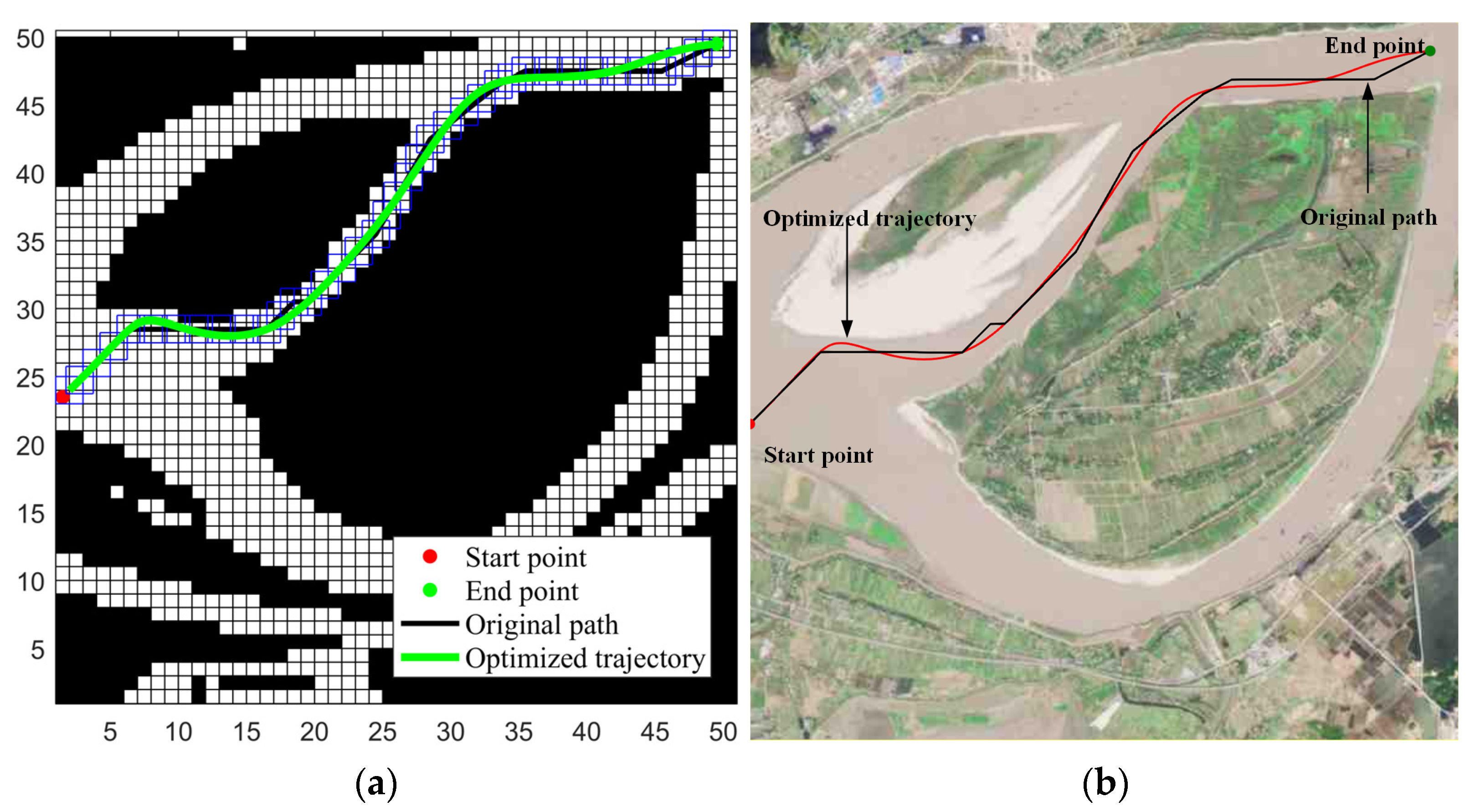
We simulate ESP in two scenes using the GCJ-02 coordinate system. In both scenes, the velocities and accelerations at the start and the end are 0. The simulated occupancy grid map is of size 50 × 50. We compare the path searching results of ESP with the A* algorithm as shown in
Figure 7. The results show that ESP effectively reduces the number of turning points and the planned path is safe.
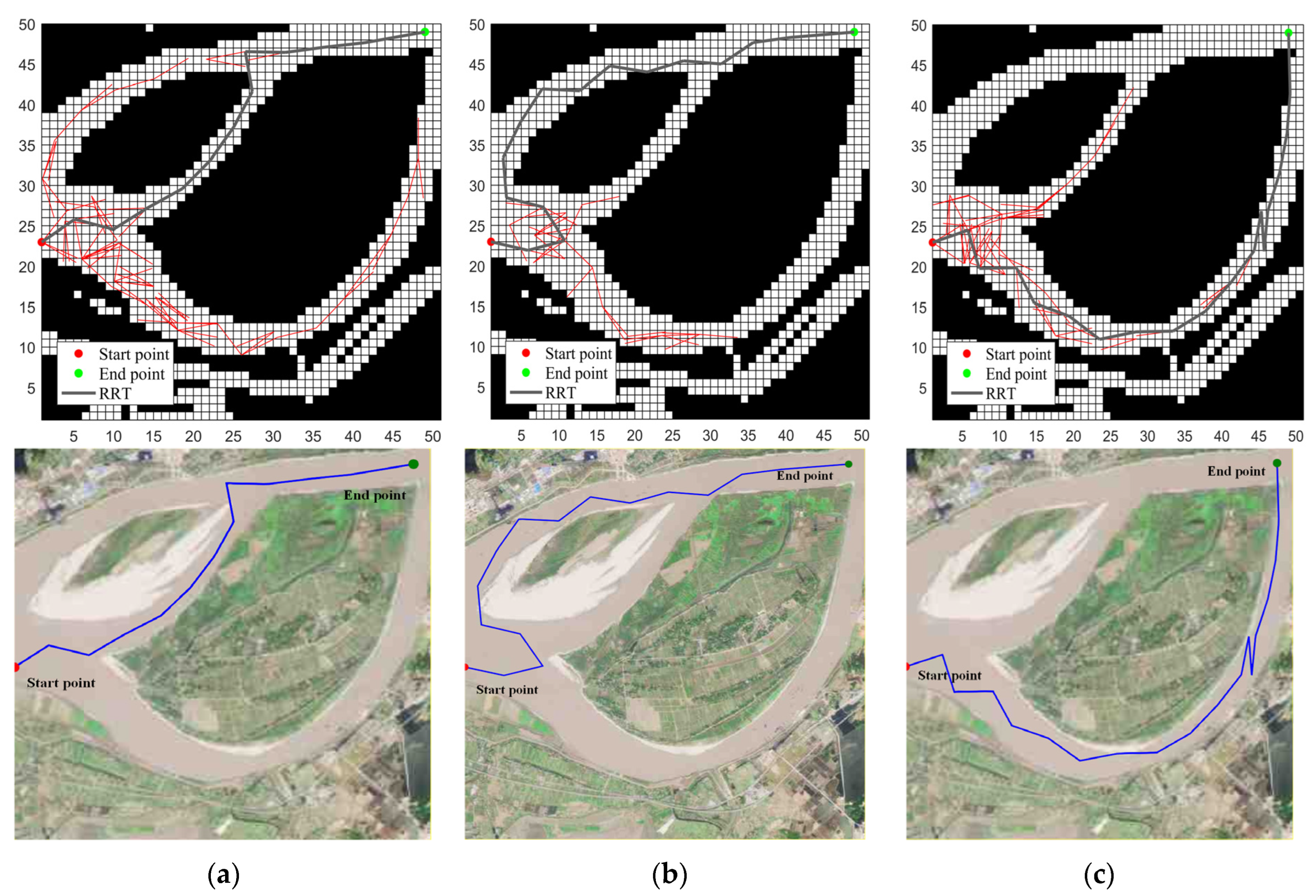
Figure 8 shows the performance of RRT. Due to the randomness of RRT, the planned paths have many unnecessary turning points, which is detrimental to the safe navigation of ships.
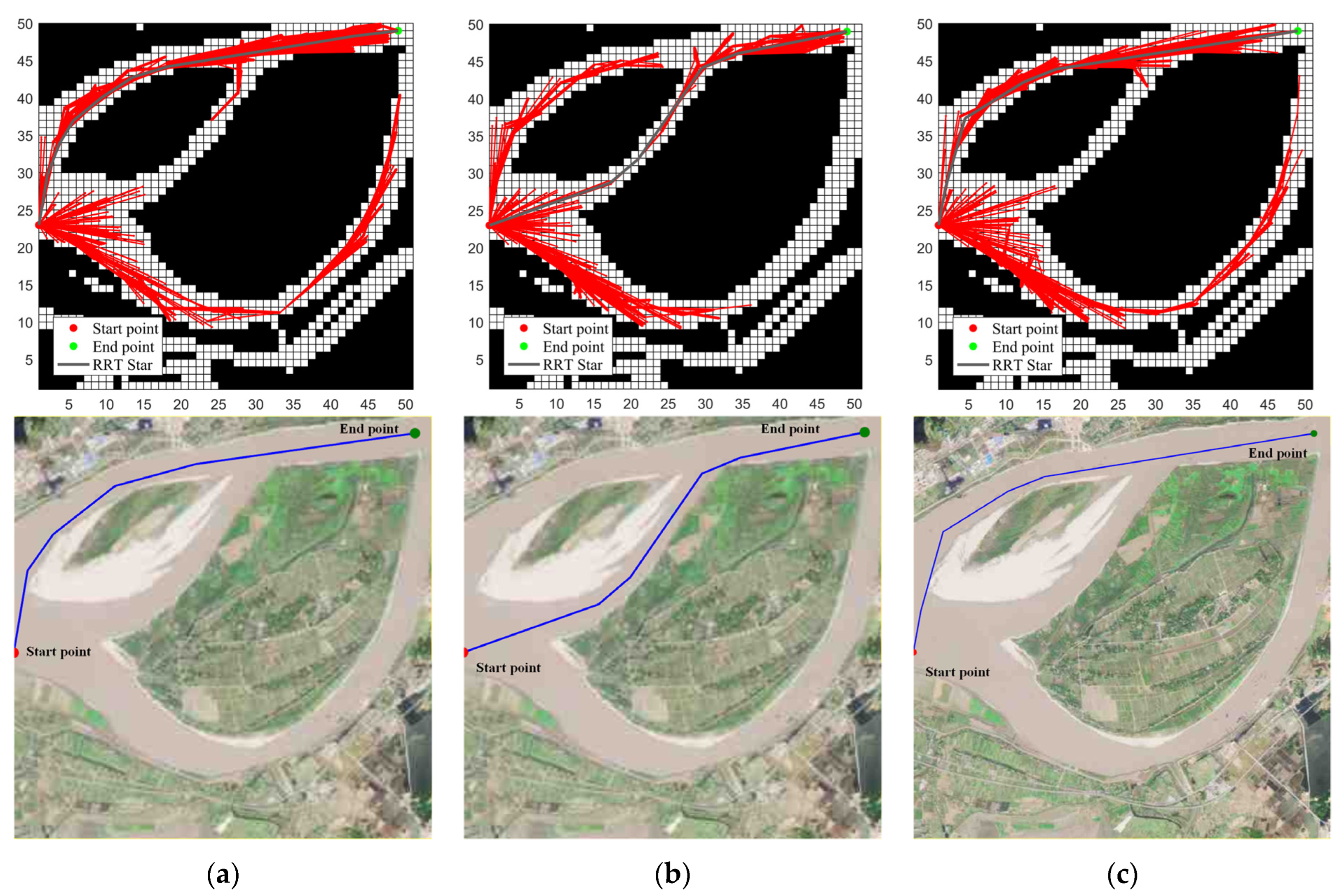
Figure 9 shows the result of RRT*. RRT* needs to rewire parents to find asymptotically optimal paths. The result will be close to the optimal solution with more iterations.
Figure 10 shows the optimized trajectory of our proposed ESP. It can be seen that the optimized trajectory (the green curve in
Figure 10a) meets the requirements of safety, feasibility, and smoothness.
Table 2 shows the numeric comparison in Scene 1 among ESP, A* [
12], RRT [
43] and RRT* [
44] in terms of computation time, number of turns, and fuel consumption. It can be seen that due to the need to measure the turning cost of the path, the searching time of ESP is 0.105 s longer than that of the A* algorithm, and the algorithm’s operating efficiency is reduced by 36.71%. Nevertheless, it is still 1.771 s shorter than that of the RRT algorithm, and 6.021 s shorter than that of the RRT* algorithm. The efficiency of the algorithm is improved by 4.35 times and 15.42 times, respectively. In addition, the number of turns of ESP is obviously less than that of the A* algorithm, which reduces the number of large-angle steers to 8 and improves the safety of ship navigation. The fuel consumption of ESP is 164.6008
less than that of the A* algorithm, 387.1543
less than that of the RRT algorithm, and 24.3311
less than that of the RRT* algorithm.
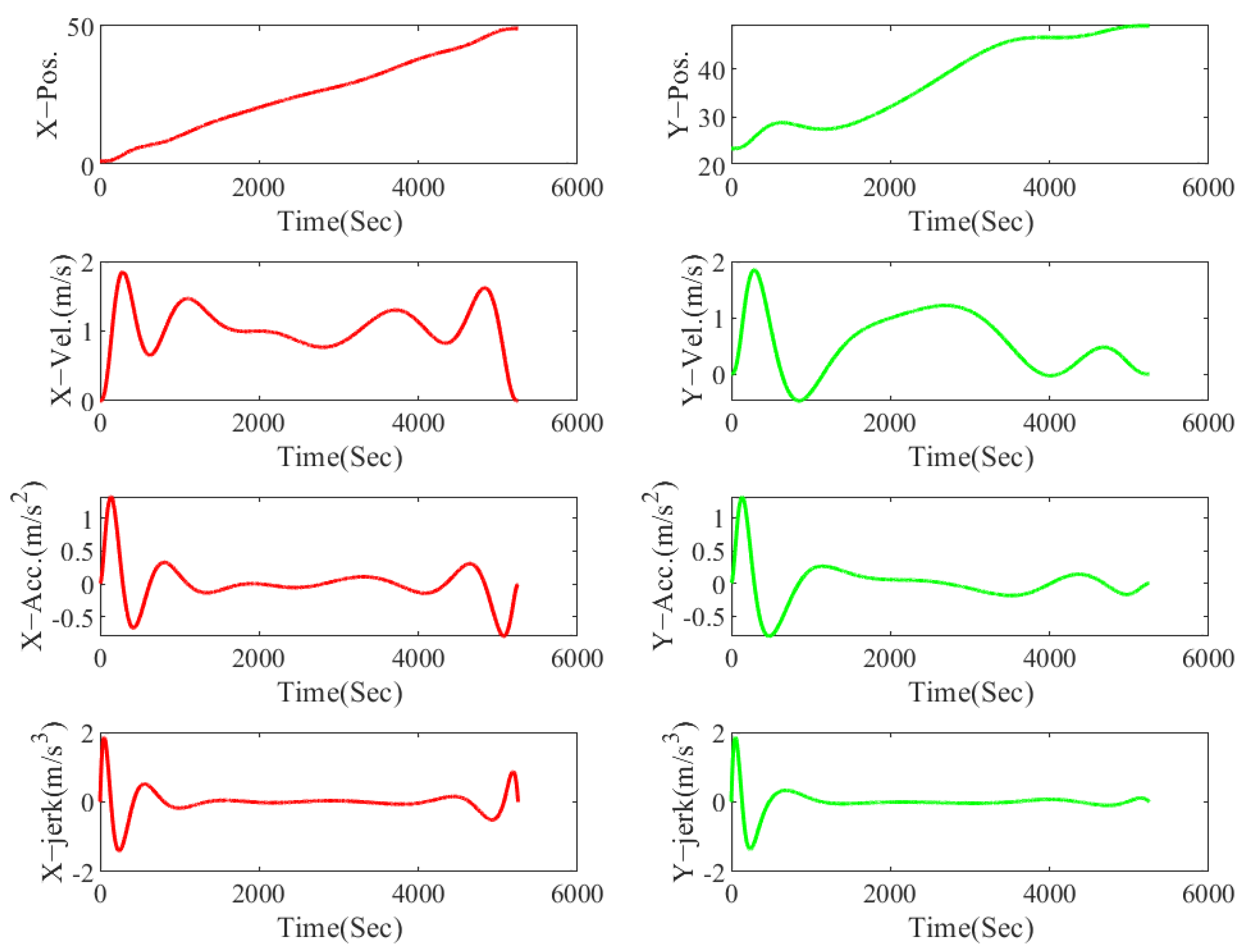
To evaluate the smoothness,
Figure 11 shows the generated positions, velocities, accelerations, and jerks. All these curves are continuous and satisfy the ship’s dynamic constraints.
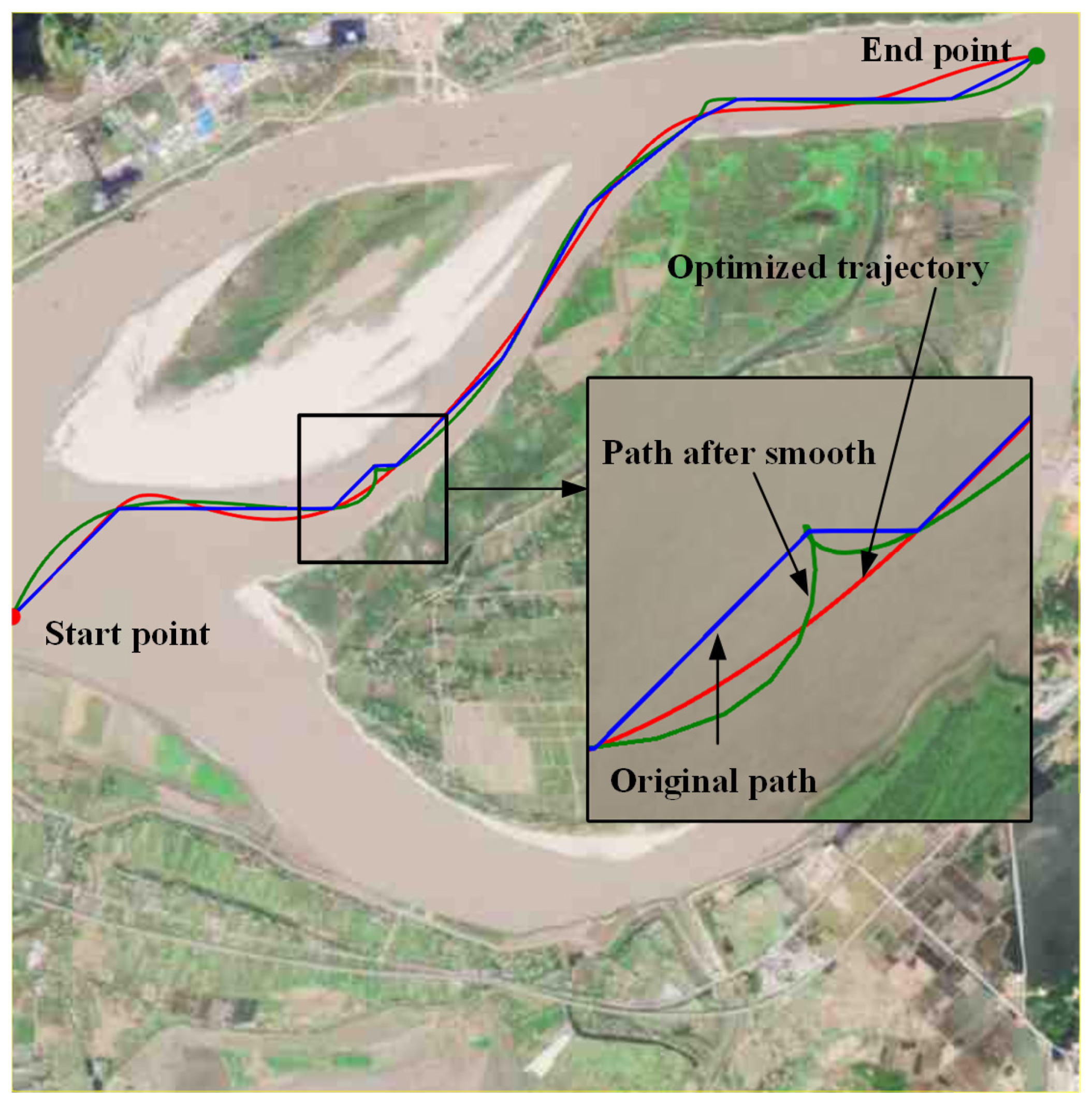
To highlight the effectiveness of ESP,
Figure 12 compares the result of ESP with that which did not consider the ship’s dynamic constraints. The blue line denotes the searched path. The green line shows that Bezier curve without considering the dynamic constraints. The red line is the optimized trajectory from ESP.
From the enlarged part, we can see that there are knots in the result without considering the dynamic constraints, making sailing control very difficult. In contrast, ESP generates a smooth and continuous trajectory with the lowest number of turns, which is safer.
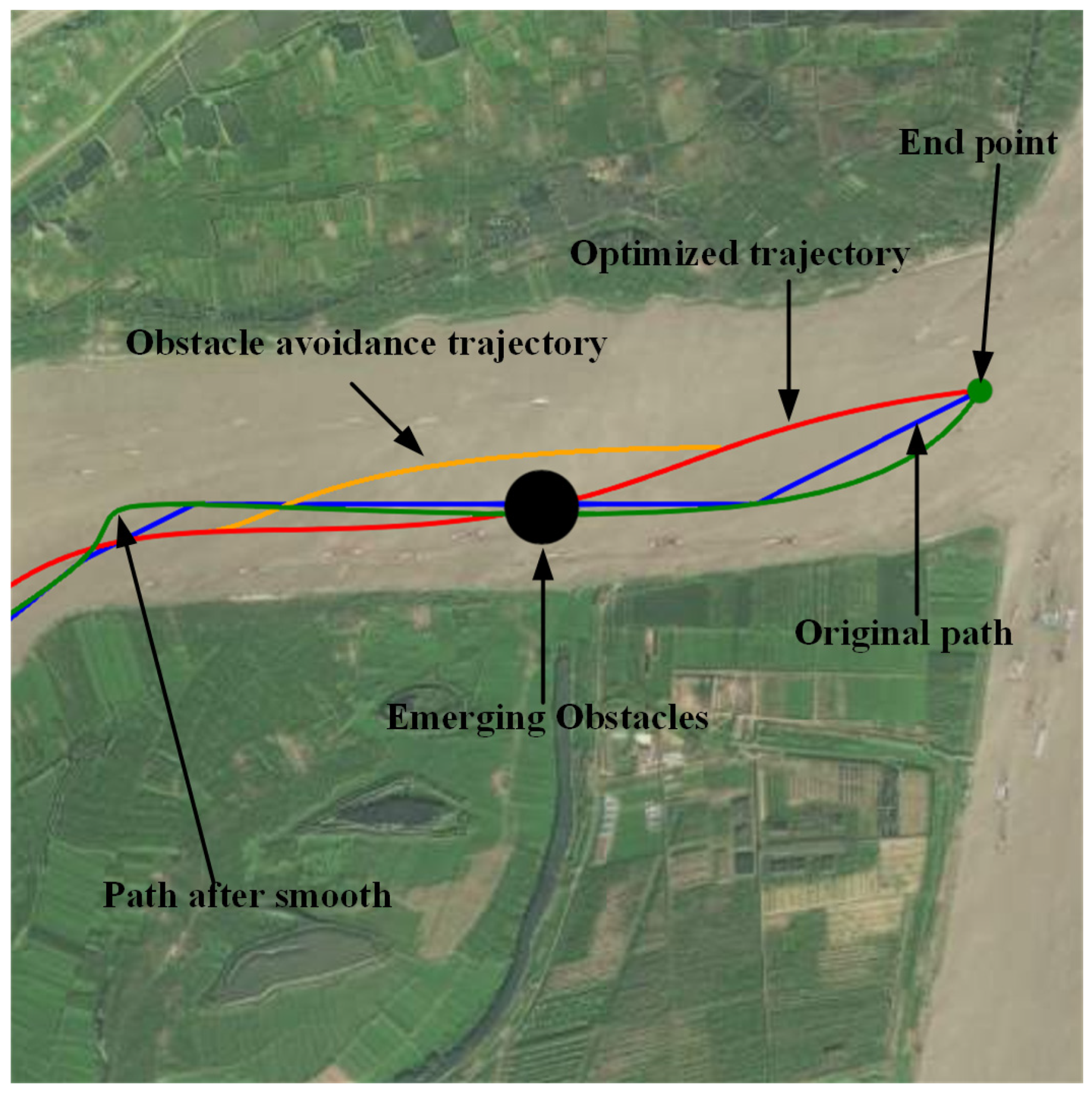
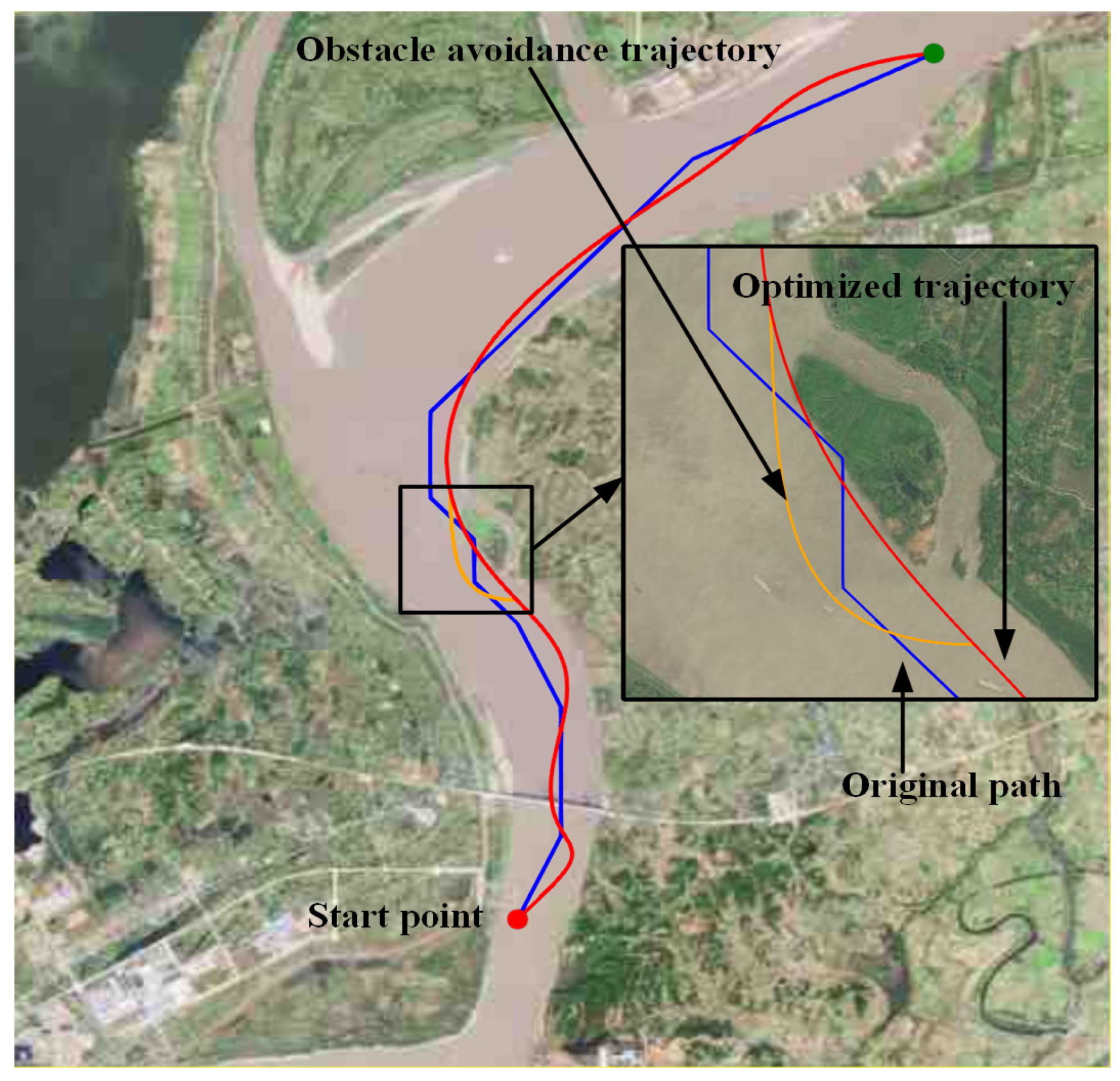
Figure 13 and
Figure 14 show the collision avoidance in Scene 1 and 2. In Scene 1, ESP generates a feasible and smooth local trajectory (the orange line) that avoids the unexpected circular obstacle. In Scene 2, the original planned trajectory is very close to the shoal, increasing the risk of the ship running aground. The local replanned trajectory effectively solves the problem. In both scenarios, the goal of safely avoiding temporarily appearing static obstacles is achieved.
The computation times of the local replanning in both scenes are listed in
Table 3. Over 1000 trials, the best calculation time is 48
, and the maximum computation time is 265
. The mean computation time is 192
in Scene 1 and 194
in Scene 2, ensuring real-time processing.
Avoiding multiple obstacles requires multiple iterations of the above process, and the response time will be multiplied by the number of iterations.
5. Conclusions
This paper proposes a GIS-data-driven method for the efficient and safe path planning of autonomous ships in maritime transportation, which makes up for the shortcomings of existing methods that ignore the motion dynamic limitations of ships in order to achieve the shortest path, leading to sudden changes in the planned route and thus lacking practical applicability. To this end, we propose ESP, a new path planner that provides comfortable sailing while saving fuel. The key intuition of our proposal is to reduce the expensive turning in path searching. The expensiveness comes from the inertia exhibited by the huge weight of the ship. To realize the above intuitive idea, we design three components for ESP. First, we quantify the ship’s turning cost based on its kinematic and dynamic model and develop a modified A* path search algorithm. Second, we formulate an optimization problem subject to dynamic ship constraints and environment constraints to produce a safe and smooth trajectory that consumes minimal fuel. Finally, we use the B-spline representation to perform real-time local replanning, enabling autonomous ships to quickly respond to unexpected risks while maintaining the previous optimization objectives. The data-driven experiments demonstrate the effectiveness of ESP. However, we currently only consider the effect of ocean currents on the dynamic ship model. In future, we will consider the influence of other environmental factors, e.g., sea wind, to build a more robust model for autonomous ships. The avoidance of dynamic obstacles and the real-time avoidance of multiple static obstacles will also be investigated on this basis.