Trajectory Planning for an Articulated Tracked Vehicle and Tracking the Trajectory via an Adaptive Model Predictive Control
Abstract
1. Introduction
- Using the Hybrid A-star path planning method to obtain a feasible kinematic trajectory.
- Using the minimum snap method to optimize the planned trajectory and obtain the reference vehicle kinematic states.
- Designing a kinematic controller based on the AMPC control scheme to achieve robust trajectory tracking control.
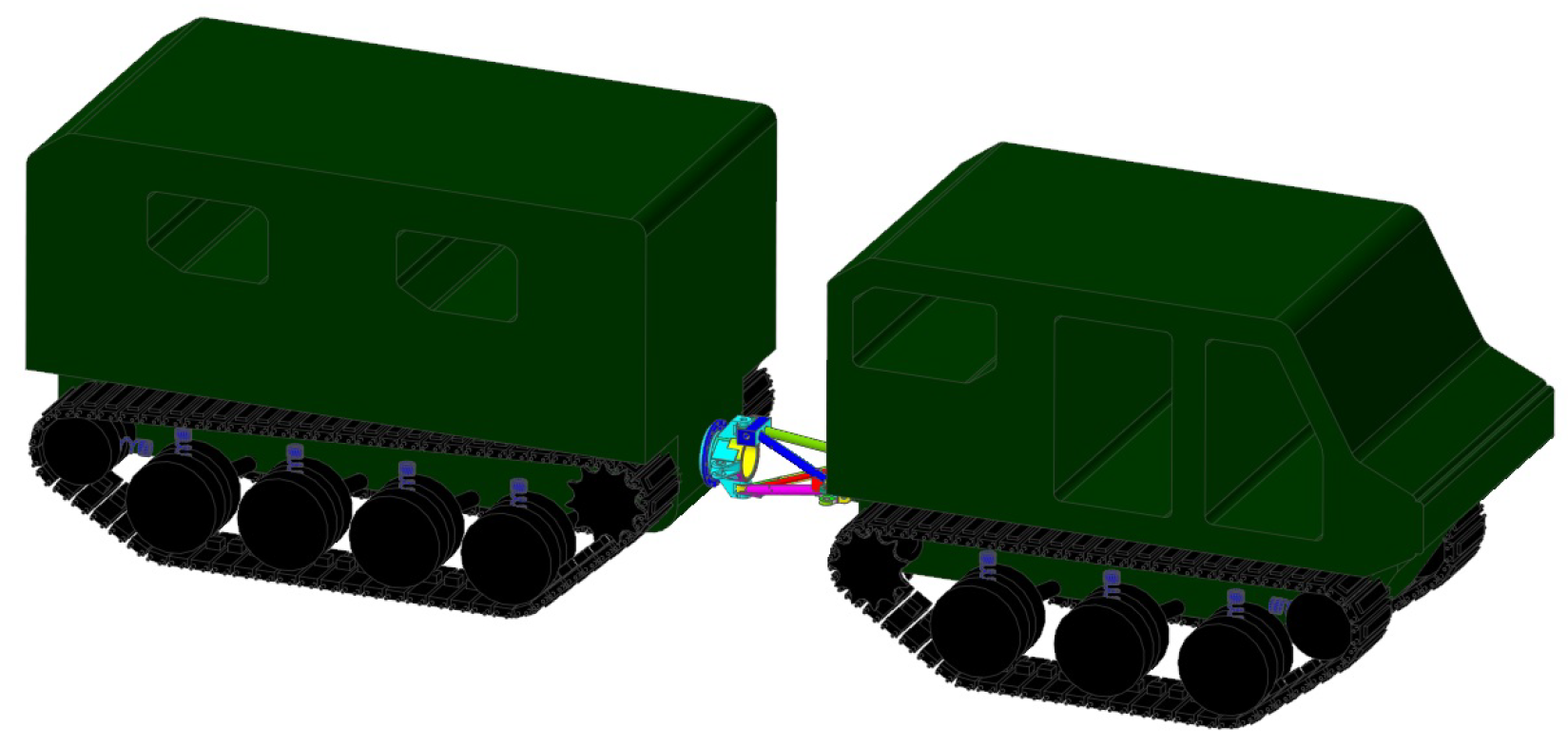
2. Autonomous Articulated Vehicle System
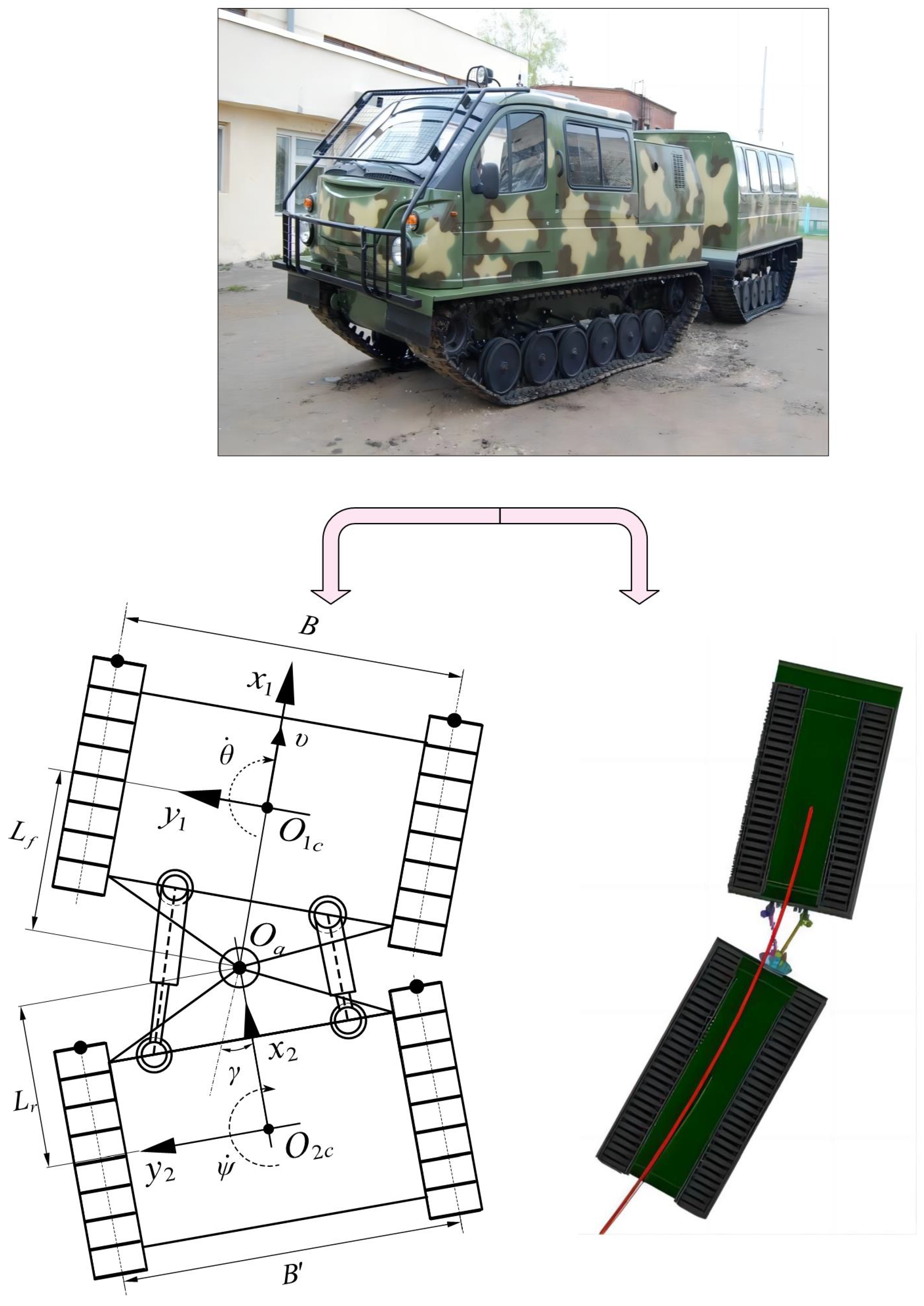
2.1. Kinematic Vehicle Models
2.2. Tracking Error Dynamics Model
2.3. Kinematic LPV Modelling
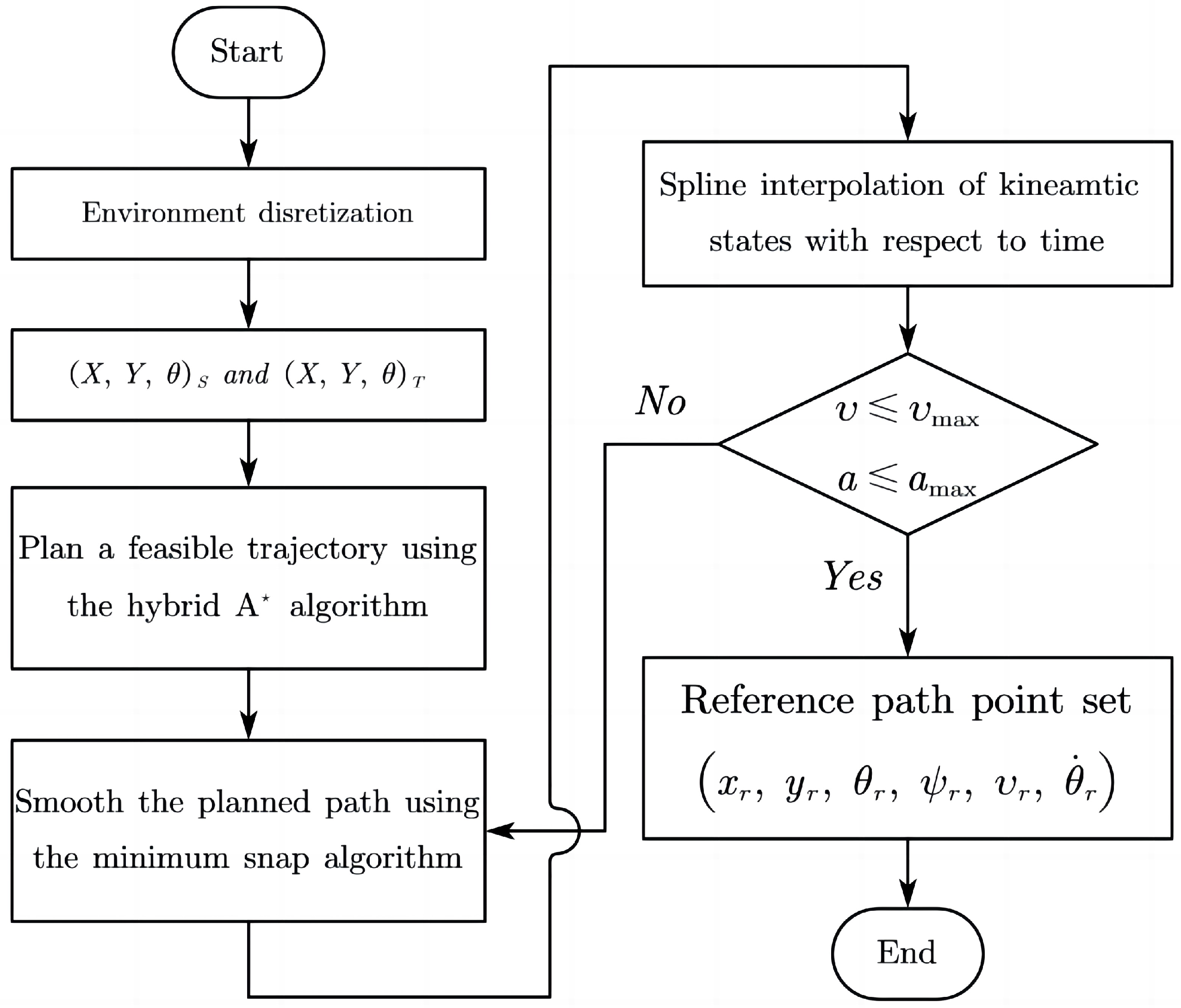
3. Trajectory Planning
3.1. Node Expansion
3.2. Heuristics Cost
3.3. Analytical Expansion
3.4. Trajectory Optimized
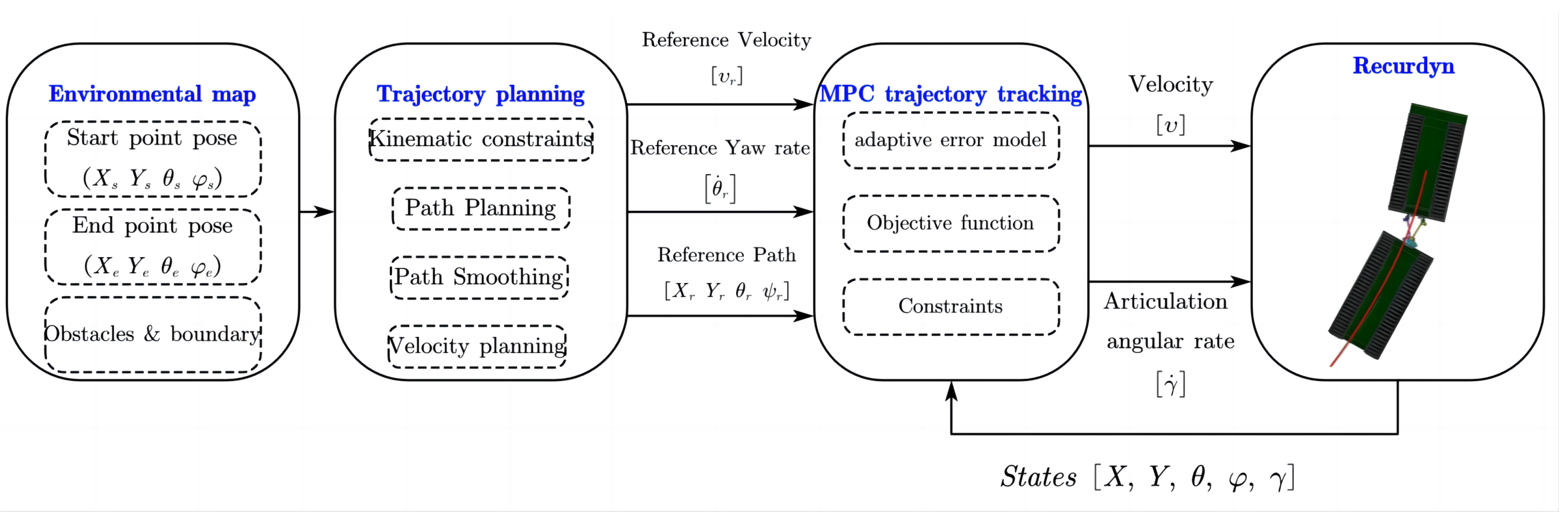
4. Control Design
4.1. Reference Trajectory
4.2. Adaptive MPC Controller
4.3. Track-Speed Control
5. Simulation and Discussion
5.1. Simulation Setup
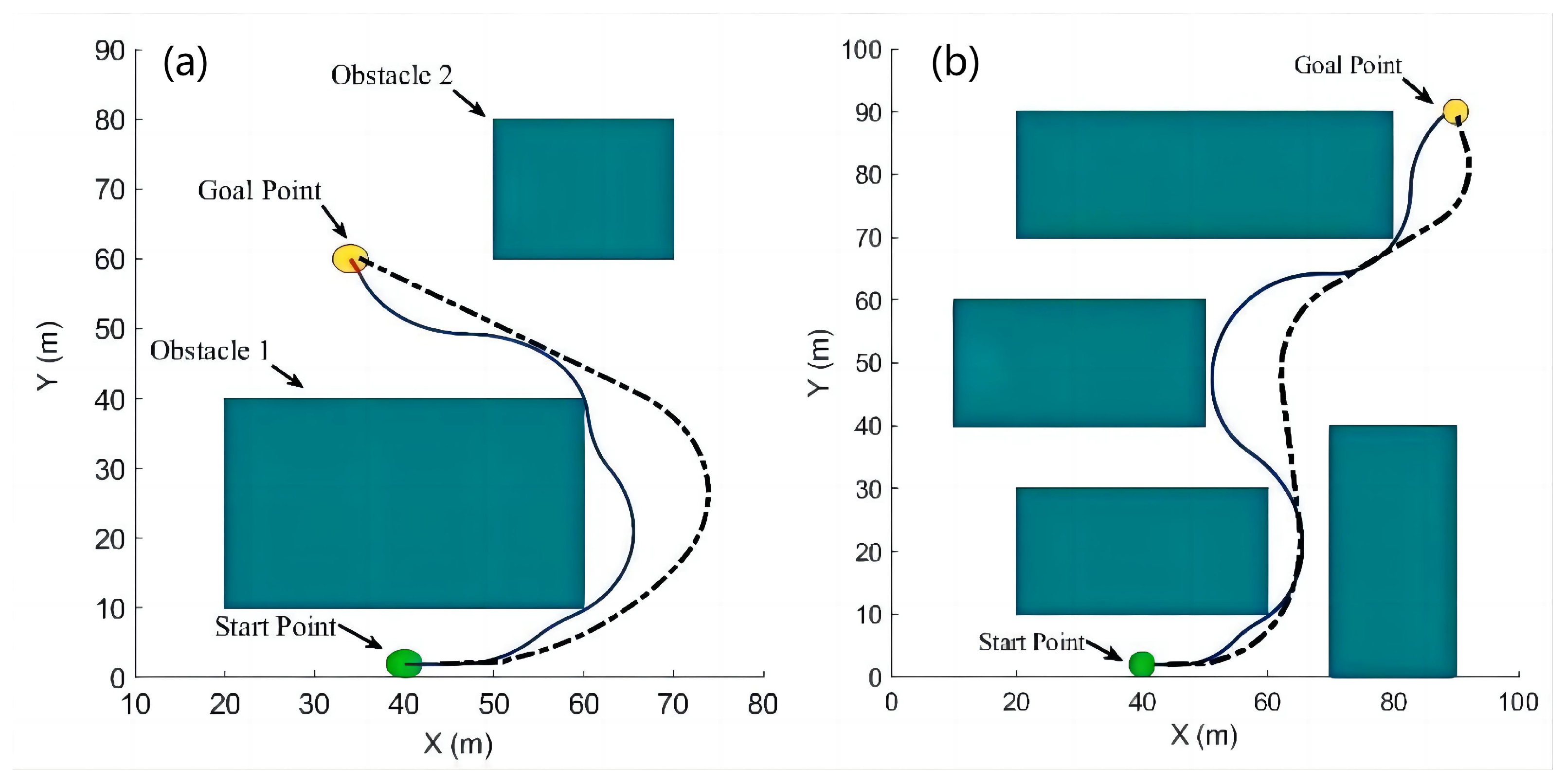
5.2. Simulation of Path Planning
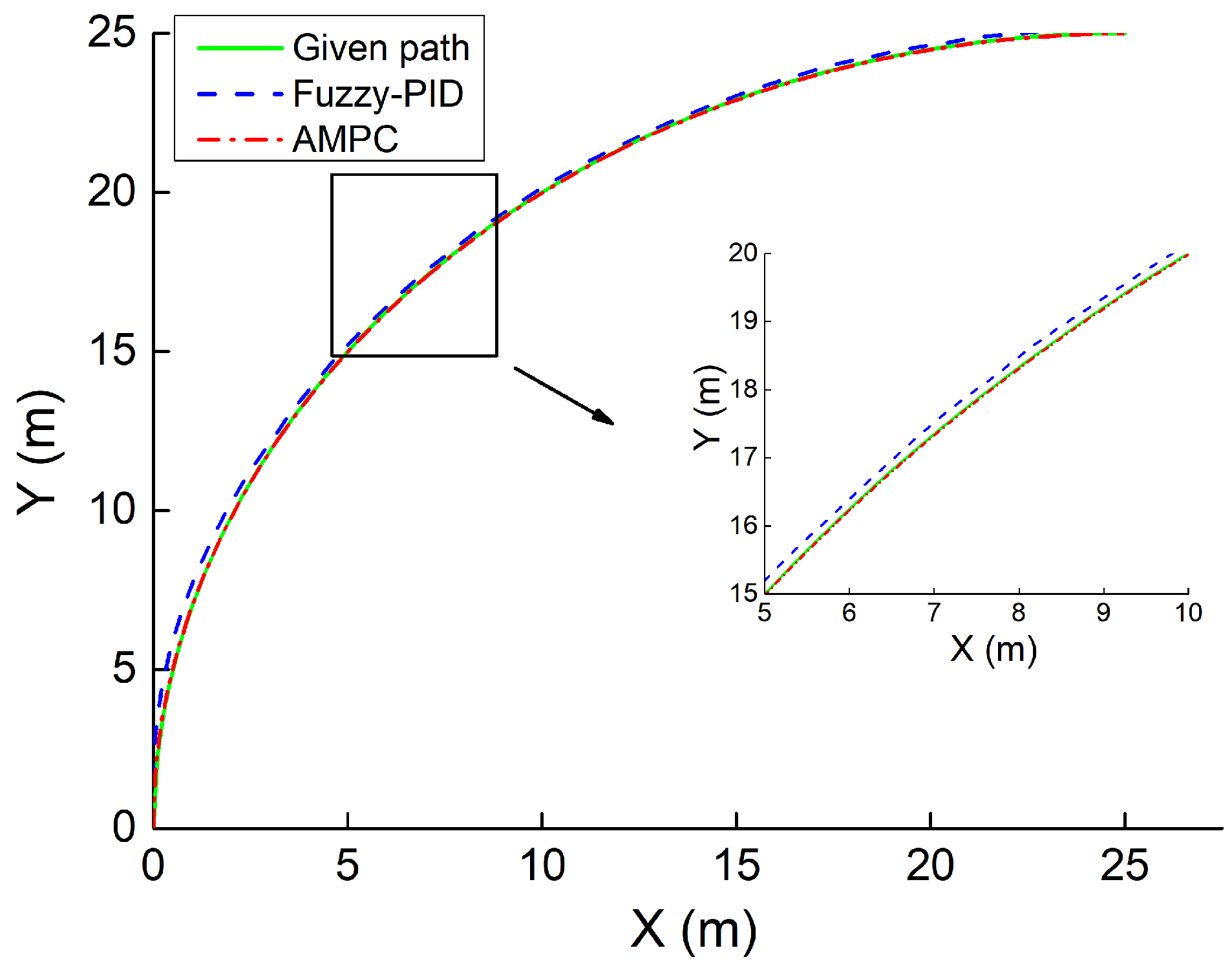
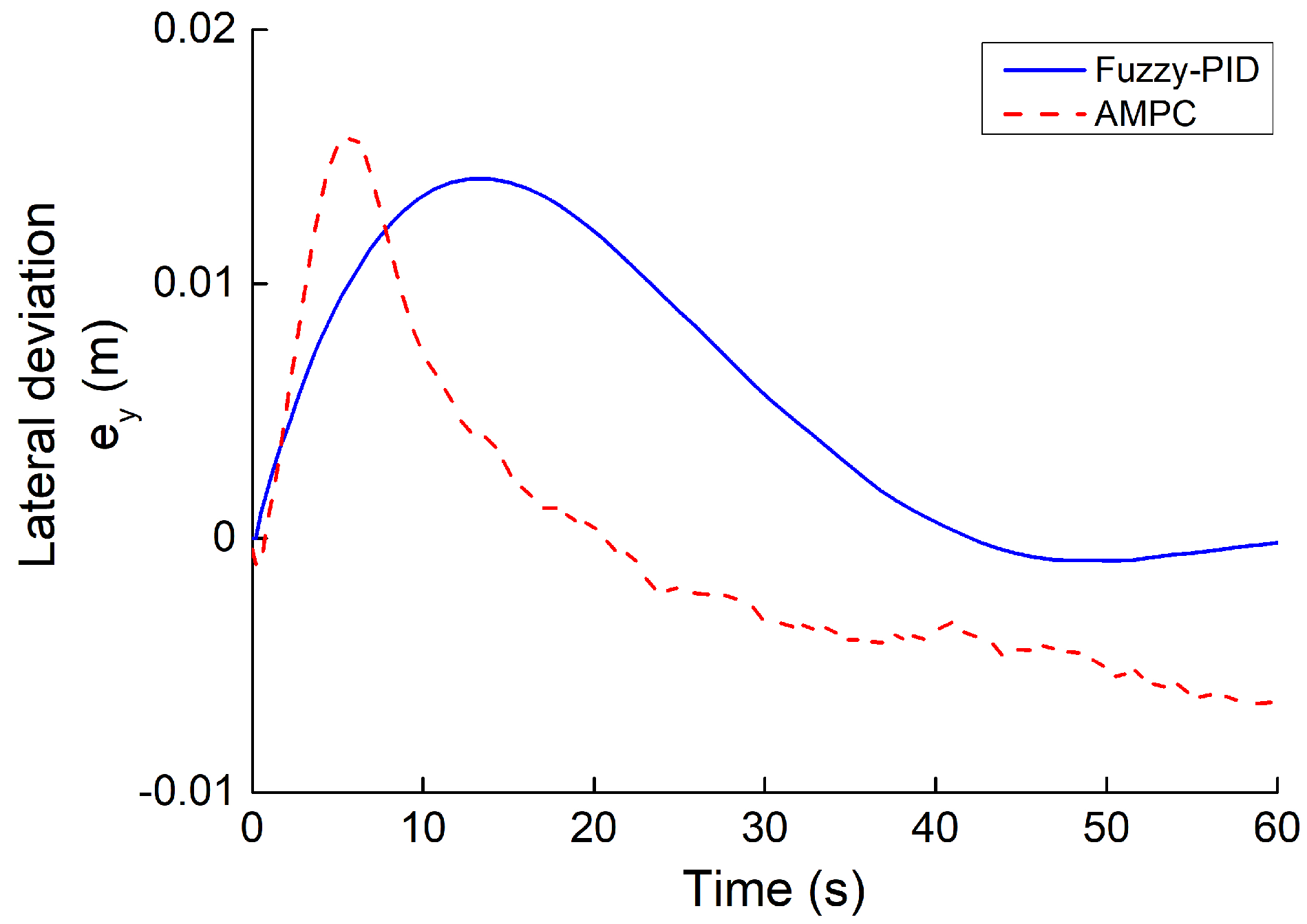
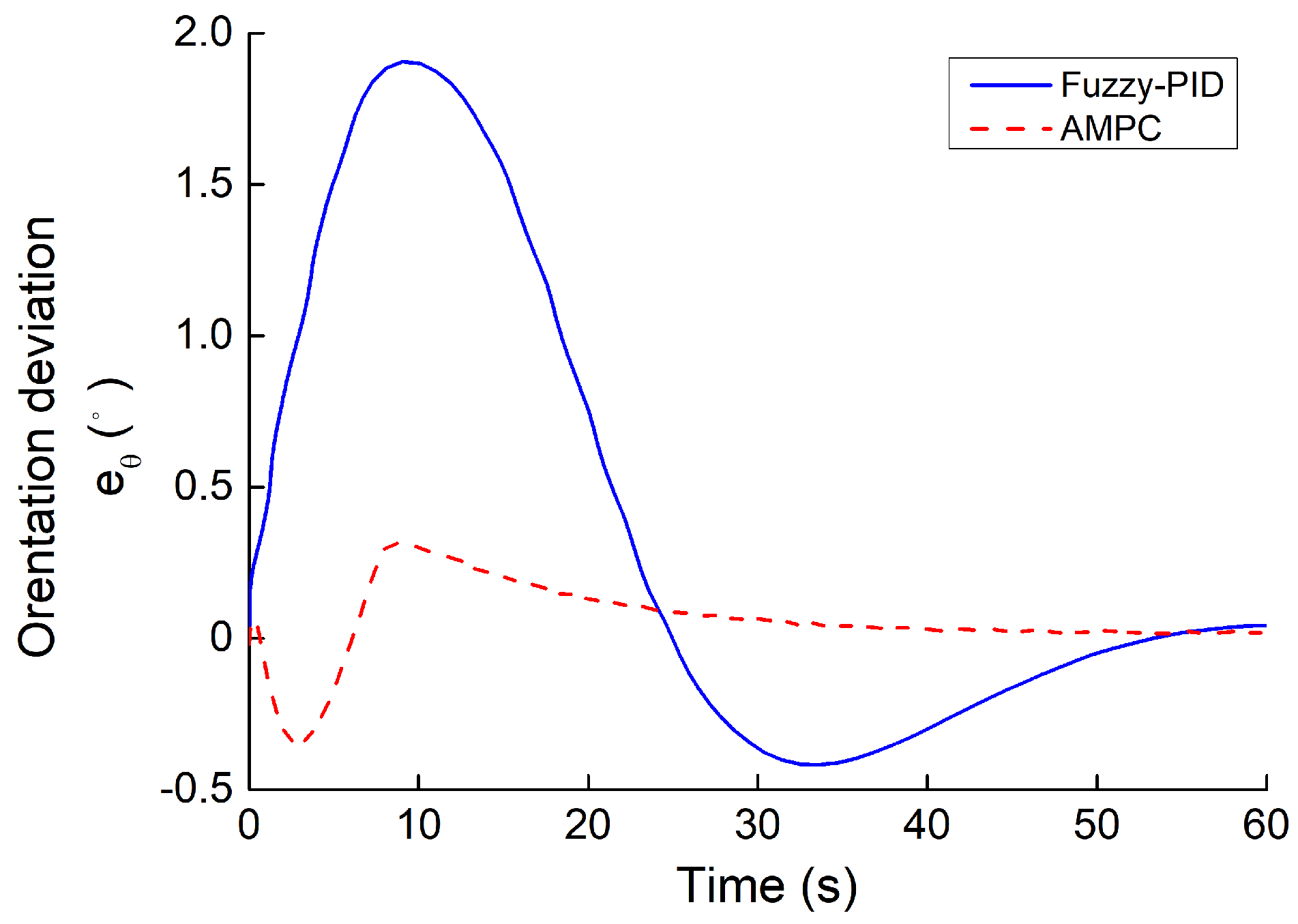
5.3. Simulation of the Trajectory Tracking
5.3.1. Simulation Result of Case 1
5.3.2. Simulation Result of Case 2
5.3.3. Simulation Result of Case 3
5.3.4. Simulation Result of Case 4
6. Conclusions
- Although the adaptive model predictive control algorithm has been applied in the path-tracking of the mobile robot, its application in the articulation vehicle is not mature. The MPC algorithm has yet to be applied in the path-tracking control of the articulated tracked vehicle. Thus, our work has extended the application of the MPC algorithm in the field of ATVs.
- The ATVs have unique steering characteristics compared to the skid-steering tracked vehicles. The path tracking of the ATVs also needs to consider its kinematic characteristics, for example, the multi-input and multi-output for the ATV control system. Thus, it is challenging for the developed control methods to control the ATV in a complex maneuver accurately. To this end, our work provides a practical method for the path planning and path tracking of ATVs.
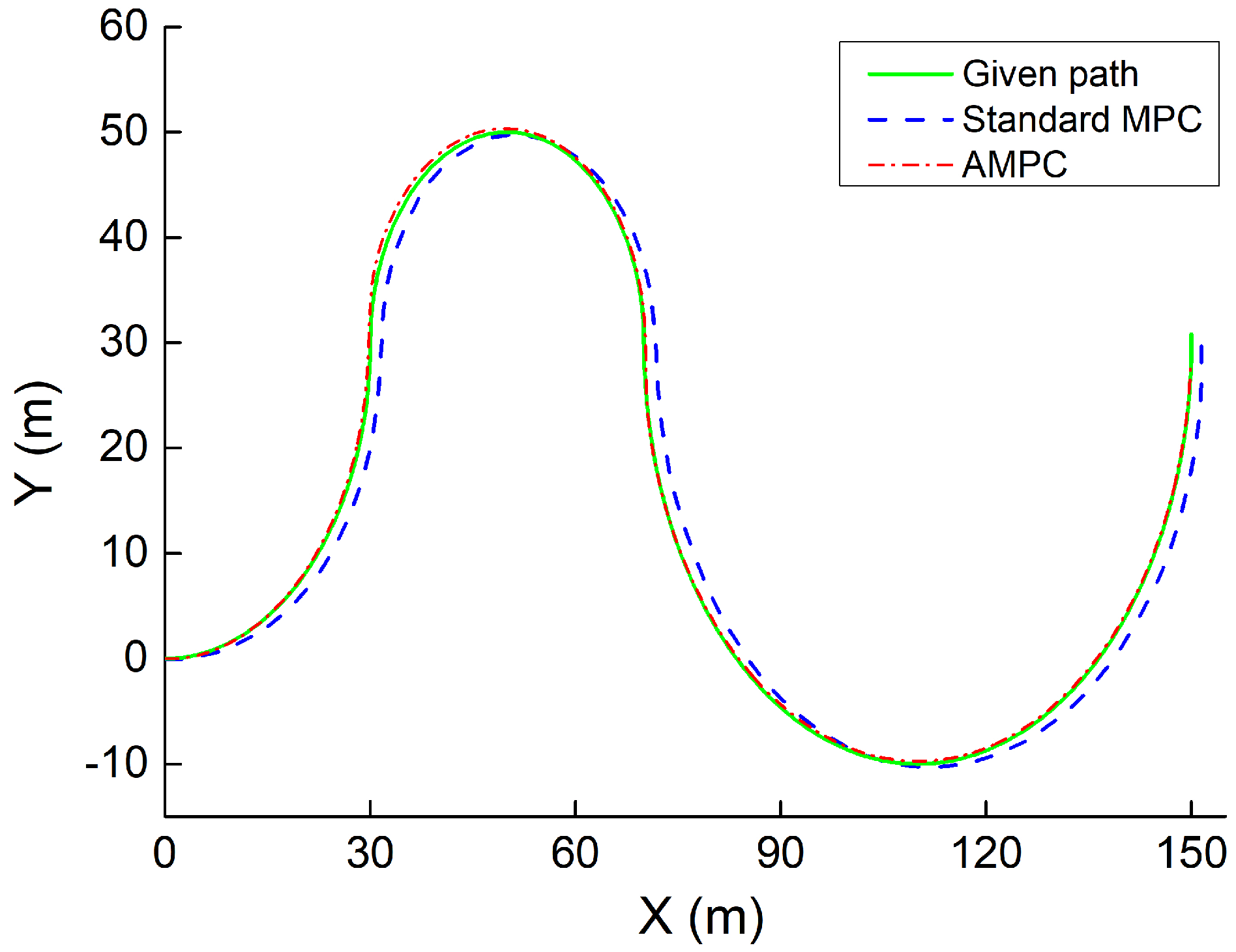
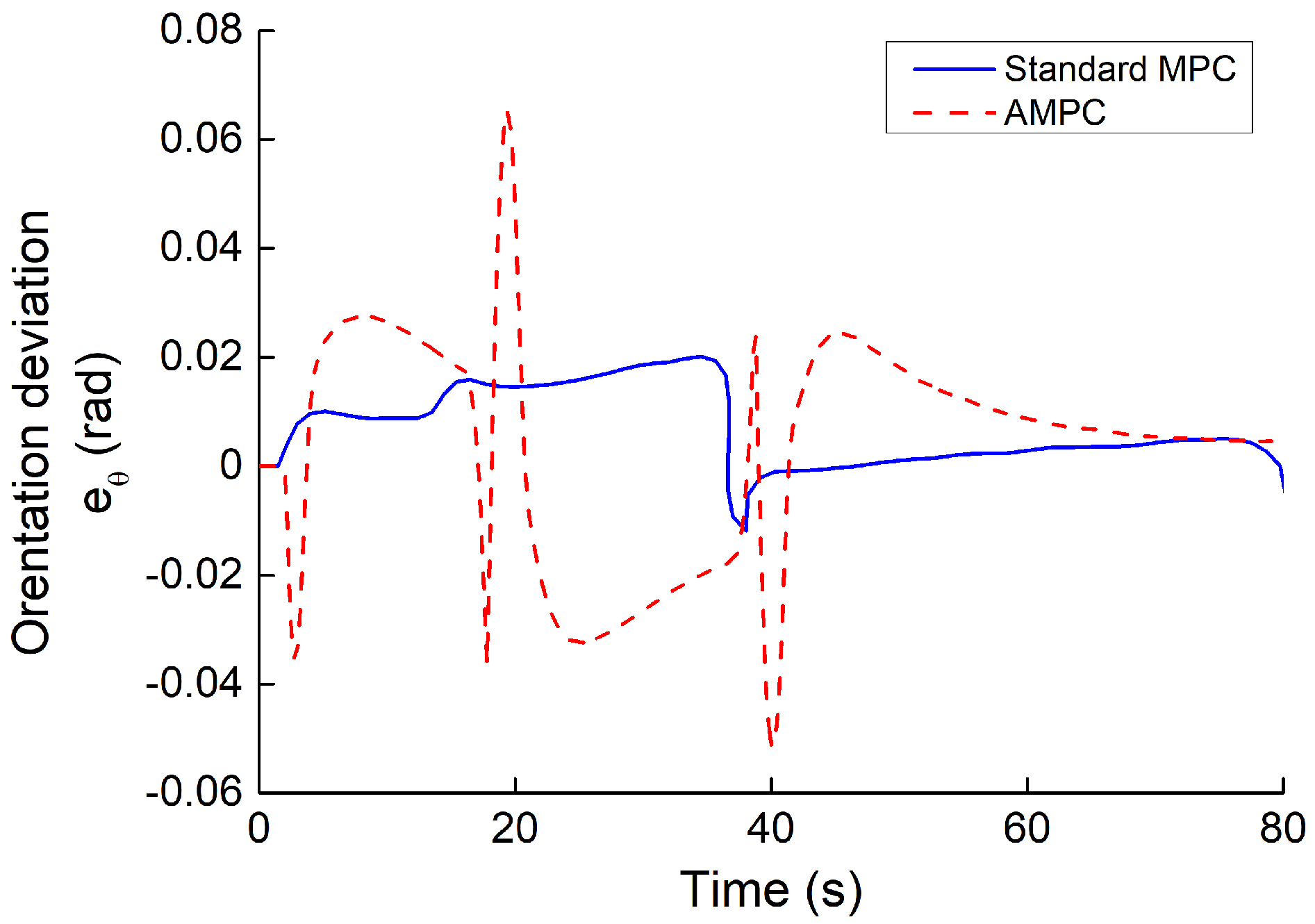
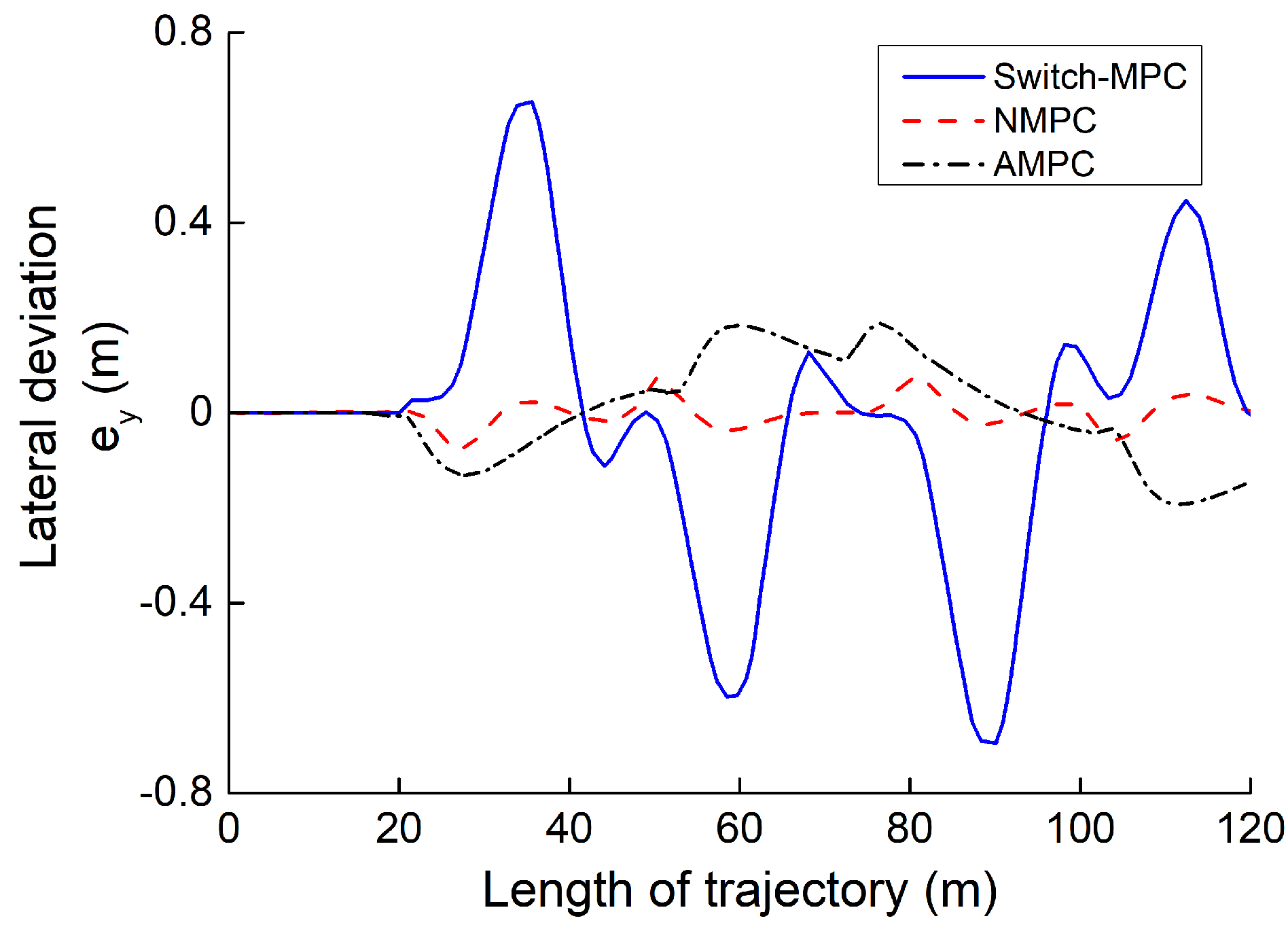
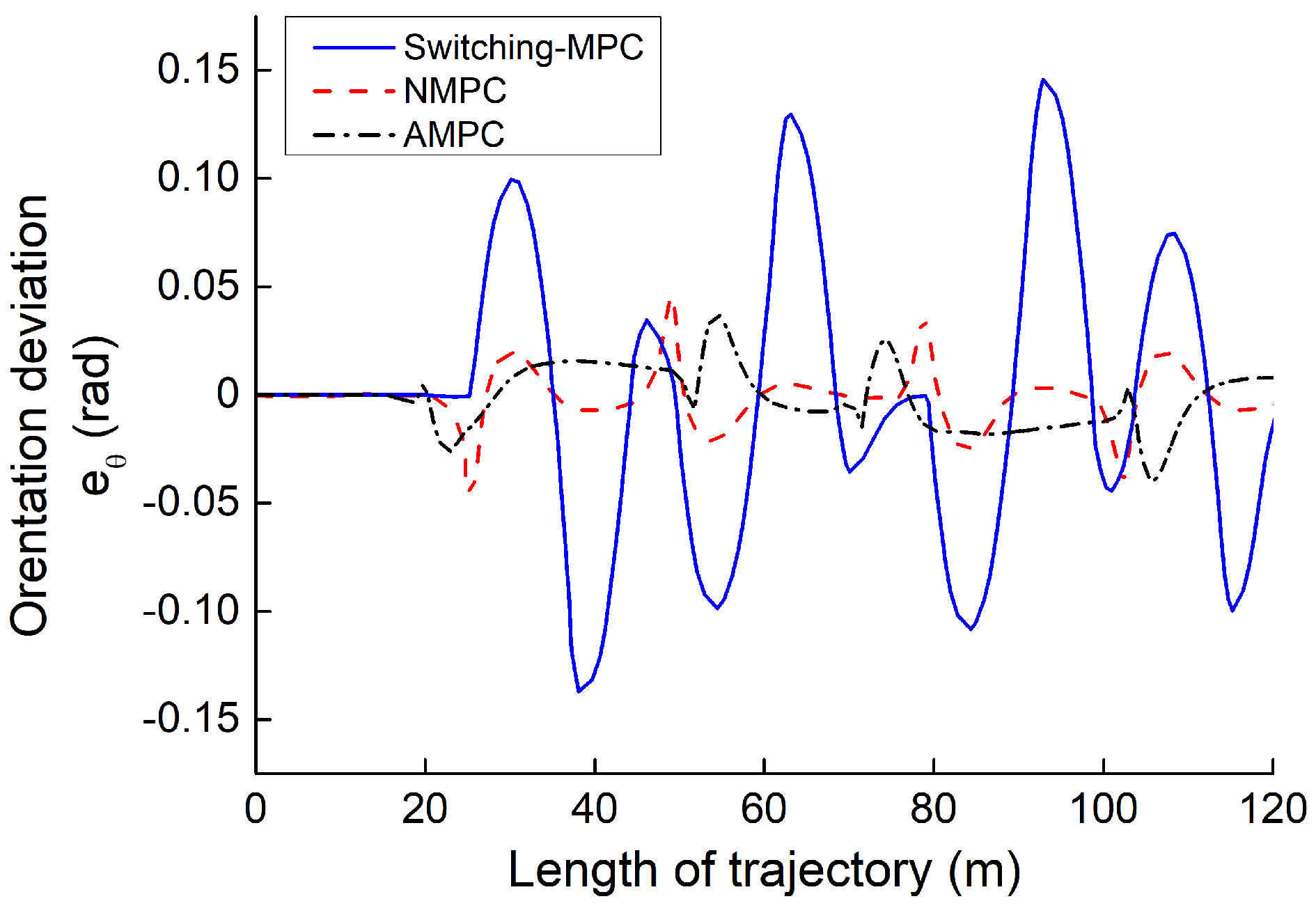
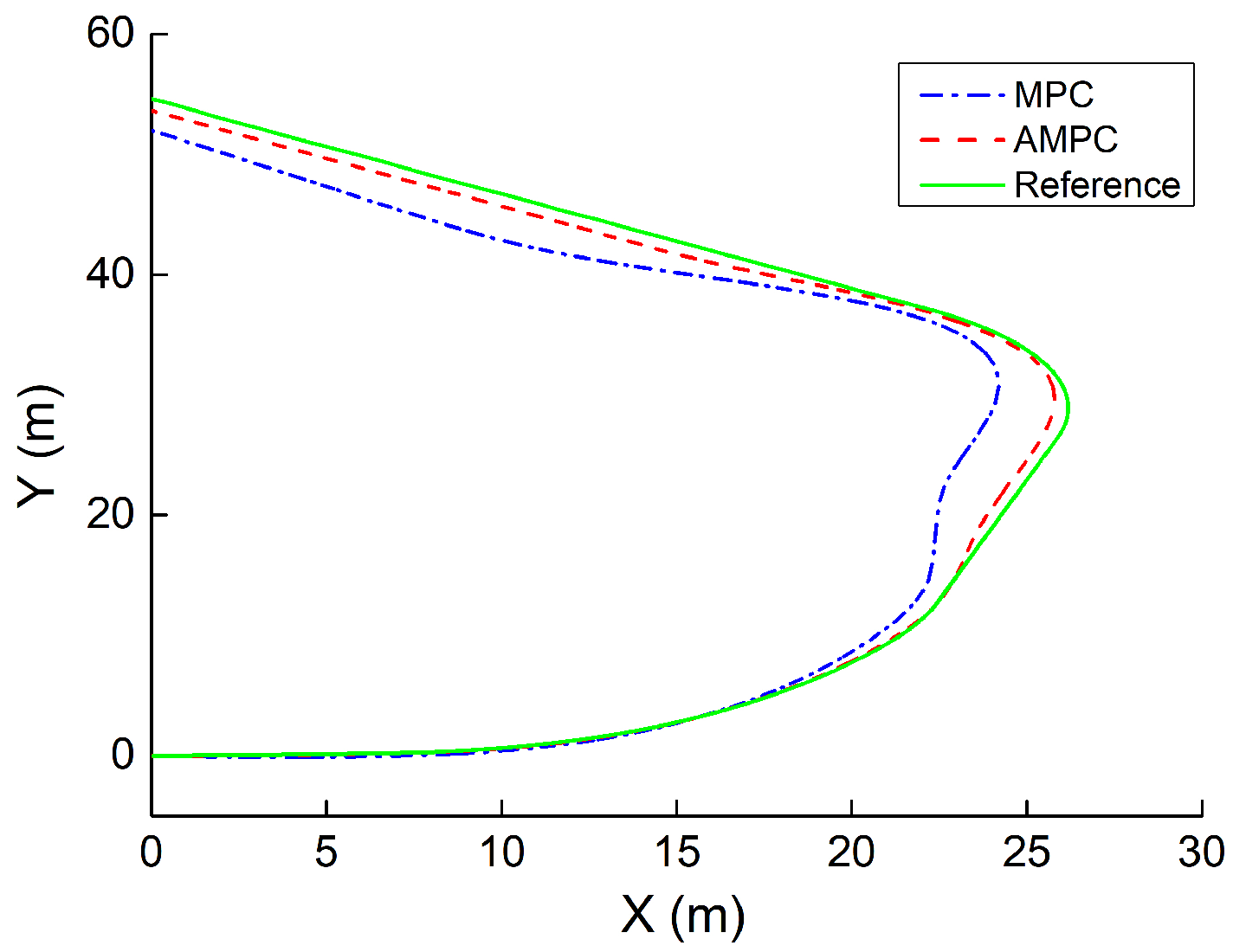
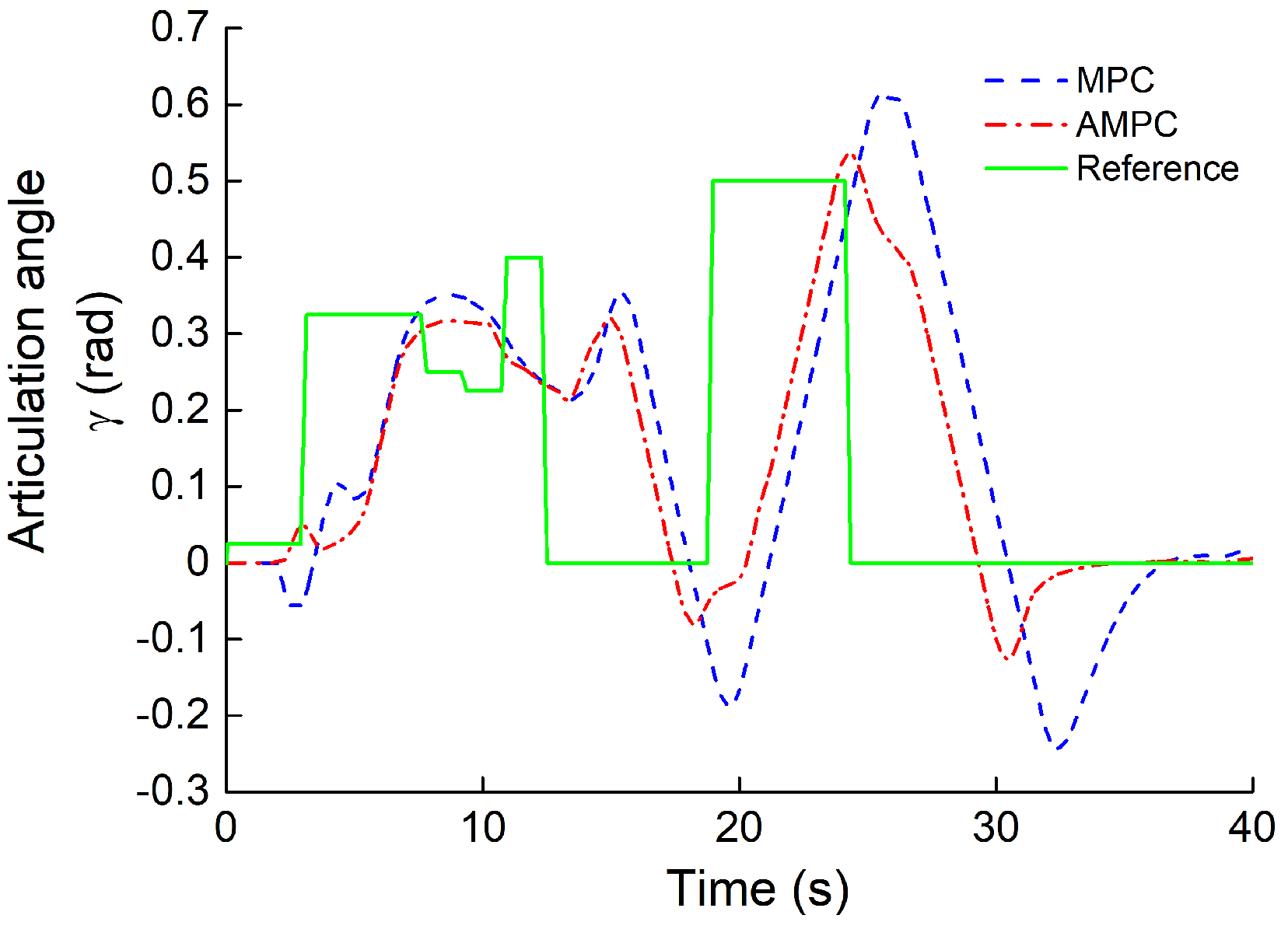
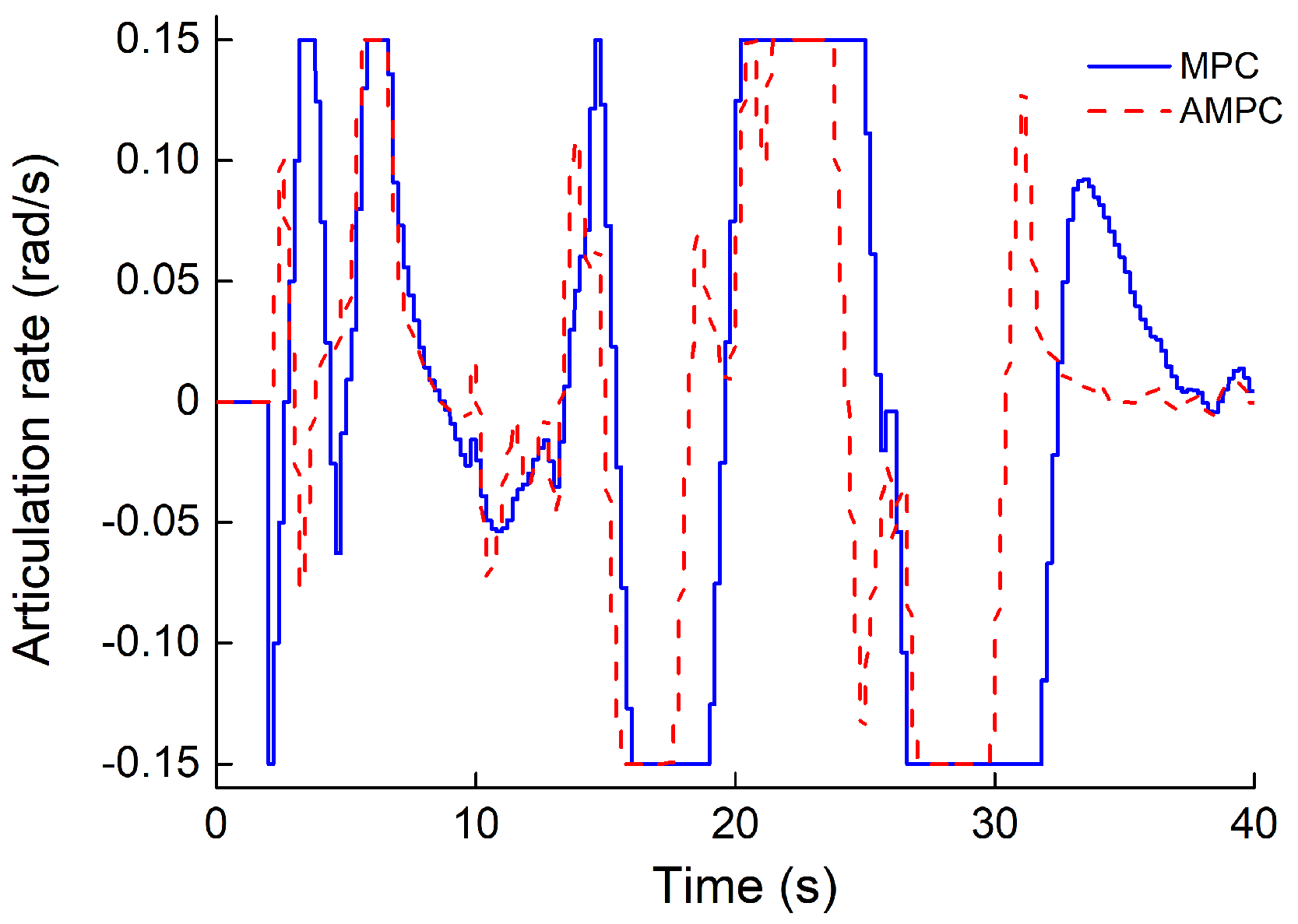
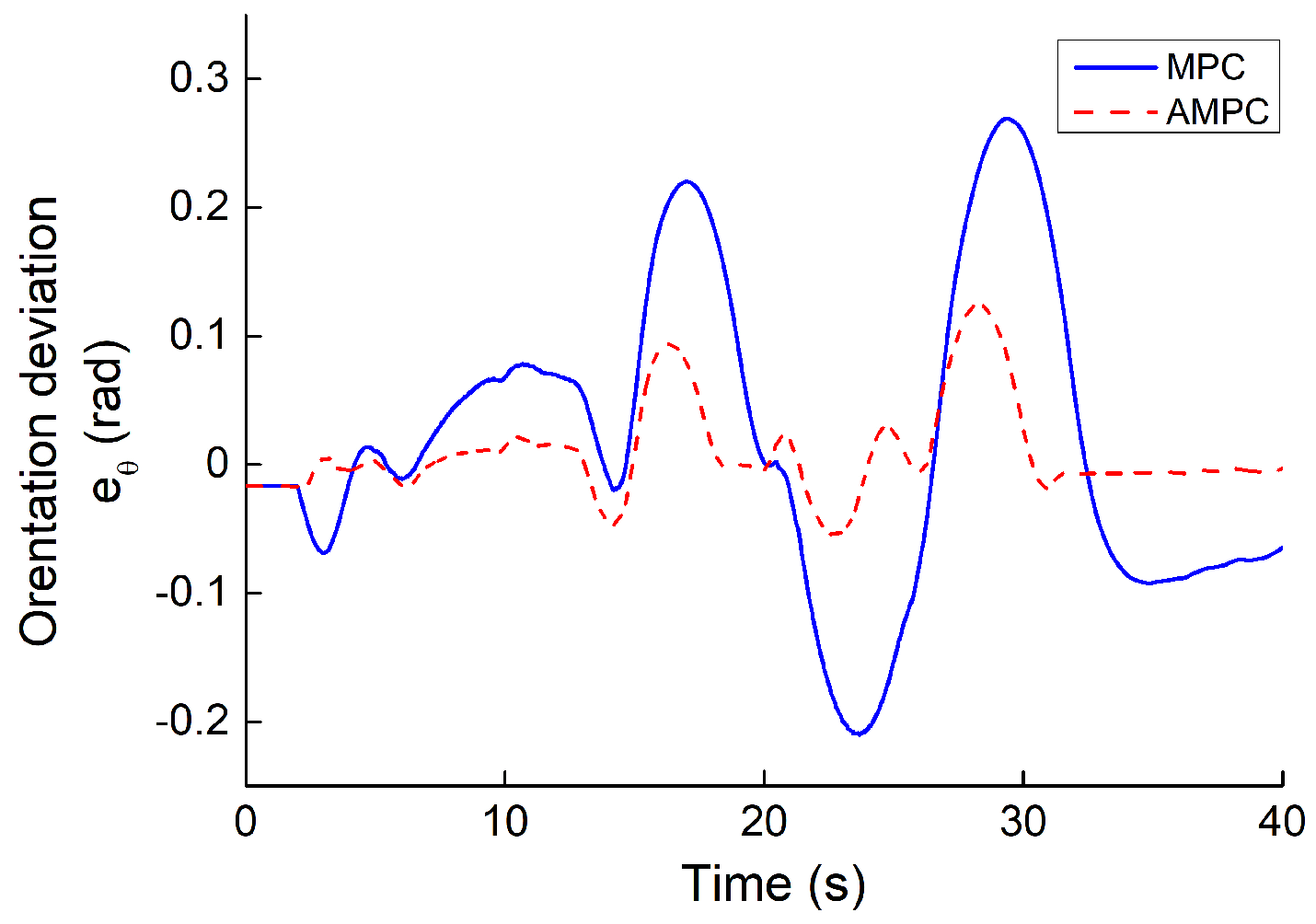
- The simulation of several path-tracking cases has demonstrated that the standard-MPC controller cannot accurately control the ATV to follow a path with varying curvature. However, the proposed AMPC controller outperforms the standard-MPC controller, while the AMPC controller can achieve the same level of tracking performance compared to the nonlinear MPC controller.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASV | Articulated steering vehicle |
| ATV | Articulated tracked vehicle |
| AMPC | Adaptive model predictive control |
| NMPC | Nonlinear model predictive control |
| MPC | Model predictive control |
| RS | Reeds Shepp |
References
- Lopatka, M.J.; Rubiec, A. Concept and preliminary simulations of a driver-aid system for transport tasks of articulated vehicles with a hydrostatic steering system. Appl. Sci. 2020, 10, 5747. [Google Scholar] [CrossRef]
- Watanabe, K.; Kitano, M. Study of Steerability of Articulated Tracked Vehicles—Part 1. Theoretical and Experimental Analysis. J. Terramech. 1986, 23, 69–83. [Google Scholar] [CrossRef]
- Marshall, J.; Barfoott, T.; Larsson, J. Autonomous Underground Tramming for Center-Articulated Vehicles. J. Field Robot. 2008, 25, 400–421. [Google Scholar] [CrossRef]
- Alshaer, B.J.; Darabseh, T.T.; Alhanouti, M.A. Path planning, modeling and simulation of an autonomous articulated heavy construction machine performing a loading cycle. Appl. Math. Model. 2013, 37, 5315–5325. [Google Scholar] [CrossRef]
- Qing, G.; Li, L.; Bai, G. Longitudinal and Lateral Trajectory Planning for the Typical Duty Cycle of Autonomous Load Haul Dump. IEEE Access 2019, 7, 126679–126695. [Google Scholar]
- Xu, T.; Xu, Y.; Wang, D.; Feng, L.H. Path Planning for Autonomous Articulated Vehicle Based on Improved Goal-Directed Rapid-Exploring Random Tree. Math. Probl. Eng. 2020, 1–14. [Google Scholar] [CrossRef]
- Sabiha, A.D.; Kamel, M.A.; Said, E.; Hussein, W.M. Trajectory Generation and Tracking Control of an Autonomous Vehicle Based on Artificial Potential Field and Optimized Backstepping Controller. In Proceedings of the 2020 12th International Conference on Electrical Engineering (ICEENG), Cairo, Egypt, 7–9 July 2020. [Google Scholar]
- Chien, V.D.; Heungju, A.; Doo, S.L.; Sang, C.L. Improved Analytic Expansions in Hybrid A-Star Path Planning for Non-Holonomic Robots. Appl. Sci. 2022, 12, 5999. [Google Scholar]
- Xu, Y.; Liu, R. Path planning for mobile articulated robots based on the improved A * algorithm. Int. J. Adv. Robot. Syst 2017, 14, 1–10. [Google Scholar] [CrossRef]
- Nayl, T.; Nikolakopoulos, G.; Gustafsson, T. A full error dynamics switching modeling and control scheme for an articulated vehicle. Int. J. Control Autom. Syst. 2015, 13, 1221–1232. [Google Scholar] [CrossRef]
- Kayacan, E.; Ramon, H.; Saeys, W. Robust trajectory tracking error model-based predictive control for unmanned ground vehicles. IEEE-ASME Trans. Mechatron. 2015, 21, 806–814. [Google Scholar] [CrossRef]
- Ridley, P.; Corke, P. Load haul dump vehicle kinematics and control. J. Dyn. Syst. Meas. Control-Trans. ASME 2003, 125, 54–59. [Google Scholar] [CrossRef]
- Barbosa, F.M.; Marcos, L.B.; Grassi, V. Robust path-following control for articulated heavy-duty vehicles. Control Eng. Practice 2019, 85, 246–256. [Google Scholar] [CrossRef]
- Oreh, S.T.; Kazemi, R.; Azadi, S. A new desired articulation angle for directional control of articulated vehicles. Proc. Inst. Mech. Eng. Part K J.-Multi-Body Dyn. 2012, 226, 298–314. [Google Scholar] [CrossRef]
- Nayl, T.; Nikolakopoulos, G.; Gustafsson, T. Design and experimental evaluation of a novel sliding mode controller for an articulated vehicle. Robot. Auton. Syst. 2018, 103, 213–221. [Google Scholar] [CrossRef]
- Astolfi, A.; Bolzern, P.; Locatelli, A. Path-tracking of a tractor-trailer vehicle along rectilinear and circular paths: A Lyapunov-based approach. IEEE Trans. Robot. Autom. 2004, 20, 154–160. [Google Scholar] [CrossRef]
- Sampei, M.; Tamura, T.; Kobayashi, T.; Shibui, N. Arbitrary path tracking control of articulated vehicles using nonlinear control theory. IEEE Trans. Control Syst. Technol. 1995, 3, 125–131. [Google Scholar] [CrossRef]
- Ruslan, N.A.I.; Amer, N.H.; Hudha, K.; Kadir, Z.A.; Ishak, S.A.F.M.; Dardin, S.M.F.S. Modelling and control strategies in path tracking control for autonomous tracked vehicles: A review of state of the art and challenges. J. Terramech. 2023, 105, 67–79. [Google Scholar] [CrossRef]
- Nayl, T.; Nikolakopoulos, G.; Gustafsson, T. Effect of kinematic parameters on MPC based on-line motion planning for an articulated vehicle. Robot. Auton. Syst. 2015, 70, 16–24. [Google Scholar] [CrossRef]
- Kayacan, E.; Saeys, W.; Ramon, H.; Belta, C.; Peschel, J.M. Experimental Validation of Linear and Nonlinear MPC on an Articulated Unmanned Ground Vehicle. IEEE/ASME Trans. Mechatron. 2018, 23, 2023–2030. [Google Scholar] [CrossRef]
- Kayacan, E.; Kayacan, E.; Ramon, H.; Saeys, W. Robust tube-based decentralized nonlinear model predictive control of an autonomous tractor-trailer system. IEEE/ASME Trans. Mechatron. 2015, 20, 447–456. [Google Scholar] [CrossRef]
- Shi, J.; Sun, D.; Qin, D.; Hu, M.; Kan, Y.; Ma, K.; Chen, R. Planning the trajectory of an autonomous wheel loader and tracking its trajectory via adaptive model predictive control. Robot. Auton. Syst. 2020, 131, 103570. [Google Scholar] [CrossRef]
- Dong, C.; Cheng, K.; Hu, W.; Yao, Y. Dynamic modelling of the steering performance of an articulated tracked vehicle using shear stress analysis of the soil. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2016, 231, 653–683. [Google Scholar] [CrossRef]
- Dong, C.; Cheng, K.; Hu, K.; Hu, W. Dynamic modeling study on the slope steering performance of articulated tracked vehicles. Adv. Mech. Eng. 2017, 9, 1–26. [Google Scholar] [CrossRef]
- Wu, J.; Wang, G.Q.; Zhao, H.; Sun, K. Study on electromechanical performance of steering of the electric articulated tracked vehicles. J. Mech. Sci. Technol. 2019, 33, 3171–3185. [Google Scholar] [CrossRef]
- Hu, K.; Cheng, K. Dynamic modelling and stability analysis of the articulated tracked vehicle considering transient track-terrain interaction. J. Mech. Sci. Technol. 2021, 35, 1343–1356. [Google Scholar] [CrossRef]
- Cui, D.; Wang, G.Q.; Zhao, H.; Wang, S. Research on a path-tracking control system for articulated tracked vehicle. Strojniski Vestn.-J. Mech. Eng. 2020, 66, 311–324. [Google Scholar] [CrossRef]
- Tota, A.; Galvagno, E.; Veladocchia, M. Analytical study on the cornering behavior of an articulated tracked vehicle. Machines 2021, 9, 38. [Google Scholar] [CrossRef]
- Alcala, E.; Puig, V.; Quevedo, J. TS-MPC for Autonomous Vehicles Including a TS-MHE-UIO Estimator. IEEE Trans. Veh. Technol. 2019, 68, 6403–6413. [Google Scholar] [CrossRef]
- DeSantis, R.M. Path-tracking for a tractor-trailer-like robot: Communication. Int. J. Robot. Res. 1994, 13, 533–544. [Google Scholar] [CrossRef]
- Dou, F.; Huang, Y.; Liu, L.; Wang, H.; Meng, Y. Path planning and tracking for autonomous mining articulated vehicles. Int. J. Heavy Vehicle Systems 2019, 26, 315–333. [Google Scholar] [CrossRef]
- Bai, G.; Liu, L.; Meng, Y.; Luo, W.; Gu, Q.; Ma, B. Path Tracking of Mining Vehicles Based on Nonlinear Model Predictive Control. Appl. Sci. 2019, 9, 1372. [Google Scholar] [CrossRef]



| Symbol | Description | Value | Unit |
|---|---|---|---|
| B | Width of ATVs | 2.1 | [m] |
| D | Length of ATVs | 4.8 | [m] |
| Distance from the hitch point to front unit | 2.6 | [m] | |
| Distance from the hitch point to rear unit | 2.2 | [m] | |
| Articulation angle | [−0.75, 0.75] | [rad] | |
| Articulation angular rate | [−0.18, 0.18] | [rad/s] | |
| Vehicle longitudinal speed | [−1, 4] | [m/s] |
| Description | Value | Unit |
|---|---|---|
| Minimum turn radius | 10.4 | [m] |
| Maximum velocity | 5 | [m/s] |
| Maximum acceleration | 2 | [m/s] |
| Maximum steering angle | 0.5 | [rad] |
| Maximum steering rate | 0.15 | [rad/s] |
| Grid resolution in distance | 2 | [m] |
| Grid resolution in yaw angle | 15 | [degree] |
| Motion step size | 1 | [m] |
| Number of steering angle candidate | 20 | |
| Steer angle change weighting coefficient | 2 | |
| Steer angle weighting coefficient | 1 | |
| Heuristic weighting coefficient | 2 |
| Symbol | Description | Value |
|---|---|---|
| The sample time of controller | 0.2 [s] | |
| Length of the prediction horizon | 10 | |
| Length of the control horizon | 5 | |
| Weighting coefficient for states | diag(0.5 0.5 1 0.1 0) | |
| Weighting coefficient for control input | diag(0.1 0.2) | |
| Terminal cost coefficient | diag(0.1 0.1 1 1 0) |
| Map | Method 1 | Method 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Curvature 1 | Number 2 | Length 3 | Time 4 | Curvature | Number | Length | Time | |
| Map A | 0.095 | 4 | 88.46 | 15.5 | 0.059 | 1 | 96.06 | 23.3 |
| Map B | 0.098 | 5 | 128.94 | 26.4 | 0.096 | 2 | 116.09 | 40.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Cheng, K. Trajectory Planning for an Articulated Tracked Vehicle and Tracking the Trajectory via an Adaptive Model Predictive Control. Electronics 2023, 12, 1988. https://doi.org/10.3390/electronics12091988
Hu K, Cheng K. Trajectory Planning for an Articulated Tracked Vehicle and Tracking the Trajectory via an Adaptive Model Predictive Control. Electronics. 2023; 12(9):1988. https://doi.org/10.3390/electronics12091988
Chicago/Turabian StyleHu, Kangle, and Kai Cheng. 2023. "Trajectory Planning for an Articulated Tracked Vehicle and Tracking the Trajectory via an Adaptive Model Predictive Control" Electronics 12, no. 9: 1988. https://doi.org/10.3390/electronics12091988
APA StyleHu, K., & Cheng, K. (2023). Trajectory Planning for an Articulated Tracked Vehicle and Tracking the Trajectory via an Adaptive Model Predictive Control. Electronics, 12(9), 1988. https://doi.org/10.3390/electronics12091988






