Abstract
Spin-Hall-effect nano-oscillators are promising beyond the CMOS devices currently available, and can potentially be used to emulate the functioning of neurons in computational neuromorphic systems. As they oscillate in the 4–20 GHz range, they could potentially be used for building highly accelerated neural hardware platforms. However, due to their extremely low signal level and high impedance at their output, as well as their microwave-range operating frequency, discerning whether the SHNO is oscillating or not carries a great challenge when its state read-out circuit is implemented using CMOS technologies. This paper presents the first CMOS front-end read-out circuitry, implemented in 180 nm, working at a SHNO oscillation frequency up to 4.7 GHz, managing to discern SHNO amplitudes of 100 µV even for an impedance as large as 300 Ω and a noise figure of 5.3 dB300 Ω. A design flow of this front end is presented, as well as the architecture of each of its blocks. The study of the low-noise amplifier is deepened for its intrinsic difficulties in the design, satisfying the characteristics of SHNOs.
1. Introduction
Computers have become essential to all aspects of modern life—from process controls, engineering, and science to entertainment and communications—and are omnipresent all over the globe. Currently, about 5–15% of the world’s energy is spent in some form of data manipulation, transmission, or processing, and thus its reduction is of paramount importance [1].
Parallel computing is presently one of the ultimate solutions to cope with problems where the Von Neumann approach is no longer valid for manifold reasons, including prohibitive power consumption and limited data processing due to memory–CPU data transfers. One powerful flavor of parallel computing is reflected presently in the neuromorphic computing system paradigm.
Neuromorphic computing [2] describes the use of very-large-scale integration systems containing electronic data, event-driven circuits to mimic neuro-biological architectures present in the nervous system. It overcomes the limitation of the word-at-a-time thinking of conventional computers by doing massive parallel data processing, similar to the brain, by co-locating data-storage and data-processing elements. Improvements in CMOS technology enable, presently, mass-produced chip processors with over 5 billion transistors per die to exist which feature 10-nm sizes with an unimaginable power consumption reduction per device. These CMOS enhancements, as well as the advances in materials and emerging nano-devices, have made possible a revolution in parallel computing, which is reflected in neuromorphic computing systems (NCS). One recent accomplishment in this field has come from IBM research, namely a biologically inspired chip (“TrueNorth”) that implements one million spiking neurons and 256 million synapses on a chip with 5.5 billion transistors with a typical power draw of 70 milliwatts. As impressive as this system is, if scaled up to the size of the human brain, it is still about 10,000 times more power intensive. A similar approach is taken by the Intel Loihi processor, which additionally includes learning capability [3,4].
However, despite NCS built with CMOS technologies achieving good results, the short-term range of physical limits of CMOS will cause that many CMOS NCS applications to be unfeasible due to prohibitive power figures, silicon area or frequency limitations. Fortunately, several groups worldwide are studying new approaches to overcome these CMOS drawbacks. These problems are being addressed using beyond-CMOS technologies. For non-CMOS synapses, memristors are used for this purpose due to programmability being currently under extensive research. Furthermore, for non-CMOS neurons, alternatives such as Magnetic Tunneling Junctions are being investigated. In particular, an interesting novel option for non-CMOS neurons is to use weighted nano-oscillators in, for instance, the flavors of weighted mutually synchronized nano-constriction spin-Hall nano-oscillators (SHNOs) [5,6].
SHNOs have recently aroused a lot of interest compared to other oscillators of their kind (i.e., STNOs) due to the straightforward fabrication of their simple structure, frequency tunability in a wide range, optical access and freedom in layer and layout selection [7,8,9,10]. Thanks to their particular potential to become synchronized in 1D chains [5] and 2D arrays [11], SHNOs have turned into a great candidate for several applications such as wireless communication [12], signal generation [13] and novel computation schemes, such as neuromorphic computing [14,15,16].
Given the characteristics of these nano-oscillators, they allow an increment in the frequency of operation of the whole neural network, reaching the GHz range while potentially reducing drastically the consumption of the NCS by orders of magnitude.
To detect whether the nano-oscillators are on or not, a system that performs this detection is necessary. In this work, we propose an implementation of a CMOS front end that works in the GHz environment and detects very low-amplitude signals.
The scheme representing the feed-forward neural network using the SHNOs together with the individual front ends is outlined in Section 2. Section 3 describes the electrical characteristics of the SHNO, used as the specifications of the front end to be designed. Section 4 goes in depth, describing the architecture of the chosen front end and those of the blocks that compose it. Finally, Section 5 and Section 6 give the front-end designed characteristics and the conclusions, respectively.
2. NCS Scheme
Considering the novel idea of building an NCS with SHNO neurons and memristive synapses [17], and CMOS front-end interface, in this paper, we present the radiofrequency front-end (RF-FE) architecture placed after the SHNOs of the NCS, as sketched in Figure 1. The first layer of the system, contained in the light blue box of Figure 1 comprises a neural network (NN) and the CMOS RF-FE. The NCS receives m input signals, which are injected into the NN. The NN has p SHNOs neurons with their synapses. Since the SHNOs work at RF frequencies, each of the outputs of the NN must be carefully processed in the p RF-FEs, to continuously detect the state of the SHNO (on or off). Other implementations of NN, such as the one shown in [18], can be used here, substituting the neuron for the SHNO, and then using the RF-FE presented here to read its state.
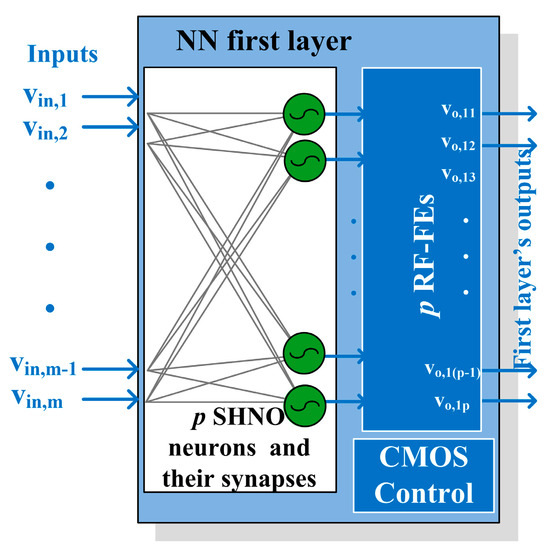
Figure 1.
Feed-forward neural network implemented in SHNOs [17] with its p RF-FE blocks.
A homogeneous integration of the SHNOs, the memristors, and the front-end circuitry was adopted to make the overall system area much smaller. This is one of the main specifications of our RF-FE because it forces the technology to be the same as that used to manufacture the SHNOs. In this design, it is a 180 nm CMOS node, which, as will be seen, affects the RF-FE performance.
3. SHNO Electrical Model
The electrical characteristics of the SHNO strongly determine the specifications of the RF-FE. In this section, we present the simplified SHNO electrical model used in the FE design. Due to the novelty in the SHNO device, its electrical model has not been extensively developed yet. In this work, the model used is derived from SHNO experimental characterization architectures created by the University of Gothenburg [11].
The SHNO electrical model used in this work corresponds to a sinusoidal voltage source, VSHNO(t), in series with a complex output impedance, ZSHNO (Thevenin’s model). Available output power, PSHNO, and oscillation frequency, fSHNO, are fixed by SHNO nanomaterial used in the fabrication procedure, the applied magnetic field, H, and the electrical operation point given by its bias current, IB,SHNO. From extracted measurements in a setup such as that of Figure 2, typical values for oscillator parameters are around PSHNO ≈ −65 dBm, ZSHNO ≈ 300 + 0j Ω, and fSHNO ≈ 5 GHz. Despite the excellent capability of SHNOs in high-frequency signal generation (up to 22 GHz [19]), due to the limitations in the CMOS-FE circuitry in conjunction with the high value of ZSHNO, SHNO operating conditions are modified to oscillate at a lower frequency, such as 4 GHz. Under these conditions, the expected peak voltage values for oscillations entering in the RF-FE in the case of considering a standard input impedance of Zin,FE = 50 Ω will be around Vin,FE ≈ 100 µVpk.
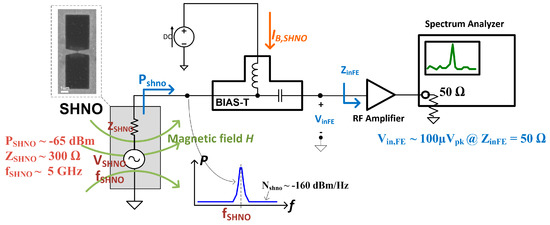
Figure 2.
SHNO parameters, simplified scheme of the oscillator under test, at a fixed external magnetic field and IB,SHNO, and the measurement setup are shown.
Regarding electronic noise, considering the values estimated in the preliminary characterization experiments, we will consider an additive white-noise model with very low densities, around NSHNO,(SSB) ≈ −160 dBm/Hz. This value leaves enough room for the RF-FE noise figure.
4. RF Front End
Contrary to what happens in RF communications systems receivers, where not only the system gain is important but also parameters such as nonlinearity (e.g., the IIP3) or very low-noise figures [20], in this application, as it is only necessary to detect whether or not the SHNO is oscillating with a sufficient output power, it is unnecessary to exactly detect the amplitude, frequency and phase of the SHNO output. This fact implies that no limitation is imposed on the nonlinearity of the RF-FE (e.g., the IIP3), simplifying the design of the blocks that compose it.
This is the first time that the design of a CMOS circuit to detect the signal at the output of a SHNO is addressed, and it implies the possible existence of several solutions to realize this sensing front end, which is, in itself, an area of study. With the above considerations, we propose the front-end architecture presented inside the blue box of Figure 3, based on a super-heterodyne receiver architecture [20].
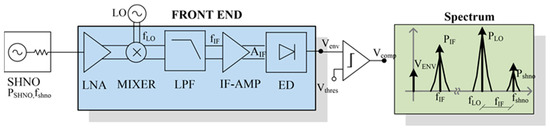
Figure 3.
Frond-end scheme proposed to sense the SHNO output signal.
The choice of a super-heterodyne system, as opposed to a zero-IF or low-IF heterodyne [21] system, is justified by the following. On one hand, the working frequency of the SHNO, fSHNO, has a certain drift in time, which would not allow the exact translation of the frequency to zero Hz or to intermediate-frequency, fIF. On the other hand, a zero-IF or low-IF system cannot be used because the large power difference between the SHNO signal, PSHNO, and that of the local oscillator, PLO, and its noise, would cause the signal to be hidden under the noise of the local oscillation (LO). In addition, finally, we wanted to take advantage of the high working frequency of the SHNOs. Reducing the output frequency of the data processed by the FE-RF means that the SHNO state detection time (on/off) increases, losing the potential offered by working at GHz. For the reasons given above, we chose the intermediate-frequency fIF = |fLO-fSHNO|= 100 MHz, with fLO the local oscillator frequency, as sketched in the green box of Figure 3.
The building blocks of the RF-FE are, from left to right: (i) low-noise amplifier (LNA), (ii) mixer, (iii) low-pass filter, (iv) intermediate-frequency (IF) amplifier, (v) envelope detector (ED), (vi) comparator. Its input signal, with frequency fSHNO, is amplified by the LNA, and translated to an intermediate-frequency fIF via a mixer, to be finally filtered, amplified and envelope detected.
The LNA boosts the SHNO output signal by a gain, GV,LNA, providing a good input return loss with a low-noise figure (NF), as well as a good reverse isolation, especially to reject spurs of the LO signal used in mixer. Next, there is a low-pass filter (LPF). Since one of the operating assumptions of the SHNO is that the noise at its output is much below the SHNO output signal (when considering an integrating bandwidth BWSHNO of ~100 MHz), an LPF with a bandwidth of 100 MHz is placed to remove, in particular, the spurs generated by the mixer noise and the out of band noise. After the LPF, an intermediate-frequency amplifier is added to sufficiently boost the LPF output to reach the ED minimum input to work properly. Finally, the ED DC output level is fed to the input of a comparator, which decides whether the oscillator oscillates with enough power, or not.
In this RF-FE, the gain is the parameter of the chain (up to the rectifier) must be maximized, regardless of the possible decrease in system linearity, only controlling that the noise figure at the input is below an acceptable limit, set here at 5 dB.
Since this is the first time that this architecture has been designed with the specifications imposed by the SHNO, the top-down design approach could not be directly applied. We apply a bottom-up approach, where the choice of the circuit architecture of each block could not be decided from the beginning, as the implementation of one block influenced the performance of the rest.
We propose the RF-FE design flow presented in Figure 4:
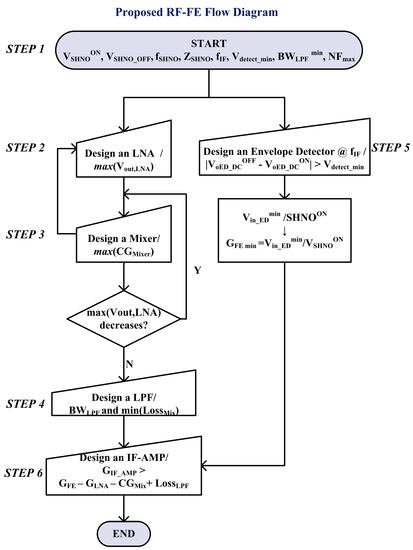
Figure 4.
Proposed RF-FE flow diagram.
- STEP 1.
- Start by fixing a set of initial parameters and limits: SHNO voltage where it is considered to be turned on and off, VSHNOON/OFF, SHNO oscillation frequency fSHNO, SHNO output impedance ZSHNO, intermediate-frequency fIF, voltage difference that the comparator can discern, Vdetect_min, minimum bandwidth of the LPF, BWLPFmin, and maximum noise figure NFmax of the RF-FE.
- STEP 2.
- Design an LNA that maximizes its output voltage, Vout,LNA at fSHNO, and whose noise figure NF is below NFmax. (Maximizing Vout,LNA implicitly means improve a good LNA input matching).
- STEP 3.
- Design a mixer (co-designed with the LNA) that maximizes its conversion gain CGMixer. If Vout,LNA is substantially reduced (i.e., if the mixer excessively loads the LNA), a new mixer should be designed. If it is not possible, a new LNA architecture should be chosen to cope with the load fixed by the mixer.
- STEP 4.
- Design an LPF (the simplest and with the smallest possible area) whose 3-dB bandwidth, BWLPF, is fIF, and with a minimum loss in the transfer magnitude, LossLPF.
- STEP 5.
- In parallel, design an Envelope Detector whose output DC voltage, VoED_DC, is proportional to its output input and VoED_DCOFF − VoED_DCON| > Vdetect_min. The envelope detector fixes a minimum input voltage Vin_EDmin.
- STEP 6.
- With the information found in STEP 4 and STEP 5, design an intermediate-frequency amplifier IF-AMP, with a gain higher than GIF_AMP = GFE − GLNA − CGMix + LossLPF. The RF-FE gain is defined as GFE = Vin_EDmin /VSHNOON. Now the design is finished.
Throughout the design of all the blocks, the premise in all of them has been to look for architecture that would consume as little energy as possible and occupy the least area, meeting the design requirements of the RF-FE.
Next, we discuss the architecture chosen for each block of the RF-FE, with special emphasis on the LNA.
4.1. LNA
In the present application, the LNA design is particularly challenging due to the SHNO output low signal levels, high working frequency near the microwave band, and the SHNO high-output resistance. This leads to the need for the LNA: (1) to provide as much voltage gain as possible; (2) to present the best possible matching to maximize power with the SHNO output impedance; and (3) to have a low input noise figure. In addition, it should have reduced area and low power consumption because p-RF-FEs are needed in the NCS. All these factors lead to stringent design trade-offs.
The front end is designed to work with internal differential signals due to well-known advantages. However, since the SHNO is a single-ended device, the LNA must be a single-ended to differential architecture; subsequent blocks will henceforth be differential.
Since the SHNO output signal is inherently a narrow-band signal, initially, both wideband LNAs (WB-LNAs) and narrow-band LNAs (NB-LNAs) can be employed. Let us evaluate them qualitatively in terms of area, input matching, gain and noise figure.
- Area: since p RF-FEs are needed, with p > 1 (see Figure 1), using NB-LNAs implies the take-up of a lot of silicon area due to passive inductors. WB-LNAs with no inductors occupy much less area.
- Input matching: since SHNO output impedance is far from (50 + 0j) Ω, input matching is better achieved in NB-LNAs due to inductors. Conversely, in WB-LNAs, the real part of the LNA input impedance Re(Zin) is generally adjusted using the input transistor connected in a common-gate fashion, being Re(Zin) ≅ 1/gm at low frequency. If there were no combination of transistor size and bias such that it generates a gm that gives a good return loss, the matching would be compromised.
- Gain: for WB-LNAs, their gain can be low because this is, generally, directly proportional to input transistor gm. Therefore, if ZSHNO is high, gm is low, and gain is reduced. For NB-LNAs, the inductor input matching network helps both to boost the gain and provides more degrees of freedom to achieve the matching.
- Noise Figure: Since improving matching and gain has a direct impact on noise reduction, it is expected that NB-LNAs have better noise figure than WB-LNAs.
Despite the drawbacks of working with WB-LNAs, we tried to use them to reduce the occupied area, as in the first instance, they would not use inductors. We designed several WB-LNA architectures trying to maximize gain, for a reasonable matching. We choose the two most promising WB-LNAs architectures: (1) the basic WB CG-CS LNA [22] of Figure 5a; and (2) the WB resistive feedback LNA [23] of Figure 5b. Regarding the NB-LNAs, we choose a modified version of the LNA of [24], presented in Figure 5c, where we replace the resistive loads by inductors L1 so as to reach higher gain without limiting the current the LNA can drain without cutting off the transistors. The methodology applied was presented in [25,26] with the semi-empirical MOS transistor model of [27].
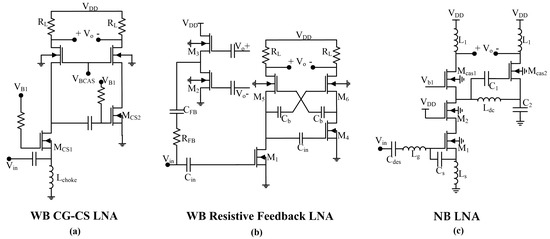
Figure 5.
LNAs designed in this work: (a) WB-CG-CS LNA [22]; (b) WB resistive feedback LNA [23]. (c) NB-LNA (modified architecture from [24]) (Bias not shown for clarity).
For WB-LNA schemes, we found that it is extremely difficult to achieve a good matching between the SHNO and the LNA. On the one hand, canceling out the imaginary part of the WB-LNA input impedance is an issue when working at 180 nm CMOS technologies. Parasitic capacitances are so large that not reducing their effect means completely losing the matching. Discarding the use of neither on-chip inductors, nor external matching networks between the SHNO and the LNA, to mitigate this problem, we considered using a bonding inductor between the SHNO and the LNA as part of its input matching network. Here, so as not to place LNA and SHNO too far apart, we limit the wire-bond length to 3 mm, with its inductance value around 3 nH, reducing the effect of the LNA input parasitic capacitances.
On the other hand, for these WB-LNAs, even improving the imaginary part, the matching is very poor when RSHNO = 300 Ω, since the resistive part of the input impedance Re(Zin) is constrained to low values. For these WB-LNAs, the Re(Zin) is around 1/gm or even lower. However, the gm value cannot be reduced without compromising the gain of the WB-LNAs (gm is that of the input transistor MCS1 of the WB CG-CS LNA of Figure 5a, and of transistor M3 of the WB resistive feedback LNA of Figure 5b.
For each of the LNAs of Figure 5, we chose a design with a good trade-off between insertion loss and gain for RSHNO = 300 Ω at frequencies in the range of 5 GHz, and whose electrical characteristics, obtained from an electrical simulator, are presented in Figure 6a,c,e (left column of plots). In particular, for the NB-LNA, we applied the design meth-odology of [25,26] with the semi-empirical MOS transistor model of [27].
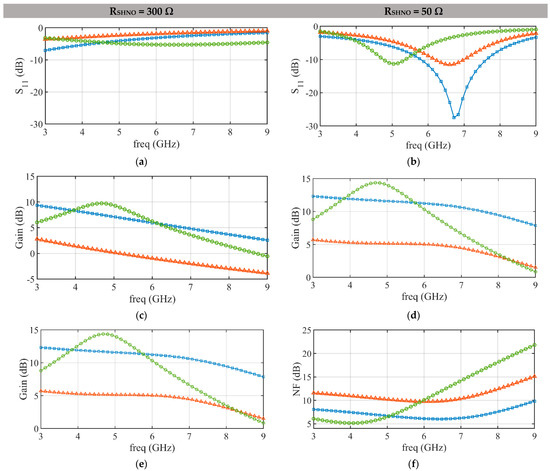
Figure 6.
S11 (a,b); Gain (c,d); NF (e,f) for CG–CS LNA, resistive feedback LNA and, NB–LNA, for RSHNO = 50 Ω and RSHNO = 300 Ω, under schematic simulations.
Let us now observe the performances of the designed LNAs at RSHNO = 300 Ω. The matching is given in Figure 6a: for both WB-LNAs the matching is unacceptable at 5 GHz (S11 much above −10 dB), and only for the NB-LNA, S11 is acceptable, reaching −12 dB. Regarding the gain (shown in Figure 6c, we see that, at 5 GHz, the WB resistive feedback LNA reaches values of only 5 dB, the WB CG-CS LNA reaches 11.5 dB; and the NB-LNA achieves almost 14 dB. Likewise, the noise figure for RSHNO = 300 Ω is plotted in Figure 6e. When evaluated for 5 GHz, we observe an unacceptable noise figure (NF) of 10 dB in the WB resistive feedback LNA, and a NF around 5 dB both for the WB CG-CS LNA and the NB-LNA.
Finally, the LNAs designed for RSHNO = 300 Ω are also characterized for RSHNO = 50 Ω (see Figure 6b,d,f, right column of plots) because (1) the LNA characterization in the laboratory is made under this standard condition; and (2) in a possible reduction of RSHNO by SHNO designers in the future, it is important to know how the LNA would behave in such a case.
For both RSHNO = 50 Ω and RSHNO = 300 Ω, the WB Feedback LNA has much lower yield with respect to the other architectures for the three characteristics evaluated (S11, NF, Gain) in the frequency range considered, so it was finally discarded, even though it would be the ideal in terms of area for the lack of on-chip inductors.
The WB CG-CS LNA has much better performance but the choke Lchoke at the source of MCS1 is a drawback for our application. If it is external, the p RF-FEs need p chokes, which is unfeasible due to the practical difficulty of assembling the system. On the other hand, integrated chokes are discarded due to their very low quality factor, which makes the amplitude of the negative output, Vo−, much smaller than the positive one, Vo+, and the differential signals Vo+ and Vo− would be very unbalanced (the phase between them is far from being 180°), losing the advantages of working with a differential architecture.
Consequently, from the above data, and considering the fact that performance will be reduced when layout parasitics are taken into account, and since as much gain as possible is needed in this application, it was decided to use the NB-LNA, despite the surplus of silicon area due to the on-chip inductors.
The NB-balun LNA was fabricated under TSMC 180 nm technology. Its area is (740 × 660) µm2, and whose microphotograph is shown in Figure 7a. Its current consumption is 7.0 mA for VDD = 1.8 V at the frequency of interest. The LNA is fabricated with an output buffer for test purposes. The equipment used for test purposes has been the Agilent N5230A Network Analyzer, the Agilent N8974A Noise Figure Analyzer, the Marki BALH-0010 balun, and the Cascade Microtech M150 measurement platform (see Figure 7b). After de-embedding setup effects, the measured S11 and S21 (with the standard 50 Ω impedance of the Network Analyzer) are plotted in Figure 8 in blue, and the simulated ones are plotted in orange. We also include S11 and S21 values translated to 300 Ω (in green) for comparison purposes with the simulations presented in Figure 6. As observed, the matching, gain and noise figure lost some performance, but we consider it acceptable at the frequency of interest.

Figure 7.
(a) Microphotograph of the NB-balun LNA. (b) Measurement setup.
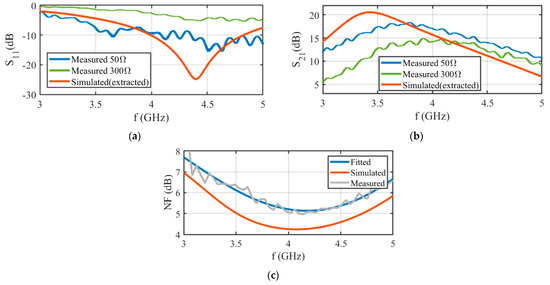
Figure 8.
Characterization of the fabricated NB-balun LNA: (a) S11, (b) S21, (c) NF measured and simulated for Rs = 50 Ω (extracted vied).
4.2. Mixer
From the perspective of power reduction of the whole system, the best mixer architecture should be a passive mixer, so it was the first choice despite it not contributing any gain to the system. The passive mixer of [22], which includes the classic passive mixer together with a trans-impedance amplifier (TIA), was first designed with a conversion gain of GPassiveMix = 0.45 V/V @{5 GHz}. Without the mixer, the LNA gain GNB-balun LNA = 14 dB @ {5 GHz, RSHNO = 300 Ω} but, after coupling the passive mixer to the NB-balun LNA the total gain was of only −2 dB. This means that the mixer excessively loads the LNA, causing the LNA performance to break down so much as to make the LNA-mixer block contribute no gain. This fact led to discarding this mixer architecture.
Thus, we move to active mixers, among which we chose the one by Klumperink et al. [28] (Figure 9) over others such as the Gilbert architecture because the noise produced by the input transistors and LO port is common mode noise, which is rejected at its differential output, reducing the NF of the mixer; also, the conversion gain would be lower in the Gilbert cell at our working frequencies. The mixer was co-designed with the LNA [29], by reducing the mixer input transistors to decrease, as much as possible, the load of the LNA without diminishing the conversion gain of the mixer excessively. Despite the mixer gain achieves GActiveMix = 8.5 V/V (see Figure 10), the gain of the combined block [LNA + mixer] achieves 30 V/V (schematic view) because of the interaction between them.
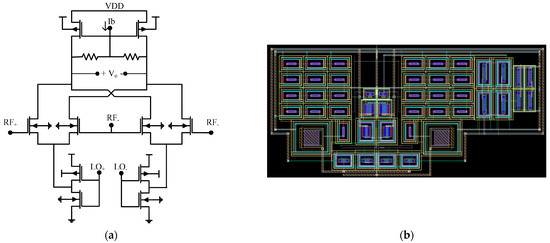
Figure 9.
(a) Mixer schematic; and (b) implemented layout.
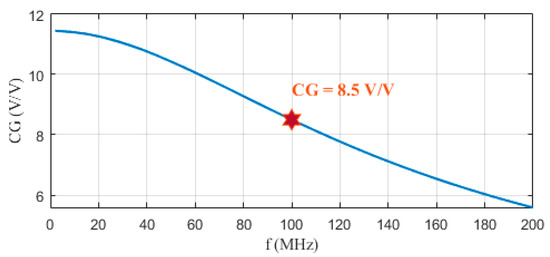
Figure 10.
Mixer conversion gain versus the intermediate-frequency fIF.
4.3. Filter and Intermediate-Frequency Amplifier
The low-pass filter is implemented using the OTA-C architecture of [30], and the schematic and layout are presented in Figure 11. Figure 12 displays its transfer function (simulated under extracted view), where its −3 dB bandwidth falls at 580 MHz. Additionally, the 180-degree phase difference between its output ports remains up to 2.5 GHz.
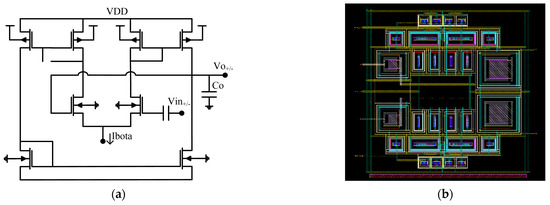
Figure 11.
(a) LPF schematic [30]. (b) Layout of the BPF.
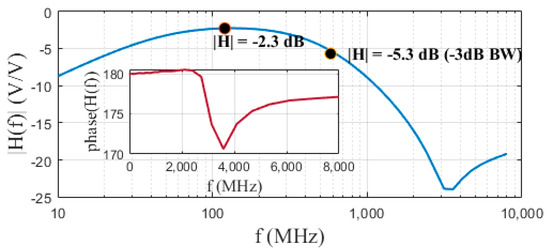
Figure 12.
Low-pass filter transfer function: Magnitude (blue) and phase (inset).
The intermediate-frequency amplifier is designed using the two-stage differential pair-type architecture of Figure 13a, where pseudo-resistors were used to bias the input transistors of both stages. In Figure 13b its layout is given.
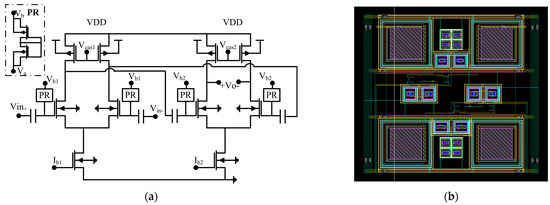
Figure 13.
(a) Intermediate-frequency amplifier architecture. (b) Layout.
Furthermore, the magnitude of its transfer function is given in Figure 14, where the −3 dB bandwidth is in 106 MHz, providing at this point a gain of 16.85 dB.
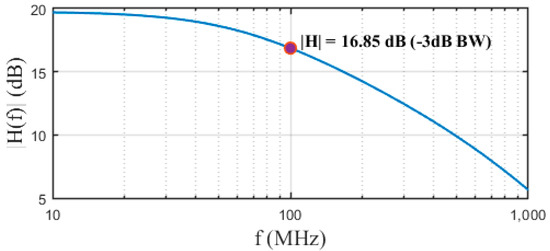
Figure 14.
Transfer function (magnitude) of the IF amplifier.
4.4. Envelope Detector
The following block after the intermediate-frequency amplifier is the envelope detector. Its function is to try to differentiate when the SHNO oscillator is on or off. Here, our intention is not to generate a perfectly shaped envelope signal, especially because, with this technology and at the working frequency fif in the order of 100 MHz, it is not feasible. The architecture we use is a modified version of the envelope detector presented by Xia in [31], and shown in Figure 15. To have a detectable signal at its output (with respect to when the input signal is negligible), its input voltage should be higher than 40 mVpp (i.e., the SHNO is oscillating with a reasonable amplitude), which imposes a strong constraint to the FE blocks behind it. It forces the gain of the previous blocks to be of, at least, 100 V/V, i.e., 40 dB. The envelope detector is adjusted to have an output whose DC component is proportional to the input signal amplitude. Its behavior is exemplified in Figure 16, whose output is given for four envelope-detector inputs, Vin,env = {1, 10, 20, 30} µV as well. It should be noted that in this architecture, the relationship is inverse, i.e., the higher the amplitude, the lower the DC output. Whether the system considers that the SHNO oscillates (SHNO ON) or not (SHNO OFF) depends on the threshold voltage, Vthres, chosen. In the case exemplified here, Vthres = 1.4 V was taken, above which the SHNO is considered OFF and below which is considered ON.
Figure 15.
(a) Single-ended core of the envelope-detector block. (b) Whole ED. (c) ED layout.
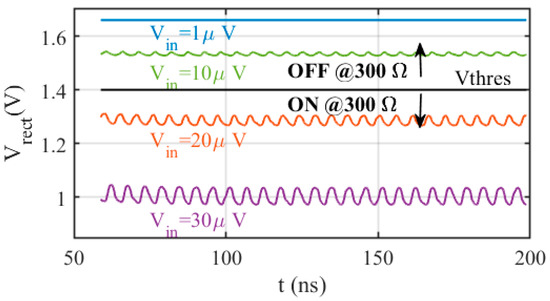
Figure 16.
Stand-alone envelope-detector outputs of Vin,env = {1, 10, 20, 30} µV.
4.5. Complete FE Block
With the blocks described above, the FE has been assembled and simulated. The layout of the complete front end is presented Figure 17, whose area is of (1000 × 660) µm2.

Figure 17.
Layout of the complete designed RF-FE.
Considering the designs of the LNA and mixer as almost fixed—they were optimized in their extracted layout version—the design of the rest of the blocks were slightly adjusted to adapt them to the real load imposed by the consecutive block that follows each of them.
Given the complexity of the RF-FE and the application in which it will be used, it was decided to gradually test the complete system blocks. Therefore, it was first decided to independently characterize the LNA by manufacturing it separately. This approach will make it possible to experimentally verify how good the coupling of the SHNO with the LNA is, and to isolate possible problems that may arise in the next stages.
5. FE Results and Discussion
When only the NB-LNA is considered, and the extracted view is used, as shown in Figure 8.a, the circuit is matched at 4.4 GHz with S11 = −25 dB, for RSHNO = 50 Ω. However, when all the front end is simulated (with post-layout), the best coupling between the SHNO and the LNA frequency is maintained at 4.4 GHz, with a S11 = −16 dB (see Figure 18).
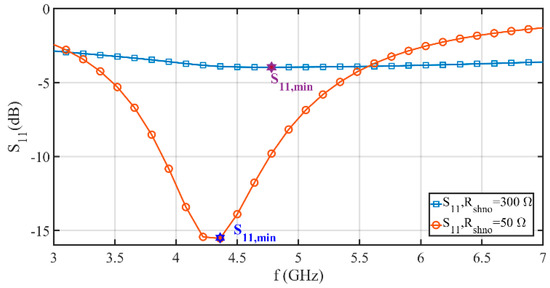
Figure 18.
S11 of the front end (extracted view).
Relaxing the matching condition up to −10 dB, the LNA can be used up to 4.7 GHz. Therefore, the local oscillator frequency fLO was fixed at 4.8 GHz to adjust, approximately, the value of the intermediate-frequency fIF ≈ 100 MHz. The amplitude of the LO is fixed at the supply voltage, VDD = 1.8 V. The reduction in operating frequency is possible because the SHNO parameters can be adjusted to lower the frequency, keeping in mind that this could reduce the performance of the SHNO at the output power level.
With the IF amplifier connected after the LPF, the capacitor that sets the LPF pole was adjusted. The gain of the IF amplifier was then corrected to reach 20.5 mVpk for RSHNO = 300 Ω, and 57 mVpk at RSHNO = 50 Ω at the input of the ED. This ensured the correct operation of the ED in the most stringent situation.
Finally, we evaluated the complete front end by injecting two possible input voltages: (1) Vin,FE = 1 µV, which exemplifies the SHNO output when it is switched off, and (2) Vin,FE = 100 µV, in which the SHNO is oscillating with a sufficient amplitude. The output of the envelope detector for both voltage values are reported in Figure 19. Depending on the RSHNO value, a correct choice of the threshold voltage will enable or not the correct discrimination of the SHNO operating state. Here, for RSHNO = 50 Ω, Vthres = 1.3 V, and for RSHNO = 300 Ω, Vthres = 1.475 V, to do the distinction of the status of the SHNO.
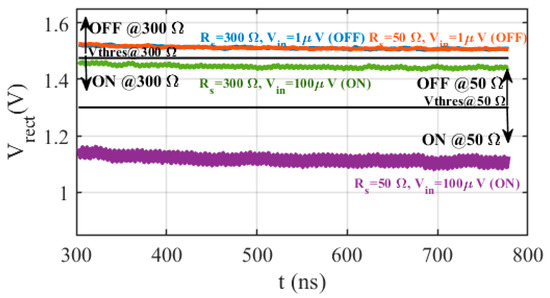
Figure 19.
Output of the FE for RSHNO= {50,300} Ω and Vin,FE = {1,100} µV.
The power consumption of the total FE is 15.4 mA at a supply voltage VDD = 1.8 V, and whose distribution is presented in Figure 20. As expected, most of the power consumption is divided between the LNA and the ED block; the former drains such a high amount of current due to the need to match the LNA input with RSHNO = 300 Ω and to increase its gain, and the latter because of the chosen high-frequency fIF.
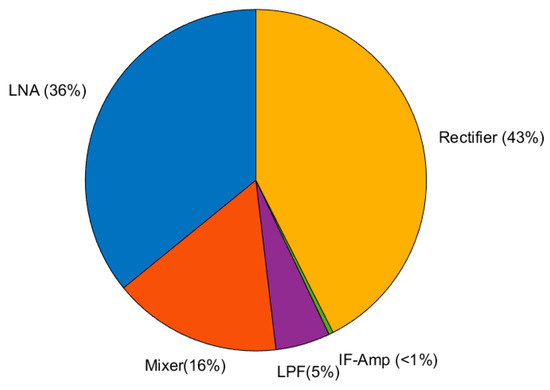
Figure 20.
Power-breakdown chart. The total current consumption is 15.4 mA at VDD = 1.8 V.
6. Conclusions and Future Work
The design of a signal-detection system for SHNOs is highly complex due to the peculiar characteristics of these devices, specifically their high oscillation frequencies, very low output amplitudes and high-output resistances. This is further aggravated if the 180-nm technological node, due to the external FE requirements (homogeneous fabrication with the SHNO), is fixed and it is not as low as it should be, considering the high working frequencies that have been handled. It is expected that, if it is possible to design the SHNOs and memristors in a smaller CMOS node, i.e., 65 nm, the whole performance improves, enabling working at oscillation frequencies of 6 GHz.
A good coupling between the LNA block and the SHNO is hard to achieve due to the SHNO high-output resistance, and forced to work with narrow-band architectures, although this was detrimental to the FE due to the area occupied by its inductors. In this first implementation, a low-pass filter has been used for simplicity, since a negligible noise was considered at the SHNO output with respect to its oscillation signal. Further experimental work should be done to confirm this hypothesis.
Given the complexity of the RF-FE and its application, the different RF-FE blocks have been separately manufactured. This approach will make it possible to experimentally verify how good the coupling of the SHNO with the LNA is, and to isolate possible problems that may arise in the next RF-FE stages. This paper reports experimental characterization of the isolated LNA block, which satisfies the needed requirements. Further work will be done to experimentally characterize other RF-FE stages and their couplings. Once this characterization is complete, the fabrication of the complete RF-FE will take place.
Author Contributions
Conceptualization, R.F.; methodology, R.F.; validation, R.F., E.P. and R.M.-R.; formal analysis, R.F., E.P., R.M.-R., M.R., A.K. and M.Z.; investigation, R.F., E.P., R.M.-R., M.R., A.K., M.Z., T.S.-G. and B.L.-B.; resources, R.F., E.P., R.M.-R., M.R., A.K. and M.Z.; data curation, R.F., E.P., M.R., A.K. and M.Z.; writing R.F.; writing—review and editing, R.F., E.P., T.S.-G. and B.L.-B.; visualization, R.F.; supervision, T.S.-G., B.L.-B., F.M. and J.Å.; funding acquisition, J.Å., F.M., T.S.-G. and B.L.-B.; project administration, F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Horizon 2020 Research and Innovation Program No. 899559 “SpinAge”, DOI 10.3030/899559.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tsunami of Data Could Consume one Fifth of Global Electricity by 2025|Environment|The Guardian. Available online: https://www.theguardian.com/environment/2017/dec/11/tsunami-of-data-could-consume-fifth-global-electricity-by-2025 (accessed on 3 March 2022).
- Mead, C. Neuromorphic Electronic Systems. Proc. IEEE 1990, 78, 1629–1636. [Google Scholar] [CrossRef]
- Human Brain Project Home. Available online: https://www.humanbrainproject.eu/en/ (accessed on 3 March 2022).
- Research Groups: APT—Advanced Processor Technologies (School of Computer Science—The University of Manchester). Available online: http://apt.cs.manchester.ac.uk/projects/SpiNNaker/project/ (accessed on 3 March 2022).
- Awad, A.A.; Dürrenfeld, P.; Houshang, A.; Dvornik, M.; Iacocca, E.; Dumas, R.K.; Åkerman, J. Long-range mutual synchronization of spin Hall nano-oscillators. Nat. Phys. 2016, 13, 292–299. [Google Scholar] [CrossRef]
- Demidov, V.E.; Urazhdin, S.; Ulrichs, H.; Tiberkevych, V.; Slavin, A.; Baither, D.; Schmitz, G.; Demokritov, S.O. Magnetic nano-oscillator driven by pure spin current. Nat. Mater. 2012, 11, 1028–1031. [Google Scholar] [CrossRef] [PubMed]
- Demidov, V.E.; Urazhdin, S.; Zholud, A.; Sadovnikov, A.V.; Demokritov, S.O. Nanoconstriction-based spin-Hall nano-oscillator. Appl. Phys. Lett. 2014, 105, 172410. [Google Scholar] [CrossRef]
- Dürrenfeld, P.; Awad, A.A.; Houshang, A.; Dumas, R.K.; Åkerman, J. A 20 nm spin Hall nano-oscillator. Nanoscale 2017, 3, 1285–1291. [Google Scholar] [CrossRef]
- Kumar, A.; Rajabali, M.; González, V.H.; Zahedinejad, M.; Houshang, A.; Åkerman, J. Fabrication of voltage-gated spin Hall nano-oscillators. Nanoscale 2022, 14, 1432–1439. [Google Scholar] [CrossRef]
- Muralidhar, S.; Houshang, A.; Alemán, A.; Khymyn, R.; Awad, A.A.; Åkerman, J. Optothermal control of spin Hall nano-oscillators. Appl. Phys. Lett. 2022, 120, 262401. [Google Scholar] [CrossRef]
- Zahedinejad, M.; Awad, A.A.; Muralidhar, S.; Khymyn, R.; Fulara, H.; Mazraati, H.; Dvornik, M.; Åkerman, J. Two-dimensional mutually synchronized spin Hall nano-oscillator arrays for neuromorphic computing. Nat. Nanotechnol. 2020, 15, 47–52. [Google Scholar] [CrossRef]
- Tarequzzaman, M.; Böhnert, T.; Decker, M.; Costa, J.D.; Borme, J.; Lacoste, B.; Paz, E.; Jenkins, A.S.; Serrano-Guisan, S.; Back, C.H.; et al. Spin torque nano-oscillator driven by combined spin injection from tunneling and spin Hall current. Commun. Phys. 2019, 2, 20. [Google Scholar] [CrossRef]
- Zahedinejad, M.; Mazraati, H.; Fulara, H.; Yue, J.; Jiang, S.; Awad, A.A.; Akerman, J. CMOS compatible W/CoFeB/MgO spin Hall nano-oscillators with wide frequency tunability. Appl. Phys. Lett. 2018, 112, 132404. [Google Scholar] [CrossRef]
- Romera, M.; Talatchian, P.; Tsunegi, S.; Araujo, F.A.; Cros, V.; Bortolotti, P.; Trastoy, J.; Yakushiji, K.; Fukushima, A.; Kubota, H.; et al. Vowel recognition with four coupled spin-torque nano-oscillators. Nature 2018, 563, 230–234. [Google Scholar] [CrossRef] [PubMed]
- Houshang, A.; Zahedinejad, M.; Muralidhar, S.; Chęciński, J.; Khymyn, R.; Rajabali, M.; Fulara, H.; Awad, A.A.; Dvornik, M.; Åkerman, J. Phase-Binarized Spin Hall Nano-Oscillator Arrays: Towards Spin Hall Ising Machines. Phys. Rev. Appl. 2022, 17, 014003. [Google Scholar] [CrossRef]
- Zahedinejad, M.; Fulara, H.; Khymyn, R.; Houshang, A.; Dvornik, M.; Fukami, S.; Kanai, S.; Ohno, H.; Åkerman, J. Memristive control of mutual spin Hall nano-oscillator synchronization for neuromorphic computing. Nat. Mater. 2021, 21, 81–87. [Google Scholar] [CrossRef]
- Leroux, N.; De Riz, A.; Sanz-Hernández, D.; Marković, D.; Mizrahi, A.; Grollier, J. Convolutional neural networks with radio-frequency spintronic nano-devices. Neuromorphic Comput. Eng. 2022, 2, 034002. [Google Scholar] [CrossRef]
- Ding, S.; Wang, N.; Bao, H.; Chen, B.; Wu, H.; Xu, Q. Memristor synapse-coupled piecewise-linear simplified Hopfield neural network: Dynamics analysis and circuit implementation. Chaos Solitons Fractals 2023, 166, 112899. [Google Scholar] [CrossRef]
- Fulara, H.; Zahedinejad, M.; Khymyn, R.; Awad, A.A.; Muralidhar, S.; Dvornik, M.; Akerman, J. Spin-orbit torque–driven propagating spin waves. Sci. Adv. 2019, 5, 9. [Google Scholar] [CrossRef] [PubMed]
- Ginés, A.; Fiorelli, R.; Villeagas, A.; Doldan, R.; Barragan, M.; Vazquez, D.; Rueda, A. Design of an Energy-Efficient ZigBee Transceiver, in Mixed-Signal Circuits; CRC Press: Boca Raton, FL, USA, 2018; pp. 192–223. [Google Scholar] [CrossRef]
- Razavi, B. RF MICROELECTRONICS, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 2011. [Google Scholar]
- Bagheri, R.; Mirzaei, A.; Chehrazi, S.; Heidari, M.E.; Lee, M.; Mikhemar, M.; Tang, W.; Abidi, A.A. An 800-MHz—6-GHz Software-Defined Wireless Receiver in 90-nm CMOS. IEEE J. Solid-State Circuits 2006, 41, 2860–2876. [Google Scholar] [CrossRef]
- Im, D.; Nam, I.; Lee, K. A CMOS active feedback balun-LNA with high IIP2 for wideband digital TV receivers. IEEE Trans. Microw. Theory Tech. 2010, 58, 3566–3579. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, C.; Liu, J.; Liao, H. 1.8dB NF 3.6mW CMOS active balun low noise amplifier for GPS. Electron. Lett. 2010, 46, 251–252. [Google Scholar] [CrossRef]
- Fiorelli, R.; Silveira, F.; Peralías, E. MOST moderate-weak-inversion region as the optimum design zone for CMOS 2.4-GHz CS-LNAs. IEEE Trans. Microw. Theory Tech. 2014, 62, 556–566. [Google Scholar] [CrossRef]
- Fiorelli, R.; Silveira, F. Common gate LNA design space exploration in all inversion regions. In Proceedings of the 2008 Argentine School of Micro-Nanoelectronics, Technology and Applications, Buenos Aires, Argentina, 18–19 September 2008. [Google Scholar]
- Fiorelli, R.; Peralías, E. Semi-empirical RF MOST model for CMOS 65 nm technologies: Theory, extraction method and validation. Integration 2016, 52, 228–236. [Google Scholar] [CrossRef]
- Klumperink, E.; Louwsma, S.; Wienk, G.; Nauta, B. A CMOS switched transconductor mixer. IEEE J. Solid-State Circuits 2004, 39, 1231–1240. [Google Scholar] [CrossRef]
- Fiorelli, R.; Villegas, A.; Peralias, E.; Vazquez, D.; Rueda, A. 2.4-GHz single-ended input low-power low-voltage active front-end for ZigBee applications in 90 nm CMOS. In Proceedings of the 2011 20th European Conference on Circuit Theory and Design (ECCTD), Linköping, Sweden, 29–31 August 2011; pp. 829–832. [Google Scholar] [CrossRef]
- Deliyannis, T.; Sun, Y.; Fidler, J. Continuous-Time Active Filter Design; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Xia, J.; Boumaiza, S. A Novel Broadband Linear-in-Magnitude RF Envelope Detector With Enhanced Detection Speed and Accuracy. IEEE Microw. Wirel. Compon. Lett. 2015, 25, 325–327. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).