Differentiable Constraints’ Encoding for Gradient-Based Analog Integrated Circuit Placement Optimization

Abstract

Analog IC design is characterized by non-systematic re-design iterations, often requiring partial or complete layout re-design. The layout task usually starts with device placement, where the several performance figures and constraints to be met escalate its complexity immensely, and, due to the inherent tradeoffs, an “optimal” floorplan solution does not usually exist. Deep learning models are now establishing for the automation of the placement task of analog integrated circuit layout design, promising to bypass the limitations of existing approaches based on: time-consuming optimization processes with several constraints; or placement retargeting from legacy designs/templates, which rely heavily on legacy layout data. However, as the complexity of analog design cases tackled by these methodologies increases, a broader set of topological constraints must be supported to cover the different layout styles and circuit classes. Here, model-independent differentiable encodings for regularity, boundary, proximity, and symmetry island constraints are formulated for the first time in the literature, and an unsupervised loss function is used for the artificial neural network model to learn how to generate placements that follow them. The use of a deep learning model makes push-button speed placement generation possible, additionally, as only sizing data are required for its training, it discards the need to acquire legacy layouts containing insights into this vast set of, often neglected, constraints. The model is ultimately used to produce floorplans from scratch at push-button speed for real state-of-the-art analog structures, including technology nodes not used for training. A case-study comparison with a floorplan design made by a human-expert presents improvements in the fulfillment of every constraint, reaching an overall improvement of around 70%, demonstrating the approach’s value in placement design.

1. Introduction

A vast number of techniques for automatic analog integrated circuit (IC) layout synthesis have been proposed in the past decades, which are mostly based on: (1) optimization processes with several topological constraints [1,2] or (2) placement retargeting from legacy designs [3,4] or templates [5,6]. In the first, every solution is generated from scratch in a, generally, time-consuming optimization process where several metrics (e.g., area, wiring topology estimates) are minimized while fulfilling the constraints. Still, even though this process moves toward a global optimum solution, it does not necessarily mean that a meaningful layout solution has been found for the circuit designer. In the second, the solution being generated matches its structure with those found on a library (or more frequently, a single instance) of legacy layouts/templates. While the solution is quickly produced from the guidelines of validated data, these methodologies struggle to generalize beyond the legacy data available, which is often scarce and may not necessarily correspond to the exact topology being generated. Nonetheless, the limitations of these approaches have been identified for long, which have hampered their widespread propagation across established commercial computer-aided design tools for analog IC design.

However, tremendous advances in machine learning (ML), and more specifically, deep learning (DL), in the past decade, are offering new alternatives to the electronic design automation (EDA) of electronic circuits [7,8]. Similarly, for analog IC placement, DL-based approaches were recently proposed [9,10,11,12], attempting to match the fast generation abilities of placement retargeting with the flexibility of optimization. Nonetheless, as the complexity of real-world analog design cases tackled by these methodologies increases, a wider set of topological constraints must be supported to cover multiple layout styles and circuit classes, e.g., device symmetry or SIs, proximity, preplaced, regularity, boundary, separation, current/signal-flows, among others [13]. Therefore, the research described in this manuscript follows the most recent trials on analog placement automation by using a non-linear unsupervised artificial neural network (ANN) model, trained with thousands of sizing solutions which can be generated via established automatic methods such as [14,15], where innovative differentiable encodings for regularity, boundary, proximity, and symmetry island (SI) are introduced for the first time in the literature. Ultimately, the model supports different circuit topologies on its input layer and outputs at push-button speed the placement coordinates of each device for any given sizing and constraints, as shown in Figure 1.

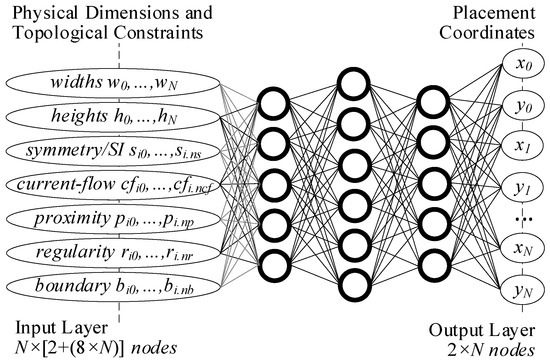
Figure 1. ANN architecture used to solve the map from the physical dimensions and topological constraints to the placement coordinates. N represents the maximum number of circuit devices supported by the model.

This document is organized as follows. Section 2 provides the related work and contributions. Section 3 details the input vector features, constraints’ encodings, and loss function. Finally, Section 4 and Section 5 address the results and conclusions.

2. Related Work and Contributions

Some of the recent ML applications for analog IC layout include building block recognition from circuit netlists in order to build the circuit’s hierarchy automatically [16], generation of wells during layout design that imitate human-designer choices [17], or even assistance/guidance for traditional path-finding routing algorithms [18]. In the particular case of analog IC placement, a straightforward fully supervised ANN that reproduces the layout patterns of a dataset of legacy placement solutions was proposed [10]. In [11], it was enhanced, providing a multi-circuit model that distinguishes between topologies by describing the topological constraints at the ANN’s input layer. Still, both models are highly dependent on the description of the circuits’ traits on the model’s input layer, preventing them from scaling for circuits with a larger number of devices than those found in the dataset. Therefore, an attention-based graph-to-sequence model was recently proposed, where the encoder-decoder architecture is scalable and invariant to the order in which the devices are provided at the input layer. These unsupervised placement techniques have proved to compete or outperform those generated by state-of-the-art optimization-based placement approaches in [12]. Note that the DL models produced these results in milliseconds, while the optimization techniques took from several seconds up to several minutes, thus, establishing the DL approach as a competitive alternative to the more traditional methods. Nonetheless, due to the intricate formulations required for efficient training of a DL model, only fundamental topological constraints were effectively supported, i.e., symmetry, proximity, and current-flows.

Supporting a broader set of topological constraints is mandatory to tackle a more comprehensive set of industry-standard analog IC design cases and produce aesthetic-wise solutions for the circuit designer. However, their implementation in DL-based tools is not trivial. Therefore, the major contributions of this work are:

• In this paper, differentiable implementations of boundary, regularity, and SI constraints are formulated for the first time in the literature. These are inherently model-independent, i.e., they can be used to train simple models, such as the multilayer perceptron [11], or even complex encoder-decoder architectures [12];
• Existent automatic approaches for analog IC placement that focus on retargeting from legacy designs/templates [3,4], or even ML-based approaches [10], use previously designed placement solutions (layouts) that comprise expert design knowledge. These examples are used as a surrogate for the explicit definition of the constraints to be met. However, legacy layouts containing robust implementations of the abovementioned constraints are scarce and expensive to obtain, and thus, here, the model’s training requires only sizing data, which is way easier to produce, and the model is focused on complying with the explicitly and efficiently described topological constraints. When compared with optimization processes with several topological constraints [1,2], which also explore the possibility of explicitly defining the constraints to be met, the inherent time-consuming optimization cycles are bypassed by the use of deep models. This is, once the model is fully trained, it can produce several valid solutions for a singular problem at push-button speed through its generative characteristics;
• The novel formulations for the boundary, regularity, proximity, and SI constraints are used to train a model that produces placement solutions from scratch at push-button speed for several state-of-the-art block-level analog IC structures, including circuit topologies and technology nodes not used for training, ultimately proving its generalization capabilities.

3. Unsupervised ANN Model with a Broader Topological Constraints Coverage

The general architecture of the proposed ANN model was previously illustrated in Figure 1.

3.1. Notation

Table 1 introduces the notation used through this document.

Table 1. Notation.

Notation	Definition
$N$	Number of devices in the model
$A_{r\times c}$	An $r\times c$ matrix
$A_{r\times c\times l}$	An $r\times c\times l$ matrix
$v_r$	An $r\times 1$ column vector
$A_{i,j}$	Entry $i,j$ of matrix $A$
$v_i$	ith entry of vector $v$
$I_n$	$n\times n$ identity matrix
$1_{n\times m}$	$n\times m$ matrix filled with ones
$diag\left(v_r\right)$	Diagonal matrix $D_{r\times r}$ where each entry in the diagonal is $D_{i,i}=v_i$ ${\forall }_{i\in \left\{1,r\right\}}$ and zero otherwise
$diag\left(A_{r\times r}\right)$	Column vector $d_r$ obtained from the entries on the main diagonal of the square matrix $A_{r\times r}$, $d_i=A_{i,i}$ ${\forall }_{i\in 1\dots ,r\}}$
$A^T$	Transpose of a two-dimensional matrix $A_{r\times c}$. $A^T={\left[\begin{array}{lll}{A}_{1,1}\hfill & \cdots \hfill & A_{r,1}\hfill \\ ⋮\hfill & \ddots \hfill & ⋮\hfill \\ A_{1,c}\hfill & \cdots \hfill & A_{r,c}\hfill \end{array}\right]}_{c\times r}$
${\Delta }^u\left(A\right)$	Upper triangular matrix $T_{r\times r}$ obtained from the entries on and above the main diagonal of the square matrix $A_{r\times r}$, $T_{i,j}=A_{i,j}$ ${\forall }_{i\le j; i,j\in \left\{1,\dots ,r\right\}}$ and zero otherwise
${\mathsf{\Sigma }}^n\left(A\right)$	Matrix obtained from summing the values of the multi-dimensional matrix $A$ (dimensionality greater or equal to 2) along dimension $n$.
${\mathsf{\Sigma }}^{n,m}\left(A\right)$	Matrix obtained from summing the values of the multi-dimensional matrix $A$ (dimensionality greater or equal to 3) first along dimension $n$ then $m$.
$\mathsf{\Sigma }\left(A\right)$	Sum of all elements of $A$
${\mathrm{M}}^n\left(A\right)$	Compute the maximum of the multi-dimensional matrix $A$ over dimension $n$
${\mathrm{m}}^n\left(A\right)$	Compute the minimum of the multi-dimensional matrix $A$ over dimension $n$
$\mathrm{m}\left(k,A\right),\mathrm{M}\left(k,A\right)$	Compute a multi-dimensional matrix with the dimension of $A$ whose entries are respectively, the minimum or maximum of each value of $A$ and $k$.
$\mathrm{m}\left(A,B\right), \mathrm{M}\left(A,B\right)$	A multi-dimensional matrix with the dimension of $A$ and $B$ whose entries are the respectively, the minimum or maximum of each value of $A$ and $B$.
$A\circ B$	Hadamard (or Schur) product of two multi-dimensional matrices with the same dimension. Example for two dimensional matrices: $A_{r\times c}\circ B_{r\times c}={\left[\begin{array}{lll}{A}_{1,1}{B}_{1,1}\hfill & \cdots \hfill & A_{1,c}{B}_{1,c}\hfill \\ ⋮\hfill & \ddots \hfill & ⋮\hfill \\ A_{r,1}{B}_{r,1}\hfill & \cdots \hfill & A_{r,c}{B}_{r,c}\hfill \end{array}\right]}_{r\times c}$
$a^T,b$	Inner product of two vectors. ${⟨\left(a_{r\times 1}\right)}^T,b_{\mathrm{r}\times 1}⟩={\mathsf{\Sigma }}^1\left(a\circ b\right)$
$A\otimes B$	Kronecker product of two multi-dimensional matrices with the same number of dimensions. Example for two-dimensional matrices: $A_{r\times c}\otimes B_{s\times d}={\left[\begin{array}{lll}{A}_{1,1}B\hfill & \cdots \hfill & A_{1,c}B\hfill \\ ⋮\hfill & \ddots \hfill & ⋮\hfill \\ A_{r,1}B\hfill & \cdots \hfill & A_{r,c}B\hfill \end{array}\right]}_{rs\times cd}$

3.2. Input Vector Features

As in its baseline implementation, the model inputs the scaled width/height of the physical implementation (bounding box dimensions) of each device composing the circuit, i.e., a vector of size 2N, where N is the number of devices within that circuit topology, resulting from flattening the device size dimension matrix $D_{N\times 2}$. Additionally, as thoroughly described in [11], symmetry (that restricts two devices to a mirrored placement along a symmetry axis (SA)), proximity (that describes groups of devices that should be placed closely), and current-flow (that force a monotonic path between the different devices composing the ‘current-flow’) requirements are passed to the ANN by three N × N unweighted adjacency matrices: $S^r, P$, and $C$ respectively. This work proposes the use of five more matrices to encode the boundary ($B_{N\times N}^x,B_{N\times N}^y$), regularity ($R_{N\times N}^x, R_{N\times N}^y$), and SI constraints ($S_{N\times N}^g$). While the sets of topological constraints used for the circuit topologies under study in this work were specified by experienced analog designers, these can be obtained directly by using works that automate their extraction process. These works can be either based on deterministic approaches [19,20], or, as developed recently, by using graph-based ML techniques [16,21,22]. Given the circuit’s sizing and the different constraint graphs, the model is trained to output a placement that fulfills the specified constraints. The placement is output as a $2N$ long vector, which can be interpreted as an $N\times 2$ matrix $L$, whose columns correspond to each devices’ coordinates in the $x$ and $y$ axis respectively.

3.3. Boundary

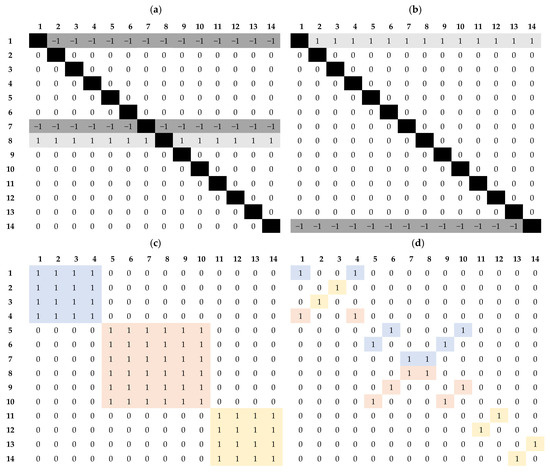
This constraint leads to easier routing access to the interfaces and fewer parasitic interactions, as shown in Figure 2b. A device with a boundary constraint must be placed between the remaining devices of the circuit and the “virtual” enclosing shape that contains all the devices, and, since this verification must be made in one of the four directions, the boundary error is divided into two axes, $x$ and $y$. The matrices $B_{N\times N}^x$ and $B_{N\times N}^y$ encode the boundary constraint graphs for the $x$ and y axis respectively. Figure 3a,b show the $B^x$ and $B^y$ matrix respectively for the circuit shown in Figure 2.

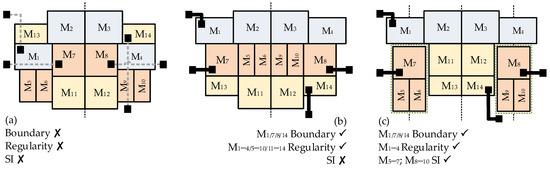
Figure 2. Three symmetric placements of the generic circuit: (a) Devices connected to the input/output ports are placed inside the circuit layout; (b) devices are placed within the circuit boundary and three horizontal regularity constraints are implemented; (c) two symmetry islands are formed.

Figure 3. One-hot encoded matrices used to provide: (a) boundary constraints in the $x$ axis (Figure 2b); (b) boundary constraints in the $y$ axis (Figure 2b); (c) row regularity constraints (Figure 2b); (d) symmetry relations (Figure 2c); and (e) symmetry island grouping (Figure 2c) to the deep model.

In practice, the $B^x$ and $B^y$ matrices encode an ordering along each axis, where $B_{i,j}^x=1$ encodes that device $i$’s maximum $x$ coordinate should be greater than $j$’s maximum $x$ coordinate, and an analogous meaning is given to $B_{i,j}^y$. On the other hand, $B_{i,j}^x=-1$ encodes that device $i$’s minimum $x$ coordinate should be lesser than $j$’s minimum $x$ coordinate, and an analogous meaning is given to $B_{i,j}^y$. Thus, if device $i$ should be on the top boundary, then $B_{i,k}^y=1, \forall k\in \left[1,N\right]$. Or if device $i$ should be on the left boundary, then $B_{i,k}^x=-1, \forall k\in \left[1,N\right]$.

Thus, to estimate the boundary error relative to the $y$ axis, the TopTop and BottomBottom errors between each device pair must be considered, each respectively represented by $B_{N\times N}^{tt}$ and $B_{N\times N}^{bb}$, calculated through:

$$B^{tt/bb}=\mathrm{M}\left(0,\mathrm{M}\left(B^y,0\right)\circ \left[{\mathbf{1}}_{N\times 1}\otimes {\left(y^{+/-}\right)}^T-{\mathbf{1}}_{1\times N}\otimes y^{+/-}\right]\right)$$

(1)

where $y_N^{-}$ corresponds to the vector containing the minimum $y$ coordinate of each device in the evaluated placement, defined as $y_i=L_{i,2}, \forall i\in \left[1,N\right]$, and $y_N^{+}$ corresponds to the maximum $y$ coordinate vector defined a $y_i^{+}=L_{i,2}+D_{i,2}, \forall i\in \left[1,N\right]$.

Similarly, for the $x$ axis, the RightRight and LeftLeft errors between each device pair, represented by $B_{N\times N}^{rr}$ and $B_{N\times N}^{ll}$ respectively, are given by:

$$B^{rr/ll}=\mathrm{M}\left(0,\mathrm{M}\left(B^x,0\right)\circ \left[{\mathbf{1}}_{N\times 1}\otimes {\left(x^{+/-}\right)}^T-{\mathbf{1}}_{1\times N}\otimes x^{+/-}\right]\right)$$

(2)

where $x_N^{-}$ corresponds to the vector containing the minimum $x$ coordinate of each device in the evaluated placement, defined as $x_i=L_{i,1}, \forall i\in \left[1,N\right]$, and $x_N^{+}$ corresponds to the maximum $x$ coordinate vector defined as $x_i^{+}=L_{i,1}+D_{i,1}, \forall i\in \left[1,N\right]$.

Finally, another factor must be considered to maximize the boundary constraint’s effectiveness: whether a device is located between a boundary-constrained device and its objective (the placement’s boundary). This can be estimated by measuring the overlap between the devices’ projections in the axis perpendicular to the corresponding boundary axis for every device pair with an ordering error greater than zero (i.e., $B_{i,j}^{tt}>0$ or $B_{i,j}^{bb}>0$ or $B_{i,j}^{rr}>0$ or $B_{i,j}^{ll}>0$, since this means that device $j$ is closer to the objective boundary than $i$, and it must be checked whether it is blocking device $i$’s path).

To measure the overlap between each device pair’s projections, consider the distance that separates the opposing faces of the two rectangles. For example, matrix $d{X}_{N\times N}^{+-}$ measures, for every pair of devices $i$ and $j$, the distance between device $i$’s maximum $x$ coordinate face and device $j$’s minimum $x$ coordinate face. Resulting in four $N\times N$ matrices, two for each axis: $d{X}^{+-}, d{X}^{-+}, d{Y}^{+-}$ and $d{Y}^{-+}$:

$$d{X}^{+-/-+}=\left|{\mathbf{1}}_{1\times N}\otimes x^{+/-}-{\mathbf{1}}_{N\times 1}\otimes {\left(x^{-/+}\right)}^T\right|$$

(3)

$$d{Y}^{+-/-+}=\left|{\mathbf{1}}_{1\times N}\otimes y^{+/-}-{\mathbf{1}}_{N\times 1}\otimes {\left(y^{-/+}\right)}^T\right|$$

(4)

The matrices $d{X}_{N\times N}^o$ and $d{Y}_{N\times N}^o$ that define the measured distance to solve the overlap in each axis are given through:

$$d{X}^o=\frac{1}{{\mathbf{1}}_{N\times 1}\otimes w^T}\left(S{x}^{+-}d{X}^{+-}+S{x}^{-+}d{X}^{-+}\right)$$

(5)

$$d{Y}^o=\frac{1}{{\mathbf{1}}_{N\times 1}\otimes h^T}\left(S{y}^{+-}d{Y}^{+-}+S{y}^{-+}d{Y}^{-+}\right)$$

(6)

where $h_N$ is the column vector containing the devices’ heights given by $h_i=D_{i,2}, i\in \left[1,N\right]$, $w_N$ is the column vector containing the devices’ widths given by $w_i=D_{i,1}, i\in \left[1,N\right]$ and the four $N\times N$ matrices $S{x}^{+-},S{x}^{-+},S{y}^{+-}$, and $S{y}^{-+}$ are scaling weights that function as a soft minimum for the distance between the devices’ opposing faces in each direction, and are defined by:

$$S{x}^{+-}=\frac{d{X}^{-+}}{d{X}^{-+}+d{X}^{+-}}$$

(7)

$$S{x}^{-+}={\mathbf{1}}_{N\times N}-S{x}^{+-}$$

(8)

$$S{y}^{+-}=\frac{d{Y}^{-+}}{d{Y}^{-+}+d{Y}^{+-}}$$

(9)

$$S{y}^{-+}={\mathbf{1}}_{N\times N}-S{y}^{+-}$$

(10)

The use of these scaling weights was introduced in [11], where it is explained in detail, and results in an output with a value between the minimum term and the maximum term, but, proportionally closer to the minimum term, such that when the minimum term approaches $0$, its weight approaches $1$.

Thus, given $d{X}^o$ and $d{Y}^o$, the two matrices, $B_{N\times N}^h$ and $B_{N\times N}^v$ that evaluate how much devices stand in the way of the boundary constrained devices are given by:

$$B^h=\mathrm{M}\left(0,\frac{B^{tt}+B^{bb}}{\left|B^{tt}+B^{bb}\right|}\right)\circ d{X}^o$$

(11)

$$B^v=\mathrm{M}\left(0,\frac{B^{rr}+B^{ll}}{\left|B^{rr}+B^{ll}\right|}\right)\circ d{Y}^o$$

(12)

The inclusion of these two errors results from a gradient-aware approach since the objective of the boundary error is not only to identify situations where the constraint is fulfilled but also to, given two distinct placements, rank them faithfully to a designer’s preferences. Locally, this results in defining the function’s gradients and information regarding how to update a placement to correct its errors intelligently. In particular, this added overlap error results in a gradient that pushes devices away from the path of the boundary-constrained devices, resulting in cooperative behavior. Figure 4 shows an example placement where the device $D_1$ should be placed in the top boundary, resulting in three distinct errors $B_{1,2}^{tt}$, $B_{1,3}^{tt}$, and $B_{1,2}^h$. Note that no error exists between $D_1$ and $D_4$ despite the existing horizontal overlap between them since there is no $B_{1,4}^{tt}$ error, thus the max function from Equation (11) returns 0 and $B_{1,4}^h=0$. Intuitively, $D_4$ does not stand between $D_1$ and its objective (the top boundary), thus, it should not be pushed away.

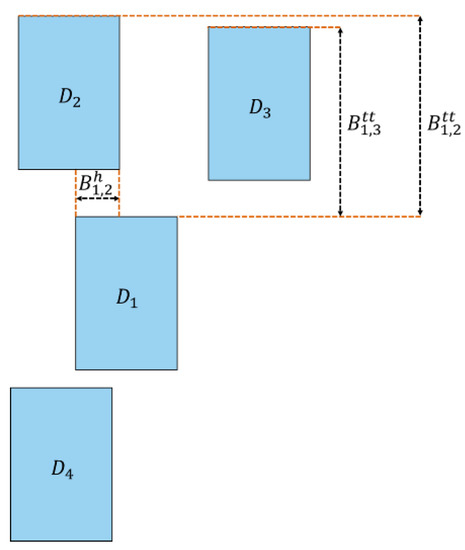
Figure 4. Example placement where device $D_1$ should be placed in the top boundary, resulting in three distinct errors $B_{1,2}^{tt}$, $B_{1,3}^{tt}$, and $B_{1,2}^h$. Note that no error exists between $D_1$ and $D_4$ despite the existing horizontal overlap between them since $D_4$ is not closer to the top boundary than $D_1$.

The pairwise boundary error ${\ddot{B}}_{N\times N}$ is calculated via:

$$\ddot{B}=B^{tt}+B^{bb}+B^{rr}+B^{ll}+B^h+B^v$$

(13)

Finally, this pairwise error could then be properly normalized and pooled through the methods discussed in [12], resulting in a final error $B$.

3.4. Regularity

This constraint arranges the devices into regular layout structures such as rows and columns, often resulting in a compact and meaningful layout, as shown in Figure 2b. The regularity constraint is split into two constraints, one for each axis, $x$ and $y$. The regularity constraint applied to the $x$ axis constrains device pairs to be vertically aligned, i.e., their centroids should have the same $x$ coordinate. Whereas the $y$ regularity constrains the pair’s centroids to have the same $y$ coordinate. For a given axis, the regularity axis between every pair of devices can be determined by calculating the pair’s centroid’s $x$ and $y$ position through ${\hat{X}}_{N\times N}$ and ${\hat{Y}}_{N\times N}$:

$$\hat{X}=\frac{1}{2}\left({\left(x^{-}+\frac{w}{2}\right)}^T\otimes {\mathbf{1}}_{N\times 1}+\left(x^{-}+\frac{w}{2}\right)\otimes {\mathbf{1}}_{1\times N}\right)$$

(14)

$$\hat{Y}=\frac{1}{2}\left({\left(y^{-}+\frac{h}{2}\right)}^T\otimes {\mathbf{1}}_{N\times 1}+\left(y^{-}+\frac{h}{2}\right)\otimes {\mathbf{1}}_{1\times N}\right)$$

(15)

where $w_N$ and $h_N$ each respectively contain each device’s width and height and are defined as $w_i=D_{i,1}, h_i=D_{i,2}, \forall i\in \left[1,N\right]$.

After calculating each regularity column and row axis between each pair of devices, given by $\hat{X}$ and $\hat{Y}$ respectively, the errors $d{R}^x{}_{N\times N}$ and $d{R}^y{}_{N\times N}$ that measure the deviation between each device to its correspondent column and row axis per pair is calculated, using:

$$d{R}^x=R^x\circ {\left({\left(x^{-}+\frac{w}{2}\right)}^T\otimes {\mathbf{1}}_{N\times 1}-\hat{X}\right)}^2$$

(16)

$$d{R}^y=R^y\circ {\left({\left(y^{-}+\frac{h}{2}\right)}^T\otimes {\mathbf{1}}_{N\times 1}-\hat{Y}\right)}^2$$

(17)

where $R_{N\times N}^x$ and $R_{N\times N}^y$ are the adjacency matrices of the graphs that encode the column and row regularity constraints respectively. These graphs encode, for a pair of devices $i$ and $j$, whether they should be aligned over a vertical or horizontal axis, respectively. Figure 3c shows the row regularity constraint graph’s adjacency matrix for the placement in Figure 2b.

Note how the regularity errors calculated in (16) and (17) measure, for each device pair $i$ and $j$, their distance to the pair’s centroid given by ${\hat{X}}_{i,j}$ or ${\hat{Y}}_{i,j}$. The alternative would be to directly calculate the distance between each device’s centroid through ${\left(x_i^{-}+\frac{w_i}{2}-x_j^{-}-\frac{w_j}{2}\right)}^2$. However, experimentally, the used errors proved to be more stable. For the same placement, the alternative errors will measure a higher value than the centroid error proposed. Thus, considering the use of momentum-based optimization algorithms (e.g., Adam), the devices will build more momentum and are more likely to overshoot their target and oscillate around the minimum. Whereas the centroid approach presents a common goal for both devices, a “compromise”. That way, the devices will not build as much momentum and are more likely to stabilize around the minimum.

Given the constraint’s pairwise $x$ and $y$ errors, the final pairwise regularity error ${\ddot{R}}_{N\times N}$ is given by:

$$\ddot{R}=d{R}^x+d{R}^y$$

(18)

Finally, this pairwise error can then be normalized appropriately and pooled through the methods proposed in [12], resulting in the final constraint error $R$.

3.5. Relative Proximity

In the boundary error, the overlap error components from Equations (5) and (6) were proposed to make unconstrained devices aware of the constrained devices’ objectives, inducing a collaborative behavior. Similarly, in order to encourage the model to group devices in the same symmetry group in an island (i.e., there is a contiguous shape that can contain all devices in the same symmetry group while not containing any device outside of the group), the implementation of the proximity constraint proposed in [11,12] was updated to behave in the same cooperative manner and used in the SI error to promote island formation. Additionally, note how in past works [12], all of the symmetry, current-flow, and overlap constraints can be satisfied, i.e., their error can be 0. The same, however, is unlikely to happen to the proximity error since the pairwise proximity error is only zero if the two devices are touching each other. This is an unnecessarily strict constraint that actively promotes overlap. A possible approach to turn this constraint satisfiable is to define a maximum threshold distance, under which the proximity error is zero, however, the size of this threshold would be, in practice, a hyperparameter to be optimized, and consequently, subject to overfitting.

Instead, a different approach was taken: the definition of proximity group was changed to a relative sense instead of an absolute one. In this implementation, the devices that form a proximity group (symmetry groups share proximity constraints as well, meaning that all symmetry groups are a proximity group) should be closer to each other than they are to all other devices. Thus, the measured error estimates how close, on average, device $i$ is to all devices that do not belong to its proximity group compared to devices that do belong to the same symmetry group. To estimate the error associated to this constraint, first it is necessary to estimate the effective minimum distance (EMD) between every pair of devices, as defined in [12]. The distance measured by this metric corresponds to the minimum distance between any two points belonging to each rectangle (device). The pairwise EMD is represented by the matrix $E_{N\times N}$. Given this, the multi-dimensional matrix $E_{N\times N\times N}^r$ measures, for a triplet of devices $i$, $j$, and $k$, how closer is device $i$ to j than it is to $k$, through:

$$E^r=\left(P\circ E\right)\otimes {\mathbf{1}}_{1\times 1\times N}-\left(\left({\mathbf{1}}_{N\times N}-P\right)\circ E\right)\otimes {\mathbf{1}}_{1\times N\times 1}$$

(19)

Note how the compared distances are those between devices in the same proximity group (represented by the term $\left(P\circ E\right)\otimes {\mathbf{1}}_{1\times 1\times N}$) with those between devices not in the same proximity group (represented by the term $\left(\left({\mathbf{1}}_{N\times N}-P\right)\circ E\right)\otimes {\mathbf{1}}_{1\times N\times 1}$). To measure the pairwise island formation error, the relative distance matrix $E^r$ must be first filtered for only occurrences where $E_{i,j}>E_{i,k}$, i.e., $E_{i,j,k}^r>0$, and then averaged over the number of devices with which device $i$ does not have a proximity constraint:

$$\ddot{P}={\mathsf{\Sigma }}^3\left(\mathrm{M}\left(E^r, 0\right)\right)\circ \frac{1}{{\left({\mathsf{\Sigma }}^2\left({\mathbf{1}}_{N\times N}-P\right)\right)}^T\otimes {\mathbf{1}}_{N\times 1}}$$

(20)

By considering a relative definition of proximity, not only does the constraint become satisfiable, but also the devices start behaving cooperatively. Instead of only pushing devices in the same proximity group close, the proximity error now pushes the devices not proximity-bounded away, opening space for the proximity-bounded devices to get close to one another. This is especially important because of the overlap error that often stops other constraints from fulfilling themselves, resulting in a local minimum around which the system oscillates. It should also be highlighted that this change comes at a computational cost, increasing the constraint’s complexity from $\mathrm{O}\left(N^2\right)$ to $\mathrm{O}\left(N^3\right).$ Finally, and as before, this pairwise error can then be adequately normalized and pooled through the methods proposed in [12], resulting in the final constraint error $P$.

3.6. Symmetry Island

The SI groups symmetric devices are close to each other, minimizing their mismatch. Therefore, multiple SA are considered, as well as hierarchical symmetry, as shown in Figure 2c. The SI error is separated into two different calculations, the error related to the intra-group interactions and the error related to the axes that separate two different symmetry groups. Thus, this approach is limited to two hierarchical levels of symmetry, but unlimited symmetry axes are supported.

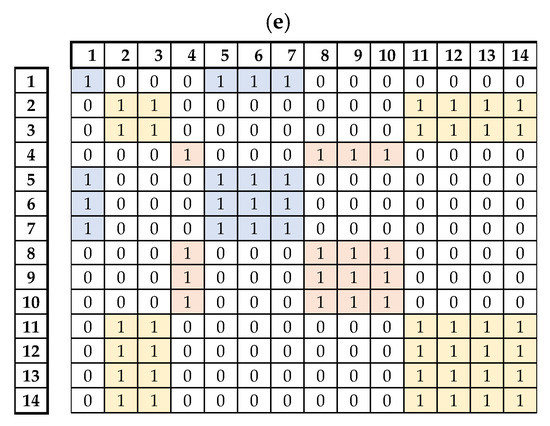
To identify the SI constraints, two different matrices are used: one, the symmetry relations matrix $S_{N\times N}^r$, to identify pairs of devices that are symmetric to one another in relation to any of the SA in the circuit; and a second, the symmetry group matrix $S_{N\times N}^g$, that signals whether two devices share the same SA set, where the SA set of a device is the set of SAs in relation to which the device is symmetric to another. For example, in Figure 2c, three Sas are marked in a dashed line, these can be denominated, from the left to the right: $S_1, S_2$, and $S_3$. For device $M_1$, its SA distribution is the set $\left\{S_1,S_2\right\}$ since it is symmetric to itself in relation to $S_1$ and symmetric to $M_4$ in relation to $S_2$. By defining the SA sets of each device, it is possible to conclude that devices M₁, M₅, M₆, M₇ all share the same SA set and thus, belong to the same symmetry group. Figure 3d,e show the two matrices $S^r$ and $S^g$ for the circuit shown in Figure 2.

Since this implementation is limited to two hierarchical levels of symmetry, a device can at most have two symmetry constraints, i.e., $\mathrm{M}\left({\mathsf{\Sigma }}^2\left(S^r\right)\right)\le 2$. This makes it possible to separate the constraints into two levels, intra-group constraints and inter-group constraints. Intra-group constraints are identified for bounding two devices of the same symmetry group, whereas inter-group constraints bound devices in different symmetry groups.

3.6.1. Intra-Group Axis

For each device, the $x$ coordinate of its intra-group symmetry relation is defined in the vector $s_N^{intra,x}$, given by:

$$s^{intra,x}=\frac{\left(S^r\circ S^g\right)+diag\left({\mathsf{\Sigma }}^1\left(S^r\circ S^g\right)\right), x^{-}+0.5w}{2}$$

(21)

where $\left(S^r\circ S^g\right)$ identifies the intra-group relations. By adding the term $diag\left({\mathsf{\Sigma }}^1\left(S^r\circ S^g\right)\right)$, a 1 is added to the main diagonal if the corresponding device has an intra-group symmetry constraint. Then the dot product adds the $x$ coordinates of the devices’ centroids, which when halved gives the pair’s centroid.

It is possible to build a three-dimensional matrix $S_{N\times N\times N}^{intra,r}$ that for a device $i$, the matrix $S_i^{intra,r}=s_i^g\otimes 1_{1\times N}\circ S^r$. Thus, $S_{N\times N\times N}^{intra,r}$ can be seen as a stack of $N$ $S_{N\times N}^r$ matrices where each layer $i$ is filtered such that only the relations relative to the group to which device $i$ belongs to are considered (i.e., only consider edges to and from a device in the group). It is important to define this matrix so that the number of symmetry constraints associated to each SA can be accurately calculated. One naïve approach to defining the number of constraints associated with each SA is through the $S^g$ matrix, where for each device, the number of elements in its group would be counted as the number of constraints. For example, for device $M_1$, its group is defined by the set $\left\{M_1,M_5,M_6,M_7\right\}$ with cardinality 4, however, since devices $M_5$ and $M_6$ are symmetric to one another, then only 3 symmetry constraints are associated to this intra-group axis. This matrix is estimated via:

$$S^{intra,r}=\left(S^r\otimes {\mathbf{1}}_{N\times 1\times 1}\right)\circ \left(S^g\otimes {\mathbf{1}}_{1\times N\times 1}\right)\circ \left(S^g\otimes {\mathbf{1}}_{1\times 1\times N}\right)$$

(22)

Now, a matrix $S_{N\times N\times N}^{intra, x}$ whose values are 0 if $S_{i,j,k}^{intra,r}=0$ and otherwise, its values are the x coordinates of the symmetric pair’s centroid. The values of $s^{intra,x}$ and $S^{intra,r}$ are used to compute the matrix $S_{N\times N\times N}^{intra,x}$ through:

$$S^{intra,x}=S^{intra,r}\circ \left(s^{intra,x}\otimes {\mathbf{1}}_{N\times 1\times N}\right)$$

(23)

The reference symmetry axis for each device, represented by the vector ${\tilde{s}}_N^{intra}$, is computed through:

$${\tilde{s}}^{intra}={\mathsf{\Sigma }}^{3,2}\left({\mathsf{\Delta }}^u\left({\mathbf{1}}_{N\times N}\right)\otimes {\mathbf{1}}_{N\times 1\times 1} \circ S^{intra,x}\right)\circ \frac{1}{{\mathsf{\Sigma }}^{3,2}\left({\mathsf{\Delta }}^u\left({\mathbf{1}}_{N\times N}\right)\otimes {\mathbf{1}}_{N\times 1\times 1} \circ S^{intra,r}\right)}$$

(24)

where the term ${\mathsf{\Sigma }}^{3,2}\left({\mathsf{\Delta }}^u\left({\mathbf{1}}_{N\times N}\right)\otimes {\mathbf{1}}_{N\times 1\times 1} \circ S^{intra,x}\right)$ adds, for each layer $i$ in $S_{N\times N\times N}^{intra,x}$, all values in the upper triangular region of the matrix, which corresponds to the different $x$ coordinates of the centroids of all devices that belong to the same symmetry group as device $i$. Then, the term ${\mathsf{\Sigma }}^{3,2}\left({\mathsf{\Delta }}^u\left({\mathbf{1}}_{N\times N}\right)\otimes {\mathbf{1}}_{N\times 1\times 1} \circ S^{intra,r}\right)$ computes for each device $i$, how many symmetry constraints are being considered to properly average out the group’s centroid’s $x$ coordinate.

The pairwise error associated with the deviation of a pair’s symmetry axis with its reference, represented by ${\ddot{S}}_{N\times N}^{intra,x}$, can be thus estimated via:

$${\ddot{S}}^{intra,x}={\mathbf{1}}_{1\times N}\otimes {\left(s^{intra,x}-{\tilde{s}}^{intra}\right)}^2\circ S^r\circ S^g$$

(25)

The pairwise error associated to the vertical misalignment between an intra-group symmetric pair ${\ddot{S}}_{N\times N}^{intra,y}$ is given by:

$${\ddot{S}}^{intra,y}={\left(\left(y^{-}\otimes {\mathbf{1}}_{1\times N}\right)-\left({\left(y^{-}\right)}^T\otimes {\mathbf{1}}_{N\times 1}\right)\right)}^2\circ S^r\circ S^g$$

(26)

3.6.2. Inter-Group Axis

Similarly, the inter-group pairwise error associated to the deviation of the symmetry axis from the mean is calculated by first estimating, for each device, the $x$ coordinate of its symmetry axis with a device from another group $s_N^{inter,x}$, then estimating, for each device, the symmetry constraints between devices in its group with devices from another group $S_{N\times N\times N}^{inter,r}$, then calculating $S_{N\times N\times N}^{inter,x}$ and ${\tilde{s}}_N^{inter}$ the same way they calculated for the intra-group constraints, and finally, calculating the error matrix ${\ddot{S}}_{N\times N}^{inter,x}$:

$$s^{inter,x}=\frac{\left[S^r\circ \left(1-S^g\right)\right]+diag\left({\mathsf{\Sigma }}^1\left[S^r\circ \left(1-S^g\right)\right]\right)}{2} ,x^{-}+0.5w$$

(27)

$$S^{inter,r}=\left(S^r\otimes {\mathbf{1}}_{N\times 1\times 1}\right)\circ \left[\left(\left(1-S^g\right)\otimes {\mathbf{1}}_{1\times N\times 1}\right)\circ \left(S^g\otimes {\mathbf{1}}_{1\times 1\times N}\right)+\left(S^g\otimes {\mathbf{1}}_{1\times N\times 1}\right)\circ \left(\left(1-S^g\right)\otimes {\mathbf{1}}_{1\times 1\times N}\right)\right]$$

(28)

$$S^{inter,x}=S^{inter,r}\circ \left(s^{inter,x}\otimes {\mathbf{1}}_{N\times 1\times N}\right)$$

(29)

$${\tilde{s}}^{inter}={\mathsf{\Sigma }}^{3,2}\left({\mathsf{\Delta }}^u\left({\mathbf{1}}_{N\times N}\right)\otimes {\mathbf{1}}_{N\times 1\times 1} \circ S^{inter,x}\right)\circ \frac{1}{{\mathsf{\Sigma }}^{3,2}\left({\mathsf{\Delta }}^u\left({\mathbf{1}}_{N\times N}\right)\otimes {\mathbf{1}}_{N\times 1\times 1} \circ S^{inter,r}\right)}$$

(30)

$${\ddot{S}}^{inter,x}=\left(S^r\circ \left(1-S^g\right)\right)\circ ({({(s^{inter,x}-{\tilde{s}}^{inter})}^2)}^T\otimes {\mathbf{1}}_{N\times 1}))$$

(31)

where in Equation (28), the term $\left(\left(1-S^g\right)\otimes {\mathbf{1}}_{1\times N\times 1}\right)\circ \left(S^g\otimes {\mathbf{1}}_{1\times 1\times N}\right)$ considers relations to outer-group devices from group devices, and the term $\left(S^g\otimes {\mathbf{1}}_{1\times N\times 1}\right)\circ \left(\left(1-S^g\right)\otimes {\mathbf{1}}_{1\times 1\times N}\right)$ considers the opposite.

The pairwise error associated to the vertical misalignment between an inter-group symmetric pair ${\ddot{S}}_{N\times N}^{inter,y}$ is given by:

$${\ddot{S}}^{inter,y}={\left(\left(y^{-}\otimes {\mathbf{1}}_{1\times N}\right)-\left({\left(y^{-}\right)}^T\otimes {\mathbf{1}}_{N\times 1}\right)\right)}^2\circ S^r\circ \left(1-S^g\right)$$

(32)

The pairwise error associated to the symmetry island constraint ${\ddot{S}}_{N\times N}$ is given by:

$$\ddot{S}={\ddot{S}}^{intra,x}+{\ddot{S}}^{intra,y}+{\ddot{S}}^{inter,x}+{\ddot{S}}^{inter,y}$$

(33)

Finally, this pairwise error can then be normalized and pooled through the methods proposed in [12], resulting in the final constraint error $S_I$. It should be noted that devices in the same symmetry group form a clique in the proximity constraint graph, thus, these groups will tend to form islands.

3.7. Loss Function

The deep model is ultimately trained to minimize a loss function whose inputs are the placement of the devices (i.e., the model’s output), the circuits’ constraint graphs, and respective sizing (i.e., the model’s inputs). This loss, shown in Equation (34), accounts for the satisfiability topological constraints considered, i.e., proximity (P), symmetry/SI (S_I), current-flows (C_F), boundary (B), and regularity (R). Still, two other metrics are also utilized to regulate the quality of produced layouts, i.e., overlaps and wasted area (W_A and O, respectively). The total loss is then given by the weighted sum of each of these constraint losses, where the w_{a,pg,si,cf,o,bou,reg} variables in Equation (34) represent said weights. Note that each of these constraint-specific losses is calculated in function of the circuit’s sizing (matrix $D_{N\times 2}$), its positional constraints (specified by the graphs $P_{N\times N}$, $S_{N\times N}^r$, $S_{N\times N}^g, C_{N\times N}$, $B_{N\times N}^x$, $B_{N\times N}^y$, $R_{N\times N}^x$, $R_{N\times N}^y$) and the produced placement (matrix $L_{N\times 2}$). Moreover, by using this unsupervised formulation, the model can be easily trained with unlabeled data, reinforcing its generalized application.

$$loss=w_a{W}_A+w_{pg}P+w_{si}{S}_I+w_{cf}{C}_F+w_{o}O+w_{bou}B+w_{reg}R$$

(34)

4. Experimental Results

The methodology was coded in Python using PyTorch ML library, and demonstrated with a dataset containing sizing solutions (split into training, validation, and test) for different state-of-the-art amplifiers on two foundries/nodes: the voltage-combiners (VC)-biased amplifier [23] (VCB, umc130), the folded VC-biased amplifier [24] (FVC, umc130, and tsmc65), and the VC-biased single-stage operational transconductance amplifier [25] (VCOTA, umc130), as shown in Table 2. Note that FVC in tsmc65 node was kept for validation and test only. The largest circuit is the VCOTA with 22 devices, whose schematic is illustrated in Figure 5. For it, 11 symmetry pairs were set by an experienced IC designer, 12 current-flows, 6 boundary constraints, 5 regularity constraints (row only), and 15 proximity constraints, as detailed in Table 3. This procedure was performed for the remaining amplifiers, with VCB being the only case study with SIs. Additionally, to balance the dataset, the sizing solutions of FVC were augmented by shuffling the order of the devices. To place larger analog circuit/system topologies, this work can be directly applied to each of the sub-blocks of the system, which, when placed, would be assembled at the top level given a set of topological constraints. As an alternative, the methodology could be used to place the entire complete mixed-signal or system in one single step, the major drawback being the deep model’s training which would escalate proportionally.

Table 2. Dataset details.

Topology	VCB [23]	FVC [24]		VCOTA [25]
Technology	umc130 nm	umc130 nm	tsmc65 nm	umc130 nm
Number of Devices	14	15		22
Number of Sizing Examples	5000	258	40	5979
Training Set	70%	70%	0%	70%
Validation Set	15%	15%	50%	15%
Number of Train and Validation Samples	4250	2213 *	1260 *	5082
Test Set/Number of Test Samples	15%/750	15%/391 *	50%/1260 *	15%/897

* Augmented data through shuffling and padding.

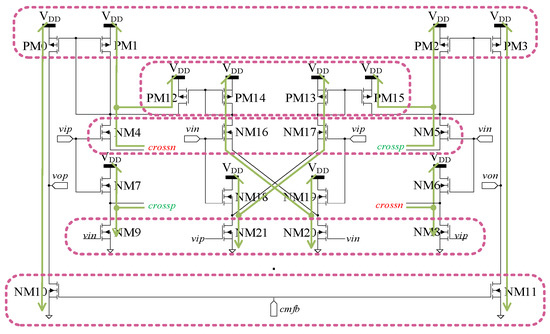
Figure 5. Schematic of the VCOTA [25]. Current-paths highlighted in green and row regularity constraints highlighted in pink.

Table 3. List of topological constraints specified for the VCOTA.

Symmetry		Current-Flow					Boundary			Row Regularity				Proximity
PM0	PM3	PM0	→	NM10			Right	NM5	NM11	PM0	PM1	PM2	PM3	PM0	NM10
PM1	PM2	PM3	→	NM11			Left	NM4	NM10	PM12	PM14	PM13	PM15	PM3	NM11
PM12	PM15	PM1	→	NM4	→	NM8	Top	NM10	NM11	NM4	NM16	NM17	NM5	PM0	PM1	PM12
PM14	PM13	PM2	→	NM5	→	NM9				NM9	NM21	NM20	NM8	PM3	PM2	PM15
NM4	NM5	PM12	→	NM4	→	NM8				NM10	NM11			PM12	PM14	NM16
NM18	NM19	PM15	→	NM5	→	NM9								PM15	PM13	NM17
NM7	NM6	PM14	→	NM16	→	NM20								NM4	NM7
NM17	NM16	PM13	→	NM17	→	NM21								NM5	NM6
NM10	NM11	NM7	→	NM9										NM4	NM9
NM9	NM8	NM6	→	NM8										NM5	NM8
NM20	NM21	NM18	→	NM21										NM16	NM18
		NM19	→	NM20										NM17	NM19
														NM16	NM19	NM20
														NM17	NM18	NM21
														NM10	NM11

The model’s input vector has size 3916, and the weights of Equation (34) were empirically chosen and set to: w_a = 0.1, w_s = 95, w_cf = 80, w_bou = 20, w_reg = 2, w_o = 90, and w_pg = 25. The ANN model comprises 5 hidden layers (with 5000/2500/1000/250/100 neurons each) and 1 output layer (44 nodes). The model was trained for 1000 epochs using Adam optimizer, and its parameters were set to: α = 0.001, ${\beta }_1$= 0.9, and ${\beta }_2$ = 0.999. A batch size of 500 samples was adopted, and dropout with a drop rate of 0.2 was used to prevent overfitting. The activation function used was the exponential linear unit (ELU) and linear function in the output layer. Table 4 fully details the train, validation, and test set errors. As observable, the test set errors are similar to those obtained on validation, with only a significant difference in the current-flow constraints on VCB and VCOTA. Moreover, its generalization ability is observed on FVC (tsmc65), with errors even lower than validation circuits. Figure 6 shows that the ANN is producing workable solutions.

Table 4. Train (TrE), validation (VaE), and test (TeE) errors.

Constraint	VCB [23]/umc130 nm				FVC [24]/umc130 nm				FVC [24]/tsmc65 nm				VCOTA [25]/umc130 nm
	TrE	VaE	TeE	Comp. (%)	TrE	VaE	TeE	Comp.(%)	TrE	VaE	TeE	Comp.(%)	TrE	VaE	TeE	Comp. (%)
Wasted Area	0.90	0.86	0.85	−0.7	1.02	0.86	0.91	+5.2	-	0.67	0.59	−10.8	0.77	0.61	0.59	−3.6
Symmetry/SI (×10−2)	0.62	9.47	9.18	−3.1	0.87	12.9	13.3	+3.1	-	10.6	9.75	−8.0	10.7	11.0	10.6	−3.6
Current-Flow (×10−2)	0.14	2.13	2.60	+22.1	<0.1	1.78	1.90	+6.7	-	3.78	3.05	−19.3	< 0.1	4.93	5.88	+19.2
Boundary (×10−2)	0.92	2.71	2.91	+7.4	7.65	4.20	4.53	+7.9	-	3.89	2.11	−45.8	5.15	4.52	4.24	−6.2
Regularity (×10−7)	3.01	1.27	1.32	+3.9	2.79	4.56	3.85	−15.6	-	2.84	2.78	−2.1	23.4	16.3	15.0	−8.0
Proximity	0.47	0.61	0.61	−0.8	0.21	0.43	0.44	+3.5	-	0.36	0.30	−17.9	0.21	0.34	0.32	−3.9
Overlap (×10−2)	4.83	7.81	8.05	+3.1	6.13	12.7	12.1	−4.7	-	14.4	14.9	+3.5	7.85	15.1	15.4	+2.0

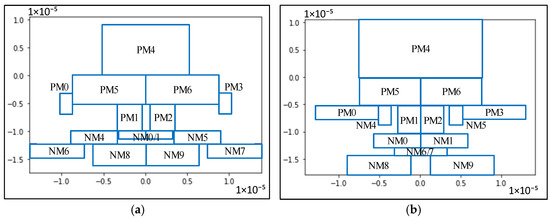
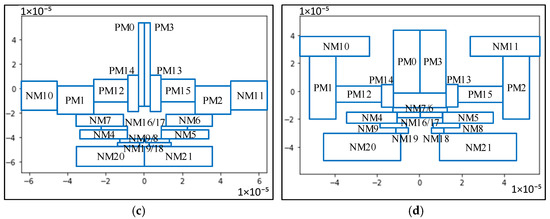
Figure 6. Test set predictions: (a,b) FVC (tsmc65); (c,d) VCOTA.

Finally, to further demonstrate the value of this work, the proposed approach’s performance was compared to a human expert designer. In this experiment, a human-designed placement for the VCOTA architecture was compared to an automatically generated placement using the approach here proposed. The ANN generated, for a single sizing, 500 different predictions, by shuffling the order of the devices in the input layer. Due to the batch capabilities of the model, the time required for this process is in the order of milliseconds (push-button speed). The best prediction was selected as the final solution produced by the ANN. The two final placements are shown side-by-side in Figure 7. Table 5 compares the numeric values for the compactness, proximity, current flow, regularity, and boundary errors for both solutions. Since the post-processing fixes overlaps and symmetry errors, these are zero and are not compared. Still, no major importance is given to the compactness comparison, as the remaining common-mode feedback circuitry used to bias the original circuit (and fill the empty spaces in the layout) were not included in this work. Nonetheless, in every metric, the automatic approach improves upon the human-designed floorplan, presenting decreases of up to 15-fold in the case of the current-flow error. Overall, the automatic approach is capable of carefully balancing all the different constraints, resulting in a placement with around 70% improvement over the human-designed solution.

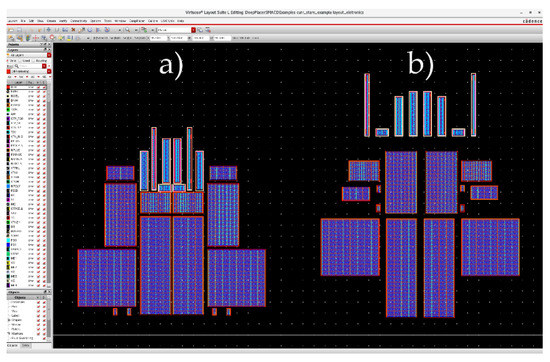
Figure 7. Placements generated for the VCOTA: (a) generated by this work, (b) designed by a human expert designer [25].

Table 5. Comparison of the automatically produced and human-designed floorplan solutions.

Placement	Compactness	Comp.	Proximity	Comp.	Current-Flow	Comp.	Regularity	Comp.	Boundary	Comp.	Total	Comp.
Human [25]	6.72	1.10×	8.33	2.19×	0.89	17.8×	0.54	4.50×	1.53	3.26×	18.01	1.70×
This Work	6.12	-	3.81	-	0.05	-	0.12	-	0.47	-	10.57	-

5. Discussion

Reliable automatic placement tools must support a broad set of topological constraints to tackle industry-standard analog IC design cases and produce aesthetic-wise solutions for the circuit designer. This paper proposes different model-independent and differentiable implementations of boundary, regularity, and SI constraints. The proposed constraints not only enforce the correct placement of the devices but were also designed to maximize the training of DL models. Their design was aware of the gradient produced and used matrix representation for improved performance using hardware parallelization (GPUs). The proof of concept was made with an ANN trained on sizing data of three different state-of-the-art amplifiers, generating workable solutions at push-button speed.

Even though the methodology proposed in this manuscript is tested in a family of state-of-the-art amplifiers, it can be applied to any real circuit class as long as there are well-defined topological constraints (i.e., symmetry pairs, current-flows, proximity, boundary, etc., constraints) for the circuit topologies within that class. If no topological constraints are requested, the deep models will still attempt to minimize the layout’s wasted area/compactness and the overlap among devices, and components of the placement loss indicated in Equation (34). However, the resulting solution may not be meaningful for the circuit designer, as no criteria to place the devices with respect to each other is being set. The experiments carried intend to show that if the deep model is trained in a dataset that shares some of the characteristics regarding topological constraints’ fulfillment of the circuit topologies to be generated, the acquired knowledge can be reused and generalized.

Even if the placement of a relatively small analog integrated circuit block is not extremely time-consuming, once several performance figures have to be considered its complexity increases immensely, and an optimal floorplan solution may not exist due to the inherent tradeoffs. Moreover, analog IC design is characterized by non-systematic re-design iterations, most of which impact the layout design, requiring partial or complete floorplan re-design. By using deep models, these floorplans can be generated instantly, while the human-designed floorplan may take from dozens of minutes to a couple of hours. These times are multiplied through every re-design iteration further conducted on a design.