Modeling of the Crystallization Conditions for Organic Synthesis Product Purification Using Deep Learning
Abstract
:1. Introduction
2. Related Work
3. Formal Definition of a Solving Task
4. The Data
5. Materials and Methods
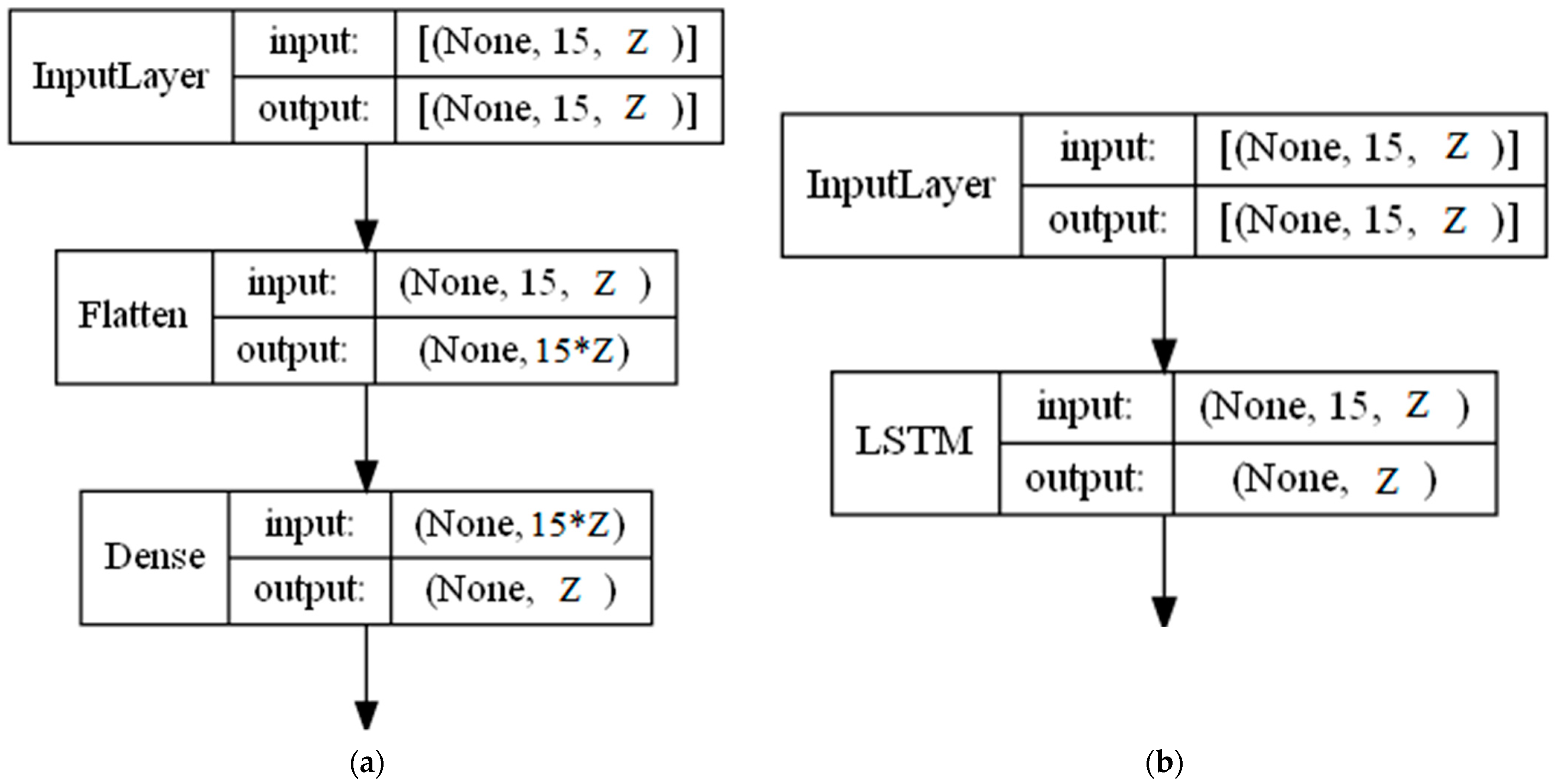
5.1. Vectorization
- Extended-connectivity fingerprints (ECFP) that can capture representations of molecular structures [55]: ECFPs are based on the Morgan algorithm, and are commonly used in such applications as virtual screening or ML [56]. ECFPs denote the absence or existence of specific substructures by scanning atom neighbors. The vectorization method works by transforming each molecule into a binary vector (containing zeros and ones) of a chosen length. In our experiments, we tested 512 and 1024 lengths of vectors. Because an instance in the dataset is multiple reactants, the vectors are combined into a matrix.
- ECFP encoders (ECFP + E): Autoencoders can be effective in reducing dimensionality for sparse matrices, such as ECFP. The main advantage of autoencoders is that they are trained in an unsupervised manner (they do not require labeled data). Additionally, autoencoders can learn the principal components, i.e., the created model can capture important patterns while ignoring the noise. This technique is often utilized in information retrieval, text analysis, and recommender systems. An autoencoder is trained to take in ECFPs and reproduce identical ECFPs in the output layer. The middle layer, the so-called bottleneck layer, is smaller than the input; therefore, the network must learn to compress the input data in a meaningful way [57]. Encoder weights are learned separately, but later can be used as the “starting point” of the deeper ANN architecture for different downstream tasks (e.g., solvent labeling, as in our case). The main advantage is that encoders may learn how to map sparse inputs to a denser latent space, which results in the detection of relevant parts, and often leads to higher accuracy.
5.2. Supervised Machine-Learning Approach
- A Feed-Forward Neural Network (FFNN) is an ANN in which the information flows through different layers, but only in one direction, i.e., forward. In its feed-forward, non-recurrent structure, the input is passed through the layers of nonlinearities or neurons (Logistic Sigmoid or Hyperbolic Tangent) until it reaches the output. The number of nodes in the input layer corresponds to the number of predictors (independent variables) from the dataset, and the number of nodes in the output layer corresponds to the number of response classes. FFNN is a simple network that can be trained faster than other networks; besides this, it usually serves as a baseline approach.
- Long Short-Term Memory (LSTM) is an ANN that can learn long-term dependencies between time steps of sequence data. LSTMs work well even when the input or output sequences are long (e.g., hundreds or thousands of time steps long), and can capture both long-term and short-term trends in the input sequence. The sigmoid function is used to control how much of each input or output is kept or forgotten across different time steps. The forget gate controls which information has to be removed from this layer’s state. Meanwhile, the input and output gates determine what information from the current time step and carryover information from previous time steps has to be combined to produce this layer’s output at the current time step. Considering the nature of the chemical molecules with significant parts in the structure, it is important to notice that, from the theoretical perspective, LSTMs should be the most suitable option for our solving task.
- Activation functions: Activation functions in ANN are important because they introduce non-linearity into the network. Without activation functions, ANNs would be limited to representing only linear models of data. They also determine whether a neuron should be activated or not by calculating the “weighted sum” and later adding bias to it. In this research, we tested several activation functions: GELU [58], SELU [59], ReLU, ELU, and tanH. The ReLU activation function is commonly chosen because it can be quickly computed, and therefore the model converges quickly, which is useful if training multiple models, and in optimization. GELU, SELU, and ELU are nonlinear modifications of ReLU. The last ANN’s layer’s activation function depends on the type of the solving task. We chose the sigmoid activation function because it is the only compatible function with the binary cross-entropy loss function used for loss calculation. The output vector contains multiple independent binary variables, and the sigmoid function returns the corresponding values in the range (0–1).
- The optimizer is also an important hyper-parameter that controls the training process. The Adam optimizer is probably the most popular choice due to its ability to effectively control the learning rate, and due to its high speed compared to other methods, such as Stochastic Gradient descent (SGD). The classic gradient descent algorithm is an iterative method of finding the minimum of a function. Starting from a random point on the function, the gradient descent algorithm follows the slope down towards the minimum value of that function. At each step, the gradient descent algorithm updates its current position based on the learning rate and loss of a given point plus momentum [60]. Nadam and Adamax optimizers that are modifications of the Adam algorithm were also tested.
- The batch size and the number of training epochs are both important hyperparameters. The batch size determines how many samples can be sent to the network for a single update iteration. The number of training epochs determines how many times the entire dataset is passed to the network. It is important to evaluate your results after each epoch in order to determine whether the model is overfitting or still underfitting the data. The batch size and the number of training epochs are both significant parameters that affect the training process overall. A larger batch size is usually beneficial, as it may prevent overfitting because the model is forced to approximate larger batches of instances. Multiple tests have shown that the most optimal batch size is 128. The number of epochs depends on the batch size. Once the optimal batch size is found, most of the models will have have successfully converged at epoch 25 or before. Typically, the training process is monitored and terminated if the accuracy metric is no longer improved. A binary cross-entropy loss function was used for loss calculation, as the output vector contains multiple independent binary variables.
5.3. Optimization
- Neural network layer size: 16, 32, 64, 128, 256, 512, and 1024 neurons
- Activation functions: GELU, SELU, ReLU, ELU, and tanH
- Optimizers: Adam, Nadam, SGD, and Adamax
- Batch sizes: 32, 64, 128, 256, 512, and 1024
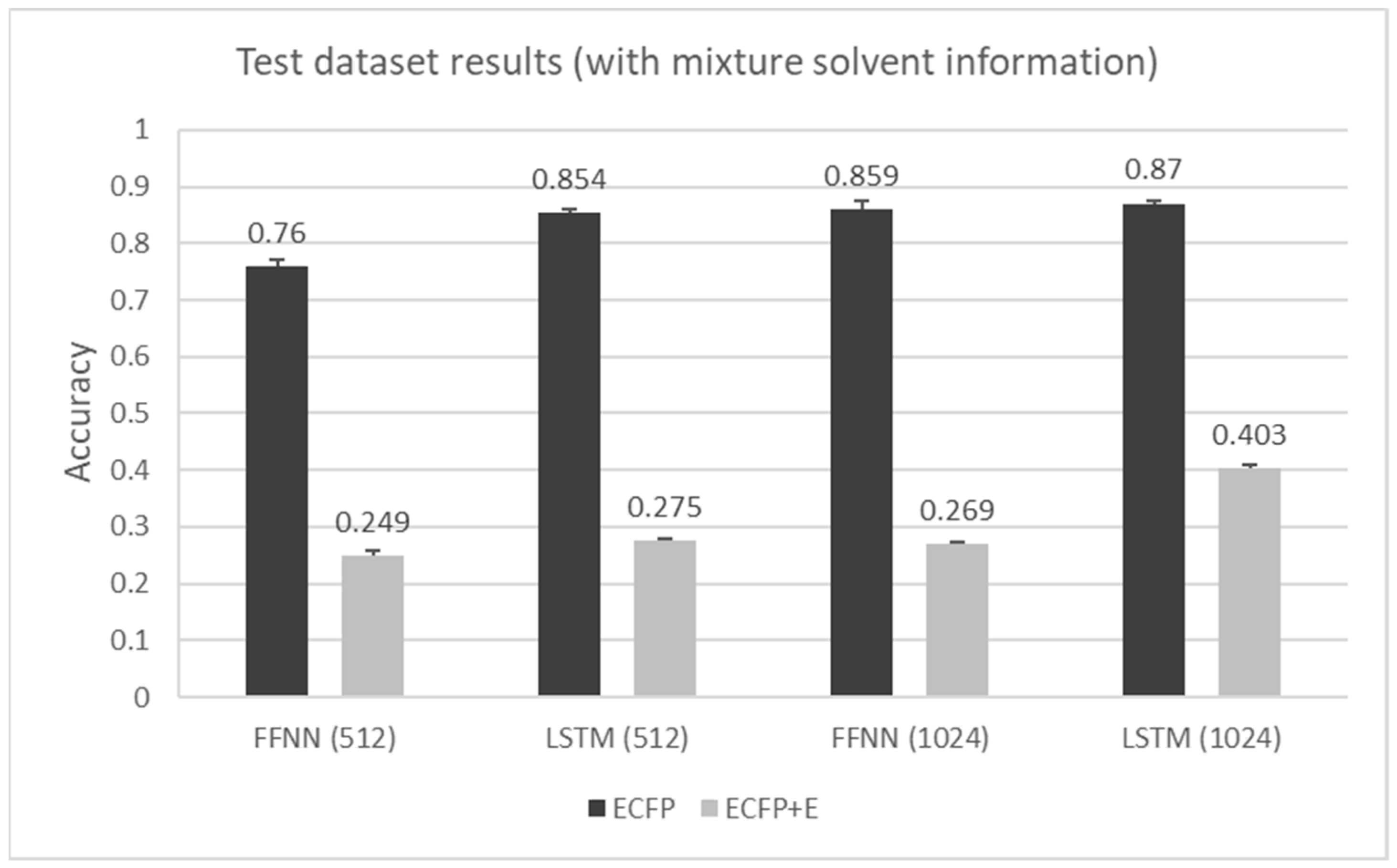
6. Results
7. Discussion
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Erdemir, D.; Lee, A.Y.; Myerson, A.S. Nucleation of Crystals from Solution: Classical and Two-Step Models. Acc. Chem. Res. 2009, 42, 621–629. [Google Scholar] [CrossRef]
- Weng, J.; Huang, Y.; Hao, D.; Ji, Y. Recent Advances of Pharmaceutical Crystallization Theories. Chin. J. Chem. Eng. 2020, 28, 935–948. [Google Scholar] [CrossRef]
- Gao, Z.; Rohani, S.; Gong, J.; Wang, J. Recent Developments in the Crystallization Process: Toward the Pharmaceutical Industry. Engineering 2017, 3, 343–353. [Google Scholar] [CrossRef]
- Cote, A.; Erdemir, D.; Girard, K.P.; Green, D.A.; Lovette, M.A.; Sirota, E.; Nere, N.K. Perspectives on the Current State, Challenges, and Opportunities in Pharmaceutical Crystallization Process Development. Cryst. Growth Des. 2020, 20, 7568–7581. [Google Scholar] [CrossRef]
- Nordstrom, F.L.; Linehan, B.; Teerakapibal, R.; Li, H. Solubility-Limited Impurity Purge in Crystallization. Cryst. Growth Des. 2019, 19, 1336–1346. [Google Scholar] [CrossRef]
- Su, W.; Jia, N.; Li, H.; Hao, H.; Li, C. Polymorphism of D-Mannitol: Crystal Structure and the Crystal Growth Mechanism. Chin. J. Chem. Eng. 2017, 25, 358–362. [Google Scholar] [CrossRef]
- Black, S.N. Crystallization in the Pharmaceutical Industry. In Handbook of Industrial Crystallization; Cambridge University Press: Cambridge, UK, 2019; pp. 380–413. [Google Scholar] [CrossRef]
- Capellades, G.; Bonsu, J.O.; Myerson, A.S. Impurity Incorporation in Solution Crystallization: Diagnosis, Prevention, and Control. CrystEngComm 2022, 24, 1989–2001. [Google Scholar] [CrossRef]
- Artusio, F.; Pisano, R. Surface-Induced Crystallization of Pharmaceuticals and Biopharmaceuticals: A Review. Int. J. Pharm. 2018, 547, 190–208. [Google Scholar] [CrossRef]
- Gini, G.; Zanoli, F.; Gamba, A.; Raitano, G.; Benfenati, E. Could Deep Learning in Neural Networks Improve the QSAR Models? SAR QSAR Environ. Res. 2019, 30, 617–642. [Google Scholar] [CrossRef]
- Lee, A.Y.; Erdemir, D.; Myerson, A.S. Crystals and Crystal Growth. In Handbook of Industrial Crystallization; Cambridge University Press: Cambridge, UK, 2019; pp. 32–75. [Google Scholar] [CrossRef] [Green Version]
- Keshavarz, L.; Steendam, R.R.E.; Blijlevens, M.A.R.; Pishnamazi, M.; Frawley, P.J. Influence of Impurities on the Solubility, Nucleation, Crystallization, and Compressibility of Paracetamol. Cryst. Growth Des. 2019, 19, 4193–4201. [Google Scholar] [CrossRef]
- Nagy, Z.K.; Fujiwara, M.; Braatz, R.D. Monitoring and Advanced Control of Crystallization Processes. In Handbook of Industrial Crystallization; Cambridge University Press: Cambridge, UK, 2019; pp. 313–345. [Google Scholar] [CrossRef]
- Fickelscherer, R.J.; Ferger, C.M.; Morrissey, S.A. Effective Solvent System Selection in the Recrystallization Purification of Pharmaceutical Products. AIChE J. 2021, 67, e17169. [Google Scholar] [CrossRef]
- Malwade, C.R.; Qu, H. Process Analytical Technology for Crystallization of Active Pharmaceutical Ingredients. Curr. Pharm. Des. 2018, 24, 2456–2472. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Sarma, B.; Evans, J.M.B.; Myerson, A.S. Pharmaceutical Crystallization. Cryst. Growth Des. 2011, 11, 887–895. [Google Scholar] [CrossRef] [Green Version]
- Watson, O.L.; Galindo, A.; Jackson, G.; Adjiman, C.S. Computer-Aided Design of Solvent Blends for the Cooling and Anti-Solvent Crystallisation of Ibuprofen. Comput. Aided Chem. Eng. 2019, 46, 949–954. [Google Scholar] [CrossRef]
- Karunanithi, A.T.; Achenie, L.E.K.; Gani, R. A Computer-Aided Molecular Design Framework for Crystallization Solvent Design. Chem. Eng. Sci. 2006, 61, 1247–1260. [Google Scholar] [CrossRef]
- Winter, R.; Montanari, F.; Noé, F.; Clevert, D.-A. Learning Continuous and Data-Driven Molecular Descriptors by Translating Equivalent Chemical Representations. Chem. Sci. 2019, 10, 1692–1701. [Google Scholar] [CrossRef] [Green Version]
- Mauri, A.; Consonni, V.; Todeschini, R. Molecular Descriptors. In Handbook of Computational Chemistry; Springer: Berlin/Heidelberg, Germany, 2017; pp. 2065–2093. [Google Scholar] [CrossRef]
- Kotsias, P.-C.; Arús-Pous, J.; Chen, H.; Engkvist, O.; Tyrchan, C.; Bjerrum, E.J. Direct Steering of de Novo Molecular Generation with Descriptor Conditional Recurrent Neural Networks. Nat. Mach. Intell. 2020, 2, 254–265. [Google Scholar] [CrossRef]
- Fernández-Torras, A.; Comajuncosa-Creus, A.; Duran-Frigola, M.; Aloy, P. Connecting Chemistry and Biology through Molecular Descriptors. Curr. Opin. Chem. Biol. 2022, 66, 102090. [Google Scholar] [CrossRef]
- Coley, C.W.; Barzilay, R.; Jaakkola, T.S.; Green, W.H.; Jensen, K.F. Prediction of Organic Reaction Outcomes Using Machine Learning. ACS Cent. Sci. 2017, 3, 434–443. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Bombarelli, R.; Wei, J.N.; Duvenaud, D.; Hernández-Lobato, J.M.; Sánchez-Lengeling, B.; Sheberla, D.; Aguilera-Iparraguirre, J.; Hirzel, T.D.; Adams, R.P.; Aspuru-Guzik, A. Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules. ACS Cent. Sci. 2018, 4, 268–276. [Google Scholar] [CrossRef]
- Khan, M.; Naeem, M.R.; Al-Ammar, E.A.; Ko, W.; Vettikalladi, H.; Ahmad, I. Power Forecasting of Regional Wind Farms via Variational Auto-Encoder and Deep Hybrid Transfer Learning. Electronics 2022, 11, 206. [Google Scholar] [CrossRef]
- Samanta, S.; O’Hagan, S.; Swainston, N.; Roberts, T.J.; Kell, D.B. VAE-Sim: A Novel Molecular Similarity Measure Based on a Variational Autoencoder. Molecules 2020, 25, 3446. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.; Ryu, S.; Kim, J.W.; Kim, W.Y. Molecular Generative Model Based on Conditional Variational Autoencoder for de Novo Molecular Design. J. Cheminform. 2018, 10, 31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baum, Z.J.; Yu, X.; Ayala, P.Y.; Zhao, Y.; Watkins, S.P.; Zhou, Q. Artificial Intelligence in Chemistry: Current Trends and Future Directions. J. Chem. Inf. Modeling 2021, 61, 3197–3212. [Google Scholar] [CrossRef] [PubMed]
- Virshup, A.M.; Contreras-García, J.; Wipf, P.; Yang, W.; Beratan, D.N. Stochastic Voyages into Uncharted Chemical Space Produce a Representative Library of All Possible Drug-Like Compounds. J. Am. Chem. Soc. 2013, 135, 7296–7303. [Google Scholar] [CrossRef] [Green Version]
- Lipkus, A.H.; Yuan, Q.; Lucas, K.A.; Funk, S.A.; Bartelt, W.F., III; Schenck, R.J.; Trippe, A.J. Structural Diversity of Organic Chemistry. A Scaffold Analysis of the CAS Registry. J. Org. Chem. 2008, 73, 4443–4451. [Google Scholar] [CrossRef] [Green Version]
- Gawehn, E.; Hiss, J.A.; Schneider, G. Deep Learning in Drug Discovery. Mol. Inform. 2015, 35, 3–14. [Google Scholar] [CrossRef]
- Ekins, S. The Next Era: Deep Learning in Pharmaceutical Research. Pharm. Res. 2016, 33, 2594–2603. [Google Scholar] [CrossRef]
- Chen, H.; Engkvist, O.; Wang, Y.; Olivecrona, M.; Blaschke, T. The Rise of Deep Learning in Drug Discovery. Drug Discov. Today 2018, 23, 1241–1250. [Google Scholar] [CrossRef]
- Lee, A.A.; Yang, Q.; Bassyouni, A.; Butler, C.R.; Hou, X.; Jenkinson, S.; Price, D.A. Ligand Biological Activity Predicted by Cleaning Positive and Negative Chemical Correlations. Proc. Natl. Acad. Sci. USA 2019, 116, 3373–3378. [Google Scholar] [CrossRef] [Green Version]
- Mayr, A.; Klambauer, G.; Unterthiner, T.; Steijaert, M.; Wegner, J.K.; Ceulemans, H.; Clevert, D.-A.; Hochreiter, S. Large-Scale Comparison of Machine Learning Methods for Drug Target Prediction on ChEMBL. Chem. Sci. 2018, 9, 5441–5451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schwaller, P.; Vaucher, A.C.; Laino, T.; Reymond, J.-L. Prediction of Chemical Reaction Yields Using Deep Learning. Mach. Learn. Sci. Technol. 2021, 2, 015016. [Google Scholar] [CrossRef]
- Feng, S.; Zhou, H.; Dong, H. Using Deep Neural Network with Small Dataset to Predict Material Defects. Mater. Des. 2019, 162, 300–310. [Google Scholar] [CrossRef]
- Yuan, Y.-G.; Wang, X. Prediction of Drug-Likeness of Central Nervous System Drug Candidates Using a Feed-Forward Neural Network Based on Chemical Structure. Biol. Med. Chem. 2020. [Google Scholar] [CrossRef]
- Yuan, Q.; Wei, Z.; Guan, X.; Jiang, M.; Wang, S.; Zhang, S.; Li, Z. Toxicity Prediction Method Based on Multi-Channel Convolutional Neural Network. Molecules 2019, 24, 3383. [Google Scholar] [CrossRef] [Green Version]
- Hirohara, M.; Saito, Y.; Koda, Y.; Sato, K.; Sakakibara, Y. Convolutional Neural Network Based on SMILES Representation of Compounds for Detecting Chemical Motif. BMC Bioinform. 2018, 19, 83–94. [Google Scholar] [CrossRef]
- Cui, Q.; Lu, S.; Ni, B.; Zeng, X.; Tan, Y.; Chen, Y.D.; Zhao, H. Improved Prediction of Aqueous Solubility of Novel Compounds by Going Deeper with Deep Learning. Front. Oncol. 2020, 10, 121. [Google Scholar] [CrossRef]
- Rao, J.; Zheng, S.; Song, Y.; Chen, J.; Li, C.; Xie, J.; Yang, H.; Chen, H.; Yang, Y. MolRep: A Deep Representation Learning Library for Molecular Property Prediction. bioRxiv 2021. Available online: https://www.biorxiv.org/content/10.1101/2021.01.13.426489v1 (accessed on 19 January 2022).
- Wieder, O.; Kohlbacher, S.; Kuenemann, M.; Garon, A.; Ducrot, P.; Seidel, T.; Langer, T. A Compact Review of Molecular Property Prediction with Graph Neural Networks. Drug Discov. Today Technol. 2020, 37, 1–12. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, S.; Bai, B.; Chan, H.C.S.; Yuan, S. Accurate Physical Property Predictions via Deep Learning. Molecules 2022, 27, 1668. [Google Scholar] [CrossRef]
- Segler, M.H.S.; Kogej, T.; Tyrchan, C.; Waller, M.P. Generating Focused Molecule Libraries for Drug Discovery with Recurrent Neural Networks. ACS Cent. Sci. 2017, 4, 120–131. [Google Scholar] [CrossRef] [Green Version]
- Ertl, P.; Lewis, R.; Martin, E.; Polyakov, V. In Silico Generation of Novel, Drug-like Chemical Matter Using the LSTM Neural Network. arXiv 2017, arXiv:1712.07449. [Google Scholar] [CrossRef]
- Gupta, A.; Müller, A.T.; Huisman, B.J.H.; Fuchs, J.A.; Schneider, P.; Schneider, G. Generative Recurrent Networks for De Novo Drug Design. Mol. Inform. 2017, 37, 1700111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grisoni, F.; Moret, M.; Lingwood, R.; Schneider, G. Bidirectional Molecule Generation with Recurrent Neural Networks. J. Chem. Inf. Modeling 2020, 60, 1175–1183. [Google Scholar] [CrossRef] [PubMed]
- Lim, H.; Jung, Y. Delfos: Deep Learning Model for Prediction of Solvation Free Energies in Generic Organic Solvents. Chem. Sci. 2019, 10, 8306–8315. [Google Scholar] [CrossRef]
- Ruiz Puentes, P.; Valderrama, N.; González, C.; Daza, L.; Muñoz-Camargo, C.; Cruz, J.C.; Arbeláez, P. PharmaNet: Pharmaceutical Discovery with Deep Recurrent Neural Networks. PLoS ONE 2021, 16, e0241728. [Google Scholar] [CrossRef]
- Shin, B.; Park, S.; Bak, J.; Ho, J.C. Controlled Molecule Generator for Optimizing Multiple Chemical Properties. In Proceedings of the Conference on Health, Inference, and Learning, Online, 8 April 2021. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chen, Y.P. Descriptive Prediction of Drug Side-effects Using a Hybrid Deep Learning Model. Int. J. Intell. Syst. 2021, 36, 2491–2510. [Google Scholar] [CrossRef]
- Lowe, D. Chemical Reactions from US Patents (1976-Sep2016). 2017. Available online: https://figshare.com/articles/dataset/Chemical_reactions_from_US_patents_1976-Sep2016_/5104873 (accessed on 6 January 2022).
- Weininger, D. SMILES, a Chemical Language and Information System. 1. Introduction to Methodology and Encoding Rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Rogers, D.; Hahn, M. Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef]
- Wójcikowski, M.; Kukiełka, M.; Stepniewska-Dziubinska, M.M.; Siedlecki, P. Development of a Protein–Ligand Extended Connectivity (PLEC) Fingerprint and Its Application for Binding Affinity Predictions. Bioinformatics 2018, 35, 1334–1341. [Google Scholar] [CrossRef] [Green Version]
- Duan, C.; Sun, J.; Li, K.; Li, Q. A Dual-Attention Autoencoder Network for Efficient Recommendation System. Electronics 2021, 10, 1581. [Google Scholar] [CrossRef]
- Sarkar, A.K.; Tan, Z.-H. On Training Targets and Activation Functions for Deep Representation Learning in Text-Dependent Speaker Verification. arXiv 2022, arXiv:2201.06426. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, C.; Gong, X. Deep Convolutional Neural Network for Decoding Motor Imagery Based Brain Computer Interface. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017. [Google Scholar] [CrossRef]
- Ketkar, N. Stochastic Gradient Descent. In Deep Learning with Python; Apress: Berkeley, CA, USA, 2017; pp. 113–132. [Google Scholar] [CrossRef]
- Vaškevičius, M.; Kapočiūtė-Dzikienė, J.; Šlepikas, L. Prediction of Chromatography Conditions for Purification in Organic Synthesis Using Deep Learning. Molecules 2021, 26, 2474. [Google Scholar] [CrossRef] [PubMed]


| Name | Compounds | Pre-Crystallization Solvents | Solvent (Prediction) |
|---|---|---|---|
| DS1 | OC=O.CC(C)N(C(CN)=O)c1ccccc1>>Cc1ccccc1>>CC(C)N(C(CNC=O)=O)c1ccccc1 | Toluene | Hexane |
| DS2 | Nc1cccc(O)c1.N#Cc1cccc([N+]([O-])=O)c1C#N>>Nc1cccc(Oc(cc2)cc(C#N)c2C#N)c1 | - | Pyridine |
| Class Label | Training Subset (Number of Instances) | Testing Subset (Number of Instances) | Total (Number of Instances) |
|---|---|---|---|
| Hexane | 42,421 | 4713 | 47,134 |
| Ethyl acetate | 41,983 | 4665 | 46,648 |
| Ethanol | 31,658 | 3518 | 35,175 |
| Ether | 21,975 | 2442 | 24,417 |
| Methanol | 18,796 | 2088 | 20,884 |
| Acetonitrile | 8398 | 933 | 9331 |
| Isopropanol | 7227 | 803 | 8030 |
| Water | 5612 | 624 | 6236 |
| Toluene | 4930 | 548 | 5478 |
| Acetone | 3874 | 430 | 4304 |
| DCM | 3704 | 412 | 4115 |
| Chloroform | 1815 | 202 | 2017 |
| DMF | 1765 | 196 | 1961 |
| Total number of instances | 162,131 | 18,015 | 180,145 |
| Number | Neural Network Type | Vectorization | Vector Size | Pre-Mix Info |
|---|---|---|---|---|
| 1 | FFNN | ECFP | 512 | no |
| 2 | LSTM | ECFP | 512 | no |
| 3 | FFNN | ECFP | 1024 | no |
| 4 | LSTM | ECFP | 1024 | no |
| 5 | FFNN | ECFP | 512 | yes |
| 6 | LSTM | ECFP | 512 | yes |
| 7 | FFNN | ECFP | 1024 | yes |
| 8 | LSTM | ECFP | 1024 | yes |
| 9 | FFNN | ECFP + E | 512 | no |
| 10 | LSTM | ECFP + E | 512 | no |
| 11 | FFNN | ECFP + E | 1024 | no |
| 12 | LSTM | ECFP + E | 1024 | no |
| 13 | FFNN | ECFP + E | 512 | yes |
| 14 | LSTM | ECFP + E | 512 | yes |
| 15 | FFNN | ECFP + E | 1024 | yes |
| 16 | LSTM | ECFP + E | 1024 | yes |
| Vectorization | Metric | FFNN (512) | LSTM (512) | FFNN (1024) | LSTM (1024) |
|---|---|---|---|---|---|
| ECFP | Accuracy | 0.617 ± 0.003 | 0.832 ± 0.008 | 0.836 ± 0.004 | 0.836 ± 0.004 |
| Precision | 0.842 ± 0.005 | 0.899 ± 0.006 | 0.847 ± 0.008 | 0.905 ± 0.004 | |
| Recall | 0.689 ± 0.003 | 0.877 ± 0.004 | 0.759 ± 0.008 | 0.880 ± 0.006 | |
| F1-score | 0.758 ± 0.004 | 0.888 ± 0.005 | 0.800 ± 0.002 | 0.892 ± 0.002 | |
| LE | Accuracy | 0.267 ± 0.005 | 0.257 ± 0.006 | 0.371 ± 0.006 | 0.862 ± 0.003 |
| Precision | 0.576 ± 0.007 | 0.655 ± 0.012 | 0.568 ± 0.003 | 0.928 ± 0.011 | |
| Recall | 0.354 ± 0.005 | 0.336 ± 0.013 | 0.502 ± 0.007 | 0.889 ± 0.002 | |
| F1-score | 0.439 ± 0.005 | 0.444 ± 0.009 | 0.533 ± 0.003 | 0.908 ± 0.006 | |
| ECFP + E | Accuracy | 0.617 ± 0.003 | 0.832 ± 0.008 | 0.836 ± 0.004 | 0.836 ± 0.004 |
| Precision | 0.842 ± 0.005 | 0.899 ± 0.006 | 0.847 ± 0.008 | 0.905 ± 0.004 | |
| Recall | 0.689 ± 0.003 | 0.877 ± 0.004 | 0.759 ± 0.008 | 0.880 ± 0.006 | |
| F1-score | 0.758 ± 0.004 | 0.888 ± 0.005 | 0.800 ± 0.002 | 0.892 ± 0.002 |
| Vectorization | Metric | FFNN (512) | LSTM (512) | FFNN (1024) | LSTM (1024) |
|---|---|---|---|---|---|
| ECFP | Accuracy | 0.617 ± 0.003 | 0.832 ± 0.008 | 0.836 ± 0.004 | 0.836 ± 0.004 |
| Precision | 0.842 ± 0.005 | 0.899 ± 0.006 | 0.847 ± 0.008 | 0.905 ± 0.004 | |
| Recall | 0.689 ± 0.003 | 0.877 ± 0.004 | 0.759 ± 0.008 | 0.880 ± 0.006 | |
| F1-score | 0.758 ± 0.004 | 0.888 ± 0.005 | 0.800 ± 0.002 | 0.892 ± 0.002 | |
| LE | Accuracy | 0.267 ± 0.005 | 0.257 ± 0.006 | 0.371 ± 0.006 | 0.862 ± 0.003 |
| Precision | 0.576 ± 0.007 | 0.655 ± 0.012 | 0.568 ± 0.003 | 0.928 ± 0.011 | |
| Recall | 0.354 ± 0.005 | 0.336 ± 0.013 | 0.502 ± 0.007 | 0.889 ± 0.002 | |
| F1-score | 0.439 ± 0.005 | 0.444 ± 0.009 | 0.533 ± 0.003 | 0.908 ± 0.006 | |
| ECFP + E | Accuracy | 0.617 ± 0.003 | 0.832 ± 0.008 | 0.836 ± 0.004 | 0.836 ± 0.004 |
| Precision | 0.842 ± 0.005 | 0.899 ± 0.006 | 0.847 ± 0.008 | 0.905 ± 0.004 | |
| Recall | 0.689 ± 0.003 | 0.877 ± 0.004 | 0.759 ± 0.008 | 0.880 ± 0.006 | |
| F1-score | 0.758 ± 0.004 | 0.888 ± 0.005 | 0.800 ± 0.002 | 0.892 ± 0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaškevičius, M.; Kapočiūtė-Dzikienė, J.; Šlepikas, L. Modeling of the Crystallization Conditions for Organic Synthesis Product Purification Using Deep Learning. Electronics 2022, 11, 1360. https://doi.org/10.3390/electronics11091360
Vaškevičius M, Kapočiūtė-Dzikienė J, Šlepikas L. Modeling of the Crystallization Conditions for Organic Synthesis Product Purification Using Deep Learning. Electronics. 2022; 11(9):1360. https://doi.org/10.3390/electronics11091360
Chicago/Turabian StyleVaškevičius, Mantas, Jurgita Kapočiūtė-Dzikienė, and Liudas Šlepikas. 2022. "Modeling of the Crystallization Conditions for Organic Synthesis Product Purification Using Deep Learning" Electronics 11, no. 9: 1360. https://doi.org/10.3390/electronics11091360
APA StyleVaškevičius, M., Kapočiūtė-Dzikienė, J., & Šlepikas, L. (2022). Modeling of the Crystallization Conditions for Organic Synthesis Product Purification Using Deep Learning. Electronics, 11(9), 1360. https://doi.org/10.3390/electronics11091360







