Preliminary Design of a Receding Horizon Controller Supported by Adaptive Feedback
Abstract
:1. Introduction
2. Formulation of the Optimization Problem without Using Constraint Terms
- It is given the horizon for design in the discrete time steps containing the state variables as , and , the exerted control forces , and the second coordinate time derivatives as ;
- in the discrete time representation the above data contain certain redundancy because the relationship must be valid for , and for ;
- the dynamic model of the system determines ; and
- the initial conditions are determined by redundantly with .
3. Solution for the Minimization
- The minimization was commenced from zero force components, and started with a big step using the Newton–Raphson algorithm. A parameter was introduced in the first step.
- Until the Newton–Raphson algorithm with the given step-length yielded a smaller cost value than the previously visited point, it proceeded forward with this big step length;
- When in the suggested next point the function value found was bigger than that in the starting point, has been halved, and times the step-length of the Newton–Raphson algorithm was applied. If it yielded a better point, the calculated step-length was used; otherwise was kept halved until it either provided a better next point, or it achieved a preset minimum value at which point the algorithm stopped.
4. Utilization of the Result of Cost Minimization
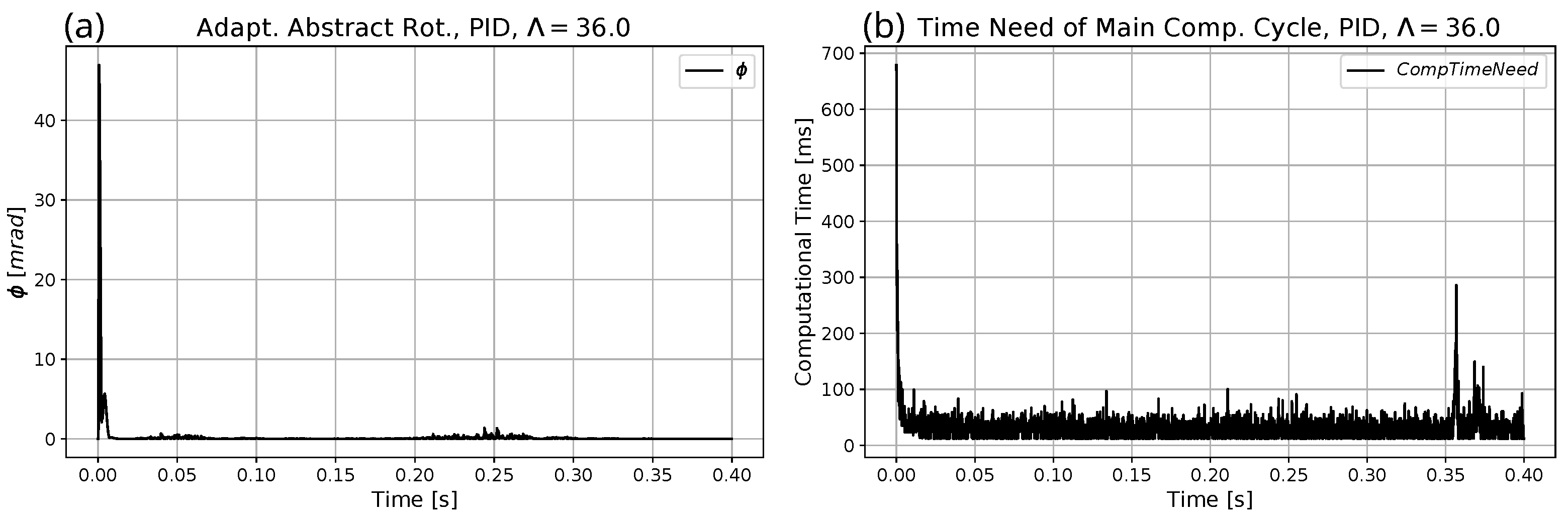
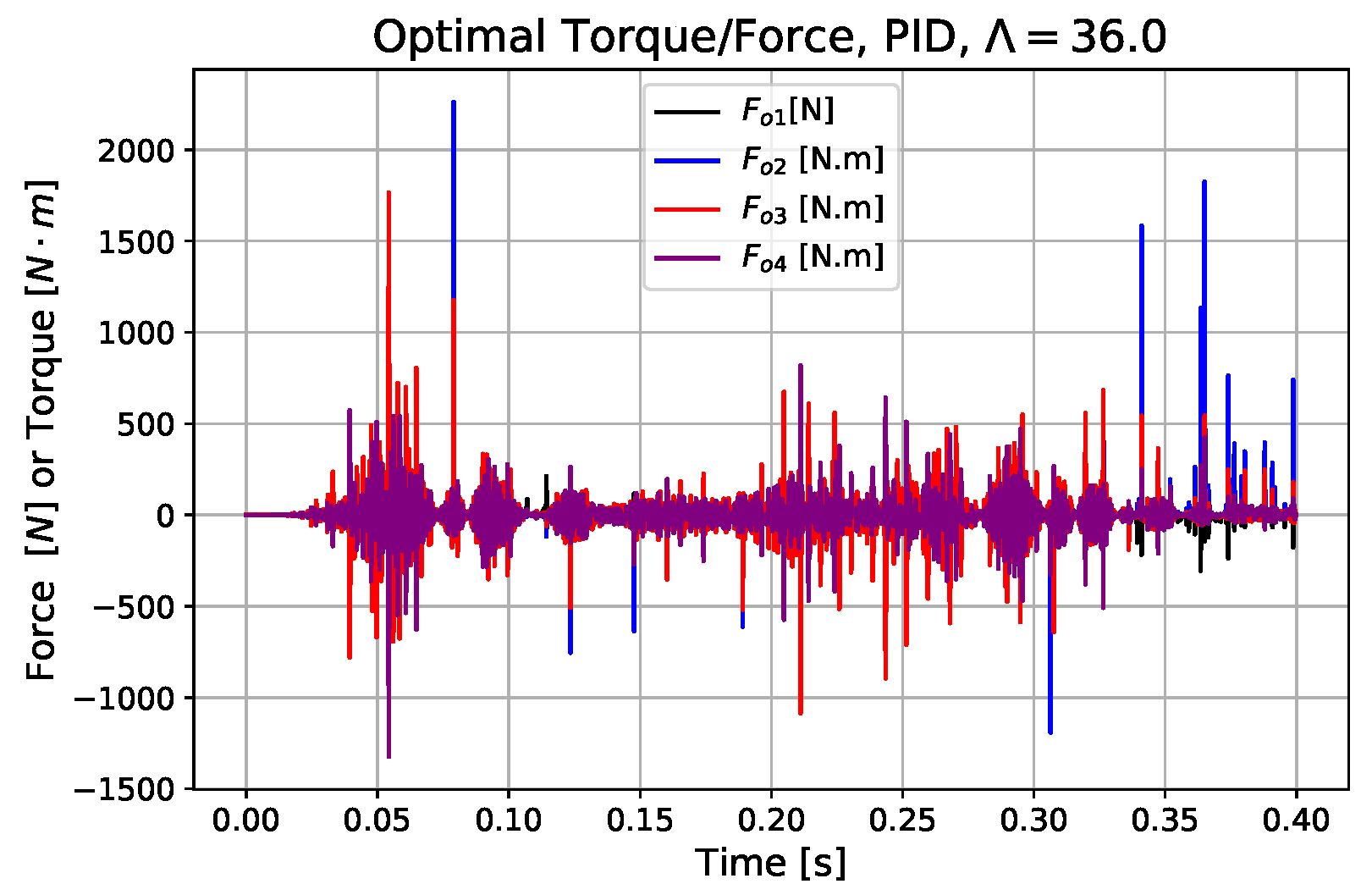
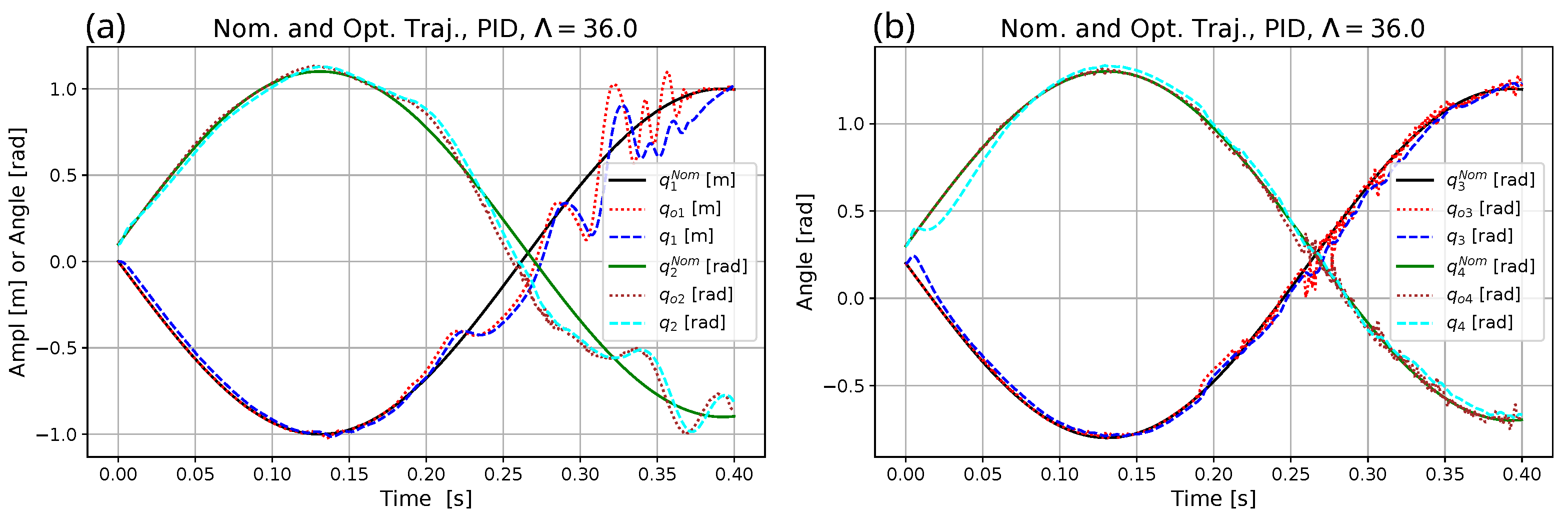
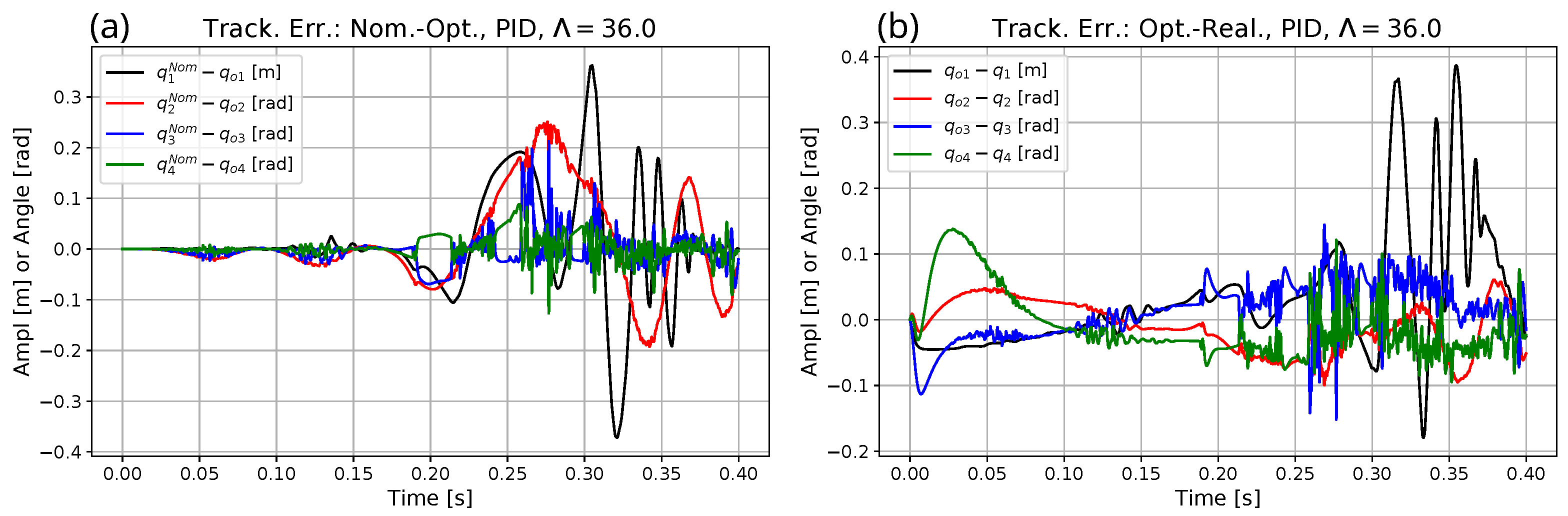
5. Simulation Results
5.1. Simulations without Force Limitation
5.1.1. Investigations for Different Time Resolutions
5.1.2. Computations for Less Precise Minimum Seeking
5.2. With Force Limitation
6. Discussion
- In general it seems to be an interesting research area to consider the problem of adaptive optimal control design for a wider set that is exempt of the limitations of linear time-invariant dynamic system models and quadratic cost function contributions.
- The prevailing general approach in this field is linear programming that tackles the problem in discrete time grid approach and the use of Lagrange’s reduced gradient algorithm that is professionally implemented e.g., in the EXCEL’s Solver package.
- It is evident that the direct problem formulation applied for evading the use of the constraint-based formalism leads to considerable reduction in complexity and computational needs. The number of the independent variables of the original approach is considerably decreased. Instead of the variables , , only the variables remain the independent ones, and there is no need to calculate the Lagrange multipliers .
- The problem of small steps in the case of the suggested solution can be tackled by a modification of the Newton–Raphson algorithm (generally it is an issue in using the reduced gradient method, too).
- It was found that for keeping the computational time low, it is expedient to use not very precise minimum seeking.
- The scattering of the force values and the related effects rather can be tackled by a simple noise-filtering approach applied for the optimized trajectory to be adaptively tracked.
- The suggested adaptive controller can well track the smoothed signal.
- The mathematical frameworks of optimization and adaptive tracking can be separated from each other in a simple manner.
- The basic concept was that the force-limited optimization can be executed by the use of a heavy dynamic model. Therefore, the force limitation issues can be tackled in the optimization phase. It can be expected that the trajectory that was optimized for the heavy model can be tracked by an easier mechanical construction for the acceleration of the components of which smaller force or torque components can be expected. For tracking the optimized trajectory, a simple CTC type or an improved adaptive CTC type control strategy can be used that is free of the burden of the force-limitation issues.
- The necessary time grid resolution depends on various factors as the dynamics of the nominal trajectory to be tracked, the structure of the cost function applied, the parameters used in smoothing the optimized trajectory, and that of the adaptive controller that tracks the smoothed trajectory.
- In general all the above factors can be clarified via making numerical simulations for a given problem or problem class.
- In the given investigations, the execution time was measured by the use of the given hardware that was a laptop with a single CPU and a multitasking operating system. Consequently, the measured data also contain the time sections during which the actual task was interrupted and the processor was working on other tasks. However, because during the calculations no heavy software application was running, these data provide approximate and reliable information. (Parallel or simultaneous’use for instance of a video player drastically modifies these observed data.)
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bennett, S. Nicholas Minorsky and the automatic steering of ships. IEEE Control Syst. Mag. 1984, 4, 10–15. [Google Scholar] [CrossRef]
- Armstrong, B.; Khatib, O.; Burdick, J. The Explicit Dynamic Model and Internal Parameters of the PUMA 560 Arm. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 7–10 April 1986; pp. 510–518. [Google Scholar]
- Corke, P.; Armstrong-Helouvry, B. A Search for Consensus Among Model Parameters Reported for the PUMA 560 Robot. In Proceedings of the IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 1608–1613. [Google Scholar]
- Mohd Zaihidee, F.; Mekhilef, S.; Mubin, M. Robust speed control of PMSM using sliding mode control (SMC)—A review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef] [Green Version]
- Sagara, S.; Ambar, R. Performance comparison of control methods using a dual-arm underwater robot-Computed torque based control and resolved acceleration control for UVMS. In Proceedings of the 2020 IEEE/SICE International Symposium on System Integration (SII), Honolulu, HI, USA, 12–15 January 2020; pp. 1094–1099. [Google Scholar]
- Hamandi, M.; Tognon, M.; Franchi, A. Direct acceleration feedback control of quadrotor aerial vehicles. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 5335–5341. [Google Scholar]
- Bodó, Z.; Lantos, B. Integrating Backstepping Control of Outdoor Quadrotor UAVs. Period. Polytech. Electr. Eng. Comput. Sci. 2019, 63, 122–132. [Google Scholar] [CrossRef]
- Yuan, S.; Lv, M.; Baldi, S.; Zhang, L. Lyapunov-equation-based stability analysis for switched linear systems and its application to switched adaptive control. IEEE Trans. Autom. Control 2020, 66, 2250–2256. [Google Scholar] [CrossRef]
- Dogan, K.M.; Yucelen, T.; Haddad, W.M.; Muse, J.A. Improving transient performance of discrete-time model reference adaptive control architectures. Int. J. Adapt. Control Signal Process. 2020, 34, 901–918. [Google Scholar] [CrossRef]
- Riccati, J. Animadversiones in aequationes differentiales secundi gradus (Observations regarding differential equations of the second order). Actorum Erud. Quae Lipsiae Publicantur Suppl. 1724, 8, 66–73. [Google Scholar]
- Haynsworth, E. On the Schur Complement. Basel Math. Notes 1968, BMN 20, 17. [Google Scholar]
- Laub, A. A Schur method for solving algebraic Riccati equations. IEEE Trans. Autom. Control 1979, 24, 913–921. [Google Scholar] [CrossRef] [Green Version]
- Boyd, S.; Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in Systems and Control Theory; SIAM Books: Philadelphia, PA, USA, 1994. [Google Scholar]
- Gahinet, P.; Nemirovskii, A.; Laub, A.; Chilali, M. The LMI control toolbox. In Proceedings of the 1994 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; Volume 3, pp. 2038–2041. [Google Scholar] [CrossRef]
- Koch, G.G.; Maccari, L.A.; Oliveira, R.C.; Montagner, V.F. Robust State Feedback Controllers Based on Linear Matrix Inequalities Applied to Grid-Connected Converters. IEEE Trans. Ind. Electron. 2018, 66, 6021–6031. [Google Scholar] [CrossRef]
- Chang, X.H.; Liu, R.R.; Park, J.H. A Further Study on Output Feedback Control for Discrete-Time Systems. IEEE Trans. Circ. Syst. 2019, 67, 305–309. [Google Scholar]
- Li, Z.M.; Chang, X.H.; Park, J.H. Quantized static output feedback fuzzy tracking control for discrete-time nonlinear networked systems with asynchronous event-triggered constraints. IEEE Trans. Syst. Man Cyber. Syst. 2019, 51, 3820–3831. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming and a new formalism in the calculus of variations. Proc. Natl. Acad. Sci. USA 1954, 40, 231–235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lagrange, J.; Binet, J.; Garnier, J. Mécanique Analytique (Analytical Mechanics); Binet, J.P.M., Garnier, J.G., Eds.; Ve Courcier: Paris, France, 1811. [Google Scholar]
- Hestenes, M.R. Multiplier and gradient methods. J. Optim. Theory Appl. 1969, 4, 303–320. [Google Scholar] [CrossRef]
- Powell, M.J. A method for nonlinear constraints in minimization problems. Optimization 1969, 283–298. [Google Scholar]
- Mayne, D.Q.; Michalska, H. Receding horizon control of nonlinear systems. In Proceedings of the 27th IEEE Conference on Decision and Control, Austin, TX, USA, 7–9 December 1988; pp. 464–465. [Google Scholar]
- Michalska, H.; Mayne, D.Q. Robust receding horizon control of constrained nonlinear systems. IEEE Trans. Autom. Control 1993, 38, 1623–1633. [Google Scholar] [CrossRef]
- Bellingham, J.; Richards, A.; How, J.P. Receding horizon control of autonomous aerial vehicles. In Proceedings of the 2002 American control conference (IEEE Cat. No. CH37301), Anchorage, AK, USA, 8–10 May 2002; Volume 5, pp. 3741–3746. [Google Scholar]
- Cagienard, R.; Grieder, P.; Kerrigan, E.C.; Morari, M. Move blocking strategies in receding horizon control. J. Process Control 2007, 17, 563–570. [Google Scholar] [CrossRef] [Green Version]
- Kuwata, Y.; Richards, A.; Schouwenaars, T.; How, J.P. Distributed robust receding horizon control for multivehicle guidance. IEEE Trans. Control Syst. Technol. 2007, 15, 627–641. [Google Scholar] [CrossRef]
- Mattingley, J.; Wang, Y.; Boyd, S. Receding horizon control. IEEE Control Syst. Mag. 2011, 31, 52–65. [Google Scholar]
- Igreja, J.; Lemos, J.; Silva, R. Adaptive receding horizon control of a distributed collector solar field. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 1282–1287. [Google Scholar]
- Tanaskovic, M.; Fagiano, L.; Smith, R.; Morari, M. Adaptive receding horizon control for constrained MIMO systems. Automatica 2014, 50, 3019–3029. [Google Scholar] [CrossRef]
- Lukina, A.; Esterle, L.; Hirsch, C.; Bartocci, E.; Yang, J.; Tiwari, A.; Smolka, S.A.; Grosu, R. ARES: Adaptive receding-horizon synthesis of optimal plans. In Proceedings of the International Conference on Tools and Algorithms for the Construction and Analysis of Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 286–302. [Google Scholar]
- Evangelista, C.A.; Pisano, A.; Puleston, P.; Usai, E. Receding horizon adaptive second-order sliding mode control for doubly-fed induction generator based wind turbine. IEEE Trans. Control Syst. Technol. 2016, 25, 73–84. [Google Scholar] [CrossRef]
- Karabulut, H. Physical meaning of Lagrange multipliers. Eur. J. Phys. Gen. Phys. 2007, 27, 709–718. [Google Scholar] [CrossRef]
- Arnold, V. Mathematical Methods of Classical Mechanics; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Raphson, J. Analysis Aequationum Universalis (Analysis of Universal Equations); Nabu Press: Paris, France, 1702. [Google Scholar]
- Issa, H.; Tar, J. Speeding up the Reduced Gradient Method for Constrained Optimization. In Proceedings of the IEEE 19th World Symposium on Applied Machine Intelligence and Informatics (SAMI 2021), Herl’any, Slovakia, 21–23 January 2021; pp. 000485–000490. [Google Scholar] [CrossRef]
- Redjimi, H.; Tar, J.K. Approximate model-based state estimation in simplified Receding Horizon Control. Int. J. Circ. Syst. Signal Process. 2021, 15, 114–124. [Google Scholar] [CrossRef]
- Issa, H.; Khan, H.; Tar, J.K. Suboptimal Adaptive Receding Horizon Control Using Simplified Nonlinear Programming. In Proceedings of the 2021 IEEE 25th International Conference on Intelligent Engineering Systems (INES), Budapest, Hungary, 7–9 July 2021; pp. 000221–000228. [Google Scholar]
- Acosta, J. Furuta’s Pendulum: A Conservative Nonlinear Model for Theory and Practise. Math. Probl. Eng. 2010, 2010, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Issa, H.; Varga, B.; Tar, J.K. A receding horizon-type solution of the inverse kinematic task of redundant robots. In Proceedings of the 2021 IEEE 15th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 19–21 May 2021; pp. 000231–000236. [Google Scholar]
- Issa, H.; Varga, B.; Tar, J.K. Accelerated reduced gradient algorithm for solving the inverse kinematic task of redundant open kinematic chains. In Proceedings of the 2021 IEEE 15th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 19–21 May 2021; pp. 000387–000392. [Google Scholar]
- Khan, H.; Tar, J.; Rudas, I.; Eigner, G. Adaptive Model Predictive Control Based on Fixed Point Iteration. WSEAS Trans. Syst. Control 2017, 12, 347–354. [Google Scholar]
- Khan, H.; Tar, J.; Rudas, I.; Eigner, G. Iterative Solution in Adaptive Model Predictive Control by Using Fixed-Point Transformation Method. Int. J. Math. Models Methods Appl. Sci. 2018, 12, 7–15. [Google Scholar]
- Lantos, B.; Bodó, Z. High Level Kinematic and Low Level Nonlinear Dynamic Control of Unmanned Ground Vehicles. Acta Polytech. Hung. 2019, 16, 97–117. [Google Scholar]
- Tar, J.; Bitó, J.; Nádai, L.; Tenreiro Machado, J. Robust Fixed Point Transformations in Adaptive Control Using Local Basin of Attraction. Acta Polytech. Hung. 2009, 6, 21–37. [Google Scholar]
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (About the Operations in the Abstract Sets and Their Application to Integral Equations). Fund. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Dineva, A.; Tar, J.; Várkonyi-Kóczy, A. Novel Generation of Fixed Point Transformation for the Adaptive Control of a Nonlinear Neuron Model. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, (SMC 2015), Hong Kong, China, 10–13 October 2015; pp. 987–992. [Google Scholar]
- Dineva, A.; Tar, J.; Várkonyi-Kóczy, A.; Piuri, V. Generalization of a Sigmoid Generated Fixed Point Transformation from SISO to MIMO Systems. In Proceedings of the IEEE 19th International Conference on Intelligent Engineering Systems, (INES 2015), Bratislava, Slovakia, 3–5 September 2015; pp. 135–140. [Google Scholar]
- Csanádi, B.; Galambos, P.; Tar, J.; Györök, G.; Serester, A. A Novel, Abstract Rotation-based Fixed Point Transformation in Adaptive Control. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC2018), Miyazaki, Japan, 7–10 October 2018; pp. 2577–2582. [Google Scholar]
- Somló, J.; Lantos, B.; Cát, P. Advanced Robot Control; Akadémiai Kiadó: Budapest, Hugary, 2002. [Google Scholar]
- Monje, C.; Ramos, F.; Feliu, V.; Vinagre, B. Tip position control of a lightweight flexible manipulator using a fractional order controller. Control Theory Appl. IET 2007, 1, 1451–1460. [Google Scholar] [CrossRef]
- Ferreira, N.; Machado, J.T.; Tar, J. Fractional Control of Two Cooperating Manipulators. In Proceedings of the 6th IEEE International Conference on Computational Cybernetics, Stará Lesna, Slovakia, 27–29 November 2008; pp. 27–32. [Google Scholar]
- Padula, F.; Visioli, A. Tuning rules for optimal PID and fractional order PID controllers. J. Process Control 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Dumlu, A.; Erenturk, K. Trajectory tracking control for a 3-DOF parallel manipulator using fractional-order PIλDμ control. IEEE Trans. Ind. Electron. 2014, 61, 3417–3426. [Google Scholar] [CrossRef]
- Bruzzone, L.; Fanghella, P. Comparison of PDD1/2 and PDμ Position Controls of a Second Order Linear System. In Proceedings of the 33rd IASTED International Conference on Modelling, Identification and Control (MIC 2014), Innsbruck, Austria, 17–19 February 2014; pp. 182–188. [Google Scholar]
- Folea, S.; De Keyser, R.; Birs, I.R.; Muresan, C.I.; Ionescu, C. Discrete-Time Implementation and Experimental Validation of a Fractional Order PD Controller for Vibration Suppression in Airplane Wings. Acta Polytech. Hung. 2017, 14, 191–206. [Google Scholar]
- Tar, J.; Bitó, J.; Kovács, L.; Faitli, T. Fractional Order PID-Type Feedback in Fixed Point Transformation-Based Adaptive Control of the FitzHugh-Nagumo Neuron Model with Time-Delay. In Proceedings of the 3rd IFAC Conference on Advances in Proportional-Integral-Derivative Control, Ghent, Belgium, 9–11 May 2018; pp. 906–911. [Google Scholar]
- De Oliveira, E.C.; Tenreiro Machado, J.A. A Review of Definitions for Fractional Derivatives and Integral. Math. Problems Eng. 2014, 2014, 6. [Google Scholar] [CrossRef] [Green Version]
- Tenreiro Machado, J.; Kiryakova, V. The Chronicles of Fractional Calculus. Fract. Calc. Appl. Anal. 2017, 20, 307–336. [Google Scholar] [CrossRef]
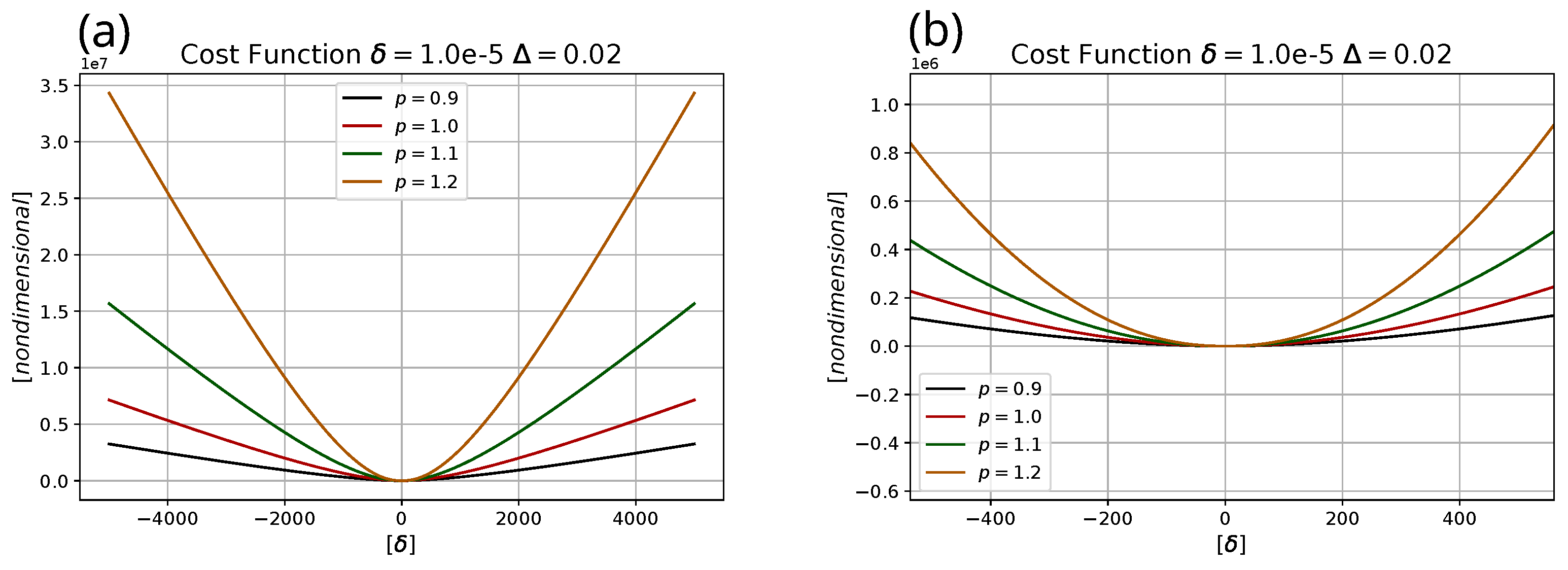



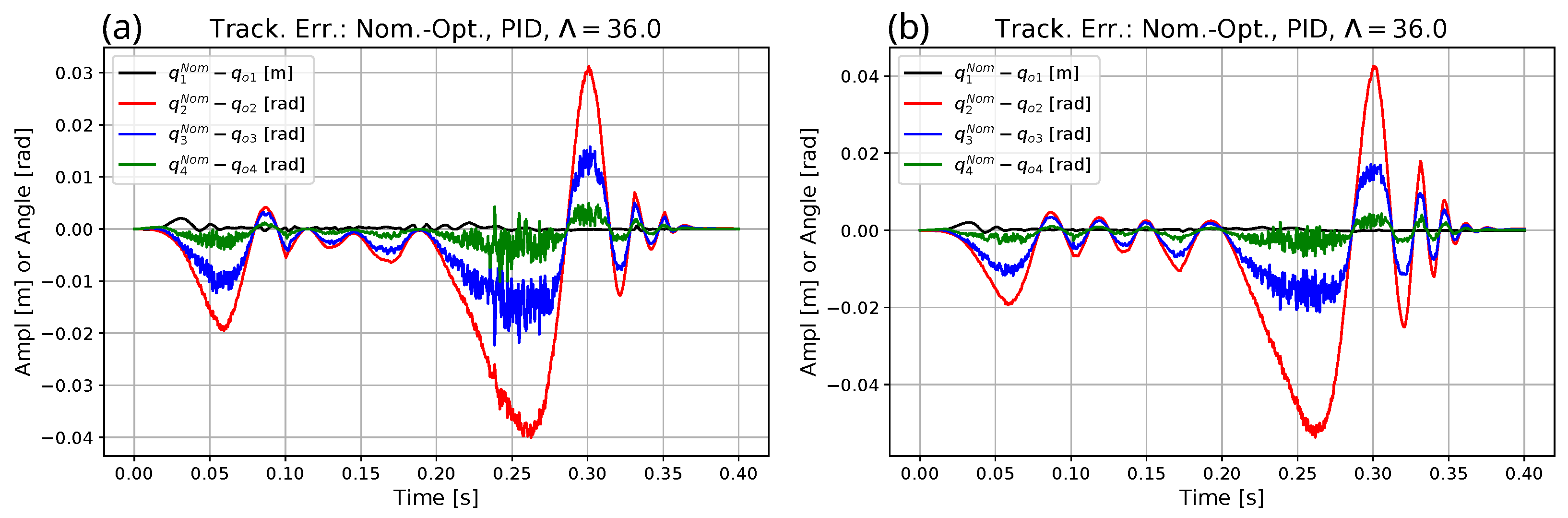

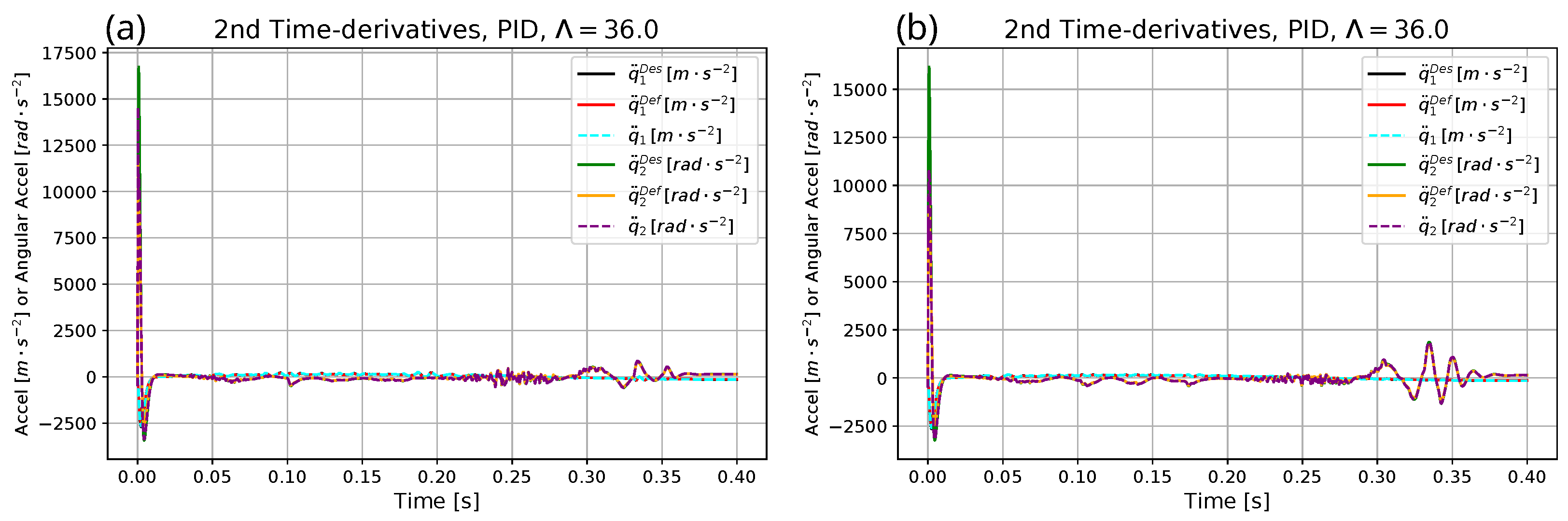
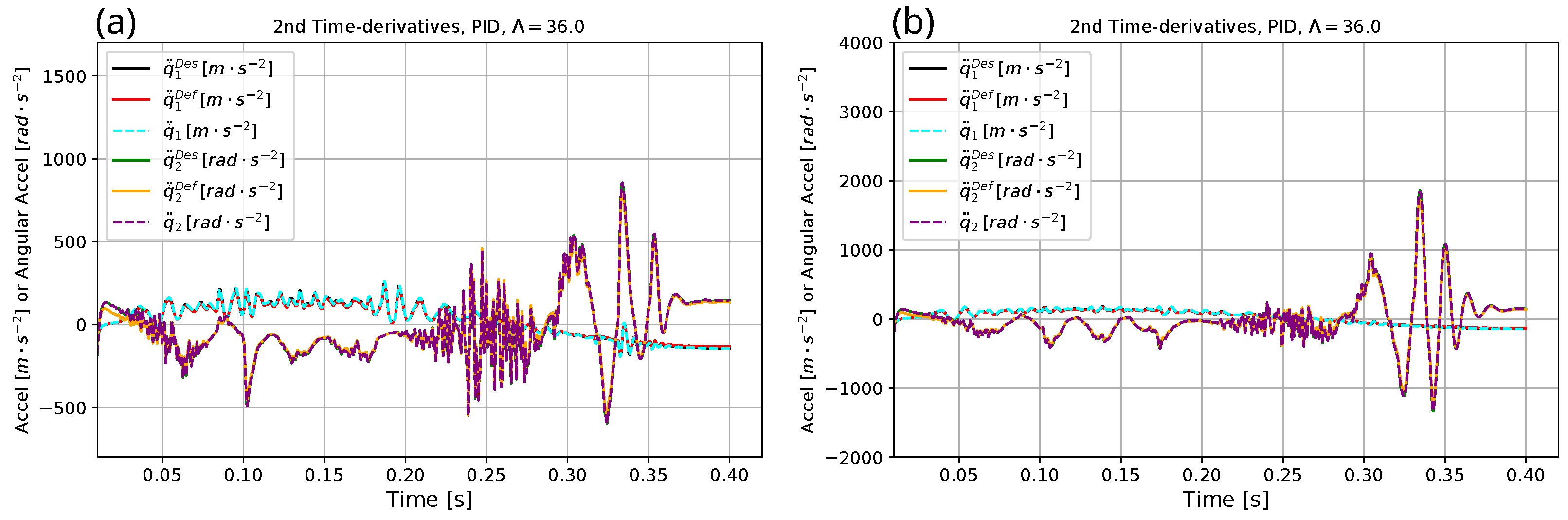
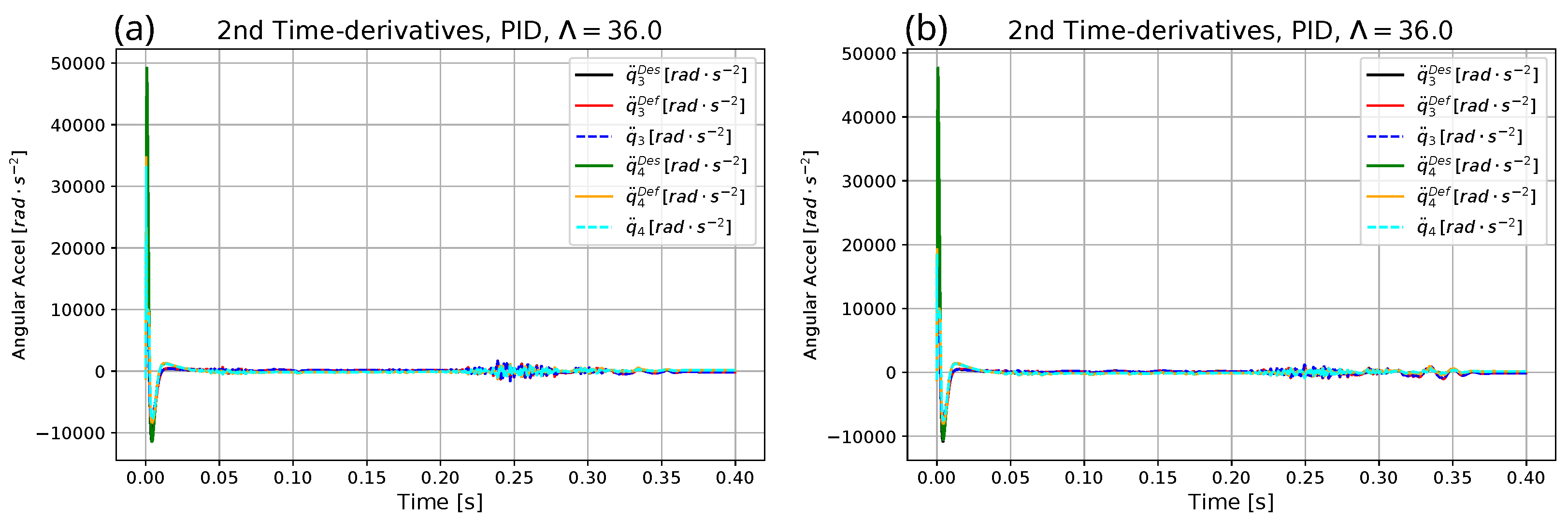


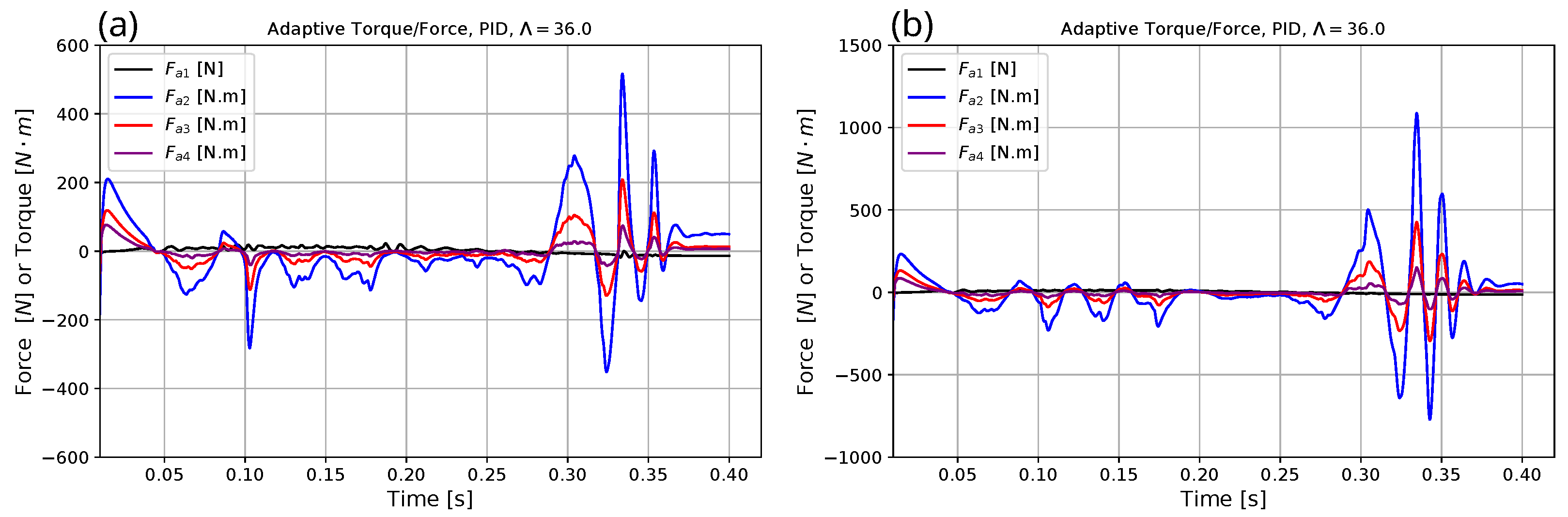
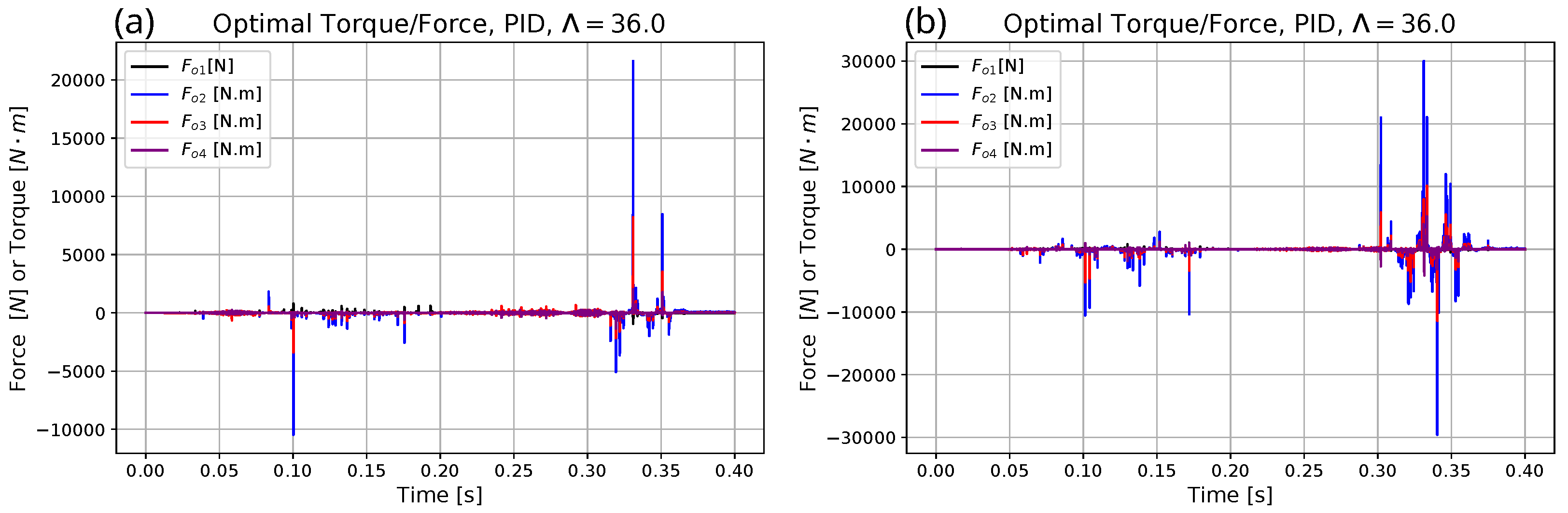
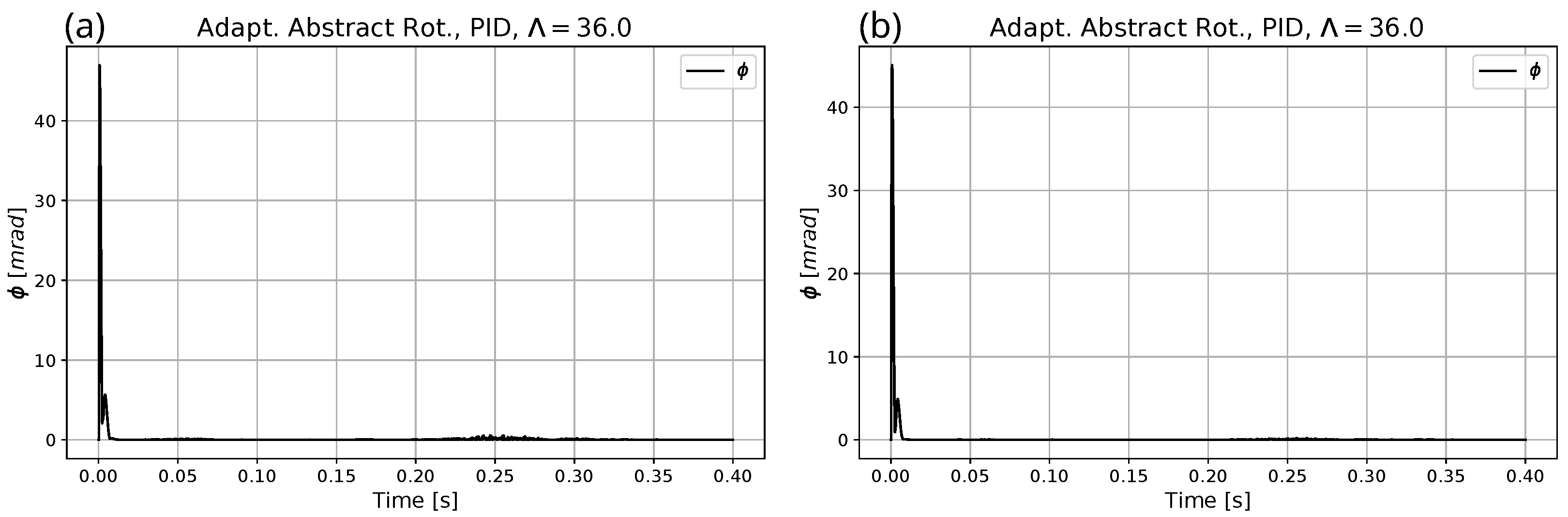
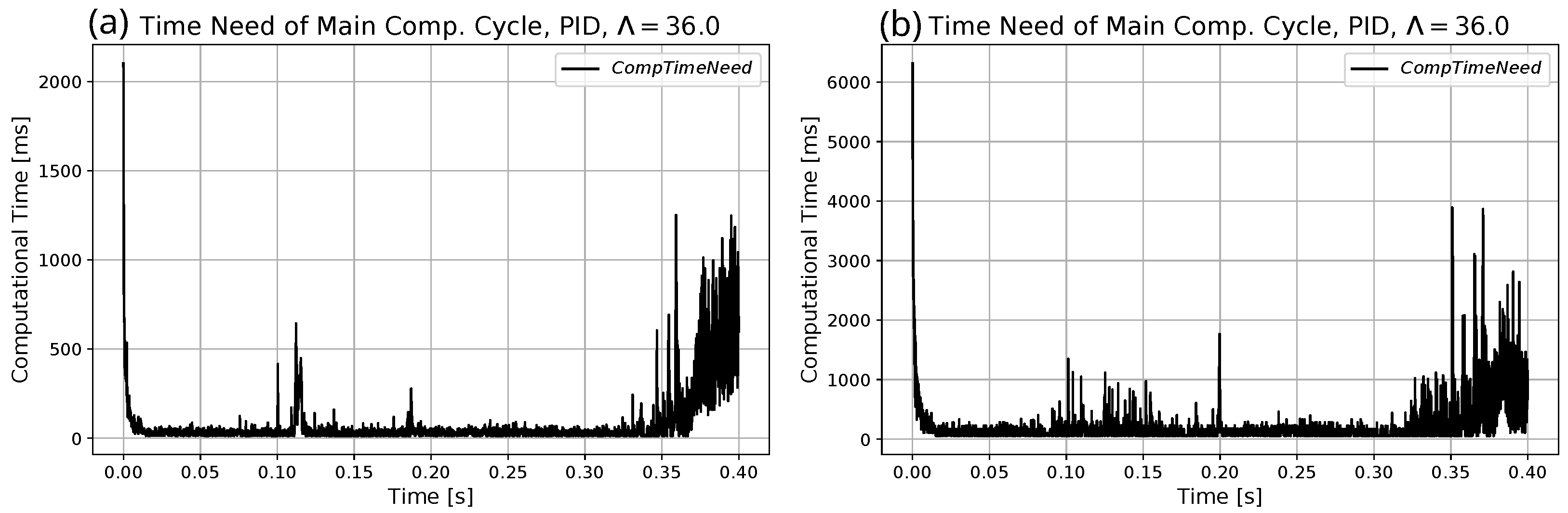
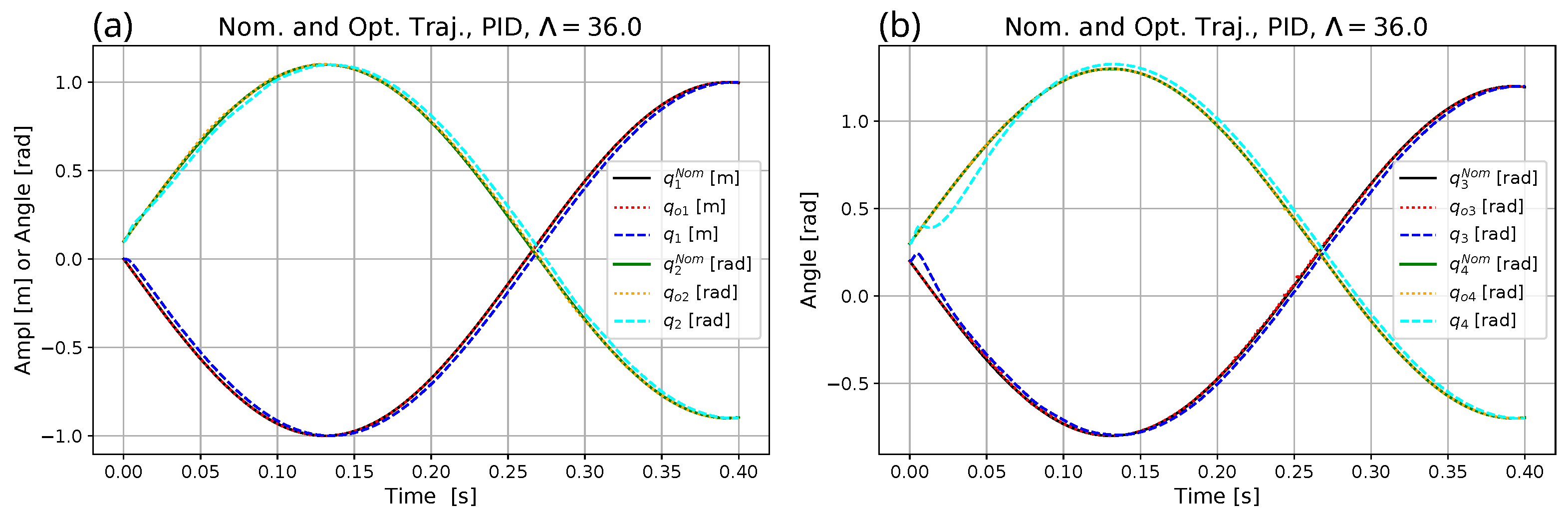


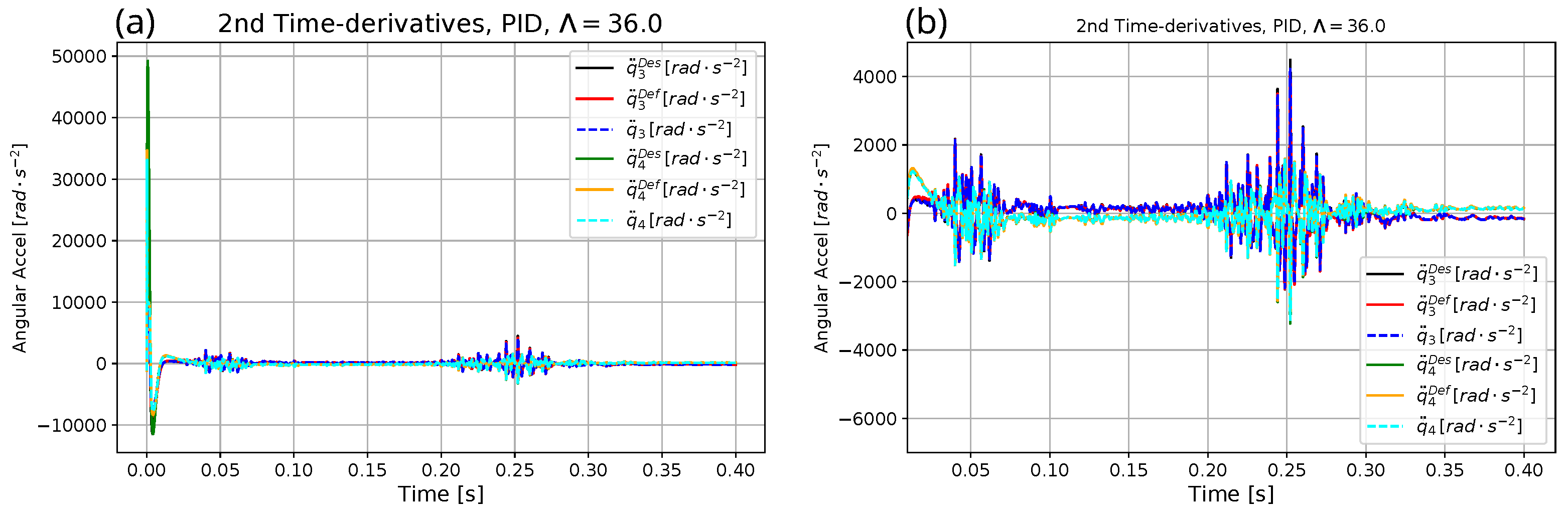
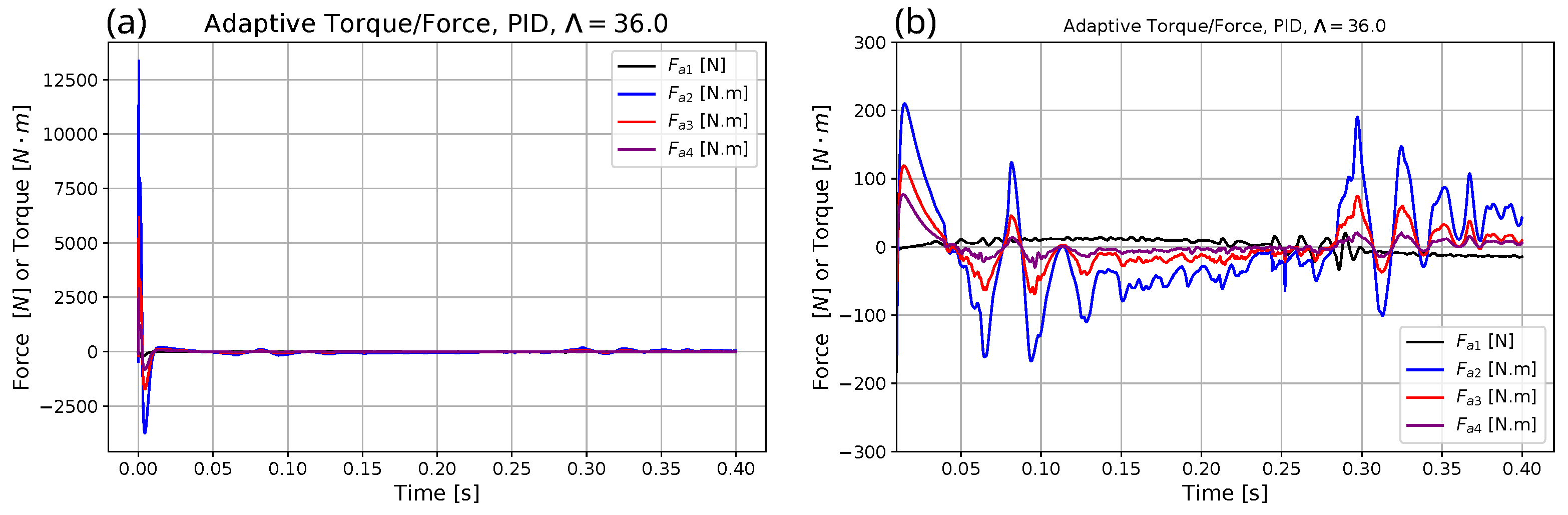
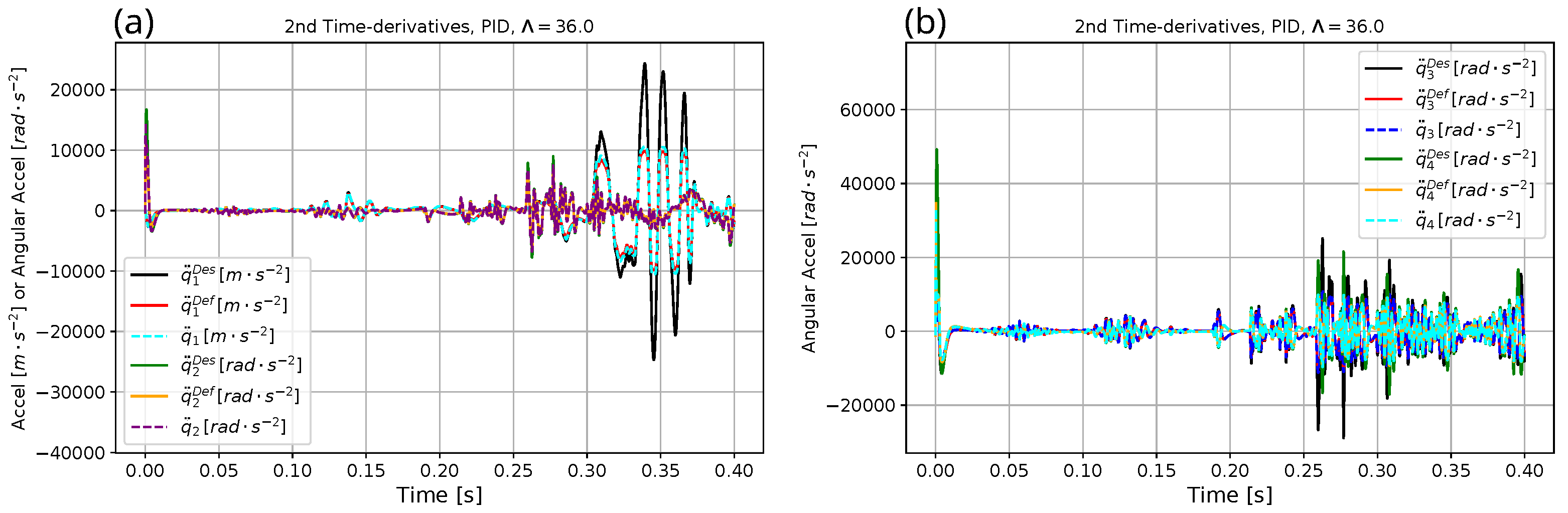
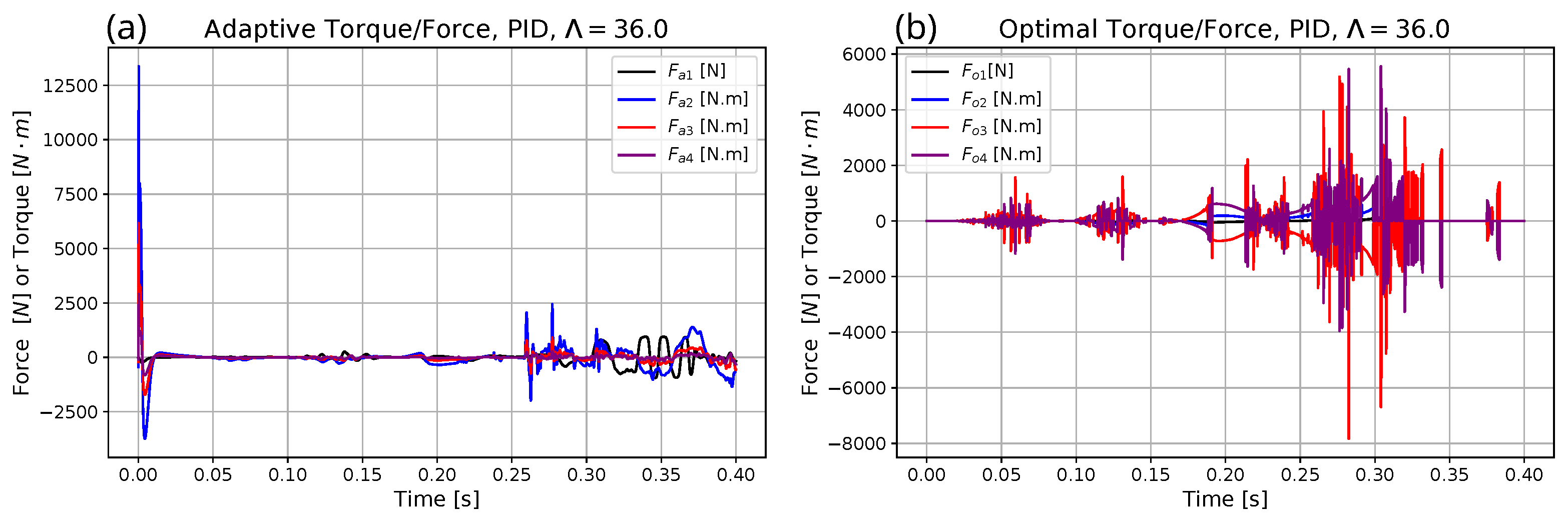
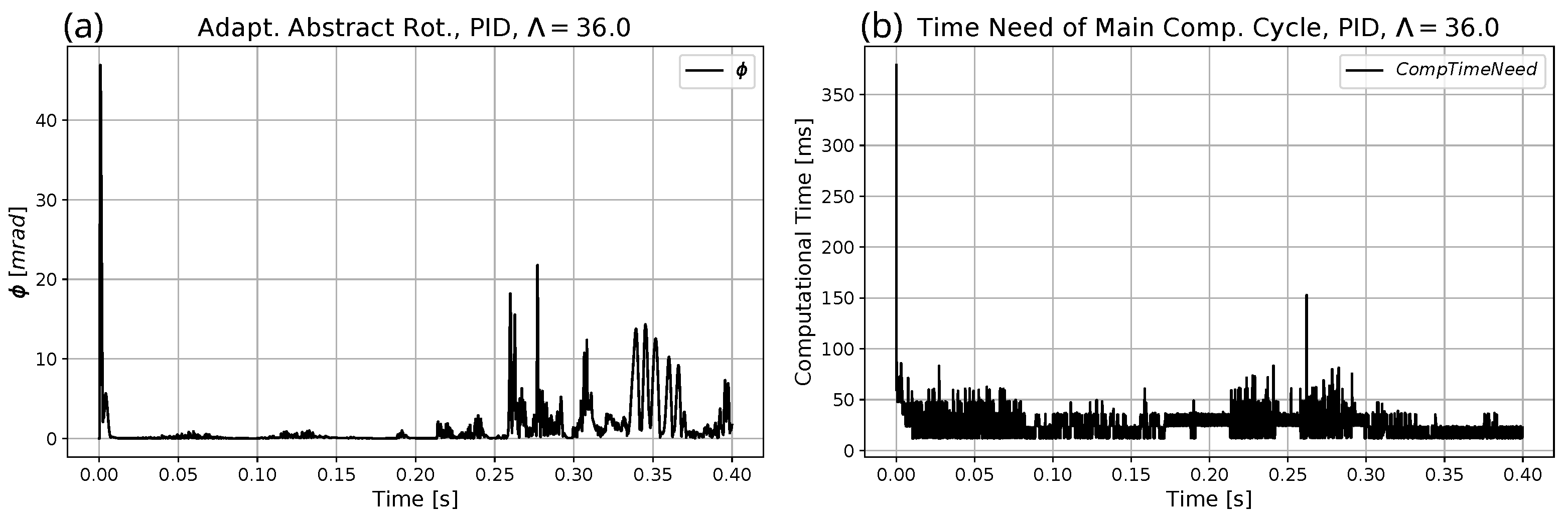

| Parameter | Exact Model for Simulation | Heavy Model for Optimization | Approximate Model for Adaptive Control |
|---|---|---|---|
| component’s mass | 10.0 | 15.0 | 12.0 |
| component’s mass | 20.0 | 25.0 | 21.0 |
| component’s mass | 10.0 | 13.0 | 12.0 |
| load’s mass | 50.0 | 55.0 | 52.0 |
| grav. accel. | 9.81 | 10.0 | 9.0 |
| load’s inertia moment | 45.0 | 50.0 | 42.0 |
| arm length | 2.0 | 2.0 | 2.0 |
| arm length | 1.0 | 1.0 | 1.0 |
| Parameter | Meaning | Value |
|---|---|---|
| Discrete time resolution | ||
| Trajectory tracking exponential coeff. | ||
| Trajectory smoothing exponential coeff. | ||
| Cost contribution coeffs. | ||
| Cost contribution coeff. | ||
| Cost parameter 1 | or | |
| Cost parameter 2 | ||
| Force cost parameter 1 | ||
| p | Cost parameter 3 | |
| Force cost parameter 2 | varying or | |
| Force cost parameter 3 | ||
| Augmented arrays’ Frobenius norm | or | |
| H | Discrete horizon length | 12 |
| Moderating factor in adaptive control | or | |
| Moderating factor in kinematic block | or | |
| Stopping limit in minimum seeking | ||
| Adaptive interpolation factor |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Issa, H.; Tar, J.K. Preliminary Design of a Receding Horizon Controller Supported by Adaptive Feedback. Electronics 2022, 11, 1243. https://doi.org/10.3390/electronics11081243
Issa H, Tar JK. Preliminary Design of a Receding Horizon Controller Supported by Adaptive Feedback. Electronics. 2022; 11(8):1243. https://doi.org/10.3390/electronics11081243
Chicago/Turabian StyleIssa, Hazem, and József K. Tar. 2022. "Preliminary Design of a Receding Horizon Controller Supported by Adaptive Feedback" Electronics 11, no. 8: 1243. https://doi.org/10.3390/electronics11081243
APA StyleIssa, H., & Tar, J. K. (2022). Preliminary Design of a Receding Horizon Controller Supported by Adaptive Feedback. Electronics, 11(8), 1243. https://doi.org/10.3390/electronics11081243






