Priority-Aware Conflict Resolution for U-Space
Abstract
:1. Introduction
- A U-space airspace may be designated within manned airspace so that manned aircraft operate alongside unmanned ones;
- Air navigation service providers (ANSPs) are responsible for carrying out dynamic reconfiguration of U-space airspace to ensure that manned and unmanned traffic remain properly delineated;
- The necessary procedures and communication facilities must be in place to provide both manned and unmanned traffic with information on airspace reconfiguration.
2. Background
2.1. Conflict Management and Priorities in U-Space
- Strategic conflict management: consists of managing conflicts before UAS take-off. It is performed taking into account the specified flight plan. The routes to be followed by the UAS will be analyzed for potential conflicts and modifications will be proposed to resolve them;
- Tactical conflict management: consists of managing conflicts once the UAS are in flight. This is done by monitoring the airspace situation to avoid that aircraft fail to respect a minimum separation between them. This management can be carried out with the help of hardware and instrumentation, taking as the main input source the data reported by the UAS to the service provider. Through tracking and monitoring, the systems will be able to detect conflict situations and propose trajectory changes to the UAS through an emergency management service;
- Collision avoidance: if none of the previous levels have been able to avoid the conflict or if an unforeseen event has occurred that prevents the navigation plan from being followed, the UAS may be equipped with different systems to detect and avoid a mid-air collision (MAC) at the last moment.
2.2. Tactical Conflict Management and Priority-Aware Previous Proposals
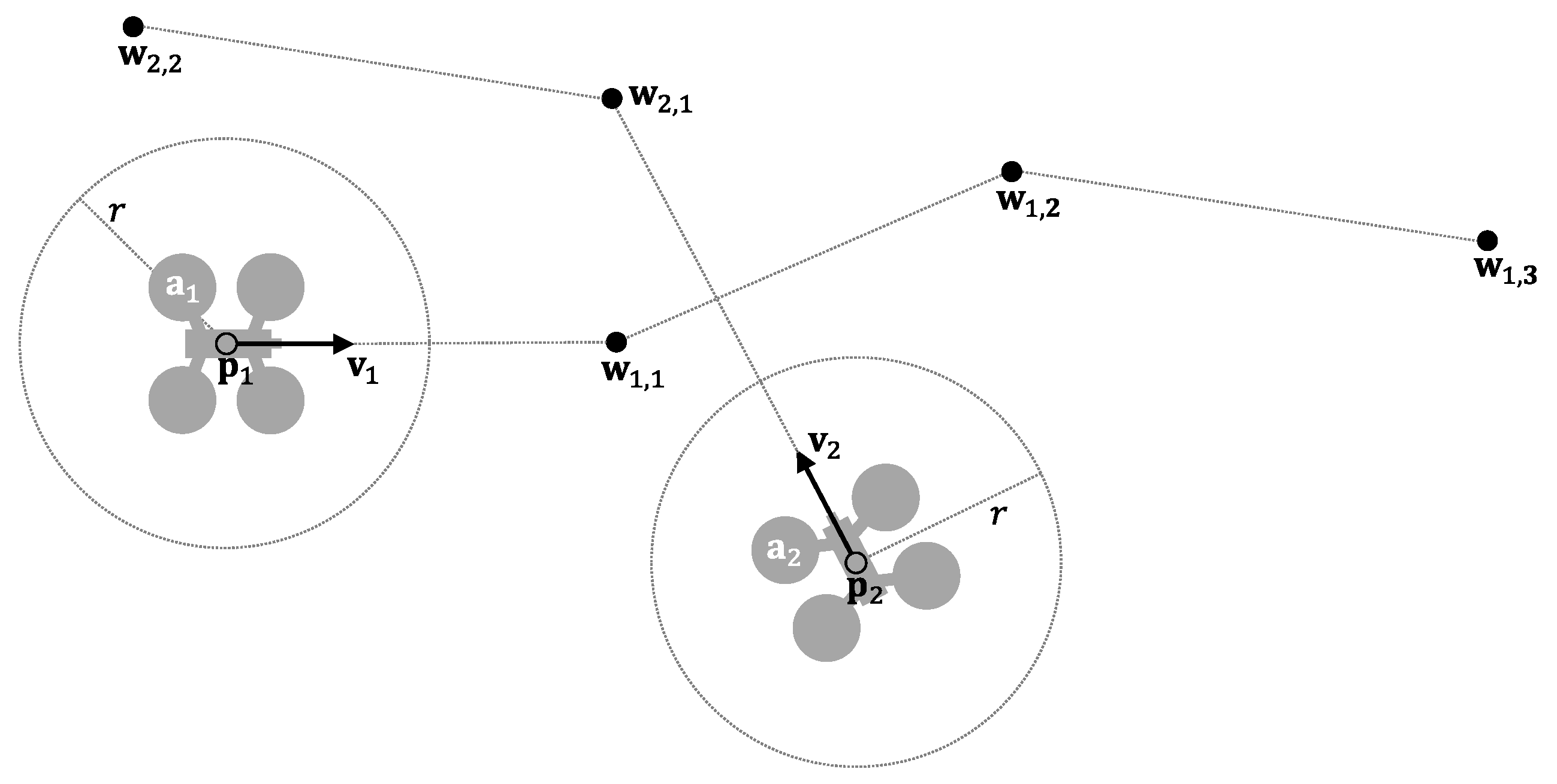
3. Managing Priorities in PCAN
3.1. PCAN General Behavior
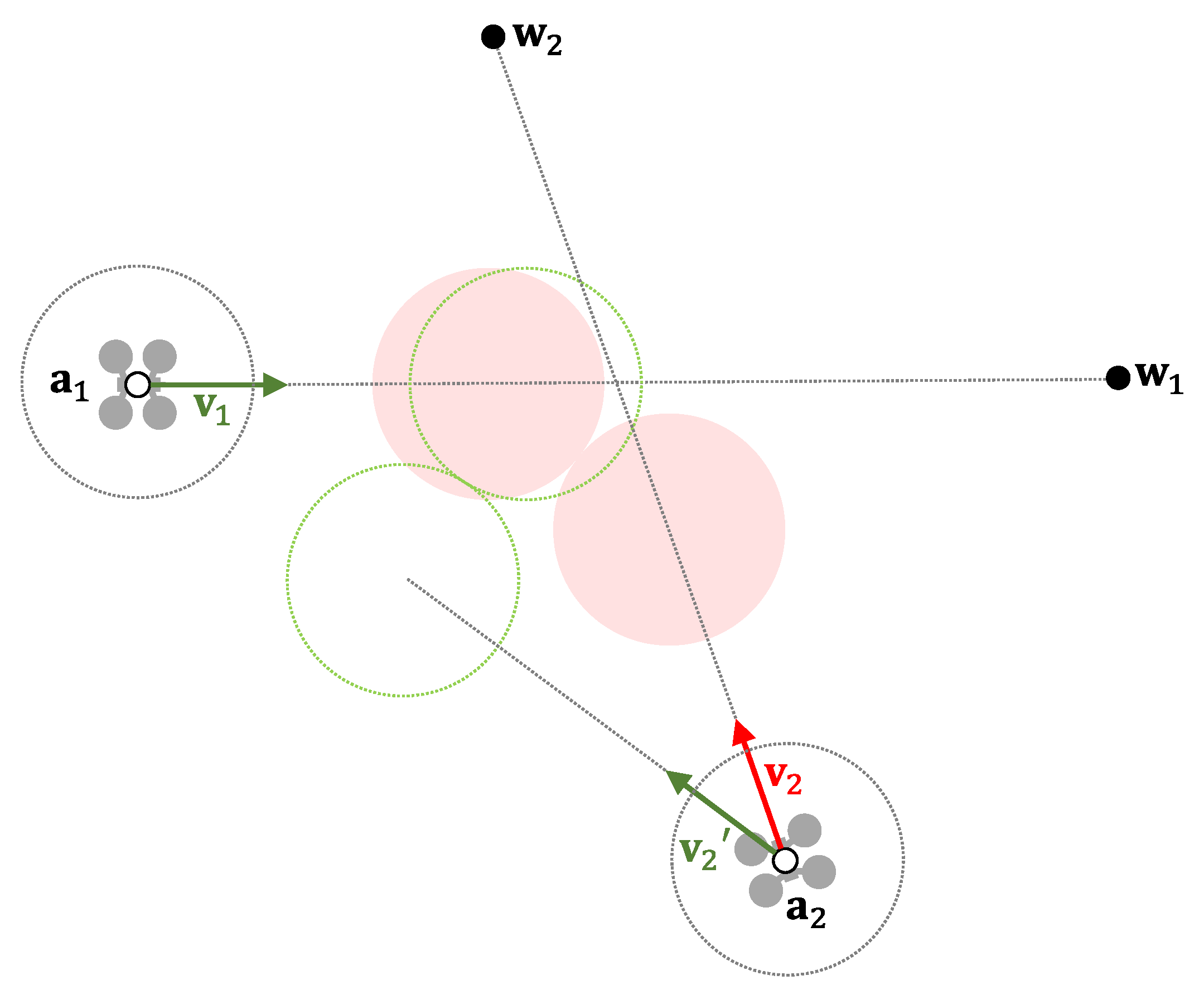
3.2. Priority Support in PCAN
3.3. Real-Time Considerations
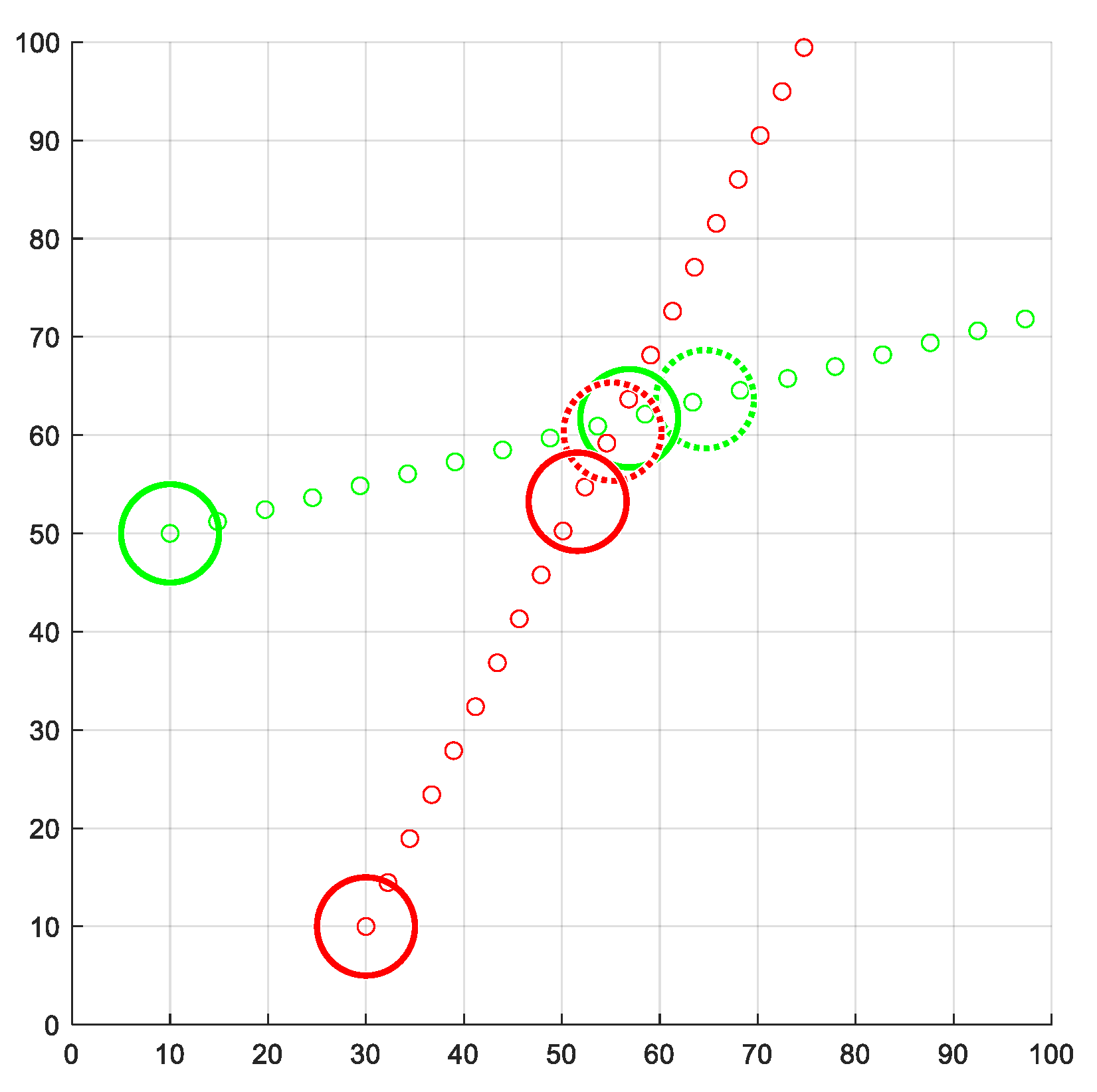
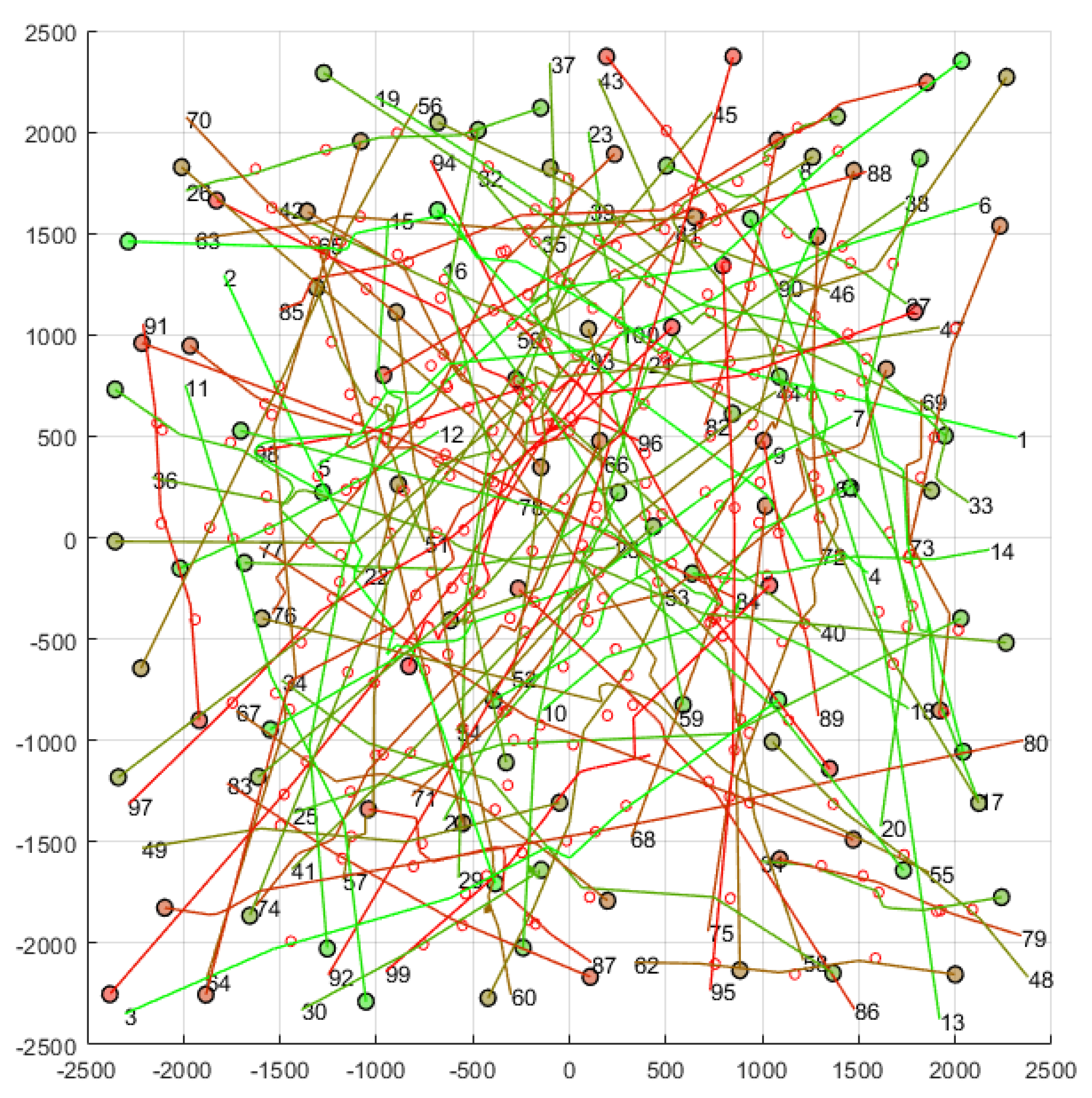
4. Performance Evaluation
4.1. PCAN Versus PCAN with Priorities
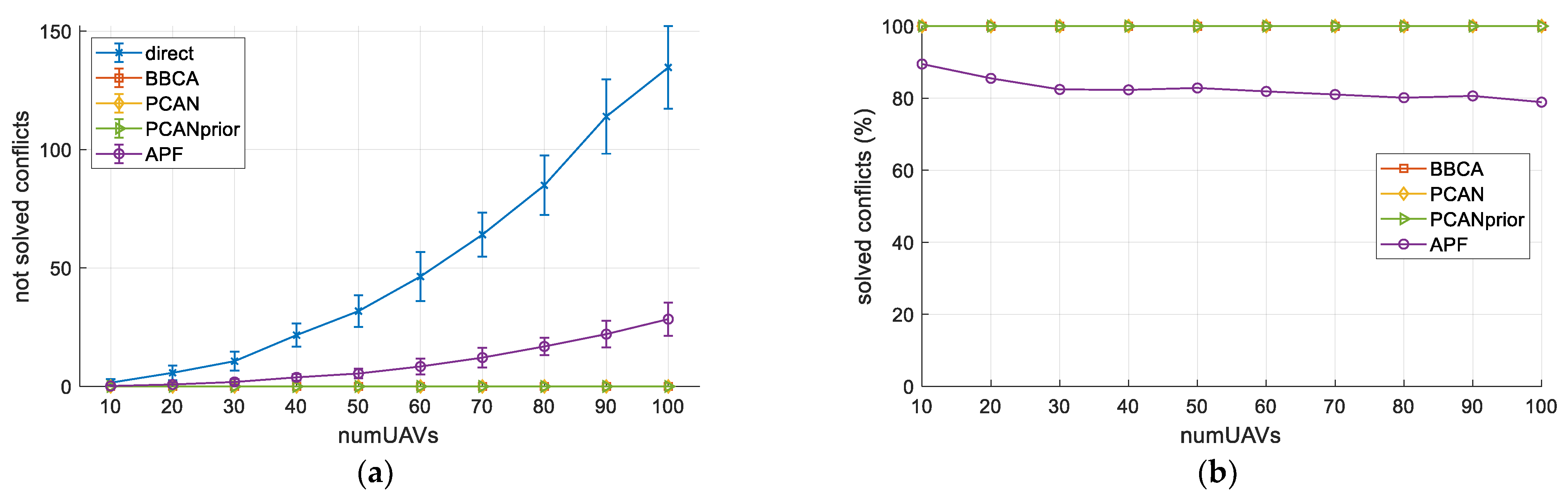
4.2. PCAN versus Other Techniques
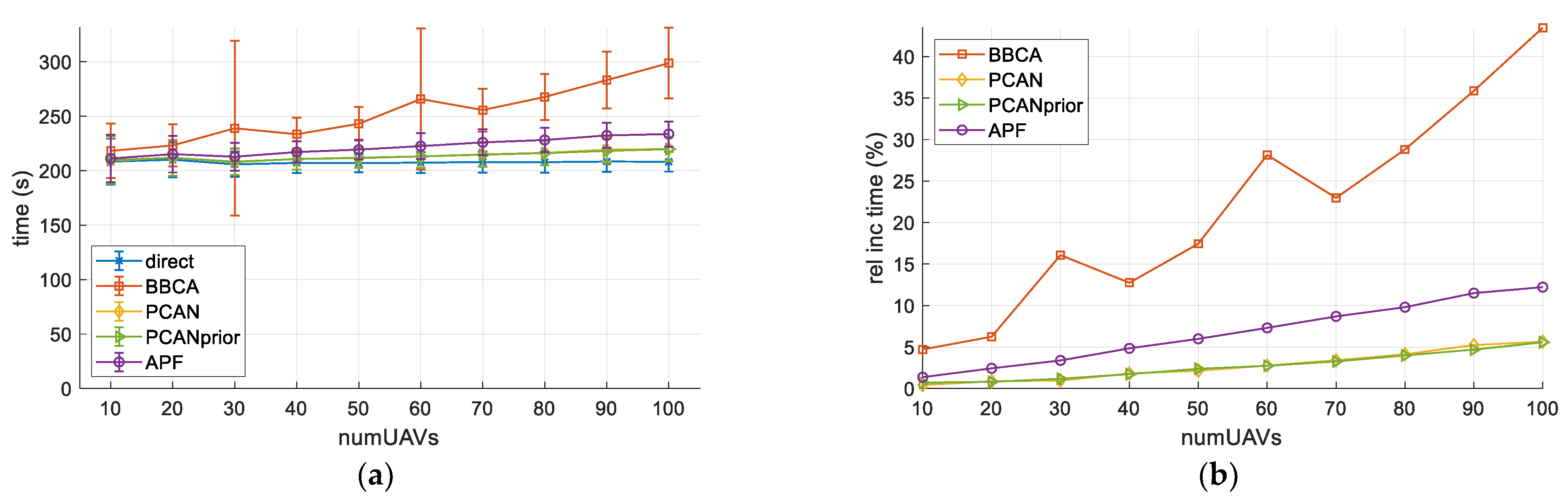
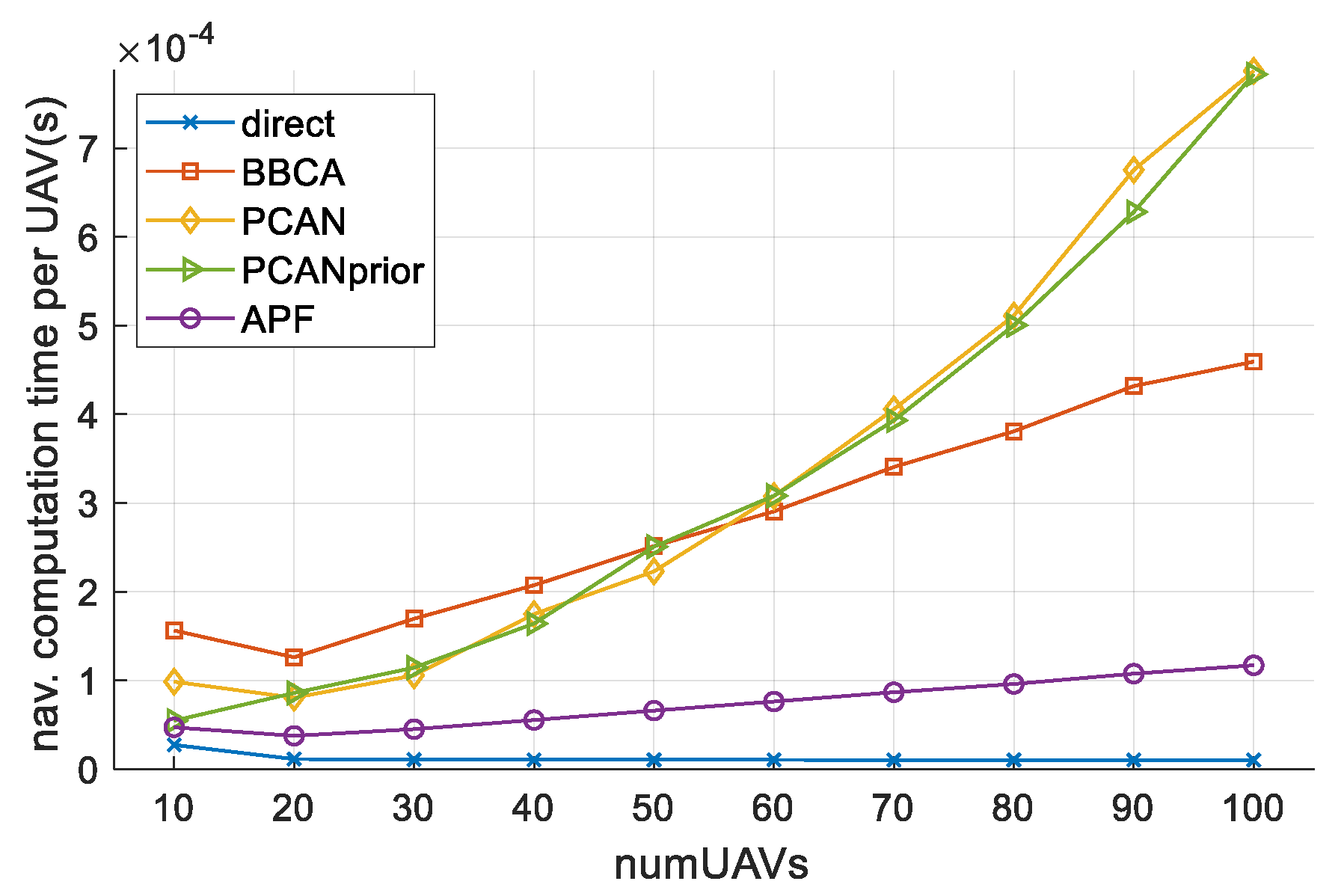
4.3. Computation Time
5. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Bauranov, A.; Rakas, J. Designing airspace for urban air mobility: A review of concepts and approaches. Prog. Aerosp. Sci. 2021, 125, 100726. [Google Scholar] [CrossRef]
- FAA NextGen Organization UTM Concept of Operations Version 2.0 (UTM ConOps Version 2.0). Available online: https://www.faa.gov/uas/research_development/traffic_management/ (accessed on 21 February 2022).
- CORUS Project U-Space Concept of Operations (U-Space ConOps). Available online: https://www.eurocontrol.int/project/concept-operations-european-utm-systems (accessed on 21 February 2022).
- Barrado, C.; Boyero, M.; Brucculeri, L.; Ferrara, G.; Hately, A.; Hullah, P.; Martin-Marrero, D.; Pastor, E.; Rushton, A.P.; Volkert, A. U-space concept of operations: A key enabler for opening airspace to emerging low-altitude operations. Aerospace 2020, 7, 24. [Google Scholar] [CrossRef] [Green Version]
- SESAR Joint Undertaking SESAR Joint Undertaking|PJ34-W3 AURA-ATM U-SPACE INTERFACE. Available online: https://www.sesarju.eu/projects/aura (accessed on 21 February 2022).
- European Commission Commission Implementing Regulation (EU) 2021/665 of 22 April 2021. Available online: https://eur-lex.europa.eu/eli/reg_impl/2021/665/oj (accessed on 21 February 2022).
- European Commission Commission Implementing Regulation (EU) 2017/373 of 1 March 2017. Available online: https://eur-lex.europa.eu/eli/reg_impl/2017/373/oj (accessed on 21 February 2022).
- International Civil Aviation Organization. Procedures for Air Navigation Services (PANS)—Air Traffic Management (Doc 4444); ICAO Store: Montreal, QC, Canada, 2016. [Google Scholar]
- Tang, J. Conflict Detection and Resolution for Civil Aviation: A literature survey. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 20–35. [Google Scholar] [CrossRef]
- Yang, X.; Wei, P. Autonomous Free Flight Operations in Urban Air Mobility With Computational Guidance and Collision Avoidance. IEEE Trans. Intell. Transp. Syst. 2021, 7, 24. [Google Scholar] [CrossRef]
- Jover, J.; Bermúdez, A.; Casado, R. A tactical conflict resolution proposal for U-Space Zu airspace volumes. Sensors 2021, 21, 5649. [Google Scholar] [CrossRef] [PubMed]
- van den Berg, J.; Guy, S.J.; Lin, M.; Manocha, D. Reciprocal n-Body Collision Avoidance. In Springer Tracts in Advanced Robotics; Pradalier, C., Siegwart, R., Hirzinger, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 70, pp. 3–19. ISBN 9783642194566. [Google Scholar]
- Sánchez, P.; Casado, R.; Bermúdez, A. Real-time collision-free navigation of multiple UAVs based on bounding boxes. Electronics 2020, 9, 1632. [Google Scholar] [CrossRef]
- Sun, J.; Tang, J.; Lao, S. Collision Avoidance for Cooperative UAVs with Optimized Artificial Potential Field Algorithm. IEEE Access 2017, 5, 18382–18390. [Google Scholar] [CrossRef]
- Alejo, D.; Cobano, J.A.; Heredia, G.; Ollero, A. Particle Swarm Optimization for collision-free 4D trajectory planning in Unmanned Aerial Vehicles. In Proceedings of the 2013 International Conference on Unmanned Aircraft Systems (ICUAS), IEEE, Atlanta, GA, USA, 28–31 May 2013; pp. 298–307. [Google Scholar]
- Yasin, J.N.; Mohamed, S.A.S.; Haghbayan, M.H.; Heikkonen, J.; Tenhunen, H.; PLoSila, J. Unmanned Aerial Vehicles (UAVs): Collision Avoidance Systems and Approaches. IEEE Access 2020, 8, 105139–105155. [Google Scholar] [CrossRef]
- Park, J.; Cho, N. Collision avoidance of hexacopter UAV based on lidar data in dynamic environment. Remote Sens. 2020, 12, 975. [Google Scholar] [CrossRef] [Green Version]
- Snape, J.; Guy, S.J.; Lin, M.C.; Manocha, D.; Van Den Berg, J. Reciprocal collision avoidance and multi-agent navigation for video games. In Proceedings of the AAAI Workshop-Technical Report, Chapel Hill, NC, USA, 15 July 2012; Volume WS-12-10, pp. 49–52. [Google Scholar]
- Cap, M.; Novak, P.; Kleiner, A.; Selecky, M. Prioritized Planning Algorithms for Trajectory Coordination of Multiple Mobile Robots. IEEE Trans. Autom. Sci. Eng. 2015, 12, 835–849. [Google Scholar] [CrossRef]
- Yang, J.; Yin, D.; Zhang, Y.; Jian, L. Multi-agent coordination in high velocity UAVs conflict detection and resolution. In Proceedings of the Chinese Control Conference, CCC, Hangzhou, China, 28–30 July 2015; Volume 2015, pp. 2621–2626. [Google Scholar]
- Fabra, F.; Zamora, W.; Sangüesa, J.; Calafate, C.T.; Cano, J.C.; Manzoni, P. A distributed approach for collision avoidance between multirotor UAVs following planned missions. Sensors 2019, 19, 2404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Du, W.; Yang, P.; Wu, T.; Zhang, J.; Wu, D.; Perc, M. A satisficing conflict resolution approach for multiple UAVs. IEEE Internet Things J. 2019, 6, 1866–1878. [Google Scholar] [CrossRef]
- Chen, H.X.; Nan, Y.; Yang, Y. Real-time conflict resolution algorithm for multi-UAV based on model predict control. Algorithms 2019, 12, 47. [Google Scholar] [CrossRef] [Green Version]
- Primatesta, S.; Scanavino, M.; Lorenzini, A.; Polia, F.; Stabile, E.; Guglieri, G.; Rizzo, A. A cloud-based vehicle collision avoidance strategy for unmanned aircraft system traffic management (UTM) in urban areas. In Proceedings of the 2020 IEEE International Workshop on Metrology for AeroSpace, MetroAeroSpace 2020-Proceedings, Pisa, Italy, 22–24 June 2020; pp. 309–313. [Google Scholar]
- Alharbi, A.; Poujade, A.; Malandrakis, K.; Petrunin, I.; Panagiotakopoulos, D.; Tsourdos, A. Rule-based conflict management for unmanned traffic management scenarios. In Proceedings of the AIAA/IEEE Digital Avionics Systems Conference-Proceedings, San Antonio, TX, USA, 11–15 October 2020; Volume 2020. [Google Scholar]
- López, B.; Muñoz, J.; Quevedo, F.; Monje, C.A.; Garrido, S.; Moreno, L.E. Path planning and collision risk management strategy for multi-UAV systems in 3D environments. Sensors 2021, 21, 4414. [Google Scholar] [CrossRef] [PubMed]
- Perez-Leon, H.; Acevedo, J.J.; Maza, I.; Ollero, A. Integration of a 4D-trajectory Follower to Improve Multi-UAV Conflict Management Within the U-Space Context. J. Intell. Robot. Syst. Theory Appl. 2021, 102, 62. [Google Scholar] [CrossRef]
- Capitán, C.; Pérez-León, H.; Capitán, J.; Castaño, Á.; Ollero, A. Unmanned aerial traffic management system architecture for u-space in-flight services. Appl. Sci. 2021, 11, 3995. [Google Scholar] [CrossRef]




| Priority | Type of Operation |
|---|---|
| Class 1 (max) | Emergency—Air ambulance, Search and rescue, catastrophe |
| Class 2 | Hospital (Hospital transport) |
| Class 3 | Authorities (Police, other), Military |
| Class 4 | Urgent Transport, Passenger transport |
| Class 5 | Agriculture, Inspection, Infrastructure, Science, Weather |
| Class 6 | Transport |
| Class 7 | Video, Filming, TV, Empty flight (ferry flight) |
| Class 8 (min) | Leisure, Sports |
| 01 | |
| 02 | do |
| 03 | |
| 04 | |
| 05 | |
| 06 | end do |
| 07 | |
| 08 | |
| 09 | do |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | break |
| 17 | end if |
| 18 | end if |
| 19 | end for |
| 20 | |
| 21 | end while |
| Priority Class | Probability |
|---|---|
| Class 1 | 2% |
| Class 2 | 5% |
| Class 3 | 3% |
| Class 4 | 10% |
| Class 5 | 15% |
| Class 6 | 50% |
| Class 7 | 10% |
| Class 8 | 5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jover, J.; Bermúdez, A.; Casado, R. Priority-Aware Conflict Resolution for U-Space. Electronics 2022, 11, 1225. https://doi.org/10.3390/electronics11081225
Jover J, Bermúdez A, Casado R. Priority-Aware Conflict Resolution for U-Space. Electronics. 2022; 11(8):1225. https://doi.org/10.3390/electronics11081225
Chicago/Turabian StyleJover, Jesús, Aurelio Bermúdez, and Rafael Casado. 2022. "Priority-Aware Conflict Resolution for U-Space" Electronics 11, no. 8: 1225. https://doi.org/10.3390/electronics11081225
APA StyleJover, J., Bermúdez, A., & Casado, R. (2022). Priority-Aware Conflict Resolution for U-Space. Electronics, 11(8), 1225. https://doi.org/10.3390/electronics11081225








