A Study on Performance Metrics for Anomaly Detection Based on Industrial Control System Operation Data
Abstract
:1. Introduction
- We create training models and perform anomaly detection using operation datasets derived from real industrial control systems;
- We propose a range-based metric suitable for evaluating anomaly detection against time series data;
- We redefine the algorithm for the ambiguous section of TaPR in consideration of the characteristics of the attack.
2. Related Works
2.1. Industrial Control System Structure and Security Requirements
2.2. Datasets
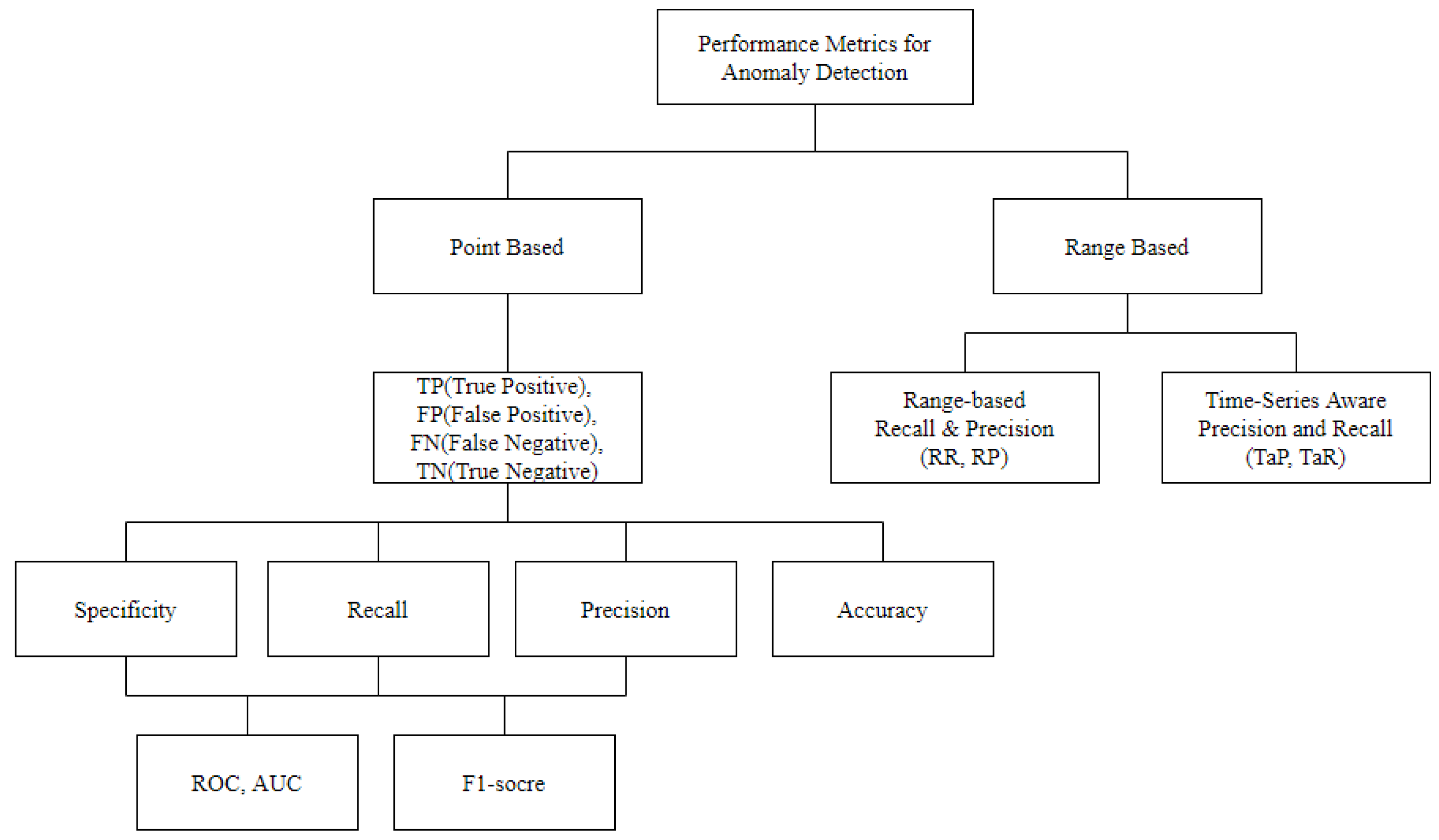
2.3. Performance Metrics for Anomaly Detection
2.3.1. Standard Metric
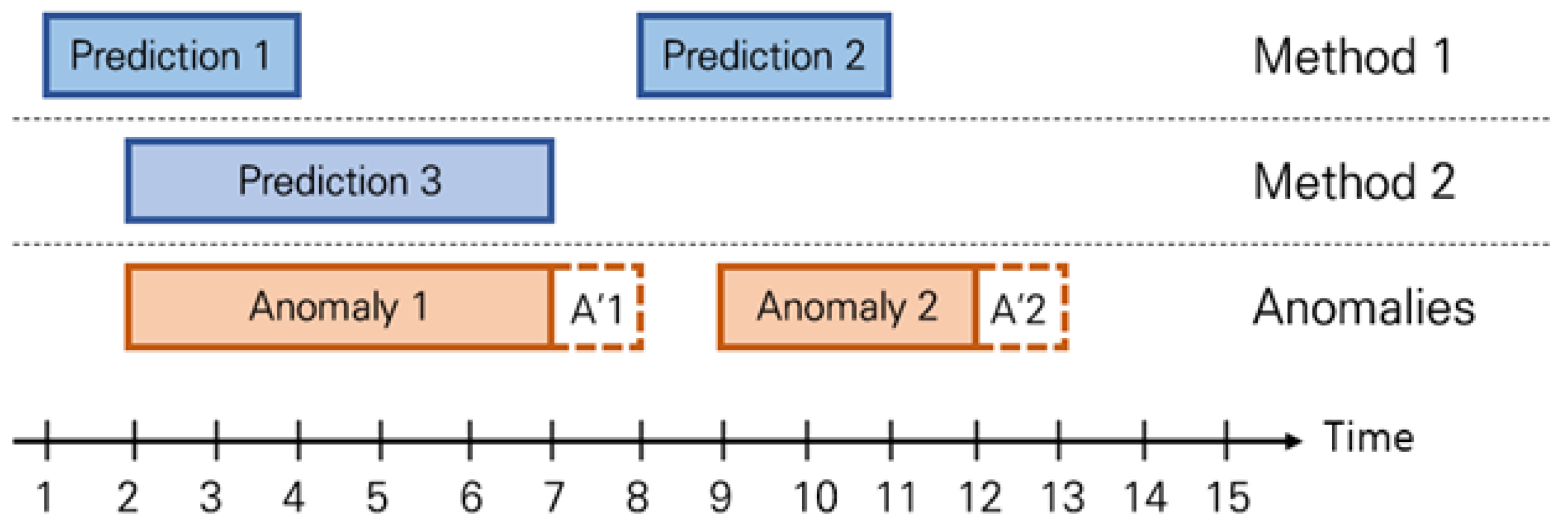
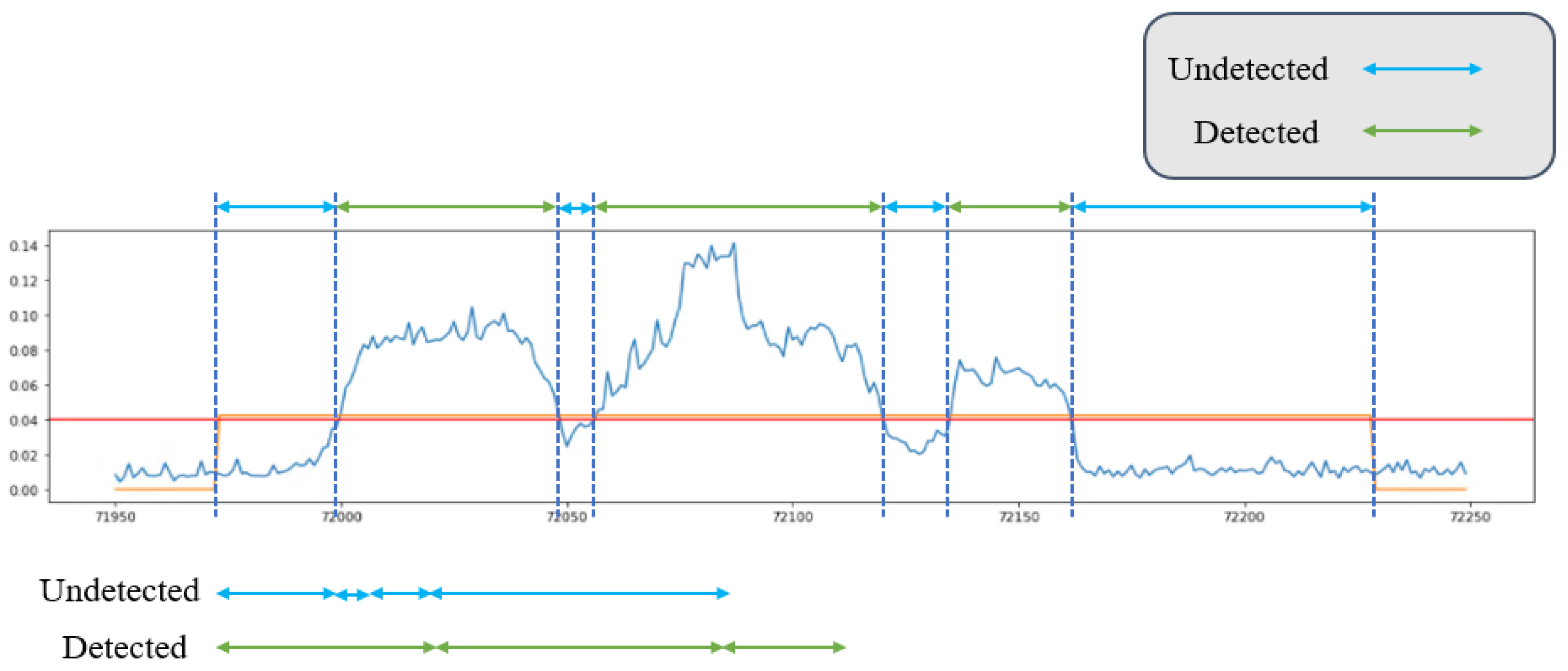
2.3.2. Range-Based Recall and Precision
2.3.3. TaPR
2.4. Requirements for Performance Metrics
- The highest score is not given to the method of detecting long-length anomalies.
- Scores are given to cases that detect various anomalies.
- Scores are given to cases that detect proactive signs.
- When an external influence such as an attack is received, the threshold value that separates normal and abnormal is exceeded, and the external influence ends; the value showing abnormality has a score for the case in which it returns to normal.
- A detection score is given according to the characteristics of the attack.
3. Proposed Performance Metrics
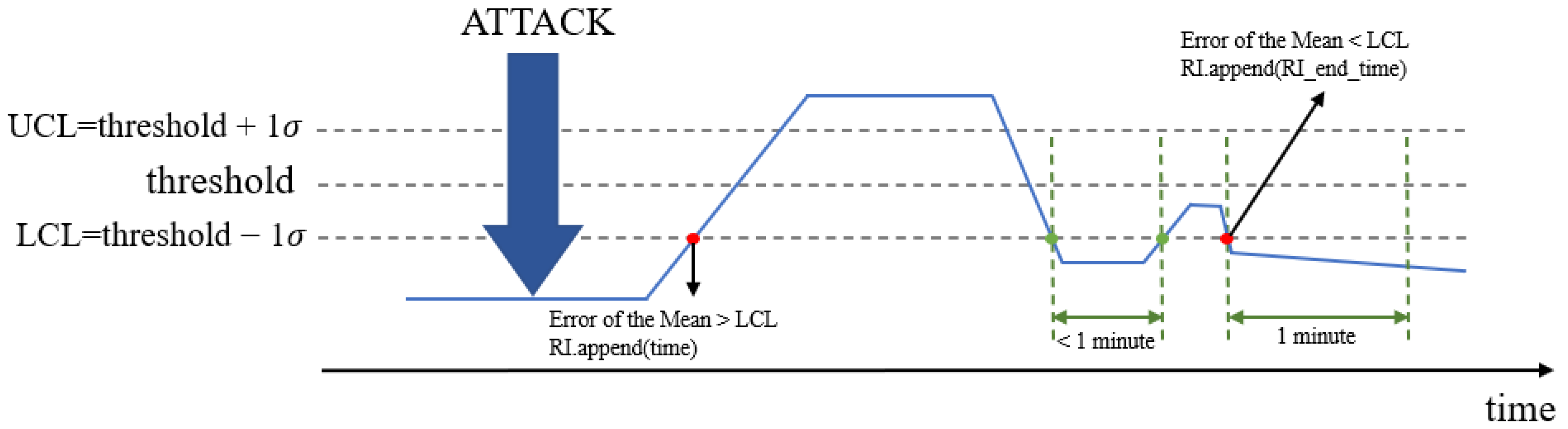
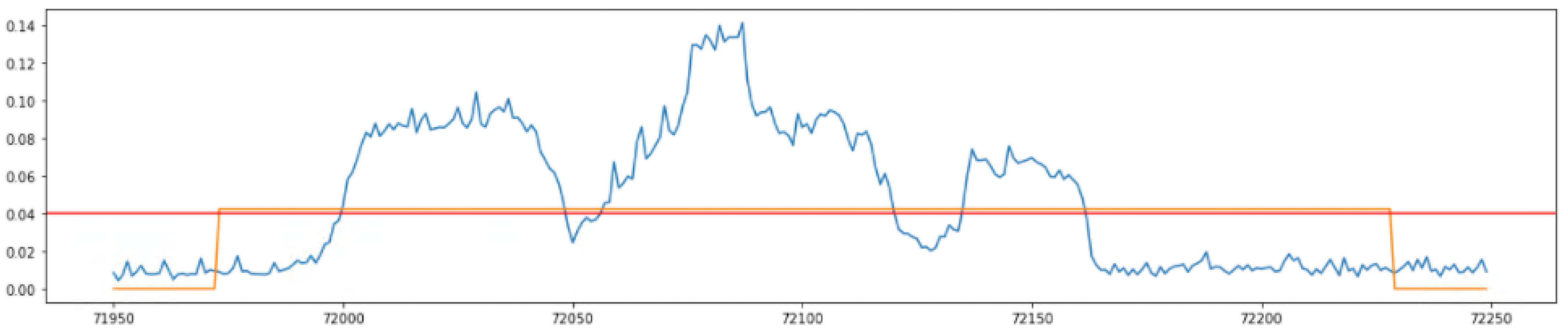
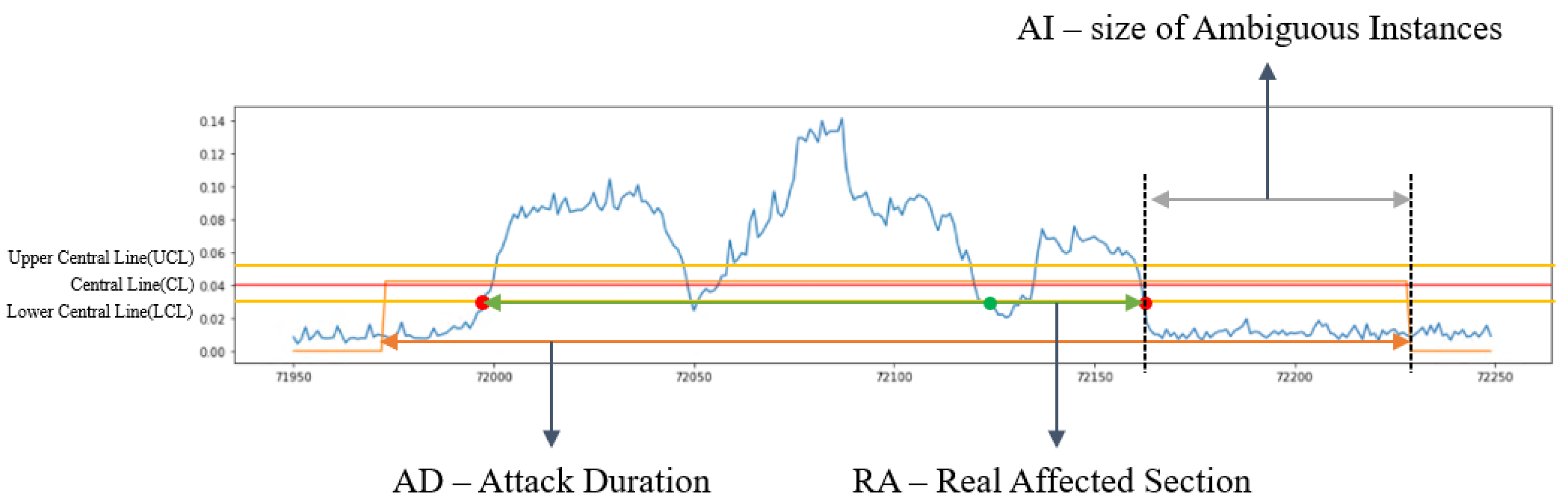
3.1. Statistical Process Control (SPC)
3.2. Defining the Real Affected Section
| Algorithm 1. Definition of the real affected section |
| INPUT: CL, UCL, LCL OUTPUT: size of ambiguous instance 1. attack duration.append(anomalies[i].get_time()[0], anomalies[i].get_time()[1]) 2. FOR attack duration do 3. IF error of the mean > LCL then 4. real affected section.append(current time) 5. ELSE IF Error of the Mean < LCL then 6. end time of real affected section = current time 7. WHILE 1 minute do 8. IF error of the mean > LCL then 9. BREAK 10. ELSE 11. real affected section.append(end time of real affected section) 12. ENDIF 13. ENDWHILE 14. ENDIF 15. ENDFOR 16. IF attack duration[1] > real affected section[1] 17. size of ambiguous instance = attack duration[1] – real affected section[1] 18. ELSE 19. size of ambiguous instance = real affected section[1] - attack duration[1] |
4. Experimentation
4.1. Model Generation Process
4.1.1. Training Data
4.1.2. Choosing a Deep Learning Model
4.1.3. Training Data Preprocessing
- Refining data by removing outliers and missing values;
- Scaling data using normalization;
- Eliminating unnecessary data points with feature graphs.
4.1.4. Model Generation
- Sliding window;
- Number of hidden layers;
- Hidden layer size.
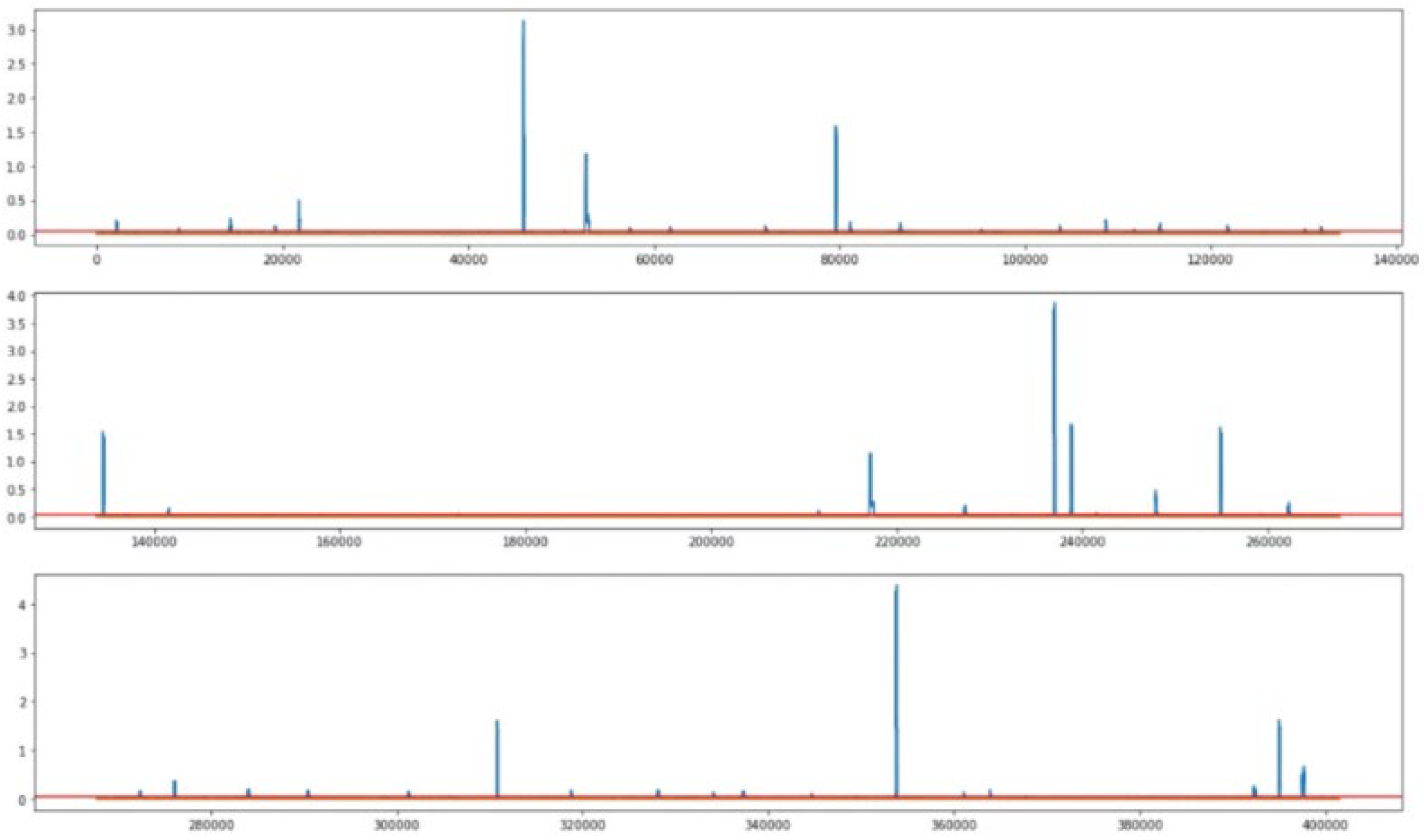
4.2. Anomaly Detection
4.3. Analysis of Performance Metrics
Comparison of Performance Metrics by Attack
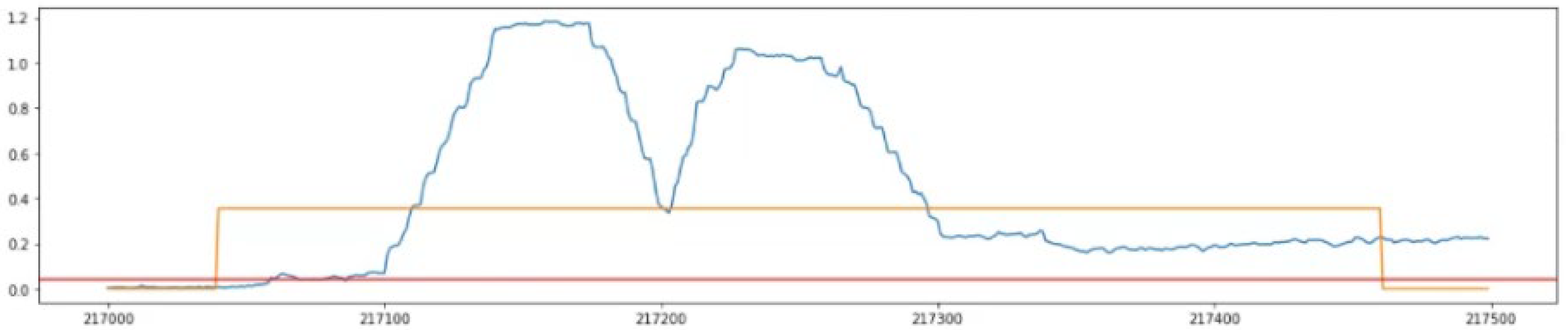
4.4. Application of the Proposed Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Kevin, E.H.; Ronald, E.F. History of Industrial Control System Cyber Incidents, Internet Publication. Available online: https://www.osti.gov/servlets/purl/1505628 (accessed on 8 April 2022).
- Joseph, S. Evolution of ICS Attacks and the Prospects for Future Disruptive Events, Internet Publication. Available online: https://www.dragos.com/wp-content/uploads/Evolution-of-ICS-Attacks-and-the-Prospects-for-Future-Disruptive-Events-Joseph-Slowik-1.pdf (accessed on 8 April 2022).
- Stampar, M.; Fertalj, K. Artificial intelligence in network intrusion detection. In Proceedings of the 38th International Convention on Information and Communication Technology, Electronics and Microelectronics, MIPRO, Opatija, Croatia, 25–29 May 2015. [Google Scholar]
- Hongyu, L.; Bo, L. Machine Learning and Deep Learning Methods for Intrusion Detection Systems: A Survey. Appl. Sci. 2019, 9, 4396. [Google Scholar]
- Hwang, W.S.; Yun, J.H.; Kim, J.; Kim, H.C. Time-Series Aware Precision and Recall for Anomaly Detection: Considering Variety of Detection Result and Addressing Ambiguous Labeling. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, CIKM ’19, Beijing, China, 3–7 November 2019; pp. 2241–2244. [Google Scholar]
- Williams, T.J. The Purdue Enterprise Reference Architecture. IFAC Proc. Vol. 1993, 26 Pt 4, 559–564. [Google Scholar] [CrossRef]
- CISCO. Network and Security in Industrial Automation Environments—Design Guide; CISCO: San Jose, CA, USA, 2020; pp. 8–13. [Google Scholar]
- SANS. The Purdue Model and Best Practices for Secure ICS Architectures. Available online: https://www.sans.org/blog/introduction-to-ics-security-part-2/ (accessed on 4 April 2022).
- Kim, G.H. Industrial Control System Security, 1981th ed.; IITP: Daejeon, Korea, 2021; pp. 5–7. [Google Scholar]
- Choi, S.O.; Kim, H.C. Energy sector infrastructure security monitoring plan based on MITRE ATT&CK framework. Rev. KIISC 2020, 30, 13–23. [Google Scholar]
- Han, G.H. Trends in Standards and Testing and Certification Technology-Smart Manufacturing Security Standardization Status. TTA J. 2018, 178, 80–90. [Google Scholar]
- Korea Industrial Standards. Security for Industrial Automation and Control Systems—Part 4-2: Technical Security Requirements for IACS Components. Available online: https://standard.go.kr/KSCI/standardIntro/getStandardSearchView.do?menuId=919&topMenuId=502&upperMenuId=503&ksNo=KSXIEC62443-4-2&tmprKsNo=KS_C_NEW_2019_3780&reformNo=00 (accessed on 9 February 2022).
- Shengyi, P.; Thomas, M.; Uttam, A. Developing a Hybrid Intrusion Detection System Using Data Mining for Power Systems. IEEE Trans. Smart Grid 2015, 6, 3104–3113. [Google Scholar]
- iTrust. BATtle of Attack Detection Algorithms (BATADAL). Available online: https://itrust.sutd.edu.sg/itrust-labs_datasets/dataset_info/ (accessed on 9 February 2022).
- iTrust. Water Distribution (WADI). Available online: https://itrust.sutd.edu.sg/itrust-labs-home/itrust-labs_wadi/ (accessed on 8 April 2022).
- iTrust. Secure Water Treatment (SWaT). Available online: https://itrust.sutd.edu.sg/itrust-labs-home/itrust-labs_swat/ (accessed on 8 April 2022).
- Shin, H.K.; Lee, W.; Yun, J.H.; Min, B.G. Two ICS Security Datasets and Anomaly Detection Contest on the HIL-based Augmented ICS Testbed. In Proceedings of the Cyber Security Experimentation and Test Workshop, CSET ’21, Virtual, CA, USA, 9 August 2021; ACM: New York, NY, USA, 2021; pp. 36–40. [Google Scholar]
- Shin, H.K.; Lee, W.; Yun, J.H.; Kim, H.C. HAI 1.0: HIL-Based Augmented ICS Security Dataset. In Proceedings of the 13th USENIX Workshop on Cyber Security Experimentation and Test (CSET 20), Boston, MA, USA, 10 August 2020. [Google Scholar]
- Lee, T.J.; Justin, G.; Nesime, T.; Eric, M.; Stan, Z. Precision and Recall for Range-Based Anomaly Detection. In Proceedings of the SysML Conference, Stanford, CA, USA, 15–16 February 2018. [Google Scholar]
- Dmitry, S.; Pavel, F.; Andrey, L. Anomaly Detection for Water Treatment System based on Neural Network with Automatic Architecture Optimization. arXiv 2018, arXiv:1807.07282. [Google Scholar]
- Kim, J.; Yun, J.H.; Kim, H.C. Anomaly Detection for Industrial Control Systems Using Sequence-to-Sequence Neural Networks. arXiv 2019, arXiv:1911.04831. [Google Scholar]
- Giuseppe, B.; Mauro, C.; Federico, T. Evaluation of Machine Learning Algorithms for Anomaly Detection in Industrial Networks. In Proceedings of the 2019 IEEE International Symposium on Measurements Networking (MN), Catania, Italy, 8–10 July 2019; pp. 1–6. [Google Scholar]
- Sohrab, M.; Alireza, A.; Kang, K.; Arman, S. A Machine Learning Approach for Anomaly Detection in Industrial Control Systems Based on Measurement Data. Electronics 2021, 10, 407. [Google Scholar]
- Kim, D.Y.; Hwang, C.W.; Lee, T.J. Stacked-Autoencoder Based Anomaly Detection with Industrial Control System. In Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing; Springer: Cham, Switzerland, 2021; pp. 181–191. [Google Scholar]
- Roland, C. Statistical process control (SPC). Assem. Autom. 1996, 16, 10–14. [Google Scholar]
- Vanli, O.A.; Castillo, E.D. Statistical Process Control in Manufacturing; Encyclopedia of Systems and Control; Springer: London, UK, 2014. [Google Scholar]
- David, E.R.; Geoffrey, E.H.; Ronald, J.W. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar]
- Sepp, H.; Jürgen, S. Long Short-Term Memory. Neural Comput. 1997, 8, 1735–1780. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Koç, C.K. Analysis of sliding window techniques for exponentiation. Comput. Math. Appl. 1995, 30, 17–24. [Google Scholar] [CrossRef] [Green Version]
- Ilya, L.; Frank, H. Decoupled Weight Decay Regularization. In Proceedings of the 7th International Conference on Learning Representations, ICLR, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]








| Name | Proposed | Attack Points | Year | |
|---|---|---|---|---|
| [13] | ICS Cyber Attack Datasets | Tommy Morris | 32 | 2015 |
| [14] | BATADAL | iTrust | 14 | 2017 |
| [15] | WADI | iTrust | 15 | 2019 |
| [16] | SWaT Datasets | iTrust | 41 | 2015 |
| [17,18] | HAI Datasets | NSR | 50 | 2020 |
| Method | Precision | Recall |
|---|---|---|
| 1 | 0.67 | 0.50 |
| 2 | 1.00 | 0.625 |
| Factor | Description | Formula |
|---|---|---|
| A set of instances | ||
| The number of instances | ||
| A set of anomalies | ||
| n | The number of anomalies | - |
| The suspicious instances | ||
| A set of predictions | ||
| m | The number of predictions | - |
| The ambiguous instances | ||
| The number of ambiguous instances | - | |
| A set of ambiguous instances |
| Performance Metrics | Req.1 | Req.2 | Req.3 | Req.4 | Req.5 | Refs. | |
|---|---|---|---|---|---|---|---|
| Point-based | Confusion Matrix | X | X | X | X | X | [20,21,22,23,24] |
| Specificity | X | X | X | X | X | ||
| Recall | X | X | X | X | X | ||
| Precision | X | X | X | X | X | ||
| Accuracy | X | X | X | X | X | ||
| Range-based | Ranged-Based Recall and Precision | O | O | X | O | X | [5,19] |
| Time-Series Aware Precision and Recall | O | O | O | O | X |
| Method | Threshold | Performance Metrics | ||
|---|---|---|---|---|
| F1-Score | TaP | TaR | ||
| RNN | 0.38 | 78.02 | 97.20 | 64.40 |
| LSTM | 0.38 | 81.60 | 97.40 | 67.66 |
| GRU | 0.38 | 83.10 | 97.50 | 71.50 |
| Time | P1_B2004 | … | Attack | … | Attack_P3 |
|---|---|---|---|---|---|
| 2020-07-11 12:00:00 AM | 0.10121 | … | 0 | … | 0 |
| 2020-07-11 12:00:01 AM | 0.10121 | … | 0 | … | 0 |
| … | … | … | … | … | … |
| Input | Output | |
|---|---|---|
| 1 | 74 | 75 |
| 2 | 79 | 80 |
| 3 | 84 | 85 |
| 4 | 89 | 90 |
| Input | Output | Wall Time | Loss Value | |
|---|---|---|---|---|
| Case 1 | 74 | 75 | 4 h 50 min 52 s | 3.266 |
| Case 2 | 79 | 80 | 5 h 9 min 44 s | 3.262 |
| Case 3 | 84 | 85 | 5 h 30 min 13 s | 3.301 |
| Case 4 | 89 | 90 | 5 h 50 min 9 s | 3.298 |
| Threshold | Number of Anomalies Detected | Performance Metrics | |||
|---|---|---|---|---|---|
| F1-Score | TaP | TaR | |||
| C1-1 | 0.042 | 36 | 0.501 | 0.413 | 0.635 |
| C1-2 | 0.04 | 36 | 0.504 | 0.416 | 0.639 |
| C1-3 | 0.38 | 35 | 0.503 | 0.415 | 0.638 |
| C1-4 | 0.36 | 35 | 0.507 | 0.417 | 0.646 |
| C2-1 | 0.05 | 36 | 0.482 | 0.396 | 0.611 |
| C2-2 | 0.047 | 36 | 0.496 | 0.413 | 0.620 |
| C2-3 | 0.044 | 35 | 0.504 | 0.425 | 0.621 |
| C2-4 | 0.04 | 34 | 0.513 | 0.437 | 0.622 |
| C3-1 | 0.047 | 35 | 0.484 | 0.401 | 0.611 |
| C3-2 | 0.044 | 34 | 0.496 | 0.417 | 0.611 |
| C3-3 | 0.04 | 33 | 0.506 | 0.428 | 0.619 |
| C3-4 | 0.038 | 31 | 0.487 | 0.409 | 0.603 |
| C4-1 | 0.046 | 34 | 0.500 | 0.417 | 0.624 |
| C4-2 | 0.044 | 34 | 0.504 | 0.421 | 0.628 |
| C4-3 | 0.042 | 34 | 0.501 | 0.415 | 0.632 |
| C4-4 | 0.04 | 32 | 0.498 | 0.420 | 0.611 |
| Section | Attack | Performance Metrics | |||
|---|---|---|---|---|---|
| Accuracy | F1-Score | TaP | TaR | ||
| 1 | 1 | 0.953 | 0.819 | 0.778 | 0.865 |
| 2 | 10 | 0.883 | 0.654 | 0.534 | 0.843 |
| 3 | 16 | 0.916 | 0.895 | 0.895 | 0.895 |
| 4 | 27 | 0.952 | 0.774 | 0.654 | 0.940 |
| 5 | 33 | 0.9875 | 0.898 | 0.820 | 0.992 |
| TaP = 0.534 | TaR = 0.843 | ||
|---|---|---|---|
| TaP_d | TaP_p | TaR_d | TaR_p |
| 1.000 | 0.365 | 1.000 | 0.729 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, G.-Y.; Lim, S.-M.; Euom, I.-C. A Study on Performance Metrics for Anomaly Detection Based on Industrial Control System Operation Data. Electronics 2022, 11, 1213. https://doi.org/10.3390/electronics11081213
Kim G-Y, Lim S-M, Euom I-C. A Study on Performance Metrics for Anomaly Detection Based on Industrial Control System Operation Data. Electronics. 2022; 11(8):1213. https://doi.org/10.3390/electronics11081213
Chicago/Turabian StyleKim, Ga-Yeong, Su-Min Lim, and Ieck-Chae Euom. 2022. "A Study on Performance Metrics for Anomaly Detection Based on Industrial Control System Operation Data" Electronics 11, no. 8: 1213. https://doi.org/10.3390/electronics11081213
APA StyleKim, G.-Y., Lim, S.-M., & Euom, I.-C. (2022). A Study on Performance Metrics for Anomaly Detection Based on Industrial Control System Operation Data. Electronics, 11(8), 1213. https://doi.org/10.3390/electronics11081213







