An Efficient Detour Computation Scheme for Electric Vehicles to Support Smart Cities’ Electrification
Abstract
:1. Introduction
2. Overview of the Electric Vehicle Routing Problem
2.1. The Rise of Electric Vehicles
2.2. Traffic Congestion
2.3. Vehicle Routing
2.4. Electric Vehicle Routing
3. Related Works
Comparative Study
4. Proposed Solution
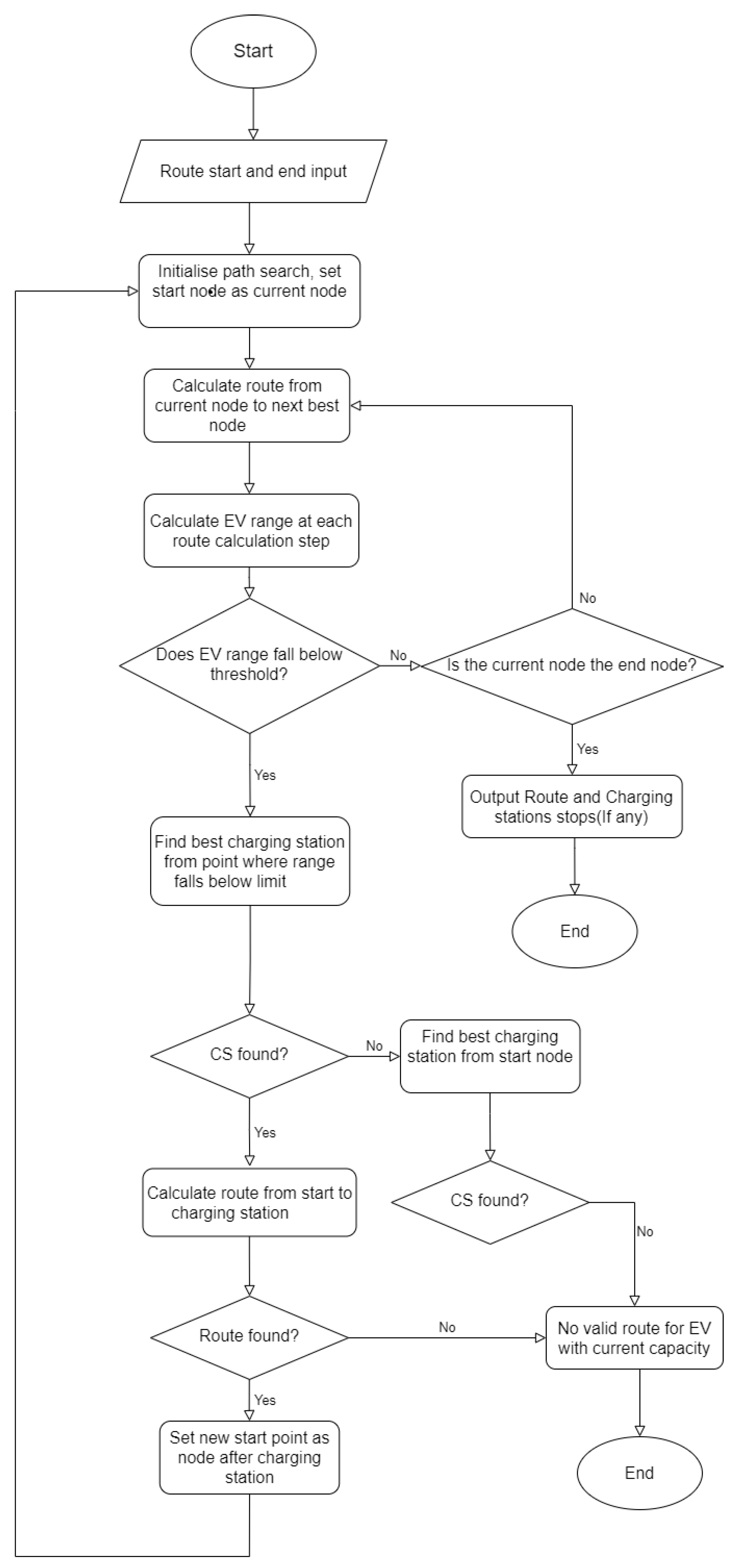
4.1. Routing Process Design
4.2. Vehicle Routing Algorithm
4.2.1. Chosen Path Search Algorithm
4.2.2. Network Costs and Heuristic
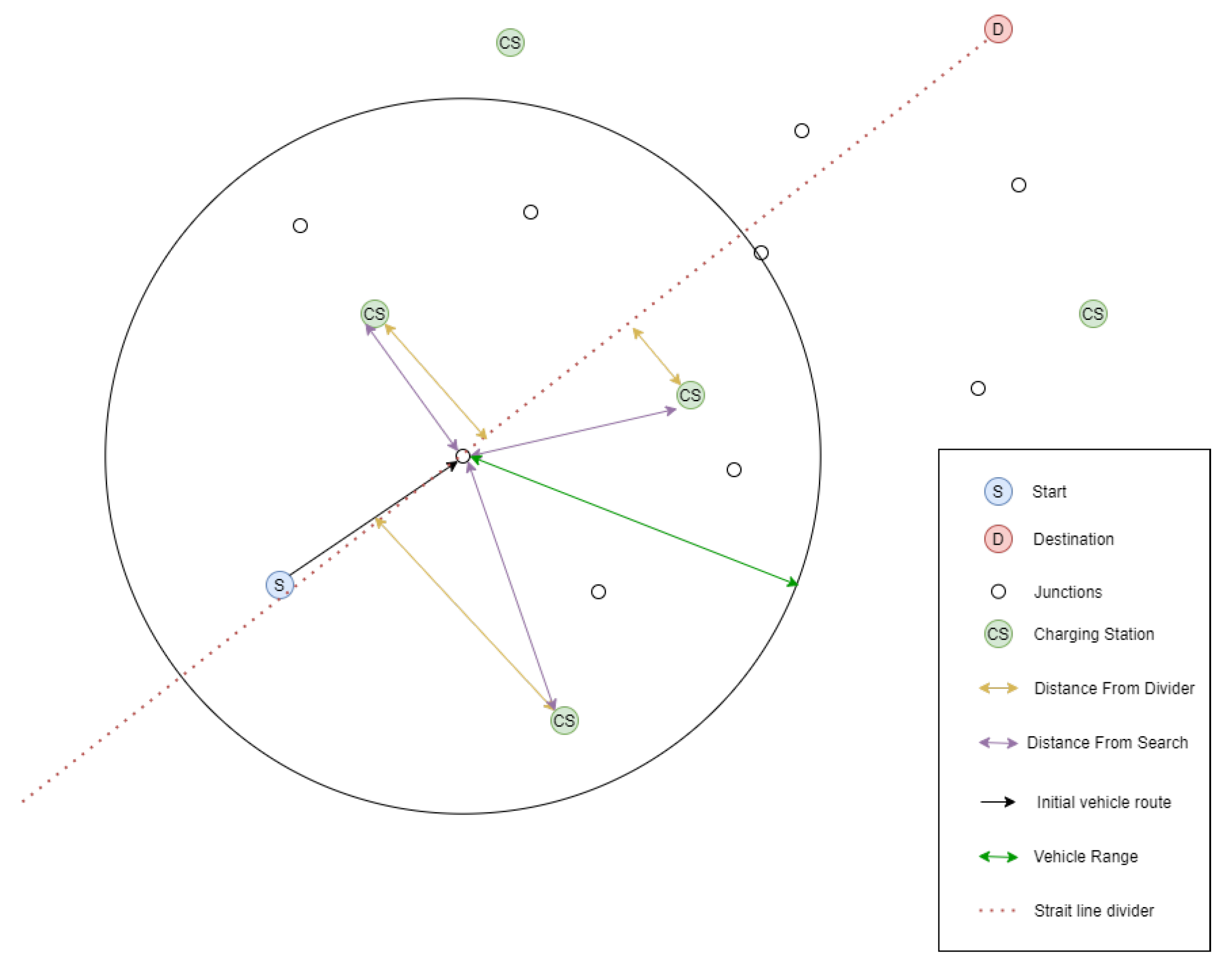
4.3. Charging Station Selection
4.3.1. Simple Additive Weighting
4.3.2. Charging Station Decision Attributes
5. Performance Evaluation
5.1. Evaluation Configuration
5.1.1. Creating Test Data
5.1.2. Evaluation Metrics
5.1.3. Evaluation Parameters
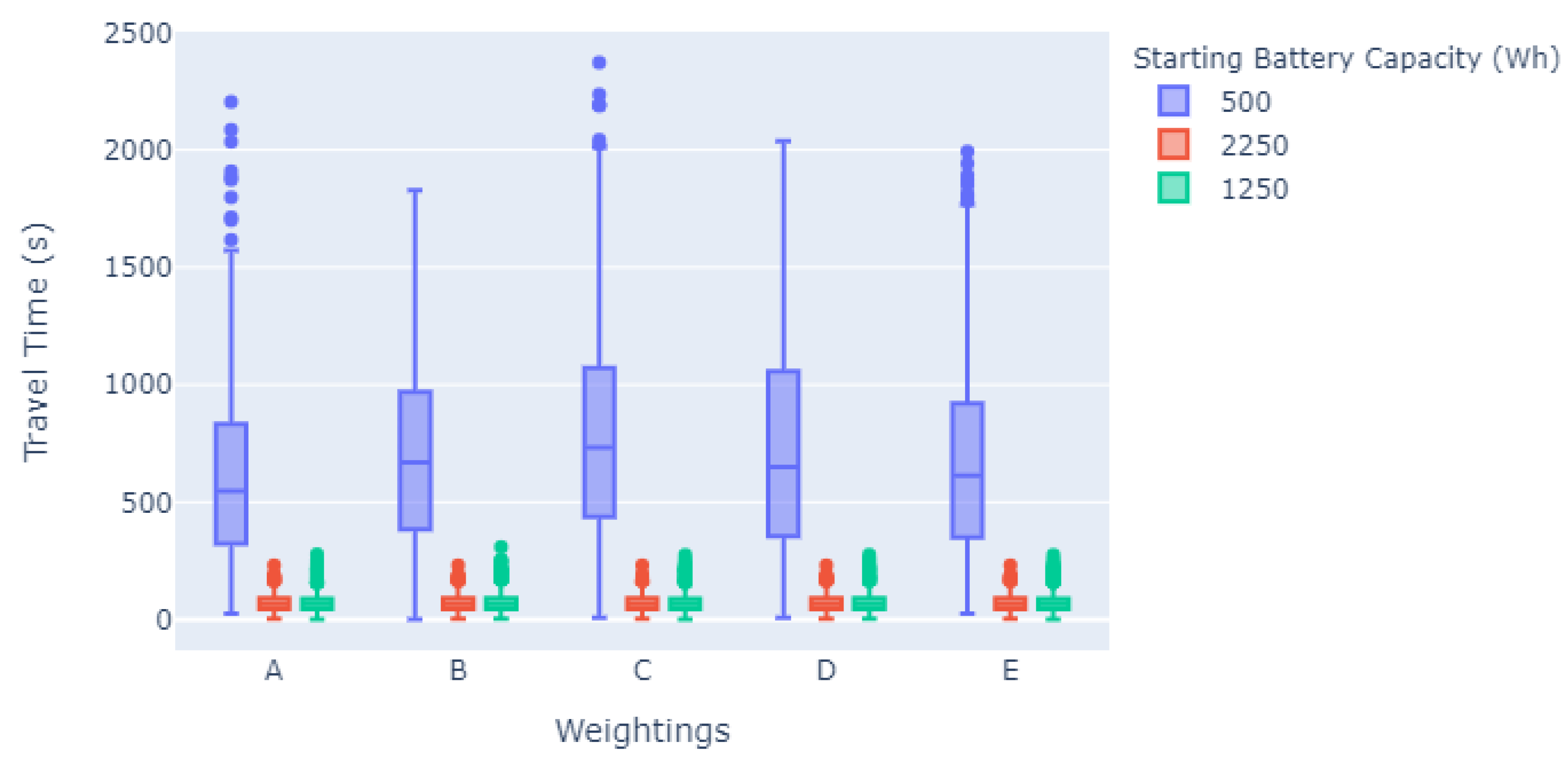
5.2. Evaluation Scenarios
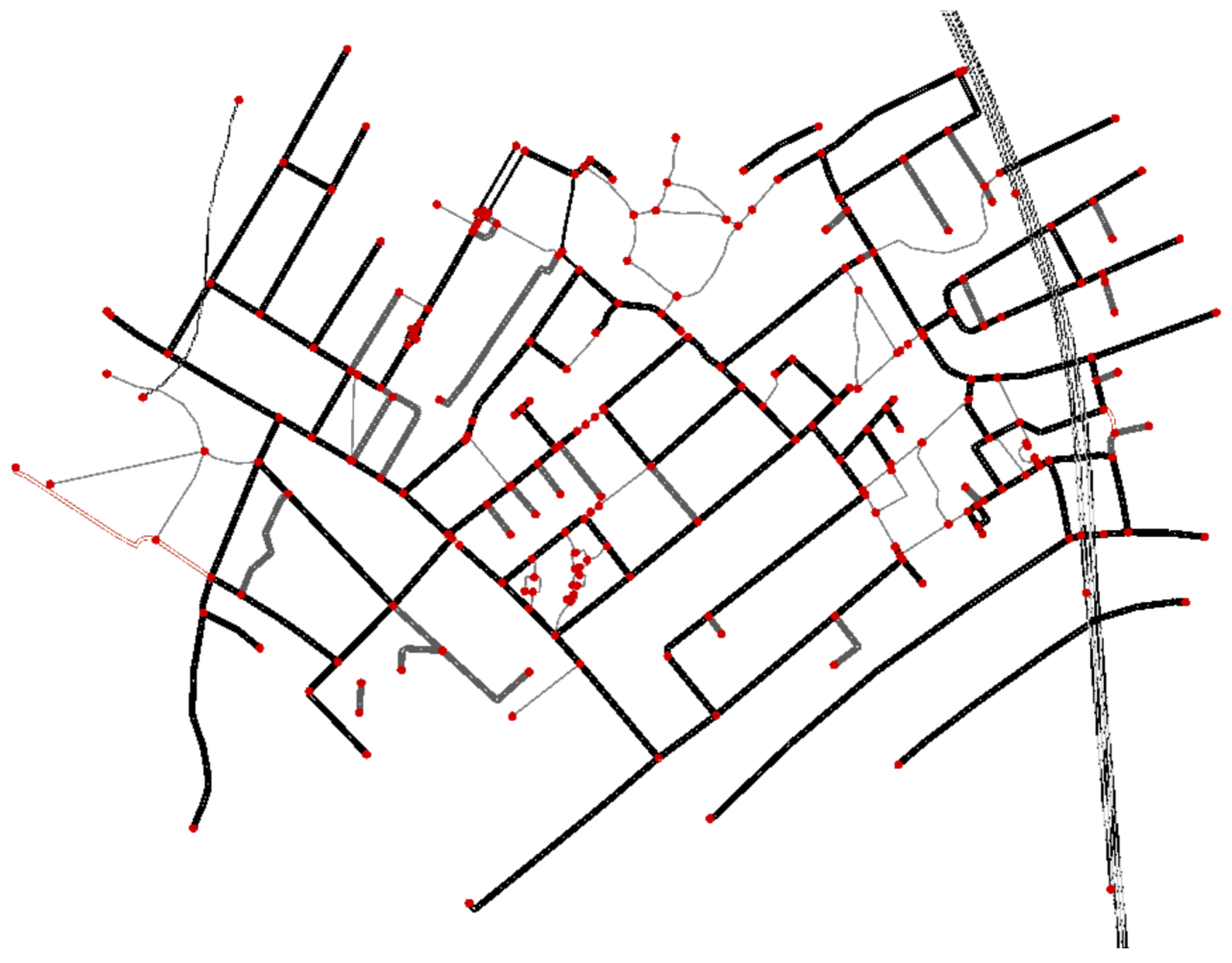
5.2.1. Grid Road Network Scenario
5.2.2. Manchester Road Network Scenario
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- A European Strategy for Low-Emission Mobility. 2018. Available online: https://www.politico.eu/wp-content/uploads/2016/07/Transport-Paper.pdf (accessed on 4 November 2021).
- Hampshire, K.; German, R.; Pridmore, A.; Fons, J. Electric vehicles from life cycle and circular economy perspectives. Version 2018, 2, 25. [Google Scholar]
- BloombergNEF Electric Vehicle Outlook 2020. Available online: https://about.bnef.com/electric-vehicle-outlook/ (accessed on 4 November 2021).
- IEA. Electric Vehicles. Available online: https://www.iea.org/reports/electric-vehicles (accessed on 4 November 2021).
- IEA. Global EV Outlook 2020. Available online: https://www.iea.org/reports/global-ev-outlook-2020 (accessed on 4 November 2021).
- Knobloch, F.; Hanssen, S.V.; Lam, A.; Pollitt, H.; Salas, P.; Chewpreecha, U.; Huijbregts, M.A.; Mercure, J.F. Net emission reductions from electric cars and heat pumps in 59 world regions over time. Nat. Sustain. 2020, 3, 437–447. [Google Scholar] [CrossRef] [PubMed]
- Malmgren, I. Quantifying the societal benefits of electric vehicles. World Electr. Veh. J. 2016, 8, 996–1007. [Google Scholar] [CrossRef] [Green Version]
- Litman, T. Smart Congestion Relief: Comprehensive Analysis of Traffic Congestion Costs and Congestion Reduction Benefits; Technical Report; Victoria Transport Policy Institute: Victoria, BC, Canada, 2016. [Google Scholar]
- Hallenbeck, M.E.; Ishimaru, J.; Nee, J. Measurement of Recurring Versus Non-Recurring Congestion; Technical Report; Department of Transportation: Washington, DC, USA, 2003.
- SMMT. January 2021-SMMT UK New Car and LCV Registrations Outlook to 2022. Available online: https://www.smmt.co.uk/wp-content/uploads/sites/2/WEBSUM-SMMT-CARLCV-MARKET-OUTLOOK-Q1-03022021FINAL.pdf (accessed on 4 November 2021).
- National Population Projections. Available online: https://www.ons.gov.uk/peoplepopulationandcommunity/populationandmigration/populationprojections/bulletins/nationalpopulationprojections/2020basedinterim (accessed on 4 November 2021).
- Wong, C. Provisional Road Traffic Estimates Great Britain; Technical Report; Department for Transport: Washington, DC, USA, 2019.
- Road Traffic Forecasts 2018—Moving Britain Ahead. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/873929/road-traffic-forecasts-2018-document.pdf (accessed on 4 November 2021).
- Reed, T. Inrix Global Traffic Scorecard. Available online: https://inrix.com/scorecard/ (accessed on 4 November 2021).
- RAC. RAC Report on Motoring 2019. Available online: https://www.rac.co.uk/drive/features/report-on-motoring-2019/ (accessed on 4 November 2021).
- Nha, V.T.N.; Djahel, S.; Murphy, J. A comparative study of vehicles’ routing algorithms for route planning in smart cities. In Proceedings of the 2012 First International Workshop on Vehicular Traffic Management for Smart Cities (VTM), Dublin, Ireland, 20 November 2012; pp. 1–6. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Gutenschwager, K.; Völker, S.; Radtke, A.; Zeller, G. The shortest path: Comparison of different approaches and implementations for the automatic routing of vehicles. In Proceedings of the 2012 Winter Simulation Conference (WSC), Berlin, Germany, 9–12 December 2012; pp. 1–12. [Google Scholar] [CrossRef] [Green Version]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Haupt, R.L.; Ellen Haupt, S. Practical Genetic Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Bagheri, A.; Akbarzadeh Totonchi, M.R. Finding shortest path with learning algorithms. Int. J. Artif. Intell. 2008, 1, 86–95. [Google Scholar]
- Gen, M.; Cheng, R.; Wang, D. Genetic algorithms for solving shortest path problems. In Proceedings of the 1997 IEEE International Conference on Evolutionary Computation (ICEC ’97), Indianapolis, IN, USA, 13–16 April 1997; pp. 401–406. [Google Scholar] [CrossRef]
- Wang, S.; Djahel, S.; McManis, J.; McKenna, C.; Murphy, L. Comprehensive performance analysis and comparison of vehicles routing algorithms in smart cities. In Proceedings of the Global Information Infrastructure Symposium-GIIS, Trento, Italy, 28–31 October 2013; pp. 1–8. [Google Scholar]
- Birkett, E.; Nicolle, W. Charging Up—Policies to Deliver a Comprehensive Network of Public EV Chargepoints. Available online: https://policyexchange.org.uk/wp-content/uploads/Charging-Up.pdf (accessed on 4 November 2021).
- Lee, H.; Clark, A. Charging the Future: Challenges and Opportunities for Electric Vehicle Adoption; Faculty Research Working Paper Series; Harvard Kennedy School: Cambridge, MA, USA, 2018. [Google Scholar]
- Neubauer, J.; Wood, E. The impact of range anxiety and home, workplace, and public charging infrastructure on simulated battery electric vehicle lifetime utility. J. Power Sources 2014, 257, 12–20. [Google Scholar] [CrossRef]
- Edmonds, E. Electric Vehicle Range Testing; Technical Report; American Automobile Association, Inc.: Heathrow, FL, USA, 2019. [Google Scholar]
- Kobayashi, Y.; Kiyama, N.; Aoshima, H.; Kashiyama, M. A route search method for electric vehicles in consideration of range and locations of charging stations. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden, Germany, 5–9 June 2011; pp. 920–925. [Google Scholar]
- Abousleiman, R.; Rawashdeh, O. A Bellman-Ford approach to energy efficient routing of electric vehicles. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 14–17 June 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Ammous, M.; Belakaria, S.; Sorour, S.; Abdel-Rahim, A. Optimal Routing with In-Route Charging of Mobility-on-Demand Electric Vehicles. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Daanish, A.R.; Naick, B.K. Implementation of charging station based electric vehicle routing problem using nearest neighbour search algorithm. In Proceedings of the 2017 2nd IEEE International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 1–3 September 2017; pp. 52–56. [Google Scholar] [CrossRef]
- Tang, X.; Bi, S.; Zhang, Y.A. Distributed Routing and Charging Scheduling Optimization for Internet of Electric Vehicles. IEEE Internet Things J. 2019, 6, 136–148. [Google Scholar] [CrossRef]
- Ding, D.; Li, J.; Tu, P.; Wang, H.; Cao, T.; Zhang, F. Electric Vehicle Charging Warning and Path Planning Method Based on Spark. IEEE Access 2020, 8, 8543–8553. [Google Scholar] [CrossRef]
- Spark. Spark Framework. Available online: https://sparkjava.com/ (accessed on 4 November 2021).
- Wang, Q.; Peng, S.; Liu, S. Optimization of Electric Vehicle Routing Problem Using Tabu Search. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 2220–2224. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. ETransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Rana, K.; Zaveri, M. A-star algorithm for energy efficient routing in wireless sensor network. In Trends in Network and Communications; Springer: Berlin/Heidelberg, Germany, 2011; pp. 232–241. [Google Scholar]
- Chakraborty, S.; Yeh, C.H. A simulation based comparative study of normalization procedures in multiattribute decision making. In Proceedings of the 6th Conference on 6th WSEAS International Conference on Artificial Intelligence, Knowledge Engineering and Data Bases, Corfu Island, Greece, 16–19 February 2007; Volume 6, pp. 102–109. [Google Scholar]
- Churchman, C.W.; Ackoff, R.L. An approximate measure of value. J. Oper. Res. Soc. Am. 1954, 2, 172–187. [Google Scholar] [CrossRef]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flötteröd, Y.P.; Hilbrich, R.; Lücken, L.; Rummel, J.; Wagner, P.; Wießner, E. Microscopic Traffic Simulation using SUMO. In Proceedings of the 21st IEEE International Conference on Intelligent Transportation Systems, Maui, HI, USA, 4–7 November 2018. [Google Scholar]
- German Aerospace Center (DLR). TraCi. Available online: https://sumo.dlr.de/docs/TraCI.html (accessed on 4 November 2021).
- Routing—SUMO Documentation. Available online: https://sumo.dlr.de/docs/Simulation/Routing.html (accessed on 4 November 2021).

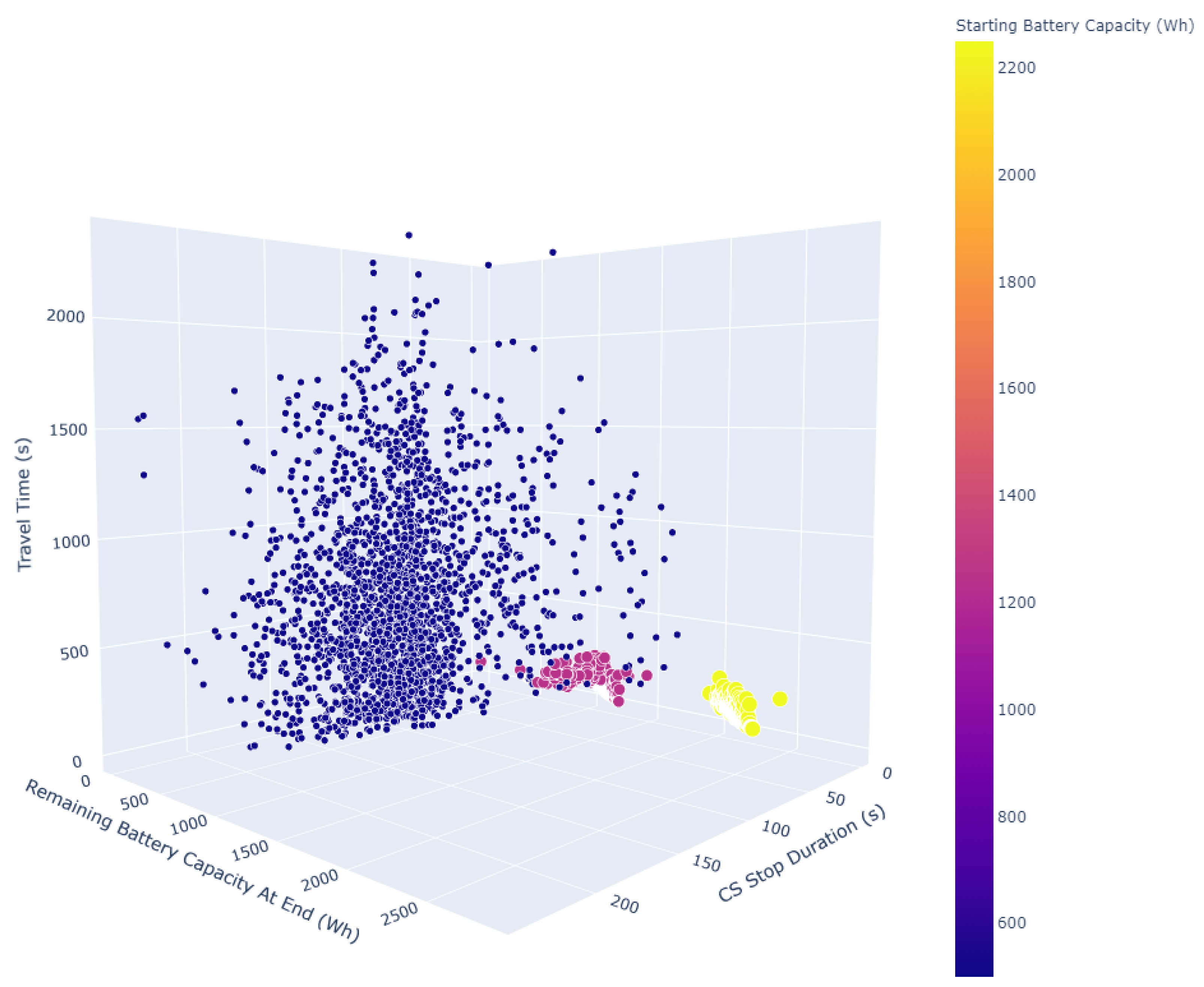

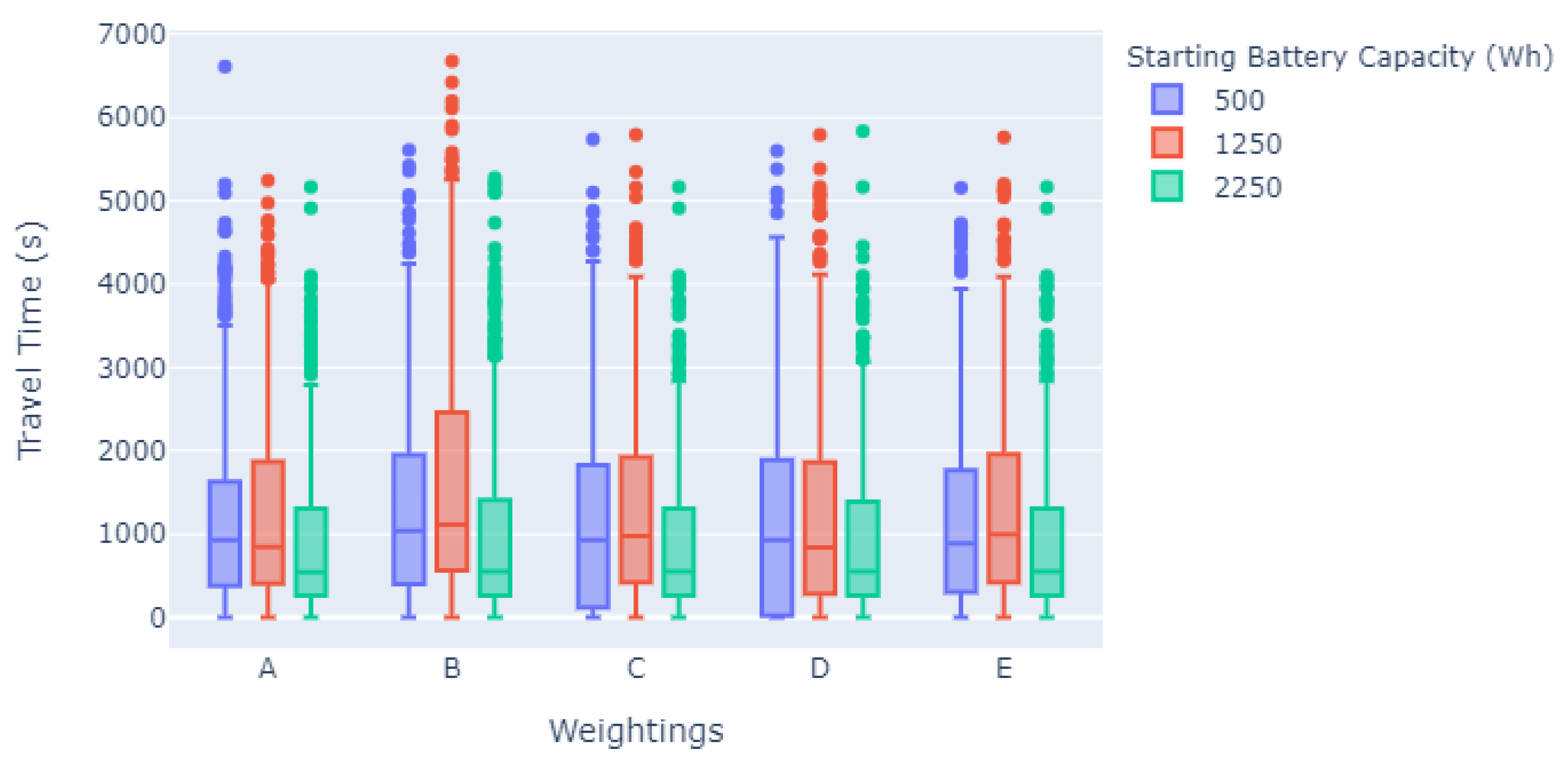
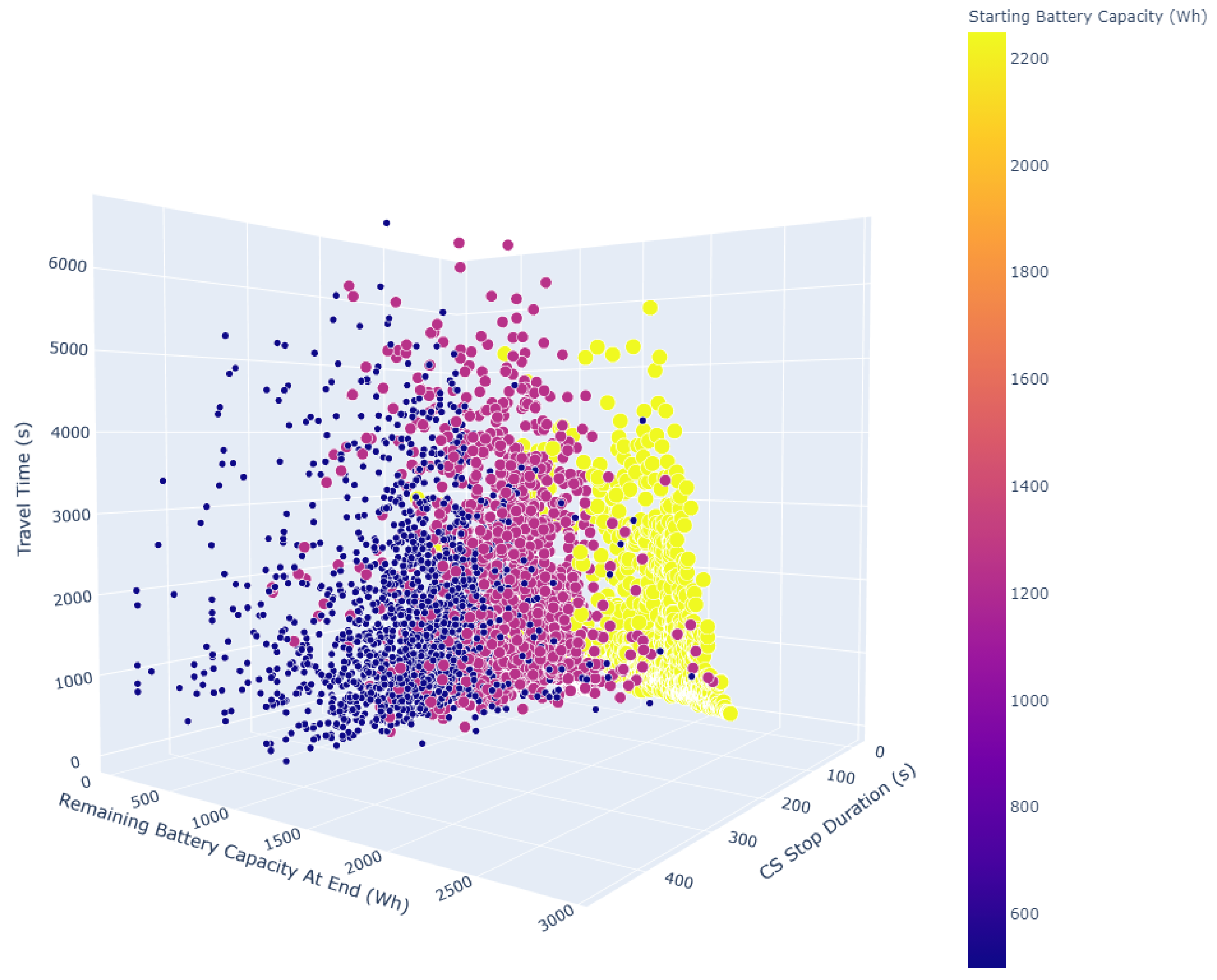
| Study | Complexity | CS Attributes Considered | Scalability | Overall Effectiveness |
|---|---|---|---|---|
| [28] | Medium | False | High | Medium |
| [29] | Low | False | Medium | Low |
| [30] | High | True | Medium | High |
| [31] | Low | False | Medium | Low |
| [32] | High | True | High | High |
| [33] | Medium | True | Very High | High |
| [35] | Very High | False | High | High |
| Our proposal | Medium | True | High | High |
| Attribute Name | Normalization |
|---|---|
| Distance From Search | Non-beneficial |
| Distance From Divider | Non-beneficial |
| Price | Non-beneficial |
| Vehicles Charging | Non-beneficial |
| Charge Per Step | Beneficial |
| Weighting | Distance from Search | Distance from Divider | Price | Waiting Time at CS | Charging Efficiency |
|---|---|---|---|---|---|
| A | 35% | 35% | 10% | 10% | 10% |
| B | 10% | 10% | 60% | 10% | 10% |
| C | 10% | 10% | 10% | 60% | 10% |
| D | 10% | 10% | 10% | 10% | 60% |
| E | 20% | 20% | 20% | 20% | 20% |
| Starting Battery Capacity (Wh) | Proposed Solution Used | %VCJ | ABE (Wh) |
|---|---|---|---|
| 500 | Yes | 100 | 1142.2 |
| 500 | No | 100 | 331.9 |
| 1250 | Yes | 100 | 1151.9 |
| 1250 | No | 100 | 872.4 |
| 2250 | Yes | 100 | 2144.2 |
| 2250 | No | 100 | 2082.0 |
| Starting Battery Capacity (Wh) | Proposed Solution Used | %VCJ | ABE (Wh) |
|---|---|---|---|
| 500 | Yes | 99.4 | 1017.9 |
| 500 | No | 55.0 | 120.7 |
| 1250 | Yes | 100 | 1180.6 |
| 1250 | No | 90.6 | 705.2 |
| 2250 | Yes | 100 | 1715.8 |
| 2250 | No | 100 | 1667.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mansfield, C.; Hodgkiss, J.; Djahel, S.; Nag, A. An Efficient Detour Computation Scheme for Electric Vehicles to Support Smart Cities’ Electrification. Electronics 2022, 11, 803. https://doi.org/10.3390/electronics11050803
Mansfield C, Hodgkiss J, Djahel S, Nag A. An Efficient Detour Computation Scheme for Electric Vehicles to Support Smart Cities’ Electrification. Electronics. 2022; 11(5):803. https://doi.org/10.3390/electronics11050803
Chicago/Turabian StyleMansfield, Cole, Jack Hodgkiss, Soufiene Djahel, and Avishek Nag. 2022. "An Efficient Detour Computation Scheme for Electric Vehicles to Support Smart Cities’ Electrification" Electronics 11, no. 5: 803. https://doi.org/10.3390/electronics11050803
APA StyleMansfield, C., Hodgkiss, J., Djahel, S., & Nag, A. (2022). An Efficient Detour Computation Scheme for Electric Vehicles to Support Smart Cities’ Electrification. Electronics, 11(5), 803. https://doi.org/10.3390/electronics11050803







