Abstract
Vital for Space Situational Awareness, Initial Orbit Determination (IOD) may be used to initialize object tracking and associate observations with a tracked satellite. Classical IOD algorithms provide only a point solution and are sensitive to noisy measurements and to certain target-observer geometry. This work examines the ability of a Multivariate GPR (MV-GPR) to accurately perform IOD and quantify the associated uncertainty. Given perfect test inputs, MV-GPR performs comparably to a simpler multitask learning GPR algorithm and the classical Gauss–Gibbs IOD in terms of prediction accuracy. It significantly outperforms the multitask learning GPR algorithm in uncertainty quantification due to the direct handling of output dimension correlations. A moment-matching algorithm provides an analytic solution to the input noise problem under certain assumptions. The algorithm is adapted to the MV-GPR formulation and shown to be an effective tool to accurately quantify the added input uncertainty. This work shows that the MV-GPR can provide a viable solution with quantified uncertainty which is robust to observation noise and traditionally challenging orbit-observer geometries.
1. Introduction
As access to space becomes more readily available, the need for robust Space Situational Awareness (SSA) increases. Space-object tracking, an integral aspect of SSA, is performed by a sequential filtering algorithm which must be initialized. To initialize these orbits, tools collectively called Initial Orbit Determination (IOD) algorithms are utilized to provide an estimate of a previously unknown orbit. Furthermore, these tracks (orbits) initialized by IOD algorithms can be used for data association purposes as shown in [1]. Although IOD algorithms have been developed to initiate orbit-tracks from radar as well as optical sensors, angles-only IOD algorithms represent an area of particular interest due to the limited availability of deep space radars.
The seminal angles-only IOD algorithms include Laplace’s method, Gauss’ method, Gooding’s method, and Double-R iteration (all detailed in [2]). Laplace’s method is often intractable for Earth-based satellites, but does provide a viable solution for heliocentric orbits. Gauss’ method may be used for Earth-based space objects, but at a limited angular separation between observations. Double-R iteration and Gooding’s method allow for longer time periods between observations, but require a guess to initialize the iteration. These classical angles-only IOD algorithms are sensitive to noise and to certain observer-target geometryas shown in both our own previous work [3,4,5] and also various other IOD studies [6,7,8,9,10,11]. All angles-only IOD algorithms mentioned utilize the observer-target geometry and assumptions defined from the Kepler problem to define a point solution, thus lacking any uncertainty information. The addition of high levels of noise essentially violates these relationships and causes severe degradation in accuracy. Additionally, a well-known failure case for these algorithms is known as a coplanar orbit. This occurs when the observation site lies close to the target’s orbital plane causing a singularity in many of the underlying algorithms. Though each of the IOD algorithms have a different formulation, all leverage the observer-target geometry; therefore, accuracy may severely degrade near coplanar orbits. In summary, many existing IOD algorithms do not inherently provide uncertainty information, are sensitive to sensor noise, and degrade in coplanar observer orbit geometries.
There exists an avenue to address the shortcomings of the classical IOD algorithms using a supervised learning method known as Gaussian Process Regression (GPR) as first proposed in our previous works [3,5]. The motivation of this paper is to examine the efficacy of GPR in providing an accurate solution with quantified uncertainty to the angles-only IOD problem both in general and in traditionally challenging observer-target sensing geometries.
While learning methods have been proposed to address the orbit determination problem, most methods focus on the range and range-rate orbit determination problem as in [12] or as a correction term to a sequential filter. GPR itself has even been introduced in the orbit determination space by Peng and Bai [13] who fuse the model estimate of a Kalman filter with the a GP model to essentially correct the orbit determination output of the sequential filter.
GPR methods outperform many regression techniques [14], and Rasmussen and Williams [15] demonstrate GPR’s ability to learn the complex, nonlinear inverse dynamics of a robotic arm with seven degrees-of-freedom. In its basic formulation, GPR assumes either a scalar output or independence between output dimensions. Many formulations exist to expand this method to vector-valued processes, as surveyed by Liu et al. [16], but the method most pertinent to this work vectorizes the process in both the data and output dimension [17,18,19]. Chen et al. [20] shows that this method is equivalent to defining a matrix-variate distribution. Additionally, GPR assumes deterministic input in the original formulation. In this work, training is performed via simulations, so perfect inputs may be assumed for training. In a real-world scenario, the inputs for inference are measurement-based with a defined uncertainty. Given GPR in inherently nonlinear, input noise cannot be directly mapped to the regression output. The work of Candela et al. [21] shows how one may exactly define the first and second statistical moments of the unknown output distribution. This defines a way to simultaneously define an initial orbit with accurate uncertainty quantification given uncertain inputs. This work builds upon our previous works [3,5,22] in showcasing the ability of Multivariate GPR (MV-GPR) to provide a solution to the IOD problem while providing accurate uncertainty characterization given uncertainty inputs at inference. The objective is to train the MV-GPR from perfect simulations and then exploit the work of Candela et al. [21] to accurately characterize the errors associated with IOD estimates while taking into account for measurement errors.
The structure of the paper is as follows: first, an overview of classical IOD algorithms is presented, followed by the review of conventional GPR process. Section 4 presents the MV-GPR formulation, followed by definition of model hyperparameters in Section 5 and testing with noisy data in Section 6. Section 7 provides results from various numerical experiments performed to assess the performance of MV-GPR for the IOD problem, and Section 8 provides the concluding remarks.
2. Classical Initial Orbit Determination
While many algorithms exist which provide a solution to the angle-only IOD problem, this work will focus on one of the oldest and well documented methods known as Gauss’ method to provide a benchmark for the GPR-based IOD method. Like most IOD algorithms, Gauss’ method leverages the geometry of the observer and target at three measurement times (), defined by
where denotes the spacecraft position vector, denotes the range and denotes the unit vector from observer to target, denotes the observer’s position vector, and i indexes the time of measurement. These lines-of-sight may be determined by topocentric measurements of the right-ascension (RA) and declination (DEC) such that
The geometry of defining Equations (1) and (2) is shown in Figure 1. With and known at each measurement, the problem becomes estimating the range in order to determine the radius vector at each measurement. Given the observer’s position is well defined, three linearly independent line-of-sight measurements, and the times of each observation, Gauss’ method provides an estimate for the position at the three observations by posing an 8-th order polynomial of . The algorithm takes advantage of the planar nature of orbits and the method of Lagrange coefficients for propagating orbits as a linear combination of position and velocity, commonly referred to as the f and g solution. Given an estimate for the three position vectors, a prediction of the instantaneous can be defined utilizing the approximate the f and g solution. With and now estimated, the target’s Cartesian state is fully defined.
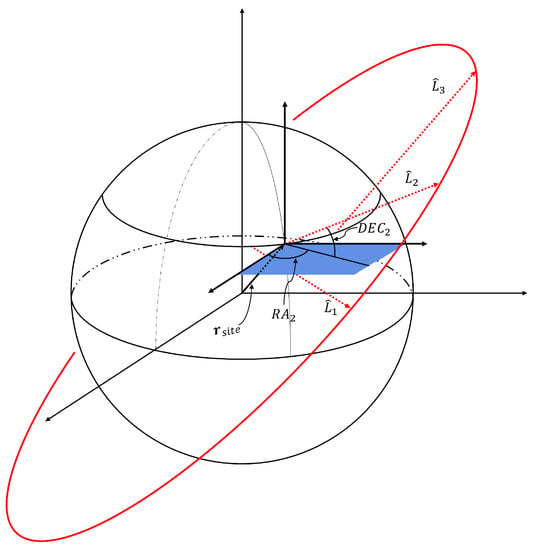
Figure 1.
Geometry of angles-only Initial Orbit Determination.
In more recent history, methods to increase the accuracy of the method have been defined. Most notably, Gauss’ method is combined with Gibbs’ or the Herrick–Gibbs methods to provide a more accurate measure [2]. Both Gibbs’ and the Herrick–Gibbs methods are IOD algorithms that start with the premise of three known position vectors and times of measurement then solve for the middle velocity. Gibbs’ method is a geometric approach while Herrick–Gibbs essentially represents a series expansion. Therefore, the Herrick–Gibbs algorithm is the best for measurement separations around or less, while Gibbs’ method is used for larger angular separations as stated in [2]. This work uses the combined Gauss–Gibbs method as the IOD benchmark. Additionally, Curtis in [23] defines an iterative scheme using universal variables which refine the “initial pass” estimated by Gauss’ method to determine the exact solution assuming perfect measurements. This will be referred to as an iterative Gauss–Gibbs method throughout the rest of this paper.
3. Standard Gaussian Process Regression (GPR)
As defined in [15], a Gaussian Process is a collection of random variables, any finite number of which have a joint Gaussian distribution. Therefore, analogous to the Gaussian distribution for random variables, the GP is completely defined by its mean and covariance functions:
where . The mean and covariance functions are defined using the expectation, such that
By defining functions as simply an infinite-dimensional vector, the GP can be compared to a Gaussian distribution with an infinitely-sized mean vector and covariance matrix. Therefore, every subset of the distribution is defined by the full distribution due to the marginalization property of Gaussian processes [15]. Now, let the model be defined as
where and represents model noise. Let there be a finite data set in the domain and range of Equation (5), then the distribution of is defined as a joint Gaussian distribution,
is the relevant submatrix defined from the covariance function of the GP in Equation (5) such that
where is any set of p vectors and is any set of q vectors .
While various kernel functions exist, we will focus on the commonly used Squared Exponential (SE) covariance function:
The matrix is often a diagonal matrix which encodes what is known as Automatic Relevance Determination (ARD). Together, and make up the hyperparameters of the SE kernel. Given that a specific form of the covariance kernel is specified, the next step involves determining the optimal hyperparameters, , to define the model, which may also include the model noise, .
Now, introducing a single test point, , the marginalization property may again be invoked such that and are defined from the same GP and therefore
The predictive distribution of consists of conditioning the prior distribution on the training observations, which returns a Gaussian defined as
4. Multivariate Gaussian Process Regression
In the formulation above, it is assumed that the output dimension is a scalar. There are many ways to expand the GPR framework to address multioutput regression problems, such that . One can pose the multidimensional output problem as one of multitask learning. By definition, multitask learning is learning one model to represent multiple data sets. We can define the training inputs and the j-th dimension as representing their own data sets, , where . In this context, the multitask learning problem will define a GPR model for each of the output dimensions, but the models share the same hyperparameters. This method is defined as ind-GPR throughout the rest of this work. The downside is that ind-GPR assumes mutual independence between the outputs, and thus limits the ability to account for output correlation during training.
Alternatively, a method to address this issue is to vectorize the output [17,18,19] such that
This reformulates the Multi-Output problem as a standard GPR method discussed in Section 3. As shown by Chen et al. [20], this may be accomplished equivocally by generalizing the Gaussian process to a vector-valued function such that
Here, encodes the covariance along the range of the D-vector GP and encodes the covariance in the m-dimensions of the vector-valued process. Again, the marginalization property holds true. Therefore if there exists a finite data set, , then the distribution of has a joint matrix-variate Gaussian distribution:
where , , and . As discussed in Chen et al. [20,24], a matrix-variate Gaussian distribution has a density of the form
Additionally, the -matrix-variate normal distribution is may be mapped to a -multivariate normal distribution:
Therefore, the work of Chen et al. [20] is similar to previous works [17,18,19] given that the matrix-variate distribution may be mapped to a multivariate one for normal distributions, as shown in Equation (15).
If a test point, , is introduced into this formulation, the marginalization property used in the standard GPR formulation may also be invoked for matrix-variate normal distributions [20,25] such that
As a property of matrix normal distributions, the test output conditioned on the training data, , is defined as
Using Equation (15), the corresponding multivariate distribution is then defined as
This method is referred to as MV-GPR throughout the rest of this paper.
5. Defining Model Hyperparameters
Though not necessarily the case, the mean function is often taken to be zero as the mean of the posterior process will not be constrained to be zero [15]. See Chapter 2.7 of [15] for details on mean function formulation and definition. Therefore, we will assume a zero-mean prior for both ind- and MV-GPR methodologies. The posterior estimation will not be confined to be zero [15], and therefore an accurate GPR model may still be learned. Additionally, we use the square-exponential kernel as defined in Equation (8) as our covariance function. Therefore, the hyperparameters associated with both GPR algorithms include , , and . For ind-GPR, this results in a set of hyperparameters to optimize for such as
By contrast, MV-GPR’s hyperparameters also include the elements of the matrix . By definition, must be a positive definite matrix since it defines the covariance between the dimensions of the vector-valued function . The Cholesky decomposition for positive definite matrices allows to be factored such that , where is a lower triangular matrix. Optimizing for the elements of not only reduced the number of hyperparameters for MV-GPR, but also ensures is positive definite. This adds an additional hyperparameters to optimize, thus giving
Under the ind-GPR assumption, the cost function for optimization of the hyperparameters is accomplished using the negative-log-likelihood
The MV-GPR algorithm directly uses its negative-log-likelihood as its cost function such that
The complexity in the training for both methods and the prediction is dominated by the inverse , assuming . There is no guarantee that optimization for either formulation will not suffer from local optima. As stated in [15], the local optima are not often devastating for less complex covariance functions and will provide differing interpretations of the data. For instance, let us state that a given problem has two optima: (1) an optimum with high and a high length-scale and (2) an optimum with the low and a low length-scale. Case (1) would correspond to a very smooth mean curve with large, smooth uncertainty bounds. Case (2) would result in a mean curve that passes much closer to the individual training points and reflect uncertainty bounds which shrink significantly near those points.
6. Estimate Given Random Test Inputs
As formulated, the GPR algorithm assumes perfect inputs into the regression model. This is not often the case in engineering systems. In this study, perfect inputs, , and perfect outputs, , generated from Equations (1) and (2) are used during training. In real world scenarios, only measurements of the input are available at inference, such that
Given that GPR is a nonlinear function in , the true predictive distribution of the GPR output will not be Gaussian. However, it may be approximated by a Gaussian with the same mean and covariance as the true distribution, i.e., moment matching. The following moment matching derivation stems from the method defined by Candela et al. [21] and presented in chapter 2 of Deisenroth [26] with amendments due to the use of MV-GPR presented in Section 4.
The mean of the predicted distribution given these approximations is
where . Given that via Equation (17) and utilizing the law of iterated expectations,
where . Using the square-exponential covariance function in Equation (8) gives an analytic definition for :
Similarly, the covariance may be defined using the law of total covariance such that
Using the definition of from Equation (17), properties of covariance, and the properties of the matrix trace,
The term may be defined analytically assuming Gaussian input noise and using the square-exponential covariance kernel such that
with . Chapter 2 of Deisenroth [26] shows additional details of this method and a numerically stable way to compute this matrix under a different multioutput GPR formulation. Due to numerical sensitivity of the noise aware MV-GPR method presented in Section 6, the method used in this work to address the numerical sensitivity is shown in Appendix A.
7. Numerical Simulations
7.1. Methodology
Often, statistical learning methods use real data for training purposes. In this work, data is simulated using the Keplerian solution to the two-body problem. The assumption of a Keplerian orbit is accurate for short intervals and is also an assumption present for most other IOD processes. A goal of this work is to study the utility of GPR in learning a solution to the IOD problem and benchmark the solution against the Gauss–Gibbs method. This work will utilize the Gauss–Gibbs method without iteration unless otherwise stated. Iterating on the Gauss–Gibbs solution will return the ground-truth to machine precision if given perfect RA and DEC measurements. The reasoning behind not including iteration is twofold. (1) The GPR method is non-iterative and so it also provides a “first pass” solution, therefore it is more informative to compare the GPR model error it to the well-studied Gauss–Gibbs “first pass” solution’s error. (2) Iteration provides very limited increase in accuracy given noisy measurements from a similarly defined noise model as shown in Chapter 3 of [22].
With respect to the GPR algorithms, it is important to inspect their performance across challenging data sets and with respect to various training levels. Orbit samples are generated from ranges of classical orbital elements shown in Table 1, which are tailored directly for the purposes of this study. The semi-major axis () is the largest semidiameter of the orbital ellipse, and the eccentricity, e, uniquely characterizes the shape. The inclination, longitude of the ascending node, argument of periapsis, and true anomaly—i, , , , respectively—are geometric relationships defined in Figure 2. For a Keplerian orbit, , e, i, , are constant for all time and define the orbit ellipse. varies with time and defines the angular position of the spacecraft within it’s orbit. The given true anomaly in Table 1, , corresponds to the 2nd measurement time.

Table 1.
Orbital regimes for each case used in GPR study.
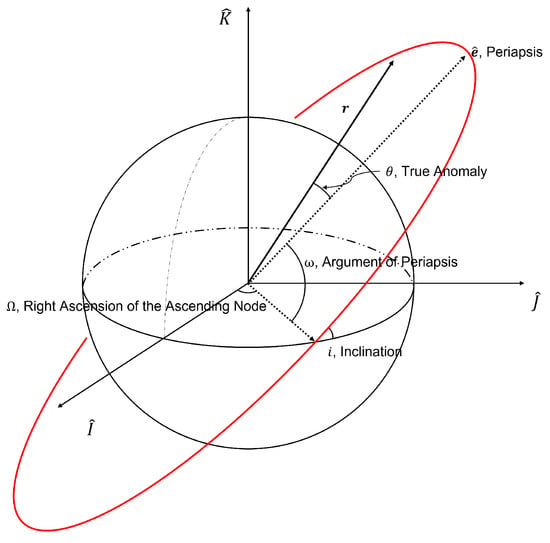
Figure 2.
Geometry classical orbital elements.
Cases A-F in Table 1 progress in the level of difficulty for the GPR methods. Case G represents a nearly-coplanar orbit regime, which has been notoriously difficult for classical IOD algorithms. The Cartesian state at the 1st and 3rd measurement time are generated such that has regressed and processed, respectively, between and . This ensures that the orbits will stay within the effective angular separation for the Gauss–Gibbs IOD algorithm. The time-of-flight (TOF) measurements are defined using Kepler’s equation and the line-of-sight vectors for each measurement are backed out using Equation (1). The observation site is at km in the -frame and rotates with Earth’s average spin rate. The number of training samples generated vary, but are specified throughout this work. There are 5000 testing orbits generated for each case in Table 1, with the resulting orbital arcs shown in Figure 3.
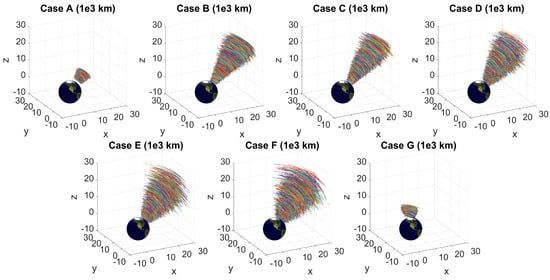
Figure 3.
Orbital arcs for 5000 test orbits of the different orbital case regions.
7.1.1. Gpr Specifics
The inputs to the GPR models are defined as the RA and DEC at each measurement time along with the time-of-flight information between the first and second measurement, , and the second and third measurement, , such that
The output is the spacecraft state vector at the second measurement time such that
where and represent the components of the Cartesian position and velocity, respectively, at the second measurement. As broken down in Table 2, the number of hyperparameters is and .

Table 2.
GPR parameters and their dimesnions in the IOD problem.
Normalization of training data is often essential for accurate optimization of machine learning algorithms. For both inputs and targets, z-score normalization is used such that the mean of the training data is subtracted and each element is divided by its standard deviation. Additionally, the Cartesian state and time-of-flight information is transformed into canonical units such that 1 = 6400 km and that prior to the z-score normalization, which proved to additionally increase performance. Testing data is normalized utilizing the same method, but with the mean and standard deviations of the training data.
The ind-GPR method is implemented using the API and optimization techniques provided by Rasmussen and Nickisch in [27], while the MV-GPR implemented in this work is based on the work of Chen [20] with modifications to the code provided in [28]. Both methods utilize three restarts in an effort to avoid the local minima problem while balancing the computational cost. Finally, the random input procedure in Section 6 is only implemented for the MV-GPR formulation and is referred to as noise aware (N.A.), while the original formulation shall be referred to as standard (STND).
In summary, training is conducted as follows. (1) The outputs—Cartesian position and velocity—are generated from the classical orbital elements reflected in Table 2. (2) The inputs—RA, DEC, and TOF—are backed out assuming Keplerian orbits and a perfectly spherical rotating earth-based observation site. (3) The outputs are written in canonical units both inputs and outputs are normalized using z-score normalization. (4) Hyperparameters in Table 2 are optimized using Equation (21) for ind-GPR and Equation (22) for MV-GPR as cost functions. The software packages [20,27] are used extensively for ind- and MV-GPR, respectively. Random initial guess and three restarts are used in an attempt to avoid local minimums.
Testing is conducted as follows. Steps (1) and (2) remain the same for training and testing on simulated data. (3) Inputs generated from the test points are transformed using the same shift and scaling generated by the z-score normalization of the training data. (4a) With the hyperparameters defined via optimization, Equations (10) and (17) are used to define the predicted state and state covariances for ind- and MV-GPR, respectively. (4b) Noise in the testing input may be accounted for using the Equation (25) for prediction mean and Equation (28) for estimated state covariance. The formulation in Appendix A overcomes some of the numerical issues that appeared when applying the noise-aware inference formulation presented in Section 6. (5) GPR estimates are transformed back into Cartesian space using the same shift and scaling used on the training outputs.
7.1.2. Noise Model
The noise model used in this work is additive Gaussian noise to the RA and DEC measurements, , where
and is the ground truth measurements defined in Equation (30). Under these assumptions, it is assumed that the time of flight measurements are deterministic while the angular measurements have an normal distribution defined by . Given the formulation provided in Section 6 does not involve , the singularity of the current covariance matrix does not affect the solution. If one were to use an equivalent algebraic expression involving the inverse matrix, then the deterministic and random elements of the input would have to be separated. For the rest of this work, one may assume unless otherwise stated and 5 samples are generated for each of the 5000 original testing orbits—giving total random noisy samples.
7.1.3. Metrics
Due to the wide range of orbits investigated, the measures used in this work include the absolute percent error (APE),
and the median absolute percent error (MdAPE),
where defines the number noisy samples and i indexes from which orbit the noisy samples were generated. Both of these measure error for each element in a given state and thus represents a vector of the same size as the state it describes. The average corresponds to the arithmetic mean of the elements in the APE or MdAPE error vector.
Our first metric, the Malanobis distance is introduced:
where is the ground-truth state and and is the GPR-predicted mean and covariance, respectively. The Mahalanobis distance is introduced to measure the accuracy of the covariance estimate. A large number of high (i.e., greater than 3) Mahalanobis distances would show that the predicted covariance is vastly overestimating the precision of the estimate. A large number of very low (i.e., less than 1) Mahalanobis distances would show that the predicted covariance is “too cautious”.
7.2. Accuracy
First, the accuracy of the GPR algorithms is benchmarked against the classical, non-iterative Gauss–Gibbs algorithm. Figure 4 compares box-plots of the APE for ind- and MV-GPR at 200, 400, 800, 1000, 1500 along with the Gauss–Gibbs method. The bars enclose the range of points between the 25th and the 75th quantiles of APE while the point represents the median APE. Figure 4 shows the APE evolving as the algorithms progress through the defined cases and as more training points are utilized. Table 3 compares the median APE of each prescribed method at the most accurate training level, defined by the median APE averaged across output dimensions. There are multiple useful trends which are important to analyze. First, the GPR models surpass Gauss–Gibbs in prediction accuracy relatively quickly across training levels in cases A and B. This is highlighted in Table 3 as ind-GPR and MV-GPR at 1500 training points provide estimates an order of magnitude more accurate than the non-iterative Gauss–Gibbs method. The GPR methods appear to slowly approach the Gauss–Gibbs accuracy in the more difficult cases E-F due to the increased sparsity of training data relative to the size of the orbit regime.
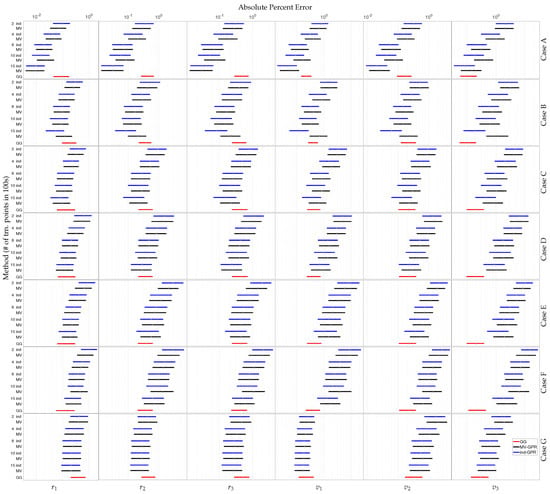
Figure 4.
Given the 5000 testing orbits, the point represents the median APE while the boxes enclose the range of points between the 25th and the 75th quantiles of APE for each Cartesian state given perfect RA and DEC measurements. The GPR methods are listed ind-GPR (blue) then MV-GPR (black) and are ordered by number of training points—200, 400, 800, 1000, and 1500—listed in 100 s. The Gauss–Gibbs results are labeled GG and shown in (red).

Table 3.
Median APE for for most accurate model in each orbit case given perfect RA and DEC measurements.
As shown in Figure 4, the MV-GPR and the ind-GPR perform similarly for most cases, with a slight advantage given to ind-GPR at a fixed training level. This edge is due to the added complexity of the cost function and the 21 additional hyperparameters associated with MV-GPR. More complex models require denser training sets to more accurately estimate their hyperparameters. Additionally, notice that the ind-GPR exhibits a steady increase in prediction accuracy as more training points are added while MV-GPR shows more erratic behavior. The MV-GPR cost function represents a much more complex surface and therefore is likely getting caught in local minimums even with the multiple restarts.
Figure 5 compares box-plots of the APE for standard and noise aware MV-GPR at 200, 400, 800, 1000, 1500 along with the Gauss–Gibbs method. The bars enclose the range of points between the 25th and the 75th quantiles of APE while the point represents the median APE. Table 4 displays the lowest median APE as averaged across the Cartesian states for each method of interest. Referring to Figure 5 and Table 4, the accuracy of the GPR state prediction is nearly identical between the standard and noise aware solutions. In fact, the state estimates provided by the STND. and N.A. are often equal to within four digits of each other as shown in Table 4. This is expected because, as shown in Equation (26), approaches when is as small as it is in this work. The benefits of the formulation presented in Section 6 will become evident in the uncertainty analysis. For Cases A-D the accuracy of the method does not steadily increase as a function of training data. In general, the output becomes more sensitive to disturbances in the inputs as the training set becomes more populated and the regression becomes more “jagged”. This cannot be the only explanation as with Case B, there is a significant drop in APE between 1000 and 1500 training points. In addition to the density of the training data, smoothness of the regression—how closely the mean curve must approach to the training point—is also a function of the signal-to-noise ratio, . In Case B, for the models using 800 and 1000 training samples is over two orders of magnitude larger than with 1500 training points. Figure 4 shows a slightly worse prediction for the Case B MV-GPR model defined by 1500 training samples, compared to 800 and 1000 samples, given the general trend of increasing accuracy given denser training sets. However, Figure 5 shows that this model is particularly robust to noisy inputs. Therefore, smaller seems to reduce regression accuracy in the deterministic input case, but provide a model which is more robust to input noise.
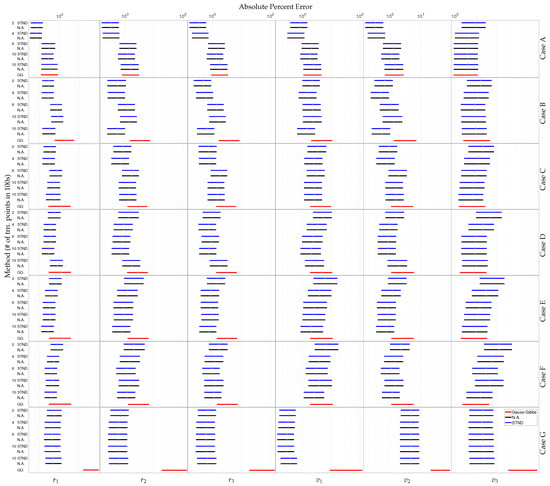
Figure 5.
The point represents the median APE while the boxes enclose the range of points between the 25th and the 75th quantiles of APE for each Cartesian state given uncertain RA and DEC measurements. The GPR methods are listed STND. (blue) Then, N.A. (black) and are ordered by number of training points—200, 400, 800, 1000, and 1500—listed in 100s. The Gauss–Gibbs results are labeled GG and shown in (red).

Table 4.
Median APE for for most accurate model in each orbit case given noisy RA and DEC measurements.
7.3. Effects of Orbit Shape
Now, the effects of the orbit regime within a given case will be investigated for MV-GPR and compared to Gauss–Gibbs method. Case C with 1000 training points is chosen as it shows an investigation of the whole orbit regime from LEO to high-MEO and provides an accurate MV-GPR model for both perfect and noisy measurements.
Figure 6a is a scatter plot of the Gauss–Gibbs and MV-GPR state estimate’s APE averaged across the Cartesian states versus the ground truth and e, which define the orbit shape. Examining the results for the Gauss–Gibbs method shown in the first row of Figure 6, the mean Cartesian APE is shown to be relatively agnostic with respect to the orbit shape given the perfect measurements. Similarly, the APEs for MV-GPR shown in the bottom row of Figure 6a are essentially agnostic to the orbit shape with one caveat being that accuracy degrades near the edges of the distribution. For example, investigating the bottom right corner of Figure 6a, there is an obvious degradation in accuracy. The reasoning for this is again related to the sparsity of data as shown in the accuracy investigation. There are no training points with an SMA greater than km nor eccentricities less than , leading to the sparsity of neighboring training points to aid in the regression.
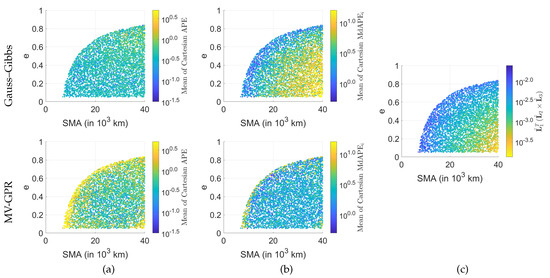
Figure 6.
Effects of orbit shape on GPR predictions for Case C: (a) average of the Cartesian APE of the GPR solution given perfect measurements, (b) the average MdAPE given noisy measurements, (c) the coplanarity of the lines-of-sight. Colorbars represent range for the 99% of points to increase readability in the presence of outliers.
Shifting focus to the effects of input noise. Figure 6b examines the state estimate’s MdAPE. There is a noticeable trend towards a degradation in MdAPE towards larger, more circular orbits for Gauss–Gibbs method. This follows the similar trend for the scalar triple product of the lines-of-sight shown in Figure 6c. The presence of noise together with nearly coplanar geometry—evident by the shrinking scalar triple product—affect the Gauss–Gibbs solution. The MV-GPR study in row 2 of Figure 6b reflects a similar conclusion to that addressed Figure 6a; accuracy is most greatly affected by sparsity of data and not orbital geometry. Unlike the Gauss–Gibbs method, the GPR prediction accuracy should not be directly related to the triple product because it is a regression based method.
7.4. Effects of Coplanarity
The classical Gauss–Gibbs method has been shown to be sensitive to coplanar geometry, as shown in Section 2. Case G is used to further study the effects of coplanarity on the Gauss–Gibbs and MV-GPR solutions. Figure 7a shows the scalar triple product of the lines-of-sight and average of the Cartesian APE of both Gauss–Gibbs and MV-GPR versus true given perfect measurements. Figure 7b shows these values with the inclusion of input noise, while Figure 7c examines the median scalar triple product and MdAPE. As shown in the second row of Figure 7a, there is a large degradation in accuracy around . This corresponds to the scalar triple product approaching zero, thus the the lines-of-sight becoming linearly dependent. As shown in Figure 7b,c, this degradation is exacerbated by the addition of noise leading to a magnitude increase in APE as far as away from the singularity at . Row 3 of Figure 7 reflects the same study but for the MV-GPR method. Again, GPR should be agnostic with respect to coplanarity of the lines-of-sight. Therefore, a decline in accuracy near the singularity at is not present for MV-GPR. Comparing the second and third rows of Figure 7, the GPR methods provide a better estimate with respect to MdAPE by at least a order of magnitude within of the leading to a coplanar singularity.
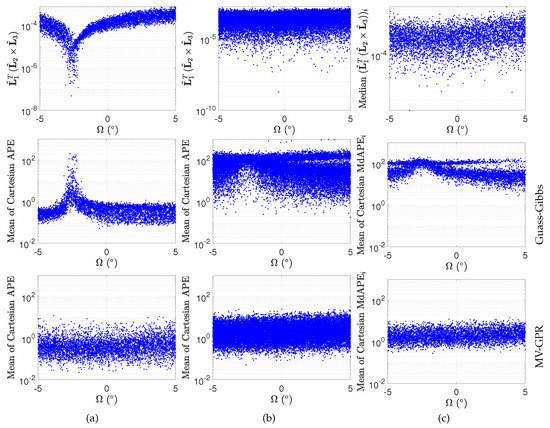
Figure 7.
Effects of coplanarity on Gauss–Gibbs and MV-GPR IOD solutions. (a) scalar triple product of the lines-of-sight and average of the Cartesian APE versus true given perfect measurements. (b) scalar triple product and average of the Cartesian APE versus true given noisy measurements. (c) median scalar triple product and average of the MdAPE versus true for each set of five random samples of the 5000 test orbits.
7.5. Bayesian Model Characterization
Unlike the deterministic Gauss–Gibbs IOD method, both ind-GPR and MV-GPR not only provide a state prediction, but also estimate the model uncertainty. This uncertainty characterization is investigated for Case G at training sample supports of 200 and 1000, as it appears to be in the most likely use-case for GPR-based IOD methods and is representative of all cases.
7.5.1. Perfect Measurements
The Mahalanobis distance from the true state to the predicted mean given the predicted covariance is shown in Figure 8. This shows that the majority of Mahalanobis distances for both GPR methods lie between 1 and 3. This is expected for accurate probability modeling of Gaussian variables and means that, in general, the predicted Gaussian model is neither over-confident nor too cautious. Comparing the two methods, ind-GPR carries a slight advantage in the number of points which stay below a Mahalanobis distance of 3, signaling a possible reduction in number of outliers.
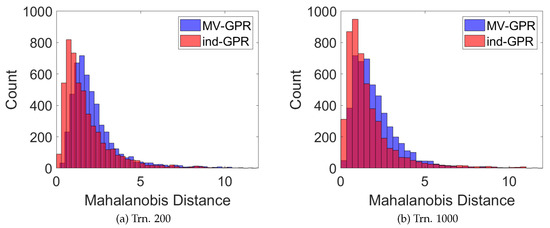
Figure 8.
The Mahalanobis distance from the true state to the GPR-predicted mean given the GPR-predicted covariance (a) 200 and (b) 1000 given perfect RA and DEC measurements.
Figure 9 shows the predicted standard deviation () versus the error between the prediction and the true Cartesian state. Note the threshold for the predicted of both methods. This threshold is defined by the hyperparameter , which in a way acts as the minimal uncertainty in the system, enforcing the fact that one cannot be more certain in predictions of test points than that of the training data. The points for both ind-GPR and MV-GPR follow along the 1- line reflecting the fact that higher errors are characterized by higher variances. Furthermore, the majority of points lie below the 3-, which further reinforces the characteristic that the model is not overly confident. The trend across training levels is that the method is overly cautious for some of its more accurate uncertainty measures, which is likely due in part to the noise term, , included in GPR model, which acts as a minimum variance term. Therefore, forcing a small variance for in the optimization process could help to reduce the over-cautious trend of the prediction covariance. However, recall this will likely reduce the model’s robustness to input noise as posited in the accuracy study. As training levels increase, the GPR estimates appear to more accurately represent that trend line, especially for the MV-GPR algorithm, because the model accuracy increases as training levels increase.
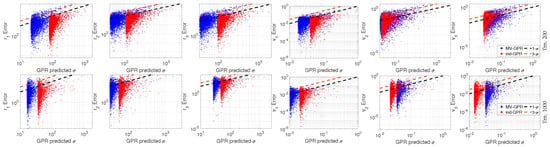
Figure 9.
Predicted standard deviation versus the error between the predicted mean and the true Cartesian state given perfect RA and DEC measurements.
Table 5 shows the percentage of points which lie within the predicted 1– and 3– bounds estimated by each GPR model. Under a normal distribution, of all estimates will lie within 1– while should lie within 3– bound. At both 200 and 1000 training points, the ind-GPR is vastly over cautious in the variance estimate for , , , and with the percentage of points within the 1– fluctuating in the high nineties. This highlights the inflexibility of the ind-GPR to provide accurate uncertainty estimation for each output dimension. In contrast, MV-GPR is able to provide more flexible variance estimation such the percentage of points within a given bound more accurately reflect the true errors.

Table 5.
Percentage of errors within –bound for ind- and MV-GPR given perfect input measurements.
Figure 10 are plots of the true Cartesian state versus the GPR prediction error with accompanying 2- bounds for a random 500 point sub-sample of the 5000 test orbits for readability. Here, MV-GPR is able to better track the true error by encoding the covariance between the components of the output state. By definition, the covariance estimate in the ind-GPR algorithm is independent and identically distributed (IID) before re-normalization. From Figure 10 and Table 5, we see that in this case the IID assumption leads to the prediction being over-cautious in the estimates. The covariance bounds for the elements in are much larger than the true error, in general. Therefore, the covariance associated with the ind-GPR only provides a measure of confidence in the output as a whole rather than providing accurate uncertainty information for each of the Cartesian dimensions. MV-GPR tunes the covariance estimation for each output dimension, therefore it is able to more accurately represent model uncertainty in each Cartesian dimension. Finally, the average covariance bounds shrink around four-fold between the case of 200 and 1000 training samples therefore showcasing the effects of sparsity in training data.
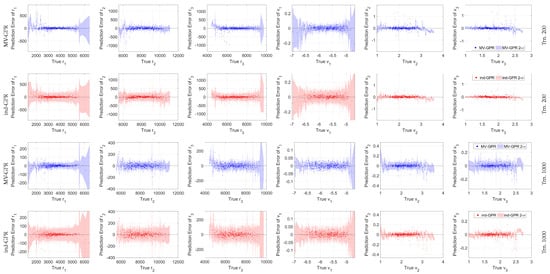
Figure 10.
Cartesian state versus the GPR output error with accompanying 3- bounds for a 500 point random sub-sample of the 5000 test orbits. Note the differing y-scale between the training levels.
7.5.2. Uncertain Angular Measurements
Recall that the Bayesian model predicted from GPR only characterizes model uncertainty as implemented in this work, therefore the predictive uncertainty characterization will suffer greatly in the presence of input noise. Figure 11 shows the Mahalanobis distance for both the standard MV-GPR formulation and the noise aware formulation presented in Section 6. For the the standard MV-GPR method, the uncertainty is grossly underestimated as the model and inference has zero uncertainty information from the test inputs. The method presented in Section 6 is meant to address this and, as reflected in the second row of Figure 11, does an excellent job at reducing the Mahalanobis distance to within more reasonable bounds. There is a more pronounced effect on the 1000 point training set because model uncertainty decreases as the number of training points increases. Therefore, the effects of uncertain inputs become the dominating term.
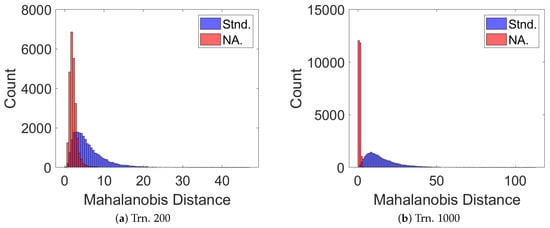
Figure 11.
The Mahalanobis distance from the true state to the GPR-predicted mean given the GPR-predicted covariance for Case G at training samples of (a) 200 and (b) 1000 given uncertain RA and DEC measurements for the standard MV-GPR (blue) and the noise-aware MV-GPR (red).
Figure 12 shows the predicted versus the estimate error for each Cartesian state for models with 200 training points in the first row and 1000 training points in the second. The ability of the noise aware MV-GPR method to accurately quantify the true error is evident. At 200 training points, the model uncertainty is very much present, so the noise aware estimation adds often less than an order of magnitude to the estimated . Since the model uncertainty is reduced at increased training levels, the noise aware MV-GPR method has a greater effect on predicted values. This results in an almost order of magnitude increase between the standard and noise aware methods.
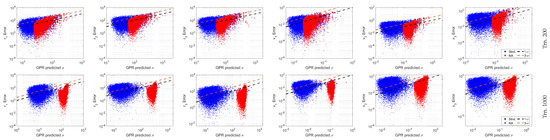
Figure 12.
Predicted standard deviation versus the error between the predicted mean and the true Cartesian state given uncertain angular measurements.
The percentage of points which lie within the GPR estimated 1– and 3– bounds are shown in Table 6. Over of points lie outside the 1– bounds predicted by standard MV-GPR at 1000 training points. This is only marginally improved examining the standard model at 200 training points, but that is largely attributed to the model error of the regression model accounting for a still significant portion of the true error. The percentage of points which lie within bounds for the noise aware MV-GPR at 200 training points hovers close to the and which define a perfect normal distribution. At 200 training points, the noise aware model over-estimates the uncertainty contribution of the input noise as evident from the high ninety percentile of points within the 1–.

Table 6.
Percentage of errors within –bound for standard and noise aware MV-GPR.
Figure 13 shows the true Cartesian elements versus the prediction error for a 500 point sub-sample of the 25,000 random noisy measurements. At 200 training points, the difference between the standard and noise aware MV-GPR inference implementations is limited as the regression uncertainty is dominated by model uncertainty. The benefits of the noise aware method is much more evident at 1000 training points. The standard inference method vastly underestimates uncertainty for the majority of samples while the noise aware method better captures the true error though being slightly over-cautious.
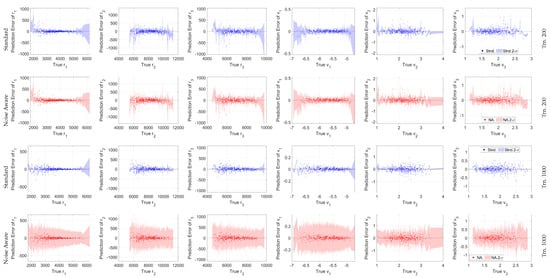
Figure 13.
Cartesian state versus the GPR output error with accompanying 3- bounds for a 500 point random sub-sample of the 25,000 total samples. Note the different y-axis scales between the training levels.
7.6. Qualitative Study
Now, with general trends established, it is important to perform a qualitative study on the proposed techniques using exemplar orbits shown in Table 7. In this section, the iterative Gauss–Gibbs method is utilized to better show the effect of GPR model bias. Orbit A represents an orbit in a regime where both Gauss–Gibbs method and the proposed GPR methods perform well. Orbit B represents a high MEO orbit in an orbit shape which the Gauss–Gibbs method with iteration is shown to begin to degrade in accuracy. Orbit C represents the failure case of a nearly coplanar orbit. In these studies, the true anomaly at the first and third measurement time are separated from . For each orbit, 250 uncertain RA and DEC measurements are generated using the noise model defined in Section 7.1.2 at pointing errors of , , and . The GPR models for Orbits A and B are generated using 1000 training samples from Case C in Table 1, while the model for Orbit C is generated from Case G training data set at 1000 training samples.

Table 7.
Exemplar orbits for qualitative study.
Figure 14 shows the distribution of the 250 samples for Orbit A at varying noise levels for both Gauss–Gibbs and noise aware MV-GPR methods. The levels of noise have very similar effects in inflating the resulting distribution between both methods. The distribution of the Gauss–Gibbs iterative method centers around the truth, while that of the GPR method shows a model bias. This bias is especially prevalent for pointing errors of and because the prediction uncertainty at these low levels of noise is still dominated by the model error. Therefore, the GPR distributions are centered around their model bias, or their prediction given perfect RA and DEC measurements. Again, this dominating model uncertainty and bias is caused by the sparsity of training data associated with the large orbit distribution of Case C.
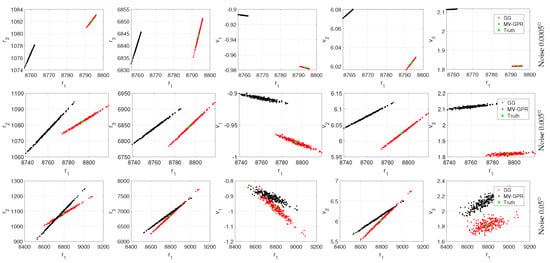
Figure 14.
Qualitative study of Orbit A at various noise levels. The black points are MV-GPR and the red are Gauss–Gibbs predictions, while the green point represents the truth.
The effects of geometry and noise in the IOD process begin to show in Figure 15, a study of the distribution of the 250 samples for Orbit B at varying noise levels for both Gauss–Gibbs and noise aware MV-GPR methods. Again, model uncertainty is the dominate term for the MV-GPR model at a noise level of . At a level of , the measurement noise begins to degrade the Gauss–Gibbs prediction accuracy. Here, the GPR methods provide a tighter distribution in all Cartesian states, though still centered around the model bias. Finally at a noise level of , the measurement noise dominates. This leads to a large distribution in the Gauss–Gibbs predictions while the MV-GPR solutions provide a tighter-distribution, closer to the truth, for all Cartesian elements.
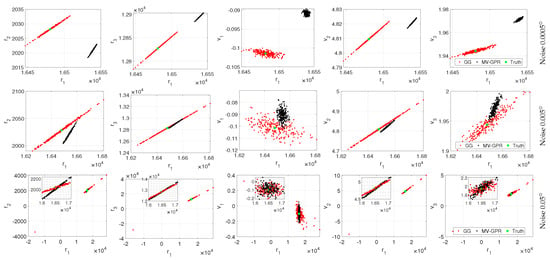
Figure 15.
Qualitative study of Orbit B at various noise levels. The black points are MV-GPR and the red are Gauss–Gibbs predictions, while the green point represents the truth.
Figure 16 shows the distribution of the 250 samples for the nearly coplanar orbital geometry case, Orbit C, at varying noise levels. Again, the near-coplanar lines-of-sight measurements present for Orbit C lead to a complete degradation in the accuracy of Gauss–Gibbs method. Even at the lowest noise levels, the MV-GPR solution provides a nearly order of magnitude decrease in the distribution of the noisy predictions. At measurement errors, the Gauss–Gibbs prediction distribution is on the order of 1000 km in position and hundreds of in velocity. In stark contrast, the MV-GPR prediction distribution is on the order of 10 km in position and tens of , providing orders-of-magnitude increase in accuracy. Finally, the Gauss–Gibbs method completely degrades at . MV-GPR’s prediction for Orbit C provides accuracy comparable to Gauss–Gibbs method for Orbit A in Figure 14, which represents an orbit where accurate Gauss–Gibbs predictions are expected.
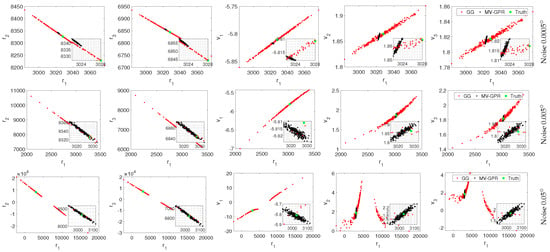
Figure 16.
Qualitative study of Orbit C at various noise levels. The black points are MV-GPR and the red are Gauss–Gibbs predictions, while the green point represents the truth.
8. Conclusions
In summary, this work examines the effects of a target’s orbit regime on the classical Gauss–Gibbs angles-only IOD method and showcases the sensitivity of the Gauss–Gibbs method to input noise and a coplanar observer-target geometry. Gauss–Gibbs method shows sensitivity to varying levels input noise dependent on the orbit regime of the target. Furthermore, the combination of input noise and nearly-coplanar observation geometry leads to complete degradation of prediction accuracy for Gauss–Gibbs method. The GPR methods implemented in this work provided a relatively accurate model less sensitive to orbital geometry and observation uncertainty. Given perfect inputs, these machine learning methods degrade in accuracy as training sets become more sparse. However, that sparsity actually proves beneficial when high levels of noise are introduced to the right ascension and declination because of the increased GPR mean-function smoothness. The GPR methods not only provide a point solution, but also characterize the model uncertainty—an added benefit over classical methods. In the case of perfect measurements, the multivariate GPR (MV-GPR) method outperforms the multitask learning GPR method (ind-GPR) in this uncertainty characterization due to the inclusion of output correlations. Given noisy RA and DEC measurements, the noise aware inference method inflates the predicted uncertainty to capture not only the model uncertainty, but also the induced uncertainty from random inputs. This results in accurate variance inflation for MV-GPR trained at 200 training points, while predicted variance is over-inflated at 1000 training points for the test case presented in this work.
Given that specific orbital regimes are more frequently encountered in practice, it could prove advantageous to tailor training data to reflect this distribution or even use true observations. Furthermore, although observation frame manipulation may make the GPR method agnostic to observation site longitude, the latitude and altitude will have a significant effect on observer-target geometry. Addressing this observation site dependence will prove beneficial. Proper characterization of the noise will likely prove extremely beneficial for model robustness with respect to input noise given the GPR signal-to-noise ratio affects on model sensitivity.
Author Contributions
Conceptualization, D.S., P.S. and S.O.; Data curation, D.S.; Formal analysis, D.S.; Funding acquisition, P.S.; Investigation, D.S.; Methodology, D.S.; Project administration, P.S.; Resources, P.S.; Software, D.S.; Supervision, P.S. and S.O.; Validation, D.S.; Visualization, D.S., P.S. and S.O.; Writing—original draft, D.S.; Writing—review & editing, P.S. and S.O. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported through United States Air Force under FA9550-20-1-0176, AFOSR grant number FA9550-17-1-0088, and the DoD’s SMART program. The contents are those of the author(s) and do not necessarily represent the official views of, nor an endorsement, by AFOSR or the U.S. Government.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IOD | Initial Orbit Determination |
| GG | Gauss–Gibbs Orbit Determination Algorithm |
| GPR | Gaussian Process Regression |
| ind-GPR | Independent Gaussian Process Regression |
| MV-GPR | Multivariate Gaussian Process Regression |
| SE | Square Exponential Covariance Function |
| STND | Standard Multivariate Gaussian Process Regression |
| NA | Noise Aware Multivariate Gaussian Process Regression |
| SSA | Space Situational Awareness |
| RA | Right Ascension |
| DEC | Declination |
| SE | Square Exponential |
| ARD | Automatic Relevance Determination |
| APE | Absolute percent error |
| MdAPE | Median absolute percent error |
| TOF | Time-of-flight |
| IID | independent and identically distributed |
Appendix A
Here, we will give a brief explanation of the numerical difficulties with the method presented in Section 6 and how they were addressed. First, Equation (28) can be rewritten such that
where is defined in Equation (17). The numerical issues are most prevalent in the term. Due to the inverse calculation, is only accurate to a finite number of digits. Therefore, the term appears to suffer from catastrophic cancellation. This is corroborated by inspection by the author. As the condition number of increased, the term became increasingly numerically sensitive as evident by producing a non-symmetric and/or a non-positive semi-definite term. To alleviate this sensitivity, the eigenvalue decomposition is performed on symmetric matrix such that , eigenvalues less than were zeroed, and the is calculated such that
This formulation significantly relieved the numerical difficulties and ensured symmetric positive definite covariance estimates.
References
- Adurthi, N.; Majji, M.; Singla, P. Quadrature-Based Nonlinear Joint Probabilistic Data Association Filter. J. Guid. Control. Dyn. 2019, 42, 2369–2381. [Google Scholar] [CrossRef]
- Vallado, D.A. Fundamentals of Astrodynamics and Applications, 4th ed.; Space Technology Library; Microcosm Press: Hawthorne, CA, USA, 2013. [Google Scholar]
- Schwab, D.; Singla, P.; Raquepas, J. Uncertainty Characterization and Surrogate Modeling for Angles-Only Initial Orbit Determination. In Proceedings of the 2019 AAS/AIAA Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019; American Astronautical Society: Springfield, VA, USA, 2019. [Google Scholar]
- Hixon, S.; Schwab, D.; Reiter, J.; Singla, P. Conjugate Unscented Transformation Based Semi-Analytic Approach for Uncertainty Characterization of Angles-Only Initial Orbit Determination Algorithms. In Proceedings of the 70th International Astronautical Congress, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Schwab, D.; Singla, P.; Huang, D. Multi-Variate Gaussian Process Regression for Angles-Only Initial Orbit Determination. In Proceedings of the 2020 AAS/AIAA Astrodynamics Specialist Conference, Lake Tahoe, CA, USA, 9–12 August 2020. [Google Scholar]
- Martínez, F.; Águeda Maté, A.; Grau, J.; Fernández Sánchez, J.; Aivar García, L. Comparison of Angles Only Initial Orbit Determination Algorithms for Space Debris Cataloguing. J. Aerosp. Eng. Sci. Appl. 2012, 4, 39. [Google Scholar]
- Schaeperkoetter, A.V. A Comprehensive Comparison between Angles-Only Initial Orbit Determination Techniques. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2011. [Google Scholar]
- Vallado, D.A. Evaluating Gooding Angles-Only Orbit Determination of Space Based Space Surveillance Measurements; Maui Economic Development Board: Maui, HI, USA, 2010. [Google Scholar]
- Weisman, R.M.; Majji, M.; Alfriend, K.T. Analytic Characterization of Measurement Uncertainty and Initial Orbit Determination on Orbital Element Representations. Celest. Mech. Dyn. Astron. 2014, 118, 165–195. [Google Scholar] [CrossRef]
- Worthy, J.L.; Holzinger, M.J. Incorporating Uncertainty in Admissible Regions for Uncorrelated Detections. J. Guid. Control. Dyn. 2015, 38, 1673–1689. [Google Scholar] [CrossRef] [Green Version]
- Binz, C.R.; Healy, L.M. Direct Uncertainty Estimates from Angles-Only Initial Orbit Determination. J. Guid. Control. Dyn. 2018, 41, 34–46. [Google Scholar] [CrossRef]
- Lee, B.S.; Kim, W.G.; Lee, J.; Hwang, Y. Machine Learning Approach to Initial Orbit Determination of Unknown LEO Satellites. In Proceedings of the 2018 SpaceOps Conference, Marseille, France, 28 May–1 June 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
- Peng, H.; Bai, X. Covariance Fusion Strategy of Gaussian Processes Covariance and Orbital Prediction Uncertainty. In Proceedings of the 2019 AAS/AIAA Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019; American Astronautical Society: Springfield, VA, USA, 2019. [Google Scholar]
- Rasmussen, C.E. Evaluation of Gaussian Processes and Other Methods for Non-Linear Regression. Ph.D Thesis, University of Toronto, Toronto, ON, Canada, 1997. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning; MIT Press: Cambridge, UK, 2006. [Google Scholar]
- Liu, H.; Cai, J.; Ong, Y.S. Remarks on Multi-Output Gaussian Process Regression. Knowl.-Based Syst. 2018, 144, 102–121. [Google Scholar] [CrossRef]
- Boyle, P.; Frean, M. Dependent Gaussian Processes. In NIPS’04: Proceedings of the 17th International Conference on Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2005; Volume 17, pp. 217–224. [Google Scholar]
- Alvarez, M.A.; Rosasco, L.; Lawrence, N.D. Kernels for Vector-Valued Functions: A Review. arXiv 2012, arXiv:1106.6251. [Google Scholar]
- Wang, B.; Chen, T. Gaussian Process Regression with Multiple Response Variables. Chemom. Intell. Lab. Syst. 2015, 142, 159–165. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Wang, B.; Gorban, A.N. Multivariate Gaussian and Student-t Process Regression for Multi-Output Prediction. Neural Comput. Appl. 2020, 32, 3005–3028. [Google Scholar] [CrossRef] [Green Version]
- Candela, J.; Girard, A.; Larsen, J.; Rasmussen, C. Propagation of Uncertainty in Bayesian Kernel Models—Application to Multiple-Step Ahead Forecasting. In Proceedings of the 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing, Hong Kong, China, 21 May 2003; Volume 2. [Google Scholar]
- Schwab, D. Efficacy of Gaussian Process Regression for Angles-Only Initial Orbit Determination. Master’s Thesis, The Pennsylvania State University, University Park, USA, 2020. [Google Scholar]
- Curtis, H.D. Orbital Mechanics for Engineering Students, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Pocuca, N.; Gallaugher, M.P.B.; Clark, K.M.; McNicholas, P.D. Assessing and Visualizing Matrix Variate Normality. arXiv 2019, arXiv:1910.02859. [Google Scholar]
- Dawid, A.P. Some Matrix-Variate Distribution Theory: Notational Considerations and a Bayesian Application. Biometrika 1981, 68, 265–274. [Google Scholar] [CrossRef]
- Deisenroth, M.P. Efficient Reinforcement Learning Using Gaussian Processes; Karlsruhe Institute of Technology: Karlsruhe, Germany, 2010. [Google Scholar]
- Rasmussen, C.E.; Nickisch, H. The GPML Toolbox Version 4.2. Available online: http://www.gaussianprocess.org/gpml/code/matlab/doc/ (accessed on 6 June 2019).
- Chen, Z. Multivariate Gaussian and Student-t Process Regression. Available online: https://github.com/Magica-Chen/gptp_multi_output (accessed on 8 April 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).