Abstract
In the paper, a new adaptive model of a neuron based on the Hindmarsh–Rose third-order model of a single neuron is proposed. The learning algorithm for adaptive identification of the neuron parameters is proposed and analyzed both theoretically and by computer simulation. The proposed algorithm is based on the Lyapunov functions approach and reduced adaptive observer. It allows one to estimate parameters of the population of the neurons if they are synchronized. The rigorous stability conditions for synchronization and identification are presented.
1. Introduction
The human brain is one of the most complex systems existing on Earth. Many researchers have been working hard for many years in order to understand how the human brain is functioning, to create its model, and to redesign its construction [1,2]. Recently, the study of the whole brain dynamics models has started [3,4]. However, the overwhelming complexity demands a variety of simplified models of different complexity degrees. The simplest models are represented as the networks of biological neuron models connected by couplings. Typical models of this class are based on the celebrated Hodgkin–Huxley model and its simplifications: FitzHugh–Nagumo (FHN), Morris–Lecar (ML), Hindmarsh–Rose (HR), etc. New models still appear in the literature, e.g., [5]. The HR model is the simplest one that can exhibit most of the biological neuron’s behavior, such as spiking or bursting.
Chong et al. [6] studied the activity of neurons at the macroscopic level, known in the literature as “neural mass models”. To estimate the neurons’ activity, a robust circle criterion observer was proposed, and its application to estimate the average membrane potential of neuron populations in the single cortical column model was demonstrated. Further steps were based on using network models. However, well-understood linear network models [7,8] are not suitable for modeling networks of biological neurons. A number of approaches to state estimation for neural populations are based on synchronization; see [9,10] and the references therein.
An important part of brain network modeling is the identification of the model parameters. Its first step is the identification of the building blocks—the models of the single neurons or their subpopulations. Ideally, it should be performed based on the neuron state measurements. However, there exists the problem of uncertainty and incomplete measurements. A number of such approaches based on adaptation and learning are described in the literature. Dong et al. [11] dealt with an identification of the FHN model dynamics, employing the deterministic learning and interpolation method. For global identification, the FHN model was transformed in [11] into a set of ordinary differential equations (ODEs), and the dynamics of the approximation system were then identified by employing deterministic learning. In [12], an approach to solving the problem of identifying topology and parameters in HR neural networks was proposed. For this purpose, the so-called generalized extremal optimization (GEO) was introduced, and a heuristic identification algorithm was employed. Identifying HR neural networks’ topology was also considered by Zhao et al. [13], who employed the sinusoidal disturbance to identify the topology at the stage when the complex network achieves synchronization. It was demonstrated by the simulations that, compared with the disturbance of all the nodes, the disturbance of the key nodes alone can achieve a very good effect. In [14], an adaptive observer for asymptotical estimation of the parameters and states of a model of interconnected cortical columns was presented. The model adopted is capable of realistically reproducing the patterns seen on (intracranial) electroencephalograms (EEGs). The assessment of the parameters and status allows a better understanding of the mechanisms underlying neurological phenomena and can be used to predict the onset of epileptic seizures. Tang et al. [15] studied the effect of electromagnetic induction on the electrical activity of neurons, and the variable for magnetic flow was used to improve the HR neuron model. By the simulations, it was demonstrated that the neuron model, proposed in [15], can show multiple modes of electrical activity, which is dependent on the time delay and external forcing current. In [16], an approach based on adaptive observers was developed for partial identification HR model parameters. Malik and Mir [17] studied the synchronization of HR neurons, demonstrating that the coupled system shows several behaviors depending on the parameters of the HR model and coupling function. Recently, Xu [18] proposed to use an impulse response identification experiment with dynamical observations with an increasing data length for capturing the real-time information of systems and serving for online identification. In Xu [18], a separable Newton recursive parameter estimation approach was developed, and its efficacy was demonstrated by the Monte Carlo tests.
The models of biological neural networks and single neurons have many applications, e.g., in brain–computer interfaces [19,20,21]. A practical application of coupled HR neural networks was also discussed in [17]. In particular, it was demonstrated that the spiking network successfully encodes and decodes a time-varying input. Synchronization of the artificial HR neurons was also studied in [22,23]. An adaptive controller that provides synchronization of two connected HR neurons using only the output signal of the reference neuron was suggested in [22]. Andreev and Maksimenko [24] considered synchronization in a coupled neural network with inhibitory coupling. It was shown in [24] that in the case of a discrete neuron model, the periodic dynamics are manifested in the alternate excitation of various neural ensembles, whereas periodic modulation of the synchronization index of neural ensembles was observed in the continuous-time model.
In this paper, the problem of HR neuron model parameters’ identification is considered. To solve this, the reduced-order adaptation algorithm based on the speed gradient (SG) method and feedback Kalman–Yakubovich lemma (FKYL) [25,26] is proposed. A rigorous statement about the convergence of the parameter estimates to the true values was formulated, and the proof is given. The performance of the identification procedure was analyzed by computer simulation.
The remainder of the paper is organized as follows. The problem statement is presented in Section 2. Section 3 presents the design of the adaptation algorithm. The main results are given in Section 4. Computer simulation results are described in Section 5. Concluding remarks and the future work intentions of Section 6 finalize the paper.
2. Problem Statement
Consider the classical Hindmarsh–Rose (HR) neuron model [27]:
The variable is the membrane potential, while are the fast and slow ionic currents, respectively. Variables represent the state vector . The values are model parameters. We considered all quantities to be dimensionless.
Assume that , , can be measured. In some cases (e.g., in in vitro experiments), this assumption is quite realistic. In order to estimate the state and parameters of the HR neuron model (1), introduce an auxiliary system—adaptive model—as follows:
The variables represent the state vector of the adaptive model (2). The term is the stabilizing term, typical for observers.
In this study, we assumed for simplicity that the value characterizing the relative rate of fast and slow currents is known. Then, one may denote the vector of tunable parameters , where , , , , , , . The problem is to design the adaptation/learning algorithm for ensuring the goals:
where .
3. Adaptation/Learning Algorithm Design
The equations for the state estimation error are as follows:
where , , ,
For the design of the adaptation/learning algorithm, we used the speed gradient method [28], suggesting to change the tunable vector in the direction of the gradient in of the speed of changing the goal function , where along the trajectories of the system (1), (2). It is suggested to choose quadratic goal function , where is a positive-definite matrix to be determined later. Since depends only on e, the error model (5) can be used instead of (1), (2) at this stage. Applying the SG methodology [25,28] yields the following algorithm:
4. Main Results
The following proposition concerning the convergence of the adaptive model to the true one holds.
Theorem 1.
The proof is based on exploiting the Lyapunov function:
Applying (6) to (8) yields . Condition is fulfilled when:
where . Since the eigenvalues of have a negative real part, P, introduced before, is the solution of Lyapunov Equation (9). The fact that is bounded is obtained from [29]. It is shown that the solutions of the system (1) are bounded, and the synchronization error is also bounded.
Definition 1.
Time-varying vector function is persistent excitation (PE) if it is bounded and there exists and such that :
Theorem 5.1 in Fradkov [25], the conditions for achieving goal (4) are derived. His theorem is reformulated below for the problem of interest.
Theorem 2.
Persistent excitation of vector is equivalent to the existence of such as satisfying [28]. The proof of PE for the signals mentioned before is quite simple. Let at some moment t, . This equation has no more then three separate solutions. Then, for an arbitrary close moment, equation does not hold. The PE of the rest of the equations is proven similarly.
Remark 1.
The identification algorithm (6) requires the measurement of all state system variables. It is aimed at studying real neural cells “in vitro”, i.e., during real experiments with single cells where the measurement of all auxiliary variables can be implemented.
5. Computer Simulation
5.1. Neuron Modeling
For the systems (1), (2) and algorithm (6), we conducted mathematical modeling to ensure that the approach adequately meets the formulated problem. We built the neuron model (1) and observed different dynamical behaviors, which are presented in Figure 1, Figure 2 and Figure 3.
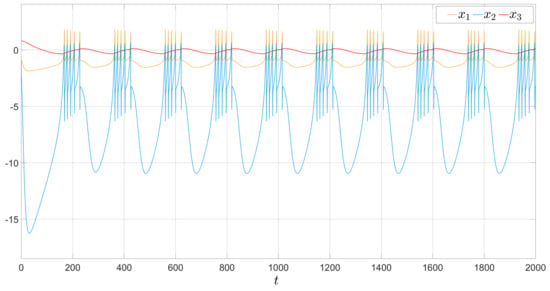
Figure 1.
Regular bursting, .
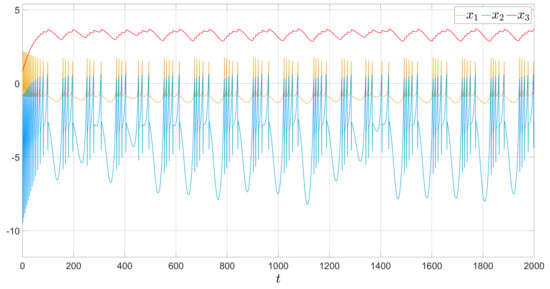
Figure 2.
Irregular bursting .
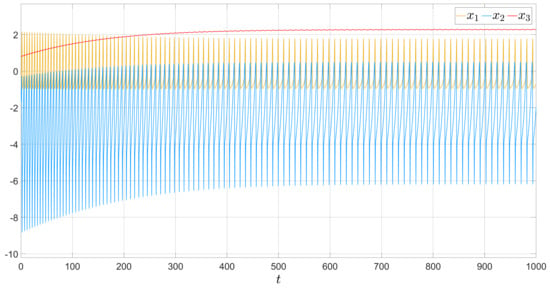
Figure 3.
Regular spiking, .
We chose numerical values of quantities from [30] where the bifurcation analysis of the HR neuron was performed. , and parameters , and I are in the figure captions.
5.2. Regular Neuron Modeling
Secondly, we modeled the difference of the systems (1) and (2) in order to perform the identification process by Algorithm (6). The parameters of the observer were calculated just in time by the adaptation algorithm. One can see the identification process in Figure 4. It is seen that the observer parameters converge to the reference neuron parameters. However, synchronization error converges to zero, which is shown in Figure 5
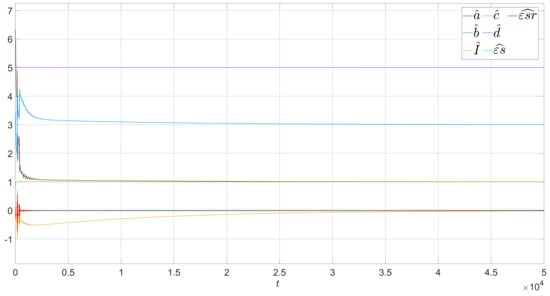
Figure 4.
Identification process, .
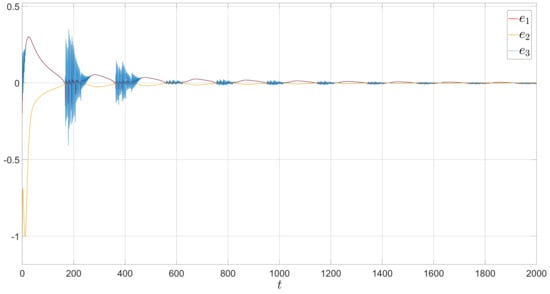
Figure 5.
Synchronization error for bursting, .
Further simulations showed that the convergence depends on the small parameter , and too small values may result in the divergence of the identification process. The reason is the liner part of error Equation (5). One may subtract regularization term from the third equation of (2). The linear part of will take the form:
After this modification, convergence becomes faster. You may see the accelerated identification process in Figure 6 and Figure 7. The synchronization error for irregular bursting is shown on Figure 8.
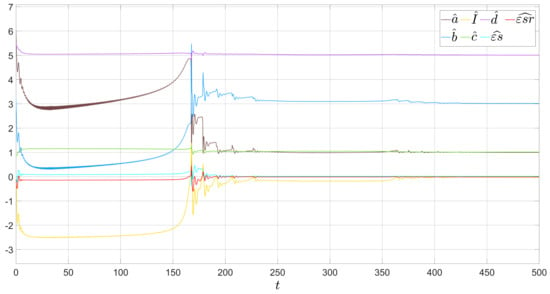
Figure 6.
Identification process for bursting regime, .
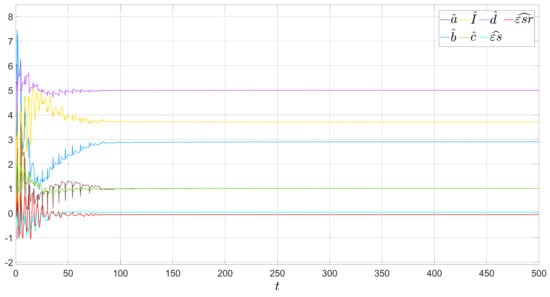
Figure 7.
Identification process for irregular bursting regime, .
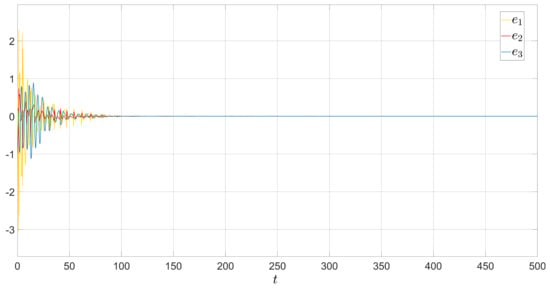
Figure 8.
Synchronization error.
5.3. Robustness of Identification with Respect to Noise
Suppose time-varying ultimately bounded disturbance . Let us propagate in the first equation on Model (1). If is small enough [31], then the adaptive system will have globally bounded solutions. The identification process for the system with disturbance is presented in Figure 9.
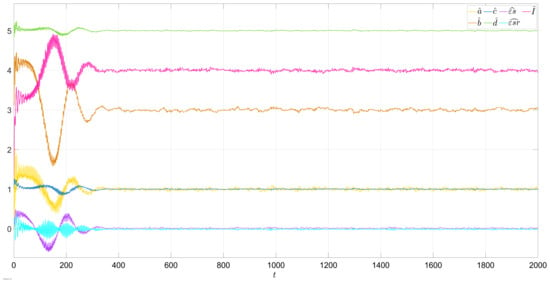
Figure 9.
Identification with bounded Gaussian disturbance .
6. Conclusions
A new algorithm for Hindmarsh–Rose neuron model parameter estimation based on the Lyapunov functions approach and reduced adaptive observer was proposed. It allows one to estimate the parameters of the population of the neurons if they are synchronized. The rigorous stability conditions for synchronization and identification were presented. Future work will be aimed at taking into account disturbances and measurement noises. It would be also interesting to use the Hindmarsh–Rose model instead of the FitzHugh–Nagumo model for studying gamma oscillation activity in the brain [32]. In future research, it is also planned to apply the results of the works [33], where the state filter for a time delay state-space system with unknown parameters from noisy observation information was proposed, and [34], where a gradient approach for the adaptive filter design based on the fractional-order derivative and a linear filter was developed.
Author Contributions
Conceptualization, A.L.F.; data curation, A.K. and B.A.; formal analysis, A.L.F. and A.K.; funding acquisition, A.L.F.; investigation, A.K. and B.A.; methodology, A.L.F.; project administration, A.L.F.; software, A.K.; supervision, A.L.F.; writing—original draft, A.K. and B.A.; writing—review and editing, A.L.F. and B.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Project No. 075-15-2021-573, performed in the IPME RAS). The mathematical formulation of the problem was performed partly in SPbU under the support of SPbU Grant ID 84912397.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EEG | electroencephalogram |
| FHN | FitzHugh–Nagumo |
| FKYL | feedback Kalman–Yakubovich lemma |
| HR | Hindmarsh–Rose |
| LTI | linear time-invariant |
| ML | Morris–Lecar |
| ODE | ordinary differential equation |
| PE | persistent excitation |
| SG | speed gradient |
References
- Ashby, W.R. Design for a Brain; Wiley: New York, NY, USA, 1960. [Google Scholar]
- Rabinovich, M.; Friston, K.J.; Varona, P. Principles of Brain Dynamics: Global State Interactions; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Breakspear, M. Dynamic models of large-scale brain activity. Nat. Neurosci. 2017, 20, 340–352. [Google Scholar] [CrossRef] [PubMed]
- Cofré, R.; Herzog, R.; Mediano, P.A.; Piccinini, J.; Rosas, F.E.; Sanz Perl, Y.; Tagliazucchi, E. Whole-brain models to explore altered states of consciousness from the bottom up. Brain Sci. 2020, 10, 626. [Google Scholar] [CrossRef] [PubMed]
- Belyaev, M.; Velichko, A. A Spiking Neural Network Based on the Model of VO2-Neuron. Electronics 2019, 8, 1065. [Google Scholar] [CrossRef] [Green Version]
- Chong, M.; Postoyan, R.; Nešić, D.; Kuhlmann, L.; Varsavsky, A. A robust circle criterion observer with application to neural mass models. Automatica 2012, 48, 2986–2989. [Google Scholar] [CrossRef] [Green Version]
- Dzhunusov, I.A.; Fradkov, A.L. Synchronization in networks of linear agents with output feedbacks. Automat. Remote Control 2011, 72, 1615–1626. [Google Scholar] [CrossRef]
- Furtat, I.; Fradkov, A.; Tsykunov, A. Robust synchronization of linear dynamical networks with compensation of disturbances. Intern. J. Robust Nonlinear Control. 2014, 24, 2774–2784. [Google Scholar] [CrossRef]
- Lehnert, J.; Hövel, P.; Selivanov, A.; Fradkov, A.L.; Schöll, E. Controlling cluster synchronization by adapting the topology. Phys. Rev. E 2014, 90, 042914. [Google Scholar] [CrossRef] [Green Version]
- Plotnikov, S. Synchronization conditions in networks of Hindmarsh–Rose systems. Cybern. Phys. 2021, 10, 254–259. [Google Scholar] [CrossRef]
- Dong, X.; Si, W.; Wang, C. Global Identification of FitzHugh–Nagumo Equation via Deterministic Learning and Interpolation. IEEE Access 2019, 7, 107334–107345. [Google Scholar] [CrossRef]
- Wang, L.; Yang, G.; Yeung, L. Identification of Hindmarsh–Rose Neuron Networks Using GEO Metaheuristic. In Proceedings of the Second International Conference on Advances in Swarm Intelligence-Volume Part I, Chiang Mai, Thailand, 26–30 July 2019; Springer: Berlin/Heidelberg, Germany, 2011; pp. 455–463. [Google Scholar]
- Zhao, J.; Aziz-Alaoui, M.A.; Bertelle, C.; Corson, N. Sinusoidal disturbance induced topology identification of Hindmarsh–Rose neural networks. Sci. China Inf. Sci. 2016, 59, 112205. [Google Scholar] [CrossRef]
- Postoyan, R.; Chong, M.; Nešić, D.; Kuhlmann, L. Parameter and state estimation for a class of neural mass models. In Proceedings of the 51st IEEE Conference Decision Control (CDC 2012), Maui, HI, USA, 10–13 December 2012; pp. 2322–2327. [Google Scholar] [CrossRef]
- Tang, K.; Wang, Z.; Shi, X. Electrical Activity in a Time-Delay Four-Variable Neuron Model under Electromagnetic Induction. Front. Comput. Neurosci. 2017, 11. [Google Scholar] [CrossRef] [Green Version]
- Mao, Y.; Tang, W.; Liu, Y.; Kocarev, L. Identification of biological neurons using adaptive observers. Cogn. Process. 2009, 10. [Google Scholar] [CrossRef]
- Malik, S.; Mir, A. Synchronization of Hindmarsh Rose Neurons. Neural Netw. 2020, 123, 372–380. [Google Scholar] [CrossRef]
- Xu, L. Separable Newton Recursive Estimation Method Through System Responses Based on Dynamically Discrete Measurements with Increasing Data Length. Int. J. Control Autom. Syst. 2022, 20, 432–443. [Google Scholar] [CrossRef]
- Bonci, A.; Fiori, S.; Higashi, H.; Tanaka, T.; Verdini, F. An Introductory Tutorial on Brain–Computer Interfaces and Their Applications. Electronics 2021, 10, 560. [Google Scholar] [CrossRef]
- Chung, M.A.; Lin, C.W.; Chang, C.T. The Human–Unmanned Aerial Vehicle System Based on SSVEP–Brain Computer Interface. Electronics 2021, 10, 25. [Google Scholar] [CrossRef]
- Choi, H.; Lim, H.; Kim, J.W.; Kang, Y.J.; Ku, J. Brain Computer Interface-Based Action Observation Game Enhances Mu Suppression in Patients with Stroke. Electronics 2019, 8, 1466. [Google Scholar] [CrossRef] [Green Version]
- Kovalchukov, A. Adaptive identification and synchronization for two Hindmarsh–Rose neurons. In Proceedings of the 2021 5th Scientific School Dynamics of Complex Networks and their Applications (DCNA), Kaliningrad, Russia, 13–15 September 2021; pp. 108–111. [Google Scholar] [CrossRef]
- Semenov, D.; Fradkov, A. Adaptive control of synchronization for the heterogeneous Hindmarsh–Rose network. In Proceedings of the 3rd IFACWorkshop on Cyber-Physical & Human Systems CPHS, Shanghai, China, 3–5 December 2020. [Google Scholar] [CrossRef]
- Andreev, A.; Maksimenko, V. Synchronization in coupled neural network with inhibitory coupling. Cybern. Phys. 2019, 8, 199–204. [Google Scholar] [CrossRef]
- Fradkov, A.L. Cybernetical Physics: From Control of Chaos to Quantum Control; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Andrievsky, B.R.; Churilov, A.N.; Fradkov, A.L. Feedback Kalman–Yakubovich lemma and its applications to adaptive control. In Proceedings of the 35th IEEE Conference Decision Control, Kobe, Japan, 13 December 1996; Volume 4, pp. 4537–4542. [Google Scholar]
- Hindmarsh, J.L.; Rose, R. A model of neuronal bursting using three coupled first order differential equations. Proc. R. Soc. London. Ser. B. Biol. Sci. 1984, 221, 87–102. [Google Scholar]
- Fradkov, A.L.; Miroshnik, I.V.; Nikiforov, V.O. Nonlinear and Adaptive Control of Complex Systems; Mathematics and Its Applications; Springer: Dordrecht, The Netherlands, 1999; Volume MAIA 491. [Google Scholar] [CrossRef]
- Semenov, D.M.; Fradkov, A.L. Adaptive synchronization in the complex heterogeneous networks of Hindmarsh–Rose neurons. Chaos Solitons Fractals 2021, 150, 111170. [Google Scholar] [CrossRef]
- Storace, M.; Linaro, D.; de Lange, E. The Hindmarsh–Rose neuron model: Bifurcation analysis and piecewise-linear approximations. Chaos Interdiscip. J. Nonlinear Sci. 2008, 18, 033128. [Google Scholar] [CrossRef]
- Annaswamy, A.; Fradkov, A. A historical perspective of adaptive control and learning. Annu. Rev. Control 2021, 52, 18–41. [Google Scholar] [CrossRef]
- Sevasteeva, E.; Plotnikov, S.; Lynnyk, V. Processing and model design of the gamma oscillation activity based on FitzHugh–Nagumo model and its interaction with slow rhythms in the brain. Cybern. Phys. 2021, 10, 265–272. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, F. Adaptive parameter estimation for a general dynamical system with unknown states. Int. J. Robust Nonlinear Control 2020, 30, 1351–1372. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, F. Optimal Adaptive Filtering Algorithm by Using the Fractional-Order Derivative. IEEE Signal Process. Lett. 2022, 29, 399–403. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).