Abstract
The use of the Hough transforms to identify shapes or images has been extensively studied in the past using software for artificial intelligence applications. In this article, we present a generalization of the goal of shape recognition using the Hough transform, applied to a broader range of real problems. A software simulator was developed to generate input patterns (straight-lines) and test the ability of a generic low-latency system to identify these lines: first in a clean environment with no other inputs and then looking for the same lines as ambient background noise increases. In particular, the paper presents a study to optimize the implementation of the Hough transform algorithm in programmable digital devices, such as FPGAs. We investigated the ability of the Hough transform to discriminate straight-lines within a vast bundle of random lines, emulating a noisy environment. In more detail, the study follows an extensive investigation we recently conducted to recognize tracks of ionizing particles in high-energy physics. In this field, the lines can represent the trajectories of particles that must be immediately recognized as they are created in a particle detector. The main advantage of using FPGAs over any other component is their speed and low latency to investigate pattern recognition problems in a noisy environment. In fact, FPGAs guarantee a latency that increases linearly with the incoming data, while other solutions increase latency times more quickly. Furthermore, HT inherently adapts to incomplete input data sets, especially if resolutions are limited. Hence, an FPGA system that implements HT is inefficient for small sets of input data but becomes more cost-effective as the size of the input data increases. The document first presents an example that uses a large Accumulator consisting of 1100 × 600 Bins and several sets of input data to validate the Hough transform algorithm as random noise increases to 80% of input data. Then, a more specifically dedicated input set was chosen to emulate a real situation where a Xilinx UltraScale+ was to be used as the final target device. Thus, we have reduced the Accumulator to 280 × 280 Bins using a clock signal at 250 MHz and a few tens input points. Under these conditions, the behavior of the firmware matched the software simulations, confirming the feasibility of the HT implementation on FPGA.
1. Introduction
Recently, we have studied new tracking capabilities in high-energy physics applications [1] for experiments at the Large Hadron Collider at CERN [2] in Geneva. In addition, we have compared the tracking capabilities of other well-known pattern recognition algorithms [3,4] with a more advanced technique based on the Hough transform (HT) [5]. Until now, the latter have primarily been used via software (SW) tools for detecting the trajectories of ionizing particles flowing inside high-energy physics detectors. There has also been a hardware (HW) implementation of HT in the CMS [6] experiment in which a time-multiplexed and highly parallelized track finder will be used. However, this is a niche application with track assumptions to reduce combinatorics in downstream data and is not necessarily adaptable to general application fields. However, as the number of tracks became even more significant, SW-based systems did not fit the purpose. In fact, some HW solutions based on associative memories have also been studied, particularly within the ATLAS [7] experiment at CERN. Furthermore, since these studies covered years of research work and since, in parallel, some commercial digital programmable components have become even more complex in terms of performance [8], we have been involved in the study of alternative solutions. In particular, we studied pattern recognition algorithms to be implemented in commodity devices characterized by a lowly fixed latency. For this reason, we have targeted the latest frontier FPGAs. We have shown the possibility of implementing the Hough transform (HT) in pattern recognition problems within “high-energy” physics experiments where “less-performing” solutions would have been abandoned. In [9], we report in detail an HW implementation (with the block diagram), while, in this paper, we broaden the field to more generic low-latency applications by using the design of an SW development tool. In [9], Xilinx UltraScale+ FPGA is investigated. The device features many gates, high-bandwidth memories, transceivers, and other high-performance electronics in a single chip, enabling the design of large, complex, and scalable architectures. We have used Xilinx Alveo U250 with a target frequency of 250 MHz and a total latency of 30 clock periods. Furthermore, we have used only 17 ÷ 53% of LUTs, 8 ÷ 12% of DSPs, 1 ÷ 3% of Block Rams, and a Flip-Flop occupancy range of 9 ÷ 28%. In contrast, in this paper, we describe a development SW tool based on HT to recognize patterns of straight-lines. This approach is derived from a high-energy physics application in which straight-lines represent possible tracks of overlapping ionizing particles with a varying amount of noise. Therefore, the main focus of our approach is to design fast, low, and fixed latency HT-based systems capable of discriminating traces within noise regardless of their quantity. Moreover, to be as general as possible, we have created a parametric SW tool for low-latency applications geared towards FPGA implementations. The ability to recognize straight-lines embedded in a noisy background can suit many other shape detection applications and images [10,11,12].
2. The Hough Transform Model
HT, in general, is a known extraction technique mainly applied in image analysis and digital processing using neural networks or other mathematical approaches [13,14]. However, the advantage of using HT in FPGAs is that latency time increases linearly with respect to the number of input data. In contrast, for combinatorial algorithms, latency time grows much more rapidly with the number of data. In addition, HT is much more tolerant to “missing” data that do not perfectly match with a given default straight-line (because of limited resolution). Hence, HT implementation on FPGAs is expensive for limited input data, but it is still convenient because its performances are significantly improved with a large set of input data. Thus, we have investigated the HT algorithm for FPGAs in detail for straight-line recognition, as shown in the (x, y) plot of Figure 1. These are representations of Input sets in a Real space (RS) since straight-lines are created from Cartesian coordinates (x, y). The same pairs can also be represented in the Hough space, i.e., the Parameter space (PS). The mathematical transformation from the lines of the RS to the corresponding elements of the PS is carried out by using the following expressions.
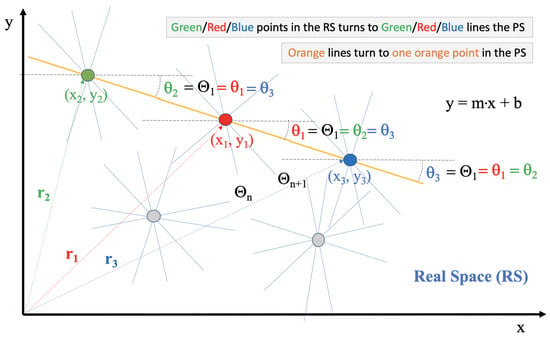
Figure 1.
Hough transform conversion for Formula in Real Space.
Then, Formula (1) can be rewritten as follows:
where is the distance from the origin and is the angle of any line with respect to the horizontal axis. is the variable angle used to execute Formula (2) as many times as needed to build the lines in the PS. Figure 1 shows three bundles of lines, with different angles crossing at one point each (colored in red, green, and blue). Only one of these lines per bundle shares the angle = with the other bundles of lines that cross at different points. These shared angles of the three bundles are, respectively, called . In particular, the three common orange lines in Figure 1 turn into the unique orange point in Figure 2. By contrast, the three green/red/blue points in the RS are converted into three colored lines in the PS, according to HT mathematics.
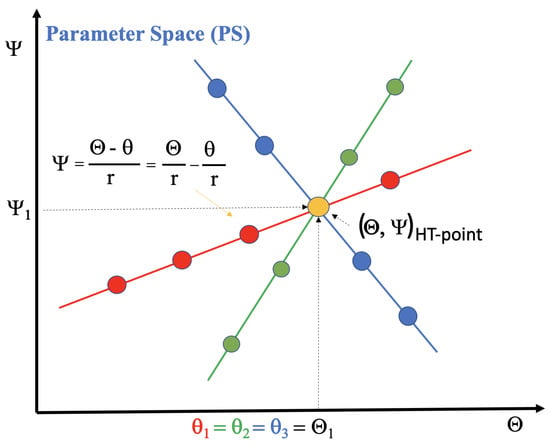
Figure 2.
Parameter Space after executing HT Formula (2).
The coordinates and in the PS graph are divided into bins to form histograms. Eventually, the orange point in Figure 2 is set as a candidate in the PS originating from the lines in the RS through the HT. This candidate, namely (HT-point), is parameterized via a data pair, i.e., (, ) = (, ).
3. Forward Process
As mentioned, through this change of coordinates, we move from RS (x, y) to PS (, ). Consequently, by recognizing and extracting a given HT-point in the PS, parameterized by a given (, ) pair, we can associate the original points, parameterized by (x, y) or (r, ) compatible with that HT-point. Hence, the HT process fills up the PS with several daughter lines originated by the Input Set, composed of the (r, ) pairs as shown in Figure 1. This task is performed by inserting a given number of angle values in Formula (2). In this manner, for each angle, correspondent is calculated, and the process is performed for all the Input Sets of values.
Following this criterion, the top plot of Figure 3 shows an example with 10 bundles of lines generated by a given Input Set composed of eight inputs providing two pairs of (r, ) each. Thus, the Input Set results in 10 × 8 (r, ) × 2 pairs of (r, ) = 160 data. Consequently, these bundles intersect in 10 (, ) pairs in the PS, i.e., 10 candidates of recognized lines of the RS.
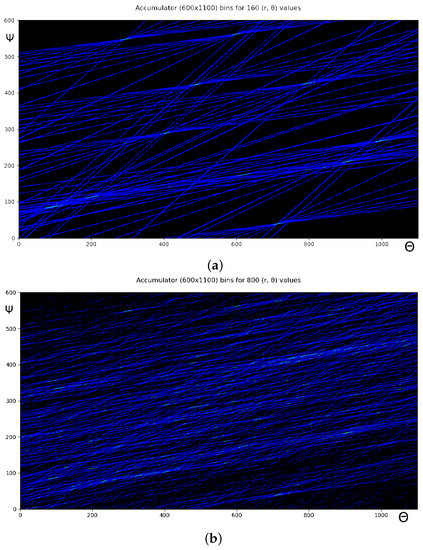
Figure 3.
The 1100 × 600 bins 2D plots of the PS after executing the HT Formula (2): (a) 10 HT-points without noise; (b) 10 HT-points with 640/800 = 80% of noise added.
The bottom plot of Figure 3 shows the same 10 bundles plus 640 random input data pairs for a total of 800 input data. These pairs also create lines in the PS, but since these do not belong to lines in the RS, they do not form cross points in PS.
The two plots in the PS are representations of the Accumulator [15], a 2D pile-up superimposition of the entire set of lines created according to Formula (2). The plots are binned horizontally along the with 1100 Bins and vertically along the variables, using 600 Bins.
Each Bin comprises N elements (8 bits in the example), where N is the number of inputs. These N elements contain the information if that Bin has been crossed, at least once, by a line originating from the inputs. If this holds, then the n-th element of that Bin is updated. This represents a point of crossing of the bundle originated using 8 input × 2 pairs of data = 16 pairs of input data. Moreover, this is repeated in the example for 10 input lines, thus resulting in 160 input data.
In the bottom plot of the figure, the same bundles have been superimposed on 640 data pairs of (r, ) representing 640/800 = 80% of background noise. If input data (r, ) belonging to the k-th input port, with 1 ≤ k ≤ N, generates a line in the Accumulator crossing the a-th brow and b-th column, then the Bin identified in the a-th row (binned with ) and the b-th column (binned with ) is updated with a “1” in its k-th element. This is performed for all Bins in the Accumulator. The entire filling process for the complete Input Set is named Forward Process.
4. Backward Process
Once the Accumulator has been filled up with all lines created by executing the Forward Process, the selection of candidate HT-points starts, and some (,) couples are eventually found. Then, the Inputs Set is scanned back to identify which (r, ) pairs were associated with the candidate (,). The HT Formula (2) has to be executed in a reverse mode for this task. This process, namely the Backward Process, is expressed by Equation (3).
The value and the (r, ) pair are used in the Formula (3) to calculate the value, which is compared to the extracted . If this difference is less than a predefined threshold, the pair (r, ) is kept aside as it belongs to the candidate input line. This task can be performed in a parallel pipeline for the entire Input Set of data, which is why it can fit into an FPGA.
5. Development Tool
An SW tool has been designed to execute the above Forward and Backward Processes. These latter tasks require an Input Set of data to carry out the processes. In particular, the SW tool envisages first the creation of a given number of HT-points composed of a definable number of (r, ) pairs, 16 in the previous example. These HT-points can be generated with or without background noise data. We started without them as we wanted to test the system’s ability to detect and reconstruct the original Input Set of data. However, the SW tool can also add a definable set of background noise in terms of randomly distributed pairs (r, ), as shown in Figure 3b. In this manner, we can also evaluate the effectiveness of the system in identifying real input data when superimposed on a background of white noise.
As mentioned, the SW tool and the HT-based system are defined independently of the Input Set, whatever the amount of noise. In parallel to SW simulations, we have designed a firmware (FW) code compatible with the SW, and we have compared the two types of simulations as shown in Figure 4a. The SW simulator follows the system described in FW step by step, regardless of the optimization of operations and the processing time. The outputs of two independent simulations can be compared to share the same input test vectors. Post-synthesis and post-layout simulations were also dealt with to consider physical connections. Hence, we have run a physical test on a Xilinx Ultrascale+ FPGAs board featuring the VU9P device [16], confirming the compatibility of the simulations, see Figure 4b.
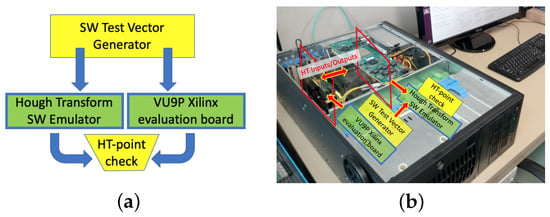
Figure 4.
Test Stand demonstrator: (a) HT SW tool, (b) HT FW implementation.
Table 1 summarizes a reduced Input Set A of the HT mounted on an FPGA. The input Data Pairs column shows the number of input data (r, ) composed of background noise along with pairs of HT-points, as shown in the HT-points column. The next column shows the Extracted HT-points, which points to which and how many input lines are potential candidate lines in the PS. This column shows higher numbers than those in the HT-points column: This is justified because noise can accidentally create false HT points that do not belong to any input line and will be eliminated by a further process outside the HT, subsequently, after the completion of the Background Process. Finally, using a reference clock period of 4 ns (250 MHz), the Processing Time is estimated in the last column.

Table 1.
Summary table for a VHDL implementation.
As mentioned above, these examples use HT-points made up of 2 × 8 pairs = 16 (r, ) couples. Thus, the first row of the Table 1 refers to 50 HT-points covering 50 × 16 = 800 pairs of input data out of 928 of column Input Data Pairs, resulting in 128 pairs of background noise data. All Input Data contain a common group of 128 noise pairs (r, ) and use eight parallel inputs.
The entire Input Set A is used to fill a 280 × 280 .8 high Accumulator, the size of which is adapted to be implementable on an FPGA.
The FW was tested on a Xilinx card, as shown in Figure 4, and physical data were sent through a 16-lane PCIe third generation port.
6. Data Analysis
The SW tool was performed to estimate the system’s ability to select input lines, especially if superimposed on background noise. Therefore, different sets of HT-points B, C, D, and E were used with a constant number of input lines and a variable number of noise data. These Input Sets are compatible extensions of the smaller Input Set A, which also had to respect a feasible FW implementation. In addition, we have set a fixed granularity and several Bins of the Accumulator to 1100 × 600 Bins for both axes. The granularity is a parameter that considers the quality of the digitized lines that fill the Accumulator. The higher the binning, the finer and more precise the lines will be at the expense of Accumulator size. The SW emulator is a representative behavioral model of the FW. Table 1 shows the processing time of the HT system after the simulation of the VHDL code on Input Set A. In contrast, Table 2 refers to the simulations of the SW emulator on Input Sets B-E. The two types of simulations proved compatible even if the SW simulation is much faster than the FW one. We use SW to validate a system, with a specific dataset and HT parameters. Furthermore, once the study is completed, we can update the FW accordingly by using the same inputs generated but running far fewer simulations and focusing on the HW implementation on FPGA. This is the most challenging phase to complete, especially for large accumulators.

Table 2.
Summary table for an SW analysis.
Table 2 shows a summary of the SW analysis listing the Input Sets B, C, D, and E, the Input Data Pairs, the HT-points generated, the Extracted HT points, the % of noise data, and the density of the Accumulator in terms of the percentage of fill compared to the total capacity. Moreover, in this example, each HT-point is composed of 2 data × 8 inputs, which correspond to 16 (r, ) data; hence 5 HT-points require 80 (r, ), 10 HT-points require 160 (r, ), and so on. These numbers reflect exactly what is shown in the first row of each Input Set B, C, D, and E. The following columns show the percentage of extra background noise applied in the simulations and the percentage of occupancy of the Accumulator.
Figure 5 shows two 3D graphs of the second, fourth, and fifth and second, fourth, and sixth columns of Table 2. The figure shows in graphs (a) and (b) that the number of HT-points extracted increases as a combination of percentage noise and Input Data pairs. When these two are simultaneously high, the number of HT-points extracted increases significantly, increasing processing time and latency. We use this type of simulation to limit the percentage of acceptable noise, depending on the application, in order to not excessively increase the total latency of the process.
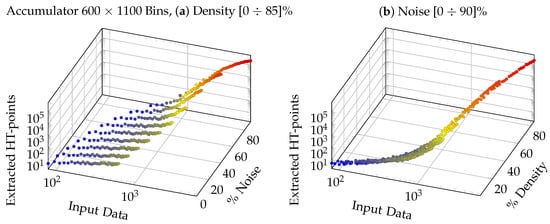
Figure 5.
(a) HT SW noise analysis; (b) HT SW density plot.
FPGAs have proved to be one of the most suitable devices for hosting mathematical algorithms such as the Hough transform. The comparison between FPGA behavior and other commercial devices has been deepened in the past by many other researchers with a general agreement that FPGAs can adapt to the best compromise for low and fixed latency, budget of power, and speed. In particular, the latest Xilinx families, such as UltraScale+, feature many integrated digital signal processors, internal (high bandwidth) memories, transceivers, and logic blocks that can be configured to be considered optimal target devices. For example, we report recent studies showing that FPGAs have become promising candidates for low-latency applications [17,18,19] and are chosen for deep neural networks instead of other commercial devices. For our tests, we used a custom card designed initially for data acquisition and triggered applications at the ATLAS experiment at CERN.
7. Conclusions
This study exploited a Hough transform system characterized by a clock signal working at 250 MHz and many Input Sets of the order of one thousand. The choice of FPGAs in this field is justified by the need for a high input–output data transmission rate, low system latencies, and management of the algorithm complexity. Compared to other similar devices, FPGA components can simultaneously provide low and fixed latency, low power budget, and high data rate. Furthermore, HT implementation on FPGAs is independent of input data and noise percentage. The system also becomes more efficient for large input data sets as the overall latency scales linearly. Emphasis was placed on simulation to monitor the design process from the FW code to the final implementation. Currently, the Hough transform FW is finalized with a description at the level of the register transfer logic, a synthesizable and routable description suitable for FPGA resources. In addition, an SW tool was designed to thoroughly investigate the system’s behavior, especially when added with background noise to emulate a real harsh environment. With this tool, many dummy test vectors have been prepared to provide HW with many input patterns to estimate the performance of the entire architecture looking for candidate input lines. In the end, we loaded the algorithm into a board equipped with an Ultrascale+ FPGA and provided the test vectors simulated earlier: the two configurations fit together perfectly.
Author Contributions
Conceptualization, A.G. and F.A.; methodology, A.G. and F.A.; software, F.A. and F.D.C.; validation, F.A. and F.D.C.; formal analysis, A.G., F.A. and F.D.C.; investigation, A.G. and F.A; resources, A.G.; data curation, A.G. and F.A; writing—original draft preparation, A.G.; writing—review and editing, A.G.; visualization, A.G. and F.A; supervision, A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tang, J.; Ren, J. Hough transform applications to particle detection of granular physics experiments. J. Comput. Inf. Syst. 2013, 9, 187–194. [Google Scholar]
- Evans, L.; Bryant, P. LHC Machine. J. Instrum. 2008, 3, S08001. [Google Scholar] [CrossRef]
- LHCb Collaboration. Performance of the LHCb outer tracker. J. Instrum. 2014, 9, 01002. [Google Scholar]
- CMS Collaboration. CMS tracking performance results from early LHC operation. Eur. Phys. J. C 2010, 70, 1165–1192. [Google Scholar] [CrossRef]
- Halyo, V.; Gresley, P.L.; Lujan, P.; Karpusenko, V.; Vladimirov, A. First evaluation of the CPU, GPGPU and MIC architectures for real time particle tracking based on Hough transform at the LHC. J. Instrum. 2014, 9, 04005. [Google Scholar] [CrossRef]
- Aggleton, R.; Ardila-Perez, L.E.; Ball, F.A.; Balzer, M.N.; Boudoul, G.; Brooke, J.; Caselle, M.; Calligaris, L.; Cieri, D.; Clement, E.; et al. An FPGA based track finder for the L1 trigger of the CMS experiment at the High Luminosity LHC. J. Instrum. 2017, 12, 12019. [Google Scholar] [CrossRef]
- Citraro, S. Highly Parallelized Pattern Matching Hardware for Fast Tracking at Hadron Colliders. IEEE Trans. Nucl. Sci. 2016, 63, 1147–1154. [Google Scholar] [CrossRef]
- HPC Wire, New Xilinx Virtex UltraScale+ FPGA Optimized for Networking and Storage Acceleration. HPC Wire. 2020. Available online: https://www.hpcwire.com/off-the-wire/new-xilinx-virtex-ultrascale-fpga-optimized-for-networking-and-storage-acceleration/ (accessed on 13 December 2021).
- Gabrielli, A.; Alfonsi, F.; Annovi, A.; Camplani, A.; Cerri, A. Hardware Implementation Study of Particle Tracking Algorithm on FPGAs. MDPI Electron. 2021, 10, 2546. [Google Scholar] [CrossRef]
- Meng, Y.; Zhang, Z.; Yin, H.; Ma, T. Automatic detection of particle size distribution by image analysis based on local adaptive canny edge detection and modified circular Hough transform. Micron 2018, 106, 34–41. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, N.; Karl, W.C. Line detection in images through regularized hough transform. IEEE Trans. Image Process. 2006, 15, 582–591. [Google Scholar] [CrossRef] [PubMed]
- Ballard, D.H. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognit. 1981, 13, 111–122. [Google Scholar] [CrossRef]
- Basak, J. Learning Hough Transform: A Neural Network Model. Neural Comput. 2001, 13, 651–676. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Xiong, H. Improved Hough transform by modeling context with conditional random fields for partially occluded pedestrian detection. Opt. Eng. 2018, 57, 063101. [Google Scholar] [CrossRef]
- Ji, J.; Chen, G.; Sun, L. A novel Hough transform method for line detection by enhancing accumulator array. Pattern Recognit. Lett. 2011, 32, 1503–1510. [Google Scholar] [CrossRef]
- UltraScale+ FPGAs, Xilinx VU9P. 2021. Available online: https://www.xilinx.com/support/documentation/selectionguides/ultrascale-plus-fpga-product-selection-guide.pdf (accessed on 13 December 2021).
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing fpga-based accelerator design for deep convolutional neural networks. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015; pp. 161–170. [Google Scholar]
- Kim, T.; Park, S.; Cho, Y. Study on the Implementation of a Simple and Effective Memory System for an AI Chip. Electronics 2021, 10, 1399. [Google Scholar] [CrossRef]
- He, D.; He, J.; Liu, J.; Yang, J.; Yan, Q.; Yang, Y. An FPGA-Based LSTM Acceleration Engine for Deep Learning Frameworks. Electronics 2021, 10, 681. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).