A Wide-Band Divide-by-2 Injection-Locked Frequency Divider Based on Distributed Dual-Resonance Tank
Abstract
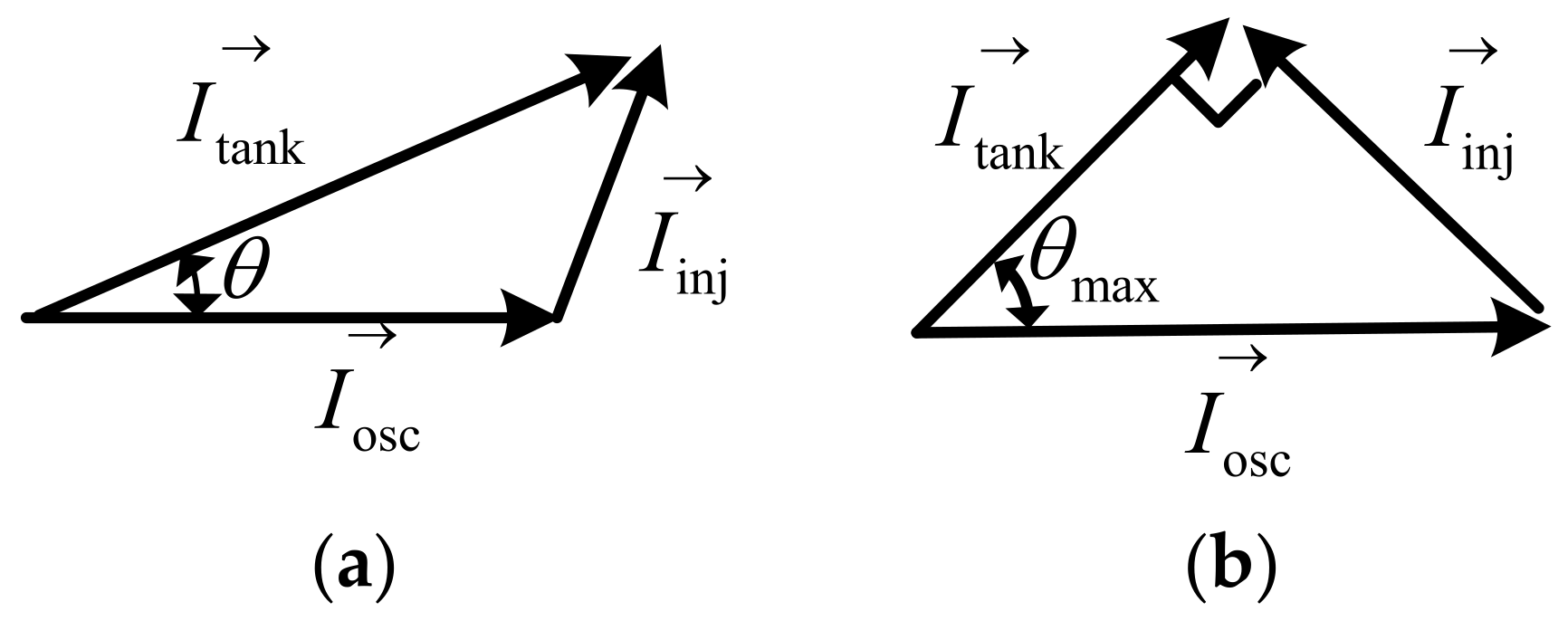
:1. Introduction
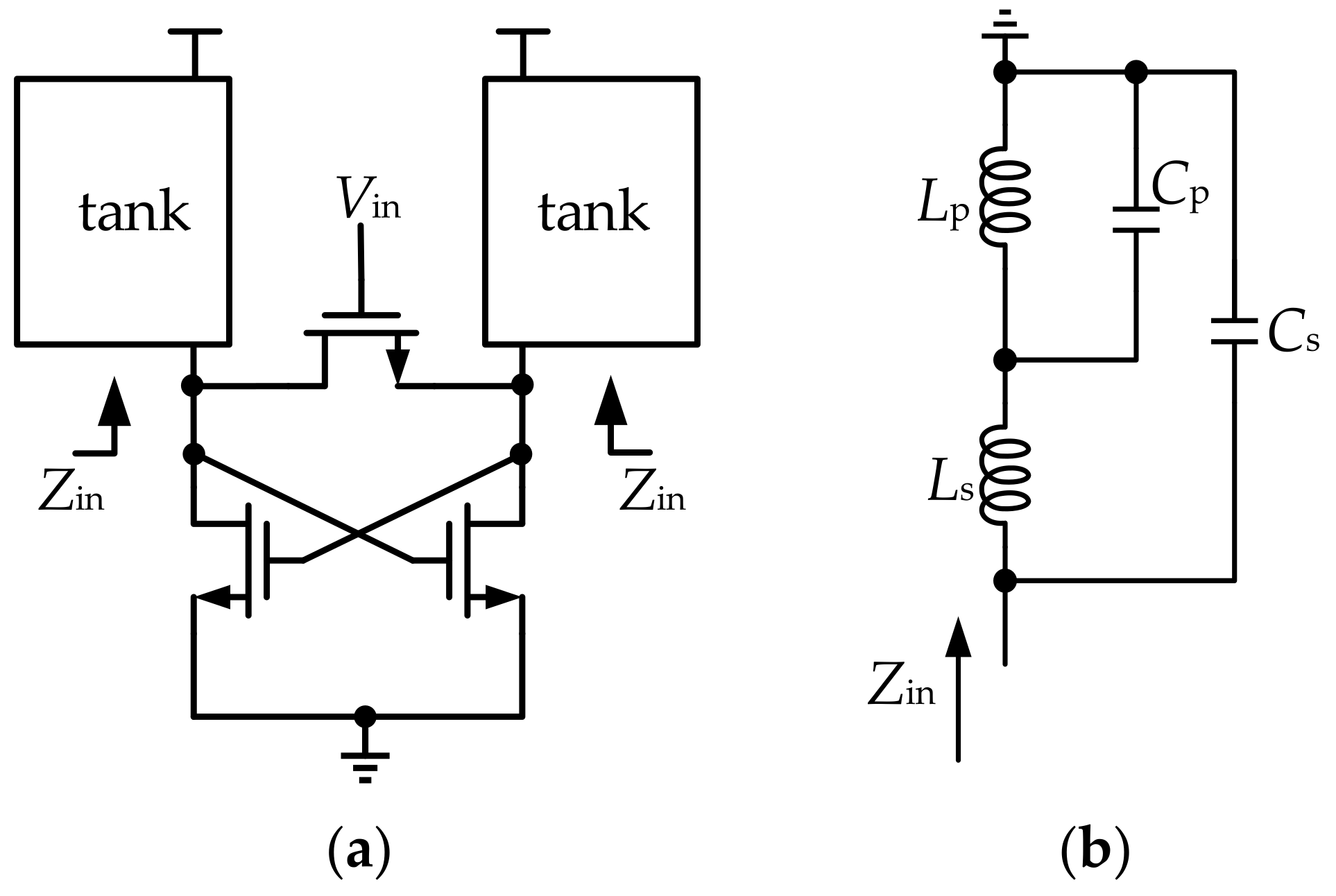
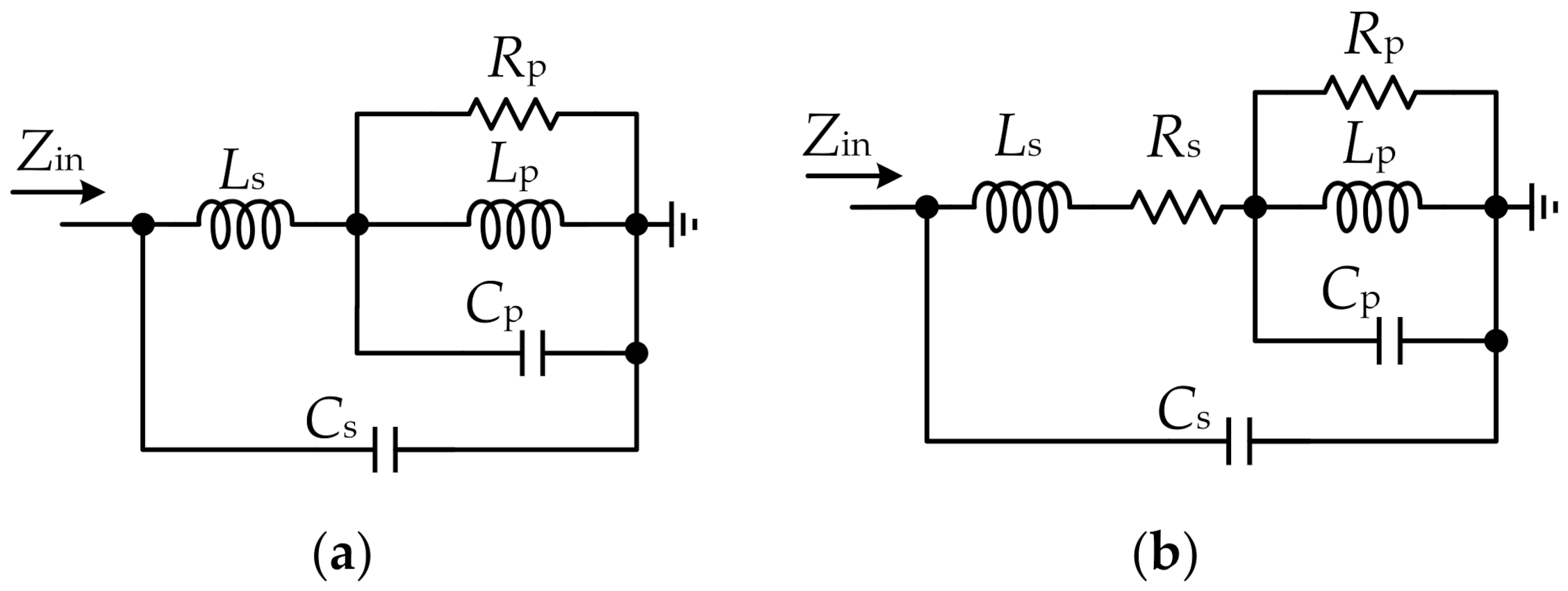
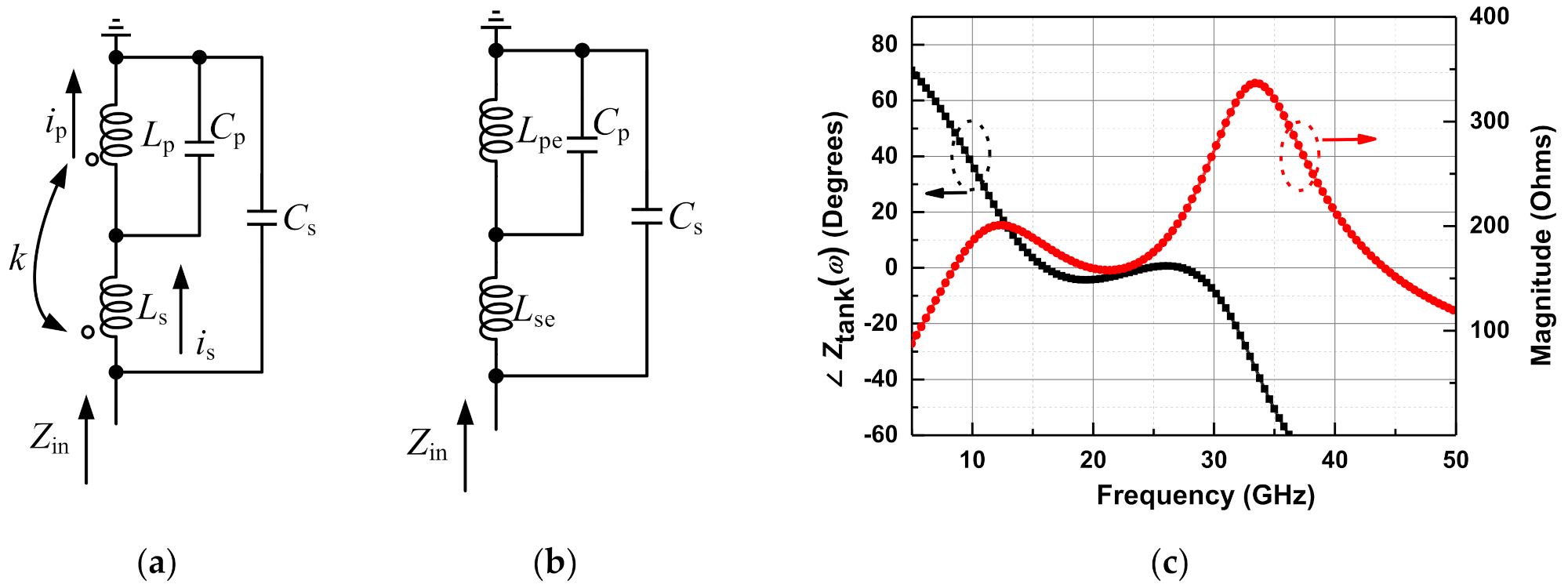
2. Analysis of the Proposed Dual-Resonance Tank
2.1. Zero and Pole Analysis
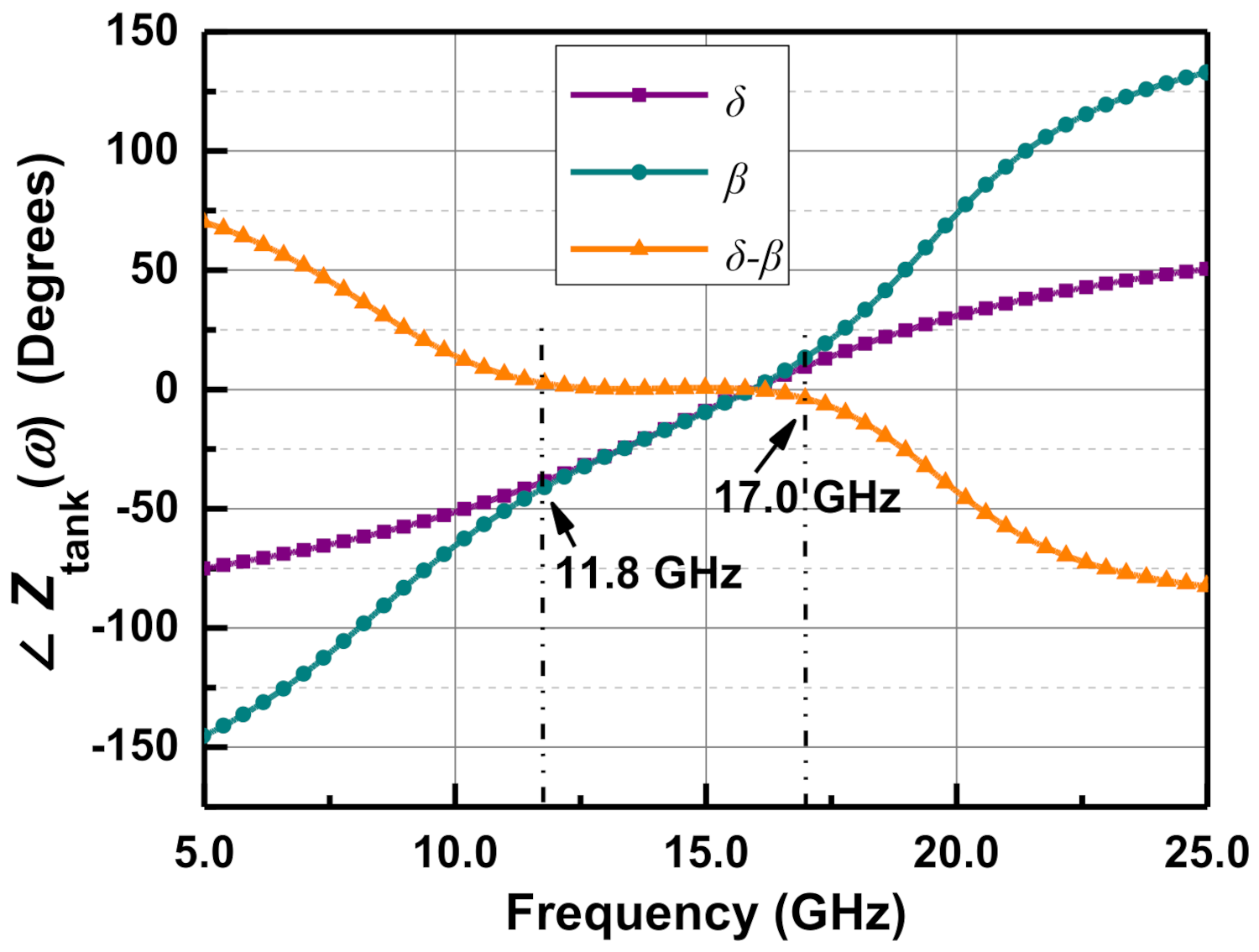
2.2. Phase Response
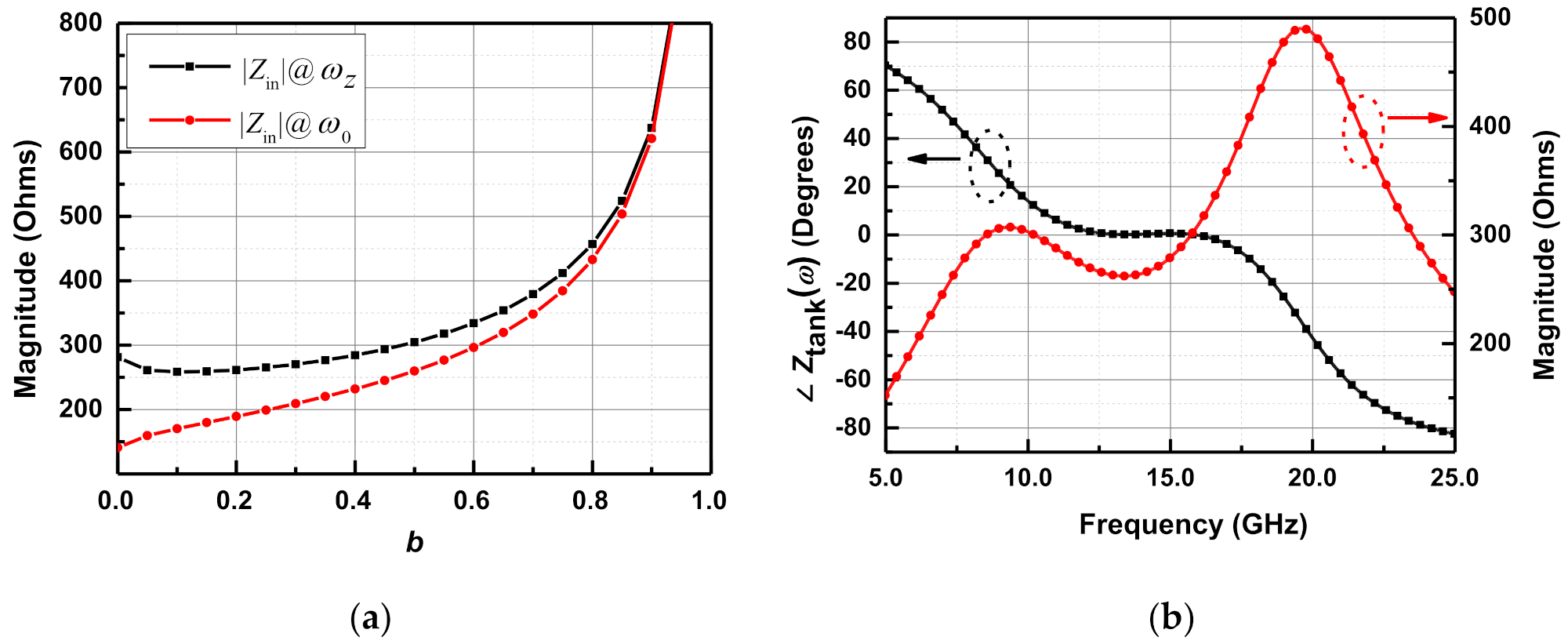
2.3. Magnitude Response
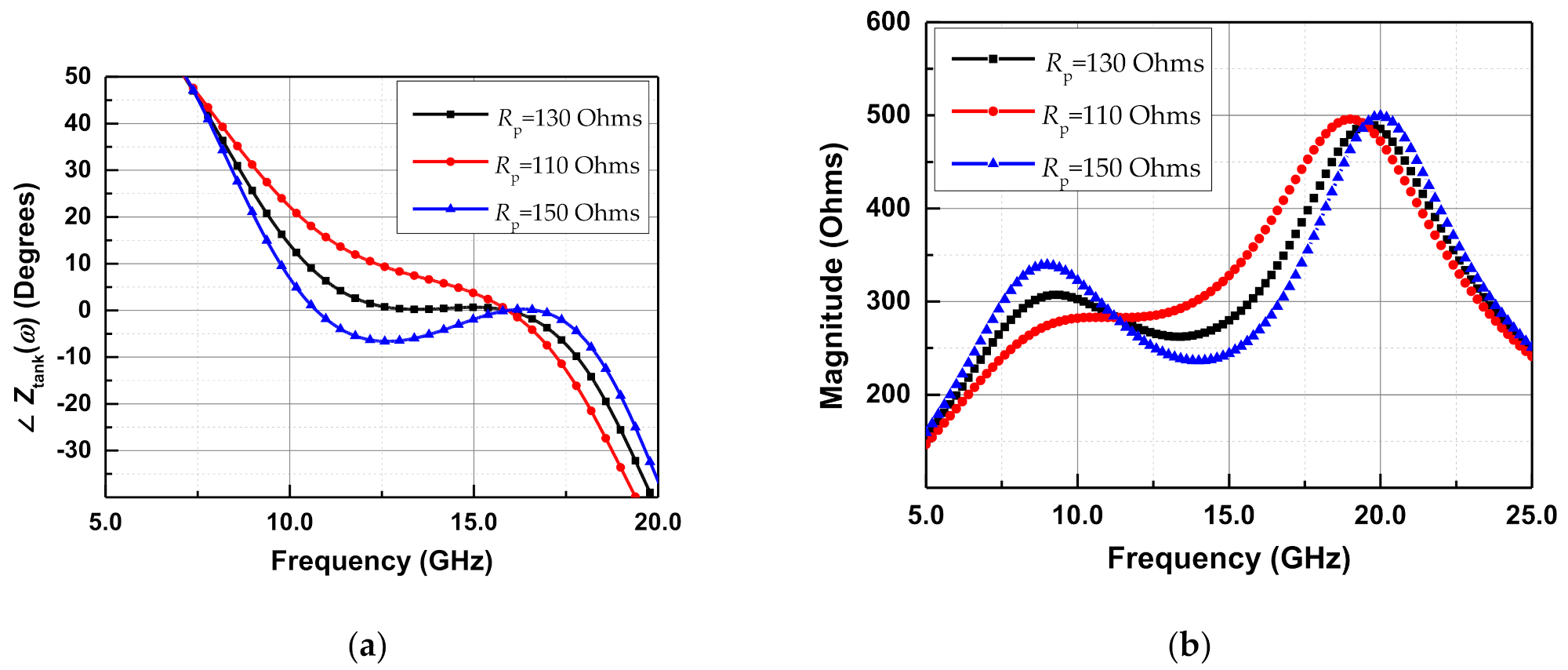
2.4. Influence of Rp and Rs
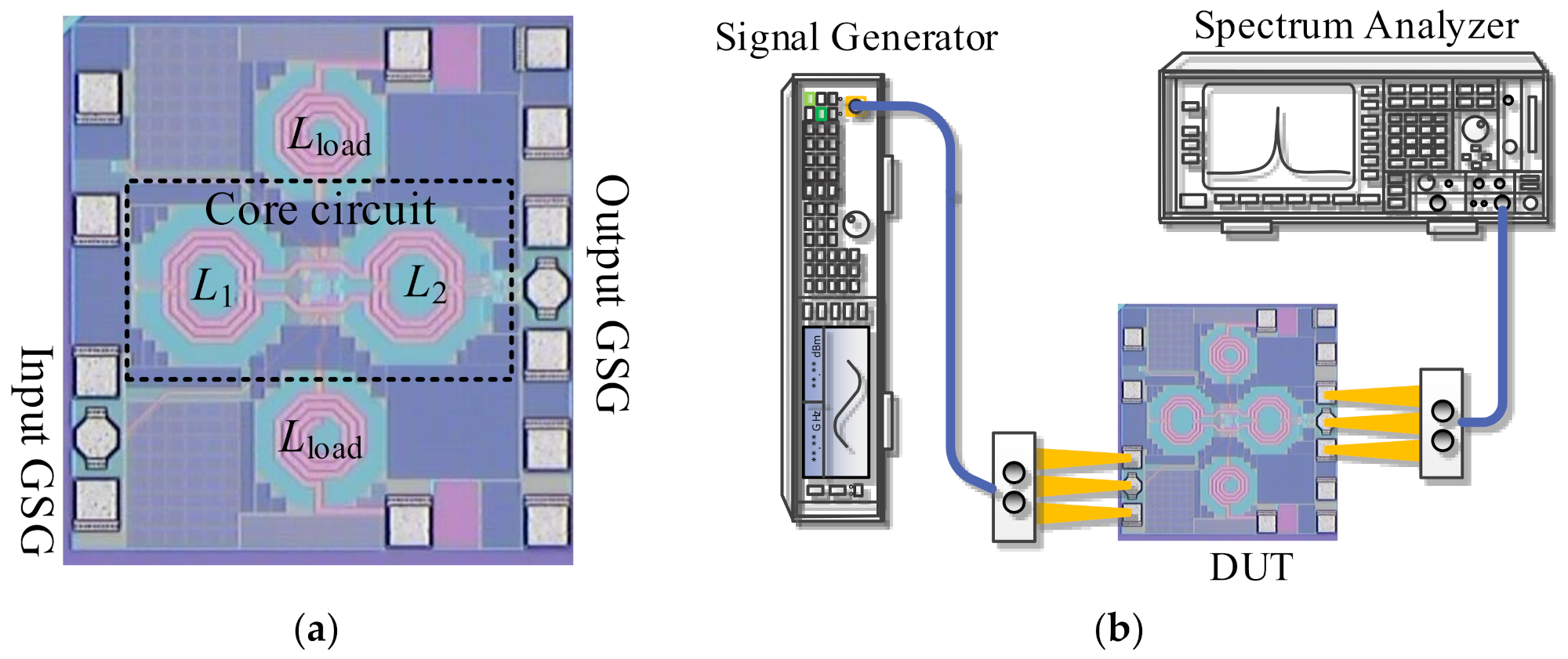
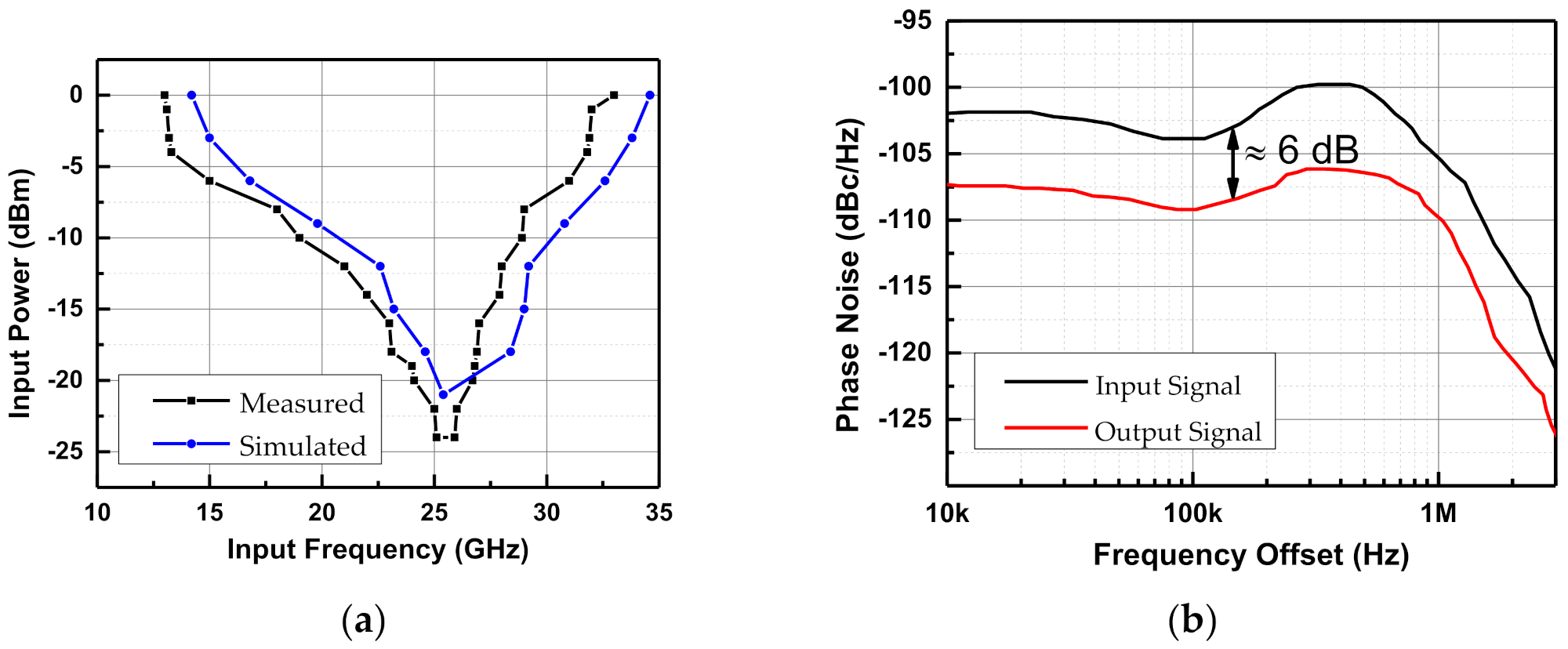
3. Implementations and Measurement Results
4. EM Coupling Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hui, W.; Hajimiri, A. A 19 GHz 0.5 mW 0.35/spl mu/m CMOS frequency divider with shunt-peaking locking-range enhancement. In Proceedings of the 2001 IEEE International Solid-State Circuits Conference. Digest of Technical Papers. ISSCC (Cat. No.01CH37177), San Francisco, CA, USA, 7 February 2001; pp. 412–413. [Google Scholar]
- Tiebout, M. A CMOS direct injection-locked oscillator topology as high-frequency low-power frequency divider. IEEE J. Solid-State Circuits 2004, 39, 1170–1174. [Google Scholar] [CrossRef]
- Takatsu, K.; Tamura, H.; Yamamoto, T.; Doi, Y.; Kanda, K.; Shibasaki, T.; Kuroda, T. A 60-GHz 1.65 mW 25.9% locking range multi-order LC oscillator based injection locked frequency divider in 65 nm CMOS. In Proceedings of the IEEE Custom Integrated Circuits Conference 2010, San Jose, CA, USA, 19–22 September 2010; pp. 1–4. [Google Scholar]
- Mangraviti, G.; Khalaf, K.; Parvais, B.; Vaesen, K.; Szortyka, V.; Vandersteen, G.; Wambacq, P. Design and Tuning of Coupled-LC mm-Wave Subharmonically Injection-Locked Oscillators. IEEE Trans. Microw. Theory Tech. 2015, 63, 2301–2312. [Google Scholar] [CrossRef]
- Lai, W.-C.; Jang, S.-L.; Huang, Y.-W.; Juang, M.-H. Divide-by-2 Injection-Locked Frequency Divider Using 3-path Transformer-Coupled Resonator. In Proceedings of the 2020 27th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Glasgow, UK, 23–25 November 2020; pp. 1–4. [Google Scholar]
- Zhang, J.; Liu, H.; Wu, Y.; Zhao, C.; Kang, K. A 27.9–53.5-GHz transformer-based injection-locked frequency divider with 62.9% locking range. In Proceedings of the 2017 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Honolulu, HI, USA, 4–6 June 2017; pp. 324–327. [Google Scholar]
- Chao, Y.; Luong, H.C. Analysis and Design of a 2.9-mW 53.4–79.4-GHz Frequency-Tracking Injection-Locked Frequency Divider in 65-nm CMOS. IEEE J. Solid-State Circuits 2013, 48, 2403–2418. [Google Scholar] [CrossRef]
- Jiang, Q.; Pan, Q. Tuning-less injection-locked frequency dividers with wide locking range utilizing 8th-order transformer-based resonator. In Proceedings of the 2021 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Atlanta, GA, USA, 7–9 June 2021. [Google Scholar]
- Mahalingam, N.; Ma, K.; Yeo, K.S. A Multi-Mode Multi-Coil Coupled Tuned Inductive Peaking ILFD for Low Injected Power with Compact Size. IEEE Access 2019, 7, 59059–59068. [Google Scholar] [CrossRef]



| Lp/H | Ls/H | Cp/F | Cs/F | Rp/Ohms | Ls/Lp | a | b | ω1/Hz | ω2/Hz | ω0/Hz | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | 4n | 2n | 75f | 50f | 146 | 0.5 | 2/3 | 1/3 | 9.19 G | 15.9 G | 12.1 G |
| Case 2 | 2n | 2n | 100f | 50f | 130 | 1 | 1/2 | 1/2 | 11.3 G | 15.9 G | 13.4 G |
| Case 3 | 1n | 2n | 150f | 50f | 112 | 2 | 1/3 | 2/3 | 13.0 G | 15.9 G | 14.4 G |
| Reference | [6] | [7] | [8] | [9] | This Work |
|---|---|---|---|---|---|
| Process | 65 nm CMOS | 65 nm CMOS | 40 nm CMOS | 65 nm CMOS | 65 nm LP-CMOS |
| Injection Power (dBm) | 0 | 0 | −4 | −5 | 0 |
| Supply Voltage (V) | 1 | 0.8 | 0.9 | 1.2 | 0.7 |
| Power Dissipation (mW) | 5.8 | 2.9 | 5.8 | 3.7 | 7 |
| Locking Range | 27.9–3.5 GHz (62.9%) | 53.4–79.4 GHz (39.2%) | 28.8–91.9 GHz (104.5%) | 58 GHz (18.3%) | 13–33 GHz (87.0%) |
| FoM * (GHz/mW) | 4.41 | 8.97 | 10.9 | 2.87 | 2.86 |
| Core Area (mm2) | 0.18 | 0.126 | 0.02 | 0.029 | 0.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Z.; Yu, Y.; Kang, K. A Wide-Band Divide-by-2 Injection-Locked Frequency Divider Based on Distributed Dual-Resonance Tank. Electronics 2022, 11, 506. https://doi.org/10.3390/electronics11040506
Xing Z, Yu Y, Kang K. A Wide-Band Divide-by-2 Injection-Locked Frequency Divider Based on Distributed Dual-Resonance Tank. Electronics. 2022; 11(4):506. https://doi.org/10.3390/electronics11040506
Chicago/Turabian StyleXing, Zhao, Yiming Yu, and Kai Kang. 2022. "A Wide-Band Divide-by-2 Injection-Locked Frequency Divider Based on Distributed Dual-Resonance Tank" Electronics 11, no. 4: 506. https://doi.org/10.3390/electronics11040506
APA StyleXing, Z., Yu, Y., & Kang, K. (2022). A Wide-Band Divide-by-2 Injection-Locked Frequency Divider Based on Distributed Dual-Resonance Tank. Electronics, 11(4), 506. https://doi.org/10.3390/electronics11040506







