A Dynamic Obstacle Avoidance Method for AGV Based on Improved Speed Barriers

Abstract

The complexity and difficulty of dynamic obstacle avoidance for AGVs are increased by the uncertainty in a dynamic environment. The adaptive speed obstacle method allows the size of the collision cone to be dynamically changed to solve this problem, but this method may cause the AGV to turn too much when it is close to obstacles, as the collision cone expands too fast, which may lead to unstable operations or even collision. In order to address these problems, we propose an improved speed obstacle algorithm. The proposed algorithm uses Kalman filtering to estimate the positions of dynamic obstacles and adopts the idea of forward simulation to build a speed obstacle buffer according to the estimated positions of obstacles, such that the AGV can use the predicted positions of obstacles in the next moment, instead of the current positions, to build a speed obstacle model. Finally, an objective function that balances efficiency and safety was established to score all the candidate speeds, such that the highest-rated speed could be selected as the candidate speed for the next moment.

1. Introduction

As a highly intelligent transport mode with various functions, such as safety, protection, and load transfer, an automated guided vehicle (AGV) can be guided by a computer or its guidance device. As such, AGVs represent important logistics equipment for realizing modern industrial processes [1]. Path planning [2], as one of the key technologies in the AGV field, is a prerequisite for automated guided motion control. Whether the AGV can travel smoothly and safely is determined by good or bad path planning. It also bridges the environmental information perception and intelligent control systems of the AGV. To be able to achieve autonomous navigation and accomplish various tasks in the environment, the AGV needs to rely on a priori map information to a large extent, and needs to reason about the next action based on known information. At present, there exist relatively mature solutions for global path planning based on static obstacles, such as the fast random search tree (RST), the ant colony algorithm, and the artificial potential field method [2,3]; however, compared with static obstacles, the limited environmental information available to AGVs and the unpredictability of the environment make obstacle avoidance and path planning based on moving obstacles challenging problems.

It is more complicated for AGVs to avoid obstacles in dynamic environments due to the uncertainty of the environment, such as the unpredictable motion state of moving obstacles, errors in sensor measurements, and slippage of wheels [4,5]. In dynamic environments, it is difficult to accurately predict the trajectory of obstacles as their motion is unknown. Most existing obstacle avoidance methods, such as the artificial potential field method, dynamic window method, velocity obstacle method, and algorithms improving upon these algorithms, simply set a region near the obstacle that prohibits the AGV from entering; however, if the region is too small, the AGV may have difficulty avoiding the obstacles in time [6]. If the region is too large, the movement space of the AGV is restricted, the movement trajectory may be prolonged, and real-time obstacle avoidance cannot be guaranteed. In [7], Gu et al. proposed an adaptive speed obstacle method in light of the above problem, which can judge the degree of danger according to the relative speed and distance between the AGV and an obstacle, adaptively changing the size of the extended radius of the mobile obstacle to ensure the safety of the path while guaranteeing obstacle avoidance of the AGV in real-time. This method also has shortcomings, as the speed obstacle method needs to calculate the speed according to the range of the collision cone, divided into a collision zone and a non-collision zone, where the AGV avoids collision by choosing the appropriate speed in the non-collision zone. However, in the adaptive velocity obstacle method, the expansion radius of the AGV near the obstacle increases exponentially, and the expansion speed becomes faster and the range larger. Therefore, there is a possibility that all candidate velocities lie inside the collision cone and there is no chance to move out of the cone in time. Furthermore, the change range of the AGV obstacle avoidance heading angle may be large, which is not conducive to the stability of the AGV operation.

To address the above problems, we propose a method based on obstacle position prediction with improved speed obstacles. The method first uses Kalman filtering to estimate the possible position of the obstacle at the next moment, and then adopts the idea of forward simulation to make the AGV aim at the predicted position of the obstacle at the next moment, instead of the current position, in order to construct the speed obstacle model. Finally, for the candidate speed, the idea of scoring is adopted, to score all candidate speeds and design a new objective that takes into account efficiency and safety functions, where the speed with the highest rating is selected as the candidate speed for the next moment. Experimental results obtained indicate that the improved algorithm presented in this paper improves the success rate of obstacle avoidance by 11% compared with the traditional adaptive speed obstacle algorithm and can maintain a safer distance from the obstacles in the process of obstacle avoidance, effectively addressing the uncertain influence caused by environmental factors on AGVs when avoiding obstacles.

2. Related Works

In the process of movement, AGVs often need to detect whether they will collide with obstacles. If an AGV fails to successfully identify and avoid an obstacle, a collision may occur, which can not only cause property damage but, in serious cases, may even pose a threat to the safety of the surrounding operators.

Dynamic obstacle avoidance with moving obstacles is one of the fundamental problems for free-moving cars to achieve autonomous navigation and, in recent years, many researchers have studied this topic [8]. The velocity obstacle method is considered a simple method to avoid moving obstacles with good real-time performance and is one of the more popular algorithms in the field of dynamic obstacle avoidance [7,9].

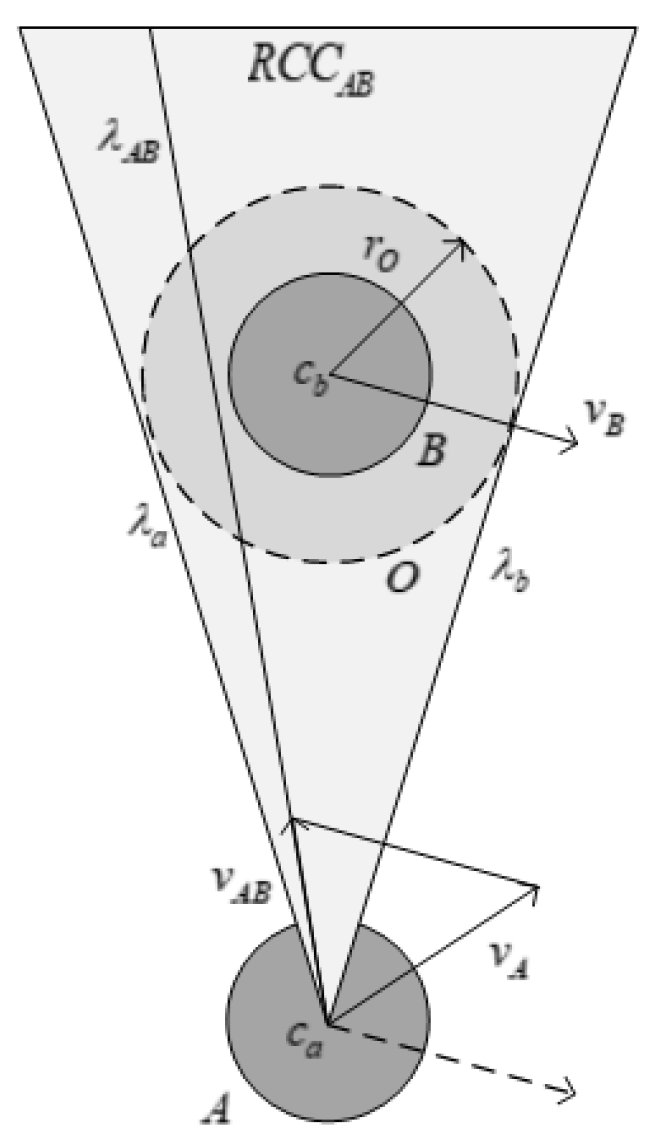
The classical velocity obstacle method was first proposed by Fiorini P et al. [4], as shown in Figure 1, where A denotes the AGV, B is the obstacle, O is the expanded obstacle, and $c_a$ and $c_b$ denote the positions of the AGV A and obstacle B, respectively. From point $c_a$, two rays ${\lambda }_a$ and ${\lambda }_b$ that are tangent to O can be formed. The obstacles can be regarded as stationary, according to the relative velocity. Supposing that the speeds of the AGV $v_A$ and obstacle $v_B$ remain unchanged, then, starting from point $c_a$, ray ${\lambda }_{AB}$ along the direction of $v_{AB}$ intersects the expanded obstacle O, and it can be considered that AGV A may collide with obstacle B at some time in the future.

Figure 1. Classical speed barrier method.

This algorithm considers the velocity and position of the obstacle and, for each obstacle, builds a conical region in the velocity space. As long as the velocity vector falls into the region for which it is determined that a collision will occur, an optimal velocity vector from the non-conical region should be chosen to ensure obstacle avoidance.

Subsequently, although many researchers have improved upon the classical speed obstacle method, most studies have tended to choose a speed that is at the boundary between the collision and non-collision zones, as it is considered the most efficient solution that will ensure that there is no collision with the obstacle in the ideal situation [9,10,11]. However, in this case, when approaching an obstacle, the probability of collision between the AGV and the obstacle may be greatly increased due to the interference of uncertainties in the environment, possible sudden changes in the speed of the obstacle, possible errors in sensor measurements, and possible wheel slippage, among other factors [12,13].

The adaptive velocity barrier method [7], as one of the improved algorithms of the classical velocity barrier method, introduces an adaptive extended radius to adjust the size of the collision cone to address the above problem, taking into account efficiency and safety.

As shown in Figure 2, the adaptive velocity barrier method adds a dynamically changing extended radius $r_{\mathrm{adaptive}}$ to the classical velocity barrier method of extending the radius to the barrier. The radius of the adaptive velocity obstacle method’s extended obstacle O is expressed as:

$$r_O=r_A+r_B+r_{\mathrm{safe}}+r_{\mathrm{adaptive}},$$

(1)

where $r_{\mathrm{adaptive}}$ is related to the relative distance and relative speed between the AGV and the obstacle. When the AGV is far away from the obstacle, the degree of danger is lower, so more attention should be paid to real-time adjustments, the extended radius is smaller, and the AGV can avoid the obstacle in a relatively short time. When the AGV is closer to the obstacle, the greater the degree of danger, the more attention should be paid to safety. At this time, the obstacle expansion radius is larger, such that the robot can maintain a relatively safe distance from the obstacle, in order to facilitate posture adjustment of the AGV, thus enabling it to escape from the obstacle.

Figure 2. Schematic diagram of adaptive speed barrier.

Therefore, the obstacle extension radius should be proportional to the relative velocity between the AGV and the obstacle and inversely proportional to the distance. The adaptive extension radius formula $r_{\mathrm{adaptive}}$ is given as

$$r_{\mathrm{adaptive}}=\frac{\delta ∥v_{AB}∥·cos\phi }{{\varphi }^{\xi d}},$$

(2)

where $\delta$ denotes the adaptive gain (a constant that needs to be set according to the actual needs), $\phi$ is the angle between the relative speed of the AGV and the obstacle and the relative distance, and $∥v_{AB}∥·cos\phi$ is the projection of the relative speed between the AGV and the obstacle onto the relative distance. When the relative distance becomes small, to make the adaptive expansion radius grow exponentially, and to make the relative speed and sliding deviation for the threat of obstacle avoidance security increase exponentially, the denominator is set to ${\varphi }^{\xi d}$, where $\varphi$ and $\xi$ are constants for adjusting the value of the denominator and the expansion radius expansion speed, respectively, and d is the relative distance between the AGV and the obstacle.

3. Improved Speed Barrier Method Based on Collision Risk Zone

Although the adaptive speed obstacle method can change the range of the collision cone adaptively, to balance the relationship between safety and efficiency based on the relative distance and relative speed between the AGV and the obstacle (as parameters reflecting the degree of danger between the AGV and the obstacle), it still faces two challenges. The first challenge is related to the distance between the AGV and the obstacle gradually decreasing, as shown in Equation (2). In this case, the adaptive expansion radius exponentially expands and, the closer the distance, the faster the collision cone expansion speed and the larger the range. At this time, to escape from the obstacles, the AGV rotation angle becomes increasingly large, which is likely to affect the operating stability of the AGV or, because of untimely steering, may lead to collision with the obstacle. The second challenge is that, as the magnitude of the collision cone expansion increases, the AGV may not be able to steer in time, resulting in all candidate speeds lying in the collision cone. Thus, the AGV is not able to move out in time, resulting in no optimal candidate speeds at the next moment. This section focuses on the first challenge, and proposes an improved velocity barrier method based on collision risk zones.

3.1. Kalman Filter-Based Obstacle Position Prediction

When humans encounter an obstacle during movement, they intuitively perceive the region where a collision may occur and, if the obstacle is dynamic, the perceived collision region will extend along the direction of the obstacle’s motion. We refer to this region as the collision risk region, which helps to guide humans in taking effective measures to avoid obstacles in advance during movement [11]. This reasoning also applies to the obstacle avoidance of AGVs; the risk collision region of dynamic obstacles will be dynamically extended due to the motion of dynamic obstacles. At this time, this risk collision region is equivalent to a buffer zone, which can help AGVs to maneuver in advance, thus improving the obstacle avoidance performance of AGVs.

Most perception information of an AGV for dynamic obstacles comes from its sensors [14]. The AGV can obtain the relative coordinates of obstacles relative to the AGV at the current moment through the LIDAR, following which, using the positioning system of the AGV, and according to the absolute coordinates of the AGV relative to the map, it can obtain the position of the obstacles in the global map using the map differencing method [15]. Other motion parameters are calculated according to the change in the position of obstacles at different moments.

In dynamic environments, the future motion trends of moving obstacles are often uncertain; however, the past motion information of moving obstacles can be used to estimate their future state, especially for short time intervals, and a high estimation accuracy can be obtained. Kalman filtering is chosen for this purpose in this paper due to its high computational efficiency, numerical stability, and practicality [16]. Therefore, the Kalman filtering algorithm was chosen for prediction of the dynamic motion parameters of obstacles.

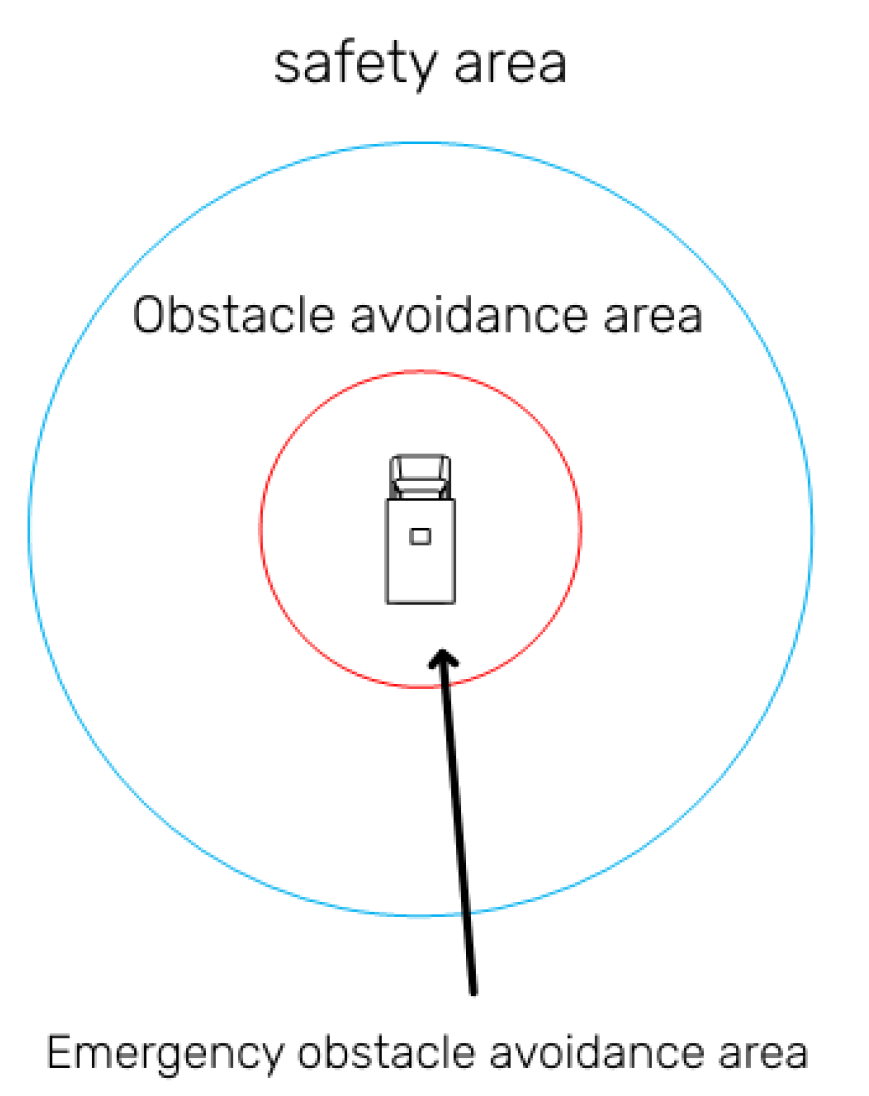
However, the prediction results of the Kalman filter are not very accurate at the beginning, with a high estimation error; however, this error will gradually decrease with several iterations and finally stabilize. Therefore, we set up a triple area in the range that an AGV can sense, as shown in Figure 3. The outermost layer is the safety zone, where the obstacle is far from the AGV distance, such that the threat level is small. We temporarily do not need to consider obstacle avoidance at this time, and Kalman filtering for the location of the obstacle is updated iteratively in order to obtain more accurate prediction results. The middle layer is the obstacle avoidance layer in which the AGV uses the Kalman filter’s estimation results to construct a risk collision buffer which guides the AGV in avoiding obstacles, such that the AGV can adjust its attitude as soon as possible to drive away from the obstacle. The final layer is the emergency obstacle avoidance layer, which seeks to avoid driving into the area of the obstacle.

Figure 3. Obstacle avoidance area.

The Kalman filtering algorithm is divided into two parts—prediction and update—which are expressed as

$$\left\{\begin{array}{c}\hfill X_k=A{x}_{k-1}+B{u}_{k-1}\hfill \\ \hfill P_k=A{P}_{k-1}{A}^T+Q\hfill \end{array}\right.,$$

(3)

$$\left\{\begin{array}{c}\hfill K_k=P_k{H}^T{\left(H{P}_k{H}^T+R\right)}^{-1}\hfill \\ \hfill X_k=X_k+K_k\left(z_k-H{x}_k\right)\hfill \\ \hfill P_k=\left(I-K_{k}H\right)P_k\hfill \end{array}\right..$$

(4)

Equation (3) represents the prediction part of the Kalman filter, while Equation (4) represents the update part of the Kalman filter, where $X_k$ denotes the state of the obstacle at the current moment; $X=\left[x,y,v_x,v_y\right]$ denotes the position and velocity of the target in the plane, where x and y are the horizontal and vertical coordinate axes, and $v_x$ and $v_y$ are the moving speed of the obstacle on the horizontal and vertical coordinate axes; Q denotes the process noise covariance matrix; H denotes the measurement matrix; R denotes the covariance matrix in the measurement noise; $Z_k$ denotes the measured value of the obstacle at the k-th moment; I denotes the unit matrix; A denotes the state transfer matrix; $P_k$ is the current covariance matrix; and $K_k$ denotes the Kalman gain.

3.2. Speed Obstacle Buffer

The concept of an obstacle avoidance risk area was first proposed by B. Guo et al. in [11]. They estimated the motion state of obstacles with a prediction algorithm and constructed a dynamic obstacle avoidance risk area along the movement direction of obstacles. The obstacle avoidance risk area was used to guide the obstacle avoidance of AGVs. However, in the selection of an obstacle avoidance strategy, this method compares the distances between the left and right sides of the AGV and the obstacle, respectively. The side with a smaller average distance is chosen for maneuvering, which is too simple to judge and does not make full use of the advantages of the dynamic obstacle avoidance risk area. Based on [11], the method proposed in this paper combines the obstacle avoidance risk area with the speed obstacle method to form the speed obstacle buffer zone. This method can solve the problem that, when the AGV passes in front of the obstacle, the uncertain factors in the environment can easily interfere, potentially leading to a collision.

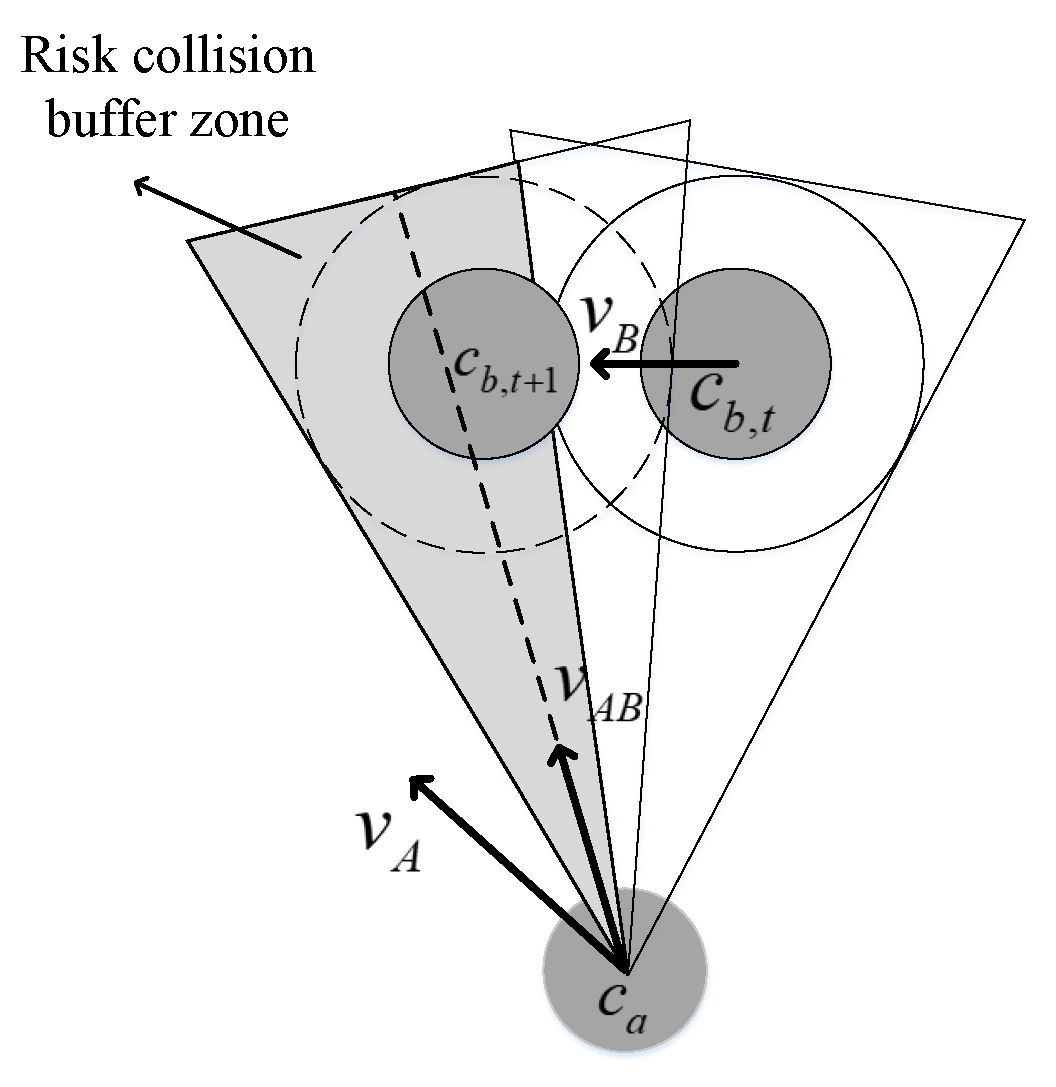
The construction process of the speed obstacle buffer is shown in Figure 4, where $c_a$ represents the position of the AGV at the current moment, $c_{b,t}$ is the actual position of the obstacle at the current moment, and $c_{b,t+1}$ is the predicted position of the obstacle at the next moment as estimated by the Kalman filtering algorithm. The gray shaded part in the figure is the speed obstacle buffer.

Figure 4. Speed barrier buffer.

Considering the interference caused by uncertain factors in the environment with AGV obstacle avoidance when the AGV chooses to overtake from the front of the obstacle, this method does not use the current position of the obstacle to construct the speed obstacle model. Instead, the estimated position of the obstacle at the next moment is selected, as shown in Figure 4. In the early stage of obstacle avoidance, the obstacles and their predicted positions are far from the AGV due to the existence of the speed obstacle buffer. At this time, the included angle of the collision cone is small, which helps the AGV to avoid the obstacles at a small angle at an earlier time and reduces the problem of unstable operation caused by the large angle when the AGV approaches the obstacles. Even if the AGV cannot turn in time due to some special circumstances during its movement, it will not collide with obstacles immediately due to the existence of a speed obstacle buffer.

4. Comprehensive Evaluation Index Based on Safety and Efficiency Factors

When the AGV detects an obstacle and determines that there is a risk of collision, according to the speed obstacle method, it is necessary to start the obstacle avoidance strategy, use appropriate methods to determine the speed interval attainable by the AGV, and select the most reasonable speed for obstacle avoidance, to ensure safety and efficiency. Efficiency denotes how fast the AGV escapes from the obstacle. When choosing the magnitude and direction of the velocity, the fastest strategy for escaping an obstacle is not necessarily the safest. If we only focus on safety and ignore efficiency, the duration of the act of obstacle avoidance of the AGV may be greatly extended, potentially leading to the AGV not arriving at the target location on time, thus causing a series of adverse effects regarding the arrangement of the task schedule.

According to the actual kinematic model of AGVs, the velocity obstacle method combined with the dynamic window can screen out the candidate speeds that the vehicle can actually reach within the next time interval, then select from this range. Assuming that, at the current moment, the range of speeds that the AGV can reach is $\left[v_{min},v_{max}\right]$, the range of the heading angle is $\left[{\omega }_{min},{\omega }_{max}\right]$, the minimum speed interval is $\Delta v$, and the minimum heading angle interval is $\Delta \omega$; then, the number of candidate speeds is given as

$$\mathrm{num}=\mathrm{floor}\left(\frac{v_{max}-v_{min}}{\Delta v}\right)·\mathrm{floor}\left(\frac{{\omega }_{max}-{\omega }_{min}}{\Delta \omega }\right).$$

(5)

On one hand, this makes the optional speed range narrower. On the other hand, as we consider the method of expanding the scope of the collision cone to ensure safety, according to Equation (2), when the AGV is closer to the obstacle, the expansion speed of the obstacle’s expansion radius is faster and the included angle of the collision cone is larger. Moreover, if the AGV heading angle is not adjusted in time, all candidate speeds may fall into the collision zone. Therefore, the traditional method of discarding all velocities in the collision zone is not feasible. In this paper, we attempt to find a qualified candidate speed that can consider both safety and efficiency by modifying the evaluation function of the dynamic window and scoring from both safety and efficiency aspects.

4.1. Velocity Gap

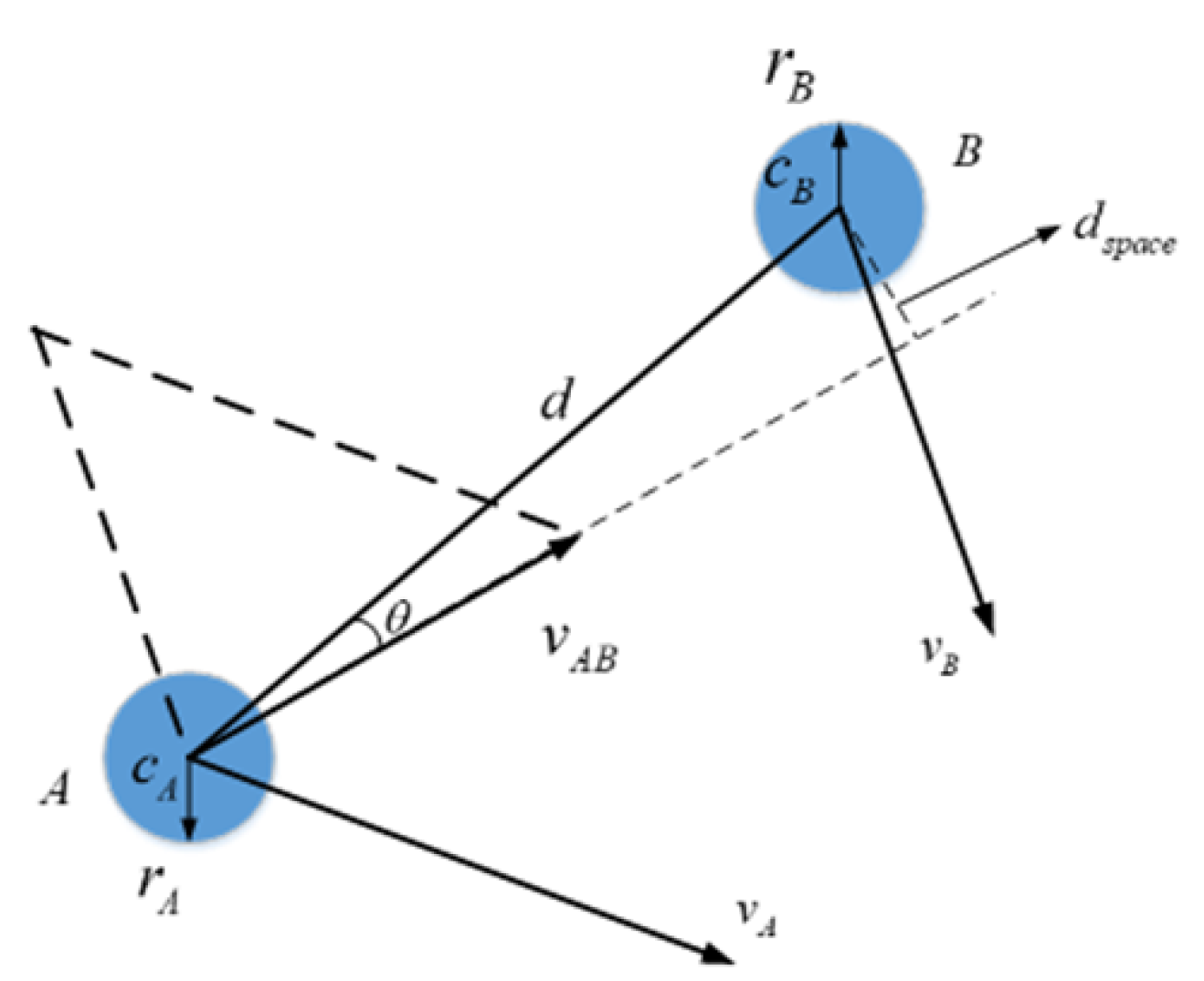
In this paper, as shown in Figure 4, the velocity gap $dist$ is defined as the vertical distance between the center of the circle where the dynamic obstacle is located and the line where the relative velocity of the AGV and the obstacle is located. When the risk of collision between the AGV and an obstacle is detected, assuming that the motion states of the AGV and obstacle do not change, the velocity gap is as shown in Figure 5, and its expression is

$$\mathrm{dist}=∥c_A-c_B∥·sin\theta .$$

(6)

Figure 5. Velocity gap schematic diagram.

4.2. Efficiency Index

Security and efficiency are the two indices that need to be considered simultaneously in the process of obstacle avoidance. If only security factors are considered, the timeliness of obstacle avoidance cannot be guaranteed.

In this paper, the boundary velocity of the collision cone in the improved velocity obstacle method is selected as the most ideal obstacle avoidance direction. The smaller the angle between the candidate velocity direction and the boundary velocity direction, the higher the candidate velocity score will be. In addition, if the two candidate velocities are on both sides of the collision cone, but the angle is the same, to preferentially select the velocity outside the collision cone, if the velocity is inside the collision cone, an additional constant k ($k>0$) should be subtracted.

When the velocity is outside the collision cone, its representation is:

$$avo=180-\phi .$$

(7)

When the velocity is in the collision cone, its representation is:

$$avo=180-\phi -\kappa ,$$

(8)

where $avo$ indicates the efficiency score of the AGV candidate speed. It can be assumed that the candidate speed is the most efficient speed that an AGV can use to escape from the obstacle under the premise of being able to consider certain safety factors. Therefore, the angle between the candidate speed direction and the speed obstacle buffer boundary is $\phi =0$, and the efficiency score is $avo=180$. In addition, considering the possible case that the candidate velocities are located on both sides of the collision cone but with the same angle, the candidate velocities located inside the collision cone may lead to additional safety factor issues, such that the safety factor score k needs to be subtracted.

4.3. Comprehensive Evaluation Indicators

Dimensionless processing is an important step in comprehensive evaluation. To avoid the lack of practical significance of the numerical accumulation results of the above two indices, due to different dimensions, it is necessary to carry out dimensionless processing on them, followed by subsequent analysis after eliminating the influence of dimensionality. Based on the premise that all evaluation index data were positive and all indicators have been transformed into positive indicators, we adopted the method of summation normalization to realize the quantification of indicators. Taking the summation value of indicators as the reference standard, the data obtained are equivalent to the sum proportion in order to convert the initial value of indicators into a dimensionless evaluation value. The calculation formula is

$$X=\frac{X}{Sum\left(X\right)},$$

(9)

where X is the evaluation index.

Subsequently, to comprehensively consider the influence of the two indicators, the results obtained after summation normalization were weighted to generate the candidate speed comprehensive evaluation score, as shown in the following:

$$G=\alpha ·dist+\beta ·avo,$$

(10)

where $\alpha$ and $\beta$ are the weights of the two evaluation indices; $dist$ is the velocity gap, used to evaluate the safety of the candidate velocity; and $avo$ is the angle between the candidate velocity direction and the velocity direction of the collision cone boundary.

Finally, all of the obtained candidate speed comprehensive evaluation indicators G are arranged in descending order, according to their numerical values, and the candidate speed with the highest score is selected as the running speed at the next moment.

5. Simulation and Result Analysis

To verify the effectiveness of the improved algorithm proposed in this paper, the MATLAB 2020 simulation software was used for simulation and analysis, as detailed in this section. The computer was configured with the Windows 10 operating system, an I5-10300H processor with main frequency 2.5 GHz, and 16 GB of operating memory.

It was assumed that the maximum speed that the AGV can achieve is 1 m/s and its maximum acceleration is 0.2 m/s${}^2$. The starting speed of the AGV was 0, and the starting direction was ${45}^{\circ }$ north by east, starting from the starting point and ending at the end point. The obstacle velocity was $0.45\mathrm{m}/\mathrm{s}$, heading due west. The time interval between the AGV and the obstacle $\Delta t$ was $0.1s$. As shown in Formula (8), according to the control variable method, the obstacle avoidance effect was best when the weight coefficients of the objective function were $\alpha =0.2$ and $\beta =0.05$. The AGV and the dynamic obstacle were regarded as two particles; the safe distance between them was set as $0.5\mathrm{m}$.

Figure 6 compares (a) a classic speed barrier method combined with a dynamic obstacle avoidance path window, (b) an adaptive speed barrier method for the obstacle avoidance path, (c) the algorithm proposed in this paper for the obstacle avoidance path, and (d) the three obstacle avoidance paths in contrast, where the blue path is the traditional method [17], red is the adaptive speed barrier method [18], and black is the proposed algorithm. In combination with the results reported in Table 1, it can be seen that the traditional obstacle avoidance method did not consider security in the obstacle avoidance process, so it chose the path with the highest efficiency when discovering and avoiding obstacles.

Figure 6. Obstacle avoidance path comparison.

Table 1. Data comparison between traditional methods and the method proposed in this paper.

Algorithms	Total Number of Obstacle Avoidance Steps	Path Length (m)	Shortest Distance from Obstacles (m)
Traditional VO algorithm	336	16.080	0.5038
Adaptive VO algorithm	344	16.241	0.6755
This article algorithm	344	16.245	0.6992

Although it took less time and the length of the path was shorter, as it came closer to the obstacle, the method cannot be considered conducive to dealing with unexpected situations in the driving process. The blue line depicts a relatively safe path when detecting obstacles. As the obstacle approached, the obstacle avoidance angle gradually became larger. Although the time and path length were longer than those of the traditional algorithm, safety could be guaranteed. The choice of path by the proposed algorithm, compared with the adaptive speed barrier method, indicates that the angle of turning in the path was relatively small, ensuring the stability of the AGV run. In addition, the proposed algorithm, when compared to the adaptive speed barrier method, although presenting a slight increase in the total length of the path, by consideration of the obstacle in the process of obstacle avoidance, provided a safer distance and, thus, had better security.

In the simulation process, considering the uncertain factors in the environment leading to interference in the process of AGV obstacle avoidance, we simulated skidding of AGV, with 0–50% random slipping included in the process of the AGV run; that is, within a given time interval, while the AGV can cover a distance of 1 m in normal circumstances, after implementing the random sliding deviation, it may only drive in the range of 0.5–1 m.

Figure 7 shows a comparison between the AGV and the distance to the obstacle from the time it detects the obstacle to the time it leaves the obstacle, with and without consideration of the slip factor. The abscissa represents the step size and the ordinate represents the distance from the obstacle. It can be seen that the speed of the AGV could not reach the expected speed due to skidding, leading to an extension of the entire obstacle avoidance cycle. Therefore, the nearest distance between the AGV and the obstacle was closer and more dangerous than the ideal case. Therefore, it is necessary to ensure a sufficient safety distance between the AGV and the obstacle in order to deal with uncertain factors in the obstacle avoidance process.

Figure 7. Comparison of distance with obstacles, with and without skidding.

Table 2 details a performance comparison between the traditional algorithm, the adaptive speed obstacle method, and the algorithm proposed in this paper when the slip factor was considered. In 200 repeated tests, the total steps, path length, and the nearest distance to the obstacle are all reported as average values. It can be seen that, although the adaptive speed obstacle method slightly increased the total steps and path length, it greatly improved the success rate of obstacle avoidance and the minimum distance from the obstacle. Compared with the adaptive speed obstacle method, the algorithm proposed in this paper achieved a higher success rate of obstacle avoidance and maintained a safer distance from the obstacle with the interference of uncertain factors. In particular, its success rate was $11\%$ higher than that of the adaptive speed obstacle method.

Table 2. Performance comparison considering skid factor.

Algorithm	Success Rate	Total Number of Steps	Path Length (m)	Closest Distance to Obstacle (m)
Traditional VO algorithm	$0\%$	348.0	16.8247	0.4113
Adaptive VO algorithm	$87\%$	360.1	17.5441	0.5310
Proposed algorithm	$98\%$	359.8	17.5525	0.5558

6. Conclusions

There are two challenges to the adaptive velocity obstacle method when avoiding dynamic obstacles. The first is that, when the AGV is close to the obstacle, the adaptive extension radius increases exponentially with the distance between the AGV and the obstacle, such that, when the AGV is closer to the obstacle, the angle needs to be adjusted to a greater extent. Too large a rotation angle may affect the stability of the AGV, potentially even leading to collision with obstacles due to delayed steering. The second challenge is that the steering speed of the AGV may not keep up with the increase in the adaptive extension radius and, if all candidate speeds come to lie in the collision zone, no alternative speed may be chosen for the next moment. In this paper, based on the idea of forward simulation, the collision obstacle method is combined with the buffer and velocity to generate a collision cone according to the estimated position of the obstacle at the next moment. This method can avoid obstacles at a small angle in the early stage of obstacle avoidance and ensure the stability of AGV operations. Furthermore, considering both efficiency and security factors, a new evaluation index was designed, which can be used to score all candidate speeds and select the one with the highest score as the running speed for the next moment. Our experimental results highlighted the superior effectiveness of the proposed algorithm.