1. Introduction
Autonomous driving vehicles have a huge potential not only for reducing the number of road accidents but also from an economic point of view, reducing emissions as well as increasing the efficiency of traffic usage by, e.g., robotaxis or avoiding traffic jams. Thus, autonomous driving already revolutionizes our view on mobility, traffic safety, and how time is spent during car journeys. The following question arises: how do we verify that an autonomous vehicle is safe enough. There are many proposals on how many kilometers an autonomous vehicle has to drive accident-free before it may be safely released on the road. The estimation reaches from several millions to even billions of kilometers. We want to stress that this is only for one system. All updates and changes in the software, occuring errors, improvements, and transformations require a rerun. Every experiment of such dimensions, if feasible at all, would be tremendously cost-intensive. This motivates a simulation-based test of autonomous vehicles.
A simulation-based framework aims to replicate real-world traffic and to validate the automated driving functionality accordingly. In this framework, robustness, reliability, and safety can be investigated in a much quicker and cost-efficient manner. It is emphasized that the validation results and investigations in the simulated environment are only as trustworthy as the virtual environment reflects the real world [
1,
2,
3,
4].
The simulation is fed with stochastic data, e.g., velocity/acceleration of the traffic participants, extracted from the real recordings of traffic events.
A huge challenge is that the stochastic parameters, such as the velocities of every traffic participants, are not independent. There are many factors that have to be considered. The weather, visibility, and the amount of traffic participants are correlated to the driving behaviour of the participants. Unfortunately, this correlation is unidentified and cannot be assumed beforehand. In this work, dependencies in stochastic data are investigated and described by so-called copulas.
The latin word copulare may be translated into “to join” or “to connect”, which already reveals the meaning and functionality of copulas. They are great tools for modeling the (nonlinear) dependence of random variables and for calculating the joint distribution. The first appearance of the term copula may be found in [
5]. Since then, substantial research and the application of copulas can be seen in the fields of statistics [
5,
6,
7], economics [
8,
9], finance [
10,
11,
12,
13], actuarial science [
14,
15], or risk management [
16,
17,
18] to name a few.
The outline of this work is as follows. In
Section 2, we examine further the subject of validating automated vehicles and the theory of copulas. The construction and usage for resimulating data are described.
Section 3 illustrates how data can be extracted from observations and how the theory on a concrete numerical example and application can be applied. A conclusion and outlook for further research and development is given in
Section 4.
2. Preliminaries
2.1. Safety Validation of Automated Vehicles
Unlike today’s cars, autonomous vehicles require additional regulations. A distinction is made between automation levels, as in the SAE J3016 standard [
19]: a
driver-only vehicle without automation,
assisting systems, and
semi-automated systems. In all three levels, the driver keeps the responsibility for the behavior of the vehicle. Furthermore, we speak of
fully automated vehicles when the driver no longer acts as a fallback [
20]. In this case, the automated systems should take over vehicle control permanently and should act safely in any environment.
The international organisation for standardisation (ISO) provides ISO/PAS (Publicly Available Specification) 21448 to ensure the safety of the functionalities [
21] and ISO 26262 to ensure that no hazards are caused by technical failures [
22]. ISO/PAS 21448, which comprises the safety of the intended funcionality (SOTIF), focuses on predictable misuse by the driver, as well as accidents that are explicitly not caused by component failure but situations that were not planned for during development. Nevertheless, this standard does not provide a detailed strategy for identifying functional deficiencies. In contrast, ISO 26262 focuses on safety in terms of intrinsic safety (the protection of the environment from the product) and, therefore, functional safety. It is an ISO standard for safety-related electrical/electronic systems in motor vehicles. It is not enough that the function has been executed correctly, but it must also be ensured that the function has been executed in the correct context. For example, an airbag must not be triggered when driving too fast over speed bumps. However, the minimum requirements for safeguarding an autonomous vehicle are not adequately described by this standard. The goal is to minimize risks to a level that is “acceptable to society”.
Consequently, the validation of autonomous vehicles cannot be based on existing ISO standards and require extension. Various approaches have been developed, starting with advanced driver assistant systems (ADAS), where function-based approaches and real-world testing operate well. In the function-based approach, requirements are defined for the operating system that are tested by simulation or on the test track. In real-world testing, a mileage-based evaluation of functionality from field tests with a driver is performed. For both methods, validating fully autonomous systems is economical infeasible in its current state. Furthermore, there is the shadow mode, presented by Wang and Winner [
23], in which the automated driving function is excecuted passively in series production vehicles. The driving function receives (real) information from the sensors, but it will not act. Its actions are evaluated afterwards by simulation.
Considering the real world as an open parameter space, with an infinite number of traffic events, the scenario-based approach tries to identify these traffic events and describe them in scenarios. It also attempts to exclude non-relevant traffic events, where neither actions nor events are observed, and to cluster similar traffic events into a representative scenario [
24]. However, this leads to the question of how to find the set of representative scenarios. A good overview of the problem of identifying critical scenarios is provided by Neurohr et al., Riedmaier et al., and Zhang et al. [
25,
26,
27].
Menzel et al. [
28] distinguished three categories of scenarios: functional, logical, and concrete scenarios. In the case of functional scenarios, the scenario space, in the same way as traffic events, is described at a sematic level by “a linguistic scenario annotation” [
28]. For the logical scenarios, this is described at the state space level. Entities and their relationships are described using parameter ranges in the state space and optionally specified using correlations and numerical relationships. A traffic event is finally mapped explicitly to the state space given a concrete scenario. Entities and their relationships are described using concrete values for each parameter. According to Zhang, the identification of critical scenarios can be performed at all three levels of abstraction. This requires a clear definition of the operational design domain (ODD), a definition of the operating conditions under which an AD system attempts to operate, and “the formulation of a functional scenario to a logical scenario”.
The German research project Pegasus (Pegasus—project for the establishment of generally accepted quality criteria, tools and methods as well as scenarios and situations for the release of highly automated driving functions; see
https://www.pegasusprojekt.de/en/home, accessed on 5 November 2022) followed the approach in [
29] of modeling the environment in layers and extended it to six layers for describing the environment of a highway. In the follow-up project VVM (VVM—verification and validation methods for level 4 and 5 automated vehicles; see
https://www.vvm-projekt.de/, accessed on 5 November 2022), the six-layer model was refined, extended to the urban environment, and provided with guidelines [
30].
To describe the operating conditions of an AD system, the parameters of the six layers are used, such as weather, the number of road users, and the number of lanes or speed of a cyclist. The assessment of whether a scenario is critical or not is based on the concrete values for these stochastic parameters. Some studies already consider realistic parameter distributions [
27] that are obtained from real-life driving databases.
In scenario-based testing, parameter distributions can be used to support the search for critical scenarios within the scenario space. In doing so, they serve to model the mutuality of the scenarios. In [
31], a risk index based on a Gaussian mixture model is used to efficiently select critical traffic conditions. Thereafter, the scenarios are replicated via simulation and used, for example, to evaluate the criticality of the AD system. For the simulation of the scenarios, real trajectories that are extracted from real data are used. In the same way, the characteristic criteria of scenarios are taken from the real data, e.g., parameter distributions or parameter dependencies, and used to reproduce trajectories or parameters. Thus, parameter distributions are applied in estimating the failure rate of a scenario. For example, Wagner et al. [
32] predicted the behavior of road users based on conditional distributions obtained by analyzing a naturalistic driving study called euroFOT (large-scale European Field Operational Test on Active Safety Systems) and determineed the criticality for each predicted event.
2.2. Copulas
Copulas allow modelling the (nonlinear) dependence of several random variables. With the help of copulas, the multivariate distribution can be split into their marginal distributions. In the following, the definition and construction as well as the main features of copulas will be discussed and illustrated.
2.2.1. Definition
For a d-dimensional random vector , we denote the joint cumulative distribution function by and the marginal distributions by . A copula is a special type of distribution function.
Definition 1 (Copulas).
A d-dimensional copula is a multivariate distribution function with standard uniform marginals. If the copula is absolutely continuous, the corresponding copula density is defined as follows. Sklar’s theorem [
5] states that any multivariate distribution can be expressed in terms of its marginal distributions and a copula.
Theorem 1 (Sklar’s Theorem, 1959).
Let be a d-dimensional random vector and let the corresponding joint distribution function be denoted by F as well as the marginal distribution functions by , where . Then, the joint distribution function is given bywhere C is a d-dimensional copula. If the distributions are absolutely continuous, then copula C is unique. Moreover, the corresponding density function is given by Sklar’s Theorem can be understood as follows. The marginal distributions characterize the behavior of each of the variables in isolation. The copula on the other hand characterizes the dependence between them. On the one hand, we can decompose any joint distribution into marginal distributions and a copula. On the other hand, we can combine any copula with arbitrary marginal distributions to form a valid multivariate disribution function.
Example 1. The copula corresponding to independent random variables is = and it is called an independence copula.
2.2.2. Bivariate Parametric Copula Models
There are two major classes of parametric copula models: elliptical copulas and Archimedean copulas. Two well-known examples of elliptical copulas are the multivariate Gaussian copula and the multivariate Student’s
t copula. They are constructed implicitly by inverting the formula in Sklar’s theorem of the following:
and they take
F to be a bivariate Gaussian or Student’s
t distribution. For further information, refer to, e.g., [
6].
Archimedean copulas are constructed more explicitly via generator functions.
Definition 2 (Bivariate Archimedean Copulas).
Let be a continuous, strictly monotone decreasing and convex function satisfying ; then, φ is the generator of the bivariate Archimedean copulawhereis the so-called pseudo-inverse of . For a specific choice of the generator, the bivariate copulas given in
Table 1 may be constructed. Note that the BB1 and BB7 families are two-parametric famlies where the others are one-parametric Archimedean copulas, but [
6] is suggested for further information.
Remark 1. Perfect dependence and independence are achieved for Clayton if and and for Gumbel if and , respectively. For the Frank copula, the indepence copula is achieved for , and for the Joe copula, the indepence copula is achieved for . For the BB1 copula, the independence copula corresponds to and and for the BB7 copula, the independence copula corresponds to and .
Copula
C is related to the distribution of random variables
,
. We thus first estimated marginal distributions
by
. Then, we generate “pseudo-observations”
, from which the copula parameters can be estimated using likelihood methods. We refer to [
6,
33,
34,
35] for more information.
2.2.3. Vine Copulas
As shown above, there is a plethora of flexible parametric models for two-dimensional vectors. The extensions of elliptical and Archimedean copulas to the d-dimensional case are much less flexible however. Elliptical copulas impose strong constraints on the symmetry of dependence. For example, large observations cannot have stronger dependence than small observations. Archimedean copulas are exchangeable, i.e., all subsets of the variables must have the same dependence.
Pair-copula constructions were introduced by [
36,
37,
38] to mitigate these issues. The idea is to construct a multivariate dependence structure from only bivariate copulas. Each of these bivariate building blocks describe the (conditional) dependence between a pair of variables. The bivariate copulas can be specified independently, e.g., with some Gaussian and some Archimedean with different strengths of dependence, which make these models extremely flexible.
The above construction relies on conditioning. To organize all admissible orders of conditioning, [
37] introduced a graphical model called
vine. A vine is a set of trees, where a tree
is a connected graph that contains no cycles; the reader can refer to [
39]. Regular vines (R-vines) are a nested set of
trees
such that a node of the next tree is built upon the edges of the previous tree. Furthermore, the edges are only joint if they have a common node in the previous tree. If additionally the degree of each node in the first tree is at most 2, then each tree is a path, and we speak of D-vines. If each tree has a unique node of degree
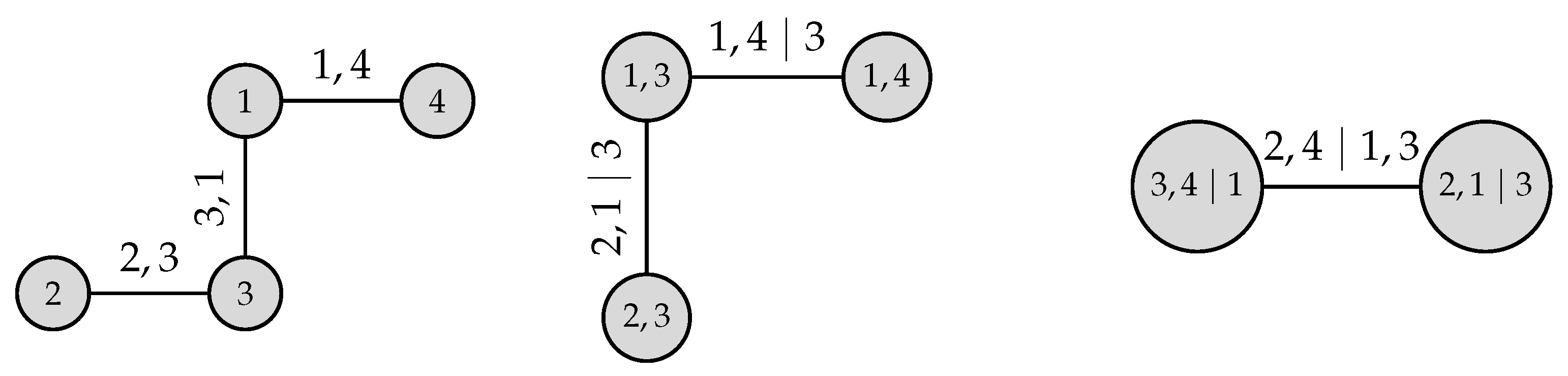
, each tree is a star, and we speak of C-vines. Hence, D- and C-vines are special cases of R-vines. An example of a four-dimensional D-vine copula can be seen in the second figure in
Section 3.
Every vine graph allows the decomposition of the joint density in a different way. To perfrom this, each edge
is assigned a label
, where
and
. Each edge is further associated with a copula
that captures the dependence of
that is conditional on all
. The reader can refer to [
6] for further details. With this notation, we obtain the following result.
Theorem 2. Let be a sequence of random variables with continuous invertible marginal distributions . Let be a R-vine tree sequence on d elements and be the set of the associated bivariate copula densities. Then, joint density f can be factorized into The conditional distributions in this formula can be computed recursively from the pair-copulas in earlier tree levels.
The formula can be simplified for a D- or C-vine. We refer to [
6,
37,
38] for further reference. In this paper, we use the R package rvinecopulib [
40], where the latter approaches are implemented. As we do not have any knowledge about the vine structure, we make use of the vine function, which performs parameter estimation and automatic model selection using the sequential procedure proposed by [
41]. The package also allows simulations from the fitted model based on the inverse Rosenblatt transform algorithm [
6,
41].
2.3. Dependence Measures
One common way to measure the dependence amongst multivariate normal random variables is to use Pearson’s correlation coefficient. This coefficient,
, is a measure of linear dependence indicated with
perfect and by
no (linear) dependence. According to [
7], the coefficient
is “generally not the best measure of dependence” since it may not yield ± 1 for non-Gaussian random variables with perfect dependence. A better choice includes rank correlation coefficients, which measure monotonic dependence. Monotone associations mean a dependence, where if one variable increases, then the other tends to decrease (or increase) and vice versa. A nice property of these measures is that they are invariant relative to strictly increasing transformations on the variables [
6,
7]. The relation can otherwise be nonlinear. The best-known rank correlation measures are Spearman’s
and Kendall’s
, which are explained in more detail in the following sections.
Definition 3 (Spearman’s
).
Let be continuous random variables with continuous marginal distributions and let . Then, Spearman’s rank correlation for is given by the following. Hence, Spearman’s rank correlation coefficient is defnined as Pearson’s correlation coefficient of the random variables and . To compute Spearman’s empirically from a sample , one replaces marginal distributions and with the respective empirical distribution functions and . The pseudo samples then correspond to , where is the rank of value among all . For example, if is the smallest value in the sample.
Definition 4 (Estimation of Spearman’s
).
An estimate of Spearman’s based on a sample of size n with ranks for is given bywhere and are the corresponding sample rank means. Kendall’s on the other hand measures dependence by comparing pairs of observations.
Definition 5 (Kendall’s
).
Let be a random vector with joint distribution F and let be another vector with the same distribution, but it is independent of . Kendall’s τ is defined as follows. In the above definition, we call the pair of vectors, and , concordant if the values and have the same sign. Otherwise, the pair is called discordant. Hence, Kendall’s is the difference of the probabilites of concordance and discordance.
To calculate Kendall’s empirically, one simply compares each observation and counts the number of concordances and ties.
Let be the number of concordant pairs, let be the number of discordant pairs, and let and be the numbers of ties in and respectively.
Definition 6 (Empirical Kendall’s
).
The empirical Kendall’s τ is given by As shown in [
6,
7], Kendall’s
and Spearman’s
are independent of the marginal distribution and only depend on the associated copula. In particular, they can be expressed as
3. Application to Traffic Data
Imagine a road that is busy on one day and has little traffic on another. The driving behavior of the road users is expected to differ. Considering the speed and traffic volume in terms of the number of vehicles, for example, it is reasonable to assume that these two parameters correlate. If we additionally take the time of day and weather conditions into account, we have already approached multi-dimensional dependencies. For example, splashy roads or low sun with high traffic volume would have another impact on the speed of the participants than dry roads or a cloudy sky. In order to reproduce traffic events in simulations, preferably as close to reality as possible, these multidimensional dependencies need to be considered. If we further want to sample or generate random values, according to their associated multidimensional distribution, copulas deliver the possibility to satisfying this request. The additional value generated by this coupled knowledge is a significant advantage for the simulative validation of autonomous driving systems in the context of scenario-based validation [
4,
26]. In particular, when calculating the probability of failure of a system, the reliability strongly depends on the distribution of the underlying parameters [
42]. The more accurate the stochastic input parameters and if their dependencies are described and therefore sampled, the more accurate the statement about the probability of critical failures and therefore the result of the reliability analysis [
42]. Precisely speaking, we want to use these multidimensional dependencies on the driver’s behavior as a stochastic input in the form of a probability distribution for the validation of autonomous systems and automated driving functions. To examine this, we focus on an explicit example, which is described in the following.
The rounD dataset is a drone dataset, specifically created for behavior planning for automated vehicles, that can also be used for downstream safety validation. Due to the high-density interactions between road users [
43], it is of special interest for the purpose and application of this work. Due to the recordings from the air, it avoids the risk of occlusion during recordings, as well as the risk, in which road users do not adopt natural behavior in traffic when being observed [
44]. This is one of the requirements that the dataset satisfies to ensure that mutual influences are reflected. To create a trajectory-based dataset, which includes more than 13746 road users, traffic was recorded at three different locations in and around Aachen, Germany. The road user types can be divided into the following classes: cars
, trucks
, vans
, trailers
, buses
, and VRUs (vulnerable road user), which include pedestrians
, bicycles
, and motorcycles
.
Most recordings were made in
Neuweiler; hence, we chose this location for our application. It is a four-armed roundabout where all access roads have two lanes and the exits are single-lane roads. The fact that there is no lane marking whithin the roundabout leads to many interactions.
Figure 1 illustrates a recording from this location. The trajectories of the traffic participant’s movement up to this point are drawn in blue and the continued trajectories are drawn in white, respectively.
According to the report of the Insurers Accident Research [
45], the most frequent accidents inside traffic circles occur due to approaching waiting vehicles too closely and disregarding the right of way when entering the traffic circle.
Based on this evaluation, we derive the four parameters shown in
Table 2. We consider the speed behavior (VelCar) per frame, which is already provided by the RounD dataset. To determine the traffic density (TrafficCar), we count the vehicles within a radius of 10 m around each car per frame. Furthermore, we consider the time of standstill (WaitTime) for each vehicle before entering the roundabout as well as inside the roundabout. Finally, we take the minimal distance (DistCar) per frame from one car to all cars in its associated surrounding. A total number of 132,409 samples result from the 22 Neuweiler recordings. Each recording is taken with 25 frames per second and has a length between 19 and 23 min. Since we count the vehicles for the representation of the traffic density, TrafficCar is a discrete parameter, whereas VelCar, WaitTime, and DistCar are continuous parameters.
In the lower triangular matrix of
Table 3, Kendall’s
is depicted and Spearman’s
in the upper triangular matrix. The values in
Table 3 of the rank correlations confirm what can be intuitively surmised. If the amount of traffic participants increase (TrafficCar), vehicle speeds (VelCar) decrease,
and
(i.e., negative correlation), along with the distances (DistCar) between vehicles,
and
; waiting times (WaitTime) increase,
and
(i.e., positive correlation). Analogously, the speeds (VelCar) decrease when the waiting times (WaitTime) increase,
and
, and the distances (DistCar) between the vehicles decrease,
and
. Furthermore, the distances (DistCar) decrease with increased waiting times (WaitTime),
and
.
Subsequently, the copula is estimated from the four parameters using the vine function from the rvinecopulib package [
40]. The resulting vine structure is shown in
Figure 2. Therein, node 1 represents parameter TrafficCar, node
VelCar, node
WaitTime, and node 4 represents DistCar.
The bivariate unconditional and conditional copula densities can be reconstructed from the tree structure such that the joint copula density
c can be written as follows:
with
TrafficCar,
VelCar,
WaitTime, and
DistCar. The unconditioned copulas
and
and conditioned copulas
and
were estimated using the local-likelihood transformation estimator (TLL). The conditioned bivariate copula
results in a (Survival) Clayton–Gumbel (BB1) family with parameters par
,
and internal coding family:
[
40]. As mentioned before, the generation of samples similar to real data is an important requirement for reliability and risk analyses.
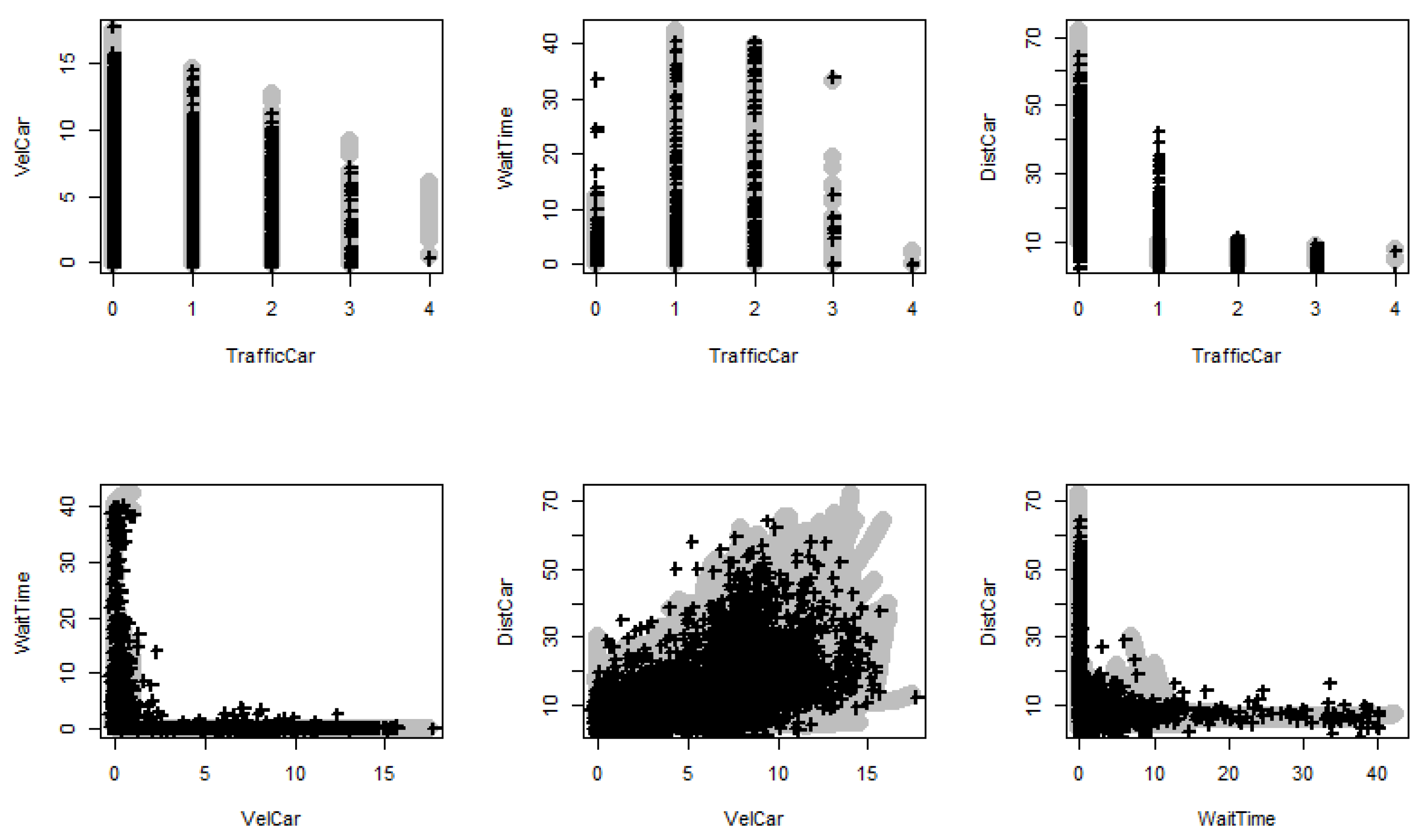
Figure 3 shows in black 5000 samples generated from the fitted vine copula model. They are plotted according to real data samples, which are depicted in grey and generated from the rounD dataset. Since the simulated data matche the original data sufficiently, the generated copula reflects the dependency structure of the four parameters and may therefore be used for further computation, such as the risk and reliability analysis. Further analysis is not performed in this study. In the next chapter, we will give an outlook for ongoing investigation and stress tests.
4. Conclusions
When it comes to describing stochastic phenomena, such as the traffic behavior, the correlation between the corresponding parameters cannot be neglected, particularly if the stochastic descriptions of the parameters are needed for ongoing analysis, such as for the validation and verification of autonomous driving and assistance systems. In this study, copulas are used as an approach for not only measuring the dependence and correlation but also to generate and calculate the joint distribution function of multivariate stochastic variables, taking the dependence into account.
The numerical example given in
Section 3 describes the application of the theory of copulas on a concrete observation and real-time measurements of a roundabout. Despite considering only four parameters, the speed, traffic density, waiting time (before entering the roundabout and within the roundabout), and the distance to other traffic participants, the usefulness of this approach is illustrated. Additionally, the plausibility of the negative and positive correlation of the parameters is discussed, which is captured via the use of a copula.
It is emphasized that more stochastic parameters can be taken into account, such as the time, since the traffic density may correlate to the time of day, e.g., rush hour at the end of the working day to give an example. Moreover, the weather, road quality, or visibility might be important parameters depending on which questions the downstream analysis tries to address. It is worth mentioning that more data and therefore more hours of recording are necessary to extract these parameters and to consider their interferences. The given approach may therefore be seen as an intial attempt to generate random variables or samples according to their dependencies, extracted from real traffic data, without the claim of the completeness of all influential parameters.
Based on the given approach, a further analysis has to be performed in the future and is not considered in this work. To provide an example of how often an autonomous vehicle causes a crash, it can be investigated with a simulated reliability analysis via, e.g., Monte Carlo simulations. It is expected that by considering the joint distribution with all correlations extracted from the real-time data, the reliability analysis is more accurate and closer to reality. However, as there are no accidents in the drone dataset, the comparison between simulation and reality is not feasible. This highlights the need for more data and more recordings.
This approach can also be helpful when it comes to studying the behavior of swarms of traffic participants and their interactions, similarly to [
46], especially when transfering this behavior from real-world to a virtual or simulated environment.