Reduced-Cost Optimization-Based Miniaturization of Microwave Passives by Multi-Resolution EM Simulations for Internet of Things and Space-Limited Applications
Abstract
1. Introduction
2. Miniaturization of Microwave Passives by Multi-Fidelity Simulations
2.1. Problem Formulation
2.2. Search Engine: Trust-Region Local Search
2.3. Model Fidelity Arrangement
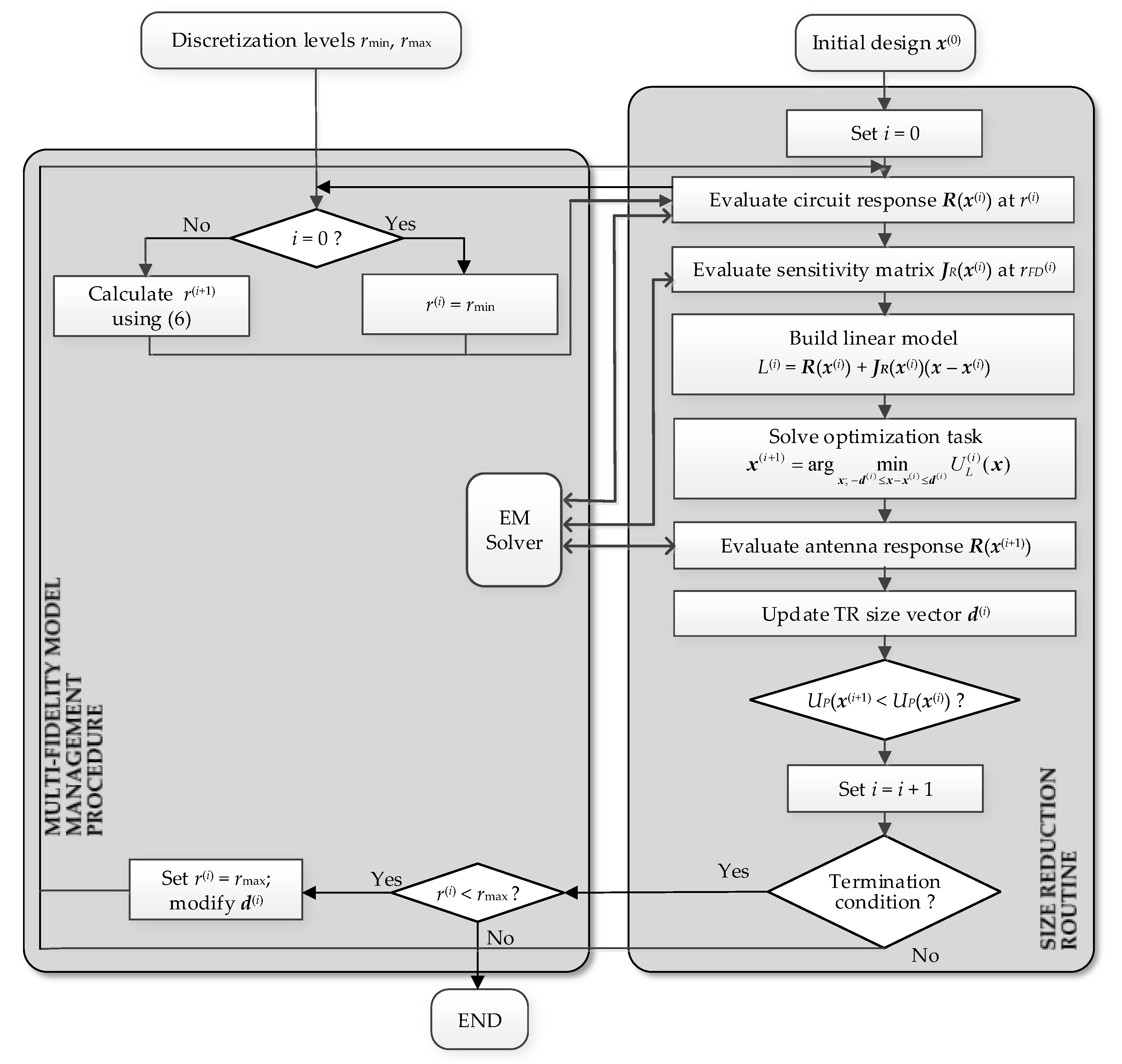
2.4. Miniaturization Framework
| Algorithm 1: Operation of the proposed multi-fidelity size reduction algorithm. |
|
1. Set the iteration counter i = 0, and r(i) = rmin; 2. Evaluate component response R(x(i)) at the discretization level r(i); 3. Evaluate component sensitivities JR(x(i)) at the discretization level rFD; 4. Construct a linear model ; 5. Obtain the design x(i+1) by solving (4); 6. Evaluate component response R(x(i+1)) at the discretization level r(i); 7. Update trust-region size vector d(i); 8. If UP(x(i+1)) < UP(x(i)), compute r(i+1) using (6); Set i = i + 1; end 9. If ||x(i+1) – x(i)|| < εx OR ||d(i)|| < εx OR | UP(x(i+1)) – UP(x(i))| < εU if r(i) < rmax Set r(i) = rmax and modify d(i); go to 3; else Go to 10; end else Go to 3; end 10. END. |
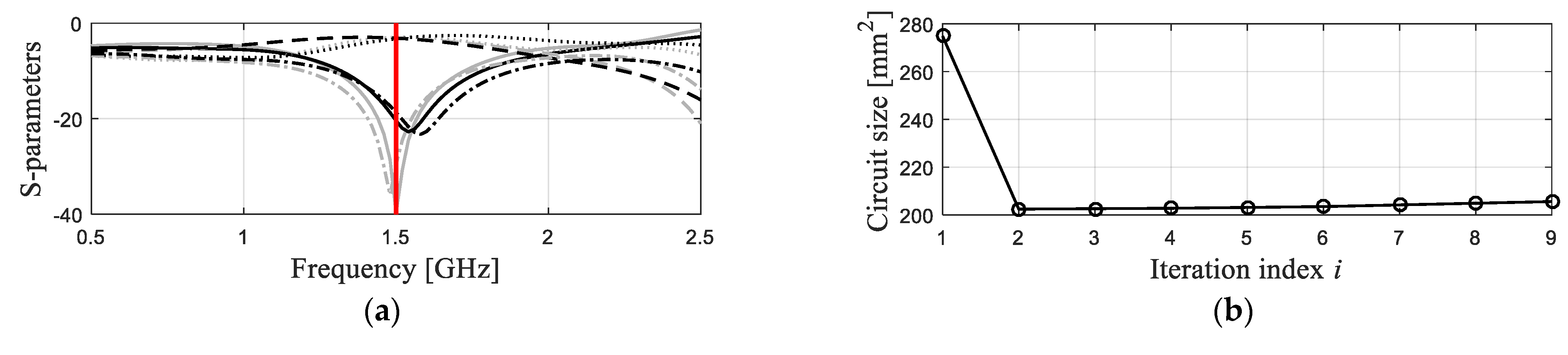
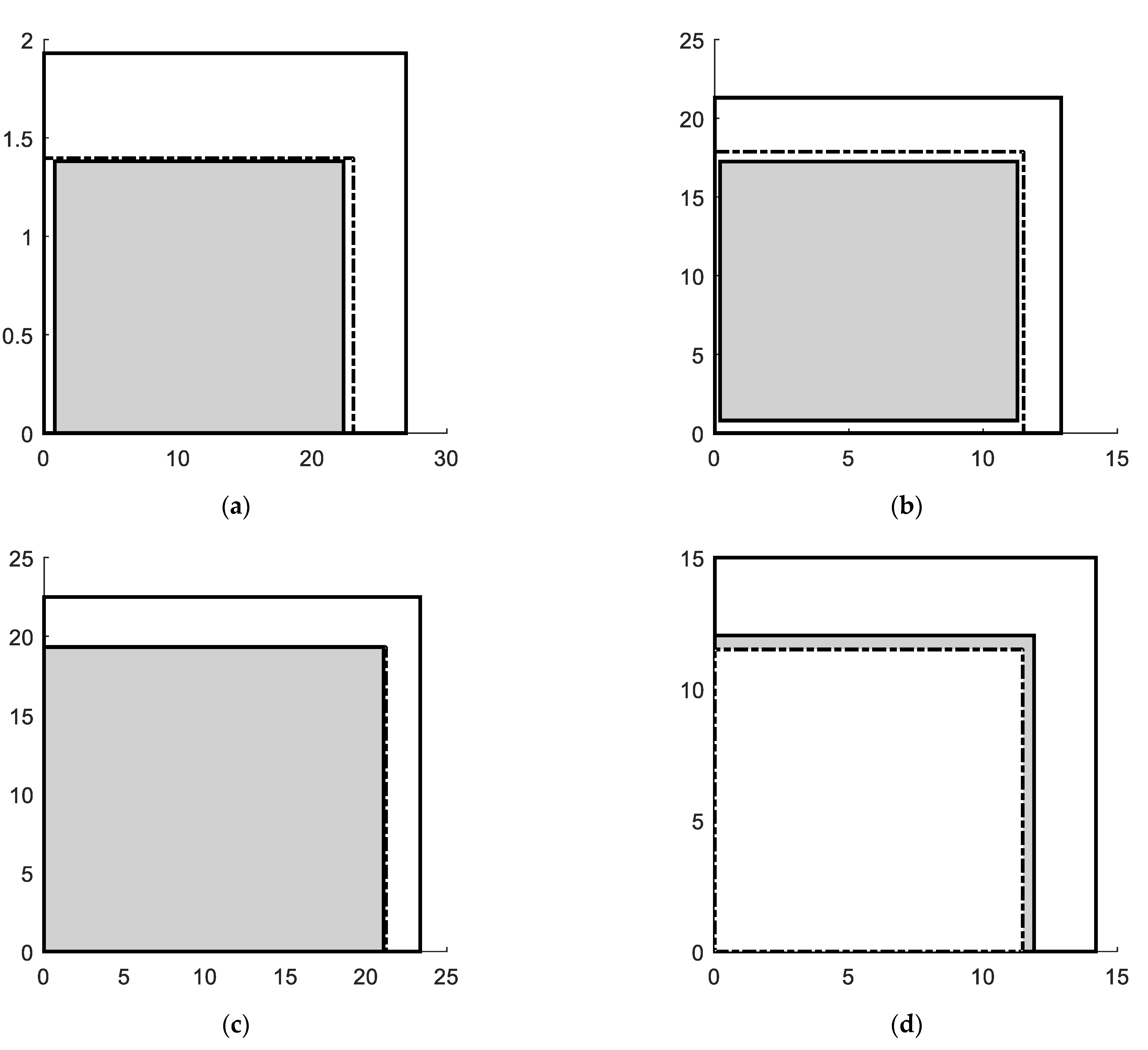
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cai, L.; Cheng, K.M. A novel design of dual-band rat-race coupler with reconfigurable power-dividing ratio. IEEE Microwave Wireless Comp. Lett. 2018, 28, 16–18. [Google Scholar] [CrossRef]
- Li, Q.; Chen, X.; Chi, P.; Yang, T. Tunable bandstop filter using distributed coupling microstrip resonators with capacitive terminal. IEEE Microw. Wirel. Comp. Lett. 2020, 30, 35–38. [Google Scholar] [CrossRef]
- Chen, S.; Yu, Y.; Tang, M. Dual-band Gysel power divider with different power dividing ratios. IEEE Microw. Wirel. Comp. Lett. 2019, 29, 462–464. [Google Scholar] [CrossRef]
- Chi, P.; Chen, Y.; Yang, T. Single-layer dual-band balanced substrate- integrated waveguide filtering power divider for 5G millimeter-wave applications. IEEE Microw. Wirel. Comp. Lett. 2020, 30, 585–588. [Google Scholar] [CrossRef]
- Seddiki, M.L.; Nedil, M.; Ghanem, F. A novel wide, dual-and triple-band frequency reconfigurable butler matrix based on transmission line resonators. IEEE Access 2019, 7, 1840–1847. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Baum, T.; Scott, J.; Ghorbani, K. Continuously tunable dual-mode bandstop filter. IEEE Microw. Wirel. Comp. Lett. 2018, 28, 419–421. [Google Scholar] [CrossRef]
- Tsai, K.; Yang, H.; Chen, J.; Chen, Y.E. A miniaturized 3 dB branch-line hybrid coupler with harmonics suppression. IEEE Microw. Wirel. Comp. Lett. 2011, 21, 537–539. [Google Scholar] [CrossRef]
- Lin, Y.-S.; Liu, Y.-R.; Chan, C.-H. Novel miniature dual-band rat-race coupler with arbitrary power division ratios using differential bridged-T coils. IEEE Trans. Microw. Theory Tech. 2021, 69, 590–602. [Google Scholar] [CrossRef]
- Mocanu, I.A. Compact dual band ring coupler using miniaturized metamaterial left-handed impedance inverters. IEEE Access 2021, 9, 86119–86131. [Google Scholar] [CrossRef]
- Hussain, R. Shared-aperture slot-based sub-6-GHz and mm-Wave IoT antenna for 5G applications. IEEE IoT J. 2021, 8, 10807–10814. [Google Scholar] [CrossRef]
- Hussain, N.; Kim, N. Integrated microwave and mm-Wave MIMO antenna module with 360° pattern diversity for 5G Internet-of-Things. IEEE IoT J. 2022, 9, 24777–24789. [Google Scholar] [CrossRef]
- Lorenz, C.H.P.; Hemour, S.; Liu, W.; Badel, A.; Formosa, F.; Wu, K. Hybrid power harvesting for increased power conversion efficiency. IEEE Microw. Wirel. Comp. Lett. 2015, 25, 687–689. [Google Scholar] [CrossRef]
- Dinh, D.D.; Lancaster, M.J. Microwave power sensors with integrated filtering function for transfer power standards. IEEE Microw. Wirel. Comp. Lett. 2020, 30, 308–311. [Google Scholar] [CrossRef]
- Kosuge, A.; Kadomoto, J.; Kuroda, T. A 6 Gb/s 6 pJ/b 5 mm-distance non-contact interface for modular smartphones using two-fold transmission line coupler and high EMC tolerant pulse transceiver. IEEE J. Solid-State Circ. 2016, 51, 1446–1456. [Google Scholar] [CrossRef]
- Shum, K.M.; Mo, T.T.; Xue, Q.; Chan, C.H. A compact bandpass filter with two tuning transmission zeros using a CMRC resonator. IEEE Trans. Microw. Theory Tech. 2015, 53, 895–900. [Google Scholar] [CrossRef]
- Han, C.; Tang, D.; Deng, Z.; Qian, H.J.; Luo, X. Filtering power divider with ultrawide stopband and wideband low radiation loss using substrate integrated defected ground structure. IEEE Microw. Wirel. Comp. Lett. 2021, 31, 113–116. [Google Scholar] [CrossRef]
- Alqadami, A.S.M.; Nguyen-Trong, N.; Mohammed, B.; Stancombe, A.E.; Heitzmann, M.T.; Abbosh, A. Compact unidirectional conformal antenna based on flexible high-permittivity custom-made substrate for wearable wideband electromagnetic head imaging system. IEEE Trans. Antennas Propag. 2020, 68, 183–194. [Google Scholar] [CrossRef]
- Wang, D.-M.; Hu, J.-G.; Wu, J. A fully integrated low-cost HF multi-standard RFID reader SoC and module for IoT applications. IEEE IoT Journal. 2022, 9, 19201–19213. [Google Scholar] [CrossRef]
- Kurgan, P.; Koziel, S. Selection of circuit geometry for miniaturized microwave components based on concurrent optimization of performance and layout area. AEÜ–Int. J. Electr. Comm. 2019, 108, 287–294. [Google Scholar] [CrossRef]
- Tomasson, J.A.; Koziel, S.; Pietrenko-Dabrowska, A. Quasi-global optimization of antenna structures using principal components and affine subspace-spanned surrogates. IEEE Access 2020, 8, 50078–50084. [Google Scholar] [CrossRef]
- Kolda, T.G.; Lewis, R.M.; Torczon, V. Optimization by direct search: New perspectives on some classical and modern methods. SIAM Rev. 2003, 45, 385–482. [Google Scholar] [CrossRef]
- Pietrenko-Dabrowska, A.; Koziel, S. Expedited antenna optimization with numerical derivatives and gradient change tracking. Eng. Comput. 2020, 37, 1179–1193. [Google Scholar] [CrossRef]
- Liu, B.; Yang, H.; Lancaster, M.J. Global optimization of microwave filters based on a surrogate model-assisted evolutionary algorithm. IEEE Trans. Microw. Theory Techn. 2017, 65, 1976–1985. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, E.-X.; Wang, B.; Gao, S.; Png, C.E. Differential evolutionary optimization of an equivalent dipole model for electromagnetic emission analysis. IEEE Trans. Electromagn. Compat. 2018, 60, 1635–1639. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P. Multiobjective particle swarm optimization to design a time-delay equalizer metasurface for an electromagnetic band-gap resonator antenna. IEEE Antenna Wirel. Comp. Lett. 2017, 16, 912–915. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, J.; Tong, M.S. An FFT-accelerated particle swarm optimization method for solving far-field inverse scattering problems. IEEE Trans. Antennas Propag. 2021, 69, 1078–1093. [Google Scholar] [CrossRef]
- Koziel, S.; Ogurtsov, S.; Cheng, Q.S.; Bandler, J.W. Rapid EM-based microwave design optimization exploiting shape-preserving response prediction and adjoint sensitivities. IET Microw. Ant. Prop. 2014, 8, 775–781. [Google Scholar] [CrossRef]
- Feng, F.; Na, W.; Liu, W.; Yan, S.; Zhu, L.; Zhang, Q.-J. Parallel gradient-based EM optimization for microwave components using adjoint- sensitivity-based neuro-transfer function surrogate. IEEE Trans. Microw. Theory Tech. 2020, 68, 3606–3620. [Google Scholar] [CrossRef]
- Pietrenko-Dabrowska, A.; Koziel, S. Numerically efficient algorithm for compact microwave device optimization with flexible sensitivity updating scheme. Int. J. RF Microw. Comput. Aided Eng. 2019, 29, e21714. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Efficient gradient-based algorithm with numerical derivatives for expedited optimization of multi-parameter miniaturized impedance matching transformers. Radioengineering 2019, 27, 572–578. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Reduced-cost design closure of antennas by means of gradient search with restricted sensitivity updates. Metrol. Meas. Syst. 2019, 26, 595–605. [Google Scholar]
- Zhang, W.; Feng, F.; Gongal-Reddy, V.-M.-R.; Zhang, J.; Yan, S.; Ma, J.; Zhang, Q.J. Space mapping approach to electromagnetic centric multiphysics parametric modeling of microwave components. IEEE Trans. Microw. Theory Tech. 2018, 66, 3169–3185. [Google Scholar] [CrossRef]
- Cai, J.; King, J.; Yu, C.; Liu, J.; Sun, L. Support vector regression-based behavioral modeling technique for RF power transistors. IEEE Microw. Wirel. Comp. Lett. 2018, 28, 428–430. [Google Scholar] [CrossRef]
- Melgarejo, J.C.; Ossorio, J.; Cogollos, S.; Guglielmi, M.; Boria, V.E.; Bandler, J.W. On space mapping techniques for microwave filter tuning. IEEE Trans. Microw. Theory Tech. 2019, 67, 4860–4870. [Google Scholar] [CrossRef]
- Koziel, S.; Bandler, J.W. Reliable microwave modeling by means of variable-fidelity response features. IEEE Trans. Microw. Theory Tech. 2015, 63, 4247–4254. [Google Scholar] [CrossRef]
- Pietrenko-Dabrowska, A.; Koziel, S. Fast design closure of compact microwave components by means of feature-based metamodels. Electronics 2021, 10, 10. [Google Scholar] [CrossRef]
- Koziel, S.; Unnsteinsson, S.D. Expedited design closure of antennas by means of trust-region-based adaptive response scaling. IEEE Antenna Wirel. Comp. Lett. 2018, 17, 1099–1103. [Google Scholar] [CrossRef]
- Gorissen, D.; Crombecq, K.; Couckuyt, I.; Dhaene, T.; Demeester, P. A surrogate modeling and adaptive sampling toolbox for computer based design. J. Mach. Learn. Res. 2010, 11, 2051–2055. [Google Scholar]
- Lophaven, S.N.; Nielsen, H.B.; Søndergaard, J. DACE: A MATLAB Kriging Toolbox; Tech. Rep. IMMTR-2002-12; Technical University of Denmark: Lyngby, Denmark, 2002. [Google Scholar]
- Marelli, S.; Sudret, B. UQLab: A framework for uncertainty quantification in MATLAB. In Vulnerability, Uncertainty, and Risk: Quantification, Mitigation, and Management; ASCE Library: London, UK, 2014; pp. 2554–2563. [Google Scholar]
- Hassan, A.S.O.; Etman, A.S.; Soliman, E.A. Optimization of a novel nano antenna with two radiation modes using kriging surrogate models. IEEE Photonics J. 2018, 10, 4800807. [Google Scholar] [CrossRef]
- Xiao, L.; Shao, W.; Jin, F.; Wang, B.; Joines, W.T.; Liu, Q.H. Semisupervised radial basis function neural network with an effective sampling strategy. IEEE Trans. Microw. Theory Tech. 2020, 68, 1260–1269. [Google Scholar] [CrossRef]
- Jacobs, J.P.; Koziel, S. Two-stage framework for efficient Gaussian process modeling of antenna input characteristics. IEEE Trans. Antennas Propag. 2014, 62, 706–713. [Google Scholar] [CrossRef]
- Prado, D.R.; Lopez-Fernandez, J.A.; Arrebola, M.; Goussetis, G. Support vector regression to accelerate design and crosspolar optimization of shaped-beam reflectarray antennas for space applications. IEEE Trans. Antennas Propag. 2019, 67, 1659–1668. [Google Scholar] [CrossRef]
- Cui, J.; Feng, F.; Na, W.; Zhang, Q.-J. Bayesian-based automated model generation method for neural network modeling of microwave components. IEEE Microw. Wirel. Comp. Lett. 2023, 31, 1179–1182. [Google Scholar] [CrossRef]
- Jin, J.; Feng, F.; Zhang, J.; Yan, S.; Na, W.; Zhang, Q.J. A novel deep neural network topology for parametric modeling of passive microwave components. IEEE Access 2020, 8, 82273–82285. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, F.; Jin, J.; Zhang, Q.-J. Parallel multiphysics optimization for microwave devices exploiting neural network surrogate. IEEE Microw. Wirel. Comp. Lett. 2021, 31, 341–344. [Google Scholar] [CrossRef]
- Liu, Z.-X.; Shao, W.; Ding, X.; Peng, L.; Jiang, B. Neural network with Fourier series-based transfer functions for filter modeling. IEEE Microw. Wirel. Comp. Lett. 2022, 32, 823–826. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A.; Plotka, P. Reduced-cost microwave design closure by multi-resolution EM simulations and model management. IEEE Access 2021, 9, 116326–116337. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Conn, A.R.; Gould, N.I.M.; Toint, P.L. Trust Region Methods; MPS-SIAM Series on Optimization; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Koziel, S.; Pietrenko-Dabrowska, A. Variable-fidelity simulation models and sparse gradient updates for cost-efficient optimization of compact antenna input characteristics. Sensors 2019, 19, 1806. [Google Scholar] [CrossRef]
- Koziel, S.; Bekasiewicz, A. Fast EM-driven optimization using variable-fidelity EM models and adjoint sensitivities. IEEE Microw. Wirel. Comp. Lett. 2016, 26, 80–82. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Reliable data-driven modeling of high-frequency structures by means of nested kriging with enhanced design of experiment. Eng. Comput. 2019, 36, 2293–2308. [Google Scholar] [CrossRef]
- Tseng, C.-H.; Chang, C.-L. A rigorous design methodology for compact planar branch-line and rat-race couplers with asymmetrical T-structures. IEEE Trans. Microw. Theory Tech. 2012, 60, 2085–2092. [Google Scholar] [CrossRef]
- Letavin, D.A.; Shabunin, S.N. Miniaturization of a branch-line coupler using microstrip cells. In Proceedings of the 2018 XIV International Scientific-Technical Conference on Actual Problems of Electronics Instrument Engineering (APEIE), Novosibirsk, Russia, 2–6 October 2018; pp. 62–65. [Google Scholar]
- Letavin, D.A.; Mitelman, E.; Chechetkin, V.A. Compact microstrip branch-line coupler with unequal power division. In Proceedings of the 2017 11th European Conference on Antennas and Propagation, EUCAP 2017, Paris, France, 19–24 March 2017; pp. 1162–1165. [Google Scholar]
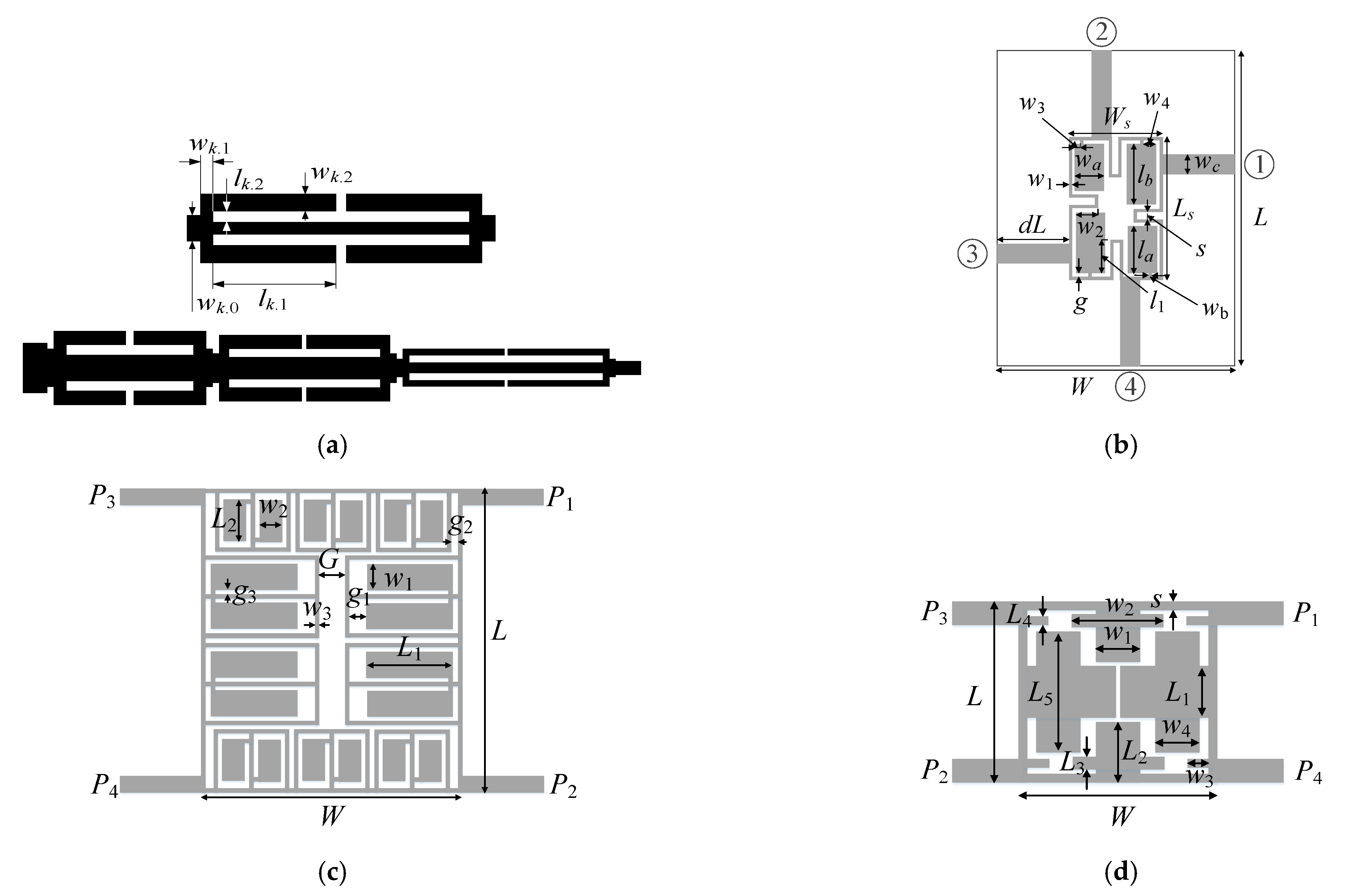




| Parameter | Purpose | Default Value |
|---|---|---|
| rmin | Governing EM-model discretization level (minimum value) | Problem specific 1 |
| rmax | Governing EM-model discretization level (maximum value) | Problem specific 1 |
| M | Launching the discretization level increase | 10–2 |
| α | Adjustment of EM-simulation model resolution | 3 |
| λ | Setting discretization level for FD | 2/3 |
| Md | TR radius increase (near convergence) | 10 |
| εx, εU | Algorithm termination | 10–3 |
| Case Study | ||||
|---|---|---|---|---|
| Circuit I | Circuit II | Circuit III | Circuit IV | |
| Substrate | RF-35 substrate (εr = 3.5, h = 0.762 mm) | RO4003 (εr = 3.38, h = 0.76 mm) | FR4 (εr = 4.4, h = 1.0 mm) | FR4 (εr = 4.4, h = 1.0 mm) |
| Design parameters | x = [l1.1 l1.2 w1.1 w1.2 w1.0 l2.1 l2.2 w2.1 w2.2 w2.0 l3.1 l3.2 w3.1 w3.2 w3.0]T | x = [g l1r la lb w1 w2r w3r w4r wa wb]T | x = [G g1 g2 g3 w1 w3 L1 L2]T | x = [W w1r w2r w3 w4 L L1r L2r L3 L4 L5r s]T |
| Other parameters | – | L = 2dL + Ls, Ls = 4w1 + 4g + s + la + lb, W = 2dL + Ws, l1 = lbl1r, Ws = 4w1 + 4g + s + 2wa, w2 = waw2r, w3 = w3rwa, w4 = w4rwa, wc = 1.9 mm | L = 4w1 + 10w3 + + 15g3 + 2L2, W = 4w3 + 2L1 + + G + 2g1 + 2g3 | w1 = w1rw2, w2 = w2r(W-2w3), l1 = L1r(L–2s–2l4), l2 = L2r(L–l1)/2, L5=L5r(L–2(W0–l4/2)–mx), mx=|l4−l3|/2+(l4+l3)/2 |
| Operating parameters | F = [1.75 4.25] GHz | f0 = 1.5 GHz | f0 = 1.0 GHz | f0 = 2.0 GHz |
| Design goals | ||||
| F1 | Minimization of footprint area | |||
| F2 | Minimization of matching |S11| within bandwidth F | Minimization of matching |S11| and isolation |S41| at f0 | ||
| F3 | – | Equal power split at f0: |S31| − |S21| = 0 at f0 | Unequal power split at f0: |S31| − |S21| = 3 dB at f0 | |
| Objective function (cf. (3)) | β = 300 | |||
| β1 = 10,000, β2 = 30 | β1 = 1000, β2 = 30 | β1 = 10,000, β2 = 100 | ||
| dsmax = 0.1 | dsmax = 0.1 | dsmax = 3.0 | ||
| Low-fidelity model | ||||
| rmin | 14 | 16 | 15 | 16 |
| Simulation time [s] # | 80.3 | 130.0 | 215.6 | 188.5 |
| High-fidelity model | ||||
| rmax | 28 | 30 | 28 | 26 |
| Simulation time [s] # | 160.4 | 237.4 | 960.3 | 283.6 |
| Time evaluation ratio | 2.0 | 1.8 | 4.5 | 1.5 |
| Initial design | x(0) = [3.58 0.19 0.79 0.38 0.3 3.75 0.24 0.33 0.39 1.46 3.9 0.18 0.23 0.28 1.0]T | x(0) = [0.59 0.7 6.7 8.3 0.84 0.91 0.72 0.13 3.3 0.63]T | x(0) = [1.0 1.0 0.6 0.25 2.4 0.25 9.0 3.75]T | x(0) = [15.0 0.63 0.93 3.45 3.0 12.4 0.42 0.81 1.50 1.0 0.9 0.5]T |
| Circuit | Algorithm | Cost 1 | Cost Savings 2 | Footprint Area A [mm2] 3 |
|---|---|---|---|---|
| I | Conventional TR search | 158 | – | 30.0 |
| Multi-fidelity (this work) | 93 | 41.1 | 32.2 | |
| II | Conventional TR search | 67 | – | 182.0 |
| Multi-fidelity (this work) | 39 | 41.8 | 205.5 | |
| III | Conventional TR search | 73 | – | 407.1 |
| Multi-fidelity (this work) | 45 | 38.4 | 409.8 | |
| IV | Conventional TR search | 152 | – | 143.1 |
| Multi-fidelity (this work) | 87 | 50.3 | 131.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pietrenko-Dabrowska, A.; Koziel, S.; Raef, A.G. Reduced-Cost Optimization-Based Miniaturization of Microwave Passives by Multi-Resolution EM Simulations for Internet of Things and Space-Limited Applications. Electronics 2022, 11, 4094. https://doi.org/10.3390/electronics11244094
Pietrenko-Dabrowska A, Koziel S, Raef AG. Reduced-Cost Optimization-Based Miniaturization of Microwave Passives by Multi-Resolution EM Simulations for Internet of Things and Space-Limited Applications. Electronics. 2022; 11(24):4094. https://doi.org/10.3390/electronics11244094
Chicago/Turabian StylePietrenko-Dabrowska, Anna, Slawomir Koziel, and Ali Ghaffarlouy Raef. 2022. "Reduced-Cost Optimization-Based Miniaturization of Microwave Passives by Multi-Resolution EM Simulations for Internet of Things and Space-Limited Applications" Electronics 11, no. 24: 4094. https://doi.org/10.3390/electronics11244094
APA StylePietrenko-Dabrowska, A., Koziel, S., & Raef, A. G. (2022). Reduced-Cost Optimization-Based Miniaturization of Microwave Passives by Multi-Resolution EM Simulations for Internet of Things and Space-Limited Applications. Electronics, 11(24), 4094. https://doi.org/10.3390/electronics11244094








