Abstract
As a popular distributed learning framework, federated learning (FL) enables clients to conduct cooperative training without sharing data, thus having higher security and enjoying benefits in processing large-scale, high-dimensional data. However, by sharing parameters in the federated learning process, the attacker can still obtain private information from the sensitive data of participants by reverse parsing. Local differential privacy (LDP) has recently worked well in preserving privacy for federated learning. However, it faces the inherent problem of balancing privacy, model performance, and algorithm efficiency. In this paper, we propose a novel privacy-enhanced federated learning framework (Optimal LDP-FL) which achieves local differential privacy protection by the client self-sampling and data perturbation mechanisms. We theoretically analyze the relationship between the model accuracy and client self-sampling probability. Restrictive client self-sampling technology is proposed which eliminates the randomness of the self-sampling probability settings in existing studies and improves the utilization of the federated system. A novel, efficiency-optimized LDP data perturbation mechanism (Adaptive-Harmony) is also proposed, which allows an adaptive parameter range to reduce variance and improve model accuracy. Comprehensive experiments on the MNIST and Fashion MNIST datasets show that the proposed method can significantly reduce computational and communication costs with the same level of privacy and model utility.
1. Introduction
Machine learning has injected a strong impetus into the practical application of artificial intelligence (AI), such as computer vision, automatic speech recognition, natural language processing, and recommender systems [1,2,3,4]. The success of these machine learning techniques, especially deep learning, is based on a large quantity of data [5,6,7,8]. However, the development of data-driven AI still faces two significant challenges: privacy issues and data silos [9].
Federated learning (FL), a new paradigm for privacy-preserving AI applications, aims to break down the two barriers. Nowadays, the intelligence of network edge devices has been dramatically improved [10,11,12]. Smartphones, wearable devices, sensors, and other devices have the necessary computing and communication capabilities. The popularity of IoT applications has promoted the rapid development of the FL framework with the core concept of decentralization [13,14,15,16]. However, federated learning still has privacy issues, even if the data are kept locally. Studies have shown that if the data structure is known in federated learning, then the shared gradient information may also be exploited, leaking additional details on the training data, such as model inversion attacks [17,18].
Differential privacy (DP) has received much attention because it provides a rigorous, quantifiable privacy-preserving method independent of the background knowledge of attacks [19]. With the development of machine learning, DP has become an active research area in privacy-preserving machine learning [20]. Nevertheless, traditional centralized differential privacy (CDP) is not suitable for FL, first because a trusted server may not exist and second because the noise accumulation at each round of aggregation causes the utility to decrease. Satisfying DP, local differential privacy (LDP) further resists privacy leakage from an untrustworthy server. In federated learning with LDP (LDP-FL), the models of the clients are subjected to a data perturbation mechanism before uploading to the server to ensure that the aggregator cannot infer more information from the model. Existing LDP-FL research has achieved specific results [21,22,23,24]. Some personalized differentially private federated learning algorithms have been proposed for complex models [25,26] and non-uniform sampling processing [27]. However, utility decline should always be a rub and challenge. Some of the research has relaxed the privacy levels for utility optimization [28,29,30].
Truex et al. integrated LDP into a federated learning system for jointly training deep neural networks. Their approach efficiently handles complex models and adversarial inference attacks while achieving personalized LDP. In addition, Wang et al. proposed FedLDA, a latent Dirichlet allocation (LDA) model based on LDP in federated learning. FedLDA employs a novel random response with priors that ensures the privacy budget is independent of the dictionary size and dramatically improves accuracy through adaptive and non-uniform sampling processing. To improve the model fitting and prediction of the scheme, Bhowmick et al. proposed a relaxed LDP mechanism. Li et al. introduced an efficient meta-learning LDP mechanism that can be used to implement personalized federated learning. LDP can be used to prevent gradients from leaking privacy for federated stochastic gradient descent (FedSGD) [31]. However, the increase in dimension d causes the privacy budget to decay rapidly, the noise scale to increase, and the accuracy of the learned model to decline. Therefore, Liu et al. proposed FedSel, selecting only the most essential k dimensions to stabilize the learning process. Recently, many studies focusing on the data perturbation mechanism to improve the model’s utility have achieved good results, such as those of Laplace [19], Duchi et al. [32], Harmony [33], PM [34], and HM [34]. The data perturbation mechanism design tries to make the aggregating disturbance statistical results meet specific usability requirements by adding positive and negative noise to individual values. They devote themselves to improving asymptotic error boundaries under private premises. However, their weaknesses include low communication efficiency and poor adaptability in complex deep learning models, since the range of model parameters for different neural network layers varies widely. Assuming a fixed range for the model parameters will introduce significant variance in the estimates, resulting in a decrease in model accuracy [35]. An adaptive method has been proposed that allows the clients in each round to adaptively select the perturbation parameters according to the model training. However, the existing process, such as Adaptive-Duchi, requires that all model information be uploaded to the server after each data perturbation, causing higher time and space complexity.
Aside from that, a technique of privacy amplification has received extensive attention for improving the model utility [36,37,38]. Based on the anonymity mechanism, the shuffler scrambles the model parameters of different clients before the global model is updated. It effectively improves the model utility of federated learning without consuming the privacy budget. Another mechanism that can amplify privacy is the client self-sampling mechanism, which realizes local differential privacy by randomly deciding whether to share updates during each iteration [39]. The latest LDP-FL based on client self-sampling theoretically proves the improvement of the privacy level and performance through the shuffler and client self-sampling design. Nevertheless, the current client self-sampling technology has some shortcomings in setting the self-sampling probability, which needs a detailed analysis of the relationship between the number of participating clients and the model’s utility. Wei et al. have shown the relationship between the number of clients participating and the model performance through detailed experimental and theoretical proof [40]. However, the existing methods [39] roughly set the client participation probability to a (0, 1) interval, which leads to a decline in the convergence and accuracy of the federated model. Moreover, more client participation is needed to avoid resource waste in the training scenario.
Building trustworthy federated learning that meets the requirements of privacy, performance, and efficiency has become the focus of future research [9]. Therefore, our study aims to balance privacy, utility, and efficiency through the optimization of federated learning. We propose an efficiency-optimized data perturbation mechanism (Adaptive-Harmony) which allows an adaptive parameter range to reduce variance and improve model accuracy. Furthermore, it randomly selects a dimension at each model layer and applies noise according to the parameter settings. Then, we keep the remaining dimensions to fixed values. As a result, this effectively reduces the communication cost with the server. We perform theoretical analysis and proofing to show that Adaptive-Harmony holds the advanced asymptotic error bounds and convergence performance with minimal communication costs. On this basis, a novel federated learning framework (i.e., Optimal LDP-FL) is proposed. In the framework, we use Adaptive-Harmony to provide the private local parameters with minor computational costs during the local model update. We introduce a parameter-shuffling mechanism that improves privacy by countering model-tracking attacks and improving communication efficiency under the same privacy level and model utility. We also propose a restrictive client self-sampling technology, which improves the shortcomings of existing methods in studying client self-sampling probability by further refining the quantitative relationship between self-sampling probability, convergence, and accuracy. It limits a more reasonable range of self-sampling probability, removes the assumption of a single datum in the past theoretical framework, extends the existing theoretical research to practical application, and improves the utility of federated learning in both theoretical and practical applications. We perform comprehensive experiments on the MNIST and Fashion MNIST datasets to verify and evaluate our algorithm from the utility, privacy budget, and communication cost. The results show that the proposed method can significantly reduce computational and communication costs with the same privacy and model utility level.
To be precise, our main contributions are as follows:
- We propose a novel LDP-FL, which integrates an efficiency-optimized data perturbation and a parameter-shuffling mechanism, and client self-sampling technology in the federated learning process to improve model utility and reduce communication costs, ensuring privacy.
- We propose an efficiency-optimized data perturbation algorithm, which supports perturbing parameter adaptive selection and minimum parameter transmission to hold the advanced asymptotic error boundary and improve communication efficiency.
- We propose restrictive client self-sampling technology which limits the range of self-sampling probability to a more reasonable one to improve the utility.
- We verify our method’s efficiency, privacy, and performance from theoretical and practical aspects. We analyze the asymptotic error boundary and communication cost and prove that our unbiased algorithm satisfies LDP. We also evaluate our algorithm on multiple databases from the utility, privacy budget, and communication cost standpoints.
2. Background and Related Works
2.1. Federated Learning
Federated learning aims to build a global model over data distributed across multiple clients without sending the raw data to any centralized server. The performance of the global model should approximate the ideal model’s performance adequately. FedAvg [41] is widely used in aggregating the models from clients. Supposing that there are K clients in a horizontal federated learning system, let denote the data set owned by the kth client and denote the index set of data points located in the kth client. Let denote the base number of ; that is, we assume that the kth client has data points. Thus, when there are K clients in total, the loss function can be written as in Equation (1):
We assume that the server has the initial model and that the clients know the optimizer settings. For each client, it contains its private dataset. Based on Equation (2), each local client updates their local models by the weight from the server. For a typical implementation of FedAvg with a fixed learning rate , when updating the global model parameters at round t, the kth client will compute , the average gradient of its local data at the current model parameter . Each local model uses gradient descent to optimize the distinct local models’ weights in parallel and sends the local weights to the server:
Next, the server calculates the weighted average of each model weight according to Equation (3) and sends the aggregated weights to each client. The training process of a federated learning system typically consists of local update, local upload, server update, and server broadcast:
2.2. Differential Privacy
Differential privacy was developed in the context of statistical disclosure control, which Dwork first proposed in 2006 [19]. For its information theory guarantee, it has been widely used to enhance data privacy in machine learning with its simplicity and low cost. The mechanisms of DP in federated learning are mainly classified into LDP [42] and CDP [19]. The traditional Laplacian mechanism of CDP can be used in FL. Each user’s data are disturbed by random noise based on the specific distribution in the mechanism. However, CDP must be based on trusted data collectors. In the case of highly sensitive machine learning models, the assumption of trusted data collectors is challenging to uphold [40,43]. Therefore, there is an urgent need for a privacy-preserving method to withstand untrustworthy third-party data collectors in the sensitive model aggregation problem. LDP is well suited for the decentralized federated learning scenarios and is naturally applicable in FL:
Definition 1
(-CDP). For two datasets D and that differ by only one record, a randomization mechanism satisfies ϵ-CDP and for all such that we have
where ϵ denotes the privacy budget.
Definition 2
(-LDP). A random function satisfies ϵ-LDP if and only if, for any two input tuples and in any case f, the output satisfies
DP introduces noise to the data, ensuring privacy but damaging the utility. Existing research has shown the algorithm has better privacy guarantees with small , which means large noise injection. However, Jayaraman et al. [44] found that few existing DP mechanisms for machine learning have an acceptable degree of a utility-privacy tradeoff. Therefore, balancing the utility and privacy is still an open issue for DP mechanism design in machine learning.
2.3. Data Perturbation in LDP
The current implementation of LDP in federated learning is mainly based on the data perturbation mechanism to perturb the local models and upload the perturbed models to the server to complete the aggregation [45,46]. Since the process of server model aggregation belongs to mean value estimation, the LDP mechanism applied in this process should also support mean statistical queries on continuous-type data. Duchi et al. [32] proposed a mean estimation method based on LDP. That aside, existing mean estimation methods include Laplace [19], Harmony [33], PM [34], and HM [34], which have achieved some results.
The main idea of Duchi et al. was to use a random response technique to perturb each user’s data according to a certain distribution probability while ensuring unbiased estimation. Each data tuple is perturbed to contain the noisy tuple , where B is determined by the data dimension d and the privacy budget , as calculated in Equations (6) and (7):
where
Although Duchi et al.’s mechanism can achieve LDP and has asymptotic error bounds, it is relatively complex. Nguyên et al. [33] have shown that Duchi et al.’s mechanism does not satisfy -LDP when d is even. Nguyên et al. proposed a possible solution and their redefinition of the Bernoulli variables u according to Equation (8):
In addition, Nguyên et al. proposed the Harmony mechanism [33], which can achieve the same privacy level and asymptotic error bounds by a more straightforward method when estimating multidimensional data using LDP. Furthermore, Wang et al. [34] further proposed the PM mechanism, which has lower variance and is easier to implement than that of Duchi et al. The Laplace mechanism and Duchi et al.’s mechanism are costly. In contrast, the Harmony and PM mechanisms are less costly. For d dimensional data, the Laplace mechanism has the most significant asymptotic error bound. In contrast, the error bounds of the other three mechanisms are lower than those of the Laplace mechanism. However, all of the above methods assume a fixed range of inputs for simplicity, and we believe that this setting has a detrimental effect on the accuracy of the neural network model.
2.4. Privacy Amplification
LDP provides privacy guarantees for federated systems with untrustworthy servers [47]. However, improving the performance of LDP-FL is necessary, since LDP makes further utility decline [48]. Privacy amplification mechanisms have been proposed to enhance the utility in LDP-FL [38,49,50]. One kind of privacy amplification mechanism is called shuffling, first derived from the Encoding, Shuffle, Analyze (ESA) architecture [51]. The shuffling model amplifies privacy through anonymization. It shuffles the local update before severe aggregation, thus preventing potential attackers from associating parameter information with individual clients. Existing LDP-FL studies based on shuffling models have improved model utility while ensuring privacy, such as model shuffling and parameter shuffling [38]. In particular, a parameter-shuffling mechanism further enhances privacy based on model shuffling. Another mechanism to amplify privacy is through randomized sampling [49], including sampling by data centers acting as servers and client self-sampling [39]. The mainly used client self-sampling realizes a participant anonymity mechanism and the effect of saving the privacy budget and enhancing utility, which avoids client coordination while keeping confidential to the server. However, the existing self-sampling is insufficient in the probability by roughly setting it within (0,1), which has theoretical and practical problems. Theoretically, suppose the participation probability is too low and even approaching zero. In that case, the number of participants in each iteration is too small, which means the algorithm needs more training iterations to achieve convergence, and the accuracy of the global model will decrease. From the perspective of application scenarios, training with too few participants results in a waste of resources. Therefore, federated learning combined with privacy amplification and efficiency enhancement becomes an urgent need. The existing methods are inadequate in setting client self-sampling probability.
3. Optimal LDP-FL
3.1. Outline
As we discussed above, the existing research remains on the problem of balancing privacy and utility. For this reason, we design a horizontal federated learning framework, Optimal LDP-FL, to address the privacy, utility, and efficiency issues and rival reconstruction attacks, model inversion, and parameter tracing. In Optimal LDP-FL, we propose a novel data perturbation mechanism (Adaptive-Harmony) in the local update, making significant efficiency improvements while satisfying LDP. In addition, it also introduces the parameter-shuffling mechanism, which can save the privacy budget, thus significantly improving the model utility. We also introduce client self-sampling in Optimal LDP-FL and propose a client self-sampling technique with restrictive probability to achieve utility optimization. Clients perform self-sampling to determine whether they participate in the local update and global update in this training iteration. The server remains ignorant of the participating clients when aggregating the model. Moreover, we restrict the client self-sampling probability to a more reasonable range to improve the performance of the global model while maintaining a high privacy level. In Section 3.4, we will describe the restrictive client self-sampling technology in detail. The architecture of our framework is shown in Figure 1.
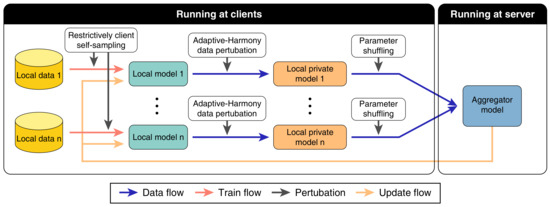
Figure 1.
Optimal LDP-FL framework. Each client has a private dataset. The clients perturb their weights by data perturbation after performing a local update, split and shuffle the parameters locally, and finally upload them to the server for server updates.
3.1.1. Local Update
Each client has his or her private training data. In each round of communication, the selected client updates the local model with the weights from the server. Next, different local models are optimized in parallel for each local model using stochastic gradient descent (SGD). LDP requires that each client not pass data and weight to each other and keep them secret from the untrustworthy server by data perturbation. Therefore, the algorithm provides privacy based on data perturbation by applying noise to the weights from the clients. After the server collects multiple models, their noise cancels each other to achieve the model accuracy.
In the process of a local update, we propose a new data perturbation algorithm, namely Adaptive-Harmony, which can satisfy the -LDP and the asymptotic error bound of under the condition of improving the communication efficiency of the algorithm to . In Section 3.2, we will describe Adaptive-Harmony with privacy and utility analysis in detail.
3.1.2. Global Update
The server randomly initializes the weights at the beginning. Let n be the number of clients, and during the rth round of communication, the server randomly selects clients for communication. These clients upload the weights to the server in preparation for updating the local model in the next round. During this process, the server does not know the exact identity of the clients, as the clients remain anonymous to the server.
In order to improve the global model utility, we introduce a parameter-shuffling mechanism into the global update process, by which the uploaded models are shuffled at the parameter level. Compared with the model-shuffling mechanism, parameter shuffling provides a better privacy amplification effect. Each client will split the weights of the local model and send them to the server anonymously after a random delay. In Section 3.3, we will describe the parameter-shuffling mechanism in detail.
Algorithm 1 gives the process of implementing the above Optimal LDP-FL framework, in which Line 5 performs clients self-sampling to determine whether the clients participate in local model updates and global aggregation in the training iteration, Line 20 performs parameter shuffling, and Line 19 performs data perturbation.
3.2. Adaptive-Harmony
Due to the complexity of deep neural networks, the range of weights varies significantly for each layer in the model. Assuming a fixed range of weights would introduce a significant variance in the model aggregation process, resulting in poor model accuracy. Sun et al. [35] first proposed the concept of weight range adaption and applied it to Duchi et al.’s mechanism, and we named it “Adaptive-Duchi” in this paper.
3.2.1. Adaptive-Duchi
Given the weights W of the model, the mechanism adds random noise to all d dimensions of W and outputs perturbed weights . Let the mechanism be , and for each , determine c and r such that , where c is the center of w and r is the radius. Both depend specifically on the method of clipping the weight. Therefore, they designed the following mechanism to perturb w in Equation (9):
where is the weight after perturbation and “w.p.” stands for “with probability”. The mechanism adds noise to all dimensions of W, so the communication cost of the method is , which means that the full model information must be uploaded to the cloud after each data perturbation. When the data dimension is high, both the time and space complexity are high, so this mechanism is not suitable for high-dimensional data.
| Algorithm 1: Optimal LDP-FL |
 |
3.2.2. Adaptive-Harmony
We propose the Adaptive-Harmony data perturbation mechanism, which improves the adaptive range based on the Harmony data perturbation mechanism. If the range of weights is adaptive, then the client can choose different c and r values for each weight in each round, and these two values depend on the way we clip the gradients. Unlike Duchi et al’s mechanism, for each dimension of the weights, only one bit of data needs to be transmitted to the subsequent process, thus significantly reducing the communication cost. Moreover, the mechanism achieves equally capable privacy-preserving and asymptotic error bounds compared to Adaptive-Duchi. In Section 4, we will analyze the privacy, unbiasedness, and asymptotic error bounds of Adaptive-Harmony.
The main idea of the algorithm is that given the weights W of the model, noise is added by randomly sampling one of the dimensions of W in j, and the algorithm outputs a perturbed tuple , which contains non-zero values only in the jth dimension. In particular, is randomly selected from dimensions of W, so obeys the following distribution in Equation (10):
The above mechanism shows that for a randomly chosen weight , the output contains only one non-zero value and only two possible values for it. Therefore, the data perturbation mechanism only needs to transfer the non-zero values and their positions to the subsequent process, so the communication cost of the mechanism is . Moreover, under the premise of uniform randomness of the selection process, the correctness of the method does not depend on the selection of .
To describe of the difference between these two mechanisms more specifically, we assume that the model has n layers, each with dimensions such that and, similarly, . According to Duchi et al.’s mechanism, we have Equation (11):
Equation (11) shows that all positions of have the value or and are related to the unperturbed M at the corresponding positions. The privacy budget is equally distributed to each w. Therefore, the time complexity and the communication cost of this mechanism are both . By contrast, in the Adaptive-Harmony mechanism we proposed, the privacy budget is assigned only to non-zero values such that , and similarly, can be obtained. Therefore, we have Equation (12):
Equation (12) shows that each layer of has one and only one dimension with non-zero values, so the time complexity and communication cost of each layer is , and the total time complexity and communication cost is , although for a single model, the weights after perturbation deviate too much and are too sparse compared with those before perturbation, making them almost unusable for neural networks. However, when enough clients upload the model for aggregation, this deviation can be offset by mean estimation, thus restoring the high availability of the model.
Algorithm 2 gives the implementation of the Adaptive-Harmony data perturbation mechanism.
| Algorithm 2: Adaptive-Harmony |
 |
According to Algorithm 2, there are only two possible values for each non-zero weight. Since the perturbation algorithm is known, the server only needs to obtain the direction of the perturbation to calculate these values using known c, d, and r values. Therefore, the position corresponding to the perturbed model contains only one bit of information, and therefore, the proposed method dramatically improves the efficiency of the algorithm.
3.3. Parameter Shuffling
In federated learning, the clients are required to upload gradient updates to the server in multiple iterations. Therefore, the privacy budget will accumulate in LDP-FL, resulting in an explosion in the total privacy budget. The studies in [38,51] show that, overall, privacy is effectively improved when data are transmitted anonymously at each point in time and are not associated with a transmission time.
However, Sun et al. [35] argue that the clients’ anonymity is insufficient to prevent side channel attacks. If clients upload models simultaneously in each aggregation, then the server can still associate a large number of weight updates together to distinguish specific clients.
As shown in Figure 2, for the local models , , , and , each model has the same structure but different weights. As shown in Figure 2a, the clients send the total weights to the server in the original federated learning. The researchers in Figure 2b [36,37,38] ensure the anonymity of the communication between the clients and the server by model shuffling. However, the work of these researchers does not consider privacy amplification in the high dimensionality of deep neural networks. Therefore, we introduce a local parameter-shuffling mechanism to break the connection between weight updates from the same clients and mix them with weight updates from other clients, thus making it more difficult for the server to combine multiple weight updates and infer more information about any client. To avoid servers tracking specific clients based on a large number of weight updates in a short period, we should employ parameter shuffling, which is performed in two steps as shown in Figure 2c. In the first step, each client splits the weights of the local model and marks each weight with to indicate the positions of the weights in the network structure. In the second step, each client samples a small random delay t for each weight from a uniform distribution , where and waits for a time t before sending the weights to the server. Since all uploads are made randomly in the same period, the server cannot distinguish them by upload time and cannot correlate weight updates from the same client.
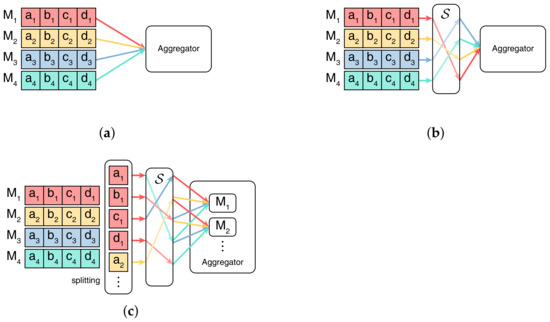
Figure 2.
Example of parameter shuffling, where is a random shuffling mechanism. (a) No shuffling. (b) Model shuffling. (c) Parameter shuffling.
Algorithm 3 gives the implementation of the above parameter shuffling mechanism.
| Algorithm 3: Parameter Shuffling |
 |
3.4. Restrictive Client Self-Sampling
In this paper, restrictive client self-sampling technology is introduced in Optimal LDP-FL. In the traditional client self-sampling, each client tosses a coin in each iteration and participates in the subsequent training process if the coin turns to heads. The data in clients’ local datasets also participate randomly in local updates with a certain probability. Since a client decides to participate or not participate locally, the server does not need to coordinate all clients to achieve LDP:
Definition 3
(Client Self-Sampling Probability). The client self-sampling probability is the probability of each client’s participation in each iteration, where m clients perform self-sampling with the probability to determine whether to participate in this iteration. Assuming that x out of m clients participate in an iteration, then we have .
Definition 4
(Client Data Sampling Probability). The client data sampling probability is the probability of data participating in training among the overall dataset . For any client i in each iteration, y entries of data are selected from to participate in training, assuming that each client contains r data entries in total, and therefore .
However, in the existing client self-sampling technology, the value of the client self-sampling probability is roughly set to (0, 1), which causes both theoretical and practical problems. From a theoretical point of view, the number of participants in federated learning has a significant impact on the model’s performance. Furthermore, considering the practical application scenario, where the number of client participants is too small, it wastes resources, and such circumstances do not conform to the realistic federated scenario. Therefore, we conducted a thorough study on the range of . Wei et al. [40] studied the relationship between the number of clients participating and the model performance in detail. Based on this, we drew the following conclusions according to the user self-sampling scenarios in Theorem 1:
Theorem 1.
There is a positive correlation between the number of participants and the convergence. In other words, the larger the number of participants, the higher the convergence. The global model accuracy changes with the number of participants as a convex function curve. Its inflection point occurs when the number of participants approaches the total number of clients.
Proof.
Since the convergence of the global model approximates to the optimum when and , the convergence of the global model approximates to optimal when . As , the relationship between the global model accuracy and is also convex. To obtain the optimal global model accuracy, the value of should be placed in (0.5, 1). □
We drew the conclusions as follows according to Theorem 1. Based on these theoretical analysis, we present a restrictive client self-sampling algorithm with a client self-sampling probability in a specific range of (0.5, 1), as shown in Algorithm 4. According to the theorem of parallel composition in DP, increasing the number of participating clients does not consume the privacy budget. Therefore, Algorithm 4 can acquire optimal convergence and global accuracy while guaranteeing a consistent privacy level.
- There exists an optimal that renders an optimal performance, since in an FL system with m clients, there is the optimal number of participating clients x which optimizes the performance. Therefore, for , there is an optimal range that guarantees the best convergence and model accuracy.
- When the number of participants approaches all participants, the performance is optimal. Therefore, the optimal FL model performance (i.e., convergence and model accuracy) can be achieved when restricting the optimal range to .
| Algorithm 4: Restrictive Self-Sampling |
 |
4. Utility Analysis
4.1. Privacy Analysis
We prove that the Adaptive-Harmony mechanism meets the definition of LDP when the weights take values in the range of :
Theorem 2.
Given an arbitrary number , where c is the center of the range of values of w and r is the radius of that range, the range is denoted as when the mechanism conforms to the definition of ϵ-LDP.
Both and r affect the privacy level, where determines how well the data are hidden in a “crowd” and r determines the size of the “crowd”. Assuming that the true average weight in each during the iteration is , the LDP mechanism in Equation (10) implements the average weight for unbiased estimation:
Lemma 1.
Algorithm 2 satisfies ϵ-LDP.
Proof.
Let be the output of this algorithm and be the only value in that is not 0. Let W and be any two tuples and u and be the Bernoulli variables generated by the input W and in line 3 of this algorithm. The following proof is for the case , and the other case is proved by the same reasoning.
According to the algorithm, we have Equation (13):
□
4.2. Utility Analysis
Model aggregation is the process of estimating the mean value of the weights. In order to maximize model utility, the data perturbation mechanism should satisfy two conditions: unbiasedness and the smallest possible asymptotic error bound. In the following, the unbiasedness of the Adaptive-Harmony algorithm will be demonstrated.
Let be the weights of all clients and N be the number of clients. Each tuple is the weight data of the ith client. Without loss of generality, the range of each weight is determined as , and the mean estimation involves estimating the weights for N clients (e.g., ). Let be the d-dimensional weights after the ith user perturbation. Given a data perturbation mechanism , let be the mathematical expectation of the output at input . The -LDP data perturbation mechanism is unbiased when it satisfies the following two equations:
As we mentioned above, Equation (14) shows that is unbiased, and Equation (15) shows that the probability of the sum of output values must be one, where is the output range of :
Lemma 2.
Let be the output of Algorithm 2 given an input d-dimensional model W. Then, for any , .
Proof.
□
Lemma 2 proves the unbiasedness of the Adaptive-Harmony algorithm so that the server can use as an unbiased estimator of the mean.
The asymptotic error bound of the Adaptive-Harmony algorithm is derived below to show that the method in this paper has an equivalent asymptotic error bound to that of Adaptive-Duchi (i.e., ). Lemma 3 provides the accuracy guarantee of our mechanism:
Lemma 3.
For any , let and . With at least probability, we have
Proof.
First, note that for any and any , the variance of is equivalent to Equation (18):
According to Bernstein’s inequality, we have Equation (19):
By the union bound, there exists such that
holds with at least probability. □
On the other hand, we proved the relationship between the global model accuracy and the number of participating clients in Algorithm 4. In Optimal LDP-FL, it was proven that the value of the loss function always has a particular functional relationship with the number of clients participating in the iteration. There was an inflection point in the curve of the loss function value, which minimized the value of the loss function. This also shows that the loss function value was the lowest when the participating clients approached the total number of clients. Therefore, Algorithm 4 set the self-sampling probability within the range of (0.5, 1), which could make the number of clients participating in the training closer to the inflection point of this function. Therefore, it could effectively improve the accuracy of the global model.
In summary, our proposed Optimal LDP-FL framework satisfies -LDP. The proposed Adaptive-Harmony mechanism is unbiased, and its asymptotic error bounds are on par with existing algorithms, as both are . However, in every layer of in the Adaptive-Harmony algorithm, there was only one dimension with a non-zero value. That means the time complexity and communication cost of each layer were reduced from to , and the total cost was reduced from to . Moreover, the parameter-shuffling mechanism and client self-sampling technology were adopted to improve the model’s performance under the same privacy level. Finally, we should also note that although for a single model, the model parameters after the perturbation were too large and too sparse compared with those before the perturbation, which were almost unusable for the neural network. However, when enough participants uploaded models for aggregation, the sparse model could be filled with a large number of parameters, and the deviation could be offset by mean value estimation, thereby restoring the high availability of the model. Therefore, when the number of clients was large enough, the convergence speed of our model would not be significantly different from the traditional method.
5. Evaluation
5.1. Experimental Setting
We tested the results of Optimal LDP-FL on the image classification task with a two-layer CNN and evaluated the global model’s accuracy and time metrics as the utility indicators. We selected the MNIST dataset [52] and FashionMNIST dataset [53], which are commonly used in deep learning. Then, we randomly sampled the training and test sets and distributed them equally to all clients. To ensure the model’s generalization, the random sampling process followed the independent and identical distribution (i.i.d.) principle. We set different ranges for the MNIST and Fashion MNIST datasets for the clipping weights. We chose the following two algorithms for comparison: the non-private federated averaging (FedAvg) the classic LDP-FL framework (Sun et al. [35]), along with our proposed framework (Optimal LDP-FL).
5.2. Utility Evaluation
5.2.1. Model Accuracy vs. Number of Clients
To analyze the effect of the number of clients on the accuracy, we designed the experiment shown in Figure 3. Figure 3a,b shows the accuracy performance of different algorithms on the MNIST and Fashion MNIST datasets, respectively, with the number of clients. As shown in Figure 3a,b, the FedAvg framework and LDP-FL model accuracy showed a slight downward trend with the increasing number of clients because the training set and test set would be directly and equally distributed to each client. The larger the number of clients, the fewer data each client could obtain, and the model accuracy decreased accordingly. As shown in Figure 3a in the MNIST dataset, for Optimal LDP-FL, the aggregated model was too sparse when the number of clients was small, resulting in lower global model accuracy. However, as the number of clients increased, the model accuracy increased back to normal with a slight upward trend, because although a smaller amount of data broke the accuracy of the local model, at the same time, a more significant number of clients could provide more local models to the server, which could better offset the effect of noise on the global model during the aggregation stage. As shown in Figure 3a,b, the model accuracies of LDP-FL and Optimal LDP-FL were slightly lower than that of FedAvg. Optimal LDP-FL reached a better model accuracy than LDP-FL, since the reasonable restriction of self-sampling probability increased the number of influential participating clients, thus effectively improving the accuracy of the global model.
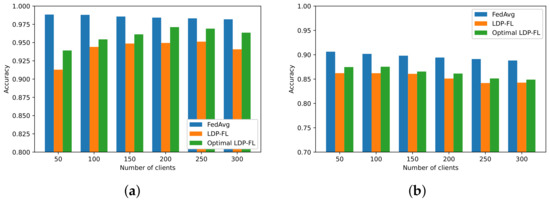
Figure 3.
Model accuracy vs. number of clients for different federated learning frameworks on MNIST and Fashion MNIST datasets: (a) MNIST and (b) Fashion MNIST.
5.2.2. Model Accuracy vs. Privacy Budget
To analyze the impact of the privacy budget on the accuracy, we compared two LDP-FL frameworks in Figure 4 on the MNIST and Fashion MNIST datasets with the privacy budget set to and chose the model accuracy of FedAvg without privacy protection as the benchmark. In our experiment, the number of clients was fixed at . The results show that Optimal LDP-FL could maintain relatively stable accuracy across various privacy budgets. Note that more complex data and tasks require more privacy budgets, mainly because complex tasks require complex neural networks with a large number of model parameters. At the same time, in complex tasks, the range of each model parameter is also more comprehensive, which leads to more considerable variance in the estimated model parameters. However, the model accuracy of Optimal LDP-FL on different datasets was slightly higher than that of LDP-FL. Therefore, the performance of Optimal LDP-FL was better.
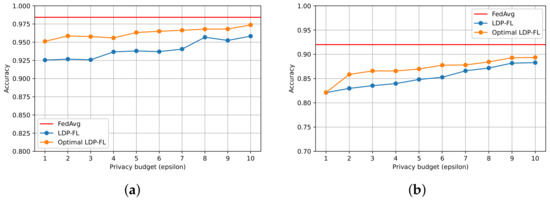
Figure 4.
Model accuracy vs. privacy budget for different federated learning frameworks on MNIST and Fashion MNIST datasets: (a) MNIST and (b) Fashion MNIST.
5.3. Efficiency Evaluation
To compare the communication costs of the two frameworks, we designed the experiment in Figure 5. The way we measured the communication cost was mainly through the running time of the program, because the difference in the network traffic consumed by different frameworks could not be reflected well in the case of a single device simulating federated learning. As shown in Figure 5a,b, the time consumed by various federated learning frameworks increased linearly with the number of clients, and the running time was roughly the same for different datasets. Compared with FedAvg, LDP-FL or Optimal LDP-FL had data perturbation and a parameter shuffling process. Due to the complex logic of data perturbation and parameter shuffling, which cannot be computed on a GPU, it consumed a lot of time. Compared with the LDP-FL mechanism, our proposed Optimal LDP-FL method saved a lot of time due to its concise data perturbation mechanism. In other words, our proposed Adaptive-Harmony mechanism could achieve a higher operating efficiency and lower communication cost under the same conditions.
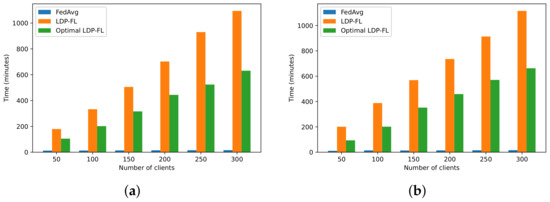
Figure 5.
Time vs. number of clients for different federated learning frameworks on MNIST and Fashion MNIST datasets: (a) MNIST and (b) Fashion MNIST.
To sum up, the experiment showed that the model with the highest accuracy was non-private FedAvg. The algorithm’s accuracy could be effectively improved by restricting the probability. Our proposed optimal LDP-FL mechanism improved the accuracy performance to a certain extent. Both frameworks were insensitive to changes in privacy budgets and could maintain high model accuracy at lower privacy budgets. However, the proposed Optimal LDP-FL mechanism significantly improved the operating efficiency. Under the same conditions, it could save more than 40% of the running time. Meanwhile, since the client sends less data to the server, optimal LDP-FL also consumes significantly less network traffic and can further save time on slower internet connections.
6. Conclusions
To achieve credible federated learning, we researched the privacy protection of federated learning and the balance of privacy, model utility, and algorithm efficiency. We proposed an efficiency-optimized data perturbation mechanism (i.e., Adaptive-Harmony). It adaptively configures the perturbation parameters, mainly the center and radius of the weight, for each client and each iteration according to the gradient descent and reduces the communication cost from each dimension to one dimension. The theoretical analysis and proof guarantee that our improved data perturbation mechanism is unbiased, convergent, and has an equivalent asymptotic error bound with the Adaptive-Duchi mechanism. We also integrated Adaptive-Harmony and privacy amplification into FL to propose a new federated learning framework (i.e., Optimal LDP-FL). It has been proven that our framework satisfies -LDP. It can avoid privacy leakages caused by server tracking clients through parameter shuffling. A restrictive self-sampling probability was also proposed which eliminated the randomness of the self-sampling probability settings in existing studies and improved the utilization of the federated system. Due to the restrictively self-sampling and efficient data perturbation, Optimal LDP-FL had good model performance, especially in terms of computational and communication costs. Model accuracy was also improved due to the combination of the restrictive client self-sampling technology. Comprehensive experiments on different datasets showed that our framework performed well in terms of classification accuracy and improved communication efficiency by 40%.
Our method proposes a restrictive self-sampling probability in the interval (0.5, 1). However, the compactness of this interval has yet to be verified. In theory, 0.5 is the relaxed lower bound of our estimate, and the tighter lower bound is an exciting direction for future research.
Author Contributions
Conceptualization and methodology, J.Z. (Jianzhe Zhao); data curation, software, and writing—original draft preparation, M.Y.; visualization, software, and investigation, W.S.; software and validation, R.Z.; software and writing—reviewing and editing, J.Z. (Jiali Zheng); software and writing—reviewing and editing, J.F.; conceptualization and writing—reviewing, S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant No. 62102074.
Institutional Review Board Statement
This is not applicable for the study since it did not involve humans or animals.
Data Availability Statement
The MNIST dataset and Fasion MNIST dataset used to support the findings of this study are available at tensorflow/g3doc/tutorials/mnist/ and tensorflow/g3doc/tutorials/Fasion-mnist/ (accessed on 15 May 2022).
Conflicts of Interest
The authors have no relevant financial or non-financial interest to disclose.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial intelligence |
| FL | Federated learning |
| DP | Differential privacy |
| CDP | Centralized differential privacy |
| LDP | Local differential privacy |
| LDP-FL | Federated learning with LDP |
| FedSGD | Federated stochastic gradient descent |
| LAD | Latent Dirichlet allocation |
| FedAvg | Federated averaging |
References
- Pouyanfar, S.; Sadiq, S.; Yan, Y.; Tian, H.; Tao, Y.; Reyes, M.P.; Shyu, M.L.; Chen, S.C.; Iyengar, S.S. A survey on deep learning: Algorithms, techniques, and applications. ACM Comput. Surv. (CSUR) 2018, 51, 1–36. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, L.; Zhou, X.; Zhou, Y.; Sun, Y.; Zhu, W.; Chen, H.; Deng, W.; Chen, H.; Zhao, H. Multi-strategy particle swarm and ant colony hybrid optimization for airport taxiway planning problem. Inf. Sci. 2022, 612, 576–593. [Google Scholar] [CrossRef]
- Song, Y.; Cai, X.; Zhou, X.; Zhang, B.; Chen, H.; Li, Y.; Deng, W.; Deng, W. Dynamic hybrid mechanism-based differential evolution algorithm and its application. Expert Syst. Appl. 2023, 213, 118834. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, P.; Zhang, R.; Yao, R.; Deng, W. A novel performance trend prediction approach using ENBLS with GWO. Meas. Sci. Technol. 2022, 34, 025018. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, X.; Ran, X.; Liu, Y.; Deng, W.; Deng, W. Co-evolutionary competitive swarm optimizer with three-phase for large-scale complex optimization problem. Inf. Sci. 2023, 619, 2–18. [Google Scholar] [CrossRef]
- Trask, A.W. Grokking Deep Learning; Simon and Schuster: New York, NY, USA, 2019. [Google Scholar]
- Deng, W.; Xu, J.; Gao, X.; Zhao, H. An Enhanced MSIQDE Algorithm with Novel Multiple Strategies for Global Optimization Problems. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1578–1587. [Google Scholar] [CrossRef]
- Jin, T.; Zhu, Y.; Shu, Y.; Cao, J.; Yan, H.; Jiang, D. Uncertain optimal control problem with the first hitting time objective and application to a portfolio selection model. J. Intell. Fuzzy Syst. 2022, 1–15, in press. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. (TIST) 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Shi, W.; Cao, J.; Zhang, Q.; Li, Y.; Xu, L. Edge computing: Vision and challenges. IEEE Internet Things J. 2016, 3, 637–646. [Google Scholar] [CrossRef]
- Chen, J.; Ran, X. Deep learning with edge computing: A review. Proc. IEEE 2019, 107, 1655–1674. [Google Scholar] [CrossRef]
- Wu, X.; Liang, Z.; Wang, J. FedMed: A Federated Learning Framework for Language Modeling. Sensors 2020, 20, 4048. [Google Scholar] [CrossRef] [PubMed]
- Mills, J.; Hu, J.; Min, G. Communication-efficient federated learning for wireless edge intelligence in IoT. IEEE Internet Things J. 2019, 7, 5986–5994. [Google Scholar] [CrossRef]
- Khan, L.U.; Saad, W.; Han, Z.; Hossain, E.; Hong, C.S. Federated learning for internet of things: Recent advances, taxonomy, and open challenges. IEEE Commun. Surv. Tutor. 2021, 23, 1759–1799. [Google Scholar] [CrossRef]
- Jin, T.; Gao, S.; Xia, H.; Ding, H. Reliability analysis for the fractional-order circuit system subject to the uncertain random fractional-order model with Caputo type. J. Adv. Res. 2021, 32, 15–26. [Google Scholar] [CrossRef]
- Liu, Y.; Qu, Y.; Xu, C.; Hao, Z.; Gu, B. Blockchain-Enabled Asynchronous Federated Learning in Edge Computing. Sensors 2021, 21, 3335. [Google Scholar] [CrossRef]
- Mohassel, P.; Zhang, Y. Secureml: A system for scalable privacy-preserving machine learning. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–24 May 2017; pp. 19–38. [Google Scholar]
- Asad, M.; Moustafa, A.; Yu, C. A Critical Evaluation of Privacy and Security Threats in Federated Learning. Sensors 2020, 20, 7182. [Google Scholar] [CrossRef]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating noise to sensitivity in private data analysis. In Proceedings of the Theory of Cryptography Conference, New York, NY, USA, 4–7 May 2006; pp. 265–284. [Google Scholar]
- Dwork, C.; Feldman, V.; Hardt, M.; Pitassi, T.; Reingold, O.; Roth, A.L. Preserving statistical validity in adaptive data analysis. In Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing, Portland, OR, USA, 14–17 June 2015; pp. 117–126. [Google Scholar]
- Ziller, A.; Trask, A.; Lopardo, A.; Szymkow, B.; Wagner, B.; Bluemke, E.; Nounahon, J.M.; Passerat-Palmbach, J.; Prakash, K.; Rose, N.; et al. Pysyft: A library for easy federated learning. In Federated Learning Systems; Springer: Berlin, Germany, 2021; pp. 111–139. [Google Scholar]
- Hesamifard, E.; Takabi, H.; Ghasemi, M.; Wright, R.N. Privacy-preserving machine learning as a service. Proc. Priv. Enhancing Technol. 2018, 2018, 123–142. [Google Scholar] [CrossRef]
- Ryffel, T.; Trask, A.; Dahl, M.; Wagner, B.; Mancuso, J.; Rueckert, D.; Passerat-Palmbach, J. A generic framework for privacy preserving deep learning. arXiv 2018, arXiv:1811.04017. [Google Scholar]
- Wang, T.; Zhang, X.; Feng, J.; Yang, X. A Comprehensive Survey on Local Differential Privacy toward Data Statistics and Analysis. Sensors 2020, 20, 7030. [Google Scholar] [CrossRef]
- Truex, S.; Liu, L.; Chow, K.H.; Gursoy, M.E.; Wei, W. LDP-Fed: Federated learning with local differential privacy. In Proceedings of the Third ACM International Workshop on Edge Systems, Analytics and Networking, Heraklion, Greece, 27 April 2020; pp. 61–66. [Google Scholar]
- Li, J.; Khodak, M.; Caldas, S.; Talwalkar, A. Differentially private meta-learning. arXiv 2019, arXiv:1909.05830. [Google Scholar]
- Wang, Y.; Tong, Y.; Shi, D. Federated latent Dirichlet allocation: A local differential privacy based framework. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2020; Volume 34, pp. 6283–6290. [Google Scholar]
- Bhowmick, A.; Duchi, J.; Freudiger, J.; Kapoor, G.; Rogers, R. Protection against reconstruction and its applications in private federated learning. arXiv 2018, arXiv:1812.00984. [Google Scholar]
- Liu, R.; Cao, Y.; Yoshikawa, M.; Chen, H. Fedsel: Federated sgd under local differential privacy with top-k dimension selection. In Proceedings of the International Conference on Database Systems for Advanced Applications, Jeju, Korea, 24–27 September 2020; pp. 485–501. [Google Scholar]
- Cao, T.; Huu, T.T.; Tran, H.; Tran, K. A federated deep learning framework for privacy preservation and communication efficiency. J. Syst. Archit. 2022, 124, 102413. [Google Scholar] [CrossRef]
- McMahan, H.B.; Moore, E.; Ramage, D.; y Arcas, B.A. Federated learning of deep networks using model averaging. arXiv 2016, arXiv:1602.05629. [Google Scholar]
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Minimax optimal procedures for locally private estimation. J. Am. Stat. Assoc. 2018, 113, 182–201. [Google Scholar] [CrossRef]
- Nguyên, T.T.; Xiao, X.; Yang, Y.; Hui, S.C.; Shin, H.; Shin, J. Collecting and analyzing data from smart device users with local differential privacy. arXiv 2016, arXiv:1606.05053. [Google Scholar]
- Wang, N.; Xiao, X.; Yang, Y.; Zhao, J.; Hui, S.C.; Shin, H.; Shin, J.; Yu, G. Collecting and analyzing multidimensional data with local differential privacy. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macau, China, 8–11 April 2019; pp. 638–649. [Google Scholar]
- Sun, L.; Qian, J.; Chen, X. Ldp-fl: Practical private aggregation in federated learning with local differential privacy. arXiv 2020, arXiv:2007.15789. [Google Scholar]
- Balle, B.; Bell, J.; Gascón, A.; Nissim, K. The privacy blanket of the shuffle model. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2019; pp. 638–667. [Google Scholar]
- Cheu, A.; Smith, A.; Ullman, J.; Zeber, D.; Zhilyaev, M. Distributed differential privacy via shuffling. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, 30 May–3 June 2019; pp. 375–403. [Google Scholar]
- Erlingsson, Ú.; Feldman, V.; Mironov, I.; Raghunathan, A.; Talwar, K.; Thakurta, A. Amplification by shuffling: From local to central differential privacy via anonymity. In Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, San Diego, CA, USA, 6–9 January 2019; pp. 2468–2479. [Google Scholar]
- Girgis, A.M.; Data, D.; Diggavi, S. Differentially private federated learning with shuffling and client self-sampling. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Melbourne, VIC, Australia, 12–20 July 2021; pp. 338–343. [Google Scholar]
- Wei, K.; Li, J.; Ding, M.; Ma, C.; Yang, H.H.; Farokhi, F.; Jin, S.; Quek, T.Q.S.; Poor, H.V. Federated Learning with Differential Privacy: Algorithms and Performance Analysis. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3454–3469. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 9–11 May 2017; pp. 1273–1282. [Google Scholar]
- Kasiviswanathan, S.P.; Lee, H.K.; Nissim, K.; Raskhodnikova, S.; Smith, A. What can we learn privately? SIAM J. Comput. 2011, 40, 793–826. [Google Scholar] [CrossRef]
- Choudhury, O.; Gkoulalas-Divanis, A.; Salonidis, T.; Sylla, I.; Park, Y.; Hsu, G.; Das, A. Differential privacy-enabled federated learning for sensitive health data. arXiv 2019, arXiv:1910.02578. [Google Scholar]
- Jayaraman, B.; Evans, D. When relaxations go bad: “differentially-private” machine learning. arXiv 2019, arXiv:1902.08874. [Google Scholar]
- Zhao, Y.; Zhao, J.; Yang, M.; Wang, T.; Wang, N.; Lyu, L.; Niyato, D.; Lam, K.Y. Local differential privacy-based federated learning for internet of things. IEEE Internet Things J. 2020, 8, 8836–8853. [Google Scholar] [CrossRef]
- Lian, Z.; Wang, W.; Su, C. COFEL: Communication-Efficient and Optimized Federated Learning with Local Differential Privacy. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Warner, S.L. Randomized response: A survey technique for eliminating evasive answer bias. J. Am. Stat. Assoc. 1965, 60, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Local privacy and statistical minimax rates. In Proceedings of the 2013 IEEE 54th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 26–29 October 2013; pp. 429–438. [Google Scholar]
- Beimel, A.; Brenner, H.; Kasiviswanathan, S.P.; Nissim, K. Bounds on the sample complexity for private learning and private data release. Mach. Learn. 2014, 94, 401–437. [Google Scholar] [CrossRef]
- Girgis, A.M.; Data, D.; Diggavi, S.; Kairouz, P.; Suresh, A.T. Shuffled model of federated learning: Privacy, communication and accuracy trade-offs. arXiv 2020, arXiv:2008.07180. [Google Scholar] [CrossRef]
- Bittau, A.; Erlingsson, Ú.; Maniatis, P.; Mironov, I.; Raghunathan, A.; Lie, D.; Rudominer, M.; Kode, U.; Tinnes, J.; Seefeld, B. Prochlo: Strong privacy for analytics in the crowd. In Proceedings of the 26th Symposium on Operating Systems Principles, Shanghai, China, 28 October 2017; pp. 441–459. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).