Adaptive Fault-Tolerant Control for Second-Order Multiagent Systems with Unknown Control Directions via a Self-Tuning Distributed Observer
Abstract
1. Introduction
2. Problem Formulation
3. Self-Tuning Distributed Observer
4. Adaptive Sliding-Mode Controller Design
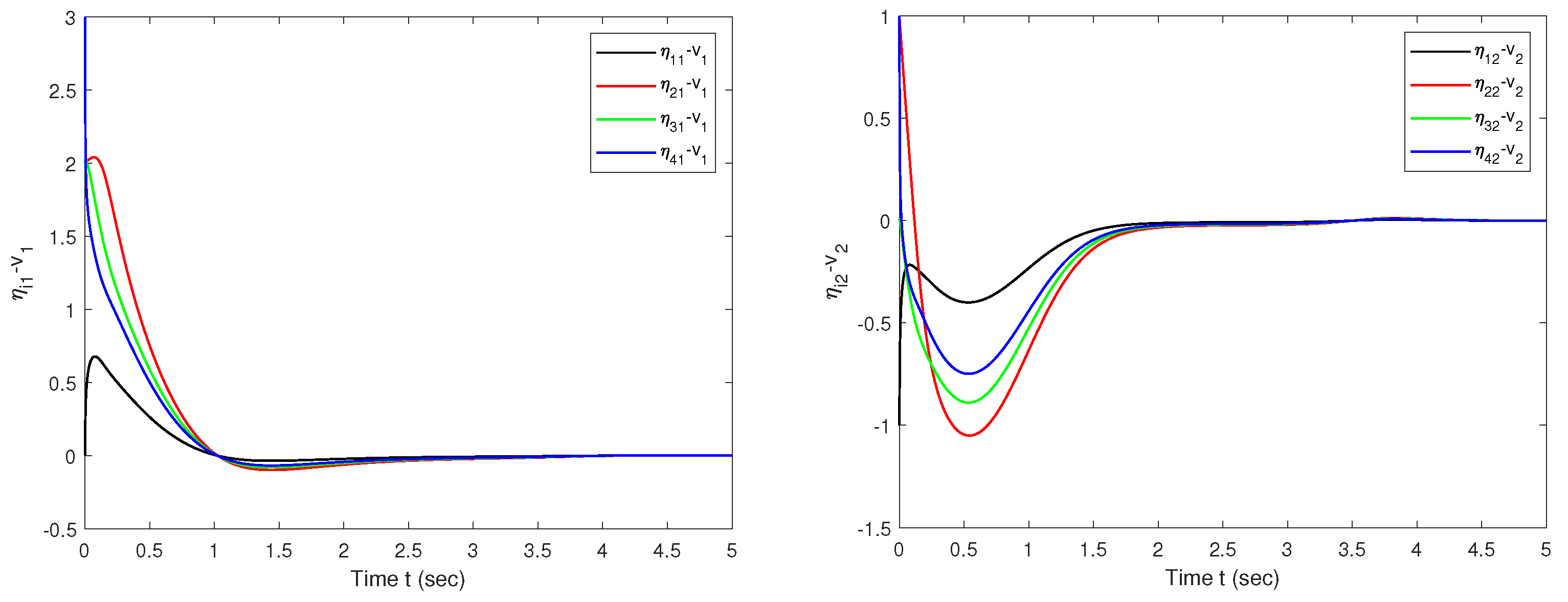
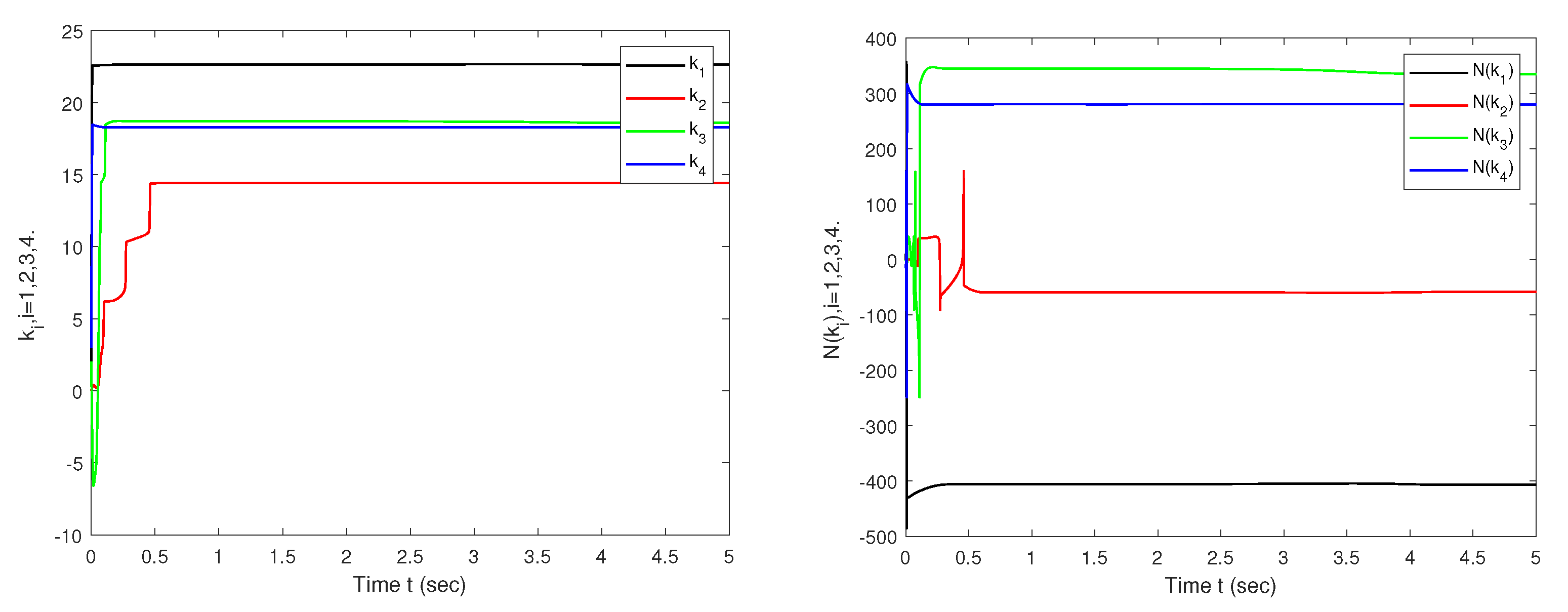
5. Simulation Studies
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PLOAE | Partial loss of actuator effectiveness |
References
- Wang, W.; Wen, C. Adaptive actuator failure compensation control of uncertain nonlinear systems with guaranteed transient performance. Automatica 2010, 46, 2082–2091. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, W.; Ye, H. Cooperative control for consensus of multi-agent systems with actuator faults. Comput. Electr. Eng. 2014, 40, 2154–2166. [Google Scholar] [CrossRef]
- Khalili, M.; Zhang, X.; Polycarpou, M.M.; Parisini, T.; Cao, Y. Distributed adaptive fault-tolerant control of uncertain multi-agent systems. Automatica 2018, 87, 142–151. [Google Scholar] [CrossRef]
- Chen, G.; Song, Y.D. Robust fault-tolerant cooperative control of multi-agent systems: A constructive design method. J. Frankl. Inst. 2015, 352, 4045–4066. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Y.; Lewis, F.L. Robust adaptive fault-tolerant control of multiagent systems with uncertain nonidentical dynamics and undetectable actuation failures. IEEE Trans. Ind. Electron. 2015, 62, 3978–3988. [Google Scholar]
- Wang, C.; Wen, C.; Guo, L. Adaptive Consensus Control for Nonlinear Multiagent Systems with Unknown Control Directions and Time-Varying Actuator Faults. IEEE Trans. Autom. Control 2020, 66, 4222–4229. [Google Scholar] [CrossRef]
- Ren, C.E.; Fu, Q.; Zhang, J.; Zhao, J. Adaptive event-triggered control for nonlinear multi-agent systems with unknown control directions and actuator failures. Nonlinear Dyn. 2021, 105, 1657–1672. [Google Scholar] [CrossRef]
- Su, Y.; Huang, J. Cooperative output regulation of linear multi-agent systems. IEEE Trans. Autom. Control 2011, 57, 1062–1066. [Google Scholar]
- Cai, H.; Huang, J. The leader-following consensus for multiple uncertain Euler-Lagrange systems with an adaptive distributed observer. IEEE Trans. Autom. Control 2015, 61, 3152–3157. [Google Scholar] [CrossRef]
- Cai, H.; Lewis, F.L.; Hu, G.; Huang, J. The adaptive distributed observer approach to the cooperative output regulation of linear multi-agent systems. Automatica 2017, 75, 299–305. [Google Scholar] [CrossRef]
- Liu, T.; Huang, J. A distributed observer for a class of nonlinear systems and its application to a leader-following consensus problem. IEEE Trans. Autom. Control 2018, 64, 1221–1227. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, J.; Huang, J. A self-tuning adaptive distributed observer approach to the cooperative output regulation problem for networked multi-agent systems. Int. J. Control 2019, 92, 1796–1804. [Google Scholar] [CrossRef]
- An, L.; Yang, G.H. Improved adaptive resilient control against sensor and actuator attacks. Inf. Sci. 2018, 423, 145–156. [Google Scholar] [CrossRef]
- Wang, W.; Wen, C.; Huang, J. Distributed adaptive asymptotically consensus tracking control of nonlinear multi-agent systems with unknown parameters and uncertain disturbances. Automatica 2017, 77, 133–142. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Y.; Krstic, M.; Wen, C. Fault-tolerant finite time consensus for multiple uncertain nonlinear mechanical systems under single-way directed communication interactions and actuation failures. Automatica 2016, 63, 374–383. [Google Scholar] [CrossRef]
- Michel, A.N.; Miller, R.K.; Vidyasagar, M. Qualitative Analysis of Large Scale Dynamical Systems. IEEE Trans. Syst. Man Cybern. 1980, 10, 689. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Qu, Z.; Lewis, F.L. On constructing Lyapunov functions for multi-agent systems. Automatica 2015, 58, 39–42. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Dong, Y.; Huang, J. Leader-following connectivity preservation rendezvous of multiple double integrator systems based on position measurement only. IEEE Trans. Autom. Control 2014, 59, 2598–2603. [Google Scholar] [CrossRef]
- Huang, J. Nonlinear Output Regulation: Theory and Applications; SIAM: Philadelphia, PA, USA, 2004. [Google Scholar]
- Nussbaum, R.D. Some remarks on a conjecture in parameter adaptive control. Syst. Control Lett. 1983, 3, 243–246. [Google Scholar] [CrossRef]
- Ge, S.S.; Wang, J. Robust adaptive neural control for a class of perturbed strict feedback nonlinear systems. IEEE Trans. Neural Netw. 2002, 13, 1409–1419. [Google Scholar] [CrossRef]
- Zhao, B.; Li, Y.; Liu, D. Self-tuned local feedback gain based decentralized fault tolerant control for a class of large-scale nonlinear systems. Neurocomputing 2017, 235, 147–156. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, J.; Su, X.; Wang, K.; Li, G. Adaptive control of second-order nonlinear systems with injection and deception attacks. IEEE Trans. Syst. Man Cybern. 2020, 52, 574–581. [Google Scholar] [CrossRef]
- Machina, A.; Ponossov, A. Differential Inclusions and Filippov Solutions in the Analysis of Piecewise Linear Models Describing Gene Regulatory Networks. Proc. AIP Conf. Proc. Am. Inst. Phys. 2009, 1168, 339–342. [Google Scholar]
- Cao, Y.; Ren, W. Distributed coordinated tracking with reduced interaction via a variable structure approach. IEEE Trans. Autom. Control 2011, 57, 33–48. [Google Scholar]
- Mei, J.; Ren, W.; Ma, G. Distributed coordinated tracking with a dynamic leader for multiple Euler-Lagrange systems. IEEE Trans. Autom. Control 2011, 56, 1415–1421. [Google Scholar] [CrossRef]
- Sun, J.; Geng, Z.; Lv, Y.; Li, Z.; Ding, Z. Distributed adaptive consensus disturbance rejection for multi-agent systems on directed graphs. IEEE/ACM Trans. Netw. 2016, 5, 629–639. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, R.; Sun, X.; Pu, D. Adaptive Fault-Tolerant Control for Second-Order Multiagent Systems with Unknown Control Directions via a Self-Tuning Distributed Observer. Electronics 2022, 11, 3939. https://doi.org/10.3390/electronics11233939
Gu R, Sun X, Pu D. Adaptive Fault-Tolerant Control for Second-Order Multiagent Systems with Unknown Control Directions via a Self-Tuning Distributed Observer. Electronics. 2022; 11(23):3939. https://doi.org/10.3390/electronics11233939
Chicago/Turabian StyleGu, Rongrong, Xudong Sun, and Dongyi Pu. 2022. "Adaptive Fault-Tolerant Control for Second-Order Multiagent Systems with Unknown Control Directions via a Self-Tuning Distributed Observer" Electronics 11, no. 23: 3939. https://doi.org/10.3390/electronics11233939
APA StyleGu, R., Sun, X., & Pu, D. (2022). Adaptive Fault-Tolerant Control for Second-Order Multiagent Systems with Unknown Control Directions via a Self-Tuning Distributed Observer. Electronics, 11(23), 3939. https://doi.org/10.3390/electronics11233939





