Abstract
Developing countries have had numerous obstacles in diagnosing the COVID-19 worldwide pandemic since its emergence. One of the most important ways to control the spread of this disease begins with early detection, which allows that isolation and treatment could perhaps be started. According to recent results, chest X-ray scans provide important information about the onset of the infection, and this information may be evaluated so that diagnosis and treatment can begin sooner. This is where artificial intelligence collides with skilled clinicians’ diagnostic abilities. The suggested study’s goal is to make a contribution to battling the worldwide epidemic by using a simple convolutional neural network (CNN) model to construct an automated image analysis framework for recognizing COVID-19 afflicted chest X-ray data. To improve classification accuracy, fully connected layers of simple CNN were replaced by the efficient extreme gradient boosting (XGBoost) classifier, which is used to categorize extracted features by the convolutional layers. Additionally, a hybrid version of the arithmetic optimization algorithm (AOA), which is also developed to facilitate proposed research, is used to tune XGBoost hyperparameters for COVID-19 chest X-ray images. Reported experimental data showed that this approach outperforms other state-of-the-art methods, including other cutting-edge metaheuristics algorithms, that were tested in the same framework. For validation purposes, a balanced X-ray images dataset with 12,000 observations, belonging to normal, COVID-19 and viral pneumonia classes, was used. The proposed method, where XGBoost was tuned by introduced hybrid AOA, showed superior performance, achieving a classification accuracy of approximately 99.39% and weighted average precision, recall and F1-score of 0.993889, 0.993887 and 0.993887, respectively.
1. Introduction
The COVID-19 pandemic has resulted in a huge worldwide catastrophe and has had a substantial impact on many lives across the world. The first instance of this deadly virus was reported in December 2019 from Wuhan, a Chinese province in [1]. After emergence, the virus quickly became a worldwide epidemic, impacting many nations across the globe. Reverse transcription-polymerase chain reaction (RT PCR) is one of the most often utilized methods in the diagnosis of COVID-19. However, since PCR has a diagnostic sensitivity of about 60–70%, radiological imaging techniques including computed tomography (CT) and X-ray have been critical in the early detection of this disease [2]. Therefore, the COVID-19 diagnosis from CT and X-ray images is an active and promising research domain, and additionally, there is much more space for improvements.
A few recent investigations have found alterations in X-ray and CT imaging scans in individuals with COVID-19 symptoms. For example, Zhao et al. [3] discovered dilatation and consolidation, as well as ground-glass opacities, in COVID-19 patients. The fast increase in the number of positive COVID-19 instances has heightened the necessity for researchers to use artificial intelligence (AI) alongside expert opinion to aid doctors in their work. Deep learning (DL) models have begun to gain traction in this respect. Due to a scarcity of radiologists in hospitals, AI-based diagnostic models may be useful in providing timely assistance to patients. Numerous research studies based on these approaches have been published in the literature; however, only the notable ones are mentioned here. Hemdan et al. [4] suggested seven convolutional neural network (CNN) models, including enhanced VGG19 and Google MobileNet, to diagnose COVID-19 from X-ray pictures. Wang et al. [5] classified COVID-19 pictures from normal and viral pneumonia patients with an accuracy of 92.4%. Similarly, Ioannis et al. [6] attained a class accuracy of 93.48% using 224 COVID-19 pictures. The Opconet, an optimized CNN, was proposed in [7] utilizing a total of 2700 pictures, giving an accuracy score of 92.8%. Apostolopoulous et al. [8] created a MobileNet CNN model utilizing extricated features. In [9], three different CNN models, namely inception v3, ResNet50, and Inception-ResNet V2, were employed for classification. In [10], a transfer learning-based method was utilized to classify COVID and non-COVID chest X-ray pictures utilizing three models such as ResNet18, ResNet50, SqueezeNet, and DenseNet121.
Although all of the above-mentioned state-of-the-art approaches use CNN, the methods do not take into consideration the spatial connections between picture pixels when training the models. As a result, when the pictures are rotated, certain resizing operations are performed, and data augmentation is executed owing to the availability of lower dataset sizes, the generated CNN models fail to properly distinguish COVID-19 instances, viral pneumonia, and normal chest X-ray scans. Although some degree of inaccuracy in recognizing viral pneumonia cases is acceptable, the misclassification of COVID-19 patients as normal or viral pneumonia might confuse doctors, leading to failure of early COVID-19 detection.
One of the promising ways for establishing an efficient COVID-19 detection model based on DL is to generate a network with proper architecture for each COVID-19 dataset. The no free lunch theorem (NFL) [11], which claims that the universal method for tackling all real-world problems does not exist, proved as right in the DL domain [12] and consequently standard DL model cannot render performance as good as models specifically tuned for COVID-19 diagnosis. The challenge of finding appropriate CNN and DL structures for each particular task is known in the literature as CNN (DL) hyperparameters tuning (optimization), and a good way to do it is by using an automated approach guided by metaheuristics optimizers [12,13,14,15,16,17,18,19,20]. The metaheuristics-driven CNN tuning has also been successfully applied to COVID-19 diagnostics [21,22,23,24].
However, the CNN tuning via metaheuristics is extremely time consuming because every function evaluation requires a generated network to be trained on large datasets for measuring solutions’ quality (fitness). Additionally, the CNN training process with standard algorithms, e.g., gradient descent (GD) [25], conjugate gradienton (CG) [26], Krylov subspace descent (KSD) [27], etc., itself is very slow, and it can take hours to obtain feedback. Taking into account that the COVID-19 diagnostics is critical and that the efficient network needs to be established in almost real time, more approaches for COVID-19 early detection from X-ray and CT images are required.
With the goal of shortening training time, while performing automated feature extraction, research presented in this manuscript adapts a sequential, two-phase hybrid machine learning model for COVID-19 detection from X-ray images. In the first phase, a well-known simple architecture alike LeNet-5 CNN [28] is used as the feature extraction to reduce structural complexities within images. The second phase uses extreme gradient boosting (XGBoost) for performing classification, where outputs from the flatten layer of the LeNet-5 structure are used as XGBoost inputs. In other words, LeNet-5 fully connected (FC) layers are replaced with XGBoost to perform almost real-time classification. The LeNet structure is trained only once, shortening execution time substantially more than in the case of CNN tuned approaches.
However, according to the NFL, the XGBoost, which efficiency depends on many hyperparameters, also needs to be tuned for specific problems. Consequently, this study also proposes metaheuristics to improve XGBoost performance for COVID-19 X-ray images classification. For the purpose of this study, modified arithmetic optimization algorithm (AOA) [29], that represents a low-level hybrid between AOA and sine cosine algorithm (SCA) [30], is developed and adapted for XGBoost optimization. The observed drawbacks of basic AOA are analyzed, and a method that outscores the original approach is developed. This particular metaheuristics is chosen because it shows great potential in solving varieties of real-world challenges [31,32]; however, since it relatively recenty emerged, it is still not investigated enough, and there are still many open spaces for its improvements.
The proposed two-phases hybrid method for COVID-19 X-ray diagnosis is validated against the COVID-19 radiography database set of images, which was retrieved from the Kaggle repository [33,34]. The classification is performed against three classes, namely normal, COVID-19 and viral pneumonia. The viral pneumonia X-rays are also taken because only subtle differences with COVID-19 X-ray images exist. However, since the source of the COVID-19 X-ray diagnosis dataset is imbalanced toward the normal class and the aim of the proposed research is not oriented toward addressing imbalanced datasets, the COVID-19 and viral pneumonia images are augmented, while the normal images are contracted from the original repository, and at the end each class, they contained 4000 observations.
The performance of the proposed methodology is compared with other standard DL methods as well as with XGBoost classifiers tuned with other well-known metaheuristics. Additionally, the proposed modified AOA, before being adopted for XGBoost tuning for COVID-19 classification, was first tested in optimizing challenging congress on evolutionary computation 2017 (CEC2017) benchmark instances.
Considering the above, this manuscript proposes a method that is guided by the two elemental problems for investigation:
- The possibility of designing a method for efficient COVID-19 diagnostics from X-ray images based on the simple CNN and XGBoost classifier and
- The possibility of further improving the original AOA apporach by performing low-level hybridization with SCA metaheuritiscs.
Established upon the experimental findings showed in Section 4 and Section 5, the contribution of the proposed study is four-fold:
- A simple light-weight neural network has been generated that obtains a decent level of performance on the COVID-19 dataset and executes fast;
- An enhanced version of AOA metaheuristics has been developed that specifically targets the observed and known limitations and drawbacks of the basic AOA implementation;
- It was shown that the proposed metaheuristics is efficient in solving global optimization tasks with combined, real and integer parameters types; and
- The proposed COVID-19 detection methodology from X-ray images that employs the light-weight network, XGBoost and enhanced AOA obtains satisfying performance within a reasonable amount of computational time.
The sections of the manuscript are outlined as follows: Section 2 provides a brief survey of the AI method employed in this study with a focus on CNN applications. Section 3 explains the basic version of the AOA, points out its drawbacks and introduces the modified AOA implementation. Bound constrained simulations of the proposed algorithm on a challenging CEC2017 benchmark set are given in Section 4. The experimental findings of the COVID-19 early diagnostics from X-ray images with the proposed methodology are provided in Section 5, while the final remarks, proposed future work and conclusions are given in Section 6.
2. Background and Preliminaries
The following section aims to give a theoretical background for the used methods and to elaborate the workings of the proposed method, which is described later on. Firstly, the deep neural networks (DNN) will be explained alongside an emphasis on CNN. Afterwards, the XGBoost architecture is described followed by the metaheuristic optimization.
2.1. Deep Neural Networks
The application of deep learning models to the analysis of X-ray captures is widely applied [35,36,37]. The performance of CNN is distinguished among deep learning models, and that is the case for X-ray image classification as well [38,39]. Input is transformed through many layers of the CNN and the application of narrow filters. The types of CNNs are various, and some of interest for this research are: ResNet [40], AlexNet [41], ZFNet [42], VGGNet [43], GoogLeNet [44], and LeNet-5 [45]. Considering the prolonged evolutionary process of the metaheuristics optimizer that is suggested for this part of the solution, the contribution of large networks can be considerable in terms of computational costs [46]. Nevertheless, operating with large networks can result in overfitting [47].
Black and white as well as grayscale images are best used with the models such as LeNet, with advantages that include simplicity alongside effectiveness. To increase the real-time processing capabilities, the authors propose the use of simple network structure such as LeNet as the primary classifier, for the structural complexity reduction and out of consideration to the previously mentioned limitations. Introduced by Yann Le-Cun, the LeNet-5 [28] is considered the simplest from the family of CNNs, and its architecture is presented in the Figure 1. This network includes only two convolutional and average pooling layers, while it uses three fully connected layers for output classification/regression.
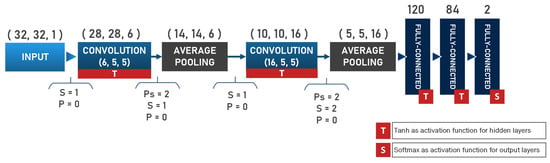
Figure 1.
The design of LeNet-5 CNN.
The visual tasks heavily employ the CNN technology [48], with contemporary progress in the field of facial recognition [49,50], analysis of documents [51,52], classification of medical images and diagnostics [53,54,55], as well as a paramount task of climate change analysis and severe weather conditions [56,57] including various other applications. In spite of the diversity of its practical implementation, the CNNs are not perfect. A considerable task is the overfitting issue and methods to avoid it. The popular solutions are regularization and dropout, early stopping, model simplification, and data augmentation [58,59,60,61,62]. The approach that the authors focused on is the dropout [63,64]. The principle of removing a unit from a layer including its connections is referred to as dropping. The selection of units to be dropped is random, and they are temporarily removed during the process of training. The neurons are detached so the network would achieve better generalization, and it does so as a result of desensitization to the neurons weights. To achieve an optimal weight set in a polynomial time is an NP-hard problem [15,65].
The architecture of the CNNs is a layer based on the goal of mimicking the human visual cortex. The types of these layers are convolutional, pooling and dense. The input goes through all layers in a specific order, which results in a high level of features allowing for high-precision image classification and optimization. The loss function has to be optimized during the weight learning of network training, and some of the optimizers are adadelta, adagrad, adamax, Adam, rmsprop, stochastic gradient descent, and momentum [66,67,68]. Non-linear output is mapped through the transfer (activation) function, and examples of such functions are rectified linear unit (ReLU) [69], tanh, and sigmoid. The de facto standard has been achieved by the ReLu transfer unction with a value amounting to .
Hyperparameters heavily influence the accuracy of the model and are a key subject of optimization [13]. The number of kernels and kernel size of each convolutional layer, the learning rate, the batch size, the number of convolutional and fully connected (dense) layers, the weight regularization in the dense layers, the activation function, the dropout rate, and so on are some examples of hyperparameters. Hyperparameter optimization is not a process that can be universally solved across all problems; hence, the “trial and error” approach is necessary. Such methods can be time exhaustive and do not guarantee results. This process is deemed as NP-hard. Metaheuristic methods have yielded results with such endeavors [70,71,72].
The detailed CNN mathematical formulation is provided in [73], and a more recent study on the same topic is given in [74].
2.2. The XGBoost Algorithm
An adaptive training method is used by the XGBoost algorithm for objective function optimization. Consequentially, every step in the optimization process depends on the previous step in terms of the result. The mathematical expression of the objective function of the XGBoost model is listed below:
where the t-th iteration loss term is given as l, the constant term is C, and the regularization parameter R of the model is additionally described as:
Generally, the simplicitty of the tree structure is proportional to the value of and customization parameters. The larger the value of the parameters is, the simpler the tree structure. First and second derivatives of the model, g and h, respectively, are given as follows:
The following formulas are used for obtaining the solution:
where the loss function score is given as , while the solution weights are given as .
2.3. Metaheuristic Optimization
Metaheuristics optimization algorithms are stochastic approaches that can be utilized to solve NP-hard problems where deterministic algorithms cannot obtain the solution in a reasonable amount of time with a reasonable amount of resources. Several families of algorithms exist in this group; however, different authors classify them in a different way. One of the most commonly used taxonomies divides metaheuristics with respect to the type of phenomena that was used to model the search mechanism of the algorithm [75,76,77]. This categorization divides metaheuristics approaches into swarm intelligence and genetic algorithms (both being inspired by the nature and a variety of behavior exhibited by animals in large groups), algorithms inspired by physical processes (such as gravitational search, water waves or electromagnetism), human-based algorithms (social network behavior, teaching, learning, and brainstorming process for example) and the most recent group of algorithms inspired by the mathematical properties (sine, cosine, arithmetic operations and so on).
The field of swarm intelligence belongs to the group of metaheuristic algorithms that apply the behavior of animals that live in swarms to the algorithms that are used in the domain of artificial intelligence [78,79]. This type of algorithm has proven efficient in tackling NP-hard problems for a large variety of applications. The true potential of swarm intelligence algorithms is accomplished through the process of hybridization. With the use of this method, the convergence speed can be substantially increased. The foundation is the stochastic methodology with the search mechanism for global optima. This results in heavy reliance on the amount of iterations. The search process recognizes two different phases alike with the training and testing phases in machine learning. These two phases are exploration, which is focused on searching locally, and exploitation, which is directed toward global search. The problem is balancing these two phases. Swarm algorithms are not expected to provide the certainly best solution but rather a very close one to it referred to as sub-optimal. Evolutionary principles immensely improve the search process if applied to the algorithm. The idea is to transfer the information from the current population to the following one. Evolution recognizes three different operations: selection, mutation, and crossover. The simplest one is the selection of the best units and using them in their original form in the next population. The same is completed with the mutation process but with some changes to the value that the unit carries over. Finally, the crossover operation combines two units. The most acclaimed SI solutions consist of ant colony optimization (ACO) [80], bat algorithm (BA) [81,82], (PSO) [83], artificial bee colony (ABC) [84], firefly algorithm (FA) [85], and a more recent quantum-based avian navigation optimizer [86].
Even though the mentioned algorithms have individual high performance, the hybrid solutions still outperform them. The trend of hybridization is increasing, and the researchers gravitate toward modified solutions. Noteworthy examples of these algorithms are the ABC-BA [87], interactive search algorithm (ISA) [88], Swarm-TWSVM [89], and two-stage GA-PSO-ACO algorithm [90].
The most recent group of metaheuristics algorithms draws inspiration from the mathematical processes and laws. Two of the most significant representatives of this group are the sine–cosine algorithm (SCA) [30] and arithmetic optimization algoritm (AOA) [29]. The SCA algorithm is inspired by mathematical fluctuations of the sine and cosine functions, while the AOA utilizes fundamental mathematical operators, and both of them were utilized in the approach suggested in this paper. There are also other recently proposed algorithms that fall into this group, including golden sine algorithm (Gold-SA) [91], for example.
The main obstacle with the use of population-based algorithms is natural to the machine learning field to which they belong, and that is that there is no universally best solution for all problems. The no free lunch (NFL) theorem provides the theory to support this claim [11]. Hence, the high diversity in algorithms and their versions so that every use case has the best adapted solution.
The real-life application of the population-based metaheuristics algorithms is various, and some of them are cloud computing [92,93,94], cloud-edge computing [95], wireless sensor networks [96,97,98,99], COVID-19 case number prediction [100,101], feature selection problem [102,103], classification of glioma MRI images [17], global optimization problems and engineering optimization [104,105,106], credit card frauds detection [107,108], pollution prediction [109] as well as general machine learning optimization [110,111].
The tuning of deep neural networks is an additional trend that has emerged in the field of swarm intelligence. As already mentioned, these algorithms have proven excellent performance in solving NP-hard problems. This problem with the DNN emerges with hyperparameter optimization, and the swarm algorithms have solved this problem in countless different cases [4,5,6].
The XGBoost method used in this work also had its fair share of improvements through metaheuristic optimization. Notable cases of these types of solutions are: [112], which tests the classification of different metaheuristic approaches alongside XGBoost, ref. [113] applies PSO to the problem of network intrusion, and [114] for stock price prediction utilizing XGBoost and genetic algorithm (GA). Additionally, XGBoost tuned by the metaheuristics was used in intrusion detection and network security models [115,116,117,118].
3. Proposed Methodology
This section first shows a brief overview of original AOA metaheuristics, which is followed by its observed drawbacks and devised modified hybrid metaheuristics approach for the purpose of this study. Finally, this section concludes with a presentation of the two-phase sequential DL and XGboost method, which is used for COVID-19 X-ray images categorization.
3.1. Arithmetic Optimization Algorithm
A novel method called arithmetic optimization algorithm (AOA) is a metaheuristic method which draw inspiration from mathematics fundamental operators introduced by Abuligah et al. [29].
The optimization process of AOA initializes with X, a randomly generated matrix, for which the single solution is represented as , , and , which represents the initial optimization space for solutions. The best-obtained solution is decided after each iteration and is considered a candidate for the best solution. The operations subtraction, addition, division, and multiplication control the computation of the near-optimal solution areas. The search phase selection is calculated according to the Math Optimizer Accelerated (MOA) function applied during both phases:
where the t-th iteration function value is given as , while the range is 1 to the maximum iterations number T in which the current iteration is signified as t. and , respectively, represent the minimum and maximum accelerated function values.
The search space is randomly explored with the use of division (D) and multiplication (M) operators during the exploration phase. This mechanism is given with Equation (8). When the condition is satisfied, the search is limited by the MOA for the current phase. The operator (M) will not be applied until the first operator (D) does not finish its task conditioned by as the first rule of Equation (8). Otherwise, operator D is substituted by the (M) operator for the completion of the same task.
where the arbitrary small integer is , the fixed control parameter is , the i-th solution of the next iteration is , the current location j of the current iteration’s i-th solution is , and the current best solution’s j-th position is . Standardly, the lower and upper boundaries of the j-th position are and .
where the t-th iteration function value is denoted as the Math Optimizer Probability , the current iteration is t, the maximum iterations number is T, and the fixed parameter is with the purpose of measuring the accuracy of exploitation over iterations.
The deep search of the search space for exploitation is afterwards performed by the search strategies employed with addition (A) and subtraction (S) operators. This process is provided in Equation (10). The bounds of the first rule of Equation (10) are which similarly links the operator (A) to the operator (S) as in the previous phase as (M) to (D). Furthermore, (S) is substituted by (A) to finish the task,
Conclusively, the near-optimal solution candidates tend to diverge when , while they gravitate to near-optimal solutions in case of . For the stimulation of exploration and exploitation, the values from to are incrementally increased for the parameter. Additionally, note that the computational complexity of AOA is computational complexity.
3.2. Cons of Basic AOA and Introduced Modified Algorithm
The basic version of the AOA is regarded as a potent optimizer with a wide range of practical applications, but it stills suffer from several known drawbacks in its original implementation. These flaws are namely insufficient exploitation power and an inadequate intensity of exploration process. This is reflected in the fact that in some cases, AOA is susceptible to dwell in the proximity of the local optima and also to the slow converging speed [32,119,120], as it can clearly be observed in CEC2017 simulations presented in Section 4.
One of the root causes of these deficiencies is that the solutions’ update procedure in basic AOA is focused on the proximity of the single current global best solution. As discussed by [119,121], it results in an extremely selective search procedure, where other solutions depend on the solitary centralized guidance to update their position, with no guarantees to converge to the global optimum. Hence, it is necessary to improve the exploration capability of the basic AOA to escape the local optimums.
Due to the above-mentioned cons, during the search process, the original AOA converges too fast toward the current best solution, and the population diversity is disturbed. Since the AOA’s efficiently depends to some extent on the generated pseudo-random numbers due to its stochastic nature, in some runs, when the current best individual in the initial population is close to optimum regions of the search domain, the AOA shows satisfying performance. However, when the algorithm is “unlucky” and the initial population is further away from optimum, the whole population quickly converges toward sub-optimum regions, and the final results have lower quality.
Additionally, besides poor exploration, the AOA’s intensification process can be also improved. As already noted, the search is conducted mostly in the neighborhood of the current best individual, and exploitation around other solutions from the population is not emphasized enough.
The enhanced AOA proposed in this manuscript addresses both observed drawbacks by improving exploration, exploitation and its balance of the original version. For that reason, the proposed method introduces the search procedure from another metaheuristics and an additional control parameter that enhances exploration, but it also establishes better intensification–diversification trade-off.
The authors were inspired by the low-level methodology of hybridization employing the principles from SCA to the AOA. This process results in satisfactory performance from both phases of the metheuristic solutions and a superior hybrid solution. The basic equations for position updating with the SCA are given (11):
where the current option’s setting for the i-th measurement at the t-th model is , arbitrary numbers //, the location factor placement in the i-th dimension is , and the absolute value is given as .
As stated above, after conducting extensive examination of the search equations of AOA and SCA algorithms, it was determined that AOA search equations are not sufficient for efficient exploitation, which to a large extent depends on the current best solution, and it is required to cover a wider search space. Hence, this research aimed to merge two algorithms combined with using a quasi-reflection-learning based (QRL) procedure [122] in the following way. Every solution life-cycle consists of two phases, where the solution performs an AOA search (phase one) and SCA search (phase two), which are controlled by the value of one additional control parameter.
Each solution is assigned a attribute, which is utilized to monitor the improvement of the solutions. In the beginning, after producing the initial population, all solutions start with an AOA search. In each iteration, if the solution was not improved, the parameter is increased by 1. When reaches the threshold value (control parameter in the proposed hybrid algorithm), that particular solution continues the search by switching to the SCA search mechanism. Again, every time when the solution is not improved, is increased by 1. If the reaches the value, that solution is removed from the population and replaced by the quasi-reflexive-opposite solution of the solution X, which is generated by applying Equation (12) over each component j of solution X.
where part of the equation has a role to generate a random value derived from the uniform distribution inside , and and represent the lower and upper limits of the search space, respectively. This procedure is executed for each parameter of every solution X within D dimensions.
However, the replacement is not performed for the current best solution, because, practically, if the solution manages to maintain the best rank within iterations, there is a great chance that this solution hits the right part of the search space. If such a replacement would have occured, then the search process might diverge from the optimum region.
It must be noted that when replacing the solution with its opposite, additional evaluation is not performed. The logic behind utilizing the quasi-reflexive opposite solutions is based on the fact that if the original solution did not improve for a long time, it was located far away from the optimum (or in one of the sub-optimum domains), and there is a reasonable chance that the opposite solution will fall significantly closer to the optimum. Discarding so-called exhausted solutions from the population ensures stable exploration during the whole search process in the run. The novel solution starts its life-cycle as described above, with the parameter reset to 0, and by conducting the AOA search first.
The value of the threshold was determined empirically, and it is calculated by using the following expression: , where T denotes the maximal number of iterations, and N is the size of the population. Therefore, there is no need for the researcher to fine-tune this parameter.
For simplicity reasons, the introduced AOA method is named hybrid AOA (HAOA) and its pseudo-code is provided in Algorithm 1. The introduced changes do not increase the complexity of the original AOA algorithm; hence, the complexity of the proposed HAOA is estimated as . Moreover, the HAOA introduces just one additional control parameter (), and it is automatically determined as it depends on T and N.
| Algorithm 1: Hybrid arithmetic optimization algorithm. |
|
3.3. Deep Learning Approach for Image Classification
As is it was already mentioned in Section 1, the proposed approach is executed in two phases, where the first phase performs feature extraction and the second phases employs XGBoost for performing classification.
In the first phase of the proposed approach, a simple CNN architecture, similar to LeNet5 [28] that consists of 3 convolutional and 3 max pooling layers, followed by 3 fully-connected layers, is employed. This network structure was determined empirically with the goal of being as simple as possible (allowing easier training and fast execution), while achieving a decent level of performance on the COVID-19 dataset, by performing hyperparameters optimization during the pre-research phase via a simple grid search. The hyperparameters that were tuned included the number of convolutional layers (range , integer), number of cells in convolutional layers (range , integer), number of fully connected layers (range , integer) and learning rate (range , continuous). The determined network structure is as follows: the first convolutional layer uses 32 filters with 3 × 3 kernel size, while the second and third convolutional layers employ 16 filters with 3 × 3 kernels, which is followed by 3 dense layers. The complete CNN network structure is shown in Figure 2.
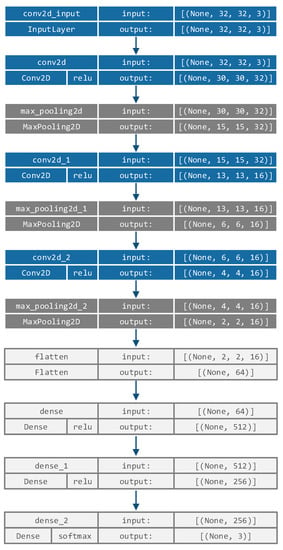
Figure 2.
CNN structure used in the proposed approach.
All images are resized to pixel size and used as CNN input, where the input size is . The convolutional layers’ weights are pre-trained on a COVID-19 dataset, as described in Section 5.1 with the Adam optimizer and a learning rate () of 0.001, sparseCatagoricalCrossEntropy loss function and a batch size of 32 over 100 epochs. The CNN uses a training set and validation set, which is a 10% fraction of the training data, and an early stopping condition with respect to validation loss with patience set to 10 epochs.
Due to the stochastic nature of the Adam optimizer, the whole training process is repeated 50 times, and the best performing pre-training model is used for the second phase. Training and validation loss for the best model during the training is shown in Figure 3, where it can be seen that the due to early stopping criteria, training terminated after only 60 epochs.
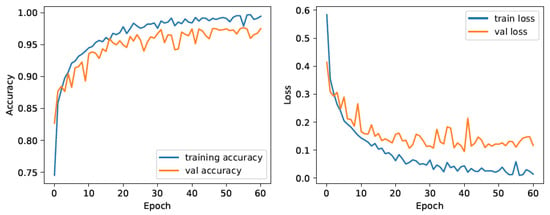
Figure 3.
The CNN training model.
After determining the sub-optimal weights and biases of the used simple CNN in the first phase, in the second phase, all fully connected layers from the CNN are removed, and the outputs from CNN’s flatten layer are used as inputs for the XGBoost classifier. Therefore, all CNN’s fully connected layers are replaced with XGBoost, where XGBoost inputs represent features extracted by the convolutional and maxpooling layers of CNN.
However, as it was also pointed out in Section 1, the XGBoost should be optimized for every particular dataset. Therefore, the proposed HAOA is used for XGBoost tuning, where each HAOA solution is of length 6 (), with every solution’s component representing one the XGBoost hyperparameters.
The collection of XGBoost hyperparameters that were addressed and tuned in this research is provided below, together with their boundaries and variable types:
- Learning rate (), limits: , category: continuous;
- , limits: , category: continuous;
- Subsample, limits: , category: continuous;
- Collsample_bytree, limits: , category: continuous;
- Max_depth, limits: , category: integer; and
- , limits: , category: continuous.
The parameter count required by softprob objective function (‘num_class’:self.no_classes) is further being passed as the parameter to XGBoost as well. All other parameters are determined and set to default XGBoost values.
Finally, the hybrid proposed approach is named after the used models—CNN-XGBoost-HAOA, and its flowchart is depicted in Figure 4.
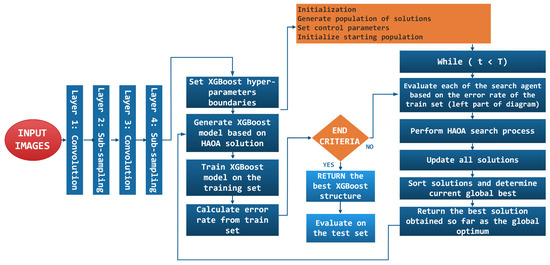
Figure 4.
The CNN-XGBoost-HAOA flowchart.
4. CEC2017 Bound-Constrained Experiments
The XGBoost tuning belongs to the group of NP-hard global optimization problems with mixed, real values and integer parameters (see Section 3.3). However, to prove the robustness of the optimizer, it should be first tested on a larger set of global optimization benchmark instances before being validated against the practical problem such as XGBoost hyperparameters optimization.
Therefore, the HAOA was validated on exceedingly challenging global optimization benchmark functions from the CEC2017 testing suite [123] with 30 parameters. The total number of instances is 30, and they are divided into 4 groups: from to —uni-modal, from to —multi-modal, hybrid functions are instances from to , and finally, the most challenging functions are the composite ones that include instances from to . The composite benchmarks exhibit all characteristics of the previous 3 groups; plus, they have been rotated and shifted.
The instance was discarded from experimentation due to its unstable behavior, as pointed out in [124]. The full specification of benchmark functions including name, class, parameters search range and global optimum value are shown in Table 1. More details, such as its visual representation, can be seen in [123].

Table 1.
The CEC2017 benchamrk instances specifications.
All simulations were performed with 30-dimensional CEC2017 instances (), and results for obtained mean (average) and standard deviation (std) averaged over 50 separate runs are reported. These two metrics are the most representative due to the stochastic behavior of metaheuristics. A relatively extensive evaluation of metaheuristics performance for the CEC2017 benchmark suite is provided in [125], where state-of-the-art improved harris hawks optimization (IHHO) was introduced; therefore, a similar experimental setup as in [125] was used in this study.
The research proposed in [125] validated all approaches in simulations with 30 individuals in the population () and 500 iterations () throughout one runtime. However, some metaheuristics spare more FFEs in one run, and setting the termination condition in terms of iterations may not be the most objective strategy. Therefore, to compare the proposed HAOA with other methods without biases, and at the same time to be consistent with the above-mentioned study, this research uses 15,030 FFEs () as the termination condition.
Additionally, most of the methods presented for validation purposes in [125] were also implemented in this study with the same adjustments of control parameters. The comparison between the proposed HAOA and the following methods was performed: basic AOA, SCA, cutting-edge IHHO [125], HHO [126], differential evolution (DE) [127], grasshopper optimization algorithm (GOA) [128], gray wolf optimization (GWO) [129], moth flame optimization (MFO) [130], multi-verse optimizer (MVO) [131], particle swarm optimization (PSO) [83] and whale optimization algorithm (WOA) [132].
Results for the CEC2017 simulations are displayed in Table 2. The text in bold emphasizes the best results for every performance indicator and instance. In the case of equal performance, these results are also bolded. Regardless whether the experimentation in [133] was performed with T as the termination condition, the results reported in this study are similar. However, due to the stohastic behavior of the optimizer, subtle differences exist.

Table 2.
The CEC2017 results and comparative analysis—HAOA vs. others.
The best mean results for 21 functions were achieved by the HAOA, and they include , , , , , , , , , , , , , , , , , , , , and . The functions are shown in Table 2. The second best approach proved the best cutting-edge IHHO, and in some tests, the IHHO showed better performance than HAOA, while in others, the results of HAOA and IHHO were tied. The HAOA and IHHO obtained the same mean indicator values in the following tests: , , , , and . The small number of cases in which the HAOA performed worse than the IHHO includes and experiments. There are also some cases where other methods achieved the best results, e.g., the instance, where MVO and PSO showed superior performance. Lastly, the HAOA tied DE in the cases of and instances.
Additionally, it is very important to observe that the original AOA never beat HAOA. Moreover, there are instances where the HAOA tremendously outscored AOA, even by more than 1000 times, e.g., in the function test. Finally, it is also significant to compare HAOA and SCA, because the HAOA uses SCA search expressions. In all simulations, the HAOA outperformed SCA for both indicators. Accordingly, it can be concluded that the HAOA successfully managed to combine the advantages of basic AOA and SCA methods as a low-level hybrid approach.
The magnitude of results’ variances between the HAOA and every other method implemented in CEC2017 simulations can be determined from a Friedman test [134,135] and two-way ranks variance analysis. This was performed for the reasons of statistical importance of an improvement’s proof that is more thorough than simply putting outcomes into comparison. Table 3 summarizes the results of the Friedman test over 29 CEC2017 instances for 12 compared methods.

Table 3.
Friedman test ranks for the compared algorithms over 29 CEC2017 functions.
Observing Table 3, the HAOA undoubtedly performs better than any of the other 11 algorithms taken into account for comparative analysis. As expected, the second best approach is IHHO, while the original AOA and SCA take the ranks of 6 and 11, respectively. Additionally, the calculated Friedman statistics is , and as such, it is greater than the critical value with 11 degrees of freedom () at the threshold level of . The conclusion of this analysis is that the null hypothesis () can be rejected, implying that the HAOA achieved results which are substantially better than other algorithms.
The convergence speed visual difference between the proposed HAOA and AOA, SCA, as well as between the other three best-performing metaheuristics, IHHO, DE and PSO for , , , , and instances, is shown in Figure 5. From the sample functions convergence graphs, it can be observed that the HAOA converges on average faster than other methods, which is particularly emphasized in cases of , and instance. It can also be seen that the results’ quality generated by HAOA is much higher than its base algorithms, AOA and SCA.
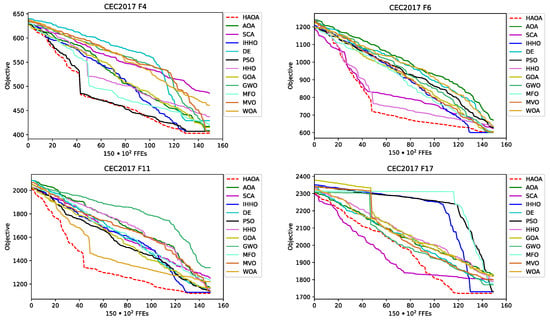
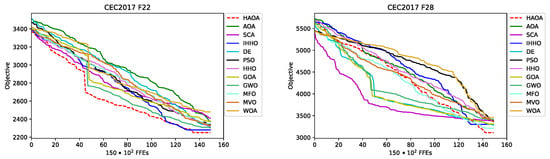
Figure 5.
CEC 2017 experiments convergence speed graphs for , , , , and benchmarks for some approaches.
5. The COVID-19 X-ray Images Classification Findings
This section first provides an overview of datasets used in experiments, which is followed by details of experimental setup and comparative analysis. This section concludes with the validation of experimental findings.
5.1. Dataset Description
The majority of images for the dataset employed in this research is taken from the COVID-19 radiography database, which can be retreived from the following URL: https://www.kaggle.com/datasets/tawsifurrahman/covid19-radiography-database (accessed on 25 October 2022). The lung opacity images are excluded, and the remaining three groups are taken for experiments. The images are categorized as follows: normal (class 0), COVID-19 (class 1) and viral pneumonia (class 2). The retrieved dataset includes sets of 3616, 10,192 and 1345 images for COVID-19, normal and viral pneumonia classes, respectively. The COVID-19 radiography database images were also employed in other research [33,34]. Random sample images from the COVID-19 radiography database are shown in Figure 6.
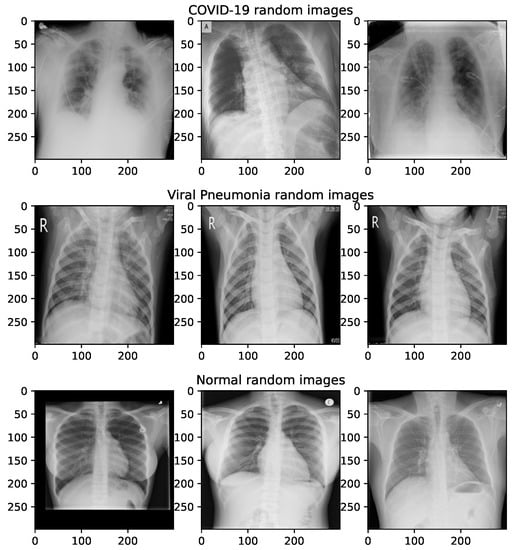
Figure 6.
Sample X-ray images for normal, COVID-19 and pneumonia taken from the COVID-19 radiography database.
According to the above description, the COVID-19 radiography repository is unbalanced, containing a majority of non-infected (normal) lung images. Since the area of the proposed research is not related to addressing imbalanced datasets, the utilized dataset is balanced so that each class has 4000 images. The balancing is performed in the following way: a random subset of 4000 normal images is taken from the original set, and the COVID-19 images are supplemented up to 4000 by taking some X-ray COVID-19 images from the Augmented COVID-19 X-ray Images Dataset [136] and by generated dedicated augmented images for this research, while 2655 viral pneumonia additional figures are generated by performing geometric augmentation of the original ones.
Samples for COVID-19 and viral pneumonia generated augmented images for the purpose of this research are shown in Figure 7, while the classes distribution of the original (imbalanced) COVID-19 radiography repository and artificially generated (balanced) dataset used in this research are presented in Figure 8.
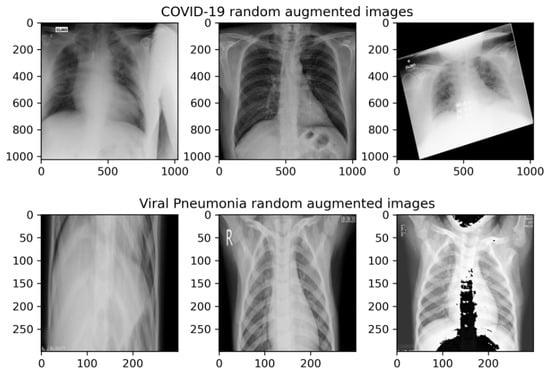
Figure 7.
Sample X-ray images for augmented COVID-19 and viral pneumonia classes generated for this research.
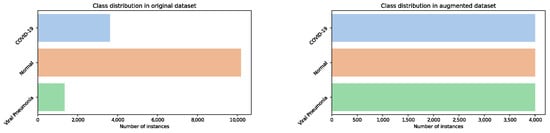
Figure 8.
Distribution of classes in original and augmented COVID-19 radiography dataset.
5.2. Experimental Setup, Comparative Analysis Reports and Discussion
The research shown in this paper uses a similar experimental setup as in [137], where chimp optimization algorithm (ChOA) was used to determine initial weights and biases for extreme learning machine (ELM) which is used to classify features extracted from simple CNN for smaller COVID-19 X-ray images dataset. Converserly to [137], this research uses even simpler CNN for feature extraction and XGBoost classifier and a much larger COVID-19 X-ray image set.
To establish the performance of the CNN–XGBoost–HAOA proposed approach, a comparative analysis with other evolved XGBoost structures by using eight other metaheuristics is performed. The comparative analysis considered the following metaheuristics: basic AOA, SCA, IHHO [125], HHO [126], PSO [83], DE [127], teaching–learning-based optimization (TLB) [138] and ChOA [139]. Therefore, besides AOA and SCA as baseline methods for HAOA, the algorithm set for comparative analysis also included three best-performing approaches in CEC2017 simulations (Section 4), as well as a few other metaheuristics. It is noted that in the results’ tables, as well as figures, for readability reasons, the XGBoost is abbreviated as XG.
All methods were tested under the same experimental condition. The COVID-19 X-ray dataset is first split by using a stratified train_test_split method in proportions of 70%, 30% for the train and test sets, respectively. Afterwards, simple CNN, as shown in Figure 2 is trained on the training set and tested on the testing set in the first phase of the proposed methodology, as described in Section 3.3. Afterwards, outputs from the CNN’s flatten layer were extracted separately for training and testing sets, and those sets were used as inputs for XGBoost, which is then tuned by metaheurisitcs.
All methods were tested with 20 solutions in the population (), and XGBoost structures were tuned throughout 30 iterations () and 15 separated runs (). The classification error rate for the training set is used as an objective function. After completing one runtime, the best-performing XGBoost model was validated against the testing set, and this was reported as the best solution in the run. Afterwards, the best, mean, worst, median, standard deviation and variance metrics of the best solutions’ testing set objective (error rate) for each metaheuristics over 15 runs are captured and reported in Table 4.

Table 4.
The best, worst, mean, median, standard deviation and variance of classification error rate for 15 independent runs—CNN–XGBoost–HAOA vs. others.
As shown in Table 4, the proposed CNN–XGBoost–HAOA approach obtained predominant results by achieving the best values for best, worst, mean and median metrics, while CNN–XGBoost–IHHO finished second. Both baseline methods, CNN–XGBoost–AOA and CNN–XGBoost–SCA, obtained average results, and were far behind the hybrid approach proposed in this research. The best values for and metrics were obtained by CNN–XGBoost–PSO, indicating that this approach delivers the most stable results (consistent, but even the best score obtained by the CNN–XGBoost–PSO was behind the mean result of the proposed algorithm).
Additionally, detailed metrics in terms of precision, recall and F1-score per classes along with accuracy and micro weighted metrics are also captured for the best-performing metaheuristics solution and for the CNN structure introduced in Section 3.3 and shown in Figure 2, which was used for feature extraction. These results are presented in Table 5. For clarity reasons, the prefix ‘CNN-XGBoost’ is omitted in the header of the detailed results table.

Table 5.
Detailed metrics for best-performing solution and baseline CNN.
From Table 5, the first thing that is interesting to emphasize is that all metaheuristics performed much better than the CNN used for feature extraction. Therefore, the XGBoost showed better performance for the classification of extracted features than standard fully connected layers of the CNN. When analyzing the performance level of metaheuristics-based models, the proposed CNN–XGBoost–HAOA obtained the best results for eight out of thirteen metrics, while the CNN–XBGBoost–IHHO finished second by obtaining the best scores for four metrics. The highest accuracy of almost 99.4% was also achieved by the CNN–XGBoost–HAOA method. Again, it is worth noting that the hybrid algorithm significantly outperformed both baseline metaherustics (AOA and SCA) in all observed categories.
Additionally, the results of the best-performing solutions in terms of true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN), true positive rate (TPR, sensitivity or recall), true negative rate (TPR, specificity), positive predicted values (PPV, precision), negative predictive values (NPV), false positive rate (FPR), false negative rate (FNR) and false discovery rate (FDR) are shown in Table 6.

Table 6.
Results of the best-performing solutions of each algorithm.
The set of hyperparameters’ values for best evolved XGBoost structures is shown in Table 7.

Table 7.
Best solutions’ XGBoost hyperparameters value.
The convergence speed graph for the best quality CNN-XGBoost metaheuristics solutions along with diversity over 15 runs are visualized in Figure 9. It can be noticed that the proposed CNN–XGboost–HAOA establishes fastest convergence and how it performs a search with huge improvements—for some iterations, it becomes stuck in sub-optimal regions; however, it eventually manages to get away and converge toward optimum.
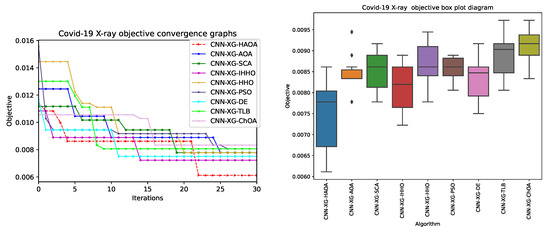
Figure 9.
Convergence speed graph for best-quality CNN-XGBoost metaheuristics solution and solutions’ diversity over 15 runs.
Finally, to better visualize the performance of CNN–XGBoost–HAOA, the confusion matrix, receiver operating characteristics (ROC) and precision–recall (PR) curves along with ROC all vs. rest (OvR) for the best solution are visualized in Figure 10.
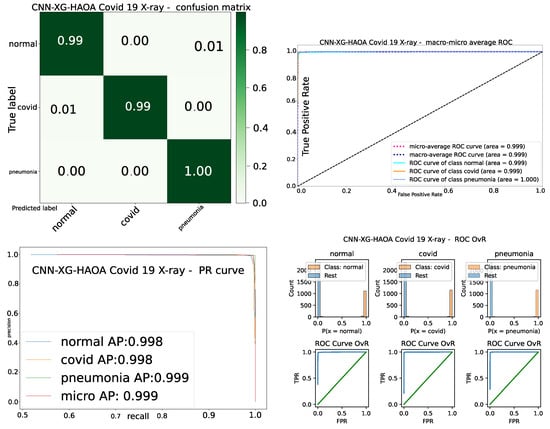
Figure 10.
Convergence speed graph for best-quality CNN–XGBoost metaheuristics solution and solutions’ diversity over 15 runs.
To validate the findings from COVID-19 X-ray simulations, the best values for each of the 15 independent runs are taken for comparison for every metaheuristics method, and all algorithms were compared by using a non-parametric test. However, prior to rendering the decision of using a non-parametric test, the safe use of parametric tests, which includes the independence, normality, and homoscedasticity of the data variances, was checked [140]. The condition of independence is satisfied because each run starts with different pseudo-random number seeds. The homoscedasticity is validated by performing Levene’s test [141], and the p-value of 0.67 is obtained in all cases, rendering the conclusion that the homoscedasticity is satisfied.
Finally, the Shapiro–Wilk test for single-problem analysis [142] was conducted to check whether or not the results from independent runs originated from normal distribution in the following way: results series that include the best solution in each run are constructed for each metaheuristics, and Shapiro–Wilk p-values are calculated for each method separately. The obtained p-value for each algorithm was lower than 0.05, allowing the conclusion that the hypothesis was rejected for both and . This means that the results are not originated from the normal distribution. The results of the Shapiro test are briefly summarized in Table 8.

Table 8.
Shapiro–Wilk test results.
Therefore, since the normality condition was not satisfied, it was proceeded with a non-parametric Wilcoxon signed-rank test [143] with the same data series containing the best values obtained in each run. The proposed HAOA was used as the control algorithm, and a Wilcoxon signed-rank test was executed on the above-mentioned data series. The obtained p-value in all cases was less than 0.05, (p-values were namely 0.03 vs. IHHO, 0.025 vs. HHO, 0.022 vs. SCA, 0.025 vs. AOA, 0.018 vs. PSO, 0.017 vs. DE, 0.026 vs. TLB, and finally, 0.028 vs. ChOA). It is possible therefore to conclude that the proposed HAOA method is statistically significantly better out of all the contending algorithms for both threshold values and . The results of the Wilcoxon test are summarized in Table 9.

Table 9.
Wilcoxon signed-rank test results.
6. Conclusions
Fast diagnostics is crucial in modern medicine. The ongoing COVID-19 epidemic has shown how important it is to quickly determine whether or not a patient has been infected, and fast treatment is often the key factor to saving lives. This paper introduces a novel early diagnostics method to detect the disease from lungs X-ray images. The proposed model utilizes a novel HAOA metaheuristics algorithm, which was created by hybridizing AOA and SCA algorithms with a goal to overcome the deficiencies of the basic variants. The solutions in the proposed hybrid algorithm start by performing an AOA search procedure, and if the solution does not improve over the iterations, it will switch to the SCA search mechanism (controlled by the additional parameter). If the solution still does not improve, ultimately, it will be replaced by a quasi-reflective opposite solution, as defined by the QRL procedure.
The HAOA algorithm was put to test on a set of hard CEC2017 benchmark functions and compared to the results of the basic AOA and SCA and another cutting-edge metaheuristics algorithm. It can be concluded that the HAOA undoubtedly achieves a higher level of performance than the other eleven tested algorithms. After proving the superior performance on the benchmark functions, the algorithm was employed in the machine learning framework, consisting of the simple CNN used for feature extraction and an XGBoost classifier, where HAOA was used to tune the XGBoost hyperparameters. The model was named CNN–XGBoost–HAOA, tested on a large COVID-19 X-ray images benchmark dataset, and compared to eight other metaheuristics algorithms used to evolve the XGBoost structure. The proposed CNN–XGBoost–HAOA obtained predominant accuracy of almost 99.4% on this dataset, leaving behind all other observed models.
The contribution of the proposed research can be defined on three levels. First—a simple light-weight network was generated, that is easy to train, operates fast and achieves decent performance on the COVID-19 dataset, where the XGBoost classifier was used instead of fully connected layers. Second—AOA metaheuristics was improved and used in the model. Finally, the whole model has been adapted to the COVID-19 dataset. The limitations of the proposed work are closely bound to these three levels of contributions. First, it was possible to execute more detailed experiments with the hyperparameters of the simple neural network to begin with, and it was also possible obtain another light structure that could have an even better level of performance; however, this was out of the scope of this work. Second, each metaheuristics algorithm can be modified in an infinite number of theoretically possible improvements (minor modifications and/or hybridization), leading to the conclusion that in theory, the level of improvements of the basic AOA could be even higher without increasing the complexity of the algorithm. It was also possible to include other XGBoost parameters to the tuning process, as there are many of them, but it was not possible to cover all this with just one study. Finally, experiments were executed with just one dataset, which has been balanced. The experiments with imbalanced datasets were not executed, because addressing imbalanced datasets was not goal of presented study.
Based on these encouraging results, the future work will be centered around gaining even more confidence in the suggested model by testing it further on the additional real-life COVID-19 X-ray datasets before considering the practical implementation as a part of the system that could be used in the hospitals to help in early COVID-19 diagnostics.
Author Contributions
Conceptualization, M.Z., N.B. and B.N.; methodology, N.B., G.K. and M.M.; software, N.B. and M.Z.; validation, B.N., M.M. and N.S.; formal analysis, N.S.; investigation, N.B., M.Z. and M.A.; resources, M.A., B.N., N.B. and N.S.; data curation, M.Z., M.A. and N.B.; writing—original draft preparation, B.N., G.K. and M.Z.; writing—review and editing, N.B., B.N. and G.K.; visualization, N.B., G.K. and N.S.; supervision, N.B.; project administration, M.Z. and M.M.; funding acquisition, B.N. and G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by Ministry of Education and Science of Republic of Serbia, Grant No. III-44006.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Partial source code along with csv containing extracted features from CNN is available via the following Github URL: https://github.com/nbacanin/Electronics2022 (accessed on 12 November 2022).
Conflicts of Interest
All authors declare no conflict of interest.
References
- Zhu, N.; Zhang, D.; Wang, W.; Li, X.; Yang, B.; Song, J.; Zhao, X.; Huang, B.; Shi, W.; Lu, R.; et al. A novel coronavirus from patients with pneumonia in China, 2019. N. Engl. J. Med. 2020, 382, 727–733. [Google Scholar] [CrossRef] [PubMed]
- Zu, Z.Y.; Jiang, M.D.; Xu, P.P.; Chen, W.; Ni, Q.Q.; Lu, G.M.; Zhang, L.J. Coronavirus disease 2019 (COVID-19): A perspective from China. Radiology 2020, 296, E15–E25. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Zhong, Z.; Xie, X.; Yu, Q.; Liu, J. Relation between chest CT findings and clinical conditions of coronavirus disease (COVID-19) pneumonia: A multicenter study. Am. J. Roentgenol. 2020, 214, 1072–1077. [Google Scholar] [CrossRef] [PubMed]
- Hemdan, E.E.D.; Shouman, M.A.; Karar, M.E. Covidx-net: A framework of deep learning classifiers to diagnose covid-19 in X-ray images. arXiv 2020, arXiv:2003.11055. [Google Scholar]
- Linda, W.; Lin, Z.Q.; Wong, A. A tailored deep convolutional neural network design for detection of covid-19 cases from chest radiography images. J. Netw. Comput. Appl. 2020, 20, 19549. [Google Scholar]
- Apostolopoulos, I.D.; Mpesiana, T.A. COVID-19: Automatic detection from X-ray images utilizing transfer learning with convolutional neural networks. Phys. Eng. Sci. Med. 2020, 43, 635–640. [Google Scholar] [CrossRef]
- Goel, T.; Murugan, R.; Mirjalili, S.; Chakrabartty, D.K. OptCoNet: An optimized convolutional neural network for an automatic diagnosis of COVID-19. Appl. Intell. 2021, 51, 1351–1366. [Google Scholar] [CrossRef]
- Apostolopoulos, I.D.; Aznaouridis, S.I.; Tzani, M.A. Extracting possibly representative COVID-19 biomarkers from X-ray images with deep learning approach and image data related to pulmonary diseases. J. Med. Biol. Eng. 2020, 40, 462–469. [Google Scholar] [CrossRef]
- Narin, A.; Kaya, C.; Pamuk, Z. Automatic detection of coronavirus disease (COVID-19) using X-ray images and deep convolutional neural networks. Pattern Anal. Appl. 2021, 24, 1207–1220. [Google Scholar] [CrossRef]
- Minaee, S.; Kafieh, R.; Sonka, M.; Yazdani, S.; Jamalipour Soufi, G. Deep-COVID: Predicting COVID-19 from chest X-ray images using deep transfer learning. Med. Image Anal. 2020, 65, 101794. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M. Monarch butterfly optimization based convolutional neural network design. Mathematics 2020, 8, 936. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Zhang, G. cPSO-CNN: An efficient PSO-based algorithm for fine-tuning hyper-parameters of convolutional neural networks. Swarm Evol. Comput. 2019, 49, 114–123. [Google Scholar] [CrossRef]
- Mohakud, R.; Dash, R. Skin cancer image segmentation utilizing a novel EN-GWO based hyper-parameter optimized FCEDN. J. King Saud-Univ.-Comput. Inf. Sci. 2022. [Google Scholar] [CrossRef]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M. Optimizing convolutional neural network hyperparameters by enhanced swarm intelligence metaheuristics. Algorithms 2020, 13, 67. [Google Scholar] [CrossRef]
- Anaraki, A.K.; Ayati, M.; Kazemi, F. Magnetic resonance imaging-based brain tumor grades classification and grading via convolutional neural networks and genetic algorithms. Biocybern. Biomed. Eng. 2019, 39, 63–74. [Google Scholar] [CrossRef]
- Bezdan, T.; Zivkovic, M.; Tuba, E.; Strumberger, I.; Bacanin, N.; Tuba, M. Glioma Brain Tumor Grade Classification from MRI Using Convolutional Neural Networks Designed by Modified FA. In Proceedings of the International Conference on Intelligent and Fuzzy Systems, Istanbul, Turkey, 21–23 July 2020; pp. 955–963. [Google Scholar]
- Bezdan, T.; Milosevic, S.; Venkatachalam, K.; Zivkovic, M.; Bacanin, N.; Strumberger, I. Optimizing convolutional neural network by hybridized elephant herding optimization algorithm for magnetic resonance image classification of glioma brain tumor grade. In Proceedings of the 2021 Zooming Innovation in Consumer Technologies Conference (ZINC), Novi Sad, Serbia, 26–27 May 2021; pp. 171–176. [Google Scholar]
- Strumberger, I.; Tuba, E.; Bacanin, N.; Zivkovic, M.; Beko, M.; Tuba, M. Designing convolutional neural network architecture by the firefly algorithm. In Proceedings of the 2019 International Young Engineers Forum (YEF-ECE), Costa da Caparica, Portugal, 10 May 2019; pp. 59–65. [Google Scholar]
- Bacanin, N.; Zivkovic, M.; Al-Turjman, F.; Venkatachalam, K.; Trojovskỳ, P.; Strumberger, I.; Bezdan, T. Hybridized sine cosine algorithm with convolutional neural networks dropout regularization application. Sci. Rep. 2022, 12, 6302. [Google Scholar] [CrossRef]
- Pathan, S.; Siddalingaswamy, P.; Ali, T. Automated Detection of COVID-19 from Chest X-ray scans using an optimized CNN architecture. Appl. Soft Comput. 2021, 104, 107238. [Google Scholar] [CrossRef]
- Zivkovic, M.; Petrovic, A.; Bacanin, N.; Milosevic, S.; Veljic, V.; Vesic, A. The COVID-19 Images Classification by MobileNetV3 and Enhanced Sine Cosine Metaheuristics. In Mobile Computing and Sustainable Informatics; Springer: Singapore, 2022; pp. 937–950. [Google Scholar]
- Khan, M.A.; Alhaisoni, M.; Tariq, U.; Hussain, N.; Majid, A.; Damaševičius, R.; Maskeliūnas, R. COVID-19 case recognition from chest CT images by deep learning, entropy-controlled firefly optimization, and parallel feature fusion. Sensors 2021, 21, 7286. [Google Scholar] [CrossRef]
- R-Prabha, M.; Prabhu, R.; Suganthi, S.; Sridevi, S.; Senthil, G.; Babu, D.V. Design of Hybrid Deep Learning Approach for COVID-19 Infected Lung Image Segmentation. J. Phys. Conf. Ser. 2021, 2040, 012016. [Google Scholar] [CrossRef]
- Rawat, W.; Wang, Z. Deep convolutional neural networks for image classification: A comprehensive review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef] [PubMed]
- Le, Q.V.; Ngiam, J.; Coates, A.; Lahiri, A.; Prochnow, B.; Ng, A.Y. On optimization methods for deep learning. In Proceedings of the ICML, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Vinyals, O.; Povey, D. Krylov subspace descent for deep learning. In Proceedings of the Artificial Intelligence and Statistics, La Palma, Canary Islands, Spain, 21–23 April 2012; pp. 1261–1268. [Google Scholar]
- LeCun, Y. LeNet-5, Convolutional Neural Networks. 2015, Volume 20, p. 14. Available online: http://yann.Lecun.Com/exdb/lenet (accessed on 25 October 2022).
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Khodadadi, N.; Snasel, V.; Mirjalili, S. Dynamic arithmetic optimization algorithm for truss optimization under natural frequency constraints. IEEE Access 2022, 10, 16188–16208. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamedani, K.B. Improved arithmetic optimization algorithm and its application to discrete structural optimization. Structures 2022, 35, 748–764. [Google Scholar] [CrossRef]
- Chowdhury, M.E.; Rahman, T.; Khandakar, A.; Mazhar, R.; Kadir, M.A.; Mahbub, Z.B.; Islam, K.R.; Khan, M.S.; Iqbal, A.; Al Emadi, N.; et al. Can AI help in screening viral and COVID-19 pneumonia? IEEE Access 2020, 8, 132665–132676. [Google Scholar] [CrossRef]
- Rahman, T.; Khandakar, A.; Qiblawey, Y.; Tahir, A.; Kiranyaz, S.; Kashem, S.B.A.; Islam, M.T.; Al Maadeed, S.; Zughaier, S.M.; Khan, M.S.; et al. Exploring the effect of image enhancement techniques on COVID-19 detection using chest X-ray images. Comput. Biol. Med. 2021, 132, 104319. [Google Scholar] [CrossRef]
- Nayak, S.R.; Nayak, D.R.; Sinha, U.; Arora, V.; Pachori, R.B. Application of deep learning techniques for detection of COVID-19 cases using chest X-ray images: A comprehensive study. Biomed. Signal Process. Control 2021, 64, 102365. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, H.; Chatterjee, I.; Kauppila, J.S.; Bhuva, B.L.; Massengill, L.W. Power-Aware SE Analysis of Different FF Designs at the 14-/16-nm Bulk FinFET CMOS Technology Node. IEEE Trans. Nucl. Sci. 2018, 65, 1866–1871. [Google Scholar] [CrossRef]
- Pan, D.; Xia, X.X.; Zhou, H.; Jin, S.Q.; Lu, Y.Y.; Liu, H.; Gao, M.L.; Jin, Z.B. COCO enhances the efficiency of photoreceptor precursor differentiation in early human embryonic stem cell-derived retinal organoids. Stem Cell Res. Ther. 2020, 11, 366. [Google Scholar] [CrossRef]
- Gilanie, G.; Bajwa, U.I.; Waraich, M.M.; Asghar, M.; Kousar, R.; Kashif, A.; Aslam, R.S.; Qasim, M.M.; Rafique, H. Coronavirus (COVID-19) detection from chest radiology images using convolutional neural networks. Biomed. Signal Process. Control 2021, 66, 102490. [Google Scholar] [CrossRef]
- Li, B.H.; Liu, Y.; Zhang, A.M.; Wang, W.H.; Wan, S. A survey on blocking technology of entity resolution. J. Comput. Sci. Technol. 2020, 35, 769–793. [Google Scholar] [CrossRef]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 818–833. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- LeCun, Y. Gradient-Based Learning Applied to Document Recognition. 2015. Available online: http://yann.lecun.com/exdb/lenet/ (accessed on 22 October 2022).
- Lv, X.; Li, N.; Xu, X.; Yang, Y. Understanding the emergence and development of online travel agencies: A dynamic evaluation and simulation approach. Internet Res. 2020, 30, 1783–1810. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, B.; Feng, Y.; Lv, X.; Ji, D.; Niu, Z.; Yang, Y.; Zhao, X.; Fan, Y. Development of 340-GHz Transceiver Front End Based on GaAs Monolithic Integration Technology for THz Active Imaging Array. Appl. Sci. 2020, 10, 7924. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Ranjan, R.; Sankaranarayanan, S.; Castillo, C.D.; Chellappa, R. An all-in-one convolutional neural network for face analysis. In Proceedings of the 2017 12th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2017), Washington, DC, USA, 30 May–3 June 2017; pp. 17–24. [Google Scholar]
- Balaban, S. Deep learning and face recognition: The state of the art. In Proceedings of the SPIE Defense + Security, Baltimore, MD, USA, 15 May 2015; Volume 9457, pp. 68–75. [Google Scholar]
- Afzal, M.Z.; Capobianco, S.; Malik, M.I.; Marinai, S.; Breuel, T.M.; Dengel, A.; Liwicki, M. Deepdocclassifier: Document classification with deep convolutional neural network. In Proceedings of the 2015 13th international conference on document analysis and recognition (ICDAR), Tunis, Tunisia, 23–26 August 2015; pp. 1111–1115. [Google Scholar]
- Lombardi, F.; Marinai, S. Deep learning for historical document analysis and recognition—A survey. J. Imaging 2020, 6, 110. [Google Scholar] [CrossRef]
- Špetlík, R.; Franc, V.; Matas, J. Visual heart rate estimation with convolutional neural network. In Proceedings of the British Machine Vision Conference, Newcastle, UK, 3–6 September 2018; pp. 3–6. [Google Scholar]
- Cai, L.; Gao, J.; Zhao, D. A review of the application of deep learning in medical image classification and segmentation. Ann. Transl. Med. 2020, 8, 713. [Google Scholar] [CrossRef]
- Ting, F.F.; Tan, Y.J.; Sim, K.S. Convolutional neural network improvement for breast cancer classification. Expert Syst. Appl. 2019, 120, 103–115. [Google Scholar] [CrossRef]
- Liu, Y.; Racah, E.; Correa, J.; Khosrowshahi, A.; Lavers, D.; Kunkel, K.; Wehner, M.; Collins, W. Application of deep convolutional neural networks for detecting extreme weather in climate datasets. arXiv 2016, arXiv:1605.01156. [Google Scholar]
- Chattopadhyay, A.; Hassanzadeh, P.; Pasha, S. Predicting clustered weather patterns: A test case for applications of convolutional neural networks to spatio-temporal climate data. Sci. Rep. 2020, 10, 1317. [Google Scholar] [CrossRef] [PubMed]
- Gavrilov, A.D.; Jordache, A.; Vasdani, M.; Deng, J. Preventing model overfitting and underfitting in convolutional neural networks. Int. J. Softw. Sci. Comput. Intell. (IJSSCI) 2018, 10, 19–28. [Google Scholar] [CrossRef]
- Ng, A.Y. Feature selection, L 1 vs. L 2 regularization, and rotational invariance. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff Alberta, AL, Canada, 4–8 July 2004; p. 78. [Google Scholar]
- Souza, V.L.; Oliveira, A.L.; Cruz, R.M.; Sabourin, R. Improving BPSO-based feature selection applied to offline WI handwritten signature verification through overfitting control. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference Companion, Cancún, Mexico, 8–12 July 2020; pp. 69–70. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Wan, L.; Zeiler, M.; Zhang, S.; Le Cun, Y.; Fergus, R. Regularization of neural networks using dropconnect. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1058–1066. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Wu, H.; Gu, X. Towards dropout training for convolutional neural networks. Neural Netw. 2015, 71, 1–10. [Google Scholar] [CrossRef]
- Thoma, M. Analysis and optimization of convolutional neural network architectures. arXiv 2017, arXiv:1707.09725. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Zeiler, M.D. Adadelta: An adaptive learning rate method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the Icml, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Yamasaki, T.; Honma, T.; Aizawa, K. Efficient optimization of convolutional neural networks using particle swarm optimization. In Proceedings of the 2017 IEEE Third International Conference on Multimedia Big Data (BigMM), Laguna Hills, CA, USA, 19–21 April 2017; pp. 70–73. [Google Scholar]
- Qolomany, B.; Maabreh, M.; Al-Fuqaha, A.; Gupta, A.; Benhaddou, D. Parameters optimization of deep learning models using particle swarm optimization. In Proceedings of the 2017 13th International Wireless Communications and Mobile Computing Conference (IWCMC), Valencia, Spain, 26–30 June 2017; pp. 1285–1290. [Google Scholar]
- Bochinski, E.; Senst, T.; Sikora, T. Hyper-parameter optimization for convolutional neural network committees based on evolutionary algorithms. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3924–3928. [Google Scholar]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Stegherr, H.; Heider, M.; Hähner, J. Classifying Metaheuristics: Towards a unified multi-level classification system. Natural Comput. 2020, 21, 155–171. [Google Scholar] [CrossRef]
- Emmerich, M.; Shir, O.M.; Wang, H. Evolution strategies. In Handbook of Heuristics; Springer: Cham, Switzerland, 2018; pp. 89–119. [Google Scholar]
- Fausto, F.; Reyna-Orta, A.; Cuevas, E.; Andrade, Á.G.; Perez-Cisneros, M. From ants to whales: Metaheuristics for all tastes. Artif. Intell. Rev. 2020, 53, 753–810. [Google Scholar] [CrossRef]
- Beni, G. Swarm intelligence. In Complex Social and Behavioral Systems: Game Theory and Agent-Based Models; Springer: New York, NY, USA, 2020; pp. 791–818. [Google Scholar]
- Abraham, A.; Guo, H.; Liu, H. Swarm intelligence: Foundations, perspectives and applications. In Swarm Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2006; pp. 3–25. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Yang, X.S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Yang, X.S.; Slowik, A. Firefly algorithm. In Swarm Intelligence Algorithms; CRC Press: Boca Raton, FL, USA, 2020; pp. 163–174. [Google Scholar]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intell. 2021, 104, 104314. [Google Scholar] [CrossRef]
- Nguyen, T.; Pan, J.S.; Dao, T.K.; Kuo, M.Y.; Horng, M.F. Hybrid bat algorithm with artificial bee colony. In Intelligent Data Analysis and Its Applications, Volume II; Springer: Cham, Switzerland, 2014; pp. 45–55. [Google Scholar]
- Mortazavi, A.; Toğan, V.; Nuhoğlu, A. Interactive search algorithm: A new hybrid metaheuristic optimization algorithm. Eng. Appl. Artif. Intell. 2018, 71, 275–292. [Google Scholar] [CrossRef]
- Ding, S.; Yu, J.; Huang, H.; Zhao, H. Twin Support Vector Machines Based on Particle Swarm Optimization. J. Comput. 2013, 8, 2296–2303. [Google Scholar] [CrossRef]
- Tam, J.H.; Ong, Z.C.; Ismail, Z.; Ang, B.C.; Khoo, S.Y. A new hybrid GA- ACO- PSO algorithm for solving various engineering design problems. Int. J. Comput. Math. 2019, 96, 883–919. [Google Scholar] [CrossRef]
- Tanyildizi, E.; Demir, G. Golden sine algorithm: A novel math-inspired algorithm. Adv. Electr. Comput. Eng. 2017, 17, 71–78. [Google Scholar] [CrossRef]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M.; Zivkovic, M. Task scheduling in cloud computing environment by grey wolf optimizer. In Proceedings of the 2019 27th Telecommunications Forum (TELFOR), Belgrade, Serbia, 26–27 November 2019; pp. 1–4. [Google Scholar]
- Bezdan, T.; Zivkovic, M.; Tuba, E.; Strumberger, I.; Bacanin, N.; Tuba, M. Multi-objective Task Scheduling in Cloud Computing Environment by Hybridized Bat Algorithm. In Proceedings of the International Conference on Intelligent and Fuzzy Systems, Istanbul, Turkey, 21–23 July 2020; pp. 718–725. [Google Scholar]
- Bezdan, T.; Zivkovic, M.; Antonijevic, M.; Zivkovic, T.; Bacanin, N. Enhanced Flower Pollination Algorithm for Task Scheduling in Cloud Computing Environment. In Machine Learning for Predictive Analysis; Springer: Singapore, 2020; pp. 163–171. [Google Scholar]
- Zivkovic, M.; Bezdan, T.; Strumberger, I.; Bacanin, N.; Venkatachalam, K. Improved Harris Hawks Optimization Algorithm for Workflow Scheduling Challenge in Cloud–Edge Environment. In Computer Networks, Big Data and IoT; Springer: Singapore, 2021; pp. 87–102. [Google Scholar]
- Zivkovic, M.; Bacanin, N.; Tuba, E.; Strumberger, I.; Bezdan, T.; Tuba, M. Wireless Sensor Networks Life Time Optimization Based on the Improved Firefly Algorithm. In Proceedings of the 2020 IEEE International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 1176–1181. [Google Scholar]
- Zivkovic, M.; Bacanin, N.; Zivkovic, T.; Strumberger, I.; Tuba, E.; Tuba, M. Enhanced Grey Wolf Algorithm for Energy Efficient Wireless Sensor Networks. In Proceedings of the 2020 Zooming Innovation in Consumer Technologies Conference (ZINC), Novi Sad, Serbia, 25–26 May 2020; pp. 87–92. [Google Scholar]
- Bacanin, N.; Tuba, E.; Zivkovic, M.; Strumberger, I.; Tuba, M. Whale Optimization Algorithm with Exploratory Move for Wireless Sensor Networks Localization. In Proceedings of the International Conference on Hybrid Intelligent Systems, Bhopal, India, 10–12 December 2019; pp. 328–338. [Google Scholar]
- Zivkovic, M.; Zivkovic, T.; Venkatachalam, K.; Bacanin, N. Enhanced Dragonfly Algorithm Adapted for Wireless Sensor Network Lifetime Optimization. In Data Intelligence and Cognitive Informatics; Springer: Singapore, 2021; pp. 803–817. [Google Scholar]
- Zivkovic, M.; Bacanin, N.; Venkatachalam, K.; Nayyar, A.; Djordjevic, A.; Strumberger, I.; Al-Turjman, F. COVID-19 cases prediction by using hybrid machine learning and beetle antennae search approach. Sustain. Cities Soc. 2021, 66, 102669. [Google Scholar] [CrossRef] [PubMed]
- Zivkovic, M.; Venkatachalam, K.; Bacanin, N.; Djordjevic, A.; Antonijevic, M.; Strumberger, I.; Rashid, T.A. Hybrid Genetic Algorithm and Machine Learning Method for COVID-19 Cases Prediction. In Proceedings of the International Conference on Sustainable Expert Systems: ICSES 2020, Lalitpur, Nepal, 28–29 September 2020; Volume 176, p. 169. [Google Scholar]
- Bezdan, T.; Cvetnic, D.; Gajic, L.; Zivkovic, M.; Strumberger, I.; Bacanin, N. Feature Selection by Firefly Algorithm with Improved Initialization Strategy. In Proceedings of the 7th Conference on the Engineering of Computer Based Systems, Novi Sad, Serbia, 26–27 May 2021; pp. 1–8. [Google Scholar]
- Nadimi-Shahraki, M.H.; Zamani, H.; Mirjalili, S. Enhanced whale optimization algorithm for medical feature selection: A COVID-19 case study. Comput. Biol. Med. 2022, 148, 105858. [Google Scholar] [CrossRef] [PubMed]
- Strumberger, I.; Tuba, E.; Zivkovic, M.; Bacanin, N.; Beko, M.; Tuba, M. Dynamic search tree growth algorithm for global optimization. In Proceedings of the Doctoral Conference on Computing, Electrical and Industrial Systems, Costa de Caparica, Portugal, 8–10 May 2019; pp. 143–153. [Google Scholar]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. Starling murmuration optimizer: A novel bio-inspired algorithm for global and engineering optimization. Comput. Methods Appl. Mech. Eng. 2022, 392, 114616. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H. DMDE: Diversity-maintained multi-trial vector differential evolution algorithm for non-decomposition large-scale global optimization. Expert Syst. Appl. 2022, 198, 116895. [Google Scholar] [CrossRef]
- Jovanovic, D.; Antonijevic, M.; Stankovic, M.; Zivkovic, M.; Tanaskovic, M.; Bacanin, N. Tuning Machine Learning Models Using a Group Search Firefly Algorithm for Credit Card Fraud Detection. Mathematics 2022, 10, 2272. [Google Scholar] [CrossRef]
- Petrovic, A.; Bacanin, N.; Zivkovic, M.; Marjanovic, M.; Antonijevic, M.; Strumberger, I. The AdaBoost Approach Tuned by Firefly Metaheuristics for Fraud Detection. In Proceedings of the 2022 IEEE World Conference on Applied Intelligence and Computing (AIC), Sonbhadra, India, 17–19 June 2022; pp. 834–839. [Google Scholar]
- Bacanin, N.; Sarac, M.; Budimirovic, N.; Zivkovic, M.; AlZubi, A.A.; Bashir, A.K. Smart wireless health care system using graph LSTM pollution prediction and dragonfly node localization. Sustain. Comput. Inform. Syst. 2022, 35, 100711. [Google Scholar] [CrossRef]
- Milosevic, S.; Bezdan, T.; Zivkovic, M.; Bacanin, N.; Strumberger, I.; Tuba, M. Feed-Forward Neural Network Training by Hybrid Bat Algorithm. In Proceedings of the Modelling and Development of Intelligent Systems: 7th International Conference, MDIS 2020, Sibiu, Romania, 22–24 October 2020; Revised Selected Papers 7. pp. 52–66. [Google Scholar]
- Gajic, L.; Cvetnic, D.; Zivkovic, M.; Bezdan, T.; Bacanin, N.; Milosevic, S. Multi-layer Perceptron Training Using Hybridized Bat Algorithm. In Computational Vision and Bio-Inspired Computing; Springer: Singapore, 2021; pp. 689–705. [Google Scholar]
- Qiu, Y.; Zhou, J.; Khandelwal, M.; Yang, H.; Yang, P.; Li, C. Performance evaluation of hybrid WOA-XGBoost, GWO-XGBoost and BO-XGBoost models to predict blast-induced ground vibration. Eng. Comput. 2021, 1–18. [Google Scholar] [CrossRef]
- Jiang, H.; He, Z.; Ye, G.; Zhang, H. Network intrusion detection based on PSO-XGBoost model. IEEE Access 2020, 8, 58392–58401. [Google Scholar] [CrossRef]
- Yun, K.K.; Yoon, S.W.; Won, D. Prediction of stock price direction using a hybrid GA-XGBoost algorithm with a three-stage feature engineering process. Expert Syst. Appl. 2021, 186, 115716. [Google Scholar] [CrossRef]
- Zivkovic, M.; Tair, M.; Venkatachalam, K.; Bacanin, N.; Hubálovskỳ, Š.; Trojovskỳ, P. Novel hybrid firefly algorithm: An application to enhance XGBoost tuning for intrusion detection classification. PeerJ Comput. Sci. 2022, 8, e956. [Google Scholar] [CrossRef]
- Zivkovic, M.; Jovanovic, L.; Ivanovic, M.; Bacanin, N.; Strumberger, I.; Joseph, P.M. XGBoost Hyperparameters Tuning by Fitness-Dependent Optimizer for Network Intrusion Detection. In Communication and Intelligent Systems; Springer: Singapore, 2022; pp. 947–962. [Google Scholar]
- AlHosni, N.; Jovanovic, L.; Antonijevic, M.; Bukumira, M.; Zivkovic, M.; Strumberger, I.; Mani, J.P.; Bacanin, N. The XGBoost Model for Network Intrusion Detection Boosted by Enhanced Sine Cosine Algorithm. In Proceedings of the International Conference on Image Processing and Capsule Networks, Bangkok, Thailand, 20–21 May 2022; pp. 213–228. [Google Scholar]
- Tair, M.; Bacanin, N.; Zivkovic, M.; Venkatachalam, K.; Strumberger, I. XGBoost Design by Multi-verse Optimiser: An Application for Network Intrusion Detection. In Mobile Computing and Sustainable Informatics; Springer: Singapore, 2022; pp. 1–16. [Google Scholar]
- Fang, H.; Fu, X.; Zeng, Z.; Zhong, K.; Liu, S. An Improved Arithmetic Optimization Algorithm and Its Application to Determine the Parameters of Support Vector Machine. Mathematics 2022, 10, 2875. [Google Scholar] [CrossRef]
- Zheng, R.; Jia, H.; Abualigah, L.; Liu, Q.; Wang, S. An improved arithmetic optimization algorithm with forced switching mechanism for global optimization problems. Math. Biosci. Eng. 2022, 19, 473–512. [Google Scholar] [CrossRef] [PubMed]
- Momin, J.; Yang, X.S. A literature survey of benchmark functions for global optimization problems. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M.A. Quasi-oppositional Differential Evolution. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 2229–2236. [Google Scholar]
- Awad, N.; Ali, M.; Liang, J.; Qu, B.; Suganthan, P.; Definitions, P. Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization; Technical Report; Nanyang Technological University: Singapore, 2016. [Google Scholar]
- Gupta, S.; Deep, K. Improved sine cosine algorithm with crossover scheme for global optimization. Knowl.-Based Syst. 2019, 165, 374–406. [Google Scholar] [CrossRef]
- Hussien, A.G.; Amin, M. A self-adaptive Harris Hawks optimization algorithm with opposition-based learning and chaotic local search strategy for global optimization and feature selection. Int. J. Mach. Learn. Cybern. 2022, 13, 309–336. [Google Scholar] [CrossRef]
- Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Mirjalili, S.Z.; Mirjalili, S.; Saremi, S.; Faris, H.; Aljarah, I. Grasshopper optimization algorithm for multi-objective optimization problems. Appl. Intell. 2018, 48, 805–820. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Liu, J.; Mao, Y.; Liu, X.; Li, Y. A dynamic adaptive firefly algorithm with globally orientation. Math. Comput. Simul. 2020, 174, 76–101. [Google Scholar] [CrossRef]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Alqudah, A.M. Augmented COVID-19 X-ray Images Dataset. 2020. Available online: https://data.mendeley.com/datasets/2fxz4px6d8 (accessed on 25 October 2022).
- Hu, T.; Khishe, M.; Mohammadi, M.; Parvizi, G.R.; Karim, S.H.T.; Rashid, T.A. Real-time COVID-19 diagnosis from X-ray images using deep CNN and extreme learning machines stabilized by chimp optimization algorithm. Biomed. Signal Process. Control 2021, 68, 102764. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- LaTorre, A.; Molina, D.; Osaba, E.; Poyatos, J.; Del Ser, J.; Herrera, F. A prescription of methodological guidelines for comparing bio-inspired optimization algorithms. Swarm Evol. Comput. 2021, 67, 100973. [Google Scholar] [CrossRef]
- Glass, G.V. Testing homogeneity of variances. Am. Educ. Res. J. 1966, 3, 187–190. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Francia, R. An approximate analysis of variance test for normality. J. Am. Stat. Assoc. 1972, 67, 215–216. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).